The van der Waals interactions in systems involving superheavy elements: the case of oganesson (Z = 118)†
Luiz Guilherme
Machado de Macedo
a,
Charles Alberto Brito
Negrão
 b,
Rhuiago Mendes
de Oliveira
c,
Rafael Ferreira
de Menezes
d,
Fernando
Pirani
ef and
Ricardo
Gargano
b,
Rhuiago Mendes
de Oliveira
c,
Rafael Ferreira
de Menezes
d,
Fernando
Pirani
ef and
Ricardo
Gargano
 *d
*d
aFederal University of São João del Rei, Campus Centro Oeste Dona Lindu (CCO/UFSJ), 35501-296, Divinópolis, MG, Brazil
bPrograma de Pós-Graduação em Química (PPGQ), Universidade Federal do Pará, Belém, 66075-110, Brazil
cInstituto Federal de Educação, Ciência e Tecnologia do Maranhão, Campus Bacabal, MA 65700-000, Brazil
dInstituto de Física, Universidade de Brasília, Campus Darcy Ribeiro, Brasília, DF, Brazil. E-mail: gargano@unb.br
eDipartimento di Chimica, Biologia e Biotecnologie, Universitá degli studi di Perugia, via Elce di Sotto 8, Perugia, Italy
fDipartimento di Ingegneria Civile ed Ambientale, Università di Perugia, via Duranti 93, 06125 Perugia, Italy
First published on 29th November 2022
Abstract
This work presents a study involving dimers composed of He, Ne, Ar, Kr, Xe, Rn, and Og noble gases with oganesson, a super-heavy closed–shell element (Z = 118). He–Og, Ne–Og, Ar–Og, Kr–Og, Xe–Og, Rn–Og, and Og–Og ground state electronic potential energy curves were calculated based on the 4-component (4c) Dirac–Coulomb Hamiltonian and were counterpoise corrected. For the 4c calculations, the electron correlation was taken into account using the same methodology (MP2-srLDA) and basis set quality (Dyall's acv3z and Dunning's aug-cc-PVTZ). All calculations included quantum electrodynamics effects at the Gaunt interaction level. For all the aforementioned dimers the vibration energies, spectroscopic constants (ωe, ωexe, ωeye, αe, and γe), and lifetime as a function of the temperature (which ranged from 200 to 500 K) were also calculated. The obtained results suggest that the inclusion of quantum electrodynamics effects reduces the value of the dissociation energy of all hetero-nuclear molecules with a percentage contribution ranging from 0.48% (for the He–Og dimer) to 9.63% (for the Rn–Og dimer). The lifetime calculations indicate that the Og–He dimer is close to the edge of instability and that Ng–Og dimers are relatively less stable when the Gaunt correction is considered. Exploiting scaling laws that adopt the polarizability of involved partners as scaling factors, it has also been demonstrated that in such systems the interaction is of van der Waals nature (size repulsion plus dispersion attraction) and this permitted an estimation of dissociation energy and equilibrium distance in the Og–Og dimer. This further information has been exploited to evaluate the rovibrational levels in this symmetric dimer and to cast light on the macroscopic properties of condensed phases concerning the complete noble gas family, emphasizing some anomalies of Og.
1 Introduction
Research involving relativistic quantum chemistry of super-heavy atoms is attracting a lot of attention from the scientific community with the emergence of new elements in the periodic table. For instance, Eliav et al.1 calculated the electron affinity of oganesson (Og), the most recently discovered noble gas, to be Z = 118,2 by using the relativistic coupled-cluster method based on the Dirac–Coulomb–Breit Hamiltonian. The obtained value was 0.056 eV (with an estimated error of 0.01 eV) when relativistic corrections were included. However, no Og electron affinity was found when non-relativistic or uncorrelated calculations were performed.1 This fact shows that relativistic theoretical chemistry plays an extremely relevant role, often being the exclusive chemical information source useful in describing the properties of systems involving super-heavy elements.3Since few isotopes of the transactinide elements can be obtained, what is known about their properties comes mostly from theory. A theoretical study becomes very important, especially when the chemical/physical properties of the heaviest elements usually cannot be predicted from extrapolations of known characteristics in the groups or periods of the Periodic Table.3 In fact, the higher the nuclear charge of an atom, the faster the speed of the innermost electrons, which reach speeds corresponding to a considerable fraction of the light speed, and substantially affect the atomic behaviour. Thus, the relativistic mass of the electrons increases and causes the contraction and stabilization of the orbitals. This fact allows other outermost orbitals to expand and destabilize. Therefore, theoretical calculations for super-heavy elements need to include the special relativity theory for a correct description of the atomic properties of the heaviest elements.4
In the systems involving super-heavy atoms, the effects of quantum electrodynamics (QED) must be included in the rationalization of their behavior. For instance, the ionization potential of the lawrencium atom has recently been determined and the obtained result agreed with the experimental value (4.96 eV) only when QED effects were included. On the other hand, the understanding of the nature of the main components determining non-covalent interactions is very important since it allows us to rationalize and predict a large number of chemical/physical phenomena.5–9 In the literature, however, there are a limited number of experimental/theoretical studies available that focus on characterization of the weak interaction, vibrational energies, spectroscopy, and lifetime of the dimers involving Ng and super-heavy atoms.
Based on these facts, the present paper reports on the characterization of the interaction in Ng–Og (Ng = He, Ne, Ar, Kr, Xe, Rn, and Og) systems considering relativistic effects at the 4-component level and with the inclusion of QED effects at the Gaunt interaction level and basis set superposition error (BSSE).10 More precisely, our work aimed to obtain the Ng–Og ground state electronic potential energy curves (PECs) by applying a combination of the second-order Moller–Plesset long-range theory (MP2-srDFT) with the DFT short-range approach within the framework of the 4-component relativistic method. These PECs have then been used to calculate the vibrational energies, spectroscopic constants, and lifetime of the Ng–Og dimers.
A further effort, addressed to better define the nature, strength and range of the leading interaction components, determining binding energy and equilibrium distance in systems involving Og, has also been performed fully exploiting all the obtained theoretical results. In particular, it has been demonstrated that the obtained interaction potentials are of van der Waals type, depending exclusively on the polarizability value of the involved partners,11 which is a collective property of all electrons (mostly the external ones and partially the internal ones) defining both size repulsion and dispersion attraction. For the Og atom, a polarizability value consistent with that recently proposed by Jerabek et al.12 has been adopted. The use of correlation formulas,11 providing the potential well features of van der Waals interactions in terms of polarizability, also allowed the prediction of binding features and of the strength of the long-range attraction in the Og2 dimer. Exploiting this information, the dependence of melting (Tmp) and boiling (Tbp) temperature on the two-body interaction components has been analyzed for the complete family of noble gas atoms. With respect to the general trend of all other noble gas atoms, some deviations of Og have been appropriately emphasized. In particular, an increased role of multi-body interaction contributions extends in an anomalous way the stability of the oganesson liquid phase, probably due to the highest relativistic effects, as recently proposed by Smits et al.14
2 Methodologies
The determination for any system of energies and rovibrational spectroscopic constants, involves an accurate fitting of radial dependence of the interaction energy, indicated as the potential energy curve (PEC). This fitting is necessary to characterize the dissociation energy, De, the equilibrium distance, Re, and the shape of the potential well. For these purposes, two analytical forms were used. The first option to fit the PEC of the studied systems was the adoption Improved Lennard Jones (ILJ) function. This model, defined in terms of only three parameters, has been extensively used in several molecular systems and it has proved to be very efficient to describe van der Waals-type interactions.15–19 For neutral-neutral systems, the ILJ form assumes the following expression:20–22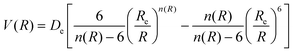 | (1) |
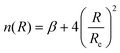 and the β parameter describes the softness/hardness of the elements involved in the molecular system. It is of relevance to stress that the shape of the potential well, obtained from the ILJ formulation, is of great significance for the present study and is in agreement with that provided by other important potential models.23–25 A detailed probe of the ILJ formulation, applied to the noble gas interactions and performed on high-resolution scattering experiments, has been discussed by Pirani et al.20 In particular, the analysis of the velocity dependence of the integral cross section represented a critical test of the radial dependence of the long-range attraction strength, arising from the critical balance of appropriately damped long-range dispersion coefficients. At the same time, the observed interference effects have been exploited to control basic features of the potential well. Moreover, for a He–He molecule a direct comparison of the ILJ potential formulation with results of ab initio calculations and of other more sophisticated potential models26 has been discussed in ref. 15 and 27.
and the β parameter describes the softness/hardness of the elements involved in the molecular system. It is of relevance to stress that the shape of the potential well, obtained from the ILJ formulation, is of great significance for the present study and is in agreement with that provided by other important potential models.23–25 A detailed probe of the ILJ formulation, applied to the noble gas interactions and performed on high-resolution scattering experiments, has been discussed by Pirani et al.20 In particular, the analysis of the velocity dependence of the integral cross section represented a critical test of the radial dependence of the long-range attraction strength, arising from the critical balance of appropriately damped long-range dispersion coefficients. At the same time, the observed interference effects have been exploited to control basic features of the potential well. Moreover, for a He–He molecule a direct comparison of the ILJ potential formulation with results of ab initio calculations and of other more sophisticated potential models26 has been discussed in ref. 15 and 27.
The second analytical form was the extended-Rydberg28 function, which has been used successfully to describe various molecular systems29–31 and it is described according to the equation:
 | (2) |
 | (3) |
As far as we know, there is no experimental data for the systems studied here. Thus, it is necessary to determine the spectroscopic constants using another methodology to ensure the reliability of the current results. The Dunham method,33 which depends on the derivatives of the potential energy curves in the equilibrium position, was chosen as a second option to calculate the rovibrational spectroscopic constants.
To determine the lifetime as a function of temperature for each Ng–Og dimer within Slater theory,34,35 the following equation was employed:
 | (4) |
3 Computational details
All calculations were performed using the DIrac1736 program package, were based on 4-component (4c) Dirac-Coulomb Hamiltonian37,38 and were counterpoise corrected.10 In the 4c calculations, the (SS|SS) two electron integrals were neglected and replaced by a charge39 using Dirac's default settings. Since the Dirac program can include the Gaunt interaction only at the Dirac–Hartree–Fock level, it was treated additively.40,41For the 4c calculations, the electron correlation was taken into account using the long-range Moller–Plesset perturbation Theory MP2-lrDFT42 and its short-range srLDA version43,44 since it has a better performance than MP2-srPBE for rare gas dimers.42 For all systems, at least 60 different distances were calculated from the repulsion region (from around 2.5–3.4 Å) up to the dissociation limit. The electrons correlated were the valence (n − 1)dnsnp and the energy threshold for inclusion of virtual orbitals for MP2-srLDA calculations was set to +20 hartrees due to computational limitations. For He, Ne and Ar atoms we employed the aug-CC-PVTZ basis sets of Dunning and coworkers.45–48 For heavier atoms (Kr, Xe, Rn and Og), we employed the acv3z basis set of Dyall.49,50
Finally, the obtained electronic energies were fitted with both the ILJ model and extended-Rydberg analytical form (with ten coefficients) via Powell's method.51 In the fitting process, the equilibrium distance and the dissociation energy were kept fixed. With the potential energy curves in hand, calculations of rovibrational energies, spectroscopic constants and the lifetime were carried out for each system.
4 Results and discussion
We found it appropriate to present the obtained results with their discussion in four subsections in order to better emphasize their relevance and to exhibit their general implications.4.1 Dissociation energy and equilibrium distance
Tables S1–S7 of the ESI† show the calculated ground state electronic energies of the He–Og, Ar–Og, Kr–Og, Xe–Og, Rn–Og, and Og–Og dimers for several different internuclear distances R, considering the inclusion of quantum electrodynamics effects at the Gaunt interaction level (QEEGIL), without inclusion of QEEGIL, and with inclusion of QEEGIL + BSSE correction. Table 1 presents the dissociation energies (De) and equilibrium distances (Re) for each diatomic system. From this table, it is observed that the inclusion of quantum electrodynamics effects reduces the value of the dissociation energy of these molecules, which may be attributed to retardation since it could be significant in dispersion interactions.52 The percentage contribution of the quantum electrodynamics effect on the dissociation energy ranged from 0.56% (for the He–Og dimer) to 9.63% (for the Rn–Og dimer), that is, as the atomic number of the noble gases increases, the more significant is the contribution of the Gaunt correction. When the BSSE correction is considered, there is a decrease of the dissociation energy of the dimers. The greatest decrease (1.53 meV) occurred for the Og–Ne system. On the other hand, the equilibrium distance remains practically unchanged when the BSSE correction is taken into account. The De results found for the Og–Og system were compared with those available in the literature. The differences between the values determined by Gaunt + BSSE and predicted by correlation formulas with those obtained by Saue et al. were 0.0272 eV (0.6270 kcal mol−1) and 0.0236 eV (0.5447 kcal mol−1), respectively. When a comparison is made taking into account the results of Jerabek et al., these values are 0.02685 eV (0.6191 kcal mol−1) and 0.02394 eV (0.5526 kcal mol−1), respectively. It can also be inferred from Table 1 that De increases as the noble gas atomic mass also increases, but the same trend does not happen with the Re. The He–Og equilibrium distance is comparable (or even larger) with respect to that of the largest among all the systems. This feature can be explained by exploring the fact that the Re of a van der Waals complex is determined through the balance between the terms of repulsion (exchange) and of attraction (dominated by dispersion effects). Both these terms depend on the electronic polarizability of the interacting partners as a measure of their size and provides also the probability of induced dipole formation. Knowing that Og shows the larger size, being more polarizable than He, Ne, Ar, Kr, Xe, and Rn atoms, then it is expected that the size-repulsion (term of exchange) is practically the same for the He–Og, Ne–Og, Ar–Og, Kr–Og, Xe–Og, and Rn–Og molecule and this determines equilibrium distances of comparable value.| Systems | D e (meV) | R e (Å) | C6 (eV Å6) | Source |
|---|---|---|---|---|
| He–Og | 1.77 | 4.62 | (Without Gaunt) | |
| He–Og | 1.76 | 4.62 | (With Gaunt) | |
| He–Og | 1.61 | 4.55 | (Gaunt + BSSE) | |
| He–Og | 2.91 | 4.37 | 20.2 | (Predicted by correlation formulas) |
| Ne–Og | 6.38 | 4.20 | (Without Gaunt) | |
| Ne–Og | 6.39 | 4.20 | (With Gaunt) | |
| Ne–Og | 4.86 | 4.30 | (Gaunt + BSSE) | |
| Ne–Og | 6.73 | 4.33 | 44.3 | (Predicted by correlation formulas) |
| Ar–Og | 19.40 | 4.33 | (Without Gaunt) | |
| Ar–Og | 19.25 | 4.33 | (With Gaunt) | |
| Ar–Og | 19.00 | 4.30 | (Gaunt + BSSE) | |
| Ar–Og | 20.13 | 4.40 | 145.9 | (Predicted by correlation formulas) |
| Kr–Og | 26.17 | 4.39 | (Without Gaunt) | |
| Kr–Og | 25.57 | 4.40 | (With Gaunt) | |
| Kr–Og | 24.98 | 4.40 | (Gaunt + BSSE) | |
| Kr–Og | 27.34 | 4.46 | 215.8 | (Predicted by correlation formulas) |
| Xe–Og | 34.94 | 4.48 | (Without Gaunt) | |
| Xe–Og | 33.44 | 4.49 | (With Gaunt) | |
| Xe–Og | 32.76 | 4.50 | (Gaunt + BSSE) | |
| Xe–Og | 35.53 | 4.56 | 320.7 | (Predicted by correlation formulas) |
| Rn–Og | 55.14 | 4.40 | (Without Gaunt) | |
| Rn–Og | 51.34 | 4.40 | (With Gaunt) | |
| Rn–Og | 50.50 | 4.40 | (Gaunt + BSSE) | |
| Rn–Og | 43.44 | 4.63 | 426.7 | (Predicted by correlation formulas) |
| Og–Og | 104.58 | 4.25 | (Gaunt + BSSE) | |
| Og–Og | 53.79 | 4.76 | 626.5 | (Predicted by correlation formulas) |
| Og–Og | 77.73 | 4.31 | Jerabek et al.12 | |
| Og–Og | 77.39 | 4.33 | Saue et al.13 | |
Indeed, all Re values are confined within 10% of their average value, and any small reduction, such as that observed when passing from He–Og to Ne–Og, and the general small increase along the Ng–Og family is due to the fine balance of size repulsion with dispersion attraction. On the other hand, the De value critically depends on the strength of the global attraction at Re which is related to the polarizability product of involved partners. Since the polarizability of the He atom is lower than that of the other noble gases, the associated De is the smallest one and its value increases regularly along the family by a factor larger than 20. Therefore, the observed behavior is typical of systems whose repulsion component, controlling Re, is mostly dominated by the size of the most polarizable atom (Og), while De varies along a homologous family (Ng–Og) according to the polarizability change of the Ng partner.
Fig. S1 and S2 (ESI†) show the ab initio (with and without Gaunt interaction) and ILJ adjusted PEC of the He–Og, Ne–Og, Ar–Og, Kr–Og, Xe–Og, and Rn–Og molecules, while Fig. S3 and S4 (ESI†) presents the ab initio (with and without Gaunt interaction) and Rydberg adjusted PEC of the same systems. Through these figures one notes that the Og–He electronic energies have small oscillations. Ab initio (with Gaunt + BSSE correction) and ILJ adjusted PEC of the He–Og, Ne–Og, Ar–Og, Kr–Og, Xe–Og, and Rn–Og dimers are shown in Fig. S5 (ESI†), while the ab initio (with Gaunt + BSSE correction) and Rydberg adjusted PEC of the same complexes are represented in Fig. S6 (ESI†). From these figures it is possible to verify that, even when the BSSE correction is taken into account, the small oscillations in the electronic energies of the Og–He system continue.
Tables 2 and 3 present the fitted values of the β ILJ parameter and the extended-Rydberg analytic coefficients, respectively. The β fitted values, depending on the softness of the interaction partners, ranged between 5.80 and 9.58. For this range, the ILJ analytical form works very well for various complexes formed by neutral–neutral and ion–neutral species, i.e., they provided an adequate description of the role of the van der Waals interaction component in the formation of weak hydrogen and halogen intermolecular bonds.53,54Tables 2 and 3 also show that the RMSD are very small, evidencing the good quality of the He–Og, Ar–Og, Kr–Og, Xe–Og, Rn–Og, and Og–Og electronic energy fits with Gaunt + BSSE correction and the Ne–Og electronic fits with only Gaunt interaction.
| Systems | RMSD (Hartree) | β parameter |
|---|---|---|
| He–Og | 2.0976 × 10−6 | 9.5808 |
| Ne–Og | 2.7833 × 10−6 | 7.2151 |
| Ar–Og | 1.0030 × 10−5 | 8.0185 |
| Kr–Og | 1.2681 × 10−5 | 6.6153 |
| Xe–Og | 1.2135 × 10−5 | 6.9770 |
| Rn–Og | 6.3491 × 10−6 | 6.8909 |
| Og–Og | 1.0493 × 10−4 | 5.8012 |
| c n (Å−n) | He–Og | Ne–Og | Ar–Og | Kr–Og | Xe–Og | Rn–Og | Og–Og |
|---|---|---|---|---|---|---|---|
| C 1 | 1.47710955 | 1.38672315 | 1.79983909 | 3.39536153 | 2.77583010 | 1.70196661 | 1.75418289 |
| C 2 | −1.12088589 | −0.81105960 | −0.45115730 | 3.94296832 | 2.15135216 | −0.24350070 | −0.00576175 |
| C 3 | 1.18081113 | 0.23626192 | 0.47373096 | 2.03562284 | 0.75799095 | 0.23677149 | 0.21663296 |
| C 4 | 0.51099513 | −0.25504175 | 0.23110898 | 0.77943221 | 0.19755360 | 0.01311309 | 0.05863362 |
| C 5 | −1.30890474 | 0.50599162 | −0.35933640 | 2.41706278 | 0.97262535 | 0.00125084 | 0.06468921 |
| C 6 | 0.13378930 | −0.30124010 | 0.12987214 | 1.02490653 | 0.06621025 | −0.02737260 | −0.03353552 |
| C 7 | 0.62722811 | 0.03474181 | 0.00452929 | −1.44895344 | −0.68265120 | 0.02038624 | 0.00327290 |
| C 8 | −0.38639035 | 0.02387602 | −0.01121581 | 0.28371066 | 0.41795297 | −0.00607865 | 0.00397981 |
| C 9 | 0.08922130 | −0.00815757 | 0.00216509 | 0.18217579 | −0.08852640 | 0.00084895 | −0.00112308 |
| C 10 | −0.00739282 | 0.00074162 | −0.00012930 | −0.04479104 | 0.00542335 | −0.00004265 | 0.00010223 |
| RMSD | 1.5224 × 10−6 | 1.1589 × 10−6 | 8.5612 × 10−6 | 6.3886 × 10−6 | 1.2681 × 10−5 | 6.3491 × 10−6 | 1.0493 × 10−4 |
Fig. S7 (ESI†) shows the Og–Og ab initio electronic energies (with Gaunt + BSSE correction) and those adjusted by both the ILJ and Rydberg forms. It can be seen from this figure that the ILJ analytical form does not adjust well the ab initio energies at the anharmonic region of the PEC. This fact suggests that the results of rovibrational energies, spectroscopic constants and the lifetime of the Og–Og molecule are more reliable when the Rydberg analytical function is used.
4.2 Nature of the interatomic interaction
As anticipated in Section 4.1, for all systems under investigation the potential energies are determined by a critical balance of size repulsion with dispersion attraction. This means that they exhibit the nature of typical van der Waals interactions. Further confirmation of this general aspect comes from the prediction of correlation formulas, representing both Re and De for all systems in terms of polarizability (α) of the involved partners.11 It is interesting to note that all correlation formulas here exploited, defined in terms of the electronic polarizability α of the interacting partners and first proposed 37 years ago,55 have been suggested on the phenomenological ground.11 Moreover, the one defining Re, showing a dependence on α1/7 values, has been recently confirmed by a refined quantum mechanical treatment.56 Therefore, the two approaches provide coincident-internally consistent results for symmetric and asymmetric noble gas dimers, respectively. Predicted values of the basic De and Re quantities are given in Table 1, where they are compared with the results of the present ab initio calculations. Considering the good agreement between the calculated and predicted values, the same correlation formulas have been exploited to estimate Re and De also for the Og–Og dimer. For all systems, the same correlation formulas are given and also the C6 coefficient that provides the leading term of the dispersion attraction due to induced dipole–induced dipole interaction.Considering the high number of internal and external electrons, with associated relativistic effects, the fundamental properties of the heavy Og monomer are not easy to evaluate. Therefore, for the Og–Og dimer, the De value predicted by the correlation formulas and that obtained by the present calculations (see Table 1) can be reasonably taken as the lower and the upper limit of the dissociation energy. In particular, considering the mutual-combined uncertainty, they are in reasonable agreement, within ≈0.5 kcal mol−1 (1 kcal mol−1 = 43.32 meV) with theoretical estimates given in ref. 12 and 13 (only for De predicted by correlation formulas does the uncertainty amount to 20–30%). Note also that the long-range C6 attraction coefficients, evaluated for Og–Og inserting De and Re of Table 1 in the asymptotic behavior of ILJ, and defined as C6 = DeRe6, agree within 20% with the results of correlation formulas.
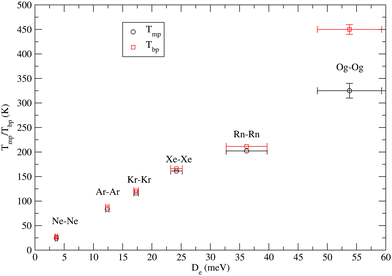
4.3 Some speculations on the macroscopic properties
We also researched a possible correlation between the macroscopic properties of noble gas atoms in their condensed phases and the intermolecular forces involved. In particular, the focus has been on the temperatures Tmp and Tbp of melting and boiling points of prototype van der Waals systems provided by noble gases, whose solid phase is usually classified as typical of close (compact)-packing. It is well known that for such systems the repulsive components are mainly responsible for melting while attractive components are responsible for boiling. For a family of systems, where many-body components directly relate to two-body contributions, it can be expected that the balance of their attraction and repulsion components affects the cohesive energy. Eqn (1) and (2) suggest that at R = Re both components scale approximately with De. Therefore, we have attempted to find a possible correlation between Tmp and Tbp with De. All involved values are given in Table 4, while Fig. 1 shows the obtained plot. For all systems from He to Rn, the reported Tmp and Tbp are experimental values while for Og they have been recently proposed by Smits et al.14 The first important feature to be emphasized is that for all systems, including the super-heavy Og, Tmb scales almost linearly with De. The second important feature concerns Tbp which follows an approximately linear dependence on De for all systems, except the super-heavy Og. In particular, for most systems, the existence zone of the liquid phase is confined in the range of a few K, while Og exhibits a range of liquid larger than 100 K. This anomalous behavior probably arises from the largest many-body contributions which are triggered by relativistic effects.| System | T mp (K) | T bp (K) | D e (meV) | Source |
|---|---|---|---|---|
| Ne–Ne | 24.5 | 27.1 | 4.28 | Predicted by correlation formulas |
| 3.66 | Exp.15 | |||
| 3.75 | Calculations15 | |||
| Ar–Ar | 83.8 | 87.5 | 11.61 | Predicted by correlation formulas |
| 12.37 | Exp.15 | |||
| 12.36 | Calculations15 | |||
| Kr–Kr | 116.6 | 120.9 | 17.61 | Predicted by correlation formulas |
| 17.30 | Exp.15 | |||
| 17.05 | Calculations15 | |||
| Xe–Xe | 161.3 | 166.1 | 25.36 | Predicted by correlation formulas |
| 24.20 | Exp.15 | |||
| 24.31 | Calculations15 | |||
| Rn–Rn | 202.2 | 211.4 | 36.20 | Predicted by correlation formulas |
| 30.32 | Calculations15 | |||
| Og–Og | 335 ± 30 | 350 ± 30 | 53.79 | Predictions-two body extrapolation 14 |
| 325 ± 15 | 450 ± 10 |
4.4 Rovibrational levels of dimers
Vibrational energy values (not shown in this work) obtained for both Og–He ILJ and Rydberg PEC with Gaunt and without Gaunt interaction are very similar, suggesting that gaunt correction is not important for this particular system. The PEC's of both Ne–Og and Ar–Og with and without Gaunt corrections have very close vibrational energy values (a total of 6 and 16, respectively) indicating that the Gaunt correction is also not very important for these dimers. It was also found that the Kr–Og ILJ PEC with and without Gaunt correction have the same number of vibrational levels (a total of twenty-six levels). Moreover, the vibrational energies calculated with Gaunt correction are smaller than those calculated without Gaunt correction. The Xe–Og dimer presents thirty-seven and thirty-six vibrational levels with and without Gaunt corrections, respectively, while the Rn–Og system contains fifty-five and fifty-two levels. Also, for both systems, the values of Gaunt vibrational energies are smaller than without Gaunt correction. These features clearly show that the Gaunt correction becomes more important as the atomic number of atoms increases.Tables 5 and 6 present the He–Og, Ar–Og, Kr–Og, Xe–Og, and Rn–Og pure vibrational (j = 0) and rovibrational (j = 1) energies for the ILJ PEC with Gaunt + BSSE correction. For the Og–Ne system, both the used ILJ and Rydberg PEC were obtained only with the Gaunt interaction for the reasons explained in Section 4.1. From these tables, it can be seen that the He–Og system has only a single vibrational level considering both the ILJ and Rydberg PEC with Gaunt + BSSE correction (Tables S8 and S9 of the ESI†). Vibrational energies are very sensitive to PEC adjustments. In fact, small differences in adjustments can produce changes in the amount of vibrational levels within the well of each adjusted PEC. This fact was observed for some systems involved in the present study. For example, for the Og–Ar, Og–Kr, Og–Xe, and Og–Rn systems, 16, 26, 36, and 52 vibrational levels were obtained for the PEC ILJ, respectively, while for the PEC Rydberg these values were 14, 20, 27, and 50. Og–Og vibrational energies (80 levels) obtained via ILJ PEC adjusted from Gaunt + BSSE electronic energies are shown in Table 7, while the Rydberg PEC contains 107 vibrational levels (Table S10 of the ESI†). With the values of Re and De estimated (correlation formulas) for the Og–Og dimer, it was also possible to construct the ILJ PEC of this system.
| ν | j | He–Og | Ne–Og | Ar–Og | Kr–Og | Xe–Og | Rn–Og |
|---|---|---|---|---|---|---|---|
| 0 | 8.087589 | 7.557380 | 11.719211 | 9.145629 | 8.856483 | 9.512609 | |
| 1 | — | 20.082742 | 33.622236 | 26.770172 | 26.089224 | 28.181499 | |
| 2 | — | 29.220193 | 53.505590 | 43.507955 | 42.684451 | 46.377093 | |
| 3 | — | 35.116381 | 71.388952 | 59.358726 | 58.642633 | 64.099541 | |
| 4 | — | 38.161975 | 87.296729 | 74.322389 | 73.964313 | 81.349010 | |
| 5 | — | 39.171675 | 101.260169 | 88.399103 | 88.650133 | 98.125690 | |
| 6 | — | — | 113.320322 | 101.589424 | 102.700861 | 114.429800 | |
| 7 | — | — | 123.532024 | 113.894481 | 116.117435 | 130.261593 | |
| 8 | — | — | 131.968954 | 125.316218 | 128.901003 | 145.621367 | |
| 9 | — | — | 138.729297 | 135.857706 | 141.052978 | 160.509470 | |
| 10 | — | — | 143.940704 | 145.523552 | 152.575108 | 174.926314 | |
| 11 | — | — | 147.762342 | 154.320420 | 163.469549 | 188.872385 | |
| 12 | — | — | 150.382299 | 162.257693 | 173.738967 | 202.348253 | |
| 13 | — | — | 152.011351 | 169.348290 | 183.386644 | 215.354596 | |
| 14 | — | — | 152.876593 | 175.609621 | 192.416619 | 227.892208 | |
| 15 | — | — | 153.227384 | 181.064657 | 200.833844 | 239.962023 | |
| 16 | — | — | — | 185.742987 | 208.644363 | 251.565141 | |
| 17 | — | — | — | 189.681710 | 215.855529 | 262.702847 | |
| 18 | — | — | — | 192.925912 | 222.476230 | 273.376646 | |
| 19 | — | — | — | 195.528566 | 228.517142 | 283.588290 | |
| 20 | — | — | — | 197.549798 | 233.990987 | 293.339822 | |
| 21 | — | — | — | 199.055775 | 238.912788 | 302.633612 | |
| 22 | 0 | — | — | — | 200.117520 | 243.300080 | 311.472406 |
| 23 | — | — | — | 200.809866 | 247.173075 | 319.859375 | |
| 24 | — | — | — | 201.210565 | 250.554727 | 327.798170 | |
| 25 | — | — | — | 201.411283 | 253.470702 | 335.292986 | |
| 26 | — | — | — | — | 255.949227 | 342.348622 | |
| 27 | — | — | — | — | 258.020855 | 348.970548 | |
| 28 | — | — | — | — | 259.718178 | 355.164974 | |
| 29 | — | — | — | — | 261.075536 | 360.938917 | |
| 30 | — | — | — | — | 262.128754 | 366.300264 | |
| 31 | — | — | — | — | 262.914910 | 371.257832 | |
| 32 | — | — | — | — | 263.472121 | 375.821406 | |
| 33 | — | — | — | — | 263.839330 | 380.001781 | |
| 34 | — | — | — | — | 264.056097 | 383.810769 | |
| 35 | — | — | — | — | 264.169466 | 387.261196 | |
| 36 | — | — | — | — | — | 390.366872 | |
| 37 | — | — | — | — | — | 393.142551 | |
| 38 | — | — | — | — | — | 395.603860 | |
| 39 | — | — | — | — | — | 397.767234 | |
| 40 | — | — | — | — | — | 399.649835 | |
| 41 | — | — | — | — | — | 401.269475 | |
| 42 | — | — | — | — | — | 402.644549 | |
| 43 | — | — | — | — | — | 403.793971 | |
| 44 | — | — | — | — | — | 404.737111 | |
| 45 | — | — | — | — | — | 405.493744 | |
| 46 | — | — | — | — | — | 406.083994 | |
| 47 | — | — | — | — | — | 406.528272 | |
| 48 | — | — | — | — | — | 406.847220 | |
| 49 | — | — | — | — | — | 407.061634 | |
| 50 | — | — | — | — | — | 407.192395 | |
| 51 | — | — | — | — | — | 407.263120 |
| ν | j | He–Og | Ne–Og | Ar–Og | Kr–Og | Xe–Og | Rn–Og |
|---|---|---|---|---|---|---|---|
| 0 | 8.405667 | 7.649373 | 11.770146 | 9.172055 | 8.874696 | 9.526304 | |
| 1 | — | 20.164716 | 33.671288 | 26.796031 | 26.107153 | 28.195047 | |
| 2 | — | 29.290414 | 53.552666 | 43.533230 | 42.702090 | 46.390492 | |
| 3 | — | 35.172352 | 71.433944 | 59.383401 | 58.659977 | 64.112788 | |
| 4 | — | 8.200502 | 87.339514 | 74.346444 | 73.981355 | 81.362104 | |
| 5 | — | 39.191075 | 101.300607 | 88.422519 | 88.666865 | 98.138628 | |
| 6 | — | — | 113.358254 | 101.612177 | 102.717277 | 114.442579 | |
| 7 | — | — | 123.567271 | 113.916547 | 116.133527 | 130.274212 | |
| 8 | — | — | 132.001316 | 125.337570 | 128.916762 | 145.633822 | |
| 9 | — | — | 138.758560 | 135.878315 | 141.068397 | 160.521759 | |
| 10 | — | — | 143.966642 | 145.543384 | 152.590176 | 174.938435 | |
| 11 | — | — | 147.784726 | 154.339439 | 163.484257 | 188.884333 | |
| 12 | — | — | 150.400893 | 162.275861 | 173.753304 | 202.360027 | |
| 13 | — | — | 152.025912 | 169.365564 | 183.400598 | 215.366192 | |
| 14 | — | — | 152.886857 | 175.625958 | 192.430179 | 227.903622 | |
| 15 | — | — | 153.233754 | 181.080007 | 200.846995 | 239.973253 | |
| 16 | — | — | — | 185.757302 | 208.657093 | 251.576182 | |
| 17 | — | — | — | 189.694938 | 215.867824 | 262.713695 | |
| 18 | — | — | — | 192.938003 | 222.488073 | 273.387297 | |
| 19 | — | — | — | 195.539469 | 228.528517 | 283.598740 | |
| 20 | — | — | — | 197.559463 | 234.001879 | 293.350066 | |
| 21 | — | — | — | 199.064152 | 238.923178 | 302.643646 | |
| 22 | 1 | — | — | — | 200.124558 | 243.309952 | 311.482225 |
| 23 | — | — | — | 200.815512 | 247.182410 | 319.868974 | |
| 24 | — | — | — | 201.214765 | 250.563508 | 327.807544 | |
| 25 | — | — | — | 201.414366 | 253.478910 | 335.302129 | |
| 26 | — | — | — | — | 255.956845 | 342.357528 | |
| 27 | — | — | — | — | 258.027866 | 348.979211 | |
| 28 | — | — | — | — | 259.724563 | 355.173389 | |
| 29 | — | — | — | — | 261.081278 | 360.947077 | |
| 30 | — | — | — | — | 262.133834 | 366.308164 | |
| 31 | — | — | — | — | 262.919310 | 371.265464 | |
| 32 | — | — | — | — | 263.475821 | 375.828765 | |
| 33 | — | — | — | — | 263.842309 | 380.008860 | |
| 34 | — | — | — | — | 264.058337 | 383.817561 | |
| 35 | — | — | — | — | 264.171150 | 387.267694 | |
| 36 | — | — | — | — | — | 390.373070 | |
| 37 | — | — | — | — | — | 393.148442 | |
| 38 | — | — | — | — | — | 395.609439 | |
| 39 | — | — | — | — | — | 397.772493 | |
| 40 | — | — | — | — | — | 399.654768 | |
| 41 | — | — | — | — | — | 401.274076 | |
| 42 | — | — | — | — | — | 402.648811 | |
| 43 | — | — | — | — | — | 403.797887 | |
| 44 | — | — | — | — | — | 404.740675 | |
| 45 | — | — | — | — | — | 405.496948 | |
| 46 | — | — | — | — | — | 406.086831 | |
| 47 | — | — | — | — | — | 406.530736 | |
| 48 | — | — | — | — | — | 406.849302 | |
| 49 | — | — | — | — | — | 407.063326 | |
| 50 | — | — | — | — | — | 407.193690 | |
| 51 | — | — | — | — | — | 407.264090 |
| ν | j | Og–Og | ν | j | Og–Og | ν | j | Og–Og | ν | j | Og–Og |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 12.501425 | 40 | 702.818996 | 0 | 12.514080 | 40 | 702.827310 | ||||
| 1 | 37.221281 | 41 | 712.188881 | 1 | 37.233850 | 41 | 712.197050 | ||||
| 2 | 61.563577 | 42 | 721.182957 | 2 | 61.576058 | 42 | 721.190979 | ||||
| 3 | 85.527891 | 43 | 729.803055 | 3 | 85.540284 | 43 | 729.810928 | ||||
| 4 | 109.113793 | 44 | 738.050734 | 4 | 109.126098 | 44 | 738.058455 | ||||
| 5 | 132.320846 | 45 | 745.927666 | 5 | 132.333061 | 45 | 745.935235 | ||||
| 6 | 155.148607 | 46 | 753.436238 | 6 | 155.160732 | 46 | 753.443653 | ||||
| 7 | 177.596626 | 47 | 760.580076 | 7 | 177.608659 | 47 | 760.587334 | ||||
| 8 | 199.664447 | 48 | 767.364268 | 8 | 199.676388 | 48 | 767.371365 | ||||
| 9 | 221.351612 | 49 | 773.795154 | 9 | 221.363461 | 49 | 773.802085 | ||||
| 10 | 242.657659 | 50 | 779.879770 | 10 | 242.669413 | 50 | 779.886529 | ||||
| 11 | 263.582122 | 51 | 785.625209 | 11 | 263.593782 | 51 | 785.631790 | ||||
| 12 | 284.124537 | 52 | 791.038169 | 12 | 284.136101 | 52 | 791.044568 | ||||
| 13 | 304.284438 | 53 | 796.124843 | 13 | 304.295905 | 53 | 796.131057 | ||||
| 14 | 324.061362 | 54 | 800.891129 | 14 | 324.072732 | 54 | 800.897155 | ||||
| 15 | 0 | 343.454852 | 55 | 0 | 805.342998 | 15 | 1 | 343.466122 | 55 | 1 | 805.348837 |
| 16 | 362.464454 | 56 | 809.486880 | 16 | 362.475624 | 56 | 809.492530 | ||||
| 17 | 381.089724 | 57 | 813.329935 | 17 | 381.100793 | 57 | 813.335396 | ||||
| 18 | 399.330227 | 58 | 816.880194 | 18 | 399.341194 | 58 | 816.885466 | ||||
| 19 | 417.185546 | 59 | 820.146578 | 19 | 417.196409 | 59 | 820.151660 | ||||
| 20 | 434.655274 | 60 | 823.138828 | 20 | 434.666032 | 60 | 823.143718 | ||||
| 21 | 451.739031 | 61 | 825.867378 | 21 | 451.749683 | 61 | 825.872074 | ||||
| 22 | 468.436455 | 62 | 828.343216 | 22 | 468.447000 | 62 | 828.347716 | ||||
| 23 | 484.747218 | 63 | 830.577753 | 23 | 484.757653 | 63 | 830.582053 | ||||
| 24 | 500.671020 | 64 | 832.582698 | 24 | 500.681345 | 64 | 832.586794 | ||||
| 25 | 516.207603 | 65 | 834.369970 | 25 | 516.217816 | 65 | 834.373860 | ||||
| 26 | 531.356753 | 66 | 835.951643 | 26 | 531.366852 | 66 | 835.955321 | ||||
| 27 | 546.118305 | 67 | 837.339899 | 27 | 546.128290 | 67 | 837.343362 | ||||
| 28 | 560.492154 | 68 | 838.547020 | 28 | 560.502022 | 68 | 838.550263 | ||||
| 29 | 574.478257 | 69 | 839.585378 | 29 | 574.488006 | 69 | 839.588399 | ||||
| 30 | 588.076645 | 70 | 840.467439 | 30 | 588.086274 | 70 | 840.470234 | ||||
| 31 | 601.287437 | 71 | 841.205765 | 31 | 601.296943 | 71 | 841.208331 | ||||
| 32 | 614.110862 | 72 | 841.813012 | 32 | 614.120244 | 72 | 841.815344 | ||||
| 33 | 626.547268 | 73 | 842.301919 | 33 | 626.556525 | 73 | 842.304015 | ||||
| 34 | 638.597113 | 74 | 842.685305 | 34 | 638.606241 | 74 | 842.687162 | ||||
| 35 | 650.260928 | 75 | 842.976041 | 35 | 650.269926 | 75 | 842.977655 | ||||
| 36 | 661.539322 | 76 | 843.187028 | 36 | 661.548188 | 76 | 843.188397 | ||||
| 37 | 672.433049 | 77 | 843.331171 | 37 | 672.441781 | 77 | 843.332291 | ||||
| 38 | 682.943163 | 78 | 843.421348 | 38 | 682.951758 | 78 | 843.422215 | ||||
| 39 | 693.071161 | 79 | 843.472547 | 39 | 693.079617 | 79 | 843.473215 |
Table 8 shows the calculated values for the rovibrational spectroscopic constants of all systems under study. An important fact that can be observed from this table is the good agreement of the results obtained with both methods, i.e., eqn (3) (named with the DVR method) and Dunham's method. With the exception of the He–Og dimer, there is a good agreement between the values of the rovibrational spectroscopic constants obtained with the ILJ and extended-Rydberg PEC. It can be seen that it was not possible to determine the spectroscopic constants for the He–Og system (for both ILJ and Rydberg PECs) viaeqn (3). The reason lies in the fact that this equation can only be used if there are at least 4 vibrational levels within the well of the potential energy curve. Table 8 shows also the Og–Og spectroscopic constant results available in the literature. When the results of ωe obtained with Dunham-Rydberg and correlation formulas are compared with Jerabek's results, the differences are 2.05 cm−1 and 5.45 cm−1, respectively. When we make the same comparisons for the ωexe vibrational constant, we have the following differences 0.001 cm−1 and 0.21 cm−1, respectively. When the ωe harmonic spectroscopic constants calculated with Dunham-Rydberg and Correlation formulas are compared with the value obtained by Saue, we have the following differences 2.70 cm−1 and 4.80 cm−1, respectively. From these comparisons, it can be noted that the values found in the present work for the Og–Og spectroscopic constants (mainly those obtained with Dunham-Rydberg) agree well with the results of Jerabek and Saue.
| System | Methods | ω e (cm−1) | ω e x e (cm−1) | ω e y e (cm−1) | α e (cm−1) | γ e (cm−1) |
|---|---|---|---|---|---|---|
| He–Og | DVR-ILJ | — | — | — | — | — |
| Dunham-ILJ | 20.88670 | — | — | — | — | |
| DVR-Rydberg | — | — | — | — | ||
| Dunham-Rydberg | 22.14117 | — | — | — | — | |
| DVR-ILJ | 15.96782 | 1.73275 | 0.00403 | 4.14 × 10−3 | −4.33 × 10−4 | |
| Ne–Og | Dunham-ILJ | 16.05381 | 1.80394 | 0.02444 | 4.40 × 10−3 | −2.45 × 10−4 |
| DVR-Rydberg | 16.46278 | 1.93427 | 0.04158 | 3.65 × 10−3 | −6.00 × 10−4 | |
| Dunham-Rydberg | 15.75879 | 1.28925 | −0.12236 | 3.93 × 10−3 | −3.12 × 10−4 | |
| DVR-ILJ | 23.94156 | 1.02459 | 0.00328 | 8.94 × 10−4 | −2.35 × 10−5 | |
| Ar–Og | Dunham-ILJ | 23.93896 | 1.02207 | 0.00236 | 8.99 × 10−4 | −1.94 × 10−5 |
| DVR-Rydberg | 24.71511 | 1.29686 | 0.02626 | 9.23 × 10−4 | −2.55 × 10−5 | |
| Dunham-Rydberg | 24.66753 | 3.39022 | −1.61570 | 9.96 × 10−4 | 9.27 × 10−4 | |
| DVR-ILJ | 18.51106 | 0.44319 | −0.00004 | 2.76 × 10−4 | −3.94 × 10−6 | |
| Kr–Og | Dunham-ILJ | 18.51139 | 0.44315 | −0.00006 | 2.76 × 10−4 | −3.47 × 10−6 |
| DVR-Rydberg | 19.50191 | 0.41346 | −0.01355 | 1.72 × 10−4 | −2.14 × 10−5 | |
| Dunham-Rydberg | 19.47647 | 0.47659 | −0.09941 | 1.70 × 10−4 | 3.35 × 10−5 | |
| DVR-ILJ | 17.87071 | 0.31911 | 0.00008 | 1.39 × 10−4 | −1.40 × 10−6 | |
| Xe–Og | Dunham-ILJ | 17.87086 | 0.31906 | 0.00006 | 1.39 × 10−4 | −1.29 × 10−6 |
| DVR-Rydberg | 18.28701 | 0.27636 | −0.00593 | 1.12 × 10−4 | −4.67 × 10−6 | |
| Dunham-Rydberg | 18.27687 | 0.31902 | −0.11668 | 1.12 × 10−4 | 3.31 × 10−5 | |
| DVR-ILJ | 19.14233 | 0.23676 | 0.00002 | 7.23 × 10−5 | −4.97 × 10−7 | |
| Rn–Og | Dunham-ILJ | 19.14251 | 0.23674 | 0.00002 | 7.27 × 10−5 | −4.67 × 10−7 |
| DVR-Rydberg | 19.16661 | 0.24821 | 0.00018 | 7.37 × 10−5 | −5.68 × 10−7 | |
| Dunham-Rydberg | 19.16455 | 0.28186 | −0.10395 | 7.37 × 10−5 | 2.04 × 10−5 | |
| DVR-ILJ | 25.09701 | 0.18846 | −0.00007 | 4.33 × 10−5 | −1.84 × 10−7 | |
| Og–Og | Dunham-ILJ | 25.09726 | 0.18846 | −0.00007 | 4.29 × 10−5 | −1.73 × 10−7 |
| DVR-Rydberg | 24.44471 | 0.20151 | −0.00024 | 4.54 × 10−5 | −2.68 × 10−7 | |
| Dunham-Rydberg | 24.44251 | 0.21228 | −0.05290 | 3.85 × 10−5 | 6.75 × 10−6 | |
| Og–Og (correlation formulas) | DVR-ILJ | 16.9382 | 0.1740 | 0.00001 | 4.41 × 10−5 | 2.48 × 10−7 |
| Og–Og (correlation formulas) | Dunham-ILJ | 16.9384 | 0.1740 | 0.00001 | 4.44 × 10−5 | 2.37 × 10−7 |
| Og–Og (Jerabek et al.12) | 22.39 | 0.2132 | 0.00017 | 1.8 × 10−4 | — | |
| Og–Og (Saue et al.13) | 21.74 | — | — | — | — |
Fig. 2 shows the behavior of lifetime as a function of temperature (which ranged from 200 to 500 K) for each molecule studied. This figure reveals that the lifetime determined by both ILJ and Rydberg PEC essentially has the same behavior for the entire temperature range considered. The He–Og lifetime obtained via Rydberg PEC and ILJ PEC are slightly above 1.0 picosecond and they are the ones with the lowest lifetime values between 200 and 500 K. All other systems have a lifetime above 1.0 picosecond within the temperature range of 200–500 K. Thus, according to Wolfgang's study,58 a lifetime of a complex above 1.0 picoseconds means that the well of the potential energy is deep enough to assure its stability and the interacting complex must be considered stable. Therefore, based on this condition, the Og–He system is close to the edge of instability and it is expected, as this system has only one vibrational level inside of the well of ILJ and Rydberg PEC. On the other hand, the Og–Og dimer has the longest lifetime in the entire temperature range considered, confirming its great stability.
 | ||
| Fig. 2 Lifetime as a function of temperature for the Ng–Og (Ng = He, Ne, Ar, Kr, Xe, Rn, and Og) systems using ILJ PEC, (a) and (c), and Rydberg PEC, (b) and (d). | ||
5 Conclusions
Using the relativistic 4-component Dirac–Fock method and with the inclusion of quantum electrodynamics effects at the Gaunt interaction level and with BSSE correction, this work presents the ground state electronic potential energy curves, the vibrational energies, spectroscopic constants, and lifetime of the He–Og, Ne–Og, Ar–Og, Kr–Og, Xe–Og, Rn–Og, and Og–Og dimers.The inclusion of quantum electrodynamics effects reduces the value of the dissociation energy of the studied dimers, which can be attributed to the fact that interactions between electrons are no longer treated as instantaneous. Furthermore, the percentage contribution of the quantum electrodynamics effect on the dissociation energy ranged from 0.48% (for the He–Og dimer) to 9.63% (for the Rn–Og dimer). This fact is also reflected in the number of vibrational levels, mainly in the dimers composed of the heaviest noble gases.
The current results obtained for the Og–Og spectroscopic constants (mainly those obtained with Dunham-Rydberg) agree well with the theoretical results of Jerabek and Saue. The lifetime as a function of temperature (which ranged from 200 to 500 K) indicates that the Og–He molecule is close to the edge of instability as expected, because this dimer has only one vibrational level inside both ILJ and Rydberg PEC. It is expected that the results of this study can motivate future spectroscopy experiments involving the He, Ne, Ar, Kr, Xe, and Rn noble gases with the oganesson (Z = 118) super-heavy element.
In the present work, the ILJ function has been adopted to fit the ab initio points. However, the obtained De and Re are not only fitting parameters, but they exhibit an appropriate meaning since they are related to the fundamental physical properties of the interacting partners. This is confirmed (see Table 1) by the good agreement (except for Og–Og) between the fitting values and predictions of correlation formulas that relate the value of the basic potential parameters with the electronic polarizability of the involved partners. Moreover, ILJ provides an asymptotic attraction, where the leading C6 coefficient, given by C6 = DeRe6 scales along with the Ng–Og family as those predicted by correlation formulas, and for any system, their absolute values are within ≈20%.
An accurate analysis of basic intermolecular force components involved in all Ng–Og (Ng = He, Ne, Ar, Kr, Xe, and Rn) family of dimers confirmed the nature of van der Waals of the global interaction. This is also proved by the behavior of the equilibrium distance Re whose values, along the Ng–Og family, remain confined in the restricted range of Re = 4.50 ± 0.25 Å, while the dissociation energy De changes by a factor of 40± 20. This is typical behavior of systems whose repulsion component, controlling Re, is effectively dominated by the size of the most polarizable atom (Og), while De varies according to the polarizability change of the Ng partner. The use of correlation formulas, defined in terms of polarizability, which represents the basic physical properties useful to scale both size repulsion and dispersion attraction, permitted us to evaluate not only the C6 dispersion coefficient for Ng–Og systems but also the basic Re, De, and C6 interaction features of the Og–Og dimer. It has been also emphasized that with respect to the other Ng, Og exhibits an unexpected high Tbp value which determines a range of temperature, defining the liquid stability, significantly larger than 100 K. This anomalous behavior probably arises from non-conventional many-body attractive interaction contributions controlled by high relativistic effects.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Brazilian Research Councils: CAPES, CNPq and FAPDF. LGMM would like to acknowledge Desenvolvimento Científico e Tecnologico (CNPQ, under grant 408085/2021-5) and also Universidade Federal de Sao João del Rei (CCO-UFSJ).Notes and references
- E. Eliav, U. Kaldor, Y. Ishikawa and P. Pyykkö, Element 118: The First Rare Gas with an Electron Affinity, Phys. Rev. Lett., 1996, 77, 5350–5352, DOI:10.1103/PhysRevLett.77.5350.
- Y. T. Oganessian, V. K. Utyonkov, Y. V. Lobanov, F. S. Abdullin, A. N. Polyakov, R. N. Sagaidak, I. V. Shirokovsky, Y. S. Tsyganov, A. A. Voinov, G. G. Gulbekian, S. L. Bogomolov, B. N. Gikal, A. N. Mezentsev, S. Iliev, V. G. Subbotin, A. M. Sukhov, K. Subotic, V. I. Zagrebaev, G. K. Vostokin, M. G. Itkis, K. J. Moody, J. B. Patin, D. A. Shaughnessy, M. A. Stoyer, N. J. Stoyer, P. A. Wilk, J. M. Kenneally, J. H. Landrum, J. F. Wild and R. W. Lougheed, Synthesis of the isotopes of elements 118 and 116 in the Cf249 and Cm245 + Ca48 fusion reactions, Phys. Rev. C: Nucl. Phys., 2006, 74, 044602, DOI:10.1103/PhysRevC.74.044602.
- A. Turler and V. Pershina, Advances in the production and chemistry of the heaviest elements, Chem. Rev., 2013, 113, 1237–1312, DOI:10.1021/cr3002438.
- P. Pyykkö, Theoretical chemistry of gold, Angew. Chem., Int. Ed., 2004, 43, 4412–4456, DOI:10.1002/anie.200300624.
- E. Pastorczak and C. Corminboeuf, Perspective: Found in translation: Quantum chemical tools for grasping non-covalent interactions, J. Chem. Phys., 2017, 146, 120901, DOI:10.1063/1.4978951.
- Q. Cui, Perspective: Quantum mechanical methods in biochemistry and biophysics, J. Chem. Phys., 2016, 145, 140901, DOI:10.1063/1.4964410.
- A. D. Buckingham, P. W. Fowler and J. M. Hutson, Theoretical studies of van der Waals molecules and intermolecular forces, Chem. Rev., 1988, 88, 963–988, DOI:10.1021/cr00088a008.
- K. Liu, Y. Kang, Z. Wang and X. Zhang, 25th Anniversary Article: Reversible and Adaptive Functional Supramolecular Materials: “Noncovalent Interaction” Matters, Adv. Mater., 2013, 25, 5530–5548, DOI:10.1002/adma201302015.
- J. Řezáč and P. Hobza, Benchmark calculations of interaction energies in noncovalent complexes and their applications, Chem. Rev., 2016, 116, 5038–5071, DOI:10.1021/acs.chemrev.5b00526.
- S. F. Boys and F. Bernardi, The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors, Mol. Phys., 1970, 19, 553–566, DOI:10.1080/00268977000101561.
- R. Cambi, D. Cappelletti, G. Liuti and F. Pirani, Generalized correlations in terms of polarizability for van der Waals interaction potential parameter calculations, J. Chem. Phys., 1991, 95, 1852–1861, DOI:10.1063/1.461035.
- P. Jerabek, O. R. Smits, J. M.l Mewes, K. A. Peterson and P. Schwerdtfeger, Solid Oganesson via a Many-Body Interaction Expansion Based on Relativistic Coupled-Cluster Theory and from Plane-Wave Relativistic Density Functional Theory, J. Phys. Chem. A, 2019, 123, 4201–4211, DOI:10.1021/acs.jpca.9b01947.
- A. Shee, S. Knecht and T. Saue., A theoretical benchmark study of the spectroscopic constants of the very heavy rare gas dimers, Phys. Chem. Chem. Phys., 2015, 17, 10978–10985, 10.1039/c5cp01094b.
- O. R. Smits, J. M. Mewes, P. Jerabek and P. Schwerdtfeger, Oganesson: A Noble Gas Element That Is Neither Noble Nor a Gas, Angew. Chem., Int. Ed., 2020, 59, 23636–23640, DOI:10.1002/anie.202011976.
- R. M. de Oliveira, L. G. M. de Macedo, T. F. da Cunha, F. Pirani and R. Gargano, A Spectroscopic Validation of the Improved Lennard-Jones Model, Molecules, 2021, 26, 3906, DOI:10.3390/molecules26133906.
- W. F. Cunha, R. M. Oliveira, L. F. Roncaratti, J. B. L. Martins, G. M. Silva and R. Gargano, Rovibrational energies and spectroscopic constants for H2O–Ng complexes, J. Mol. Model., 2014, 20, 2498, DOI:10.1007/s00894-014-2498-8.
- A. L. A. Oliveira, M. A. Silva, F. Pirani, L. G. M. de Macedo and R. Gargano, Hydrogen sulphide H2S and noble gases (Ng = He, Ne, Ar, Kr, Xe, Rn) complexes: A theoretical study of their dynamics, spectroscopy, and interactions, Int. J. Quantum. Chem., 2020, 120, e26266, DOI:10.1002/qua.26266.
- F. M. Carvalho, A. S. Kiametis, A. L. A. Oliveira, F. Pirani and R. Gargano, Spectroscopy, lifetime, and charge-displacement of the methanol-noble gas complexes: An integrated experimental-theoretical investigation, Spectrochim. Acta, Part A, 2021, 246, 119049, DOI:10.1016/j.saa.2020.119049.
- A. L. A. Oliveira, L. G. M. de Macedo, Y. A. de Oliveira Só, J. B. L. Martins, F. Pirani and R. Gargano, Nature and role of the weak intermolecular bond in enantiomeric conformations of H2O2-noble gas adducts: a chiral prototypical model, New J. Chem., 2021, 45, 8240–8247, 10.1039/D0NJ06135B.
- F. Pirani, S. Brizi, L. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Beyond the Lennard-Jones model: A simple and accurate potential function probed byhigh resolution scattering data useful for molecular dynamics simulations, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503, 10.1039/B808524B.
- F. Pirani, M. Alberti, A. Castro, M. Moix Teixidor and D. Cappelletti, Atom-bond pairwise additive representation for intermolecular potential energy surfaces, Chem. Phys. Lett., 2004, 394, 37–44, DOI:10.1016/j.cplett.2004.06.100.
- P. Candori, D. Cappelletti, S. Falcinelli, F. Pirani, L. F. Roncaratti, F. Tarantelli and F. Vecchiocattivi, Benchmarking a model potential for the investigation of intermolecular interactions, Phys. Scr., 2008, 78, 038102, DOI:10.1088/0031-8949/78/03/038102.
- C. Douketis, G. Scoles, S. Marchetti, M. Zen and A. J. Thakkar, Intermolecular forces via hybrid Hartree-Fock-SCF plus damped dispersion (HFD) energy calculations. An improved spherical model, J. Chem. Phys., 1982, 76, 3057–3063, DOI:10.1063/1.443345.
- K. T. Tang and J. P. Toennies, An improved simple model for the van der Waals potential based on universal damping functions for the dispersion coefficients, J. Chem. Phys., 1984, 80, 3726–3741, DOI:10.1063/1.447150.
- K. T. Tang and J. P. Toennies, The van der Waals potentials between all the rare gas atoms from He to Rn, J. Chem. Phys., 2003, 118, 4976–4983, DOI:10.1063/1.1543944.
- K. T. Tang, J. P. Toennies and C. L. You, Accurate Analytical He-He van der Waals Potential Based on Perturbation Theory, Phys. Rev. Lett., 1995, 74, 1546–1549, DOI:10.1103/PhysRevLett.74.1546.
- S. Longo, P. Diomede, A. Laricchiuta, G. Colonna, M. Capitelli, D. Ascenzi, M. Scotoni, P. Tosi and F. Pirani, Lect. Notes Comput. Sci., 2008, 5072, 1131 Search PubMed.
- J. N. Murrel, S. Carter, S. C. Farantos, P. Huxley and A. J. C. Varandas, Molecular Potential Energy Functions, John Wiley & Sons, Chichester, Sussex, UK, 1984 Search PubMed.
- H. V. R. Vila, L. A. Leal, A. L. A. Fonseca and R. Gargano, Calculation of the H2+ rovibrational energies and spectroscopic constants in the 2π, 3dσ, 4dσ, 4fπ, 4fσ, 5gσ, and 6iσ electronic states, Int. J. Quantum Chem., 2012, 112, 829–833, DOI:10.1002/qua.23070.
- E. N. C. Paura, W. F. da Cunha, P. H. de Oliveira Neto, G. M. e Silva, J. B. L. Martins and R. Gargano, Vibrational and Electronic Structure Analysis of a Carbon Dioxide Interaction with Functionalized Single-Walled Carbon Nanotubes, J. Phys. Chem. A, 2013, 3013(117), 2854–2861, DOI:10.1021/jp312622s.
- W. F. Cunha, R. Gargano, E. Garcia, J. R. S. Politi, A. F. Albernaz and J. B. L. Martins, Rovibrational energy and spectroscopic constant calculations of CH4⋯H2O, CH4⋯CHF3, and H2O⋯CHF3 dimers, J. Mol. Model., 2014, 20, 2298, DOI:10.1007/s00894-014-2298-1.
- J. Soares Neto and L. Costa, Numerical Generation of Optimized Discrete Variable Representations, Braz. J. Phys., 1998, 28, 1–11, DOI:10.1590/S0103-97331998000100001.
- J. L. Dunham, The Energy Levels of a Rotating Vibrator, Phys. Rev., 1932, 41, 721–731, DOI:10.1103/PhysRev.41.721.
- J. C. Slater, The theory of complex spectra, Phys. Rev., 1929, 34, 1293, DOI:10.1103/PhysRev.34.1293.
- R. F. de Menezes, L. G. M. de Macedo, J. B. L. Martins, F. Pirani and R. Gargano, Investigation of strength and nature of the weak intermolecular bond in NH2 radical-noble gas atom adducts and evaluation of their basic spectroscopic features, Chem. Phys. Lett., 2021, 769, 138386, DOI:10.1016/j.cplett.2021.138386.
- DIRAC17, a relativistic ab initio electronic structure program, Release DIRAC17 (2017), written by L. Visscher, H. J. A. Jensen, R. Bast, T. Saue, with contributions from V. Bakken, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A. S. P. Gomes, E. D. Hedegård, T. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, H. S. Nataraj, M. K. Nayak, P. Norman, G. Olejniczak, J. Olsen, J. M. H. Olsen, Y. C. Park, J. K. Pedersen, M. Pernpointner, R.di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, A. Shee, J. Sikkema, A. J. Thorvaldsen, J. Thyssen, J.van Stralen, S. Villaume, O. Visser, T. Winther, S. Yamamoto. http://www.diracprogram.org.
- K. Dyall and K. Faegri. Introduction to relativistic quantum chemistry, Oxford University Press, 2007 Search PubMed.
- T. Saue, Relativistic Hamiltonians for chemistry: A primer, ChemPhysChem, 2011, 12, 3077–3094, DOI:10.1002/cphc.201100682.
- L. Visscher, Approximate molecular relativistic Dirac-Coulomb calculations using a simple Coulombic correction, Theor. Chem. Acc., 1997, 98, 68–70, DOI:10.1007/s002140050280.
- T. Hangele and M. Dolg, Coupled-cluster and DFT studies of the Copernicium dimer including QED effects, Chem. Phys. Lett., 2014, 616, 222–225, DOI:10.1016/j.cplett.2014.10.048.
- D. H. T. Amador, H. C. B. de Oliveira, J. Sambrano, R. Gargano and L. G. M. de Macedo, 4-Component correlated all-electron study on Eka-actinium Fluoride (E121F) including Gaunt interaction: Accurate analytical form, bonding and influence on rovibrational spectra, Chem. Phys. Lett., 2016, 662, 169–175, DOI:10.1016/j.cplett.2016.09.025.
- O. Kullie and T. Saue., Range-separated density functional theory: a 4-component relativistic study of the rare gas dimers He2, Ne2, Ar2, Kr2, Xe2, Rn2 and Uuo2, Chem. Phys., 2012, 395, 54–62, DOI:10.1016/j.chemphys.2011.06.024.
- P. M. W. Gill, R. D. Adamson and J. A. Pople., Coulomb-attenuated exchange energy density functionals, Mol. Phys., 1996, 88, 1005–1009, DOI:10.1080/00268979609484488.
- I. C. Gerber and J. G. Angyan., London dispersion forces by range-separated hybrid density functional with second order perturbational corrections: The case of rare gas complexes, J. Chem. Phys., 2007, 126, 044103, DOI:10.1063/1.2431644.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153.
- R. A. Kendall, T. H. Dunning and R. J. Harrison., Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806, DOI:10.1063/1.462569.
- D. E. Woon and T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98, 1358–1371, DOI:10.1063/1.464303.
- D. E. Woon and T. H. Dunning Jr., Gaussian Basis Sets for Use in Correlated Molecular Calculations. IV. Calculation of Static Electrical Response Properties, J. Chem. Phys., 1994, 100, 2975–2988, DOI:10.1063/1.466439.
- K. G. Dyall, Relativistic quadruple-zeta and revised triple-zeta and double-zeta basis sets for the 4p, 5p, and 6p elements, Theor. Chem. Acc., 2006, 115, 441–447, DOI:10.1007/s00214-006-0126-0.
- K. Dyall, Relativistic double-zeta, triple-zeta, and quadruple-zeta basis sets for the 7p elements, with atomic and molecular applications, Theor. Chem. Acc., 2012, 131, 1172–1174, DOI:10.1007/s00214-012-1172-4.
- A. D. Powell and R. Dawes, Calculating potential energy curves with fixed-node diffusion Monte Carlo: CO and N2, J. Chem. Phys., 2016, 145, 224308, DOI:10.1063/1.4971378.
- M. J. Jamieson, G. W. F. Drake and A. Dalgarno, Retarded dipole-dipole dispersion interaction potential for helium, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 3358, DOI:10.1103/PhysRevA.51.3358.
- F. Nunzi, G. Pannacci, F. Tarantelli, L. Belpassi, D. Cappelletti, S. Falcinelli and F. Pirani, Leading interaction components in the structure and reactivity of noble gases compounds, Molecules, 2020, 25, 2367, DOI:10.3390/molecules25102367.
- D. Cappelletti, E. Ronca, L. Belpassi, F. Tarantelli and F. Pirani, Revealing Charge-Transfer Effects in Gas-Phase Water Chemistry, Acc. Chem. Res., 2012, 45, 1571–1580, DOI:10.1021/ar3000635.
- G. Liuti and F. Pirani, Regularities in van der Waals forces: correlation between the potential parameters and polarizability, Chem. Phys. Lett., 1985, 122, 245–250, DOI:10.1016/0009-2614(85)80571-6.
- D. V. Fedorov, M. Sadhunkhn, M. Stöhr and A. Tkatchenko, Quantum-Mechanical Relation between Atomic Dipole Polarizability and the van der Waals Radius, Phys. Rev. Lett., 2018, 121, 183401, DOI:10.1103/PhysRevLett.121.183401.
- D. R. Lide, Handbook of Chemistry and Physics, CRC Press, Florida, 67th edn, 2005, pp. 1986–1987 Search PubMed.
- R. Wolfgang, Energy and chemical reaction. II. intermediate complexes vs. direct mechanisms, Acc. Chem. Res., 1970, 3, DOI:10.1021/ar50026a002.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04456k |
| This journal is © the Owner Societies 2023 |