Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Overlapping hydration shells in salt solutions causing non-monotonic Soret coefficients with varying concentration†
Shilpa
Mohanakumar
 a,
Hartmut
Kriegs
a,
Hartmut
Kriegs
 a,
W. J.
Briels
a,
W. J.
Briels
 ab and
Simone
Wiegand
ab and
Simone
Wiegand
 *ac
*ac
aIBI-4:Biomacromolecular Systems and Processes, Forschungszentrum Jülich GmbH, D-52428 Jülich, Germany. E-mail: s.wiegand@fz-juelich.de
bUniversity of Twente, Computational Chemical Physics, Postbus 217, 7500 AE Enschede, The Netherlands. E-mail: w.j.briels@utwente.nl
cChemistry Department – Physical Chemistry, University Cologne, D-50939 Cologne, Germany
First published on 28th October 2022
Abstract
We investigate the thermodiffusive properties of aqueous solutions of sodium iodide, potassium iodide and lithium iodide, using thermal diffusion forced Rayleigh scattering in a concentration range of 0.5–4 mol kg−1 of solvent, large enough to deal with associated salts, and a temperature range of 15 to 45 °C. All systems exhibit non-monotonic variations of the Soret coefficient ST with concentration, with a minimum at one mol kg−1 of solvent in all three cases. We take this as an indication that the relevant length and energy scales are very similar in all cases. On this basis we develop an intuitive picture in which the relevant objects are the fully hydrated salt molecules, including all water molecules that behave differently from bulk water. Preliminary, somewhat sketchy calculations indicate that indeed Soret coefficients begin to rise beyond concentrations where the fully hydrated particles are randomly close packed. Indications are given as to why the model will fail at large concentrations.
1 Introduction
Thermophoresis, also called thermodiffusion or Ludwig–Soret effect, describes mass transport in temperature gradients and is one of the interesting unsolved puzzles in physical chemistry. Nowadays the most prominent application of this effect is in the determination of binding constants in protein–ligand reactions,1,2 but the effect also plays an important role in, for example, the conversion of waste heat into electricity by means of thermogalvanic cells.3–5 In both cases a deeper understanding of thermodiffusion of ions in aqueous solutions is desirable. Since the pioneering work of Hofmeister, it is known that many physicochemical processes in aqueous salt solutions do not only depend on ion concentrations and valencies, but also on the ion type.6–8 We therefore present experimental results of thermodiffusion in a range of concentrations and temperatures of solutions of three different salts with equal valencies but of different ion type, in casu lithium, sodium and potassium iodide.In principle, in systems like ours there are four mass fluxes, i.e. those of the two types of ions, the one of the intact, non-dissociated salt molecules, and that of the solvent. Because of macroscopic electro-neutrality the two ionic fluxes must be equal. If we further assume that the dissociation equilibrium does not change with the very small temperature changes, the flux of the intact salt molecules must be equal to that of the individual ions. At the end we are left with only two independent mass fluxes, that of the solvent and that of the solute as a whole. From a phenomenological point of view we are therefore left with binary systems. From a microscopic point of view, the measured transport coefficients are combinations of those of the individual components.
In a binary fluid mixture exposed to a temperature gradient a stationary non-equilibrium state sets in, where the ordinary diffusive mass flux of the solute, proportional to the diffusion coefficient D, balances a thermophoretic mass flux of the solute, proportional to the thermal diffusion DT. The Soret coefficient ST defined as the ratio DT/D describes the value of the concentration gradient that develops as a result of the applied temperature gradient. It can be positive, indicating that the solute accumulates in the cold region, or negative, in case the solute moves towards the warm region.9,10 Especially in aqueous systems, variations of concentration or temperature may lead to sign changes and non-monotonous variations of ST. While early studies of more than 20 different salts in water indicated monotonous behavior of the Soret coefficient with concentration,11 later works reported a minimum of ST for aqueous solutions of various salts.12–14 A recent indication for a minimum of ST with concentration was observed experimentally15 and by computer simulations16 for lithium chloride at very low temperatures. The simulations showed that the minimum disappeared with increasing temperature, and especially that artificially decreasing the size of the anion increased the depth of the minimum. Until now, all these phenomena are basically not understood on a microscopic level.10,17–19
According to Onsager's irreversible thermodynamics20–22 the Soret coefficient ST of a binary mixture may be written as
 | (1) |
Variations of the Soret coefficient ST with temperature often follow an empirical equation proposed by Iacopini and Piazza34
 | (2) |
Several computer simulation studies of thermodiffusion have appeared in the literature, some of which have been cited above, but none of these addresses salt solutions over a range of temperatures and concentrations. We will therefore not review these studies here in any detail. However, because we will refer to them on several occasions below, we do briefly discuss the results of thermophoretic simulations of binary Lennard-Jones mixtures by Artola and Rousseau.39 All particles in their simulations were of equal mass and equal size. Simulations were performed over the full range of mole-fractions and a range of temperatures. Moreover they studied several different systems by varying like–like (εAA, εBB) and cross-interactions (εAB). Clearly, with Lennard-Jones energies εAA = εBB, and εAB such that component A goes to cold at small mole-fractions xA, component B must go to cold at small mole-fractions xB, i.e. at large mole-fractions xA; as a consequence component A will go to hot at large mole-fractions xA. The Soret coefficient of component A must therefore obey ST(xA) = −ST(1 − xA), and change sign at 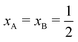 . From the simulations it follows that in all cases the Soret coefficient changes linearly with mole-fraction, and indeed obeys the rule just mentioned. Moreover, it was found that changing kAB in
. From the simulations it follows that in all cases the Soret coefficient changes linearly with mole-fraction, and indeed obeys the rule just mentioned. Moreover, it was found that changing kAB in  changes the slope of this line, while varying the ratio ψ = εBB/εAA induces a vertical (or horizontal if you prefer) shift of the line. Before ending this paragraph on computer simulations we mention one more study on Lennard-Jones mixtures by Bresme et al.,40 where the authors perform in depth calculations of all properties of their mixtures relevant for testing several theories proposed to describe Soret coefficients so far. Their calculations are restricted however to one particular set of Lennard-Jones parameters, and therefore cannot be used for our purposes (see below).
changes the slope of this line, while varying the ratio ψ = εBB/εAA induces a vertical (or horizontal if you prefer) shift of the line. Before ending this paragraph on computer simulations we mention one more study on Lennard-Jones mixtures by Bresme et al.,40 where the authors perform in depth calculations of all properties of their mixtures relevant for testing several theories proposed to describe Soret coefficients so far. Their calculations are restricted however to one particular set of Lennard-Jones parameters, and therefore cannot be used for our purposes (see below).
Even when no theoretical explanation for the occurrence of a minimum in the Soret coefficient with variations of concentration is available, some hypotheses/speculations concerning the origin of the phenomenon may be found in the literature. Chanu,13 and later Gaeta et al.14 pointed at the perturbation of local order of water in the neighborhood of the ions and its dependence on salt concentration as a possible starting point for an understanding of the non-monotonous dependence of Soret. This picture of perturbed water goes back to Frank and Wen.41 Evidently, in dense solutions, solvent molecules must organize their structure in order to accommodate to the presence of the solutes. Indeed, strong variations of water densities around NaI, among other salts, have been confirmed in a paper by simulations and neutron diffraction experiments42–46 and around CO2 by Mitev et al.47 A closer look at the structure in the latter case reveals that water molecules very close to the solute are strongly bound to that solute, either by expressing their negative oxygen atom to the slightly positive carbon atom on CO2, or by embracing the slightly negative oxygen atom on CO2 with their hydrogen atoms. Similar structures may be assumed to occur around dissolved salt molecules. Beyond this first shell of water molecules, a second shell of decreasingly perturbed water molecules is needed to gradually adjust to bulk water. As a result, the CO2 molecule plus perturbed water is roughly a sphere with a radius of about 6–7 Å.47
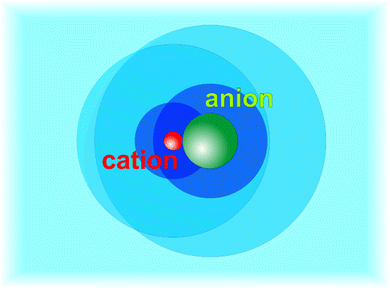
In this paper we will adopt a similar picture for salt solutions. For simplicity we assume that the measured effective transport coefficients may be attributed to non-dissociated salt molecules. Further discussion of this assumption will be given in Section 3.1. We define three types of particles, the bare salt molecule consisting of a cation paired with an iodide ion, the hydrated salt molecule (HSP) consisting of a bare salt molecule plus a first layer of Z strongly bound solvent molecules, and the fully hydrated salt molecule (FHP) consisting of the hydrated salt molecule plus the shell of perturbed water molecules. A caricaturist picture of these definitions is shown in Fig. 1. We expect that the Soret coefficient will change monotonously with concentration up to random close packing of the FHPs, beyond which the behavior will change. Random close packing occurs at a volume fraction of ϕ = 0.64,48 which with a radius of 6–7 Å corresponds to a molality of about 1.0 mole of salt per kilogram of water. This indeed turns out to roughly coincide with the minimum of Soret in all systems that we studied. We will use this observation as the starting point of our analysis of the thermophoresis of salt solutions with molalities on the order of one mole kg−1 of water.
2 Results
2.1 Concentration dependence
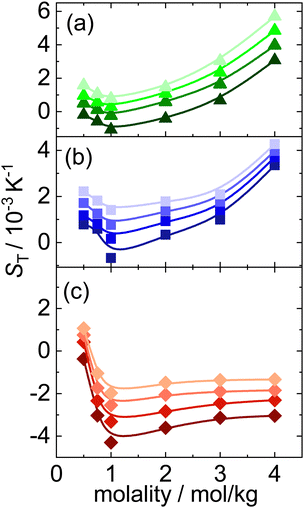
We used Infrared Thermal Diffusion Forced Rayleigh Scattering (IR-TDFRS) to investigate the thermophoretic behavior quantitatively. A schematic diagram of the setup is discussed in ESI† (Section S1) By way of example, we present in Fig. 2 the diffusion coefficient D, the thermal diffusion coefficient DT, and the Soret coefficient ST of NaI at four different temperatures as function of concentration. The solid lines are guides to the eye. As a measure of concentration we use molality m, i.e. the number of moles of salt per kilogram of water. At all temperatures DT shows a minimum around a molality of 1 mol kg−1, which survives in ST, only slightly smoothed by increasing D. In all cases the diffusion coefficient D increases monotonously with concentrations, with the increase at higher concentrations being less than that at lower concentrations, due to an increase of viscosity with increasing salt concentration.49 At the lowest measured temperature ST and DT change sign twice with concentration. Around m = 1 mol kg−1 NaI is thermophilic (goes to hot), while at lower and higher concentrations it reveals thermophobic behavior (goes to cold). Potassium and lithium iodide behave similarly, but none of them shows a double sign change (cf. Fig. S4 and S5, ESI†).Fig. 3 displays the concentration dependence of ST values at 25 °C of the three iodide salts that have been studied. The lines are guide to the eye. All ST of the investigated systems show a minimum with concentration, around 1 mol kg−1, as has been observed for several other electrolytes.13–15,38 The concentration at which the minimum is observed varies only marginally for different salt systems. The steepest decay at low concentrations is found for LiI, which is the most hydrophilic of the investigated systems.
2.2 Temperature dependence
Fig. 4 shows the measured ST as function of temperature at a molality of 1 and 4 mol kg−1. The curves have been fitted using eqn (2). The Soret coefficient shows an increase with increasing temperature for all salt systems investigated, which is typical for aqueous solutions at low concentrations. At 1 mol kg−1ST of KI and NaI show a sign change with temperature (cf. Fig. 4a), while LiI, as expected from the previous literature, shows thermophilic behavior at all concentrations.50 Additionally, ST of LiI remains almost constant with increasing concentration, while the thermophobicity of the other salts increases with concentration. | ||
| Fig. 4 Temperature dependence of Soret coefficient ST of KI, NaI and LiI at molalities of 1 (left panel) and 4 (right panel) mol kg−1 respectively. The open symbols mark data points by Caldwell.50 Darkest symbol corresponds to the lowest temperature of 15 °C with gradually fading to lighter symbols towards higher temperatures. | ||
In a previous investigation where ST of a number of electrolytes had been studied at 0.01 mol kg−1 of water, Snowden and Turner51 found at 25.3 °C the largest negative value of ST for LiI, −1.44 × 10−3 K−1. Also, in our study LiI exhibits large negative ST values in comparison to KI and NaI (cf. Fig. 4). In a previous study of LiI Caldwell et al.50 reported a ST value of −2.69 × 10−3 K−1, while we found an 11% lower value of −3.01 × 10−3 K−1 under the same conditions.
Fig. S6, S7 and S8 in the ESI,† display the temperature dependence of DT and D. Both DT and D show an increase with temperature. The increase in D is associated with the decrease in viscosity with temperature.
3 Discussion
3.1 Concentration dependence
In this section we infer from the characteristics of the data presented above a coarse grain picture that, in our view, contains the relevant elements to model the physics of our systems. In the second part we present results from some quick, but rather incomplete calculations on the basis of this model.It is known that in all cases that we consider about 80% of the salt molecules are dissociated into independent ions, while only 20% of them exist as non-dissociated, intact salt molecules.52–54 We notice, however, that also among the dissociated ions the cation–anion pair correlation functions have very strong first peaks, mainly as a result of the strong Coulomb interactions. In agreement with the second of the above findings we therefore assume that on average we may treat the salt molecules as single particles, sometimes consisting of strongly bound ion pairs, sometimes consisting of more loosely bound ion pairs, and sometimes even as single anions. A particle like this is called a bare salt molecule from now on. The properties attributed to such a bare salt molecule must be considered to be effective properties, very much as discussed in Section 1. Clearly, the model that we describe below will become less applicable with increasing cation sizes. If needed, a more realistic, but also more complicated model may be devised along similar lines. Referring to Fig. 1, we recall the definition of hydrated salt molecule (HSP), consisting of a bare salt molecule plus the first layer of strongly attached water molecules, and the fully hydrated salt molecule (FHP), consisting of an HSP plus the layer of perturbed water molecules. The radius of such an FHP will be denoted RHS. We obtain an estimate of this radius by assuming that the FHPs are randomly close packed when the molality is equal to mmin. The volume fraction of FHPs ϕ is given as
 | (3) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is called the molarity, the number of moles of salt per liter of solution. VHS is the volume of one FHP, i.e. one hydrated salt molecule or anion, Ns is the number of salt molecules in volume V, and ρ is the density of the solution. With mmin= 1.0 mol kg−1 for all systems and a random close packed volume fraction ϕrcp = 0.64, we obtain RHS = 6.3 Å; this is a very reasonable value according to Mitev et al.47
is called the molarity, the number of moles of salt per liter of solution. VHS is the volume of one FHP, i.e. one hydrated salt molecule or anion, Ns is the number of salt molecules in volume V, and ρ is the density of the solution. With mmin= 1.0 mol kg−1 for all systems and a random close packed volume fraction ϕrcp = 0.64, we obtain RHS = 6.3 Å; this is a very reasonable value according to Mitev et al.47
On increasing the concentration beyond mmin, the outer hydration shells of the salt molecules begin to overlap, as shown in Fig. 5. This gives rise to a type of depletion interaction between the salt molecules, which we will now explain. First we notice that concentrations are never large enough for the tightly bound water molecules, constituting the first solvation layer, of two different salt molecules or anions to touch. Therefore we take HSPs as the coarse grain particles in our model. Similarly we define coarse water particles to consist of several water molecules. The energy of a salt solution is then written as
 | (4) |
When one molecule of salt is dissolved in water, the change of energy has two contributions, one negative contribution when the first layer of water molecules is bound to the salt, and one positive contribution that takes into account the perturbation of the outer hydration shell. The total increase of energy will be negative. At low concentrations, when the FHPs do not overlap, a total energy E0 proportional to the number of salt particles will be released. When two FHPs do overlap, the energies gained by attaching the strongly bound water shells to each of the bare salt molecules, i.e. by creating the HSPs, are the same as for two non-overlapping FHPs, but the energy paid to create the outer shells of the FHPs is diminished by a positive amount, proportional to the overlap of the two outer shells. This holds for any pair of overlapping hydration shells. The self energy therefore reads
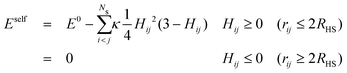 | (5a,b) |
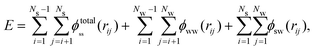 | (6a) |
 | (6b) |
On the energy scales that we are interested in, coarse salt particles may be considered to be impenetrable particles interacting through dipole–dipole interactions, so ϕ0ss may well be approximated by a Lennard-Jones potential. Given the dimensions as shown in Fig. 1 the radius of a coarse salt particle is about one half of RHS, so the salt–salt Lennard-Jones potential has a σ of about RHS, and therefore a range of about 2σ = 2RHS, which is equal to that of the overlap potential ϕoverlapss. For computational purposes it is often most convenient to have water particles of about the same size as that of the salt particle. Clearly for coarse water–water and salt–water interactions somewhat more soft potentials seem to be preferable, although Lennard-Jones potentials have been used for this purpose as well. For a review see Hadley and McCabe.55 This concludes the description of our coarse grain picture of salt solutions at low concentrations.
The results of our calculations are shown as the lines in Fig. 6. It is clearly seen that the predicted Soret coefficients increase as soon as the outer hydration shells of the big spheres begin to overlap. At larger concentrations, however, they decay again while experimental data continue to increase. Apart from the numerical inadequacies already mentioned, also the model itself will become inadequate at the larger concentrations. First, the pairwise additive corrections to the self energies will become inappropriate, and next, at even higher concentrations, one can imagine that it is profitable to form clusters of salt particles and expel the water molecules from these altogether to minimize the energy stored in the perturbed hydration shells. Both effects will lower the average salt–salt interactions faster than is done within the present model, and will drive salt to the cold.
3.2 Temperature dependence
As can be seen in Fig. 4ST of all investigated systems shows an increase in thermophobicity with temperature and can be successfully described by eqn (2) for all concentrations studied. The same behavior has been recently observed for other simple salts without large organic groups,38,56 which is in contrast to the temperature dependence of ST observed for larger organic salts37,57 and non-ionic solutes in water.29 For a typical non-ionic solute, the behavior of ST changes from increasing with temperature to decreasing with temperature as the concentration increases. It is assumed that this is correlated with the hydration of the solutes, which decreases as the concentration increases. In contrast, the Soret coefficients of simple ionic solutes show the typical temperature dependence described by eqn (2) over the entire concentration range. This might be explained by cluster formation and growth of the salts with increasing concentrations. At high salt concentrations, these clusters are hydrated by water as the fraction of ions in the interfaces decreases when more ions are part of larger clusters. This results in diluted solutions of clusters, which still exhibit the typical temperature dependence of diluted aqueous solutions.4 Conclusion
We have studied the thermophoretic properties of three iodide salt solutions over a range of temperatures and concentrations. For all three salts, LiI, NaI and KI, the variation of the Soret coefficient with concentration exhibits a minimum for all four temperatures that we investigated. On the basis of various theoretical expressions combined with the best thermodynamic enthalpies and activity coefficients available, we were not able to describe this minimum. On the contrary, in most cases we predicted a maximum in Soret coefficient with concentration.All experimental data share the same characteristics. First, Soret coefficients at low concentrations decay linearly with concentration, and second, in all cases a minimum occurs at one and the same concentration of one mole of salt per kilogram of solvent. From this we infer that the relevant objects in all systems are to a large extent equally big and behave like ideally dissolved particles at low concentrations. From the concentration where the minimum occurs we obtain an estimate for the size of these objects, which coincides with that of a salt molecule including the full hydration shell of strongly attached and perturbed water molecules. Beyond the concentration where the Soret coefficient is minimal, the hydrated objects begin to overlap which leads to stronger interactions between salt molecules, much like depletion interactions do in colloid–polymer solutions. Preliminary, somewhat sketchy calculations indicate that indeed the Soret coefficient increases when concentrations increase beyond one mole of salt per kilogram of water. The model only holds at concentrations not very much larger than close packing of the big hydrated objects. At even larger concentrations the pair wise approximation on which the model is built may not be accurate enough. Moreover at large concentrations it may be energetically profitable for the system to expel the water between the salt molecules and form salt clusters.
Conflicts of interest
There are no conflicts to declare.Appendix
In this appendix we describe how we map our model on the binary Lennard-Jones model of Artola and Rousseau in order to be able to make use of their numerical data on ST for these systems. We summarize the data of these authors as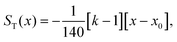 | (7a) |
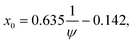 | (7b) |
 and ψ = εBB/εAA. The values of x0 are obtained from the simulations and have been fitted by us as in eqn (7b).
and ψ = εBB/εAA. The values of x0 are obtained from the simulations and have been fitted by us as in eqn (7b).
As noticed in the main text, the radius of the bare salt molecule plus the attached water layer is about half the radius of the fully hydrated salt molecule. Moreover, our concentrations will never be large enough that the attached water layers become perturbed as well. Given these two facts, we consider one salt molecule together with Z attached water molecules to be one LJs particle of diameter σ equal to RHS. A LJw particle then consists of Z + α water molecules, such that it has the same diameter and preferably the same mass as the salt particles. With this we calculate the Lennard-Jones mole-fractions for salt according to
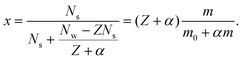 | (8) |
We now must decide about the values of k and ψ. These are determined by the three epsilon values εAA = εeffss, εBB = εww and εAB = εsw, of which εww and εsw remain constant throughout this appendix. Moreover only values of εeffss/εww are needed explicitly. First, we determine ε0ss/εww = 1/ψ0 by putting the overlap potential to zero for molalities less than mmin. By fitting the experimental data in this range with eqn (7) we get k0 and ψ0 for the zeroth order potentials. For molalities larger than mmin we assume that the total salt–salt potential, ϕtotalss(rij) may be approximated by the effective Lennard-Jones potential
 | (9) |
 | (10) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) 0ss = ϕ0ss/ε0 = ϕLJ/ε, etc. Since both the numerator and the denominator in the last term are negative, the effective epsilon is larger than the pure epsilon, so binding becomes stronger. In order to complete the calculation of k and ψ as function of concentration we must relate rNN to the concentration. To this end we approximate
0ss = ϕ0ss/ε0 = ϕLJ/ε, etc. Since both the numerator and the denominator in the last term are negative, the effective epsilon is larger than the pure epsilon, so binding becomes stronger. In order to complete the calculation of k and ψ as function of concentration we must relate rNN to the concentration. To this end we approximate | (11) |
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) =
= ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) min we get rNN = 2, and for very large concentrations rNN = 1.
min we get rNN = 2, and for very large concentrations rNN = 1.
We now have available all information to calculate k and ψ as functions of concentration:
 | (12a) |
 | (12b) |
Acknowledgements
We thank Fernando Bresme, Julia Burkhardt, Niels Hansen, Jutta Luettmer-Strathmann, Daniel Markthaler, Gunwoo Park, Annette Schmidt and Nils Zimmermann for fruitful and helpful discussions. We are grateful to Jan Dhont and Peter Lang for inspiring ideas and his generous support of our work. SM acknowledges the support of the International Helmholtz Research School of Biophysics and Soft Matter (BioSoft).References
- M. Jerabek-Willemsen, T. Andre, R. Wanner, H. M. Roth, S. Duhr, P. Baaske and D. Breitsprecher, J. Mol. Struct., 2014, 1077, 101–113 CrossRef CAS.
- D. Niether, M. Sarter, B. W. Koenig, J. Fitter, A. M. Stadler and S. Wiegand, Polymers, 2020, 12, 376 CrossRef CAS PubMed.
- B. T. Huang, M. Roger, M. Bonetti, T. J. Salez, C. Wiertel-Gasquet, E. Dubois, R. Cabreira Gomes, G. Demouchy, G. Mériguet, V. Peyre, M. Kouyaté, C. L. Filomeno, J. Depeyrot, F. A. Tourinho, R. Perzynski and S. Nakamae, J. Chem. Phys., 2015, 143, 054902 CrossRef CAS PubMed.
- M. Jokinen, J. A. Manzanares, K. Kontturi and L. Murtomäki, J. Membr. Sci., 2016, 499, 234–244 CAS.
- N. Jaziri, A. Boughamoura, J. Mueller, B. Mezghani, F. Tounsi and M. Ismail, Energy Rep., 2020, 6, 264–287 Search PubMed.
- F. Hofmeister, Arch. Exp. Pathol. Pharmakol., 1888, 24, 247–260 CrossRef.
- Y. Zhang and P. S. Cremer, Curr. Opin. Chem. Biol., 2006, 10, 658–663 CAS.
- W. Kunz, Specific ion effects, World Scientific, Singapore and Hackensack NJ, 2010 Search PubMed.
- Thermal nonequilibrium phenomena in fluid mixtures, ed. W. Köhler and S. Wiegand, Springer, Berlin, 1st edn, 2002, vol. LNP584 Search PubMed.
- D. Niether and S. Wiegand, J. Phys.: Condens. Matter, 2019, 31, 503003 CrossRef CAS PubMed.
- C. C. Tanner, Trans. Faraday Soc., 1927, 23, 75–95 RSC.
- J. Chanu, J. Chim. Phys. Phys.-Chim. Biol., 1958, 55, 743–753 Search PubMed.
- J. Chanu, in Advances in Chemical Physics, ed. I. Prigogine, John Wiley & Sons, Inc, Hoboken, NJ, USA, 1967, pp. 349–367 Search PubMed.
- F. S. Gaeta, G. Perna, G. Scala and F. Bellucci, J. Phys. Chem., 1982, 86, 2967–2974 CrossRef CAS.
- J. Colombani, J. Bert and J. Dupuy-Philon, J. Chem. Phys., 1999, 110, 8622–8627 CrossRef CAS.
- S. Di Lecce, T. Albrecht and F. Bresme, Phys. Chem. Chem. Phys., 2017, 19, 9575–9583 RSC.
- I. Prigogine, L. Debrouckere and R. Amand, Physica, 1950, 16, 851–860 CrossRef CAS.
- P. Polyakov and S. Wiegand, J. Chem. Phys., 2008, 128, 034505 CrossRef PubMed.
- Z. Wang, H. Kriegs and S. Wiegand, J. Phys. Chem. B, 2012, 116, 7463–7469 CrossRef CAS PubMed.
- S. R. de Groot, Thermodynamics of irreversible processes, North Holland, Amsterdam, 1966 Search PubMed.
- R. Haase, Thermodynamik der Irreversiblen Prozesse, Steinkopff, Heidelberg, 1963, vol. 8 Search PubMed.
- S. Kjelstrup, D. Bedeaux, E. Johannessen and J. Gross, Non-equilibrium thermodynamics for engineers, World Scientific, Hackensack, NJ, 2nd edn, 2017 Search PubMed.
- K. Shukla and A. Firoozabadi, Ind. Eng. Chem. Res., 1998, 37, 3331–3342 CrossRef CAS.
- L. J. T. M. Kempers, J. Chem. Phys., 2001, 115, 6330–6341 CAS.
- M. G. Gonzalez-Bagnoli, A. A. Shapiro and E. H. Stenby, Philos. Mag., 2003, 83, 2171–2183 CrossRef CAS.
- M. Hartung and W. Köhler, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 117–121 CrossRef CAS PubMed.
- A. Königer, B. Meier and W. Köhler, Philos. Mag., 2009, 89, 907–923 CrossRef.
- P. Blanco, H. Kriegs, B. Arlt and S. Wiegand, J. Phys. Chem. B, 2010, 114, 10740–10747 CrossRef CAS PubMed.
- D. Niether, H. Kriegs, J. K. G. Dhont and S. Wiegand, J. Chem. Phys., 2018, 149, 044506 CrossRef PubMed.
- D. Vigolo, S. Buzzaccaro and R. Piazza, Langmuir, 2010, 26, 7792–7801 CrossRef CAS PubMed.
- D. Lide, T. J. Bruno and J. R. Rumble, CRC handbook of chemistry and physics: A ready-reference book of chemical and physical data, 100th edn, 2019 Search PubMed.
- R. Heyrovská, Chem. Phys. Lett., 1989, 163, 207–211 CrossRef.
- J. A. Myers, S. I. Sandler and R. H. Wood, Ind. Eng. Chem. Res., 2002, 41, 3282–3297 CAS.
- S. Iacopini, R. Rusconi and R. Piazza, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 19, 59–67 CrossRef CAS PubMed.
- Y. Kishikawa, S. Wiegand and R. Kita, Biomacromolecules, 2010, 11, 740–747 CrossRef CAS PubMed.
- D. Niether, D. Afanasenkau, J. K. G. Dhont and S. Wiegand, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4272–4277 CAS.
- A. L. Sehnem, D. Niether, S. Wiegand and A. M. F. Neto, J. Phys. Chem. B, 2018, 122, 4093–4100 CrossRef CAS PubMed.
- S. Mohanakumar, J. Luettmer-Strathmann and S. Wiegand, J. Chem. Phys., 2021, 154, 084506 CrossRef CAS PubMed.
- P. A. Artola and B. Rousseau, Phys. Rev. Lett., 2007, 98, 125901 CrossRef PubMed.
- O. R. Gittus and F. Bresme, On the microscopic origin of Soret coefficient minima in liquid mixtures, https://arxiv.org/pdf/2207.12864.
- H. S. Frank and W.-Y. Wen, Discuss. Faraday Soc., 1957, 24, 133 RSC.
- M. Carrillo-Tripp, H. Saint-Martin and I. Ortega-Blake, J. Chem. Phys., 2003, 118, 7062–7073 CrossRef CAS.
- A. K. Soper and K. Weckström, Biophys. Chem., 2006, 124, 180–191 CrossRef CAS PubMed.
- R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, J. Phys. Chem. B, 2007, 111, 13570–13577 CrossRef CAS PubMed.
- J. Gujt, M. Bešter-Rogač and B. Hribar-Lee, J. Mol. Liq., 2014, 190, 34–41 CrossRef CAS PubMed.
- P. Gallo, D. Corradini and M. Rovere, J. Mol. Liq., 2014, 189, 52–56 CrossRef CAS.
- K. Hermansson, P. D. Mitev and W. J. Briels, J. Phys. Chem. B, 2021, 125, 13886–13895 CrossRef PubMed.
- G. D. Scott and D. M. Kilgour, J. Phys. D: Appl. Phys., 1969, 2, 863–866 CrossRef.
- D. E. Goldsack and R. Franchetto, Can. J. Chem., 1977, 55, 1062–1072 CrossRef CAS.
- D. R. Caldwell, J. Phys. Chem., 1975, 79, 1882–1884 CrossRef CAS.
- P. N. Snowdon and J. C. R. Turner, Trans. Faraday Soc., 1960, 56, 1409–1418 RSC.
- R. Heyrovska, Croat. Chem. Acta, 1997, 70, 39–54 CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2009, 113, 13279–13290 CrossRef CAS PubMed.
- A. K. Borkowski, Z. A. Piskulich and W. H. Thompson, J. Phys. Chem. B, 2021, 125, 350–359 CrossRef CAS PubMed.
- K. R. Hadley and C. McCabe, Mol. Simul., 2012, 38, 671–681 CrossRef CAS PubMed.
- S. Mohanakumar and S. Wiegand, Eur. Phys. J. E: Soft Matter Biol. Phys., 2022, 45, 10 CrossRef CAS PubMed.
- A. L. Sehnem, A. M. F. Neto, R. Aquino, A. F. C. Campos, F. A. Tourinho and J. Depeyrot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 042311 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04089a |
| This journal is © the Owner Societies 2022 |