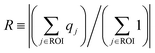Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Collision-induced torque mediates the transition of chiral dynamic patterns formed by active particles†
Tetsuya
Hiraiwa‡
 *ab,
Ryo
Akiyama‡
*ab,
Ryo
Akiyama‡
 c,
Daisuke
Inoue
c,
Daisuke
Inoue
 d,
Arif Md. Rashedul
Kabir
d,
Arif Md. Rashedul
Kabir
 e and
Akira
Kakugo
e and
Akira
Kakugo
 e
e
aMechanobiology Institute, National University of Singapore, Singapore 117411, Singapore. E-mail: mbithi@nus.edu.sg
bUniversal Biology Institute, The University of Tokyo, Hongo, Tokyo 113-0033, Japan
cDepartment of Chemistry, Kyushu University, Fukuoka 819-0395, Japan
dFaculty of Design, Kyushu University, Fukuoka 815-8540, Japan
eFaculty of Science, Hokkaido University, Sapporo 060-0810, Japan
First published on 26th October 2022
Abstract
Controlling the patterns formed by self-propelled particles through dynamic self-organization is a challenging task. Although varieties of patterns associated with chiral self-propelled particles have been reported, essential factors that determine the morphology of the patterns have remained unclear. Here, we explore theoretically how torque formed upon collision of the particles affects the dynamic self-organization of the particles and determine the patterns. Based on a particle-based model with collision-induced torque and torque associated with self-propulsion, we find that introducing collision-induced torque turns the homogeneous bi-directionally aligned particles into rotating mono-polar flocks, which helps resolve a discrepancy in the earlier observations in microfilament gliding assays.
Controlling the patterns that emerge through the dynamic self-organization of motile objects, as observed in the collective motion of living organisms,1–3 has been a long-standing great challenge. Recently, the dynamic patterns observed in nature have been mimicked in artificial systems by using the cytoskeletal filament microtubules (MTs) and F-actins. Upon propulsion by their associated biomolecular motors, the cytoskeletal filaments exhibited collective motion mediated by attractive interactions4–9 or crowded conditions.10–12 Local alignment interactions, i.e., collision-induced alignment of two self-propelled filaments, play important roles in the emergence of their collective motion.10–12 The resulting patterns of circular mesoscopic structures, streams, and vortices exhibited local or global rotational motion in the clockwise (CW) or counterclockwise (CCW) direction6–9,12,13 that resembled the coherent motion exhibited by living organisms in nature.
In nature, a rotational force or torque of cytoskeletal filaments is known to play an important role in chiral morphogenesis of cells, tissues, and organisms.14–16 Similarly, in artificial systems made of cytoskeletal proteins, chiral collective behaviors have often been observed.6,7,9,12,13,17 Such observations and demonstrations motivated to explore the collective dynamics of chiral self-propelled objects theoretically by employing analytical and numerical approaches. Among these efforts, the most popular strategy was the introduction of chirality, i.e., the left–right asymmetry, in the motion of the objects translocating in two dimensions.18–24 Chirality was also introduced in relation to the mutual interactions of the objects.25 A more straightforward strategy has been to use objects with a finite size and shape explicitly, instead of using point-objects, and put chirality or LR asymmetry in the object shape.26–28 Indeed, this approach has been useful in studying artificial systems in which the objects are of well-defined shape in mechanistic sense; e.g., gliding assay of cytoskeletal filaments.28 Such self-propelled objects with a chiral shape can exhibit varieties of dynamic self-organization.
In view of these two approaches to introduce chirality, the shape chirality can influence both the spontaneous motility and interaction of the objects. However, which chirality plays a crucial role in facilitating the emergence of dynamic self-organization patterns has not been figured out yet. For example, a recent study demonstrates well-defined chiral mono-polar flocking of MTs, or dense MT cluster in which motility directions of MTs are aligned unidirectionally, in a gliding assay on kinesins29, but it remains unclear how the chirality of MTs contributed to such mono-polar flocking. Indeed, the difference between chirality in spontaneous motility and that in interaction of the objects can be a clue to resolve this issue as follows. Experimental observations in ref. 29 suggested mono-polar flocking is attributed to chirality in interaction. In contrast, ref. 13 and 17 report a homogeneous bi-directional orientation of MTs with chiral rotational motion, instead of flocking, in a gliding assay on kinesins, and such rotating bidirectional orientation can be explained by chirality in spontaneous motion.13 Like this, to obtain a comprehensive understanding of the factors that determine such differences in dynamic self-organization patterns with chirality, it appears inevitable to dissect the effect of chirality on the motility and interactions of self-propelled objects.
Here, we have demonstrated a systematic in silico study on the collective motion of self-propelled particles (SPPs) each of which has an intrinsic chirality of both types as mentioned above, namely, chirality in self-propulsion and interaction. We consider SPPs with intrinsic polarity where the SPPs move on a two-dimensional substrate. The SPPs interact with each other through isotropic core repulsion and bi-directional alignment. We chose such a bi-directional alignment to avoid the emergence of a mono-polar phase purely by the alignment interaction, which is the case for MTs in a gliding assay. Two types of torque, self-propelled torque (ST) and collision-induced torque (CT) (see Fig. 1 and below for more details), are applied to the particles as left–right (LR) asymmetric motility due to two-dimensionality. We have investigated the emergence of patterns by tuning the strength of ST and CT without manipulating their alignment interactions. We found that when the CT is introduced, transition from the bidirectional orientation to mono-polar flocking takes place although the alignment interaction is bi-directional. The emergence of mono-polar flocking mediated by chirality was reported in ref. 28, where the authors investigated a mixture of two types of filaments having opposite chirality. In contrast, the results presented in this article predict another mechanism to account for the chirality-induced mono-polar flocking, according to which such a combination of two types of filaments is unnecessary.
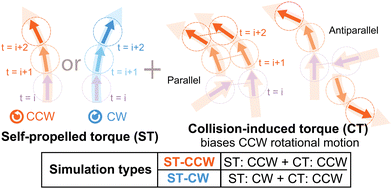 | ||
| Fig. 1 Schematic diagrams showing the application of self-propelled and collision-induced torque to SPPs. | ||
Before moving on, we recall the robust features experimentally observed in the collective motion of chiral MTs driven by kinesins, presented in ref. 29. Chirality in the MT structure was introduced by polymerizing tubulins with a certain nucleotide, GMPCPP. The GMPCPP-MTs are found to align upon collision and eventually form mono-polar flocks. Notably, these flocks rotate dominantly in the CCW direction.29 In addition, when the MT-density is increased, the mean curvature in a trajectory is also increased. These observations imply a correlation between the collision-induced torque and mono-polar flocking, which has motivated us to build up the simulation setting in this study.
We consider N SPPs, which are located at xj = (xj,yj) (j = 1,2,…,N) and have intrinsic polarity qj = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj, sin
θj, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj),30 in a regular rectangle space with periodic boundaries in two dimensions.13,31–33 We assume that locations and polarity directions of SPPs (j = 1,2,…,N) obey
θj),30 in a regular rectangle space with periodic boundaries in two dimensions.13,31–33 We assume that locations and polarity directions of SPPs (j = 1,2,…,N) obey
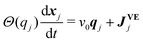 | (1) |
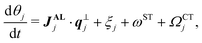 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj,cos
θj,cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θj). Eqn (1) assumes the over-damped dynamics, and each object moves along the polarity qj with a constant velocity v030 in the absence of volume exclusion interactions. The volume exclusion, by which two SPPs mechanically interact with each other, is implemented by
θj). Eqn (1) assumes the over-damped dynamics, and each object moves along the polarity qj with a constant velocity v030 in the absence of volume exclusion interactions. The volume exclusion, by which two SPPs mechanically interact with each other, is implemented by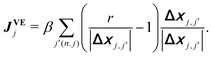 | (3) |
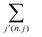 runs for all the neighbors j′ of jth SPP, defined by |Δxj,j′| < r with Δxj,j′ = xj − xj′. Eqn (1) also assumes that each SPP hardly moves along the direction perpendicular to the polarity direction, using the rescaled anisotropic friction tensor Θ(qj) = qj ⊗ qj + Rζ−1(I − qj ⊗ qj) with the ratio Rζ = ζ‖/ζ⊥ of friction coefficients in parallel ζ‖ and perpendicular directions ζ⊥13 (⊗ is the tensor product and I is the identity matrix). This anisotropy in friction has been implemented to phenomenologically reflect the observation that, when a gliding MT collides with another MT from its side, the colliding MT either stops to move or gets over the other, and the collided MT does not move in the direction perpendicular to its polarity.13 This anisotropy is not essential for the phenomenology focused in this paper, as shown below. Eqn (2) assumes that polarity is spontaneously established for each SPP with a fixed amplitude, |qi| = 1, and only its direction can evolve over time.30 The first term indicates the bidirectional alignment interaction,13
runs for all the neighbors j′ of jth SPP, defined by |Δxj,j′| < r with Δxj,j′ = xj − xj′. Eqn (1) also assumes that each SPP hardly moves along the direction perpendicular to the polarity direction, using the rescaled anisotropic friction tensor Θ(qj) = qj ⊗ qj + Rζ−1(I − qj ⊗ qj) with the ratio Rζ = ζ‖/ζ⊥ of friction coefficients in parallel ζ‖ and perpendicular directions ζ⊥13 (⊗ is the tensor product and I is the identity matrix). This anisotropy in friction has been implemented to phenomenologically reflect the observation that, when a gliding MT collides with another MT from its side, the colliding MT either stops to move or gets over the other, and the collided MT does not move in the direction perpendicular to its polarity.13 This anisotropy is not essential for the phenomenology focused in this paper, as shown below. Eqn (2) assumes that polarity is spontaneously established for each SPP with a fixed amplitude, |qi| = 1, and only its direction can evolve over time.30 The first term indicates the bidirectional alignment interaction,13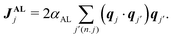 | (4) |
In this study, we also apply two different types of torque, self-propelled torque (ST) and collision-induced torque (CT), to the particles, which are represented by the last two terms in eqn (2) (Fig. 1). Note that, since SPPs are gliding on the substrate, the special directionality exists in the z-axis and here we are focusing on only the other two dimensions; reflecting this fact, we assumed torque as a representation of LR asymmetric motility. In ST, we assume that intrinsic polarity qj of each SPP rotates with a given speed ωST in either the CCW or the CW direction. ωST denotes the strength of ST [Fig. 1, left], which we assume is a given constant. It is to be noted that ST has been observed in the gliding assay of MTs.6 We further assume that, when SPPs collide, another torque is exerted on their intrinsic polarities, which we name CT. ΩCTj denotes CT [Fig. 1, right], given by ΩCTj = ωCTmj with the number mj of SPPs within the range r from the focused SPP and a constant ωCT representing the strength of CT. Indeed, in the gliding assay of MTs on a kinesin coated surface in ref. 29, an increase in the mean curvature of the trajectory was observed upon increasing the MT-density, which suggests that our assumption for CT is not artificial. In the absence of these LR asymmetries, this model is essentially the same as that given in ref. 13.
We numerically calculate eqn (1)–(4), after non-dimensionalization with characteristic length X ≡ r and time T ≡ r/v0. (For these purposes, we can simply put r = 1 and v0 = 1.) We apply Heun's method with a discretized time step dt = 0.004 up to variable total steps M. The value of M or the corresponding time t is mentioned in each figure legend. The parameters are set as follows: Rζ = 0.01, D = 0.01 (or Péclet number = 100), αAL= 1.0 and β = 0.1 unless otherwise mentioned. The number of objects and the global object density are set to be N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and ρ = 0.2, respectively, unless otherwise mentioned. The system size is
000 and ρ = 0.2, respectively, unless otherwise mentioned. The system size is 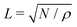 both for x and y.
both for x and y.
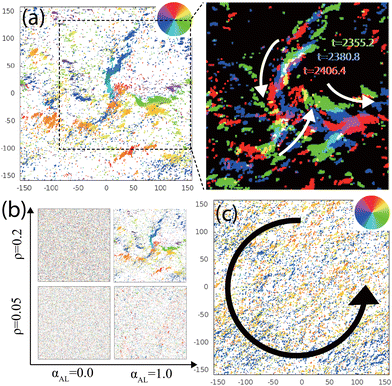
First, we examine the possible patterns which may emerge based on our theoretical model system. Typical snapshots are shown in Fig. 2. For a two-dimensional hard-disk system, the formation of an ordered phase requires a packing fraction higher than 0.7 (ρ = 0.89).36 Despite a low global particle density, ρ of 0.2, mono-polar flocks are observed in silico, as shown in Fig. 2(a). The flocking is caused by the CCW-CT (ωCT = 0.001, ωST = 0.000). The largest flock is found to be composed of several thousands of particles. Magnified time overlay images reveal the rotational motion of the flocks in the CCW direction [Fig. 2(a), right]. While rotating, the flocks collide with each other, and the particles scatter in all directions, which is followed by the regeneration of the flocks. Note that when the density is low, the giant mono-polar flocks do not emerge [Fig. 2(b)], which is consistent with the experimental results in ref. 29. Simulating the case with only ST (ωCT = 0.000, ωST = 0.002) exhibits a homogeneous bi-directional orientation pattern which always rotates counterclockwise, as shown in Fig. 2(c), consistent with those reported in previous literature.13,17
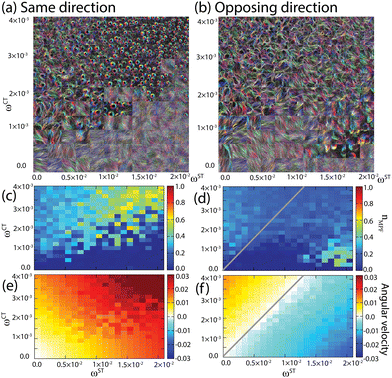
To investigate the physical principle that controls the transition of these two distinct patterns, we first examine how the two types of torque affect the pattern transition. The phase diagram against ST and CT in Fig. 3(a) and (b) shows a correlation between morphology and the torques, and Fig. 3(c), (d) and (e), (f) represent the number fraction of SPPs in mono-polar and the angular velocities, respectively. The structures formed through the collective motion of SPPs are found to be dependent of both types of torque. From the time-overlay images, two distinct morphologies, a mono-polar flocking phase and a bi-polar phase, can be identified. The doughnut-like shapes, formed by the rotating flocks, represent the mono-polar phase. Some structures shown in fuzzy color, in which rotating flocks were not observed, represent a stable bi-polar phase. For instance, rotating flocks are not observed when ωCT = 0. Since the effective attraction between particles is generated by the CT and alignment interaction, these results seem reasonable. The bi-polar phase is observed for relatively high values of ωST and low values of ωCT [Fig. 3(a) and (b)].
When the ST and CT were opposite to each other, we found an island region in the lower right of Fig. 3(b) and (d) for the flocks rotating in the CW direction. The doughnut-like shapes in the island are the same as those in the mono-polar area on the upper left region in Fig. 3(d). However, the SPP number fraction in the polar order region of the island area is larger than that of the upper left region. Thus, the collision probability in the flock increases and the density increases by the collisions as ωST becomes large. Therefore, the increase of the collision frequency caused by the ST leads to another mono-polar flocking phase in combination with the CT in the opposite direction. In contrast, when the CT is in the same direction as the ST, as shown in Fig. 3(c), this island area is not observed. This is consistent with the above statement because the density seems to always decrease with increasing ωST in this case.
As mentioned above, the rotating flocks are observed for high values of ωCT [Fig. 3(a) and (b)]. As ωST increases, the boundary between the mono-polar flocking and homogeneous bi-polar phases moves upwards towards higher ωCT. This means that ST suppresses the formation of rotating flocks, which is also supported by analysis of the SPP number fraction in mono-polar flocks. In the case of the same direction [Fig. 3(c)], the boundary appears for ωST < 2.0 × 10−2. In the case of opposing direction [Fig. 3(d)], the boundary becomes unclear when ωST > 1.0 × 10−2 because of the existence of an exceptional region for the CW-rotating flocks.
The boundary between the two phases appears as a thick band. The map in the band is speckled, which suggests that the mono-polar flocking and homogeneous phases are bi-stable (supported by hysteresis analysis in the ESI†). The speckled band is also found in the map of angular velocity for the case of the same direction [Fig. 3(e)]. Similar to the fraction in mono-polar flocks, the angular velocity is relatively high in the mono-polar flocking phase [Fig. 3(c)]. On the other hand, in Fig. 3(f), the color bands are straight and parallel, which indicates that the angular velocity is governed by the balance between ωCT and ωST. Thus, the angular velocity and the phase behavior are not strongly correlated when the ST and CT are opposite to each other.
In the case of the opposing direction [Fig. 3(f)], ωCT is positive (CCW) whereas ωST is negative (CW). The white grids, shown by the gray line, indicate that rotations are canceled by each other. Furthermore, the slope of the line was roughly 0.3. We also evaluated the mean contact number around each particle in mono-polar flocks 〈mi〉i∈MPF in the numerical calculation, for the parameter window exhibiting the polar order, and it was around 2 to 5. Hence, the above slope agrees with the condition for vanishing torque, ωST + ωCT〈mi〉i∈MPF ∼ 0. It is noted that, since the global particle density, ρ, has been set at 0.2, the contact number and the slope are the consequence of flocking.
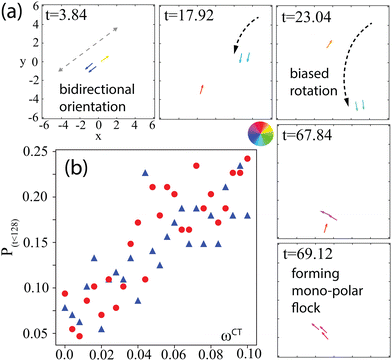
Finally, we discuss the mechanism behind the violation of bidirectional orientation and the formation of mono-polar flocks mediated by only the CT based on the three-SPP simulation (see the ESI† and Fig. S2 for the details). The increase of CT changes a stable state from the bidirectional orientation to the rotating mono-polar flock [Fig. 2(a)]. Flocking is mediated by the alignment interaction and CT. Although both the mono-polar and bidirectional orientation of motion can be stabilized by alignment interaction, simulations for a few SPPs in Fig. 4(a) and appendix reveal that, in the absence of CT, bi-polar orientation is stable and mono-polar flocks are rarely formed. In contrast, CT rotates the direction of movement of the SPPs moving in the same direction as a cluster, which breaks the bi-polar orientation and provides more chances of mono-polar flocking [Fig. 2(b)]. For particles moving in the same direction, alignment interaction worked as an effective attractive interaction and maintained the mono-polar flock once it is formed. Therefore, when alignment interaction is strong enough and the density of SPPs is large enough, this effective alignment among the SPPs moving in the same direction may result in phase separation and allow the emergence of the mono-polar flocks with high local density and large local polar order. In fact, such dependency on the associated parameters is seen in Fig. 2(b). Note that we could not find a significant difference between the cases with and without ST [compare red circles and blue triangles in Fig. 4(b)], which is a stark difference from the results shown in Fig. 3(c) and (d), where we simulated the many-SPP case (N = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and observed the ωST-dependence of the SPP number fraction within mono-polar flocks. This difference implies that the many-body effect is indispensable to recapitulate the ωST-dependence of the threshold ωCT seen in Fig. 3.
000) and observed the ωST-dependence of the SPP number fraction within mono-polar flocks. This difference implies that the many-body effect is indispensable to recapitulate the ωST-dependence of the threshold ωCT seen in Fig. 3.
As expected by this mechanism, the formation of mono-polar flocks by CT does not rely on the anisotropic setting of friction in eqn (1). In Fig. S3 (ESI†), we performed the simulations with the isotropic setting, Rζ = 1.0, and indeed obtained similar snapshots.
Conclusions
In conclusion, through an in silico study, we have clarified how the types of torque of SPPs, i.e. torque due to the collision and torque associated with their self-propulsion, can affect their coherent dynamics. By varying the magnitudes of these two types of torque, we have discovered that there is a transition between different forms of coherent dynamics that are manifested by a homogeneous bidirectional orientation and mono-polar flocking, which have been observed in microtubule-kinesin gliding assays in ref. 13, 17 and 29, respectively. When the self-propelled torque is dominant, SPPs maintain their homogeneous bidirectional orientation, although their direction rotates. We discovered that an increase in collision-induced torque breaks the homogeneous bidirectional order and the stabilized mono-polar flocks. Our results clarify the role of collision-induced torque in the emergence of their coherent dynamics and resolve the discrepancy in the observations mentioned above. The findings in this work point out the importance of the type of torque as a controlling factor in the dynamic self-organization patterns of SPPs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank S. Tanida and M. Sano for valuable discussions in the TH's previous works which help us design this work. We also thank Yuting Lou, Rakesh Das, Alok Ghosh and Ayumi Ozawa for helpful comments on this work. This work was supported by the Mechanobiology Institute, National University of Singapore, (to TH), the JSPS KAKENHI grant number JP16K17777, JP19K03764 (to TH), JP19H01863, JP19K03772, JP18K03555, JP16K05512 (to RA), JP20K15141, JP21H05886 (to DI), JP20H05972, JP21K04846 (to AMRK), and JP18H03673 (to AK), a Grant-in-Aid for Scientific Research on Innovative Areas “Molecular Engine” (JSPS KAKENHI Grant Number JP18H05423) and a Grant-in-Aid for JSPS Research Fellows (JP18F18323) (to AK), “Leading Initiative for Excellent Young Researchers (LEADER)” (JSPS Grant number RAHJ290002) (to DI), a research grant from Hirose Foundation (PK22201017) (to AMRK), and New Energy and Industrial Technology Development Organization (NEDO) (JPNP20006) (to AK).Notes and references
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140 CrossRef.
- I. D. Couzin and N. R. Franks, Proc. R. Soc. London, Ser. B, 2003, 270, 139–146 CAS.
- J. K. Parrish, S. V. Viscido and D. Grünbaum, Biol. Bull., 2002, 202, 296–305 CrossRef PubMed.
- H. Hess, J. Clemmens, C. Brunner, R. Doot, S. Luna, K.-H. Ernst and V. Vogel, Nano Lett., 2005, 5, 629–633 CrossRef CAS PubMed.
- Y. Tamura, R. Kawamura, K. Shikinaka, A. Kakugo, Y. Osada, J. P. Gong and H. Mayama, Soft Matter, 2011, 7, 5654–5659 RSC.
- R. Kawamura, A. Kakugo, K. Shikinaka, Y. Osada and J. P. Gong, Biomacromolecules, 2008, 9, 2277–2282 CrossRef CAS PubMed.
- A. Kakugo, A. M. R. Kabir, N. Hosoda, K. Shikinaka and J. P. Gong, Biomacromolecules, 2011, 12, 3394–3399 CrossRef CAS PubMed.
- S. Wada, A. M. Rashedul Kabir, M. Ito, D. Inoue, K. Sada and A. Kakugo, Soft Matter, 2015, 11, 1151–1157 RSC.
- S. Wada, A. M. R. Kabir, R. Kawamura, M. Ito, D. Inoue, K. Sada and A. Kakugo, Biomacromolecules, 2015, 16, 374–378 CrossRef CAS PubMed.
- V. Schaller, C. Weber, C. Semmrich, E. Frey and A. R. Bausch, Nature, 2010, 467, 73–77 CrossRef CAS PubMed.
- D. Inoue, B. Mahmot, A. M. R. Kabir, T. I. Farhana, K. Tokuraku, K. Sada, A. Konagaya and A. Kakugo, Nanoscale, 2015, 7, 18054–18061 RSC.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448–452 CrossRef CAS PubMed.
- S. Tanida, K. Furuta, K. Nishikawa, T. Hiraiwa, H. Kojima, K. Oiwa and M. Sano, Phys. Rev. E, 2020, 101, 032607 CrossRef CAS PubMed.
- S. R. Naganathan, S. Fürthauer, M. Nishikawa, F. Jülicher and S. W. Grill, eLife, 2014, 3, e04165 CrossRef PubMed.
- Y. H. Tee, T. Shemesh, V. Thiagarajan, R. F. Hariadi, K. L. Anderson, C. Page, N. Volkmann, D. Hanein, S. Sivaramakrishnan and M. M. Kozlov, et al. , Nat. Cell Biol., 2015, 17, 445–457 CrossRef CAS PubMed.
- M. Novak, B. Polak, J. Simunć, Z. Boban, B. Kuzmić, A. W. Thomae, I. M. ToliKuzmić and N. Pavin, Nat. Commun., 2018, 9, 3571 CrossRef PubMed.
- K. Kim, N. Yoshinaga, S. Bhattacharyya, H. Nakazawa, M. Umetsu and W. Teizer, Soft Matter, 2018, 14, 3221–3231 RSC.
- H.-S. Kuan, R. Blackwell, L. E. Hough, M. A. Glaser and M. D. Betterton, Phys. Rev. E, 2015, 92, 060501(R) CrossRef PubMed.
- B. Liebchen and D. Levis, Phys. Rev. Lett., 2017, 119, 058002 CrossRef PubMed.
- C. Chen, S. Liu, X.-q Shi, H. Chaté and Y. Wu, Nature, 2017, 542, 210–214 CrossRef CAS PubMed.
- B.-q Ai, Z.-g Shao and W.-r Zhong, Soft Matter, 2018, 14, 4388–4395 RSC.
- D. Levis and B. Liebchen, J. Phys.: Condens. Matter, 2018, 30, 084001 CrossRef PubMed.
- D. Levis, I. Pagonabarraga and B. Liebchen, Phys. Rev. Res., 2019, 1, 023026 CrossRef CAS.
- J. Zhang, R. Alert, J. Yan, N. S. Wingreen and S. Granick, Nat. Phys., 2021, 17, 961–967 Search PubMed.
- N. Kruk, J. A. Carrillo and H. Koeppl, Phys. Rev. E, 2020, 102, 022604 CrossRef CAS PubMed.
- J. Denk, L. Huber, E. Reithmann and E. Frey, Phys. Rev. Lett., 2016, 116, 178301 CrossRef PubMed.
- Y. Liu, Y. Yang, B. Li and X.-Q. Feng, Soft Matter, 2019, 15, 2999–3007 RSC.
- J. M. Moore, M. A. Glaser and M. D. Betterton, Soft Matter, 2021, 17, 4559–4565 RSC.
- F. Afroze, D. Inoue, T. I. Farhana, T. Hiraiwa, R. Akiyama, A. M. R. Kabir, K. Sada and A. Kakugo, Biochem. Biophys. Res. Commun., 2021, 563, 73–78 CrossRef CAS PubMed.
- T. Hiraiwa, A. Nagamatsu, N. Akuzawa, M. Nishikawa and T. Shibata, Phys. Biol., 2004, 11, 056002 CrossRef PubMed.
- T. Hiraiwa, Phys. Rev. E, 2019, 99, 012614 CrossRef CAS PubMed.
- T. Hiraiwa, Phys. Rev. Lett., 2020, 125, 268104 CrossRef CAS PubMed.
- M. Hayakawa, T. Hiraiwa, Y. Wada, H. Kuwayama and T. Shibata, eLife, 2020, 9, e53609 CrossRef PubMed.
- A. Baskaran and M. C. Marchetti, Phys. Rev. Lett., 2008, 101, 268101 CrossRef PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- E. P. Bernard and W. Krauth, Phys. Rev. Lett., 2011, 107, 155704 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03879j |
| ‡ These authors contributed equally to this work. |
| § The supplementary material includes ref. 13, 18, 34 and 35. |
| This journal is © the Owner Societies 2022 |