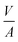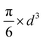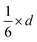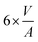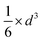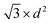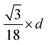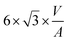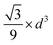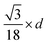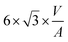Open Access Article
Open Access ArticleBCC-Cu nanoparticles: from a transient to a stable allotrope by tuning size and reaction conditions†
Jan L.
Alfke‡
ab,
Andreas
Müller‡
a,
Adam H.
Clark
 b,
Antonio
Cervellino
b,
Milivoj
Plodinec
a,
Aleix
Comas-Vives
b,
Antonio
Cervellino
b,
Milivoj
Plodinec
a,
Aleix
Comas-Vives
 cd,
Christophe
Copéret
cd,
Christophe
Copéret
 *a and
Olga V.
Safonova
*a and
Olga V.
Safonova
 *b
*b
aDepartment of Chemistry and Applied Biosciences, ETH Zurich, Vladimir Prelog Weg 2, Zurich, Switzerland. E-mail: ccoperet@ethz.ch
bPaul Scherrer Institute, Forschungsstrasse 111, CH-5232 Villigen, Switzerland
cInstitute of Materials Chemistry, TU Wien, 1060 Vienna, Austria
dDepartament de Química, Universitat Autònoma de Barcelona, 08193, Cerdanyola del Vallès, Catalonia, Spain
First published on 22nd September 2022
Abstract
Metallic copper generally adopts an FCC structure. In this work, we detect highly unusual BCC-structured Cu nanoparticles as a transient intermediate during the H2 reduction of a CuI precursor, [Cu4OtBu4], grafted onto the surface of partially dehydroxylated silica. The Cu BCC structure, assigned by in situ Cu K-edge XANES and EXAFS, as well as in situ synchrotron PXRD, converts upon heating into the most commonly found FCC allotrope. DFT calculations show that the BCC-Cu phase is in fact predicted to be more stable for small particles, and that their stability increases at lower H2 concentrations. Using this knowledge, we show that it is possible to synthesize BCC-structured Cu nanoparticles as a stable allotrope by reduction of the same grafted precursor either in 10% H2 diluted in Ar or 100% H2 at low temperature.
1. Introduction
Elements can adopt several different structures in their elemental form, which are usually referred to as allotropes.1 These allotropes can be observed in their most stable form or be kinetically trapped; their most stable form can also change upon exposure to different thermodynamic conditions such as temperature or pressure. Typical cases are Co, which changes from the hexagonal close-packed (HCP) α-Co structure to the face-centred cubic (FCC) β-Co when heated above 450 °C,2 or Fe, which changes from a body-centred cubic (BCC) structure to an HCP structure at pressures above 10 GPa,3 and to an FCC structure when heated.4 Additionally, it is also possible to form a specific allotrope of an element by tuning the synthesis conditions; textbook examples are C,5 Sb6 or P.7 In this case, a metastable allotrope, which is formed due to being favoured kinetically or thermodynamically under synthesis conditions, can become kinetically trapped, allowing access to a wide variety of structures. These different structures can differ vastly, which in turn gives these elements very diverse physicochemical properties. For instance, white phosphorus is highly reactive and widely used as a precursor to synthesize P-containing compounds,8 while the more stable black and red phosphorus are used for a wide range of catalytic and electronic applications.9–11 Some elements, most notably C, also possess some allotropes which only occur in nanostructures.12 This phenomenon has also been observed in some transition metal nanoparticles. Examples include Os13 and Ru,14 which are HCP-structured in bulk states and nanoparticles synthesized from chlorides but can adopt an FCC structure in nanoparticles synthesized from acetylacetonates. The square nanosheets of Au also transform from the common FCC structure to an HCP structure upon electron beam irradiation.15 In the case of Ag, HCP-structured nanoparticles can also be prepared by tuning the synthesis conditions and surfactants.16For Cu, very few cases of allotropy have been reported so far. Metallic Cu almost universally adopts an FCC structure. BCC structured Cu has so far only been observed as thin films synthesized via epitaxial growth of Cu on the surface of the BCC-structured metal Fe.17 A body centred tetragonal (BCT) Cu film has also been grown on the surface of Pd.18 Recently, a mixed HCP and FCC structure in alkynyl protected Cu nanoclusters has also been reported.19 Cu nanoparticles are routinely used as catalysts for a wide range of reactions: COx hydrogenation,20 CO oxidation,21,22 selective hydrogenation, including alkyne semi-hydrogenation,23,24 or click chemistry,25 to name but a few. Cu is also used extensively in electrocatalysis, where it is the only metal to effectively catalyse C–C bond forming reactions.26,27 Because Cu is useful for such a broad range of applications, manipulating its properties and structure is of high interest across different fields.28
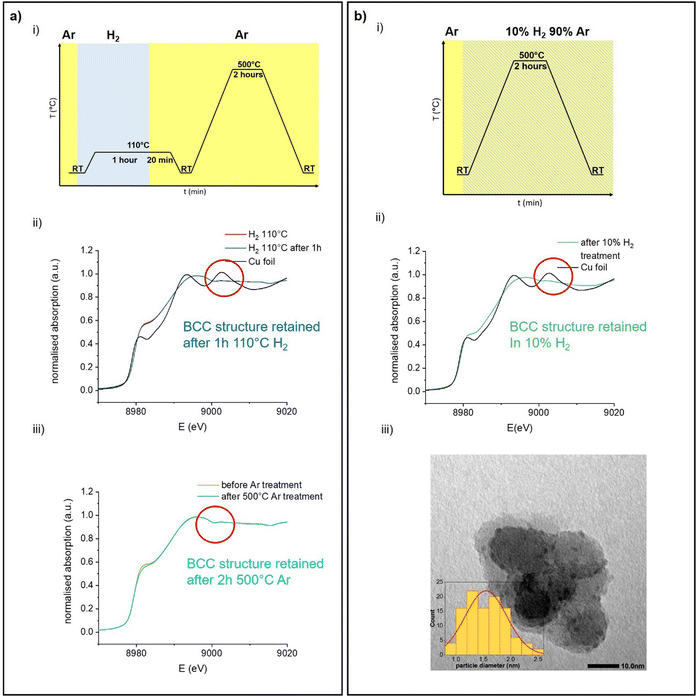
The typical FCC structure of metals results in a very characteristic K-edge X-ray absorption near edge structure (XANES), which is observed in transition metals, such as Cu or Ni,29 as well as in main group metals, such as Al.30 In the case of Cu, the XANES region consists of three distinct features (Fig. 1a):31
 | ||
| Fig. 1 Examples of the structure and the resulting K-edge XANES spectra of (a) FCC-Cu and (b) BCC-Fe. | ||
Aside from the A shoulder at ca. 8981 eV, corresponding to a 1s to 4p transition, the white line is split into a clear doublet (B peak at ca. 8993 eV and C peak at ca. 9003 eV), due to multiple scattering events in the 4th and 5th coordination spheres.31,32 In contrast, BCC-structured metals such as Fe are characterized by a different XANES profile (Fig. 1b). The shoulder A at ca. 7115 eV is less pronounced compared to that for FCC Cu. The main difference however lies in the shape of the white line, which appears as a single peak B at ca. 7131 eV. Feature C, while present at ca. 7141 eV is substantially less intense than in the FCC structure. Additionally, another small shoulder is also visible at ca. 7122 eV, between features A and B. When Fe transitions from the BCC to the FCC structure upon heating, the XANES profile changes accordingly, now exhibiting a doublet at the white line and resembling that of FCC-structured Cu.4
In BCC-structured solid solutions of Cu with metals such as Fe, a typical BCC-related XANES profile is also observed in the Cu K-edge.33 Thus, the K-edge XANES of a metal, complementary to X-ray diffraction (XRD), can be used as a fingerprint of its crystal structure, even under reactive conditions, and in particular for supported nanoparticles, the structure of which cannot be easily identified by XRD due to small size or low concentration.
In this work, we report the originally surprising observation of transient BCC-Cu nanoparticles, generated upon treatment under H2 of a silica-supported CuI surface species prepared via surface organometallic chemistry (SOMC).34 Computational studies show that Cu nanoparticles are in fact stable with a BCC structure when below a certain size threshold. Furthermore, their stability strongly depends on reaction conditions, namely temperature and H2 concentration. Based on this information, we show how one can stabilize the BCC-Cu structure.
2. Results and discussion
2.1 Observation of transient BCC-Cu particles
The silica-supported Cu nanoparticles – CuNP@SiO2 – were prepared in two steps using SOMC: grafting of the tetrameric CuI precursor [Cu4OtBu4] on silica partially dehydroxylated at 500 °C (surface OH density = 0.5 mmol g−1) generated [CuI]@SiO2, which was then treated under H2 at 500 °C to produce CuNP@SiO2.32 Further details about the synthesis are given in the ESI.† The Cu K-edge extended X-ray absorption fine structure (EXAFS) spectrum (Fig. S15, ESI†) of the grafted species, [CuI]@SiO2, reveals a Cu–O coordination number of around 2 (Table 1 and Table S2, ESI†), as well as the absence of a Cu–Cu path, consistent with the presence of a highly dispersed CuI species. This result somewhat contrasts previous findings from grafting of [Cu4OtBu4] on mesoporous silica dehydroxylated at a lower temperature, where a Cu–Cu path was still observed in the EXAFS of the grafted material.35| Temperature [°C] | N (Cu–O) | N (Cu–Cu) | σ 2 [Å]2 | R [Å] | ΔE0 [eV] |
|---|---|---|---|---|---|
| [CuI]@SiO2 | 1.7 ± 0.2 | — | 0.005 ± 0.002 | 1.86 ± 0.01 | 7 ± 2 |
| 110 | — | 5.0 ± 0.8 | 0.014 ± 0.002 | 2.498 ± 0.005 | 2.2 ± 0.4 |
| 160 | — | 5.1 ± 0.7 | 0.014 ± 0.001 | 2.494 ± 0.005 | 2.2 ± 0.4 |
| 210 | — | 5.0 ± 0.7 | 0.016 ± 0.002 | 2.486 ± 0.005 | 2.2 ± 0.4 |
| 270 | — | 2.9 ± 1.3 | 0.011 ± 0.004 | 2.43± 0.04 | 1.5 ± 1.6 |
| 2.2 ± 0.9 | 2.57 ± 0.05 | ||||
| 350 | — | 3.5 ± 1.1 | 0.013 ± 0.003 | 2.45 ± 0.02 | 2.5 ± 1.5 |
| 2.3 ± 0.3 | 2.60 ± 0.03 | ||||
| 400 | — | 4.2 ± 1.8 | 0.015 ± 0.004 | 2.45 ± 0.04 | 2.1 ± 1.6 |
| 2.5 ± 0.8 | 2.61 ± 0.05 | ||||
| 450 | — | 3.5 ± 0.8 | 0.012 ± 0.002 | 2.43 ± 0.02 | 2 ± 1.4 |
| 2.6 ± 0.3 | 2.6 ± 0.02 | ||||
| 500 | — | 3.3 ± 0.8 | 0.013 ± 0.002 | 2.42 ± 0.02 | 1.1 ± 1.5 |
| 2.6 ± 0.3 | 2.58 ± 0.03 | ||||
| CuNP@SiO2 (RT) | — | 8.5 ± 0.5 | 0.0087 ± 0.0005 | 2.526 ± 0.003 | 2.2 ± 0.4 |
The Cu K-edge XANES spectrum (Fig. 2a) also exhibits an edge shift and a pre-edge feature indicative of CuI. After treatment of the material under a flow of H2 at 500 °C for 4 hours (ramp rate 5 °C min−1), Cu nanoparticles with a narrow particle size distribution of 3 ± 0.8 nm are formed, according to transmission electron microscopy (TEM) (Fig. S1 and S2, ESI†). In order to obtain information about the nanoparticle formation, we also monitored the evolution of [CuI]@SiO2 upon H2 treatment, while continuously acquiring in situ Cu K-edge X-ray absorption spectra (XAS) with a time resolution of one second. Afterwards, the sample was allowed to cool down to room temperature to obtain high quality EXAFS data.
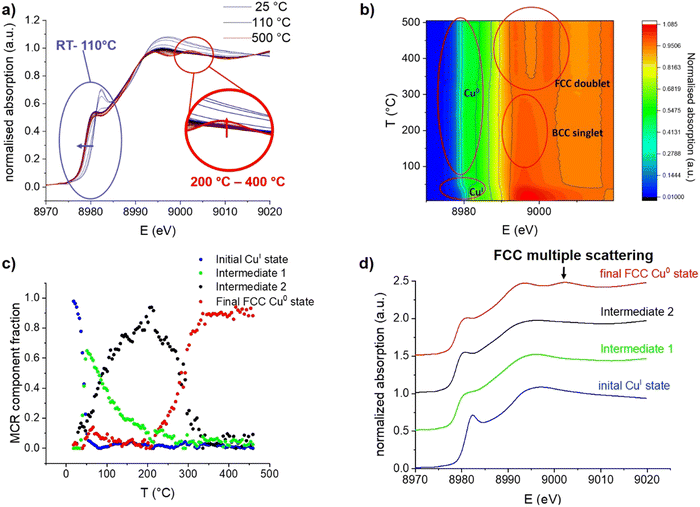
During continuous heating from room temperature to 110 °C, an edge shift towards lower energy is observed in Cu K-edge XANES spectra (Fig. 2a and b), which indicates the expected reduction from CuI to Cu0. However, the absence of the typical FCC multiple scattering feature C at around 9003 eV31 was surprising; indeed, this feature only emerges at a temperature range between 300 and 400 °C. The continuous spectral evolution process is better-highlighted using multivariate curve resolution (MCR) analysis of XANES spectra (Fig. 2c), where four components are needed to fully describe the entire temperature programmed experiment (additional details are shown in the SI). The first component (Fig. 2d) fully matches the initial state, i.e. the grafted CuI precursor [CuI]@SiO2 (100%), as evidenced by the edge position as well as the intense pre-edge feature.
Between room temperature and 110 °C, it is quickly transformed into a first intermediate component (Intermediate 1 – Int1), which is again rapidly converted into a second intermediate state (Intermediate 2– Int2). Reduction in white line intensity and the edge shift towards lower energy identify both of these intermediates as Cu0, whereas the feature C expected at 9003 eV for the FCC structure is completely absent. The two intermediates mainly differ in the edge region, with the earlier formed Int1 having a substantially less intense shoulder A, indicating a lower degree of local order around the absorbing atom.28,32 The last component (final state) begins to emerge at 200 °C, becoming the main one at 300 °C and unique at 400 °C. It exhibits all three spectral features typical for metallic FCC-structured Cu0.31
Regarding the intermediate states, the XANES signatures of these components are highly reminiscent of BCC-structured metals such as Fe3, or BCC-structured CuFe alloys.29 One can thus propose that, upon treatment under H2, the grafted CuI species yields a BCC-structured Cu0 phase, first as small clusters, then as larger nanoparticles, before being converted into the more stable FCC structure, at temperatures above 200 °C. An alternative explanation could be that the initially formed Cu clusters and particles are simply too small to give the typical FCC XANES profile. In fact, it has been predicted that small Cu clusters should not display a typical FCC profile, as it arises from higher-order multiple scattering and therefore requires a 4th and 5th shell of Cu atoms to be present, which is not the case below sizes of about 1 nm.36 This effect has even been observed before, in Cu nanoclusters with a mean diameter of only 1 nm, which were isolated in solid Ar,37 and simulated as well as observed in sub-nanometric Cu clusters on ZrO2 and ZnO supports.32 Oxide-supported FCC-structured Cu64 clusters however already exhibit the C feature as a slight shoulder, supporting that the particles observed in our experiment are BCC-structured. Multiple scattering simulations of Cu nanoclusters predict the C feature to start appearing at cluster sizes of 43 atoms.38 The feature has, however, also been observed in Cu nanoclusters with a size of only 25 atoms39 and an icosahedral Cu0 core, which shows that the shape of nanoclusters can also influence their XANES features. The aforementioned XANES simulations also predict the near-complete absence of feature A in clusters of 13 Cu atoms, highly reminiscent of the observed Int1. It is therefore likely that Int1 corresponds to very small Cu clusters formed upon initial nucleation after CuI is reduced to Cu0. However, given the known influences of particle size and shape, XANES is clearly not sufficient to confidently assign the crystal structure of small Cu nanoparticles, pointing to the need for complementary characterization techniques.
Cu K-edge EXAFS data (Fig. 3) confirms the fully metallic state of the Cu phase formed at 110 °C, consistent with the edge position in XANES.
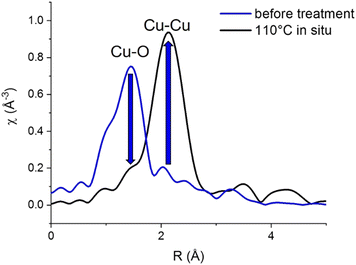 | ||
| Fig. 3 Cu K-edge EXAFS of initial [CuI]@SiO2 at room temperature and the Cu phase formed at 110 °C during in situ H2-TPR. | ||
Before hydrogen treatment, only a Cu–O path is observed, which is fully replaced by a Cu–Cu path at 110 °C, consistent with the disappearance of the initial state [CuI]@SiO2 component in XANES MCR (Fig. 2c).
At 110 °C, Cu-K edge EXAFS fit (Table 1 and Fig. S16–S18, ESI†) also reveals an unusually low Cu–Cu coordination number of 5.0 ± 0.8, compared to 12 for Cu foil and 8.5 ± 0.5 for CuNP@SiO2, the final material after completed reduction treatment, measured at room temperature in H2. This would again be consistent with the formation of a BCC-Cu phase, as in the BCC structure, a full first coordination sphere of Cu consists of only 8 atoms as opposed to 12 atoms for the FCC structure.
Moreover, a substantially shortened Cu–Cu distance of 2.498 ± 0.005 Å fitted for EXAFS data obtained at 110 °C, compared to the usual 2.556 Å for bulk FCC-structured Cu, again supports a structure different from FCC. However, particle size also has a substantial influence on EXAFS coordination number, and is known to influence bond lengths as well. At 270 °C and above, concomitant with the appearance of the FCC C feature in XANES, two Cu–Cu paths are needed to adequately fit the data, which indicates the presence of a mixed phase. The total Cu–Cu coordination number however does slightly increase between 210 °C and 400 °C. Above 400 °C, EXAFS oscillations are strongly dampened due to temperature, resulting in a possible underestimation of the coordination numbers.
It therefore appears from the in situ XAS studies that after initial reduction of Cu, a BCC-structured metallic Cu phase could be formed, which then transforms into an FCC phase at higher temperatures. Yet, the observations made in both XANES and EXAFS could also be related to the formation of very small particles.
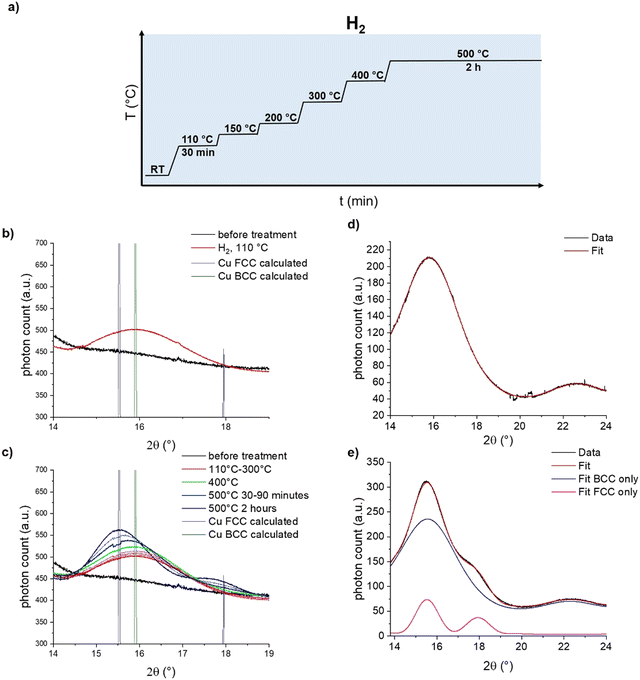
To distinguish between these two hypotheses, we turned towards in situ synchrotron powder X-ray diffraction (PXRD) at the X04SA-MS beamline of SLS40 to ascertain the structure of the Cu intermediate. [CuI]@SiO2 was loaded air free into a capillary reactor, placed under a flow of H2, and synchrotron diffraction patterns were measured with a wavelength of 0.56872(6) Å for 30 minutes at a plateau of 110 °C, 150 °C, 200 °C, 300 °C, and 400 °C, followed by 2 hours at 500 °C (Fig. 4a). At 110 °C, in agreement with the reduction temperature found by XAS, a single diffraction peak stood out against the amorphous background of SiO2, as seen in Fig. 4b.
Comparison of this feature with the calculated diffraction patterns for both BCC- and FCC-Cu identify the formed species as BCC-Cu, as the Bragg angle at 15.9°matches that of BCC-Cu, rather than the one expected for FCC at 15.5°. However, this finding alone is not sufficient to distinguish the FCC from the BCC structure. More crucially, for FCC-structured Cu, a second adjacent diffraction peak at 18° would be expected, which is not present in the data. Simulations of the diffraction pattern of a 2 nm Cu cube with Debussy41 show that this feature should be visible even for nano-objects (Fig. S19, ESI†). Fitting with DEBUSSY confirms that at 110 °C, only BCC-Cu is present in the sample (Fig. 4d) At higher temperatures, the Bragg angle of the diffraction peak shifts towards the lower value expected for FCC-Cu, and the second diffraction peak emerges at 18° (Fig. 4c). This is consistent with the phase change to FCC-Cu, slowly starting at 400 °C and strongly accelerating at 500 °C. Fitting of the data with DEBUSSY shows that upon reaching 500 °C, only 12% of Cu was converted to the FCC structure. The presence of a mixed-phase even at 500 °C is in agreement with the results of the EXAFS analysis.
Estimation of the Cu crystallite size using the Scherrer equation (Fig. S15–S18 and Table S3, ESI†) shows that upon their initial formation at 110 °C, they measure only about 1.3 nm, which is substantially smaller than the 3 ± 0.8 nm which were observed by TEM for CuNP@SiO2 (Fig. S18 and S19, ESI†). Between 110 °C and 400 °C, the crystallite size increases to 1.5 nm, indicative of the expected particle growth (Table S3, ESI†).
2.2 Thermodynamic stability of BCC- vs. FCC-structured Cu nanoparticles from DFT computations
We were interested to find out whether the unusual structure of the BCC-structured Cu particles is due to their small size or other parameters. We thus turned to Density Functional Theory (DFT) to investigate the stability of both FCC- and BCC-structured particles as a function of particle size. Indeed, the energy of a particle is defined as the total sum of the bulk energy and the surface energy and consequently depends on its size. The bulk energy of both structures was calculated by optimizing an infinite crystal and calculating the energetic contribution of one atom to the energy of the crystal. For a mathematical derivation, we refer the reader to the ESI.† The bulk energies of FCC-Cu and BCC-Cu are μfccBulk = −3.726 eV per atom and μbccBulk = −3.692 eV per atom respectively, which shows that a bulk Cu material with an FCC crystal structure is indeed more stable than one with a BCC crystal structure. To investigate the surface energy of the two crystal structures, we constructed slab models of various low-index facets, namely the (100), (110), (111) and (211) facet for FCC-Cu and the (100), (110). (111), (210) and (211) facet for BCC-Cu, and calculated the surface energies as described in one of our recent publications.42 The calculated surface energies are shown in Table 2 (values on FCC-Cu were taken from ref. 42, all calculations were carried out using the exact same method). All calculations of the surface energies are provided in the ESI.† Comparing the different surface energies for the two crystal structures in Table 2 reveals that BCC-structured Cu has, on average, a lower surface energy than FCC-structured Cu. In other words, the formation of surfaces is less disfavoured for BCC-structured Cu than for the FCC-structured Cu. Surprisingly, the (211) facet is highly stable for the BCC structure, and is much more stable than any surface observed for the FCC structure, which is unusual since lower-index facets are, in general, more stable than higher-index facets. The slab models (shown in the ESI†) reveal why this facet is so stable: even though the surface of the BCC-(211) facet is not flat, the steps are rather small and the topmost Cu atoms are not as exposed as in the FCC-(110) facet for instance. In contrast, due to the lower bulk coordination number of Cu in BCC-structured Cu, the Cu atoms in the other surface facets are more exposed than in their FCC counterpart, which leads to this highly unusual stability of a higher-index surface facet.| FCC-Cu42 | BCC-Cu | ||||
|---|---|---|---|---|---|
| Facet | γ [eV Å−2] | γ [J m−2] | Facet | γ [eV Å−2] | γ [J m−2] |
| (100) | 0.0927 | 1.486 | (100) | 0.0890 | 1.426 |
| (110) | 0.0973 | 1.559 | (110) | 0.0793 | 1.272 |
| (111) | 0.0830 | 1.330 | (111) | 0.0924 | 1.480 |
| (211) | 0.0946 | 1.516 | (210) | 0.0848 | 1.358 |
| — | (211) | 0.0614 | 0.984 | ||
Since the surface energy dominates the particle energy for small particles due to the higher surface-to-volume ratio, the small BCC-structured particles are likely thermodynamically more stable than the equivalent FCC particles, and the change in the crystal structure results from particle growth.
This would be consistent with the observation that the phase transition of Cu from the FCC to BCC structure coincided with crystallite growth during the in situ synchrotron PXRD experiments. We thus evaluated at which particle size FCC-structured Cu becomes more stable than BCC-structured Cu.
Since small BCC-structured particles are more stable due to their lower surface energy and large FCC-structured particles are more stable due to their lower bulk energy, we can propose a mean transition size (dTrans), at which the energies of BCC- and FCC-structured particles (Ebcc-Particle and Efcc-Particle) are identical. Since the particle energy is the sum of the bulk and surface energy, and the particle energies are identical, the differences in bulk and surface energies depending on the mean transition size must be equal too (eqn (1)):
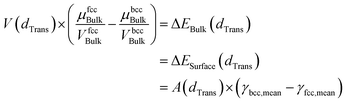 | (1) |
Rearranging eqn (1) leads to the following expression linking the volume-to-surface ratio for the transition size 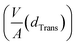 to the bulk energies, bulk atomic volumes and mean surface energies (eqn (2)):
to the bulk energies, bulk atomic volumes and mean surface energies (eqn (2)):
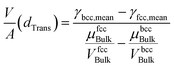 | (2) |
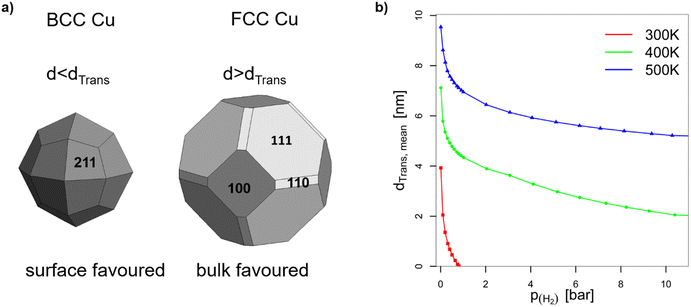 | ||
| Fig. 5 (a) Wulff constructions of BCC- and FCC-structured Cu nanoparticles in vacuum. (b) Transition sizes of Cu particles at different temperatures as a function of H2 partial pressure. | ||
The volume-to-surface ratios of all investigated particle shapes are rather similar and around 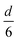 , while the mean transition sizes are around
, while the mean transition sizes are around 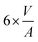 . Thus, while they both depend on the assumed particle shape, this dependency is rather weak: The difference between the two extreme cases (ideal sphere and ideal cube/octahedron) is only a factor of √3. Assuming an octahedral particle shape, we obtain the upper borders for the transition size of dTrans = 9.5 nm, which is surprisingly large and shows that the BCC-structured particles should be stable for up to rather large particle sizes. It is worth noting that this model assumes ideal particle shapes and does not factor in the influence of the support. Another simplification is that the model only considers surfaces and does not factor in the influence of edge energies. Especially for small particles (<3 nm), the influence of edge energies could somewhat alter transition sizes.
. Thus, while they both depend on the assumed particle shape, this dependency is rather weak: The difference between the two extreme cases (ideal sphere and ideal cube/octahedron) is only a factor of √3. Assuming an octahedral particle shape, we obtain the upper borders for the transition size of dTrans = 9.5 nm, which is surprisingly large and shows that the BCC-structured particles should be stable for up to rather large particle sizes. It is worth noting that this model assumes ideal particle shapes and does not factor in the influence of the support. Another simplification is that the model only considers surfaces and does not factor in the influence of edge energies. Especially for small particles (<3 nm), the influence of edge energies could somewhat alter transition sizes.
2.3 Effect of active atmosphere – hydrogen
In the context of work related to CO2 hydrogenation with Cu nanoparticles,42 computational studies have shown that FCC-Cu particles can adsorb hydrogen at rather low hydrogen partial pressures, but only on the threefold adsorption site on the (111) facet. This reduces the surface energy of that facet and stabilizes the FCC-structured particles. Since BCC-structured Cu particles have no such threefold adsorption site, BCC-Cu is unlikely to adsorb hydrogen.Ab initio thermodynamic calculations confirmed that the surface facets of BCC-Cu are not stabilized in the presence of H2 (ESI†). Through this, we can calculate the expected transition sizes as a function of temperature and H2 partial pressure, using eqn (2) (Fig. 5b). A clear dependence on both H2 pressure and temperature is visible, with the transition size decreasing strongly as soon as H2 is introduced. Transition sizes also increase at high temperatures, meaning that this is actually beneficial for the stability of BCC-Cu. The increased stability of BCC-Cu at higher temperatures however might in reality be counteracted by sintering, which takes place at higher temperatures as well.
As a result, our calculations predict that BCC-structured Cu is thermodynamically stable, but only for small particle sizes and at low H2 partial pressure. Conversely, BCC-Cu will transform into FCC-Cu upon sintering and high hydrogen partial pressures. In the absence of hydrogen however, BCC-structured Cu nanoparticles are expected to be stable, even under elevated temperatures, as long as no significant sintering takes place.
2.4 Synthesis of stable silica-supported BCC-Cu nanoparticles
Since DFT calculations predict BCC-Cu to be thermodynamically stable under the right conditions, we reasoned that it would be possible to obtain silica-supported BCC-Cu nanoparticles as a stable material, and thus set out to synthesize this unusual structure. Our calculations highlight two different ways to achieve this: (i) either by avoiding sintering, potentially through maintaining a lower temperature; or (ii) by carrying out the reduction under a lower concentration of H2. Additionally, the BCC-Cu particles, once formed, should be substantially more stable under Ar.We aimed at minimizing sintering by reducing [CuI]@SiO2 under 1 bar of pure H2 at only 110 °C while simultaneously measuring XAS to confirm retention of the BCC structure (Fig. 6a-i). Indeed, we again observed the XANES associated with BCC-Cu, with the edge position at 8979.5 eV, and the typical FCC-related C feature absent (Fig. 6a-ii) under a flow of H2 at 110 °C. The XANES spectrum does not change, even after one hour and after cooling back down to room temperature under Ar, indicating that the BCC structure remains stable. To demonstrate the increased stability under Ar predicted by computations, we now heated the sample at a ramp rate of 5 °C min−1 to 500 °C, where we held it for 2 hours. While this exact temperature program under 1 bar of pure H2 previously led to a phase transition to FCC (Fig. 2) no significant change in XANES was observed under Ar (Fig. 6a-iii).
When carrying out this temperature program under a flow of 10% H2 in Ar (Fig. 6bi), Cu K-edge XANES (Fig. 6b-ii) again reveal retention of the BCC-Cu structure throughout the entire treatment, consistent with our DFT calculations, which predict increased BCC phase stability under lower H2 chemical potential.
TEM images (Fig. 6b-iii) of the sample taken after the reduction under 10% H2, and after exposure to air, which results in oxidation as evidenced by an immediate change of colour from red-brown to black, reveal the presence of Cu nanoparticles with a particle size of 1.5 ± 0.5 nm, which is significantly lower than for the original CuNP@SiO2, which has a particle size of 3.0 ± 0.8 nm. Overall, the stabilization of the BCC nanoparticles can thus result from the use of lower H2 concentration and/or the formation of smaller particles. Nevertheless, both modified synthesis protocols can be used to synthesize stable BCC-Cu nanoparticles in a targeted manner. We also measured high-resolution TEM (HRTEM) of FCC Cu-SiO2 and BCC Cu-SiO2 without exposure to air, in an attempt to further prove the different structures (Fig. S4 and S5, ESI†). However, due to the charging nature of the SiO2 support under the electron beam and the very small particle size, we were not able to obtain enough information to differentiate the BCC from the FCC structure.
We also investigated the reduction of the CuI alkyl complex [Cu5Mes5], grafted on silica via SOMC. [Cu5Mes5] crystallizes as a pentamer, but exists as both a pentamer and a tetramer in solution.45 The grafted material, [CuI-Mes@SiO2], is known to produce smaller Cu nanoparticles (1.9 ± 0.3) nm after reduction at 300 °C.24 Cu K-edge XANES (Fig. S17, ESI†) show that when [CuI-Mes@SiO2] is reduced under H2, the BCC-Cu structure is again formed after initial reduction at 110 °C. The FCC-related C feature in XANES becomes visible at around 500 °C, however due to the small particle size, it has very low intensity. After 2 hours at 500 °C, the feature becomes significantly more pronounced. This result indicates that choosing a precursor that results in smaller particle size is another method to obtain FCC-Cu, as it has been previously demonstrated for Os[13].
3. Conclusions
During the reduction of [CuI]@SiO2 under H2, we observed by in situ Cu K-edge XANES the surprising formation of a BCC-structured metallic Cu transient intermediate. The BCC structure of non-epitaxially grown silica-supported Cu nanoparticles is confirmed by a combination of in situ XANES, EXAFS, and synchrotron PXRD. The Cu particles with a size below 1.5 nm are first formed with a BCC structure and then sinter upon time, undergoing a phase transformation to the commonly found FCC structure. DFT and ab initio thermodynamic calculations show that the existence of the BCC-Cu phase and its transition to the FCC phase are due to the comparatively lower surface energy of BCC-Cu. At very low particle sizes, the surface energy dominates the total energy of the system, while bulk energy becomes more important upon sintering (particle growth), favouring the FCC structure. The BCC structure is therefore thermodynamically preferred for smaller particle sizes, and the FCC structure at larger particle sizes. Furthermore, we show that the presence of higher hydrogen concentrations favours the FCC over the BCC structure, making it challenging to observe and stabilize the latter in hydrogen atmosphere. However, with careful, computationally driven experiments, we found conditions to generate stable BCC-Cu particles supported on SiO2, by either carrying out the reduction in hydrogen at a lower temperature, thus preventing the phase transition by maintaining a small particle size, or by using a lower concentration of H2. This unusual structure of Cu might help to broaden the range of applications for Cu nanoparticles. Furthermore, combining experiment and modelling of realistic nano-objects, as demonstrated in this work, could allow the synthesis of previously unknown allotropes of other metals as well. With this data in hand, we are now further exploring how the support can affect the stability of Cu allotropes.Author contributions
Jan L. Alfke: conceptualization, investigation, formal analysis, visualization, writing – original draft. Andreas Müller: conceptualization (computations), investigation (computations), visualization, writing – original draft. Adam H. Clark: conceptualization, formal analysis, writing – review & editing. Antonio Cervellino: investigation, formal analysis. Milivoj Plodinec: investigation, formal analysis. Aleix Comas-Vives: supervision, funding acquisition, writing – review & editing. Olga V. Safonova: conceptualization, project administration, funding acquisition, supervision, writing – review & editing. Christophe Copéret: conceptualization, project administration, funding acquisition, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Super XAS and MS Beamlines at the Swiss Light Source for technical support during the beamtimes. All DFT calculations were performed using the EULER cluster at ETH Zurich managed by the HPC team. We thank Dr María Tejeda-Serrano and Scott Docherty (ETH Zürich) for discussion and aid with beamtimes. We thank Ilia Sadykov (PSI) for aid with the in situ setups and during beamtime. Additional thanks for aid with shifts during beamtime go to Dr Darryl Nater, Dr Gina Noh, Dr Jordan Meyet, Jasper Clarysse, Dr Nicolas Kaeffer and Prof. Dr Maksym Yarema. J. L. A. and A. M. thank the SNSF project CRSII5_183495 for funding. A. C.-V. thanks the Spanish MEC and the European Social Fund (RyC-2016-19930) and the Spanish “Ministerio de Ciencia, Innovación y Universidades” (PGC2018-100818A-I00).Notes and references
- A. D. McNaught and A. Wilkinson, IUPAC. Compendium of Chemical Terminology, 2nd edn (the “Gold Book”), Blackwell Scientific Publications, Oxford, 1997 Search PubMed.
- T. Nishizawa and K. Ishida, Bull. Alloy Phase Diagrams, 1983, 4(4), 387 CrossRef.
- O. Mathon, F. Baudelet, J. P. Itie, A. Polian, M. dAstuto, J. C. Chervin and S. Pascarelli, Phys. Rev. Lett., 2004, 93, 255503 CrossRef CAS.
- C. Marini, F. Occelli, O. Mathon, R. Torchio, V. Recoules, S. Pascarelli and P. Loubeyre, J. Appl. Phys., 2014, 115, 093513 CrossRef.
- A. Hirsch, Nat. Mater., 2010, 9, 868 CrossRef CAS PubMed.
- A. A. Ashcheulov, O. N. Manyk, T. O. Manyk, S. F. Marenkin and V. R. Bilynskiy-Slotylo, Inorg. Mater., 2013, 49, 766 CrossRef CAS.
- M. E. Schlesinger, Chem. Rev., 2002, 102(11), 4267 CrossRef CAS PubMed.
- H. Diskowski and T. Hofmann, Ullman's Encyclopedia of Industrial Chemicals, 2012 Search PubMed.
- X. Ren, P. Lian, D. Xie, Y. Yang, Y. Mei, X. Huang, Z. Wang and X. Yin, J. Mater. Sci., 2017, 52, 10364 CrossRef CAS.
- Z. Shen, Y. Yuan, L. Pei, Z. Yu and Z. Zou, Chem. Eng. J., 2020, 386, 123997 CrossRef CAS.
- C. Wu, L. Jing, J. Deng, Y. Liu, S. Li, S. Lv, Y. Sun, Q. Zhang and H. Dai, Chemosphere, 2021, 274, 129793 CrossRef CAS PubMed.
- V. Georgakilas, J. A. Perman, J. Tucek and R. Zboril, Chem. Rev., 2015, 115(11), 4744 CrossRef CAS PubMed.
- T. Wakasika, K. Kusada, T. Yamamoto, T. Toriyama, S. Matsumura, G. Ibrahima, O. Seo, J. Kim, S. Hiroi, O. Sakata, S. Kawaguchi, Y. Kubota and H. Kitagawa, Chem. Commun., 2020, 56, 372 RSC.
- K. Kusada, H. Kobayashi, T. Yamamoto, S. Matsumura, N. Sumi, K. Sato, K. Nagaoka, Y. Kubota and H. Kitagawa, J. Am. Chem. Soc., 2013, 135, 5493 CrossRef CAS.
- X. Huang, S. Li, Y. Huang, S. Wu, X. Zhou, S. Li and H. Zhang, et al. , Nat. Commun., 2011, 2(1), 1 Search PubMed.
- M. Gebruers, R. A. Saha, A. V. Kubarev, L. Clinckemalie, Y. Liao, E. Debroye and M. B. Roeffaers, New J. Chem., 2022, 46(27), 13352 RSC.
- Z. Q. Wang, S. H. Lu, Y. S. Li, F. Jona and P. M. Marcus, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 15 Search PubMed.
- H. Li, S. C. Wu, D. Tian, J. Quinn, Y. S. Li, F. Jona and P. M. Marcus, Phys. Rev., 1989, 8, 8 Search PubMed.
- M. Qu, F. Zhang, D. Wang, H. Li, J. Hou and X. Zhang, Angew. Chem., Int. Ed., 2020, 59(16), 6507 CrossRef CAS PubMed.
- X. Jiang, X. Nie, X. Guo, C. Song and J. G. Chen, Chem. Rev., 2020, 120(15), 7984 CrossRef CAS PubMed.
- P. A. DeSario, C. L. Pitman, D. J. Delia, D. M. Driscoll, A. J. Maynes, J. R. Morris, A. M. Pennington, T. H. Brintlinger, D. R. Rolison and J. J. Pietron, Appl. Catal., B, 2019, 252, 205 CrossRef CAS.
- R. V. Goncalves, R. Wojcieszak, H. Wender, C. S. B. Dias, L. L. R. Vono, D. Eberhardt, S. R. Teixeira and L. M. Rossi, ACS Appl. Mater. Interfaces, 2015, 7(15), 7987 CrossRef CAS PubMed.
- N. J. Ossipoff and N. W. Cant, J. Catal., 1994, 148(1), 125 CrossRef CAS.
- A. Fedorov, H. Liu, H. Lo and C. Copéret, J. Am. Chem. Soc., 2016, 138(50), 16502 CrossRef CAS PubMed.
- F. Alonso, Y. Moglie and G. Radivoy, Acc. Chem. Res., 2015, 48(9), 2516 CrossRef CAS PubMed.
- D. Ren, N. T. Wong, A. D. Handoko, Y. Huang and B. S. Yeo, J. Phys. Chem. Lett., 2016, 7, 20 CrossRef CAS PubMed.
- T. N. Huan, G. Rousse, S. Zanna, I. T. Lucas, X. Xu, N. Menguy, V. Mougel and M. Fontecave, Angew. Chem., Int. Ed., 2017, 56, 4792 CrossRef CAS PubMed.
- G. O. Larrazábal, V. Okatenko, I. Chorkendorff, R. Buonsanti and B. Seger, ACS Appl. Mater. Interfaces, 2022, 14(6), 7779–7787 CrossRef PubMed.
- H. H. Hsieh, Y. K. Chang, W. F. Pong, J. Y. Pieh, P. K. Tseng, T. K. Sham, I. Coulthard, S. J. Naftel, J. F. Lee, S. C. Chung and K. L. Tsang, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 15204 CrossRef CAS.
- K. Nakanishi and T. Ohta, J. Phys.: Condens. Matter, 2009, 21(10), 104214 CrossRef CAS PubMed.
- G. N. Greaves, P. J. Durham, G. Diakun and P. Quinn, Nature, 1981, 294(9), 39 Search PubMed.
- J. Timoshenko, A. Halder, B. Yang, S. Seifert, M. J. Pellin, S. Vajda and A. I. Frenkel, J. Phys. Chem. C, 2018, 122(37), 21686 CrossRef CAS.
- P. J. Schilling, J. He, J. Cheng and E. Ma, Appl. Phys. Lett., 1996, 68(6), 767 CrossRef.
- C. Copéret, et al. , Chem. Rev., 2016, 116, 323 CrossRef.
- I. J. Drake, K. L. Fujdala, S. Baxamusa, A. T. Bell and T. D. Tilley, J. Phys. Chem. B, 2004, 108(48), 18421 CrossRef CAS.
- D. Bazin and J. J. Rehr, J. Phys. Chem. B, 2003, 107(45), 12398 CrossRef CAS.
- A. Montano, G. K. Shenoy and E. E. Alp, Phys. Rev. Lett., 1986, 56(19), 2076 CrossRef PubMed.
- H. Oyanagi, Z. H. Sun, Y. Jiang, M. Uehara, H. Nakamura, K. Yamashita, Y. Orimoto, L. Zhang, C. Lee, A. Fukano and H. Maeda, J. Appl. Phys., 2012, 111, 084315 CrossRef.
- T. D. Nguyen, Z. R. Jones, D. F. Leto, G. Wu, S. L. Scott and T. W. Hayton, Chem. Mater., 2016, 28(22), 8385–8390 CrossRef CAS.
- P. R. Willmott, D. Meister, S. J. Leake, M. Lange, A. Bergamaschi, M. Böge, M. Calvi, C. Cancellieri, N. Casati, A. Cervellino, Q. Chen, C. David, U. Flechsig, F. Gozzo, B. Henrich, S. Jäggi-Spielmann, B. Jakob, I. Kalichava, P. Karvinen, J. Krempasky, A. Lüdeke, R. Lüscher, S. Maag, C. Quitmann, M. L. Reinle-Schmitt, T. Schmidt, B. Schmitt, A. Streun, I. Vartiainen, M. Vitins, X. Wang and R. Wullschleger, J. Synchrotron Radiat., 2013, 20, 667 CrossRef CAS PubMed.
- A. Cervellino, R. Frison, F. Bertolotti and A. Guagliardi, J. Appl. Crystallogr., 2015, 48, 2026 CrossRef CAS.
- A. Müller, A. Comas-Vives and C. Copéret, J. Phys. Chem. C, 2021, 125, 1 Search PubMed.
- G. Wulff, Z. Krystallogr. Mineral., 1901, 34(5/6), 449 CAS.
- R. V. Zucker, D. Chatain, U. Dahmen, S. Hagege and W. C. Carter, J. Mater. Sci., 2012, 47, 8290 CrossRef CAS.
- H. Eriksson and M. Hakansson, Organometallics, 1997, 16, 4243 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp03593f |
| ‡ Shared first authorship. |
| This journal is © the Owner Societies 2022 |