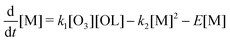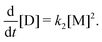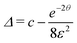Electrodynamic balance–mass spectrometry reveals impact of oxidant concentration on product composition in the ozonolysis of oleic acid

Abstract

The chemical and physical properties of atmospheric aerosol particles change upon oxidative ageing, influencing their interaction with radiation, their propensity to serve as nuclei for cloud condensation and ice formation, and their adverse effects on human health. The investigation of atmospheric aerosol oxidation processes is complicated by low oxidant concentrations and long timescales, which are difficult to represent in laboratory studies. Experimental work often attempts to compensate for short timescales with elevated concentrations of oxidative agents, assuming that the ageing progress depends only on the oxidant exposure, i.e. on the product of oxidant concentration and time, [Ox] × t, and not on [Ox] or t independently. The application of electrodynamic balance–mass spectrometry of single particles allows the validity of this assumption to be investigated, since it provides information on the molecular composition of aerosol particles for a wide range of reaction durations under well-defined oxidation conditions. Here, we demonstrate the capabilities of a new setup on levitated oleic acid droplets reacting with ozone at mixing ratios of 0.2 and 15 ppm, i.e. spanning almost two orders of magnitude in [Ox]. We show that the reactive removal of oleic acid can be accurately expressed as a function of ozone exposure [Ox] × t, whereas the product concentrations depend on [Ox] and t independently. As the underlying reason for the breakdown of the exposure metric, we suggest a competition between evaporation of volatile first-generation products and their accretion reactions with reactive Criegee intermediates, converting them into low-volatility dimers and oligomers. This hypothesis is supported by kinetic model simulations using the aerosol process model KM-SUB, which explicitly resolves the competition between evaporation and secondary chemistry as a function of the experimental timescale and ozone mixing ratio. The model successfully reproduces final product distributions. The findings are further supported by the recorded changes of droplet sizes during oxidation. As a heuristic, the breakdown of the exposure metric in a chemical reaction system is possible, when competition between first- and second-order processes of reactive intermediates determines important system properties.

---

1 Introduction

Oxidative ageing of atmospheric aerosol particles affects the constituents in terms of molecular weight and functional groups, which is reflected in different physicochemical properties such as the oxidation state, refractive index, vapour pressure or solubility. The reaction products may differ substantially from their parent compounds, which affects the relevant properties of these particles in terms of their radiative effects and their impact on human health. Most laboratory studies on aerosol ageing use significantly elevated oxidant concentrations and relatively short exposure times to study chemical reactions within aerosol particles. The assumption in these studies is that oxidant exposure (the product of oxidant concentration and reaction time) can be used as a metric for the particle ageing progress, regardless of the applied oxidant concentration.

There are only a handful of examples in the literature where the application of the exposure metric is thoroughly assessed.^1–5 In some of these studies, the exposure metric fails to represent different oxidant concentrations. For example, in modelling palmitic acid oxidation, the results differed when a short reaction time with high OH radical mixing ratio was assumed instead of a long reaction with low OH mixing ratio, due to surface renewal and secondary chemistry processes.² In a laboratory study on the oxidation of squalane with chlorine, the exposure metric failed due to the occurrence of radical chain reactions.⁴ In another experimental study, the dominating degradation pathway of linoleic acid depended on the ozone concentration, which led to different product distributions for the same exposure.⁵ These examples show that high oxidant concentrations in short experiments may lead to significantly different ratios of reaction product concentrations or even different species compared to natural atmospheric oxidant concentrations, hence biasing data interpretation.

Oleic acid has been intensively studied in the context of atmospheric aerosol ageing. As a mono-unsaturated fatty acid, it has served in numerous studies as a proxy compound for organic aerosol matter susceptible to reacting with atmospheric ozone.^6–12 A chemical mechanism of oleic acid ozonolysis, including the principal secondary reactions, is given in Fig. 1 (from top up to and including the white box). Oleic acid reacts with ozone to form a short-lived primary ozonide (reaction R1), which decays into Criegee intermediates (CI) and aldehydes (R2a and R2b).¹⁷ Because of the asymmetry of the primary ozonide, two different aldehydes (nonanal and 9-oxononanoic acid) and two CI (denoted with the m/z of the deprotonated species, CI-157 and CI-187) are formed. CI can undergo rearrangements to form the corresponding acids (nonanoic acid and azelaic acid, via R3a and R3b).¹⁸ Both the acids and the aldehydes together are referred to here as first-generation products. Instead of undergoing rearrangements, the CI may also react with other functional groups, forming dimers and higher oligomers.^7,9,10,18,19 Reactions with acids (to form α-acyloxyalkyl hydroperoxides, AAHPs, R4) and reactions with aldehydes (to form secondary ozonides, SOZs, R5) are suggested in the literature to form secondary products.

Fig. 1 Simplified reaction scheme of the ozonolysis of oleic acid. The general temporal development goes from top (oleic acid) to bottom (secondary products being thermally decomposed at time of analysis). Note that the aerosol ageing results in primary chemistry (leading to first-generation products) and secondary chemistry (leading to dimers, exemplarily summarised in the white box) whereas the final thermal decomposition is an effect of particle composition analysis. Not shown is the reaction of ozone with the dimer from the reaction of oleic acid with a Criegee intermediate. Stable monomer structures tentatively detected with MS in this study are shown in orange boxes with the m/z corresponding to deprotonated molecules. Commercially available substances are depicted with bold names. Vapour pressure for azelaic acid, nonanal, nonanoic acid and oleic acid are literature values,^13–15 all other vapour pressures are estimated using EVAPORATION.¹⁶ *Only the secondary ozonide with two unfunctionalised alkyl rests is predicted to have a significant vapour pressure (∼0.001 Pa) but is not expected to be a major aerosol constituent since its formation results from the reaction with the very volatile nonanal.

A wide variety of experiments on oleic acid ozonolysis using different experimental setups and reaction conditions were recently compiled by Berkemeier et al.²⁰ Using a numerical model explicitly treating molecular transport and chemical reactions on the surface and in the bulk of the particle, the authors were able to describe the reactive loss of oleic acid over reaction times varying from a few seconds to 20 h with associated ozone concentrations varying between 240 ppb and 100 ppm ozone. However, Berkemeier et al.²⁰ had to rely on data from very different experimental techniques with their own subtleties, most of which are able to explore only a narrow range of oxidant concentration. Moreover, most of these studies focused on the loss of oleic acid itself rather than on products. Some studies grouped secondary products into categories such as peroxides, higher molecular weight compounds or unidentified products.^7,18,21,22 Very few studies aimed to (semi-)quantitatively follow the evolution of secondary chemistry products.^9,10,12

In this study, we use single oleic acid droplets levitated in an electrodynamic balance (EDB) in combination with mass spectrometry (MS) to showcase compositional monitoring of droplets aged under strongly differing oxidant concentrations, and we investigate the validity of the exposure metric for this reaction system.

2 Instrumentation and method

An emerging tool for the detailed study of aerosol processes is the combination of an EDB with MS.^23–31 Trapping droplets in an EDB allows the contactless storage and examination of particles over hours and days under well-defined experimental conditions.³² Transfer of the stored droplets to an MS unit allows to infer the particle composition at the time of ejection. Such a system is therefore well-suited to compare oxidation reactions with very different oxidant mixing ratios.

A schematic overview of our newly built setup is given in Fig. 2. The interested reader is referred to Appendix A, which contains a detailed description of the instrumentation and describes the typical experimental procedure. Very briefly, oleic acid particles are produced from solutions using an inkjet cartridge and charged inductively by a DC ring electrode at the time of injection. In the linear quadrupole type EDB, droplets are contained in an electrodynamic field and exposed to a controlled gas phase (T, p, RH) with known ozone mixing ratio. Size information is obtained by measuring the 2-D angular scattering pattern of laser-illuminated droplets before the experiment and during ageing of the droplets. Because the droplets can be stored in the EDB over extended reaction times of several days, complete oxidation of oleic acid has been achieved with ozone mixing ratios as low as 0.2 ppm. Complementary experiments have been carried out at an ozone mixing ratio of 15 ppm. All experiments were carried out under dry conditions (RH < 15%). For the droplet composition analysis, single droplets are transferred to a heated evaporation unit, and the resulting gas-phase compounds are ionised in a very soft dielectric barrier discharge ion source prior to MS measurements using a triple quadrupole QTRAP instrument. The temperature of the evaporation unit was set at 190 °C because it allows the evaporation of most substances within a reasonable time frame and, hence, produces a signal that is well distinguishable from the background. However, elevated temperatures may lead to thermal decomposition depending on the thermal stability of the analyte.

Fig. 2 Schematic representation of the instrumentation. In the electrodynamic balance (EDB), charged particles are stored and aged under specific reaction conditions (ozone mixing ratio and reaction time). Subsequently, single particles are transferred to the evaporation unit and the resulting gas-phase compounds are transported to the ionisation region and analysed by mass spectrometry (MS). Parts are not drawn to scale.

In contrast to the previous EDB–MS setup described by Birdsall et al.,²³ the efficiency of droplet transfer from the EDB to the evaporation unit was significantly increased by introducing a gas flow through the EDB at the time of droplet transfer. Thus, in the present study MS data have been successfully obtained from every exposed droplet. Additionally, changing from a Corona discharge to dielectric barrier discharge ionisation reduced analyte fragmentation in the ion source substantially.

3 Results and discussion

3.1 Unreacted oleic acid droplets

The spectrum of an unreacted oleic acid droplet is shown in Fig. 3a and a more detailed version including information about the background subtraction is given in Fig. 8d in Appendix A. The most prominent peak is found at m/z 281, corresponding to the deprotonated oleic acid. It is accompanied by the isotope signal from oleic acid with one ¹³C at m/z 282. Further peaks are detected at m/z 85, 87, and 101 but their signal intensities are more than three times lower than the corresponding background signal intensities (see Appendix A). These peaks indicate impurities or fragments formed either during ionisation or evaporation. Apart from these peaks, there is no sign of fragmentation in the ion source, which is consistent with our experience and literature knowledge about the ionisation method.^33–36 In preliminary experiments with other mono- and dicarboxylic acids, the detected fragments could all be assigned to products from thermal decomposition in the evaporation unit (inferred from the temperature dependence of the relative signal intensities).

Fig. 3 Mass spectra from droplets of oleic acid and ozonolysis products before (a) and after different ozone exposures (b and c) aged with 10 ppm ozone.

In the following, we restrict the discussion to the unperturbed spectral range above m/z 110. Additional peaks at m/z 295, 297 and 312 most likely stem from impurities in the injected solution. However, we cannot rule out that they are caused by processes in the ion source. Because the intensity of these peaks decreases with increasing exposure (see Section 3.2), it is rather unlikely that they result from oxidation products of oleic acid. A similar pattern of additional peaks has also been reported in measurements using EESI-MS on the oleic acid ozonolysis system.¹⁰

To evaluate the quantitative capabilities of our setup and the experimental reproducibility, a calibration was carried out using a series of unreacted oleic acid droplets of different sizes. Fig. 10 in Appendix A shows the MS signals along with the estimated amount of substance, revealing a clear linear relationship between droplet volume and signal intensity. In addition, the sensitivity (signal per amount of substance) was estimated for commercially available products from the ozonolysis of oleic acid, nonanoic acid and azelaic acid, by means of mixed droplets of different compositions using the same approach (shown in Fig. 11 in Appendix A).

3.2 Heterogeneous oxidation of oleic acid by ozone

We studied the ozonolysis of oleic acid using droplet measurements at constant ozone mixing ratio and as a function of exposure. For the comparison of differently aged drops (82% with a radius in the range from 24 to 28.3 μm and 18% smaller droplets between 19.0 and 24 μm for comparison), the droplet signal was normalised by volume to a reference radius of 27 μm. Fig. 3 shows the evolution of the mass spectra at characteristic reaction times for experiments with 10 ppm of ozone.

All peaks detected in the spectra of unreacted oleic acid droplets (at m/z 281, 282, 295, 297 and 312), shown in Fig. 3(a) decrease in intensity upon exposure to ozone (b) and disappear at higher exposures (c). Product formation leads to the appearance of new peaks in the mass spectrum at m/z 141, 143, 157, 159, 171, 185, 187 and 203. Although peak intensities cannot be converted directly to amounts of substances, we note that the most intensive peaks of the product spectrum (at m/z 157, 171 and 187) are detected at the expected mass-to-charge ratios of deprotonated first-generation products nonanoic acid, 9-oxononanoic acid and azelaic acid (see Fig. 1). The additional first-generation product nonanal would be expected at m/z 141, where only a minor peak is observed (which is related to the high vapour pressure and evaporative loss of this species, see Section 3.4). The peak at m/z 143 has previously been reported as octanoic acid, a product potentially formed from CI-187 after splitting off CO₂.^21,22 The peak at m/z 203 has been associated with a fragment of a larger molecule, most likely a fragmentation product from an AAHP.^10,37

In our experiments, we did not observe any peaks at the expected m/z of molecular ions of dimers or higher oligomers, which have been reported in the literature.^6,9,10 This absence is presumably caused by the droplet evaporation scheme in our setup, leading to thermal decomposition of dimers and higher oligomers. Such decompositions have been observed at temperatures well below the temperature used in our evaporation unit.^9,18 The absence of any further decomposition product suggests that dimers and higher oligomers decay predominantly into the corresponding monomer fragments and are therefore indirectly detected with the signal at the mass-to-charge ratio of the monomers (see also Fig. 1 and discussion in Section 3.4.1).

3.3 Verification of the exposure metric for oleic acid oxidation

To test the validity of the exposure metric, ozonolysis experiments of oleic acid were performed for several reaction times at two very different ozone mixing ratios. A total of 20 drops were investigated under low ozone conditions with an average ozone mixing ratio of 0.184 ± 0.008 ppm (denoted 0.2 ppm) and 14 drops were investigated under high ozone conditions with an average ozone mixing ratio of 14.66 ± 0.20 ppm (denoted 15 ppm). For comparison, 0.2 ppm ozone is a value frequently exceeded in cities in eastern China,³⁸ and about four times higher than the annual mean tropospheric background value in the northern hemisphere;³⁹ whereas 15 ppm is a value often used or exceeded in laboratory studies but out of range of typical environmental conditions (around 300 times higher than the annual mean tropospheric background concentration in the northern hemisphere).

By combining single droplet data from multiple droplets aged for different reaction times, the temporal evolution of the droplet composition can be constructed. We first discuss the decay of oleic acid and thereafter (Section 3.4) how the various product signals evolve with time. Fig. 4a shows the evolution of the integrated signal at m/z 281 for the two mixing ratios. It is clear that the difference in ozone mixing ratio directly translates into drastically different characteristic reaction times for oleic acid depletion in the droplets. However, when these data are plotted against exposure (n_O3(g) × t) instead of reaction time, they collapse on a single decay curve with a single characteristic exposure, see Fig. 4b. This demonstrates the capability of our EDB–MS setup and proves that the exposure metric holds true for the degradation of oleic acid within a range of ozone mixing ratios of almost two orders of magnitude.

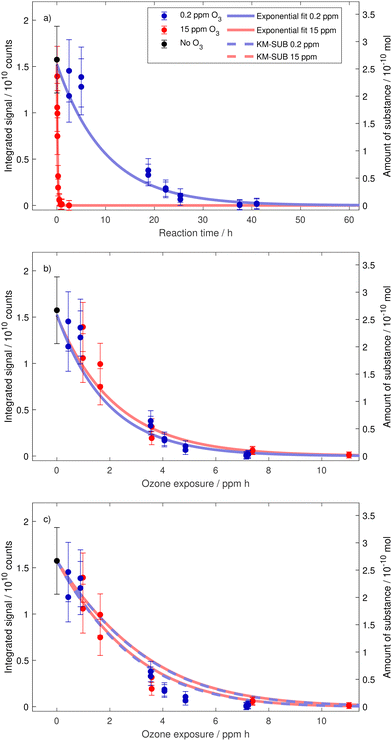Fig. 4 Decay of oleic acid as a function of reaction time (a), ozone exposure (b) and in comparison to model scenario B for MS experiments in Berkemeier et al.²⁰ (c). If the decay is caused by a rate limiting surface reaction, we expect it to depend on the exposure metric ([O₃](g) × t) in a simple exponential manner.⁴⁰ The error bars depict estimated uncertainties due to variability of the MS signal. Exponential fits take into account the uncertainties of individual data points (see Appendix B). In (c), we show the oleic acid decay predicted by KM-SUB model runs (167, each with individual parameter sets). Shown are fastest and slowest model runs.

As mentioned above, there is a broad collection of laboratory data for the specific case of oleic acid ozonolysis. Recently, Berkemeier et al.²⁰ applied the kinetic multilayer model of aerosol surface and bulk chemistry KM-SUB⁴¹ to derive model parameters that represent a best fit to a collection of 12 literature data sets. In contrast to resistor model frameworks (e.g. Worsnop et al.⁴⁰), the explicit treatment of coupled mass transport and chemistry with KM-SUB does not depend on the assumption of limiting cases⁴² and enables to also treat the product chemistry (see below). A direct comparison of our oleic acid measurements with the model output (using the obtained parameter sets from model scenario B for MS experiments in Berkemeier et al.²⁰ and applying our experimental conditions without further fitting) is shown in Fig. 4c. The experimental data agree well with the model (the model predicts a slightly slower decay than suggested by the experiments but the deviation is comparable to the differences between the model and experimental data in the original study²⁰) and, hence, fall in line with the available literature. The overlap of the model output for both mixing ratios shows that the model—without any unproven assumption—describes the decay of oleic acid to depend only on the exposure metric (n_O3(g) × t), not on n_O3(g) and t individually.

3.4 Product formation

Fig. 5 shows the evolution of the decay of oleic acid vis-a-vis the increase of the product signals at m/z corresponding to the first-generation products. The MS data for other product signals (cp. Fig. 3) can be found in Fig. 12 in Appendix C.

Fig. 5 Compilation of measured signal for MS peaks corresponding to first-generation products in dependence on exposure to ozone. For the m/z with commercially available substances, the integrated signal axis is supplemented with an additional axis showing the corresponding amount of substance. Error bars depict estimated uncertainties from MS sensitivity variability and the trend lines are the model results from the modified KM-SUB version.

In the following discussion we focus on two aspects: (i) the trend of product signal intensities with increasing exposure (Section 3.4.1) and (ii) the extension of the existing kinetic model to test the hypothesised processes (secondary chemistry vs. evaporation, Section 3.4.2) for m/z of first-generation products and the corresponding monomeric building blocks of dimers and oligomers.

3.4.1 Signals from second generation products. For all product peaks, we find that the signal intensity first increases and then remains relatively constant. Since the partitioning of semi-volatile species from the condensed phase to the gas phase affects the droplet composition, it is important to consider the evaporation of first generation products when analysing the increase of product signals. An estimate of the evaporation timescale of a given compound can be derived from Maxwell's equation for the evaporation of a droplet.²³ To estimate the relevant timescales, we simulated droplets (r = 27 μm) of binary mixtures of oleic acid and first-generation products at a 9 : 1 molar ratio and derived the time when 50% of the first-generation product had evaporated using the 'pyvap' tool presented by Birdsall et al.²³ The obtained evaporation times are summarised in Table 1.

Table 1 Evaporation timescales for first-generation products in binary droplets with oleic acid (r = 27 μm, 10% first-generation product by moles).²³ Gas-phase diffusivities D_v were calculated according to Bird et al.⁴³ using critical volumes and critical temperatures from UManSysProp.⁴⁴ Note the influence of vapour pressures on the evaporation timescales

Substance	D v (m^2 s^−1)	p (Pa)	t evap (s)
Nonanal	5.6 × 10^−6	4.9 × 10^+1 ^14	2.4 × 10^0
Nonanoic acid	5.3 × 10^−6	2.2 × 10^−1 ^14	1.2 × 10^3
9-Oxononanoic acid	5.1 × 10^−6	1.2 × 10^−2 ^16	2.3 × 10^4
Azelaic acid	4.8 × 10^−6	1.0 × 10^−4 ^13	2.9 × 10^6

---

Even though these calculations do not take into consideration the complex mixing state of the droplets, they reveal the relevant orders of magnitude to consider for the evaporation of the substances with the corresponding vapour pressures. It is therefore unlikely that products with the highest vapour pressure (i.e. nonanal and nonanoic acid) persist during an experiment with a duration of several days, which is in contrast to the observed constant product signal intensities at higher exposures ( ppm h, see Fig. 5). Similar considerations concern the additional product peaks, which are not corresponding to the first-generation products discussed above (shown in Fig. 12 in Appendix C).

The persistent signal at m/z of nonanoic acid, nonanal and 9-oxononanoic acid can only be explained with contributions of dimers and oligomers that thermally decompose in the evaporation unit prior to MS detection and are measured at the m/z of the corresponding monomers. This is in agreement with findings from thermal desorption particle beam MS and thermal desorption of filter-collected oleic acid ozonolysis products.^9,18 The vapour pressures of dimers are predicted to be lower than 10⁻⁵ Pa.† Therefore, dimers are assumed to be non-volatile for our experiment duration.

While at short exposure timescales nonanal, nonanoic acid and 9-oxononanoic acid can still contribute to the measured signal, we conclude from our data that dimers and oligomers must dominate the measured signal of the respective m/z at later reaction times. The experiment times, at which thermal decomposition products start impacting the measured signal depend on the vapour pressures of the first-generation products and on the reaction rates.

A closer look at Fig. 5 reveals some remarkable discrepancies between the final product concentrations under the two ozone mixing ratios. For the product peaks at m/z 141 and m/z 157, the final signal is substantially lower at low ozone conditions than at high ozone conditions. These peaks correspond to the first-generation products nonanal (m/z 141), nonanoic acid (m/z 157) and the respective monomeric building blocks of thermally decaying dimers and oligomers. For the other two peaks at m/z 171 and m/z 187, the final signal are similar at both ozone mixing ratios. These peaks correspond to the first-generation products 9-oxononanoic acid (m/z 171) and azelaic acid (m/z 187) and the respective monomeric building blocks.

Based on the volatility of the first-generation products and taking into account the expected contribution of dimers to the measured signal, we propose an influence of first-generation product evaporation on the final droplet composition. The faster evaporation of first-generation products with higher vapour pressure (e.g. nonanal and nonanoic acid) may lead to a stronger loss in the longer experiments with lower ozone mixing ratio. Therefore, these products are likely to be less available as reaction partners for dimerisation reactions with CI (R4 and R5 in Fig. 1) and contribute less to the non-volatile dimer and oligomer mass. A similar competition was described by Zeng and Wilson,⁴⁵ who investigated the ozonolysis of cis-9-tricosene and showed that the contributions of CI reactions (bimolecular accretion and unimolecular decomposition) could be separated using CI scavengers. In our setup, the non-volatile droplet components likely decompose thermally at the time of analysis and are then detected as monomeric building blocks.

3.4.2 Kinetic modelling of product signal curves. To test our hypothesis of competing evaporation and secondary reaction with an aerosol process model, we used the existing KM-SUB model of Berkemeier et al.²⁰ and complemented it with additional reactions following the recent study of Gallimore et al.¹⁰ and with evaporation of semi-volatile first-generation products. The rearrangement of CI and their reactions with acids and aldehydes were added as presented in Fig. 1 and ozone was implemented to react with all C=C double bonds, including double bonds of AAHPs formed in the reaction of CI with oleic acid (not shown in Fig. 1). The evaporation of semi-volatile compounds (nonanal, nonanoic acid, 9-oxononanoic acid, azelaic acid and CI) was treated based on vapour pressures as presented previously.⁴⁶ To simulate the detection of thermal decay fragments at the time of analysis, the dimers are formed in the model and thermal decay is treated by assigning dimers to the signal of the corresponding monomeric building blocks, assuming quantitative turnover. For the decay of secondary ozonides, cleavage was assumed to occur at both C–O bonds with a probability of 50%, leading to different product pairs. Details of the model setup are provided in Appendix D.

A number of unknown kinetic model parameters of product formation and detection were optimised to make the model match the experimental data. Surface and bulk reaction rates of oleic acid with ozone were used as fixed parameters as suggested by Berkemeier et al.²⁰ (R1 in Fig. 1). The bulk reaction rates for CI rearrangement (to the acid, R3) and for the reaction between CI with acids (to form AAHPs, R5) were adopted from Gallimore et al.¹⁰ Further physico-chemical properties of involved species (such as vapour pressures and diffusion coefficients) were used as fixed parameters based on best estimates from the literature. All model parameters used in this study are summarised in Table 2 in Appendix D. Fitted parameters are the surface desorption lifetime of ozone, the branching ratio of primary ozonide decay (R2a vs. R2b), the bulk reaction rate for the formation of SOZs (R4), as well as factors for the conversion between model concentration and experimentally measured signal.

Table 2 Input parameters for KM-SUB and their values to fit the experimental data set

Parameter	Parameter value (best fit)	Parameter fit range	Description^Literature
k SLR1 (cm^2 s^−1)	1.0 × 10^−9		Surface reaction rate coefficient (olefin + O3)^20
k BR1 (cm^3 s^−1)	1.0 × 10^−18		Bulk reaction rate coefficient (olefin + O3)^20
k BR3 (s^−1)	500		Bulk reaction rate coefficient (rearrangement of CI)^10,61
k BR4 (cm^3 s^−1)	1.66 × 10^−15	1.7 × 10^−21–1.7 × 10^−15	Bulk reaction rate coefficient (SOZ formation)
k BR5 (cm^3 s^−1)	2.5 × 10^−19		Bulk reaction rate coefficient (AAHP formation)^10
α R2b/R2a (—)	0.6	1.0 × 10^−4–1.0 × 10^0	Branching ratio of primary ozonide decay (share of 9-oxononanoic acid and CI(m/z 157) branch)
α s,0 (—)	0.1		Surface accommodation coefficient of O3^20
D b,O3 (cm^2 s^−1)	1.0 × 10^−6		Bulk diffusion coefficient of O3 in OL^20
(cm^2 s^−1)	1.9 × 10^−7		Diffusion coefficient of organic species
D g,O3 (cm^2 s^−1)	0.14		Gas-phase diffusion coefficient of O3^20
D g,C9 (cm^2 s^−1)	0.03		Gas-phase diffusion coefficient of C9 species
p vap,NN (atm)	4.8 × 10^−4		Vapour pressure of nonanal^14
p vap,NA (atm)	1.8 × 10^−6		Vapour pressure of nonanoic acid^14
p vap,ON (atm)	1.2 × 10^−7		Vapour pressure of 9-oxononanoic acid^16
p vap,AA (atm)	9.9 × 10^−10		Vapour pressure of azelaic acid^13
H cp,O3 (mol cm^−3 atm^−1)	4.8 × 10^−4		Henry's law solubility coefficient of O3 in OL^20
τ D,O3 (s^−1)	1.0 × 10^−7	1.0 × 10^−9–1.0 × 10^−3	Desorption lifetime of O3
T (K)	293		Temperature
F 141 (—)	0.075	1.0 × 10^−4–2.0 × 10^0	Scaling factor for signal at m/z 141
F 157 (—)	0.7	1.0 × 10^−4–2.0 × 10^0	Scaling factor for signal at m/z 157
F 171 (—)	1.5	1.0 × 10^−4–2.0 × 10^0	Scaling factor for signal at m/z 171
F 187 (—)	0.25	1.0 × 10^−4–2.0 × 10^0	Scaling factor for signal at m/z 187

---

The model output for signal intensities of oleic acid and the first-generation products is included in Fig. 5. The model consolidates the experimental finding that product concentrations reach a constant final state, which for m/z 141 and m/z 157 depends strongly on the ozone mixing ratio. For m/z 187, the model suggests a slight signal decrease after 5 ppm h in the 0.2 ppm experiment, owing to evaporation of azelaic acid present in monomeric form.

Similar to the recent study of Gallimore et al.,¹⁰ the dimer yield in our model is dominated by secondary ozonides. In their study, Gallimore et al.¹⁰ also found a faster reaction of CI with aldehydes than with acids. However, in comparison to their study, we require even higher rates of secondary reactions in order to obtain the observed final ratio of product signals. Note that in our model configuration, the competition between secondary chemistry and evaporation is reflected mainly in the reaction rates of SOZ formation. This is due to the fact that in our scheme the AAHP formation rate is fixed and (besides the quickly evaporating nonanal) only SOZs are contributing to the signal at m/z 141. The higher rates of secondary reactions in our study may be a consequence from the much higher surface accommodation coefficient applied in our model. We used a fixed surface accommodation coefficient of 0.1 based on the recent evaluation by Berkemeier et al.²⁰ to ensure that the uptake is not limited by surface accommodation. Gallimore et al.¹⁰ fitted the accommodation coefficient and obtained very low value of 0.001.

Using the kinetic model, we performed a kinetic flux analysis assessing the competition of first-order (i.e. evaporation and rearrangement) and second-order loss processes (i.e. secondary reaction) of reaction intermediates, i.e. first-generation products and CI (Fig. 13 and Table 3 in Appendix D). The analysis reveals that the applied ozone mixing ratio has an influence on the relative importance of evaporation, dimerisation, and rearrangement. The reaction rates and the vapour pressures determine the prevailing mode of action under specific reaction conditions. As the production and, hence, the concentration of CI is highest in the beginning, the relative importance of dimerisation generally decreases over time and for first-order processes it increases.

Table 3 Relative fractions of processes for first-generation products and CI depending on the applied ozone mixing ratio. The numbers represent the overall fate when integrating over the entire reaction time

Compound	O3 mixing ratio (ppm)	Dimerisation (%)	Evaporation (%)	Isomerisation (%)
Nonanal	0.2	6.5	93.5
	15	60.8	39.2
Nonanoic acid	0.2	0.5	99.5
	15	9.6	90.4
9-Oxononanoic acid	0.2	99.3	0.7
	15	99.97	0.03
Azelaic acid	0.2	73.4	26.6
	15	96.3	3.7
CI-157	0.2	65.6	10.7	23.6
	15	83.6	7.3	9.1
CI-187	0.2	73.5	0.0	26.5
	15	90.2	0.0	9.8

---

3.4.2.1 Final product concentrations for different ozone mixing ratios. For a quantitative comparison of the kinetic model with the experimental data, we fitted the experimental data for each of the MS peaks with an exponential curve

I(x) = I_∞·(1 − e^−x/τ), (1)

where I(x) is the m/z signal intensity from a droplet after exposure x, I_∞ is the signal for x → ∞ and τ is the characteristic e-folding exposure, which is inversely proportional to the initial slope of I(x) for x → 0. Eqn (1) is motivated by the fact that an exponential behaviour is a good approximation for simple reactive systems. For example, when considering the simple bulk reaction system of oleic acid + O₃ → CI + M → dimer, it can be shown that even with evaporating monomers M, the dimer concentration after reaction of the monomer M and the Criegee intermediate CI follows an exponential growth curve in cases of both, dominating or negligible evaporation (see Appendix E). Therefore, an exponential growth curve according to eqn (1) is expected to capture the obtained signal well if the products are formed from an exponentially decreasing starting material and if no other reactions or product partitioning is taking place.

Using the Bayesian inference module from the uncertainty quantification tool UQLab,^47,48 we extracted the two unknown quantities I_∞ and τ from the experimental data including their corresponding uncertainties for each MS peak individually (for more details see Appendix B). The exponential parameters were also extracted from the kinetic model curves, which (with the exception of the curve for m/z 187 at 0.2 ppm ozone) can be reasonably well described by exponential functions.

The pre-exponential factors I_∞ from the Bayesian inference analysis are compared to the corresponding pre-exponential factors from the kinetic model in Fig. 6a. For the low m/z product signals (m/z 141, 143, 157, 159), the pre-exponential factors are lower in the 0.2 ppm experiments than in their 15 ppm counterparts. For higher m/z product signals (m/z 171, 185, 187, 203), this difference becomes smaller. The kinetic model is able to reproduce this trend very well and attributes it to a lower degree of secondary chemistry for compounds with higher vapour pressure. Note that, secondary chemistry occurs through bimolecular reactions of intermediates (i.e., Criegee intermediates, volatile primary products). These intermediates decay (in the case of Criegee intermediates) and evaporate in a first-order process. At the lower ozone mixing ratio (0.2 ppm), the low steady-state concentration of reactive intermediates leads to rather slow rates of secondary chemistry and evaporation of first-generation products is favoured. In turn, at the high ozone mixing ratio (15 ppm), secondary chemistry occurs much faster due to the higher steady-state concentration of reactive intermediates and is favoured over evaporation.

Fig. 6 Final product signal I_∞ (a) and characteristic e-folding exposures τ (b) of Bayesian inference exponential fits to experimental data in comparison to KM-SUB outputs. The error bars and shaded rectangles represent the 95% confidence intervals obtained from Bayesian inference. The signals from oleic acid, from products, and from m/z with decreasing intensity are separated with vertical dashed lines. In (a), the final signals of all species are normalised to the 15 ppm signals, for comparison. Horizontal dotted lines at the 15 ppm final signal (a) and at the estimated characteristic e-folding exposure of oleic acid for 15 ppm (b) help guiding the eye. For the peak at m/z 297, the characteristic exposure of the exponential fit for 0.2 ppm ozone (*) is not shown (estimated to be >100 ppm h).

The diverging final concentrations at high exposures imply that the exposure metric, which holds for the degradation of oleic acid, is not valid for the product formation as the composition of the aerosol droplet depends ultimately on the ozone mixing ratio. For chemical schemes similar to the ozonolysis of oleic acid, where primary products may participate in further, bimolecular reactions, it is therefore possible that the concentrations of secondary products are overestimated in experiments conducted at elevated oxidant concentrations. In this matter, our findings come to different conclusions than a study in which almost identical Raman signatures were detected on droplets aged at 260 ppb ozone for 20 h and in droplets exposed to over 10 ppm ozone for 1.5 h.¹ This result may arise because Raman spectroscopy detects contributions from functional groups and single bonds within a molecule rather than individual molecules.

3.4.2.2 Characteristic exposures for achieving final state for different ozone mixing ratios. In Fig. 6b, we show the characteristic exposures τ from the Bayesian inference analysis and the kinetic model. As the sample number at low ozone exposures is lower than at the final state, the characteristic exposure data is less constrained and is therefore discussed here in terms of the 95% confidence intervals. For all products (with the exception of the signal at m/z 143), the confidence intervals from both ozone mixing ratios overlap, suggesting insignificant differences between the apparent product formation rates. Nevertheless, it is remarkable that, especially at 0.2 ppm ozone, the characteristic exposures of product formation are smaller than the oleic acid decay for many products. In a simplified chemical scheme without evaporation where products may react further but decay quantitatively back into the monomers upon thermal decomposition, the characteristic exposure of product formation is expected to be identical with the characteristic exposure of starting material decay.

The shorter characteristic exposure for experiments under low ozone conditions could be caused by evaporation of first-generation products. However, in the simple bulk reaction system (oleic acid + O₃ → M + M → dimer), evaporation can only lead to a decrease in the characteristic exponential exposure up to a factor of two in the limiting case of very strong evaporation (as shown in Appendix E). The observation that the characteristic exposure depends on the ozone mixing ratio is also not captured in the numerical model, where the products show only slight deviations from the characteristic exposure of oleic acid. Although the model is able to produce a more pronounced dependency of the characteristic product formation exposure on the ozone mixing ratio when using increased CI rearrangement rates or decreased dimerisation reaction rates, such model parameters result in an inferior agreement with the experimental data of final product composition.

Further effects, which are not included in the model, such as the influence of the degree of polymerisation on thermal decomposition and the formation of other products, may also be responsible for the differences. If, for example, the process efficiency of thermal decomposition and evaporation at the time of particle analysis was decreasing with an increasing order of oligomerisation, the initial growth of product signal (dominated by monomers and dimers) would be disproportionately higher than the incline at later stages (formation of higher oligomers). Consequently, the curve-fitting would result in shorter characteristic exposures.

Note that, in the previously published model,²⁰ the decay of oleic acid (shown in Fig. 4) was based on the assumption that for MS data, AAHPs do not contribute to the oleic acid signal, while in Raman data, AAHPs containing a double bond are detected as oleic acid. In the previous work, these unsaturated AAHPs were important reactive intermediates and the distinction between MS and Raman data significantly improved the quality of the global fit. Similarly, Zhou et al.¹² reported a higher yield of AAHPs in comparison to the SOZ yield when studying oleic acid coating ozonolysis. In the extended KM-SUB model of this present study, the formation of AAHP adducts of oleic acid, however, is only a minor channel of secondary chemistry. The good agreement in Fig. 4 may thus indicate that the monomer signal is potentially more influential than AAHP contributions. Further product studies would be needed to distinguish the contributions of secondary ozonides and AAHPs to the product spectrum.

3.4.3 Other products from the ozonolysis of oleic acid. The peaks at m/z 143, 159 and 185 (see Fig. 12 in Appendix C) show a similar behaviour as the peaks at m/z 141 or 157. Even though it remains impossible to confidently assign possible products with our MS resolution (e.g. to distinguish possible contributors to the peak at m/z 143, such as the proposed octanoic acid from nonanol, which could be formed at the time of analysis through thermal decomposition), the prevailing species in the droplet would most likely be a dimer or an oligomer. Otherwise the intensity would not remain constant after experiment durations of over two days, given the vapour pressures of these monomeric C9 acids or alcohols.

Although outside the focus of this work, it should be noticed that the signal from m/z 297 shows a significantly different behaviour between the two ozone mixing ratios. In the experiment with a high ozone mixing ratio, the decay is rather similar to that of oleic acid or other peaks at m/z 295, 312 or 328, yet a bit slower. At low ozone mixing ratios, however, there is hardly any decay detectable and the characteristic time is on the order of 100 ppm h. We can only speculate about the reason: the difference could be due to the formation of an oxidation product of oleic acid with molecular oxygen, which is favoured in the longer experiment over a reaction with either ozone or with CI. The addition of one oxygen atom would also explain the mass difference of 16 mass units between oleic acid and this additional peak. Further investigations with high resolution MS would be required to gain insight into the molecular structures and to propose a chemical mechanism.

3.5 Droplet size changes

Droplet size data from the reactions with different ozone mixing ratios allow testing the proposed evaporation effect. To do so, we tracked the change in particle radius for two particles at both ozone mixing ratios by comparing the evolution of the angular scattering pattern with simulated patterns.

The droplet size changes are shown in Fig. 7. As expected, experiments with longer reaction times lead to smaller droplets at a given exposure. The shown radius changes at 5 ppm h translate into volume decreases of about 18–22% for the droplets in 0.2 ppm ozone and about 13–14% for the droplets in 15 ppm ozone. Given the continued shrinking after 5 ppm h, the final droplet sizes agree with the measured non-volatile fraction of 50–85% reported by Dennis-Smither et al.⁸ Yet, in our experiments we observed an increased evaporation in experiments at lower ozone mixing ratios whereas they see indications that the non-volatile fraction of substances was higher at lower ozone mixing ratios. If this discrepancy is due to the presence of NaCl cores in their droplets would need further investigations.

Fig. 7 Droplet size changes during the reaction under different ozone mixing ratios. The initial radius and radius changes were obtained by comparison of the angular scattering pattern to calculated scattering patterns assuming constant refractive indices. The assumption of an unchanged refractive index is expected to have an effect of less than 3% on the obtained volume.⁸

There is an apparent deceleration of size change after an exposure of around 5 ppm h, which is most likely because the oleic acid has reacted away in large part by then. While the shrinkage under high ozone concentrations seems to stagnate at exposures above 10 ppm h, there is still a steady radius decrease detectable in the longer, low ozone experiments. Further oxidation reactions with ozone, which produce highly volatile species and therefore contribute to this size change cannot be ruled out but seem not to be the dominant reason because they would apply under both ozone mixing ratios equally.

While the change in droplet radius over the course of the experiment is not treated explicitly in the model, droplet sizes can be inferred from model output by converting particle mass to volume. For Fig. 7, we used a density of 0.89 g cm⁻³ for oleic acid and 1.12 g cm⁻³ for product species, based on findings by Katrib et al.⁴⁹ The model reproduces the general features in the droplet radius data even though this data was not used in the model fitting. The strongest diversion from the experimental data is observed at a low ozone mixing ratio and high exposure. This indicates that there is ongoing evaporation of semi-volatile species under low ozone conditions, which is not captured by the model, possibly due to a slow decomposition of dimers and oligomers, which is not treated in the model.

From measurements of the angular phase function, no major distortion in the regular patter could be observed, indicating that there is no extensive phase separation. Such a behaviour had been described for deposited droplets and films.^11,50

4 Outlook

Using a new setup for EDB–MS measurements, we demonstrate the influence of first-generation product evaporation on secondary chemistry in the heterogeneous oxidation of oleic acid with ozone. While the starting material decay can be described with the exposure metric (i.e., it is only dependent on oxidant concentration × time, for all oxidant concentrations), the metric is not fully applicable to concentrations of first-generation products, dimers and oligomers. Deviation from typical atmospheric conditions in laboratory experiments may suppress the influence of first-order processes such as evaporation, happening on longer timescales, in favour of second-order processes such as bimolecular reactions of reactive intermediates, which are less relevant under atmospheric conditions. This is not limited to evaporation, but also includes other transport processes and unimolecular chemical reactions. In other chemical systems, semi-volatile reaction products could also compete with the starting material for oxidative agents and therefore influence the primary chemistry in dependence on the applied reaction conditions, which would make the exposure metric not applicable to the starting material decay. This highlights the necessity to fully understand the chemical system under consideration to safely gain knowledge from experiments with elevated oxidant concentration.

Author contributions

M. M. and U. K. K. designed the experimental setup with E. H. M. M. carried out the experiments and analysed the data. A. M. and T. B. set up the model and A. M. ran and optimised the model. T. P. derived the mathematical treatment of the simplified chemistry using differential equations. M. M., A. M., T. B., T. P., and U. K. K. discussed the results. M. M. produced the figures and wrote the original draft with help from A. M. The draft was revised by A. M., T. B., T. P., and U. K. K.

Conflicts of interest

There are no conflicts to declare.

Appendix A instrumentation and chemicals

For the injection of new particles, a droplet on demand generator (TIJ 1.0 print cartridge, Hewlett Packard; average drop volume 220 pl) is mounted on a translatable and tilting stage, orientated towards the EDB. Droplets are charged inductively upon ejection utilising a copper ring directly below the cartridge. Voltages of 20 to 300 V were applied to the ring to imply a sufficient charge on the droplet.

The linear quadrupole EDB consists of combined rod AC electrodes and perforated disk DC electrodes.^51–53 While the quadrupolar arrangement of the AC electrodes confines the path of charged particles to the central axis, three pairs of inserted DC electrodes are used to counteract the gravitational force of injected particles. The AC electrodes are kinked, which allows laser illumination along the central axis without removing the injector. Furthermore, tilting the first part of the trap prevents uncharged (satellite) droplets accidentally ejected from colliding with already stored particles. The DC electrode pairs define storage segments in the trap: a first segment before the kink is used to verify a successful injection, a second segment below the kink is used for droplet sizing and a third segment underneath is used for droplet storage (see Fig. 2). Typically, 3 kV were applied at 150–300 Hz at the AC rod electrodes and the DC voltage at the inserted disk electrodes was varied from ground potential to 1 kV for transfer and vertical droplet positioning. All electrodes are mounted inside a polyether ether ketone (PEEK) housing which holds a manual polytetrafluorethylene (PTFE) valve on the top end and a pneumatic valve (VAT Vakuumventile AG, Switzerland) at the bottom end of the trap. The AC rods of both EDB parts are approximately 13 cm long.

In the first segment, a DPSS laser module (532 nm, 4 mW, uniform 30° fan angle, Frankfurt Laser Company, Germany) is used for particle illumination from the side. For the lower arm of the EDB, a second DPSS laser module (532 nm, 3 mW TEM₀₀, Lasermate Group Inc., USA) is used along the central axis. At each segment, a Raspberry Pi with a camera (ArduCam UC-599) is mounted to observe the droplet position. For the second segment a feedback loop is utilised to adjust the DC voltage in order to maintain the vertical droplet position while sizing. An additional camera (Raspberry Pi HQ Camera V1.0) is installed at the second segment to capture the 2-D angular scattering pattern from 94.87° to 99.13° and particle sizes are determined based on the mean peak-to-peak distance in the angular scattering pattern which is compared to simulated scattering patterns using MiePlot (v4.6.20).^54,55

To control the gas phase in the EDB and the gas flows in the evaporation unit, a set of valves and mass flow controllers (MKS Instruments, USA) are used for both nitrogen and compressed air. For ozone mixing ratios below or equal to 1.5 ppm a calibration ozone generator (Photometric O₃ Calibrator – Model 401, Advanced Pollution Instrumentation, USA) is used. For higher mixing ratios, an ambient ozone simulator (AOS 2 with bypassed pump, BMT Messtechnik, Germany) is used. An electrochemical ozone sensor (OX-B431 on Alphasense ISB, Alphasense, UK), calibrated with the ozone calibrator, is mounted at the outflow of the EDB to measure ozone concentrations. For the calibration of the ozone detector and to provide a reference signal there is a bypass between the ozone generator and the ozone detector (bypassing the EDB). The relative humidity and temperature in the outflow is measured using a digital humidity and temperature sensor (Sensirion SHT85, Switzerland).

The pneumatic valve at the bottom end of the EDB connects the EDB housing to a PEEK socket holding the evaporation unit. To allow a complete flushing of the evaporation unit, this socket also has a gas connection (labelled ‘Flushing gas’ in Fig. 2). The evaporation unit consists of a home-built combination of a jet heating cartridge (50 V, 50 W) welded together with a bored-up Swagelock Tee and connected to another heating cartridge (230 V, 100 W, both from Probag Wärmetechnik AG, Switzerland). Both heating cartridges are equipped with a Pt 100 temperature sensor and powered by temperature controllers (LTC-11, Neocera, USA and LTC-10, Conductus, USA), which allow to stabilise the temperature between 30 °C and 200 °C to better than 0.1 °C. The two remaining openings of the Swagelock Tee are connected via PEEK tubing to the ion source (towards the MS) on one side and to the gas inlet on the other side. To allow a constant gas flow through the ion source (driven by a Venturi nozzle in the interface) a nitrogen overflow tube is connected as main gas inlet accompanied by a connection for a control gas flow (nitrogen flow through a gas washing bottle filled with a mixture of 1% toluene in ethanol).

Gas-phase compounds are ionised in a cold plasma dielectric barrier discharge ion source^56,57 (SICRIT SC-30X Ionisation Set, Plasmion GmbH, Germany) operated at ambient pressure. MS analysis is carried out with a triple quadrupole mass spectrometer (QTRAP 4500, AB Sciex LLC, USA) operated in negative Q3 mode at 2000 Da s⁻¹ with unit resolution. It is operated with the provided instrument control and data processing software Analyst (Version 1.7, AB Sciex LLC, USA). For further analysis, MS data were processed in MATLAB (Version R2019a, MathWorks, USA).

Chemicals

Azelaic acid (≥99% (GC), Fluka Chemika), ethanol–toluene mix (1% toluene, 94%, Thommen-Furler AG), methanol (UHPLC for MS, Sigma-Aldrich), nonanal (95%, Aldrich chemistry), nonanoic acid (≥97%, Sigma life science) and oleic acid (selectophore, ≥99%, Sigma-Aldrich) were all used without further purification. For the carrier gas, nitrogen gas stemmed from a nitrogen generator (NGM-11, cmc Instruments GmbH, Germany) and for all other nitrogen applications, nitrogen gas was delivered from a liquid nitrogen reservoir Dewar. Zero Air was supplied by the zero air generator of the ozone calibrator or used from the in-house compressed air supply in combination with the ambient ozone simulator.

Typical experimental procedure

All measurements were carried out at ambient pressure and laboratory temperature (20–23 °C). Prior to any measurement, the EDB was flushed with 50 sccm N₂ for at least 30 minutes. Particles were produced from solutions of 2–10 wt% solute in methanol. Oleic acid solutions were stored at <6 °C and freshly prepared roughly every two weeks.

After the successful injection of two droplets the manual top valve was closed and a N₂ flow of 25 sccm was applied and maintained until the start of the experiment. The first drop was transferred to the second EDB segment and sized by recording its angular scattering pattern. It was subsequently transferred to the lowermost EDB segment and stored there. Afterwards, the second drop was transferred to the second EDB segment and its angular scattering pattern was continuously recorded for sizing throughout the whole experiment. The storage of a larger number of droplets is possible but here only one droplet in each lower segment was used. This two droplet configuration allows for an additional gas flow through the trap during droplet ejection which results in an efficient droplet transfer into the evaporation unit.

Before starting the heterogeneous oxidation reaction, the gas flow from the ozone generator (up to 400 sccm total flow, containing 0.2, 10 or 15 ppm O₃) was passed over the ozone sensor to check the sensor response in terms of magnitude and stability. To start the ozonolysis, this gas flow was redirected through the EDB and the ozone mixing ratio was monitored at the EDB outflow. These data are a lower bound of the mixing ratio of ozone in the two segments with the levitated droplets. In all experiments, the difference between ozone concentration before and after the EDB were less than 15% of the inflow mixing ratio. After the desired reaction time, the ozone generator was switched off and the EDB was purged with a nitrogen gas flow for one minute. Subsequently, the drops were ejected and analysed consecutively by an automated cascade of valve and electrode voltage switching. In a first step, the pneumatic valve between the EDB and the evaporation unit was opened and the third segment DC electrode voltage was set to zero. Afterwards, a pure nitrogen gas flow was forced through the EDB for one second (300 sccm). This led to a very reliable droplet transport from the lowest segment of the EDB to the evaporation unit with a transfer success rate of close to 100%. In a last step, the valve between the EDB and the evaporation unit was closed, the gas flow through the EDB was stopped and the evaporation unit was flushed with a flow of 300 sccm nitrogen gas. This flow was maintained for the entire MS measurement duration of 240 s. Afterwards, the remaining droplet was transferred to the third segment of the EDB and the analysis procedure was repeated.

For MS analysis, both heating cartridges in the evaporation unit were set to 190 °C and a control gas flow of 5 sccm N2 containing ethanol and toluene vapour was mixed with the carrier flow for both the background and for the droplet measurements.‡ Background measurements were used to check for inter-day variability with a focus on the stability of the ion source. These covered a range of m/z 40–340 in both positive and negative mode. Averaged peaks from ethanol and toluene (positive mode) as well as ethanol and NO₃⁻ in negative mode were extracted for comparison. Droplet measurements were carried out in negative mode either in the range of m/z 40–340 with a scan time of 0.155 s (6.45 full scans per second) or for a selection of ranges (m/z 140–145, 155–160, 168–175, 184–189, 200–204, 233–235, 278–284, 294–299, 320–315, 326–330) with a scan time of 0.075 s (13.4 full scans per second).

Because the MS signal during a droplet evaporation event is dominated by the gas-phase background signals from carrier-, flushing- and control gas (see Fig. 8b), the signal from the last 30 s of the flushing period was used for a background correction (subtraction of the average background, see Fig. 8). The main background peaks at m/z 45, 46, and 62 are produced by EtO⁻, NO₂⁻ and NO₃⁻, respectively.³⁶ In addition, also data from ejection sequences without any drop present was collected and subtracted from the droplet signal as also flushing the empty trap lead to a slight increase in signal. Individual peaks were extracted by binning the spectral data in segments of one mass unit width (containing m/z i ± 0.5 for integer i). When focusing on the most prominent MS peak from the unreacted oleic acid droplet at m/z 281, a typical droplet ‘evapogram’ is obtained (see Fig. 9).

Fig. 8 Temporal evolution of the total ion count during a single, unreacted oleic acid droplet evaporation experiment (a), expansion to integrated mass spectra for selected time spans (b) and (c) and background corrected signal (d). Time span A denotes the interval with signal from the droplet whereas time span B is treated as background signal for background subtraction. Subtracting the average background signal from the droplet interval signal yields the background corrected spectrum. The main contribution to the total ion count peak is from the deprotonated oleic acid ion [M−H]⁻ at m/z 281 and the background signal is dominated by NO₃⁻ at m/z 62.³⁶

Fig. 9 Extracted ion count for m/z 281 from the evaporation of a single oleic acid droplet at 190 °C. After a sharp increase with the introduction of the droplet in the evaporation unit the signal intensity decays as the droplet shrinks and reaches background values before the end of the experiment at 240 s. The area below the curve corresponds to the amount of oleic acid in the drop.

Calibration

The conversion from the MS signal into amount of substance was based on calibration experiments, assuming that the droplet composition (apart from the substance of interest) has no influence on the MS signal. Furthermore, it is assumed that the signal can be corrected for droplet size deviation (with the relative volume) and that the dimers and oligomers form again the same monomers when thermally decomposing.

For the calibration of oleic acid peaks, the signal at m/z 281 of 24 different droplet measurements was recorded on nine different days spread over seven weeks (see Fig. 10). A conservative uncertainty in the radius determination of 10% is assumed resulting in a corresponding uncertainty for the amount of substance of 30%.⁶⁰ The day-to-day variability of the MS-signal was estimated from gas-phase background measurements by analysing the response from ethanol, toluene and NO₃⁻. While the alcohol signals in positive mode were constant over measurements on 14 different days in seven weeks (all values less than 3% off the mean), there was a considerable spread but no clear trend in negative mode peaks of ethanol and NO₃⁻ (up to 45% above and 36% below the mean value). The relative standard deviation of the negative ethanol signal was applied to the averaged data points in Fig. 10 to illustrate the estimated uncertainty from inter-day variability. A linear regression through the unweighted data points and forced through zero results in a slope of (5.9 ± 0.20) × 10¹⁹ counts per mol. Analogously, the calibration figures for nonanoic acid (slope of (1.74 ± 0.18) × 10¹⁹ counts per mol) and azelaic acid (slope of (4.9 ± 0.4) × 10¹⁹ counts per mol) is shown in Fig. 11.

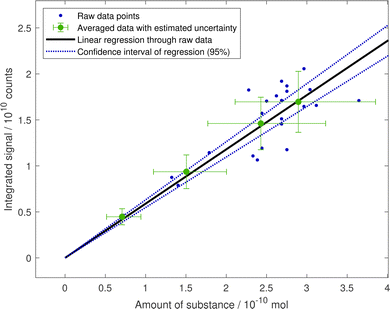Fig. 10 Calibration of oleic acid MS signal with data from the evaporation of droplets of different sizes. The amount of substance was derived from the mean peak-to-peak distance in the droplet angular scattering pattern and using molar mass and density of oleic acid at standard temperature and pressure.^54,59 Data points with similar calculated amount of substance were averaged (n = 2, 3, 7, 12) and provided with error bars depicting an estimated uncertainty in the radius measurement of 10% and the standard deviation of the day-to-day variability in sensitivity extracted from the gas-phase methanol analysis. A linear fit through zero is applied to the raw data points and it is shown with the 95% confidence interval.

Fig. 11 Calibration curves for nonanoic acid (a) and azelaic acid (b). Mixed droplets with different droplet compositions were used. For the calculation of the amount of substance, the molar volume was used and a refractive index of 1.46 was assumed for all droplets. The linear regression was forced through zero.

Appendix B uncertainty quantification of exponential fits

This section describes the procedure for the uncertainty quantification of exponential fit parameters using the Bayesian inference module from the uncertainty quantification tool UQLab.^47,48

The droplet signal from a drop after exposure x is denoted I(x). For peaks with increasing intensity as exposure increases, an exponential curve according to was fitted. Similarly, a decrease according to was assumed for all other peaks. Here, I is the maximum signal (signal at infinite exposure I_∞ for increasing intensities and signal at zero exposure I₀ for others) and τ the characteristic exponential lifetime.

The sampling range for the τ parameters was set to a uniform distribution between 0 and 5 ppm h for all peaks except m/z 297 at 0.2 ppm where a distribution between 0 and 150 ppm h was used. For the pre-exponential parameter I, the sampling range was defined from 0 to 1.25 times the maximum measured signal intensity. A discrepancy model was used to account for the uncertainty of experimental measurements using Gaussian discrepancies with standard errors composed of a percent error (estimated from the signal variability extracted from the gas-phase methanol analyses) and a minimal uncertainty of 2.5% of the maximum signal. For each peak, the Markov chain Monte Carlo sampling of the Bayesian inversion tool was run with the adaptive metropolis algorithm until 100 000 parameter combinations were accepted of which the first 50 000 were discarded to prevent burn-in artefacts. The point estimates and the distributions of parameters were extracted and used for comparisons.

Appendix C: measured signal for further MS peaks

In Fig. 12, the course of measured signal intensities is shown for further m/z, not corresponding to deprotonated primary products or oleic acid.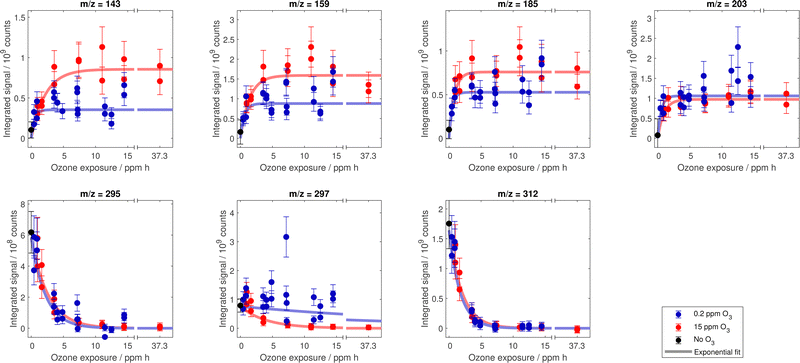

Fig. 12 Compilation of measured signal for prominent MS peaks in dependence on exposure to ozone. Error bars depict estimated uncertainties from size sensitivity variability. The trend lines are based on point estimates for the exponential parameters I and τ in and . More details on the uncertainty of these model parameters are given in Fig. 6.

Appendix D: kinetic multilayer model

The kinetic process model is based on the multilayer model of aerosol surface and bulk chemistry KM-SUB.⁴¹ The implemented scheme and model parameters are based on a recent study focusing on the degradation of oleic acid in 12 different experimental data sets that span a wide range of oxidant concentration and particle size.²⁰ The spherically-symmetric KM-SUB model compartments are, from outside to inside, gas phase, near-surface gas phase, sorption surface layer, quasi-static surface layer, and a number of bulk layers. Processes described in the KM-SUB model include gas-phase diffusion, adsorption and desorption, surface-bulk exchange, bulk diffusion of gaseous and bulk material as well as chemical reactions at the surface and in the particle bulk. The model code generates and solves a system of ordinary differential equations that describe the mass balance of each chemical species in each model layer. The corresponding Jacobian matrix is generated and evaluated explicitly to increase the numerical stability of the differential equation solver (ode23tb in Matlab).

Reaction rate coefficients and other input parameter values are presented in Table 2. The primary reaction of oleic acid with ozone was treated with a separate bulk (k_BR1) and surface reaction (k_SLR1). It was shown by Berkemeier et al.,²⁰ that the differentiation of surface and bulk reaction rates is important to reconcile the decay of oleic acid across multiple literature data sets. The secondary reactions of reactive intermediates considered in the model are the rearrangements of Criegee intermediates (CI) (k_BR3) as well as their reactions with aldehydes forming secondary ozonides (k_BR4) and with acids forming α-acyloxyalkyl hydroperoxides (AAHP) (k_BR5). We assume here that all aldehydes and acids, respectively, react with the same rate coefficients. Note that the AAHP formed in the reaction of CI with oleic acid is still able to undergo ozonolysis with a rate coefficient k_BR1/k_SLR1.

We assume that all first-generation products (nonanal, nonanoic acid, 9-oxononanoic acid and azelaic acid and the two CI) are semi-volatile and evaporate according to their vapour pressure (literature references in Table 2). The desorption flux from the particle surface to the gas phase is parameterised as a function of vapour pressure.⁴⁶ For CI, we assume the vapour pressures of the corresponding aldehydes. Oleic acid and secondary products are treated as non-volatile.

To compare primary model output to the mass spectra, mole fractions of chemical species are multiplied with scaling factors (F) to simulate the compound-specific detection efficiency in the experimental setup. Dimers are assumed to thermally decompose into their constituting monomers (nonanal, nonanoic acid, 9-oxononanoic acid and azelaic acid). For the secondary ozonides, the thermal decomposition is assumed to produce pairs of aldehydes and acids. The two possible sets of products of this decomposition are assumed to occur with equal likelihood.

The relative fractions of first order (evaporation and rearrangement) and second order processes (bimolecular reaction) are shown in Fig. 13 as a function of the remaining oleic acid concentration. Time-integrated relative fractions of the different processes are provided in Table 3. Overall, the secondary reaction dominates over evaporation for first-generation products with low volatility (azelaic acid and 9-oxononanoic acid), and for CI due to their high reaction rate coefficients. For nonanal, the vapour pressure is just high enough that evaporation dominates under low ozone conditions but dimerisation reactions dominate at the high ozone concentration. This is due to the high steady-state concentration of first-generation products and CI at high ozone mixing ratios, favouring the second-order reaction. In the case of nonanoic acid, the high volatility dictates the fate because of the low reactivity with CI (due to the absence of an aldehyde functional group, R4 vs. R5). For CI, the rearrangement provides another first-order process, which dominates over evaporation for CI-187 but is on the same order of magnitude as the evaporation for CI-157.

Fig. 13 Representation of the relative importance of evaporation, secondary reaction, and first-order rearrangement of first-generation products (a–d) and CI (e and f). The remaining fraction of oleic acid in the drop is used as abscissa.

Kinetic flux analysis reveals that, in our model, approximately 92% of the primary oleic acid loss is due to surface reaction.

Appendix E: simplified chemistry representation with differential equations

For the treatment of a simplified chemical scheme, we write oleic acid as ‘OL’, monomers as ‘M’ and dimers as ‘D’. The following derivation may help to understand the characteristics of the product formation curve under specific conditions. We consider a reaction (E.1) with reaction rate coefficient k₁,

OL + O₃ → M + M, (E.1)

and a reaction (E.2) with reaction rate coefficient k₂,

M + M → D. (E.2)

Furthermore, we consider the evaporation of M as depending linearly on an evaporation rate E and the concentration [M]. Time-dependent concentrations are given in squared brackets (e.g. [M]) and initial concentrations are denoted explicitly (e.g. [M]₀).

The change of the oleic acid concentration over time is then

the monomer concentration changes as
and the dimer concentration change is given as

If k₁[O₃] is assumed to be constant, then the time-dependent concentration of oleic acid is simply

[OL] = [OL]₀e^{−k₁[O₃]t} = [OL]₀e^−t/τ,

with the characteristic e-folding exposure . Assuming steady state conditions for [M] gives
which yields
and therefore
By introducing a dimensionless relative dimer concentration Δ = [D]/[OL]₀, a dimensionless relative evaporation and a dimensionless time surrogate θ = t/τ, we may write

In an extreme case without evaporation (i.e. ε= 0), eqn (E.3) simplifies to

for which we obtain Δ = 1 − e^−θ and therefore

[D] = [OL]₀(1 − e^−t/τ).

In the other extreme case, where the evaporation is infinitely fast, eqn (E.3) can be reduce to

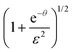using a Taylor expansion of for 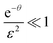to the second term. Therefore, we obtain
with constant c, which means [D] can be expressed as
Note the deviation by a factor of two for the e-folding exposure compared to the limiting case without evaporation (the exponent changes from τ to τ/2).

Acknowledgements

This work was supported by ETH Research Grant ETH-03 17-2. The authors would like to thank Nico Germann, Marco Vecellio and Uwe Weers for their contributions to design and construction of the instrumentation. Furthermore, scientific discussions with Nir Bluvshtein and support from Plasmion GmbH, Augsburg, Germany were much appreciated. A. M. was supported by the Max Planck Graduate Center with the Johannes Gutenberg University Mainz (MPGC).

Notes and references

1. A. K. Lee and C. K. Chan, Atmos. Environ., 2007, 41, 4611–4621.
2. V. F. McNeill, R. L. Yatavelli, J. A. Thornton, C. B. Stipe and O. Landgrebe, Atmos. Chem. Phys., 2008, 8, 5465–5476.
3. L. H. Renbaum and G. D. Smith, Atmos. Chem. Phys., 2011, 11, 6881–6893.
4. C. L. Liu, J. D. Smith, D. L. Che, M. Ahmed, S. R. Leone and K. R. Wilson, Phys. Chem. Chem. Phys., 2011, 13, 8993–9007.
5. Y. Chu, T. F. Cheng, M. Gen, C. K. Chan, A. K. Lee and M. N. Chan, ACS Earth Space Chem., 2019, 3, 779–788.
6. J. Zahardis and G. A. Petrucci, Atmos. Chem. Phys., 2007, 7, 1237–1274.
7. O. Vesna, M. Sax, M. Kalberer, A. Gaschen and M. Ammann, Atmos. Environ., 2009, 43, 3662–3669.
8. B. J. Dennis-Smither, R. E. Miles and J. P. Reid, J. Geophys. Res. Atmos., 2012, 117, 1–13.
9. M. Wang, L. Yao, J. Zheng, X. Wang, J. Chen, X. Yang, D. R. Worsnop, N. M. Donahue and L. Wang, Environ. Sci. Technol., 2016, 50, 5702–5710.
10. P. J. Gallimore, P. T. Griffiths, F. D. Pope, J. P. Reid and M. Kalberer, J. Geophys. Res., 2017, 122, 4364–4377.
11. A. Milsom, A. M. Squires, A. D. Ward and C. Pfrang, Atmos. Chem. Phys., 2022, 22, 4895–4907.
12. Z. Zhou, P. S. J. Lakey, M. von Domaros, N. Wise, D. J. Tobias, M. Shiraiwa and J. P. D. Abbatt, Environ. Sci. Technol., 2022, 56, 7716–7728.
13. M. Bilde, K. Barsanti, M. Booth, C. D. Cappa, N. M. Donahue, E. U. Emanuelsson, G. McFiggans, U. K. Krieger, C. Marcolli, D. Topping, P. Ziemann, M. Barley, S. Clegg, B. Dennis-Smither, M. Hallquist, Å. M. Hallquist, A. Khlystov, M. Kulmala, D. Mogensen, C. J. Percival, F. Pope, J. P. Reid, M. A. Ribeiro Da Silva, T. Rosenoern, K. Salo, V. P. Soonsin, T. Yli-Juuti, N. L. Prisle, J. Pagels, J. Rarey, A. A. Zardini and I. Riipinen, Chem. Rev., 2015, 115, 4115–4156.
14. T. E. Daubert and R. Danner, Physical and thermodynamic properties of pure chemicals: data compilation, Taylor and Francis, 1989.
15. C. D. Cappa, E. R. Lovejoy and A. R. Ravishankara, J. Phys. Chem. A, 2008, 112, 3959–3964.
16. S. Compernolle, K. Ceulemans and J. F. Müller, Atmos. Chem. Phys., 2011, 11, 9431–9450.
17. R. Criegee, Angew. Chem., Int. Ed. Engl., 1975, 14, 745–752.
18. P. J. Ziemann, Faraday Discuss., 2005, 130, 469–490.
19. J. Zahardis, B. W. LaFranchi and G. A. Petrucci, J. Geophys. Res., D: Atmos., 2005, 110, 1–10.
20. T. Berkemeier, A. Mishra, C. Mattei, A. J. Huisman, U. K. Krieger and U. Pöschl, ACS Earth Space Chem., 2021, 5, 3313–3323.
21. H. M. Hung, Y. Katrib and S. T. Martin, J. Phys. Chem. A, 2005, 109, 4517–4530.
22. S. S. Al-Kindi, F. D. Pope, D. C. Beddows, W. J. Bloss and R. M. Harrison, Atmos. Chem. Phys., 2016, 16, 15561–15579.
23. A. W. Birdsall, U. K. Krieger and F. N. Keutsch, Atmos. Meas. Tech., 2018, 11, 33–47.
24. M. I. Jacobs, J. F. Davies, L. Lee, R. D. Davis, F. Houle and K. R. Wilson, Anal. Chem., 2017, 89, 12511–12519.
25. M. I. Jacobs, R. D. Davis, R. J. Rapf and K. R. Wilson, J. Am. Soc. Mass Spectrom., 2019, 30, 339–343.
26. A. W. Birdsall, J. C. Hensley, P. S. Kotowitz, A. J. Huisman and F. N. Keutsch, Atmos. Chem. Phys., 2019, 19, 14195–14209.
27. M. D. Willis, G. Rovelli and K. R. Wilson, Anal. Chem., 2020, 92, 11943–11952.
28. R. Kaur Kohli and J. F. Davies, Analyst, 2020, 145, 2639–2648.
29. J. C. Hensley, A. W. Birdsall and F. N. Keutsch, Environ. Sci. Technol., 2021, 55, 11549–11556.
30. J. C. Hensley, A. W. Birdsall, G. Valtierra, J. L. Cox and F. N. Keutsch, Atmos. Chem. Phys., 2021, 21, 8809–8821.
31. R. K. Kohli and J. F. Davies, Anal. Chem., 2021, 93, 12472–12479.
32. U. K. Krieger, C. Marcolli and J. P. Reid, Chem. Soc. Rev., 2012, 41, 6631–6662.
33. L. Bregy, P. M. L. Sinues, M. M. Nudnova and R. Zenobi, J. Breath Res., 2014, 8, 027102.
34. J. C. Wolf, M. Schaer, P. Siegenthaler and R. Zenobi, Anal. Chem., 2015, 87, 723–729.
35. M. F. Mirabelli, J. C. Wolf and R. Zenobi, Analyst, 2017, 142, 1909–1915.
36. L. Gyr, J. C. Wolf, J. Franzke and R. Zenobi, Anal. Chem., 2018, 90, 2725–2731.
37. J. C. Reynolds, D. J. Last, M. McGillen, A. Nijs, A. B. Horn, C. Percival, L. J. Carpenter and A. C. Lewis, Environ. Sci. Technol., 2006, 40, 6674–6681.
38. G. Li, N. Bei, J. Cao, J. Wu, X. Long, T. Feng, W. Dai, S. Liu, Q. Zhang and X. Tie, Atmos. Chem. Phys., 2017, 17, 2759–2774.
39. J. Staehelin, F. Tummon, L. Revell, A. Stenke and T. Peter, Atmosphere, 2017, 8, 1–20.
40. D. R. Worsnop, J. W. Morris, Q. Shi, P. Davidovits and C. E. Kolb, Geophys. Res. Lett., 2002, 29, 19–22.
41. M. Shiraiwa, C. Pfrang and U. Pöschl, Atmos. Chem. Phys., 2010, 10, 3673–3691.
42. T. Berkemeier, A. J. Huisman, M. Ammann, M. Shiraiwa, T. Koop and U. Pöschl, Atmos. Chem. Phys., 2013, 13, 6663–6686.
43. R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, Wiley, New York, Rev. 2nd edn, 2007.
44. D. Topping, M. Barley, M. K. Bane, N. Higham, B. Aumont, N. Dingle and G. McFiggans, Geosci. Model Dev., 2016, 9, 899–914.
45. M. Zeng and K. R. Wilson, J. Phys. Chem. Lett., 2020, 11, 6580–6585.
46. T. Berkemeier, M. Takeuchi, G. Eris and N. L. Ng, Atmos. Chem. Phys., 2020, 20, 15513–15535.
47. S. Marelli and B. Sudret, Vulnerability, Uncertainty, and Risk, Reston, VA, 2014, pp. 2554–2563.
48. P.-R. Wagner, J. Nagel, S. Marelli and B. Sudret, UQLab user manual – Bayesian inversion for model calibration and validation, Chair of risk, safety and uncertainty quantification, ETHZurich, Switzerland, Technical report, 2021.
49. Y. Katrib, S. T. Martin, Y. Rudich, P. Davidovits, J. T. Jayne and D. R. Worsnop, Atmos. Chem. Phys., 2005, 5, 275–291.
50. S. Xu, F. Mahrt, F. K. A. Gregson and A. K. Bertram, ACS Earth Space Chem., 2022, 6, 1836–1845.
51. P. H. Dawson, Quadrupole mass spectrometry and its applications, Elsevier Scientific Publishing Company, Amsterdam, Netherlands, 1976.
52. M. B. Hart, V. Sivaprakasam, J. D. Eversole, L. J. Johnson and J. Czege, Appl. Opt., 2015, 54, F174.
53. M. Woźniak, G. Derkachov, K. Kolwas, J. Archer, T. Wojciechowski, D. Jakubczyk and M. Kolwas, Langmuir, 2015, 31, 7860–7868.
54. E. J. Davis and R. Periasamy, Langmuir, 1985, 1, 373–379.
55. P. Laven, Appl. Opt., 2003, 42, 436.
56. M. M. Nudnova, L. Zhu and R. Zenobi, Rapid Commun. Mass Spectrom., 2012, 26, 1447–1452.
57. L. Gyr, F. D. Klute, J. Franzke and R. Zenobi, Anal. Chem., 2019, 91, 6865–6871.
58. S. M. Kurtz, Chemical and Radiation Stability of PEEK, Elsevier Inc., 2012, pp. 75–79.
59. W. J. Glantschnig and S.-H. Chen, Appl. Opt., 1981, 20, 2499.
60. A. K. Ray, A. Souyri, E. J. Davis and T. M. Allen, Appl. Opt., 1991, 30, 3974.
61. O. Welz, J. D. Savee, D. L. Osborn, S. S. Vasu, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Science, 2012, 335, 204–207.

---

Footnotes

† Only the secondary ozonide from the reaction of nonanal with CI-157 intermediate has a vapour pressure of around 10⁻³ Pa, but it is expected to be formed only in small amounts due to the rapid partitioning of nonanal to the gas phase.¹⁶

‡ The chosen temperature lies still sufficiently below the processing temperature of PEEK and below typical autoclaving temperatures under which the bulk behaviour of reinforced PEEK is not yet affected.⁵⁸

---