Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrafast transverse relaxation exchange NMR spectroscopy†
Md Sharif
Ullah‡
 ,
Otto
Mankinen‡
,
Otto
Mankinen‡
 *,
Vladimir V.
Zhivonitko
*,
Vladimir V.
Zhivonitko
 and
Ville-Veikko
Telkki
and
Ville-Veikko
Telkki
 *
*
NMR Research Unit, Faculty of Science, University of Oulu, P.O.Box 3000, 90014 Oulu, Finland. E-mail: otto.mankinen@oulu.fi; ville-veikko.telkki@oulu.fi
First published on 2nd September 2022
Abstract
Molecular exchange between different physical or chemical environments occurs due to either diffusion or chemical transformation. Nuclear magnetic resonance (NMR) spectroscopy provides a means of understanding the molecular exchange in a noninvasive way and without tracers. Here, we introduce a novel two dimensional, single-scan ultrafast Laplace NMR (UF LNMR) method to monitor molecular exchange using transverse relaxation as a contrast. The UF T2–T2 relaxation exchange spectroscopy (REXSY) method shortens the experiment time by one to two orders of magnitude compared to its conventional counterpart. Contrary to the conventional EXSY, the exchanging sites are distinguished based on T2 relaxation times instead of chemical shifts, making the method especially useful for systems including physical exchange of molecules. Therefore, the UF REXSY method offers an efficient means for quantification of exchange processes in various fields such as cellular metabolism and ion transport in electrolytes. As a proof of principle, we studied a halogen-free orthoborate based ionic liquid system and followed molecular exchange between molecular aggregates and free molecules. The results are in good agreement with the conventional exchange studies. Due to the single-scan nature, the method potentially significantly facilitates the use of modern hyperpolarization techniques to boost the sensitivity by several orders of magnitude.
1. Introduction
Molecular exchange occurs due to diffusion or chemical transformations.1,2 When exchange occurs in a liquid or gas contained in a solid structure, its direct monitoring is challenging. Nuclear magnetic resonance spectroscopy (NMR) is used in the investigation of molecular motion in a noninvasive way, without tracers and it can be used in studying optically opaque samples.3 Different multidimensional NMR exchange methods, such as exchange spectroscopy (EXSY),4 diffusion exchange spectroscopy (DEXSY)5,6 and T2–T2 relaxation exchange spectroscopy (REXSY),7–9 have been exploited in the analysis of molecular exchange processes. For example, the REXSY method has been used to investigate exchange in urea-water systems,7,10 human cortical bone,11 geopolymers12 and shale,13 track pore-to-pore exchange,14 asphaltene adsorption,15 and water exchange in myelinated nerves16 and study aggregation of ionic liquids.17 These methods provide a two-dimensional map, in which the exchange sites and exchange are visible. However, these two-dimensional exchange NMR experiments must be repeated tens to hundreds of times with incremented evolution time or gradient strength, leading to long experiment times. Furthermore, the need for repetitions restricts the use of sensitivity increasing hyperpolarization methods.18Ultrafast (UF) NMR spectroscopy, a concept introduced by Frydman et al,19,20 enables collection of multidimensional NMR data in a single scan. This technique is based on spatial encoding, where different evolution times are encoded into the different layers of the sample. After that, the encoded data are read using the principles of magnetic resonance imaging (MRI).8,9 As a result, the two-dimensional data is collected in a single scan and is analogous to the conventional, slow, counterpart.
Swisher et al.21 described a single scan UF EXSY method, which is based on small flip angle pulses, phase accrual during the spin echo times and collection of very few points in the indirect dimension. This method facilitates the collection of a series of data with variable mixing time just in a single scan. Therefore, it can be used in the full characterization of exchange process, although with reduced number of data points.
Spatial encoding has been exploited in T1 relaxation and diffusion experiments as well.22–31 Lately, we have introduced the spatial encoding technique to many multidimensional relaxation and diffusion experiments, which enable one to correlate various LNMR parameters such as T1, T2 and diffusion coefficient D.30–36 The inverse Laplace transformation (ILT) of the data provides relaxation time or diffusion coefficient distribution.37 Therefore, these methods are referred to as UF Laplace NMR (LNMR). UF LNMR has diverse application fields ranging from the identification of intracellular and extracellular metabolites38 to porous materials research,36 and the methods are applicable even with low field single-sided NMR instruments.39–41 The UF approach shortens the experiment time by one to three orders of magnitude.42 Due to the single-scan nature of UF LNMR methods, the use of hyperpolarization is feasible.36
Recently, we introduced the first UF LNMR exchange experiment, UF DEXSY, which relies on diffusion contrast.35 The experiment was exploited to study the exchange of water in a vesicle system formed by surfactant molecules. Here, we introduce a new ultrafast T2–T2 relaxation exchange spectroscopy (UF REXSY) method. We demonstrate its feasibility by quantifying molecular exchange of an ionic liquid (IL) system, which is a novel application area of UF LNMR. ILs are salts with melting point below 100 °C, and they are attractive for many applications such as organic synthesis, catalysis, lubrication, and electrochemistry due to their favorable properties such as low vapor pressure and flammability as well as high thermal stability.43
2. Experimental
2.1 Sample
The IL sample consisting of trihexyl(tetradecyl)phosphonium cations, [P6,6,6,14]+, and bis(mandelato)borate anions, [BMB]− was previously prepared17 and reused in this study. Due to the previous 129Xe NMR analysis, the sample included also Xe gas. In the sample preparation, the residual moisture was removed from the IL in vacuum at 383 K for 4 hours. After that 300 μl of the IL was transferred in a 5 mm NMR tube and 129Xe gas at 1 atm was added to the NMR sample tube. Finally, the NMR tube was sealed by a flame.2.2 Conventional REXSY experiments
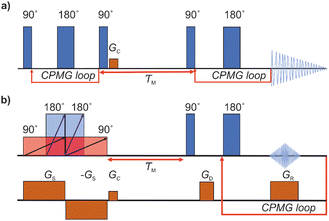
As a reference data, we used T2–T2 data measured previously.17 To make results better comparable, the original data was cut to correspond roughly same echo time window as in the UF experiments. The conventional REXSY pulse sequence includes two CPMG blocks separated by a mixing time (Fig. 1a).7 Five experiments were performed at different mixing time varying from 50 to 400 ms. The relaxation delay was 3 s and echo time was 2 ms. After the first CPMG block, 1 ms crusher gradient Gc was applied to eliminate residual transverse magnetization. A total of 32 points was collected in each dimension with 8 scans and it took 8 hours to complete one experiment.2.3 Ultrafast REXSY exchange experiments
The UF REXSY exchange experiments (Fig. 1b) were performed on a Bruker Avance III 400 MHz spectrometer at room temperature. The lengths of the 90° and 180° chirp pulses were 25 and 12.5 ms, respectively, and the sweep width Δν was 100 kHz. The strength of the spatial encoding gradient Gs was 133 mT m−1. The number of echoes in the CPMG loop was 32, the echo time was 5 ms, and each echo was consisted of 128 complex points. The strength of the trapezoidal read gradient GR was 75 mT m−1 with the gradient ramp and stabilization times of 200 and 50 μs, respectively. Five experiments were performed varying the mixing time from 30 to 400 ms. The experiment time with 512 scans and the relaxation delay of 7 s was 1 hour. The Iterative Thresholding Algorithm for Multiexponential Decay (ITAMeD)44 was used for ILT analysis. For each map, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, grid size of 25 by 25 and inversion limits from 0.001 to 1 s were used. The regularization parameter was chosen so that the inversion was stable and same value was used for all the maps for ensure comparison between measurements. The selection of suitable regularization parameter depends on the data quality and used ILT parameters such as grid size and inversion limits.
000 iterations, grid size of 25 by 25 and inversion limits from 0.001 to 1 s were used. The regularization parameter was chosen so that the inversion was stable and same value was used for all the maps for ensure comparison between measurements. The selection of suitable regularization parameter depends on the data quality and used ILT parameters such as grid size and inversion limits.
3. Results and discussion
The pulse sequence of the conventional REXSY experiment (Fig. 1a) has two CPMG blocks separated by the mixing period τM.7 This experiment shows a relationship between the initial and final T2 relaxation time. The change in the T2 relaxation time indicates that physical or chemical environment of molecule changes during the mixing period. Conventional multidimensional NMR experiments, such as the REXSY experiment, are very time consuming, because data points of indirect dimension are collected individually in separate experiments. In fact, quite often the data of the direct dimension of the conventional REXSY experiment are collected point-by-point as well, leading to even much longer experiments. On the other hand, it is possible to accelerate the conventional REXSY by collecting all the echoes of the direct dimension in a single scan.The pulse sequence for the UF REXSY experiment is shown in Fig. 1b. The sequence is identical to our previously published UF DEXSY sequence,35 but, as we describe below, it can be used also for UF REXSY measurements, when the gradient strengths are small enough and/or diffusion is slow.
The initial part of the sequence used for the single-scan spatial encoding of T2 of the indirect dimension consists of four adiabatic frequency-swept chirp pulses accompanied by two gradient pulses. The frequency of the chirp pulses increases linearly with time. On the other hand, the gradient pulses make the Larmor frequencies of the nuclei linearly dependent on position. Therefore, the first 90° chirp pulse excites the spins at the bottom layer first and the spins at the top layer last. The first 180° chirp pulse starts in the middle of the initial 90° pulse and both pulses switch off at the same time. Therefore, the length of 180° pulse is half of the length of 90° pulse. Technically, the overlapping 90° and 180° pulses were generated by the summation of two individual frequency-swept chirp pulses in the pulse shape tool of the spectrometer, and only single channel was needed for running the experiment. In principle, due to the initial 90° and 180° chirp pulses, a spin echo appears at the end of the pulses, and the echo time is linearly dependent on position, being zero at the top and equal to the length of the 90° pulse at the bottom. In practice, no echo is observed because spins in different layers experience different phases of the frequency-swept pulses.45 However, there is another pair of chirp and gradient right after the initial pulses to compensate the quadratic spatial dependence of the spin phases. In the second pair, the 180° chirp pulse overlaps with the first half of the 90° chirp pulse, and the gradient has an opposite polarity. Overall, the four chirp pulses accompanied by the bipolar gradient pulses form a double spin echo, and the double spin echo time t1 is linearly dependent on position z:35
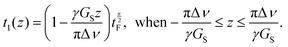 | (1) |
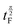 is the length of the 90° chirp pulse. The double spin-echo amplitude is35
is the length of the 90° chirp pulse. The double spin-echo amplitude is35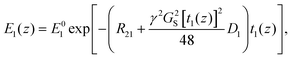 | (2) |
The final part of the sequence (after the mixing time τM) comprises of a CPMG loop for the second T2 encoding and reading data. The CPMG loop includes also gradients GD and GS for reading the spatial encoding information using the principles of 1D MRI.46 The echo amplitude in the CPMG loop in the second T2 encoding block is35
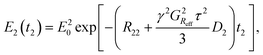 | (3) |
If the sample includes several T2 components and if the diffusion terms are negligible, then, according to eqn (2) and (3), the overall signal observed in the UF REXSY experiment is
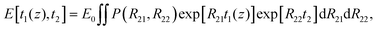 | (4) |
We demonstrate the feasibility of UF REXSY by studying a halogen-free orthoborate based ionic liquid consisting of the trihexyl(tetradecyl)phosphonium, [P6,6,6,14], cations, and bis(mandelato)borate, [BMB], anions (Fig. 2).26 In earlier studies, two significantly different diffusion components were observed from the IL.47 The smaller diffusion coefficient was proposed to arise from aggregates of ions and the higher from free ions. Our previous studies confirmed the existence of the two diffusion coefficients.17 With 2D D-T2 correlation experiments we were able to identify that the two diffusion coefficients are associated with two distinct T2 relaxation times. Our advanced relaxation modelling indicated that the aggregates include 10–70 ion pairs (cations and anions). Conventional REXSY revealed relatively slow exchange between the free ion and aggregate sites. The diffusion coefficients of both free ions and aggregates were observed to be very low, about 5 × 10−12 and 1 × 10−13 m2 s−1 at room temperature, respectively. 1H T2 values of free ions and aggregates are about 80 and 6 ms, respectively, both for cation and anion signals around 0–1 and 4–8 ppm (Fig. 2). Consequently, the IL is an excellent model system for proof-of-principles UF REXSY experiments.
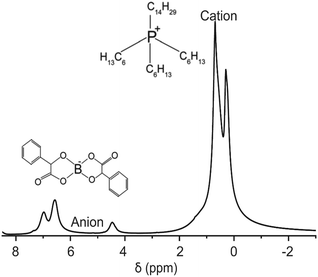 | ||
| Fig. 2 1H spectrum of the ionic liquid composed of trihexyl(tetradecyl)phosphonium, [P6,6,6,14]+, cation and bis(mandelato)borate, [BMB]−, anion measured at room temperature. | ||
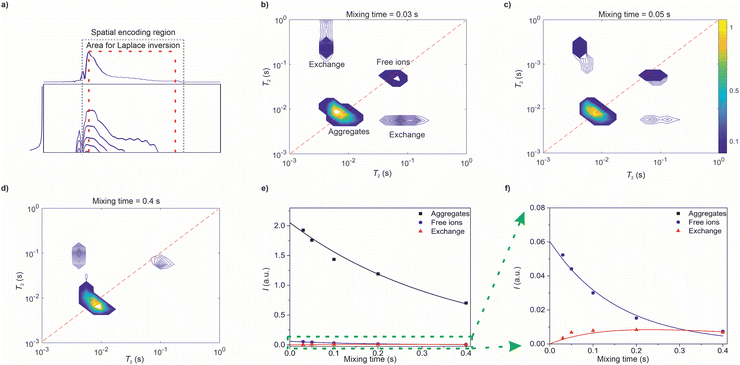
The raw data of the UF REXSY experiment after the Fourier transform along the spatial encoding direction is shown in Fig. 3a. The data was measured with the mixing time τM = 30 ms. The signal decays exponentially in both dimensions. Due to the small diffusion coefficients of the ions and relatively low gradient values used in the experiment, the signal decay is dominated by T2 relaxation, and the diffusion terms in eqn (2) and (3) are negligible. There are some artefacts at the edges of the spatial encoding region (indicated by gray dotted lines) due to imperfect performance of the chirp pulse in the beginning and at the end of the sweep.48 Furthermore, signal is slightly oscillating in the spatial encoding direction, most likely due to interference between the simultaneous 90° and 180° pulses. The data outside the spatial encoding region as well as the artificial regions close to the edges were removed.48
UF REXSY maps resulting from 2D inverse Laplace transform of the raw data are shown in Fig. 3b–d. The maps include two diagonal peaks around T2 = 8 and 80 ms corresponding to free ions and aggregates, respectively.17 Furthermore, there are off-diagonal cross-peaks revealing exchange between the aggregate and free ion sites. The exchange is physical, i.e., the IL molecules are exchanging between the aggregate and free ion sites without chemical modifications in their molecular structures. The integrals of the signals as a function of mixing time are shown in Fig. 3e and f. The integral of the cross-peaks increases first with mixing time because increased number of exchanging ions. For cross-peak integral, average value of the two cross-peaks was used in the analysis. In some maps one of the exchange peaks is not visible due to their low intensity in general compared to the diagonal peaks. However, the loss of the less intense signal does not affect significantly to the result. At the longest mixing times it starts to decay due to T1 relaxation.
Molecular exchange rates were determined by fitting a two-site exchange model (eqn (22)–(25) in ref. 4) with the integral values of diagonal and off-diagonal peaks (solid lines in Fig. 3e and f). The resulting values are k = 1.7 ± 1.1 s−1, kAI = 0.04 ± 0.03 s−1 and kIA = 1.7 ± 1.1 s−1, where subscripts A and I refer to aggregates and ions, respectively. They are in good agreement with the values determined by the conventional reference measurements using roughly same echo time window (k = 1.8 ± 0.9 s−1, kAI = 0.08 ± 0.04 s−1 and kIA = 1.8 ± 0.9 s−1).
The UF REXSY experiment took about 1 h with 512 scans and 7 s relaxation delay. In contrast, the conventional REXSY experiment with 8 scans, 32 echoes in each dimension and 3 s relaxation delay took about 8 h. In the conventional experiment, both the direct and indirect dimensions were collected point-by-point, and reduced relaxation delay was used for shortening the extremely long experiment time. Theoretically, a single-scan UF REXSY experiment is 1024 times faster than a single-scan conventional experiment, if 32 time points are collected in each direction. On the other hand, it is possible to collect the direct dimension in a single scan also in the conventional experiment, reducing the UF acceleration to the factor of 32. The number of points in the UF experiments can be increased without time penalty. However, the spatial encoding decreases slightly the sensitivity of the experiment (typically by the factor of four),36 which may require higher number of scans collected in the UF experiment, if the sensitivity is a limiting factor. On the other hand, the single-scan UF approach significantly facilitates the use of hyperpolarization to boost the sensitivity of the experiment by several orders of magnitude.18
As explained earlier, the UF sequence shown in Fig. 1b can be used for both REXSY and DEXSY experiments. The type of the contrast depends on whether the signal decay is dominated by T2 relaxation or diffusion. As shown by eqn (2) and (3), the contrast can be adjusted by gradient strengths. Low gradient strengths result in T2 contrast while high values provide diffusion contrast. On the other hand, spatial encoding requires high enough gradient strengths. Therefore, the UF REXSY experiment is best suitable for samples with relatively low diffusion coefficients. In the case of faster diffusion, it is better to rely on diffusion contrast. In the case of more complex samples, the hard 90° and 180° pulses can be replaced by corresponding frequency selective pulses in the CPMG loop to select only desired signals from the spectrum.
4. Conclusions
In this article, we demonstrated the feasibility of a novel UF T2–T2 relaxation exchange spectroscopy (REXSY) NMR experiment and showed that it can be used for reliable quantification of exchange rates between aggregate and free ion sites in an ionic liquid sample, which is a new, interesting application field of UF LNMR. Depending on experimental parameters (i.e., gradient strength) and diffusion coefficients, the same experiment can be used for T2 or diffusion contrast-based exchange experiments. The method significantly shortens the experiment time as compared to the conventional REXSY experiment, which is beneficial, e.g., in the studies of samples that evolve or degrade over time. The method allows also improving resolution of the experiment in time efficient manner. Furthermore, the single scan approach facilitates the use modern hyperpolarization methods to boost sensitivity by several orders of magnitude, allowing low concentration studies even in physiological concentrations, and the observation window can be extended by using heteronuclei such as 13C with significantly longer T1 relaxation time than 1H.36,38 The method can be exploited to study physical or chemical exchange phenomena in many disciplines ranging from chemistry and biochemistry materials science, including protein-ligand binding, rearrangement of secondary structures of RNA, metabolic processes and exchange phenomena related to novel biomarkers.38,49–51Author contributions
M. S. U and O. M contributed equally to this work; M. S. U.: formal analysis, investigation, writing – original draft, visualization; O. M.: conceptualization, methodology, formal analysis, investigation, data curation, supervision; V. V. Z: conceptualization, data curation, funding acquisition, supervision; V.-V. T.: conceptualization, supervision, funding acquisition, project administration, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the European Research Council (Project number 772110), Academy of Finland (Grant No. 323480 and 340099), KAUTE foundation and the University of Oulu (Kvantum Institute) is gratefully acknowledged. This work was carried out with the support of the Centre for Material Analysis, University of Oulu, Finland. We also acknowledge the research group of Oleg N. Antzutkin (Luleå University of Technology, Sweden) for providing the ionic liquid sample.References
- P. T. Callaghan, A. Coy, D. MacGowan, K. J. Packer and F. O. Zelaya, Nature, 1991, 351, 467–469 CrossRef CAS.
- K. Inomata, A. Ohno, H. Tochio, S. Isogai, T. Tenno, I. Nakase, T. Takeuchi, S. Futaki, Y. Ito, H. Hiroaki and M. Shirakawa, Nature, 2009, 458, 106–109 CrossRef CAS.
- P. T. Callaghan, Translational dynamics and magnetic resonance: principles of pulsed gradient spin echo NMR, Oxford University Press, 2011 Search PubMed.
- J. Jeener, B. H. Meier, P. Bachmann and R. R. Ernst, J. Chem. Phys., 1979, 71, 4546–4553 CrossRef CAS.
- Y. Qiao, P. Galvosas, T. Adalsteinsson, M. Schönhoff and P. T. Callaghan, J. Chem. Phys., 2005, 122, 214912 CrossRef CAS.
- P. T. Callaghan and I. Furó, J. Chem. Phys., 2004, 120, 4032 CrossRef CAS PubMed.
- J. H. Lee, C. Labadie, C. S. Springer, G. S. Harbison, J. H. Lee, C. Labadie, C. S. Springer and G. S. Harbison, J. Am. Chem. Soc., 1993, 115, 7761–7764 CrossRef CAS.
- K. E. Anderssen and E. R. McCarney, Food Control, 2022, 132, 108373 CrossRef CAS.
- M. N. D’Eurydice, E. T. Montrazi, C. A. Fortulan and T. J. Bonagamba, J. Chem. Phys., 2016, 144, 204201 CrossRef PubMed.
- R. D. Dortch, R. A. Horch and M. D. Does, J. Chem. Phys., 2009, 131, 164502 CrossRef CAS PubMed.
- R. A. Horch, J. S. Nyman, D. F. Gochberg, R. D. Dortch and M. D. Does, Magn. Reson. Med., 2010, 64, 680–687 CrossRef CAS PubMed.
- J. Li, S. Mailhiot, H. Sreenivasan, A. M. Kantola, M. Illikainen, E. Adesanya, L. Kriskova, V. V. Telkki and P. Kinnunen, Cem. Concr. Res., 2021, 143, 106394 CrossRef CAS.
- M. A. Javed, S. Komulainen, H. Daigle, B. Zhang, J. Vaara, B. Zhou and V. V. Telkki, Microporous Mesoporous Mater., 2019, 281, 66–74 CrossRef CAS.
- K. E. Washburn and P. T. Callaghan, Phys. Rev. Lett., 2006, 97, 175502 CrossRef CAS PubMed.
- I. Shikhov, R. Li and C. H. Arns, Fuel, 2018, 220, 692–705 CrossRef CAS.
- R. A. Horch, J. C. Gore and M. D. Does, Magn. Reson. Med., 2011, 66, 24–31 CrossRef CAS.
- M. A. Javed, S. Ahola, P. Håkansson, O. Mankinen, M. K. Aslam, A. Filippov, F. U. Shah, S. Glavatskih, O. N. Antzutkin and V. V. Telkki, Chem. Commun., 2017, 53, 11056–11059 RSC.
- V. V. Telkki, Magn. Reson. Chem., 2018, 56, 619–632 CrossRef CAS PubMed.
- L. Frydman, T. Scherf and A. Lupulescu, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15858–15862 CrossRef CAS PubMed.
- P. Pelupessy, J. Am. Chem. Soc., 2003, 125, 12345–12350 CrossRef CAS.
- C. Leon Swisher, B. Koelsch, S. Sukumar, R. Sriram, R. D. Santos, Z. J. Wang, J. Kurhanewicz, D. Vigneron and P. Larson, J. Magn. Reson., 2015, 257, 102 CrossRef CAS PubMed.
- E. McVeigh, A. Yang and E. Zerhouni, Med. Phys., 1990, 17, 131–134 CrossRef CAS PubMed.
- J. G. Pipe, J. Magn. Reson., 1992, 99, 582–589 CAS.
- M. J. Thrippleton, N. M. Loening and J. Keeler, Magn. Reson. Chem., 2003, 41, 441–447 CrossRef CAS.
- P. E. S. Smith, K. J. Donovan, O. Szekely, M. Baias and L. Frydman, ChemPhysChem, 2013, 14, 3138–3145 CrossRef CAS PubMed.
- Y. Shrot and L. Frydman, J. Magn. Reson., 2008, 195, 226–231 CrossRef CAS.
- L. Guduff, D. Kurzbach, C. van Heijenoort, D. Abergel and J. N. Dumez, Chem. – Eur. J., 2017, 23, 16722–16727 CrossRef CAS PubMed.
- L. Guduff, I. Kuprov, C. Van Heijenoort and J. N. Dumez, Chem. Commun., 2017, 53, 701–704 RSC.
- S. Ahola, O. Mankinen and V. V. Telkki, Magn. Reson. Chem., 2017, 55, 341–347 CrossRef CAS PubMed.
- V. V. Zhivonitko, M. S. Ullah and V. V. Telkki, J. Magn. Reson., 2019, 307, 106571 CrossRef CAS PubMed.
- M. Urbańczyk, Y. Kharbanda, O. Mankinen and V. V. Telkki, Anal. Chem., 2020, 92, 9948–9955 CrossRef PubMed.
- S. Ahola and V.-V. Telkki, ChemPhysChem, 2014, 15, 1687–1692 CrossRef CAS PubMed.
- O. Mankinen, J. Hollenbach, S. Ahola, J. Matysik and V. V. Telkki, Microporous Mesoporous Mater., 2018, 269, 75–78 CrossRef CAS.
- B. J. Tickner, V. V. Zhivonitko and V. V. Telkki, Phys. Chem. Chem. Phys., 2021, 23, 16542–16550 RSC.
- O. Mankinen, V. V. Zhivonitko, A. Selent, S. Mailhiot, S. Komulainen, N. L. Prisle, S. Ahola and V. V. Telkki, Nat. Commun., 2020, 11, 1–8 CrossRef PubMed.
- S. Ahola, V. V. Zhivonitko, O. Mankinen, G. Zhang, A. M. Kantola, H. Y. Chen, C. Hilty, I. V. Koptyug and V. V. Telkki, Nat. Commun., 2015, 6, 1–7 Search PubMed.
- Y. Q. Song, L. Venkataramanan, M. D. Hürlimann, M. Flaum, P. Frulla and C. Straley, J. Magn. Reson., 2002, 154, 261–268 CrossRef CAS PubMed.
- G. Zhang, S. Ahola, M. H. Lerche, V. V. Telkki and C. Hilty, Anal. Chem., 2018, 90, 11131–11137 CrossRef CAS PubMed.
- J. N. King, V. J. Lee, S. Ahola, V.-V. Telkki and T. Meldrum, Angew. Chem., Int. Ed., 2016, 128, 5124–5127 CrossRef.
- M. Urbańczyk, Y. Kharbanda, O. Mankinen and V. V. Telkki, Anal. Chem., 2020, 92, 9948–9955 CrossRef PubMed.
- Y. Kharbanda, M. Urbańczyk, V. V. Zhivonitko, S. Mailhiot, M. I. Kettunen and V. V. Telkki, Angew. Chem., Int. Ed., 2022, 61, e202203957 CrossRef CAS PubMed.
- V. V. Telkki and V. V. Zhivonitko, Annu. Rep. NMR Spectrosc., 2019, 97, 83–119 CrossRef CAS.
- M. Freemantle, An introduction to ionic liquids, Royal Society of Chemistry, 2009 Search PubMed.
- M. Urbańczyk, D. Bernin, W. Koźmiński and K. Kazimierczuk, Anal. Chem., 2013, 85, 1828–1833 CrossRef PubMed.
- A. Tal and L. Frydman, Prog. Nucl. Magn. Reson. Spectrosc., 2010, 57, 241–292 CrossRef CAS PubMed.
- R. W. Brown, Y. C. N. Cheng, E. M. Haacke, M. R. Thompson and R. Venkatesan, Magnetic Resonance Imaging: Physical Principles and Sequence Design: Second Edition, John Wiley & Sons Ltd, Chichester, UK, 2014 Search PubMed.
- A. Filippov, F. U. Shah, M. Taher, S. Glavatskih and O. N. Antzutkin, Phys. Chem. Chem. Phys., 2013, 15, 9281–9287 RSC.
- V. V. Telkki, M. Urbańczyk and V. Zhivonitko, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 126–127, 101–120 CrossRef CAS PubMed.
- M. S. Ullah, V. V. Zhivonitko, A. Samoylenko, A. Zhyvolozhnyi, S. Viitala, S. Kankaanpää, S. Komulainen, L. Schröder, S. J. Vainio and V. V. Telkki, Chem. Sci., 2021, 12, 8311–8319 RSC.
- L. Baronti, I. Guzzetti, P. Ebrahimi, S. Friebe Sandoz, E. Steiner, J. Schlagnitweit, B. Fromm, L. Silva, C. Fontana, A. A. Chen and K. Petzold, Nature, 2020, 583, 139–144 CrossRef CAS PubMed.
- C. Qi, Y. Wang and C. Hilty, Angew. Chem., Int. Ed., 2021, 60, 24018–24021 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Contains all the UF and the conventional T2–T2 exchange maps and two site fits. See DOI: https://doi.org/10.1039/d2cp02944h |
| ‡ Both authors contributed equally to this manuscript. |
| This journal is © the Owner Societies 2022 |