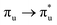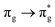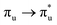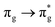A theoretical investigation of uranyl covalency via symmetry-preserving excited state structures

Abstract

Time dependent density functional theory (TDDFT) calculations have been performed on a series of symmetry-preserving excited states of the uranyl dication, UO₂²⁺. The simulated excited state electronic structures are compared to that of the ground state at both ground and excited state-optimised geometries. For the first time, the Quantum Theory of Atoms in Molecules (QTAIM) has been applied to the excited states electronic structures of uranyl in order to quantify the variation in bond covalency upon electronic excitation. QTAIM analysis of vertical excitations at the ground state geometry demonstrated an inverse relationship between the orbital mixing coefficient, λ, and the excitation energy. Furthermore, it was found that, for MOs with U 5f character, λ was more dependent on the metal–ligand Hamiltonian matrix element H_ML, whereas for those with U 6d character, λ became increasingly dependent on the difference in fragment orbital energy levels, ΔE_ML. Charge transfer from O to U reduced as the excitation energy increased, as did the degree of electron sharing between the centres. When considering the relaxed excited state geometries, a relationship between excitation energy and bond elongation was established, commensurate with the large magnitude of λ and its dependence on H_ML for MOs with U 5f character, and enhanced charge transfer otherwise.

---

1. Introduction

While covalency is well-established for the majority of the periodic table, understanding bonding interactions for actinide complexes is a continuously evolving area of research. Rationalising covalency in actinide complexes remains a challenging experimental and computational problem and deeper understanding is of great importance.^1–3 From a fundamental perspective, understanding the bonding interactions within actinide complexes aids in the assessment of the viability of novel synthetic complexes,^4,5 while in a practical application, variation in the bonding character is of particular importance for spent fuel reprocessing in the nuclear power industry. Indeed, selective complexation exploits the variation in the bonding character of complexes and is used in the chemical separation of the chemically similar trivalent actinides and lanthanides.^6,7

Covalency, as defined by Heitler and London,⁸ is fundamental to our understanding of chemical bonding. In transition metals, metal–ligand orbital mixing and overlap as descriptors of covalent character is well established; however, the prevalence of covalent bonding in actinides is heavily debated.^9–11 Therefore, understanding the role of the 5f and 6d orbitals in covalent bonding of actinides remains an important goal in fundamental actinide chemistry.^12,13 While the concept of covalency is well-established, there is no formal physical definition. At the theoretical ionic limit there is no mixing among the valence orbitals, deviations from this idealised picture can be considered through perturbation theory. The mixing between a metal (ϕ_M) and ligand (ϕ_L) orbital, with energies E_M and E_L, in a molecular orbital φ can be expressed as:

φ(r) = ϕ_M(r) + λϕ_L(r) (1)

where the mixing coefficient λ is given to first order by:¹⁴Here H_ML is the Hamiltonian matrix element between the two orbitals and is approximately proportional to the overlap (S_ML).¹⁴ Since S_ML is correlated to the bond length, it follows that the same is true for H_ML.

In uranyl, H_ML can be taken as a measure of the strength of interactions between the uranium 5f/6d and oxygen 2p orbitals, whereas, E_ML is the energy difference between the metal and ligand orbitals. The mixing coefficient (λ) is a measure of the covalent character of the bond. Values of λ are, in general, nonzero and maximum covalency is achieved when λ = 1, e.g. in a homonuclear diatomic at its equilibrium geometry.

Eqn (2) indicates that covalency can be driven by two factors:¹⁵

(i). Large values of H_ML, corresponding to overlap-driven covalency.

(ii). Small values of ΔE_ML, corresponding to (energy) degeneracy-driven covalency.

The inherent properties of actinides makes characterising the bonding interactions, and therefore the origins of covalency, challenging for both experimentalists and theorists. Actinide complexes exhibit strong relativistic effects, weak crystal fields and strongly correlated valence electronic structures.^16,17 These strongly-correlated systems result in ambiguous orbital-based descriptions of the electronic structure and as such, analysis using orbital-based methods should be contextualised with other approaches.^18–23 Analytical methods based on the experimentally observable electron density provide a robust and unambiguous alternative. In this contribution, the Quantum Theory of Atoms in Molecules (QTAIM), developed by Bader,²⁴ will be utilised. QTAIM divides a molecule up into a contiguous set of space-filling atomic basins. This method provides insight into the bonding interactions via both topological and integrated properties of the electron density, which can be used to build up a picture of the covalency in a molecule. We direct the reader to a recent article which gives a detailed overview of this analysis.¹⁵

QTAIM has been successfully used to characterise the bonding interactions in many f-element complexes.^{21,23,25–34} One of the earliest applications of QTAIM analysis in f-element chemistry was conducted by Kaltsoyannis and co-workers.^25,26 In these contributions, the covalency in AnCp₄ and AnCp₃ complexes (An = Th-Cm) were studied. The densities were generated using density functional theory (DFT) and the covalency was assigned using the magnitude of the topological QTAIM metric, ρ_BCP. This metric indicated that, in these organometallic complexes, the interaction between the actinide and coordinating carbon was mainly ionic in character and this ionic character increased with atomic number. This trend was also established by our own group³² in studies of AnCOT₂ complexes (COT = η⁵–C₈H₈) where, in contrast to the previous contributions, the complete-active-space self-consistent-field (CASSCF) method was utilised to generate the simulated density. We also analysed the degree of electron sharing between the actinide and coordinating carbon species via the delocalisation index, an integrated QTAIM metric. Both integrated and topological metrics gave the same broad trend.

Of more direct relevance to the present study, QTAIM has also been utilised to study the covalency of uranyl and its complexes. Vallet et al.²³ found that free uranyl (UO₂²⁺) has strongly covalent interactions between the uranium and oxygen as indicated by the large ρ_BCP and DI metrics. They also concluded that there is a significant decrease in the magnitude of these metrics (ρ_BCP and DI) after ligation to the equatorial plane, indicating a decrease in covalency. Comparable bonding characteristics were also established by our group⁴ using similar techniques. In this contribution, we investigate covalency in uranyl via the exploration of excitations which maintain symmetry of the electronic wavefunction, considering both ground and electronically excited state geometries. These excitations were chosen specifically to ensure that linearity of the uranyl unit is maintained since excitations are largely characterised as being from bonding to anti-bonding MOs of the same irreducible representation (Fig. 1), giving relatively simple excited state electronic structures. Throughout this work, singlet excitations comprised of transitions from bonding to antibonding orbitals of the same character (e.g.) will be investigated, along with the optically accessible triplet excitation (σ_u → δ_u), which is allowed via spin–orbit coupling.^35–39

Fig. 1 MOs involved in the excitations considered in this study. Irreps are those of the d_2h point group. For degenerate MOs, only excitations between those of the same irrep were considered to ensure A_g symmetry was maintained in the electronic structure.

The excitation energy, as well as the energy difference between a bonding (φ) and antibonding (φ*) MO of the same irrep can be linked with the terms in eqn (2). These energy differences would be expected to be large when either charge transfer character is large (implying a small value of λ) and/or H_ML is large (which implies a large value S_ML but doesn’t fully characterise λ).

2. Computational details

Initially, simulations employed version 7.3 of the TURBOMOLE code⁴⁰ to explore the excitations of A_g symmetry within the d_2h point group. Once excitations of interest were identified, Gaussian09 (Revision E.01)⁴¹ was employed and, unless explicitly stated, all presented results are derived using Gaussian. All simulations were performed at the hybrid Density Functional Theory (DFT) level, employing the B3LYP exchange-correlation functional.^42,43 The aug-cc-pVDZ basis set^44,45 was employed for oxygen along with Stuttgart RSC 1997 basis set and associated small core effective core potential for uranium.^46–48 Geometry optimisations were performed for both ground and electronic excited state geometries and structures characterised as minima by vibrational frequency analysis. Electronic excitations were calculated at both the ground and excited state geometries employing the Tamm–Dancoff Approximation (TDA)⁴⁹ to Time Dependent-DFT.^50,51 Version 19.02.13 of AIMAll⁵² and version 3.6 of Multiwfn⁵³ were used in the density-based analysis of the simulated electronic structures. The latter was also employed in the generations of density difference data.

Throughout this contribution, variations in different properties (denoted δ/Δ) are evaluated by subtracting the ground state property from the excited state property. A schematic for the specific differences considered is shown in Fig. 2.

Fig. 2 Representation of comparative quantities considered in this contribution, along with nomenclature used to represent them. Δ^GS compares ground and excited state properties at the ground state geometry, Δ^ES compares the same at the excited state geometry, and δ compares ground and excited state properties at their corresponding equilibrium geometries.

3. Results and discussion

3.1 Electronic properties at the ground state geometry

Geometry optimisation of UO₂²⁺ produced a U-O bond length of 1.70 Å, in excellent agreement with previously reported values (1.68–1.72 Å).^54–56 Electronic excitations in which the dominant orbital transitions were between MOs of the same irrep and same bonding character were identified and are summarised in Table 1. The π → π* excitations are comprised of two symmetry-equivalent transitions. The character of each excited state was assigned through a single dominant transition (>75%), with the exception of which, while the most dominant character, also presented significant (33%) character.

Table 1 Characterisation of electronic excitations at the ground state geometry of uranyl

Excitation	Δ ^GS E (eV)	Contribution (%)
	7.38	88
	12.75	44
	13.41	78
	16.65	98

---

Excitations involving transitions between MOs of u (ungerade) symmetry, possessing U 5f character, are shown to occur at lower energies than those of g (gerade) symmetry, possessing U 6d character.

It then follows that transitions involving MOs with U 5f character maintain greater covalent character, as measured by λ, and/or smaller values H_ML when compared to those involving MOs with 6d character. Clark and co-workers¹² investigated the covalency of actinide chlorides and concluded that the 6d-orbitals were available for orbital mixing to a larger extent than the 5f-orbitals. They also stated that this observation is consistent with other accounts,^57–59 which all suggest that 5f-orbitals have a small H_ML and hence limited participation in covalent bonding.

In order to further rationalise the difference in U 5f/6d bond character, integrated properties of the electron density were evaluated within the Quantum Theory of Atoms in Molecules (QTAIM) framework. Specifically, the atomic charge (q), as well as the localisation (LI) and delocalisation (DI) indices were considered (Table 2).^4,18,32 While the atomic charge is a one-electron property obtained via integration of the total electron density in an atomic basin, the localisation and delocalisation indices are formally two-electron properties. LI provides a measure of the number of electrons localised on a given atom while DI measures the number of electrons shared between two atoms and, in the absence of bond polarisation, acts as a bond order metric. Combined, these metrics can provide detailed information regarding the nature and magnitude of bonding interactions, highlighting variation in both charge transfer and covalency. Here, we consider the variation in a metric, M, by comparing its value in the excited state to that in the ground state, such that:

Δ^GSM = M(ES) − M(GS) (3)

where M(GS/ES) indicates the value of the metric in the ground/excited state. Δ^GS is reported in Table 2, with M(GS/ES) values provided in the ESI.†

Table 2 Variation in charge (q), localisation (LI) and delocalisation (DI) indices between the ground and excited state electronic structures

Excitation	ΔE (eV)	Δ ^GS q(U) (a.u.)	Δ ^GS q(O) (a.u.)	Δ ^GSLI(U)	Δ ^GSLI(O)	Δ ^GSDI(U,O)
	7.38	−0.050	+0.025	+0.395	+0.186	−0.353
	12.75	−0.106	+0.053	+0.323	+0.094	−0.228
	13.41	−0.181	+0.090	+0.278	−0.016	−0.102
	16.65	+0.215	−0.107	−0.345	−0.103	+0.129

---

Atomic charge data shows that, as excitation energy increases, increasing electronic charge is transferred to the uranium. From an orbital perspective, this implies that the bonding MO has more oxygen character and the antibonding MO more uranium character. A partial exception to this trend is the high energy excitation, where, while the direction of charge transfer is reversed, the excitation has the largest magnitude charge transfer character, and so a correlation between charge transfer character and excitation energy is established. This is commensurate with the excitation energy data which suggest reduced orbital mixing, λ, with increasing excitation energy. This observation further verifies the analysis given that charge transfer would be expected to be minimal when λ = 1.

We have previously highlighted the fact that reliance on charge data alone can lead to incorrect interpretations with regard to variation in uranyl bonding.⁴ Here, while LI(U) qualitatively mirrors the atomic charge data, with Δ^GSLI > 0 when charge is transferred to the uranium and Δ^GSLI < 0 when charge is transferred from the uranium, the overall trend is not replicated, e.g. the increase in electron localisation is largest for the lowest energy excitation. This is perhaps unsurprising, since the LI alone is insufficient to characterise the electron population, N, of an atom, which can be formally defined in QTAIM as:

A change in the LI of an atom can therefore be due to charge transfer from another atom, a change in the DI between it and other atoms, or a combination of the two. Given that the variation in DI(U,O) opposes that of LI(U) for all excitations and shows greater sensitivity to the excitation energy for the three lowest energy excitations, the atomic charge data can be rationalised. Charge transfer from O to U, as defined by the variation in LI, actually reduces with increased excitation energy, with the increase in Δ^GSq(U) strongly affected by a smaller reduction in DI(U,O) (note that the 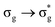excitation shows qualitatively different behaviour, although the same general reasoning applies).

In a monodeterminantal wavefunction, the DI can be interpreted in terms of the overlap between MOs⁶⁰ and, as such, Δ^GSDI would be expected to be largest when λ is closest to 1. Since DI(U,O) reduces with increasing excitation energy, with the exception of the 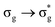state, this further supports the assertion of the anticorrelation of λ with ΔE.

Returning our attention to the excitation, it can be noted from Fig. 1 that the MO has rather diffuse character with significant O contribution. This observation allows us to better understand the electronic structure data. As previously mentioned, the large excitation energy correlates with the substantial charge transfer character of the excitation, albeit with the charge being transferred to the oxygen centres. Here, both LI(U) and LI(O) reduce upon excitation and so the apparent charge transfer is explained by an increase in DI(U,O). As we have discussed above, this is unexpected behaviour for an excitation into a formally antibonding MO and so we suggest that the increase in electronic charge on the (already anionic) oxygen centres has a substantial secondary effect on the electronic structure, causing the doubly occupied σ_u and π_g/u MOs to adopt more covalent character leading to the net increase in DI(U,O). This dramatic behaviour suggests that λ is smallest in σ_g, again strengthening the relationship between λ and ΔE that we have already identified.

In a simple two-level model, we would expect the energy difference between the bonding and antibonding MOs, and therefore the φ → φ* excitation energy, to increase monotonically with the magnitude of the Hamiltonian matrix element between the relevant metal and ligand levels. From our analysis above, this would imply an inverse relationship between λ and H_ML. However, eqn (2) states the opposite, leading us to deduce that ΔE_ML increasingly outweighs H_ML as the excitation energy increases, implying that ΔE_ML dominates in covalent interactions involving U 6d contributions, whereas H_ML dominates for covalent interactions involving U 5f orbitals. Since delocalisation indices themselves are unable to differentiate between overlap- and degeneracy-driven covalency,¹⁵ we turn our attention to topological properties of the electron density. ρ_BCP measures the electron density at the bond critical point (BCP) between two chemically bonded species and gives an indication of the charge accumulated at the BCP. This metric would be expected to reflect the degree of overlap-driven covalency, with a common rule of thumb being that ρ_BCP > 0.2 a.u. is indicative of a covalent interaction. However, this will only identify contributions due to σ-type interactions since π-interactions are characterised by a nodal plane in which the BCP typically lies. The Laplacian of ρ_BCP is a complementary metric which can further aid in the characterisation of a bonding interaction. Finally, the magnitude of the energy density, H, which is negative for interactions which have significant electron sharing, can reflect the covalency of an interaction.

The results presented in Table 3 are surprising in that ρ_BCP increases in the electronically excited state. Since the excitations are into formally antibonding MOs, one would expect ρ_BCP, which reflects the degree of covalent character, to decrease in the excited state. However, ρ_BCP also correlates strongly with bond length and so the small increases found here may simply be reflective of the constrained geometry associated with the vertical excitation (an analogous argument can also be made for H). We therefore delay our analysis of topological properties until excited state molecular structures have been considered.

Table 3 Changes in topological QTAIM metrics in electronically excited states when compared to the ground state

Excitation	Δ ^GS ρ BCP (a.u.)	Δ ^GS∇^2ρBCP (a.u.)	Δ ^GS H (a.u.)
	0.026	−0.217	−0.048
	0.028	0.036	−0.048
	0.032	−0.293	−0.057
	0.006	−0.148	−0.010

---

3.2 Electronic properties at excited state geometries

Geometry optimisations were performed for each of the electronically excited states discussed in Section 3.1 and the results of these optimisations are presented in Table 4. Fig. 3 compares the density difference generated at both the ground and excited state geometries for each excitation.

Table 4 Characterisation of electronic excitations at the excited state geometries of uranyl and the elongation of the U–O bond compared to the ground state geometry

Excitation	Δ ^ES E (eV)	Δr (Å)	Stokes shift (eV)	Contribution (%)
	5.55	0.135	1.83	47
	10.16	0.166	2.59	23
	9.91	0.194	3.50	66
	16.37	0.051	0.28	98

---

Fig. 3 Comparison of density differences at ground (left) and excited (right) state geometries. Purple/green represents positive/negative electron density.

Table 4 reveals an increase in bond length upon excitation, as expected. Again, the state exhibits a quantitatively different behaviour, with only a modest bond elongation. Inspection of density differences (Fig. 3) reveals that the state exhibits a qualitatively different redistribution of charge and consequently a variation in the interplay between ionic and covalent bond character, providing a potential origin for the calculated bond length.

For the three excited states with qualitatively similar excitation character, the variation in bond length follows the same trend as found for the vertical excitation energies in Section 3.1 and provides further evidence that the reduction in λ is due to an increasingly dominant ΔE_ML contribution, rather than a decrease in H_ML, since only the latter would be expected to directly impact on bond stability. Diabatic excitations in which Δr is large imply that H_ML is also substantial as H_ML is approximately proportional to the overlap (S_ML) which is in turn correlated to bond length.

Excitation energies, along with corresponding orbital contributions, at the relevant excited state minima are presented in Table 4. This contribution remains unchanged for the state but is significantly reduced for the other states, presumably reflecting the deviation from monodeterminantal character as the bond is stretched. The state has contributions from 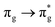orbital transitions and both the and states include contributions from other π → π* transitions.

Excitation energies are all reduced in magnitude when compared to those at the ground state minima, indicating relative destabilisation of the ground state, and so the Stokes shift, calculated here as the difference between the vertical excitation energy at the excited and ground state geometry, describes a red shift for each excited state. The Stokes shift may be utilised to provide further bonding insight, e.g. a small Stokes shift may be indicative of the dependence of λ on ΔE_ML rather than H_ML, however, it also correlates strongly with variation in bond length (see Table 4), and for the states under consideration here this latter correlation restricts further interpretation in terms of electronic structure.

We now again turn our attention again to QTAIM metrics (Table 5), comparing the ground and excited state electronic structures at their corresponding equilibrium geometries (δ in Fig. 2). For completeness, corresponding energy differences (δE, see Fig. 2) at the excited state minima are also included. Trends in all metrics are qualitatively similar to those found at the ground state geometry (cf. Table 2) although the magnitudes vary. For example, the redistribution of charge is accentuated, with enhanced electron localisation as might be expected at longer bond lengths. Uranium localisation is substantial for the three lowest energy excited states and while this is accompanied by an increase in oxygen localisation for the excitations which involve MOs with U 5f character, commensurate with enhanced ionic character, δLI(O) is negative (and substantially larger than that seen at the ground state geometry) in the 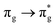state, indicative of enhanced charge transfer character in the excitation.

Table 5 Variation in charge (q), localisation (LI) and delocalisation (DI) indices between the ground and excited state electronic structures at their corresponding equilibrium geometries

Excitation	δE (eV)	δq(U) (a.u.)	δq(O) (a.u.)	δLI(U)	δLI(O)	δDI(U,O)
	6.45	−0.122	+0.061	+0.527	+0.177	−0.410
	11.45	−0.307	+0.153	+0.807	+0.153	−0.509
	11.61	−0.414	+0.207	+0.562	−0.110	−0.152
	16.52	+0.165	−0.082	−0.277	−0.112	+0.110

---

Table 6 summarises the variation in topological QTAIM parameters between ground and excited state electronic structures at their corresponding equilibrium geometries. In contrast to Table 3, ρ_BCP decreases and H increases in the excited states, as would be expected for excitations into formally antibonding MOs. The trends in these variations correlate strongly with the increase in bond length, with the strength of this correlation meaning that further bond characterisation is not possible.

Table 6 Variation in topological QTAIM between the ground and excited state electronic structures at their corresponding equilibrium geometries

Excitation	δρBCP (a.u.)	δ∇^2ρBCP (a.u.)	δH (a.u.)
	−0.066	−0.196	0.130
	−0.082	−0.082	0.159
	−0.096	−0.179	0.182
	−0.032	−0.119	0.064

---

These data allow us to make further observations regarding λ for the orbital excitations associated with each state. At the ground state geometry, it was deduced that for the π_g MO, λ was strongly dependent on H_ML and relatively small. The state provides the largest values of both Δr and the Stokes shift. This state also has the largest redistribution of charge, opposing localisation indices and a low variation in electron delocalisation. This provides further evidence that λ is indeed significantly dependent on H_ML in the π_g MO and that there is a degree of charge transfer character in the excitation, particularly apparent when considering the electronic structure at the excited state minima. This latter point again supports the view of a small value of λ in the π_g MO.

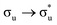The and excited state minima give similar, albeit enhanced, changes in QTAIM metrics to those found at the ground state geometry. The variation in delocalisation index is largest in these two states and this, along with the small redistribution of charge, again supports the view that λ is largest for the π_u and σ_u MOs. Since the excitation energies are lowest for these states, we tentatively suggest that H_ML is relatively small (although still substantial, as evidenced by the pronounced increase in bond lengths) and the large value of λ is due to the interplay between H_ML and ΔE_ML.

3.3. Symmetry decomposition of QTAIM metrics

The high symmetry of uranyl allows the DIs to be decomposed into their symmetry elements. We have previously employed such analysis to differentiate between 5f and 6d contributions to bonding interactions.^{15,18,32,61,62} These symmetry-decomposed DIs are used here to understand how electrons are shared in the ground state as the U=O bond is elongated. Table 7 orders the excited states in terms of increasing bond length and summarises the symmetry-decomposed DIs.

Table 7 Ground state symmetry-decomposed DIs evaluated at the equilibrium geometries of the ground and excited states

State geometry	r (Å)	DI(U,O)
		Total	σu	πu	σg	πg
GS	1.700	2.282	0.578	0.418	0.317	0.275
	1.751	2.278	0.577	0.419	0.312	0.275
	1.835	2.273	0.573	0.425	0.304	0.273
	1.866	2.272	0.572	0.426	0.302	0.273
	1.894	2.270	0.570	0.429	0.300	0.271

---

The total DI reduces with increasing bond length, as would be expected. This behaviour is mirrored in the σ_u and σ_g components, however the π_u component increases with increasing bond length. Since orbital overlap (and therefore H_ML) necessarily decreases with increasing bond length, these data can be interpreted in terms of the relative positions of the energy levels of the fragment orbitals comprising the MO. We can therefore deduce that ΔE_ML decreases more rapidly for the π_u MO in comparison to the others, suggesting that the fragment are brought more closely into resonance as the bond is elongated.

3.4 The optically active excited state

Previous computational studies^{35,37–39,56} have determined that the lowest lying optically active excited state in uranyl can be primarily described as a triplet excitation from the σ_u into the nonbonding 5f_δ orbital, allowed via spin–orbit coupling. This excitation was simulated using the same model chemistry as that employed for our studies of symmetry-preserving excitations, and a vertical excitation energy of 2.43 eV was calculated, in reasonable agreement with the CASPT2 literature value of 2.79 eV calculated in the absence of spin–orbit coupling⁵⁶ and our own CASSCF-calculated value of 2.95 eV. Relaxation of the excited state geometry produced an increase in bond length to 1.747 Å, again in reasonable agreement with the CASPT2 literature value of 1.765 Å, and an excited state energy of 2.18 eV at the excited state minimum. QTAIM metrics at both the ground and excited state geometries are summarised in Table 8.

Table 8 Variation in charge (q), localisation (LI) and delocalisation (DI) indices between the ground and excited state electronic structures at both the ground and excited state geometries. All QTAIM metrics are in a.u. with the exception of the (de)localisation indices, which are dimensionless

Geometry	Δq(U)	Δq(O)	ΔLI(U)	ΔLI(O)	ΔDI(U,O)	ΔρBCP	Δ∇^2ρBCP	ΔH
Ground state	−0.002	+0.001	−0.068	−0.073	+0.064	+0.003	−0.018	−0.004
Excited state	−0.049	+0.025	−0.013	−0.103	+0.055	−0.035	−0.041	+0.068

---

All QTAIM metrics report little to no change in electronic structure upon excitation into the U based 5f_δ orbital, which would only be expected if the σ_u MO were also entirely localised on the U centre. Since our previous analysis has revealed this not to be the case, with the σ_u MO having substantial contributions from both U and O centres, these data can therefore be interpreted as showing a reorganisation amongst the other MOs to accommodate the charge localised in the 5f_δ orbital. Since this reorganisation must therefore involve charge transfer from the U centre, and noting that DI(U,O) increases upon excitation, we can deduce that λ must increase amongst the other MOs, although our methodology cannot be used to determine which specific MOs experience this increase.

4. Conclusions and outlook

Electron-density based analyses of f-element complexes have grown in utility in recent years.^{5,12,15,18,57,61,63} In this contribution, QTAIM analysis has been applied, for the first time, to probe the excited state electronic structure of a uranyl complex. This analysis has been shown to be able to characterise bond covalency in this compound, as well as its origins. Investigations of vertical excitations at the ground state geometry demonstrated an inverse relationship between the orbital mixing coefficient, λ, and the excitation energy. Furthermore, it was found that, for MOs with U 5f character (e.g. σ_u and π_u), λ was more dependent on the metal–ligand Hamiltonian matrix element H_ML, whereas for those with U 6d character (e.g. σ_g and π_g), λ became increasingly dependent on the difference in fragment orbital energy levels, ΔE_ML. Further analysis of the electronic structure showed that charge transfer from O to U reduced as the excitation energy increased, as did the degree of electron sharing between the two centres. The excited state often exhibited quantitatively different behaviour, and this was characterised as being due to a very low value of λ in the σ_g MO and a difference in the dominant atomic contribution to this MO, leading to significant redistribution of charge amongst the other orbitals in this state.

When considering the relaxed excited state geometries, a relationship between excitation energy and bond elongation was established. This was commensurate with the large magnitude of λ and its dependence on H_ML for the σ_u and π_u MOs, however further analysis revealed that the large bond elongation associated with the state could be understood by also recognising enhanced charge transfer character in the excitation. The excitation was again an outlier, where the charge transfer character of the excitation was balanced by the redistribution of charge discussed above.

The dependence of λ on H_ML for excitations involving 5f MOs has also been investigated previously, in particular for actinide halides.^12,61 Tanti et al.⁶¹ concluded that the 5f contributions to overlap-driven covalency were larger than 6d for uranyl/uranium halide complexes. Similar findings were also observed across the actinide series by Clark and co-workers;¹² they suggest that as you traverse the actinides, “the positive effects from ΔE_ML outweigh negative impacts from H_ML and covalency increases.” This contribution complements these findings and suggests that these trends also extend into the excited state.

In contrast to previous literature however, here we conclude that excitations involving the U 5f orbitals have a larger λ than excitations involving U 6d orbitals.^57–59 This is largely due to the anticorrelation between λ and excitation energy, with the large λ value due to the interplay between H_ML and ΔE_ML, as indicated previously.¹²

The calculated ground state delocalisation indices were decomposed into their symmetry-distinct components. It would be expected that delocalisation indices would decrease with increasing bond length, but the π_u component exhibited the opposite behaviour, suggesting enhanced degeneracy-driven covalency with increasing bond length for this component.

Finally, the leading orbital contribution to the lowest energy optically accessible state in uranyl was investigated. QTAIM metrics revealed little difference between ground and excited state electronic structures, which could be interpreted in terms of the previously analysed states as an increase in covalent character amongst the bonding MOs which offset the charge localisation due to excitation into the non-bonding U 5f_δ orbital.

This contribution has demonstrated that analysis of excited state electronic structures can be used to characterise properties of the ground state that would be otherwise challenging to access. Future studies will apply these techniques to more complicated f-element systems to better understand the relative contribution of overlap- and degeneracy-driven covalency to bonding in these compounds.

Conflicts of interest

There are no conflicts to declare.

References

1. A. Formanuik, A. M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. McInnes and D. P. Mills, Actinide covalency measured by pulsed electron paramagnetic resonance spectroscopy, Nat. Chem., 2017, 9, 578–583.
2. L. R. Morss, N. Edelstein, J. Fuger and J. J. Katz, The Chemistry of the Actinide and Transactinide Elements, Springer, 4th edn, 2010.
3. L. S. Natrajan and M. H. L. Paden, F-block elements recovery, 2013, vol. 58.
4. P. Di Pietro and A. Kerridge, U-Oyl Stretching Vibrations as a Quantitative Measure of the Equatorial Bond Covalency in Uranyl Complexes: A Quantum- Chemical Investigation, Inorg. Chem., 2016, 55, 573–583.
5. P. Di Pietro and A. Kerridge, Assessing covalency in equatorial U-N bonds: Density based measures of bonding in BTP and isoamethyrin complexes of uranyl, Phys. Chem. Chem. Phys., 2016, 18, 16830–16839.
6. H. H. Dam, D. N. Reinhoudt and W. Verboom, Multicoordinate ligands for actinide/lanthanide separations, Chem. Soc. Rev., 2007, 36, 367–377.
7. F. W. Lewis, M. J. Hudson and L. M. Harwood, Development of highly selective ligands for separations of actinides from lanthanides in the nuclear fuel cycle, Synlett, 2011, 2609–2632.
8. W. Heitler and F. London, Wechselwirkung Neutraler Atome Und Homöopolare Bindung Nach Der Quantenmechanik, Eur. Phys. J. A, 1927, 6–7, 455–472.
9. J. L. Krinsky, S. G. Minasian and J. Arnold, Covalent lanthanide chemistry near the limit of weak bonding: Observation of (CpSiMe3)3Ce-ECp* and a comprehensive density functional theory analysis of Cp3Ln-ECp (E = Al, Ga), Inorg. Chem., 2011, 50, 345–357.
10. F. A. Cotton, Chemical Applications of Group Theory, John Wiley & Sons, New York, 3rd edn, 2004.
11. K. N. Raymond and C. W. Eigenbrot, Structural Criteria for the Mode of Bonding of Organoactinides and Lanthanides and Related Compounds, Acc. Chem. Res., 1980, 13, 276–283.
12. J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, Energy-Degeneracy-Driven Covalency in Actinide Bonding, J. Am. Chem. Soc., 2018, 140, 17977–17984.
13. R. M. Diamond, K. Street and G. T. Seaborg, An Ion-exchange Study of Possible Hybridized 5f Bonding in the Actinides, J. Am. Chem. Soc., 1954, 76, 1461–1469.
14. S. G. Minasian, J. M. Keith, E. R. Batista, K. S. Boland, D. L. Clark, S. D. Conradson, S. A. Kozimor, R. L. Martin, D. E. Schwarz, D. K. Shuh, G. L. Wagner, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, Determining relative f and d orbital contributions to M-Cl covalency in MCl 62- (M = Ti, Zr, Hf, U) and UOCl 5- using Cl K-edge X-ray absorption spectroscopy and time-dependent density functional theory, J. Am. Chem. Soc., 2012, 134, 5586–5597.
15. A. Kerridge, Quantification of f-element covalency through analysis of the electron density: Insights from simulation, Chem. Commun., 2017, 53, 6685–6695.
16. M. Dolg, Encyclopedia of Computational Chemistry, Wiley, Chichester, 2002.
17. M. Seth, P. Schwerdtfeger, M. Dolg and P. Fulde, Lanthanide and Actinide Contractions: Relativistic and Shell Structure Effects, J. Am. Chem. Soc., 1995, 117, 6597–6598.
18. R. Beekmeyer and A. Kerridge, Assessing covalency in cerium and uranium hexachlorides: A correlated wavefunction and density functional theory study, Inorganics, 2015, 3, 482–499.
19. M. Dolg, P. Fulde, W. Küchle, C. S. Neumann and H. Stoll, Ground state calculations of di-π-cyclooctatetraene cerium, J. Chem. Phys., 1991, 94, 3011–3017.
20. A. Kerridge, R. Coates and N. Kaltsoyannis, Is cerocene really a Ce(III) compound? all-electron spin–orbit coupled CASPT2 calculations on M(8-C8H8)2 (M = Th, Pa, Ce), J. Phys. Chem. A, 2009, 113, 2896–2905.
21. A. Kerridge, Oxidation state and covalency in f-element metallocenes (M = Ce, Th, Pu): A combined CASSCF and topological study, Dalton Trans., 2013, 42, 16428–16436.
22. O. Mooßen and M. Dolg, Two interpretations of the cerocene electronic ground state, Chem. Phys. Lett., 2014, 594, 47–50.
23. V. Vallet, U. Wahlgren and I. Grenthe, Probing the nature of chemical bonding in uranyl(VI) complexes with quantum chemical methods, J. Phys. Chem. A, 2012, 116, 12373–12380.
24. R. F. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990.
25. I. Kirker and N. Kaltsoyannis, Does covalency really increase across the 5f series? A comparison of molecular orbital, natural population, spin and electron density analyses of AnCp3 (An = Th-Cm; Cp = η5-C5H5), Dalton Trans., 2011, 40, 124–131.
26. M. J. Tassell and N. Kaltsoyannis, Covalency in AnCp4 (An = Th–Cm): a comparison of molecular orbital, natural population and atoms-in-molecules analyses, Dalton Trans., 2010, 39, 6576–6588.
27. P. L. Arnold, Z. R. Turner, N. Kaltsoyannis, P. Pelekanaki, R. M. Bellabarba and R. P. Tooze, Covalency in CeIV and UIV halide and N-heterocyclic carbene bonds, Chem. – Eur. J., 2010, 16, 9623–9629.
28. V. V. Zhurov, E. A. Zhurova, A. I. Stash and A. A. Pinkerton, Characterization of bonding in cesium uranyl chloride: Topological analysis of the experimental charge density, J. Phys. Chem. A, 2011, 115, 13016–13023.
29. M. B. Jones, A. J. Gaunt, J. C. Gordon, N. Kaltsoyannis, M. P. Neu and B. L. Scott, Uncovering f-element bonding differences and electronic structure in a series of 1:3 and 1:4 complexes with a diselenophosphinate ligand, Chem. Sci., 2013, 4, 1189–1203.
30. A. C. Behrle, C. L. Barnes, N. Kaltsoyannis and J. R. Walensky, Systematic investigation of thorium(IV)- and uranium(IV)-ligand bonding in dithiophosphonate, thioselenophosphinate, and diselenophosphonate complexes, Inorg. Chem., 2013, 52, 10623–10631.
31. Q. Y. Wu, C. Z. Wang, J. H. Lan, C. L. Xiao, X. K. Wang, Y. L. Zhao, Z. F. Chai and W. Q. Shi, Theoretical investigation on multiple bonds in terminal actinide nitride complexes, Inorg. Chem., 2014, 53, 9607–9614.
32. A. Kerridge, F-Orbital covalency in the actinocenes (An = Th-Cm): Multiconfigurational studies and topological analysis, RSC Adv., 2014, 4, 12078–12086.
33. Q. R. Huang, J. R. Kingham and N. Kaltsoyannis, The strength of actinide-element bonds from the quantum theory of atoms-in-molecules, Dalton Trans., 2015, 44, 2554–2566.
34. S. M. Mansell, N. Kaltsoyannis and P. L. Arnold, Small molecule activation by uranium tris(aryloxides): Experimental and computational studies of binding of N2, coupling of CO, and deoxygenation insertion of CO2 under ambient conditions, J. Am. Chem. Soc., 2011, 133, 9036–9051.
35. K. Pierloot, E. Van Besien, E. Van Lenthe and E. J. Baerends, Electronic spectrum of UO₂²⁺ and [UO₂Cl₄]^2- calculated with time-dependent density functional theory, J. Chem. Phys., 2007, 126, 194311.
36. L. Gagliardi, B. O. Roos, P.-Å. Malmqvist and J. M. Dyke, On the Electronic Structure of the UO ₂ Molecule, J. Phys. Chem. A, 2001, 105, 10602–10606.
37. P. Tecmer, A. S. P. Gomes, U. Ekström and L. Visscher, Electronic spectroscopy of UO22 +, NUO+ and NUN: An evaluation of time-dependent density functional theory for actinides, Phys. Chem. Chem. Phys., 2011, 13, 6249–6259.
38. P. Tecmer, R. Bast, K. Ruud and L. Visscher, Reliable are Electronic Spectra from Relativistic Time-Dependent.
39. P. Tecmer, N. Govind, K. Kowalski, W. A. De Jong and L. Visscher, Reliable modeling of the electronic spectra of realistic uranium complexes, J. Chem. Phys., 2013, 139, 034301.
40. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, TURBOMOLE, Chem. Phys. Lett., 1989, 162, 165–169.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. J. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyez, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresmann, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, L. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09 (Revision E.01), Gaussian Inc., Wallingford CT, 2015.
42. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
43. A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
44. T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023.
45. R. G. Denning, Electronic Structure and Bonding in Actinyl Ions, 1992, pp. 217–276.
46. X. Cao, M. Dolg and H. Stoll, Valence basis sets for relativistic energy-consistent small-core actinide pseudopotentials, J. Chem. Phys., 2003, 118, 487–496.
47. X. Cao and M. Dolg, Segmented contraction scheme for small-core actinide pseudopotential basis sets, J. Mol. Struct.: THEOCHEM, 2004, 673, 203–209.
48. W. Küchle, M. Dolg, H. Stoll and H. Preuss, Energy-adjusted pseudopotentials for the actinides. Parameter sets and test calculations for thorium and thorium monoxide, J. Chem. Phys., 1994, 100, 7535–7542.
49. S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314, 291–299.
50. E. Runge and E. K. U. Gross, No Title, Phys. Rev. Lett., 1984, 52, 997–1000.
51. E. K. U. Gross and W. Kohn, in Density Functional Theory of many-fermion systems, ed. P.-O. Löwdin, 1990, pp. 255–291.
52. T. A. Keith, AIMAll (Version 19.02.13), TK Gristmill Software, Overland Park KS, USA, 2019 (aim.tkgristmill.com).
53. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
54. F. Réal, S. P. Gomes, L. Visscher, V. Vallet and E. Ephraim, Benchmarking Electronic Structure Calculations on the Bare UO 22 + Ion: How Different are Single and Multireference Electron Correlation Methods?, J. Phys. Chem. A, 2009, 113, 12504–12511.
55. F. Wei, G. Wu, W. H. E. Schwarz and J. Li, Geometries, electronic structures, and excited states of UN2, NUO +, and UO22 +: A combined CCSD(T), RAS/CASPT2 and TDDFT study, Theor. Chem. Acc., 2011, 129, 467–481.
56. K. Pierloot and E. Van Besien, Electronic structure and spectrum of UO₂²⁺ and UO₂CI₄^2-, J. Chem. Phys., 2005, 123, 204309.
57. N. Kaltsoyannis, Does covalency increase or decrease across the actinide series? Implications for minor actinide partitioning, Inorg. Chem., 2013, 52, 3407–3413.
58. M. Pepper and B. E. Bursten, The Electronic Structure of Actinide-Containing Molecules: A Challenge to Applied Quantum Chemistry, Chem. Rev., 1991, 91, 719–741.
59. H. M. Crosswhite, H. Crosswhite, W. T. Carnall and A. P. Paszek, Spectrum analysis of U³⁺:LaCI₃, J. Chem. Phys, 1980, 72, 5103.
60. X. Fradera, M. A. Austen and R. F. W. Bader, The Lewis Model and Beyond, J. Phys. Chem. A, 1999, 103, 304–314.
61. J. Tanti, M. Lincoln and A. Kerridge, Decomposition of d- and f-Shell Contributions to Uranium Bonding from the Quantum Theory of Atoms in Molecules: Application to Uranium and Uranyl Halides, Inorganics, 2018, 6, 88.
62. I. Fryer-Kanssen and A. Kerridge, Elucidation of the inverse: Trans influence in uranyl and its imido and carbene analogues via quantum chemical simulation, Chem. Commun., 2018, 54, 9761–9764.
63. P. Di Pietro and A. Kerridge, U-Oyl Stretching Vibrations as a Quantitative Measure of the Equatorial Bond Covalency in Uranyl Complexes: A Quantum-Chemical Investigation, Inorg. Chem., 2016, 55, 573–583.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02878f

---