Inverse design of molecule–metal nanoparticle systems interacting with light for desired photophysical properties†
Received
24th June 2022
, Accepted 31st August 2022
First published on 16th September 2022
Abstract
Molecules close to a metal nanoparticle (NP) have significantly different photophysical properties from those of the isolated one. In order to harness the potential of the molecule–NP system, appropriate design guidelines are required. Here, we propose an inverse design method of the optimal molecule–NP systems and incident electric field for desired photophysical properties. It is based on a gradient-based optimization search within the time-dependent quantum chemical description for the molecule and the continuum model for the metal NP. We designed the optimal molecule, relative molecule–NP spatial conformation, and incident electric field of a molecule–NP system to maximize the population transfer to the target electronic state of the molecule. The design results were presented and discussed. The present method is promising as the basis for designing molecule–NP systems and incident fields and accelerates discoveries of efficient molecular plasmonics systems.
1. Introduction
Light-response properties of molecules in the close vicinity of a metal nanoparticle (NP) surface are strongly modulated by the localized surface plasmon resonance (LSPR). For example, surface-enhanced Raman scattering (SERS),1,2 modulation of the molecular fluorescence,3,4 and plasmon-mediated chemical reactions5,6 are observed. Making use of the plasmonic phenomena is promising for realizing desired photophysical properties of molecules and manipulations of (photo)chemical events.
The molecule–NP systems have huge potential for the design in terms of the designability of their components. Regarding the molecule, more than 8 million molecules have been already synthesized and are available.7 From a practical point of view, it is often important to adjust the properties of a molecule by introducing substituents. The properties of the NP, including LSPR, are determined by its chemical nature, size, shape, and environment. The NPs of coinage metals such as gold and silver support LSPR. Careful control of processing conditions enables the precise control of the NP structures.8 The relative position and orientation of the molecule and NP also affect the properties of the whole system. The control of the distance between molecule and NP can be experimentally realized, and the changes of the plasmonic phenomena were observed.9,10 The incident electromagnetic field, which produces the LSPR and mediates molecule–plasmon interaction, is highly controllable with respect to the time profile and intensity. Thus, the molecule–plasmon systems have a wealth of design possibilities and are promising for nanophotonics applications. The appropriate design guidelines of the tunable parameters of the system are important for exploiting the potential of the plasmonic systems.
For the design of the electronic dynamics, the population transfer from a specific state to a target state is important to manipulate the subsequent photochemical phenomena. The nuclear motion is negligible for the interaction of the molecule with the ultrashort laser pulse in a time scale of a few femtoseconds. In practice, minimizing fluence of the incident field is required in addition to maximization of the population of a specific electronic state.
Design approaches of molecular systems can be categorized into direct and inverse design from the relation between the system and its desired property.11,12 Conceptually, inverse design that starts from the desired performance and predicts the molecular structure is in a straightforward fashion in contrast to the direct approach by “trials and errors.” However, in practice, it is difficult to obtain a realizable molecular system from the desired property by directly solving the inverse problem of the Schrödinger equation.13,14 Thus, commonly, the inverse design indicates design strategies driven by information on functional space corresponding to chemical space.14–19
Converting discrete chemical space of candidate molecular systems into continuous one makes it possible to use gradients of the desired property with respect to characteristics of molecular systems for finding optimal systems. In alchemical transformation methods, the continuous chemical space is interpolated by alchemical systems which are not realizable. The variational particle approach13,15,20 and the linear combination of atomic potentials (LCAP)21 are alchemical transformation methods based on quantum chemical models. In this work, we used the LCAP framework based on the effective Hamiltonian22,23 for designing molecule–NP systems.
In addition to the design of molecular systems, the inverse design of a suitable perturbing agent (e.g., an incident laser pulse) is widely applied to the studies of molecular electronic states.24 The quantum optimal control theory (QOCT) is often used to refer to inverse design of an electromagnetic field applied to a molecule, but they are the same in principle. In particular, the gradient-based method efficiently tailors incident light for photo-excited systems.25,26 Combining it with molecular design provides a possibility to further optimize desired properties. Such a design by theoretical means requires the time-domain description of the phenomena involving light such as the LSPR.
To theoretically describe molecule–plasmon systems, combining the quantum chemical description of the molecule, often referred to as “QM”, with a (semi)classical model of the metal NP is effective since the applicability of full QM methods is computationally limited for the large NPs.27,28 The PCM–NP,29–31 which treats the metal NP as a homogeneous and continuous dielectric based on the polarizable continuum model (PCM),32 allows us to overcome these computational limitations and provides an effective way for interfacing with the QM description of the molecules. In particular, a numerical procedure based on the boundary element method (BEM) reduces the problem to a two-dimensional calculation of polarization charges on the discretized NP surface. Furthermore, the PCM–NP method can model complex-shaped metal NPs. Recent developments in the PCM–NP in the time domain allow simulations of real-time plasmonic phenomena.31,33–36
For the inverse design based on the theoretical description, it is necessary to represent continuous chemical space of possible molecule–NP systems. As described above, the QM/PCM–NP method can simulate photophysical properties of molecule–NP systems based on its design variables: nature, size, shape, and environment of the NP; molecular species; mutual conformation and distance between the molecule and NP; time profile and intensity of the applied electromagnetic field. Therefore, the QM/PCM–NP is well suited to the inverse design. Indeed, the BEM was recently utilized in the design toward optimal mechanical control of a plasmonic NP by incident light.37
In this work, we develop an inverse design method of molecule–NP system and incident light for the desired photophysical property based on the QM/PCM–NP method. For the molecule–NP system, the inverse design method enables the design of the molecular species and the relative molecule–NP distance and conformation. We applied this method to the design of the system with the maximized population of a target electronic state of the molecule at the desired time. The design of the molecule, incident electric field, and both of them was performed on several metal NPs with different metal natures and NP shapes. Given the nature of our work, we limited ourselves to the application of a small number of candidate molecules as a proof of concept of the new methodology. The candidate molecules were MQ and its derivatives as a representative example of the photo-active molecular dyes class, focusing mainly on substituent effects. The results were assessed in terms of the design performance.
2. Methods
Here, we describe the proposed inverse design method of the molecule–NP systems and incident electric fields. Firstly, we present the real-time description of the electronic dynamics of a molecule near a metal NP in order to establish some notations. Secondly, we present the inverse design method based on this theoretical model. Then, the chemical space and incident field for the present design are described. Finally, the computational details are given.
2.1. TD-CI coupled with TD–PCM–NP
We briefly summarize the theoretical description of molecule–NP systems by the time-dependent configuration interaction (TD-CI) method for the molecule coupled with the TD–PCM–NP within the integral equation formalism for the metal NP, developed in ref. 34. The effective Hamiltonian of the molecule near the NP includes the field-free electronic Hamiltonian Ĥ0 of the molecule, molecule–radiation interactions, and molecule–NP interactions:| | Ĥs(t) = Ĥ0 − ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) · ·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inc(t) + (qref(t) + qpol(t))· inc(t) + (qref(t) + qpol(t))·![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) | (1) |
where ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) is the electric dipole operator and
is the electric dipole operator and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inc(t) is the time-dependent incident electric field. qref(t) and qpol(t) are polarization charges of the NP due to the external field and molecule, respectively. The molecule–radiation interaction is modeled in the dipole approximation in the length gauge. In the framework of PCM–NP, the metal NP is described as a continuum body characterized by the dielectric function of the metal. The TD–PCM–NP describes the response of the metal NP to the incident field and molecule as the time-dependent polarization charges qref(t) and qpol(t), respectively, located on geometrical centers of each tessera of the discretized NP surface.
inc(t) is the time-dependent incident electric field. qref(t) and qpol(t) are polarization charges of the NP due to the external field and molecule, respectively. The molecule–radiation interaction is modeled in the dipole approximation in the length gauge. In the framework of PCM–NP, the metal NP is described as a continuum body characterized by the dielectric function of the metal. The TD–PCM–NP describes the response of the metal NP to the incident field and molecule as the time-dependent polarization charges qref(t) and qpol(t), respectively, located on geometrical centers of each tessera of the discretized NP surface. ![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) is the electrostatic potential operator acting at the tesserae positions.
is the electrostatic potential operator acting at the tesserae positions.
The wavefunction |Ψ(t)〉 of the molecule near the NP is propagated based on the time-dependent Schrödinger equation with the incident field
| | 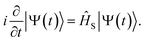 | (2) |
|
Ψ(
t)〉 is expanded using reference ground and excited states |
ΦI〉 with
I = 0 and
I > 0, respectively, of the molecule in the CI theory as
| | 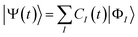 | (3) |
where
CI(
t) is the time-dependent coefficient for the reference
Ith electronic state. The reference ground state |
Φ0〉 is the Hartree–Fock wavefunction of the molecule equilibrated with the NP. The excited states |
ΦI〉 with
I > 0 are obtained at the CI singles (CIS) level of theory. The corresponding time-independent Schrödinger equation for the molecule in the presence of the fixed polarization charge
qpol(|
Φ0〉) evaluated with |
Φ0〉 is
| | [Ĥ0 + qpol(|Φ0〉)·![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) ]|ΦI〉 = EI|ΦI〉 ]|ΦI〉 = EI|ΦI〉 | (4) |
where
EI is the electronic energy of the
Ith electronic state. By using
eqn (3), eqn (2) becomes
| | 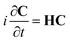 | (5) |
where
H is the Hamiltonian matrix having the elements
| | HIJ(t) = EIδIJ − ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ· IJ·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inc(t) + (qref(t) + Δqpol(t))·VIJ inc(t) + (qref(t) + Δqpol(t))·VIJ | (6) |
with
| | | Δqpol(t) = qpol(t) − qpol(|Φ0〉), | (7) |
| | ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ = 〈ΦI| IJ = 〈ΦI|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ΦJ〉, |ΦJ〉, | (8) |
| | VIJ = 〈ΦI|![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) |ΦJ〉. |ΦJ〉. | (9) |
In the TD–PCM–NP, the time evolution of
qref(
t) and
qpol(
t) can be computed using an arbitrary dielectric function (
e.g., experimentally observed one) in the frequency domain.
36 Although effective simplification of the equation of motion of the polarization charges is proposed in ref.
36, it was not used in this work.
2.2. Inverse design of the molecule near the NP and the incident field
The present inverse design uses the Hamiltonian matrix of eqn (6) to represent continuous chemical space of candidate molecule–NP systems, which allows the gradient-directed design by continuous optimization. The optimal molecule and molecule–NP configuration can be efficiently predicted among the candidates by the inverse design. For the molecule and its conformation relative to the NP, the Hamiltonian matrix of the TD-CI/TD–PCM–NP approach reads the electronic state energies (EI), electric dipole moments (![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ), and molecular potentials on tesserae of the NP (VIJ). Therefore, in the inverse design of the molecule–NP systems with respect to the molecular species and its spatial arrangement, we express these molecular characteristics as
IJ), and molecular potentials on tesserae of the NP (VIJ). Therefore, in the inverse design of the molecule–NP systems with respect to the molecular species and its spatial arrangement, we express these molecular characteristics as| | 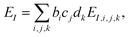 | (10) |
| | 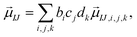 | (11) |
| | 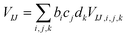 | (12) |
where EI,i,j,k, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ,i,j,k, and VIJ,i,j,k are EI,
IJ,i,j,k, and VIJ,i,j,k are EI, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ, and VIJ of the molecule of the ith candidate molecular species with the jth candidate conformation and kth candidate distance with respect to the NP, respectively. bi, cj, and dk are the corresponding participation coefficients, which are treated as optimization variables to tailor the system. The participation coefficients take a value between 0 and 1, and its sum for all the corresponding candidates is 1:
IJ, and VIJ of the molecule of the ith candidate molecular species with the jth candidate conformation and kth candidate distance with respect to the NP, respectively. bi, cj, and dk are the corresponding participation coefficients, which are treated as optimization variables to tailor the system. The participation coefficients take a value between 0 and 1, and its sum for all the corresponding candidates is 1:| | 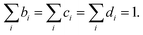 | (13) |
When all the participation coefficients are 0 or 1, the Hamiltonian matrix and time evolution of the system are identical to those of the real system. To find the optimal molecule–NP system in the chemical space, the participation coefficients are rounded-off after the optimization. Moreover, for the designed system, rounded-off values of the optimized participation coefficients need to satisfy the condition of eqn (13). When several candidates have large participation coefficients as the result of the optimization, the design ends up in having rounded participation coefficients that do not satisfy eqn (13). Thanks to the continuous chemical space represented by the participation coefficients, the derivative of the design target property P of the molecule–NP system with respect to the participation coefficients can be defined. Therefore, the inverse design of the molecule near the NP can be implemented by the efficient gradient-based optimization of the participation coefficients. By further expanding eqn (10)–(12) for the other elements of the candidate molecules, it is possible to more efficiently represent the chemical space by the combination of the different participation coefficients; for example, candidate derivatives of the molecular species can be expressed by the difference in the substituents and grouped arbitrarily. A scheme of the design is shown in Scheme S1 (ESI†).
In the design, the incident electric field irradiated to the molecule–NP system is represented by a sum over different harmonics having the frequency ω = π/T with the time duration T of the light irradiation:38
| | 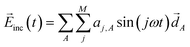 | (14) |
where
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) A
A is 1.0 a.u. for all the directions specified by the index
A running over the three Cartesian coordinates. The intensity of the field is zero at the start and end of the illumination (
t = 0 and
T, respectively) and thus more easily obtained in the experiments. The amplitudes {
aj,A} of the sine wave components are treated as optimization variables to design the optimal incident field that drives the desired time evolution of the molecule–NP system. In the design of both the incident field and the molecule of the molecule–NP system, the tailored field is further optimized for the designed molecule after rounding-off the participation coefficients.
The design of the molecule–NP system and incident electric field is achieved by maximizing the objective function J defined as a sum of the desired property P of the system and the penalty term to the high fluence of the incident field:39,40
| | 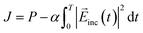 | (15) |
where
α is a penalty factor and constant over the time. The larger
α, the more negative the penalty term and the smaller
J becomes. In this work, the target property is the population of the first excited state of the molecule near the NP at the end of the molecule– and NP–radiation interactions. For the target property, to steer the intermediate participation coefficients {
bi}, {
ci}, and {
di} to the discrete values (0 or 1) in the optimization, by introducing a dimensionless penalty factor
γ, we represent the target property as
| | 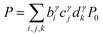 | (16) |
where
P0 is the original target property evaluated with {
bi}, {
ci}, and {
di}. When
γ is equal to 1.0,
P is identical to
P0. Using
γ that is larger than 1.0,
P and
J become smaller in the intermediate regime of the participation coefficients, while larger when closer to 1 or 0. As such, the proper
γ can be used so that the optimized participation coefficients satisfy the condition of
eqn (13).
A method for designing metal natures of NPs was also developed. Details of the method are described in ESI.†
2.3. Chemical space
As the candidate molecular species, N-methyl-6-quinolone (MQ) and its derivatives (EQ and 3tBu-MQ) shown in Fig. 1 were adopted as an example. This choice enables us to investigate substituent effects in the design, which is important from a practical point of view in making use of the plasmon to modulate properties of a molecule possessing a specific motif. MQ has been well studied in terms of its peculiar photophysical properties41 and adopted in the inverse design studies of the incident field.42,43 EQ and 3tBu-MQ were used to investigate the substituent effects.44,45 We considered two types of distances and conformations of the molecule relative to the NP as the candidates. The molecular plane is located on the xy or yz plane in the Cartesian coordinates shown in Fig. 1. The candidate distances between the mass center of the molecule and the closest NP surface are 5 and 8 Å.
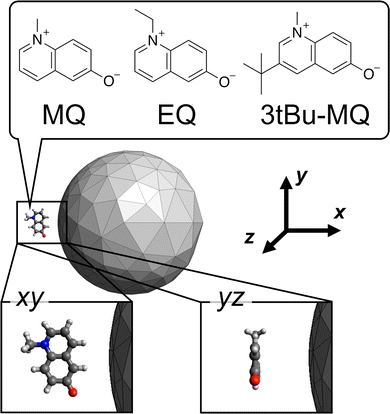 |
| | Fig. 1 Schematic representation of the candidate molecule + metal NP system. The chemical structures are of the candidate molecular species. The candidate conformation xy and yz indicate that the molecular planes are located on the xy and yz planes of the Cartesian coordinates, respectively. Drawing out of scale. | |
In this work, the inverse design was performed on the NPs with cubic, ellipsoidal, rod, and spherical shapes. The nanocube has a side length of 10 nm and a curvature radius at the edges of 1 nm. The ellipsoidal NP has a semi-major axis length of 8 nm and two semi-minor axes of 5 nm. The nanorod is 10 nm long and has a cylinder radius of 1.5 nm. The spherical NP has a 5 nm radius. These NPs have a similar surface area. The surface was divided into 664 triangular tesserae and refined near the molecule (Fig. 2) by using the Gmsh software46 for all the shapes. The metal NPs considered in this work do not have a diameter (<3 nm) where the non-local effects of the dielectric function are significant. In addition, the quasi-static approximation used here is valid in the wavelength range of the calculated electronic states because of the small object size.
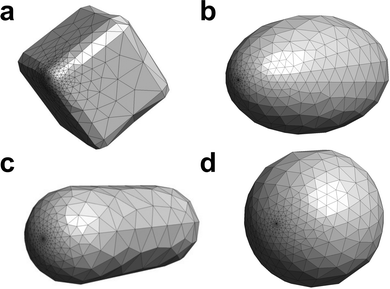 |
| | Fig. 2 Metal NPs of (a) cubic, (b) ellipsoidal, (c) rod, and (d) spherical shapes. The visualization was performed by Gmsh.46 The structures from the other views can be found in Fig. S1 and S2 (ESI†). | |
As the metal natures of the NPs, gold and silver were adopted. The parametrization of the Drude–Lorentz (DL) expansion for the TD–PCM–NP was performed using experimentally observed dielectric functions of the bulk metals.36 We used six DL terms in the expansion. The experimental data were taken from ref. 47 and 48 for gold and silver, respectively.
To illustrate dependences of photophysical properties on the NP shapes and metal natures, we computed the polarizability of the NPs, whose imaginary part is related to the photo-absorption, by using the TD–PCM–NP. The applied field to the NP for the TD calculations is the same as that adopted in ref. 36 and propagating in the x direction. Fig. S3 and S4 (ESI†) show the imaginary part of the polarizability of the silver and gold NPs, respectively. The results indicate that the difference of the NP shapes significantly changes the LSPR property and that the shape control of the NP is crucial for the design of the metal NP systems.
2.4. Computational details
We optimized geometries of the candidate molecules under the CS symmetry at the Hartree–Fock level of theory by using the Gaussian 16 software.49 The Hartree–Fock and CIS calculations of the molecules equilibrated with the metal NP were performed by a locally modified version of Gamess.50,51 The 6-31G(d) basis set was employed for these calculations.
The real-time simulation and design of the molecule–NP system and incident electric field were performed using a locally modified version of WaveT software.34,35 The ground and low-lying 10 excited states of the molecule were included in the Hamiltonian. We adopted a time step of 2.42 as (0.10 a.u.) in the time evolution of the system. The wavefunction of the molecule was propagated by the Euler algorithm. The time duration of the incident field was chosen to be 250 a.u. (≈6 fs) to focus on the ultrafast electron dynamics and its related functions. In the design of the optimal incident field, all the initial amplitudes {aj,A} of the sine wave components in eqn (14) were set to 1.0 × 10−7 a.u. The Gaussian sinusoidal wave was adopted as a fixed incident field used to demonstrate the inverse design of the molecular part of the molecule–NP system:
| | 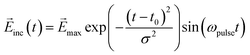 | (17) |
where the central
t0 is 125 a.u., the pulse width
σ is 49.61 a.u., and the pulse frequency
ωpulse is 3.0 eV, similar to the excitation energy for the first excited state of the MQ molecule and its derivatives. The maximum value of the electric field
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) max
max is (1.0 × 10
−6, 0.0, 0.0) a.u. ((5.142 × 10
5, 0.0, 0.0) V m
−1) for the (
x,
y,
z) directions. The orientations of the NPs with the Cartesian axes are shown in Fig. S1 and S2 (ESI
†). The time profile of this incident field along the
x direction is shown in
Fig. 3(a).
Fig. 3(b) displays the Fourier transform (FT) of the incident field.
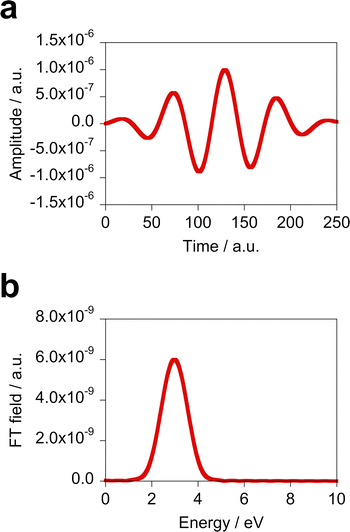 |
| | Fig. 3 (a) Time profile of the fixed incident field used in the design of the optimal molecule along the x direction and (b) its FT. | |
The continuous optimization of the participation coefficients and the amplitudes of the incident field in eqn (14) was performed by the quasi-Newton method with the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm52 implemented in the L-BFGS-B code version Lbfgsb.3.0.53,54 The derivatives of the target property with respect to the participation coefficients and the amplitudes of the field were computed as numerical differentials in the forward-finite difference formulation with the small number of 1.0 × 10−5 and 1.0 × 10−11 for the molecule and incident field, respectively. To tailor the incident field, well-established approaches such as the Rabitz algorithm39 can be used. However, in this work, the simple gradient-based optimization was adopted to combine the design of the molecule and incident field. In each design for the molecule, using the different randomized initial participation coefficients, the design was performed five times. The optimization terminated when the difference of the objective function values was smaller than a small number ε in the line search. ε was set to 2.2 × 10−13 and 2.2 × 10−7 for the design with the fixed and optimal fields, respectively. In the first ten optimization steps, ε was set to zero in order to suppress the termination of the design.
3. Results and discussion
Results of the inverse design are reported in this section. To assess the design performance, the design of components, molecule and incident electric field, of molecule–NP systems was performed, and then both of them were designed. Firstly, we report the results of the design of a molecule near a metal NP. Secondly, the results of the design of the incident field irradiated to a molecule–NP system are shown. Then, the design results of both optimal molecule close to a metal NP and incident electric field are presented. Additionally, we examine the design of a metal nature of a NP of a molecule–NP system.
3.1. Design of the molecule near the metal NP
The performance of the inverse design of the molecule of the molecule–NP system was assessed by comparing results of the screening and design. Here, the objective function of the design is the population of the first excited state of the molecule because the incident field (and its fluence) is fixed to the Gaussian sinusoidal pulse (eqn (17) and Fig. 3). In the screening, we performed calculations of all the possible systems of the design of the molecule near the silver spherical NP with the irradiation of the fixed incident field. The calculation results given in Table 1 show that the various target properties are obtained depending on the substituents of MQ and the relative distance and conformation between the molecule and NP. The target state population of the molecules in the xy conformation is larger than that in the yz one. In the same distance and molecular species, the population differs by a factor of about 102–105 in these conformations. This is possibly related to the direct transition from the ground state because the incident field directs along the x direction and the z component of the electric transition dipole moment for the ground and first excited states of the candidate molecules is null, although the other pathways of the population transfer are possible. The MQ or EQ molecule on the xy plane and at a distance of 5 Å from the nearest silver NP surface has the largest target property. In the inverse design, the MQ system with the largest population was designed in all the trials. In this design, the optimized participation coefficients for the relative orientation and distance of the molecule with respect to the NP, {ci} and {di}, respectively, are localized. On the other hand, those for the molecular species are 0.57 and 0.43 for MQ and EQ, respectively. The difference between the optimized and designed target properties is about 1% of the designed one. This gap can be large in the design of both the optimal molecule and incident field. Therefore, in eqn (16), we decided to use the penalty factor γ of 1.05, which is slightly increased from 1.00, in order to avoid obtaining optimized participation coefficients widely distributed among the candidates. Using the γ of 1.05, the optimized participation coefficients were fully localized on the MQ or EQ molecule; the MQ and EQ systems were obtained three and two times in the five trials of the design with γ = 1.05, respectively. The typical optimization history of the target property obtained in the design of the MQ system is shown in Fig. 4. The design results suggest that the target property is smooth as a function of the participation coefficients.
Table 1 Population of the first excited state of the candidate molecules near the silver spherical NP at the end of the incident field illumination. The possible molecule–NP systems are classified according to the molecular species and the relative molecule–NP conformation and distance
| Species |
Conformation |
Distancea (Å) |
Population |
|
Distance between the mass center of the molecule and the nearest NP surface.
|
| MQ |
xy
|
5 |
3.64 × 10−8 |
| EQ |
xy
|
5 |
3.64 × 10−8 |
| 3tBu-MQ |
xy
|
5 |
3.53 × 10−8 |
| MQ |
yz
|
5 |
3.35 × 10−13 |
| EQ |
yz
|
5 |
1.67 × 10−13 |
| 3tBu-MQ |
yz
|
5 |
1.51 × 10−10 |
| MQ |
xy
|
8 |
2.90 × 10−8 |
| EQ |
xy
|
8 |
2.96 × 10−8 |
| 3tBu-MQ |
xy
|
8 |
2.84 × 10−8 |
| MQ |
yz
|
8 |
1.02 × 10−13 |
| EQ |
yz
|
8 |
2.54 × 10−13 |
| 3tBu-MQ |
yz
|
8 |
1.02 × 10−10 |
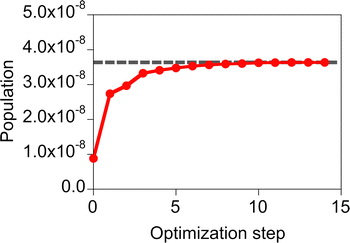 |
| | Fig. 4 Optimization history of the target property obtained in the design of the MQ molecule near the silver spherical NP with the penalty factor γ = 1.05. The gray dashed line denotes the target property after rounding off the optimized participation coefficients. | |
3.2. Design of the incident electric field
The inverse design of the incident electric field was performed using the 13 sine wave components with different harmonics (i.e., M = 13 in eqn (14)). To observe the dependence of the design results on the incident field fluence, we employed α = 1, 10, and 100 a.u. since the larger α imposes the larger penalty on the fluence. For the molecule–NP system, MQ in the xy conformation and the silver spherical NP with 5 Å distance were adopted. The design results are shown in Table 2. When α is equal to 1 a.u., we designed the incident light that realizes the perfect population transfer with the target state population of 1.00, an upper limit. The more limited the fluence and the smaller the population of the first excited state of MQ were obtained with the larger α. This means that a high-intensity electric field is needed to realize the highly populated target excited state of MQ. Fig. S5 (ESI†) displays the time profiles of the optimal incident fields. The x and y components of the incident field have large amplitudes in comparison with the z component under the restriction on the total field fluence in the optimization. As discussed above, the direct transition from the ground state by the z direction field is suppressed since the z component of the electric transition dipole moment of MQ between the ground and target excited states is null. Not only the intensity of the incoming light but also the shape of the pulse differs depending on α. The optimization histories of the objective function of the design with the different penalty factors are shown in Fig. 5, along with variations of the target state population and total fluence. The outcome value of the design decreases in the order of α = 1, 10, and 100 a.u. The optimization takes more steps to satisfy the optimization condition when the penalty becomes loose, i.e., the fluence is high. The value of the objective function monotonically increases with the optimization step; the objective function is smooth as a function of the amplitudes of the sine wave components. The results indicate that the optimal control of the incident field is effective in realizing the design of the desired photophysical property of molecule–NP systems.
Table 2 Objective function (J), target property (P), and total fluence of the incident field obtained in the design with the penalty factor α for the incident field. The molecule–NP system is composed of MQ in the xy conformation and the silver spherical NP with 5 Å distance
|
α (a.u.) |
J
|
P
|
Fluence (a.u.) |
| 1 |
0.991 |
1.000 |
8.56 × 10−3 |
| 10 |
0.933 |
0.990 |
5.68 × 10−3 |
| 100 |
0.653 |
0.862 |
2.09 × 10−3 |
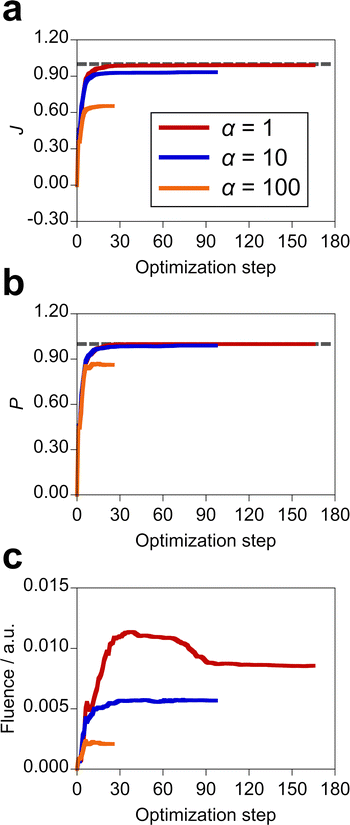 |
| | Fig. 5 (a) Optimization histories of the objective function in the design of the optimal incident field with the different penalty factors α (a.u.) for the field fluence, along with variations of (b) population of the target state and (c) total fluence of the incident field. The gray dashed line denotes the value of 1.00. The individual data are shown in Fig. S6 (ESI†). | |
3.3. Design of both the molecule and incident electric field
We conducted the inverse design of both the optimal molecule close to the metal NP and incident electric field. The design was performed on several types of metal NPs with different metal natures and NP shapes. According to the results obtained at the former section, the penalty factor of α = 100 a.u. for the incident field, which provided non-saturated population in the design of the molecular part of the system, was adopted to investigate the influence of the metal NP features on the design results. In the five trials of each design, the obtained system with the best objective function value is referred to as the designed system here. Based on the results of the molecular design in Section 3.1, we employed the penalty factor γ of 1.05. When the optimized participation coefficients did not satisfy the condition of eqn (13) by using the penalty factor γ of 1.05, we used the larger γ of 1.20 as shown in Table S1 (ESI†) to localize the optimized participation coefficients. Table 3 shows the designed systems and properties. Fig. S7 and S8 (ESI†) display the designed molecule + metal NP systems designed on the silver and gold NPs, respectively. The corresponding optimal incident fields are shown in Fig. S9 and S10 (ESI†). All the designed molecules have the xy conformation regardless of the NP type, and therefore the amplitude of the z component of the optimal incident field is small, as discussed in the former section. Comparing with the design of the electric field applied to the MQ + silver spherical NP system (Table 2, α = 100 a.u.), by the design on the same metal NP, the larger objective function value (+0.022) was obtained with the EQ molecule possessing the xy conformation at 5 Å distance from the silver spherical NP surface (Table 3). This indicates that the design of both the substituents of the molecule and the incident field is effective for realizing the desired property of the molecule–NP system. Furthermore, this designed system has the largest objective function value in all the obtained systems.
Table 3 Results of the design of both the optimal molecule and incident field on the various metal NPs.a The adopted α is 100 a.u.
| Metal NP |
Optimal molecule |
Designed properties |
| Nature |
Shape |
Species |
Conformation |
Distance (Å) |
J
|
P
|
Fluence (a.u.) |
|
In the design on the gold ellipsoidal NP, the requirements for the design (eqn (13)) were not fulfilled with γ = 1.05, 1.20, 1.50, and 2.00, and the designed system was not obtained in the five trials with the randomized initial participation coefficients.
|
| Ag |
Cube |
3tBu-MQ |
xy
|
8 |
0.575 |
0.726 |
1.51 × 10−3 |
| Ellipsoid |
EQ |
xy
|
8 |
0.652 |
0.895 |
2.42 × 10−3 |
| Rod |
3tBu-MQ |
xy
|
5 |
0.582 |
0.873 |
2.92 × 10−3 |
| Sphere |
EQ |
xy
|
5 |
0.675 |
0.881 |
2.06 × 10−3 |
| Au |
Cube |
3tBu-MQ |
xy
|
5 |
0.647 |
0.917 |
2.70 × 10−3 |
| Rod |
EQ |
xy
|
5 |
0.557 |
0.874 |
3.17 × 10−3 |
| Sphere |
MQ |
xy
|
5 |
0.394 |
0.757 |
3.63 × 10−3 |
In the design, the objective function, population of the target state, and field fluence take various values depending on the metal nature and NP shape but also the optimal molecule and incident field. As such, the control of the metal NP is important for the design of the photophysical property of the molecule. Fig. 6 shows the optimization history and deviations of the target property and field fluence of the designed system with the largest objective function value. After optimizing both the molecule and incident field, the tailored field was further optimized for the designed molecule (Scheme S1, ESI†). Therefore, the objective function value of the designed system is smaller than that of the non-physical system with the fully optimized participation coefficients. All the data of the optimization for the designed systems are shown in Fig. S11 and S12 (ESI†). The optimization histories suggest that the objective function is relatively smooth as a function of the participation coefficients.
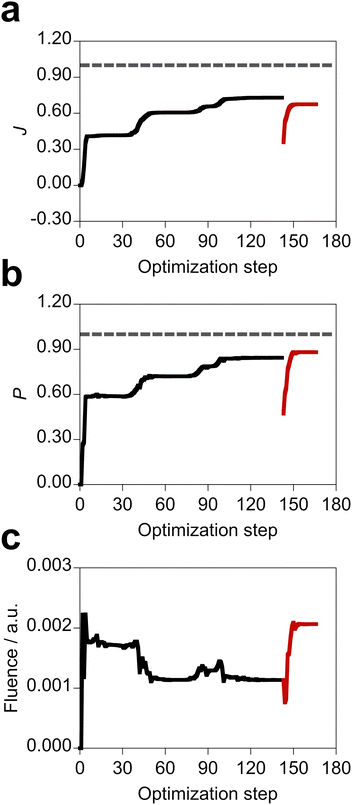 |
| | Fig. 6 Optimization history of the objective function in both the optimal molecule and incident field design, along with variations of population of the target state and total fluence of the incident field. The design was performed on the silver spherical NPs, and the EQ molecule possessing the xy conformation at 5 Å distance from the silver spherical NP surface and the incident electric field shown in Fig. S7(d) (ESI†) were obtained. The black lines are of the optimization of both the optimal molecule and incident field design. The red lines refer to the design of optimal incident field for the optimal molecule after the design of both the molecule and incident field. The gray dashed lines denote the value of 1.00. | |
3.4. Design of the metal nature of the NP
We performed the inverse design of the metal nature of the NP. The method was applied to a molecule + metal nanocube system (Fig. S13, ESI†). Ag, Al, Au, Cu, Pd, and Rh were considered as candidate metal natures. The computational details can be found in ESI.† To examine the performance of the design, we computed the target property of the design, which is the population of the first excited state of the MQ of the MQ–nanocube system at the end of the light irradiation, for all the candidate metal natures of the NP. The results show that Ag gives the largest population of the target electronic state of MQ (Table S2, ESI†). In the design, Ag was successfully obtained using five different conditions of the randomized initial participation coefficients. One of the design results is shown in Fig. S14 (ESI†). The local field generated on the Ag nanocube surface due to the incident field is resonant with molecular excitation energy and therefore contributes to the large population of the target state of the molecule (Fig. S15 and S16, ESI†).
The proposed design method for the metal nature of the NP is not computationally effective (ESI†). Therefore, we do not combine this method with the inverse design method for molecule–NP systems and incident fields, while it may be useful for combining with constraint conditions which need to be accounted for in the design of realistic materials.
4. Summary
In summary, we proposed an inverse design method of optimal molecule near metal NPs and incident electric field based on the time-dependent QM/PCM–NP approach. In this method, both the molecular species and spatial arrangements with respect to the NP are designed. The design of each component and both of them was performed to maximize the population of the target excited state as an example of a non-trivial molecular properties to be maximized. Although the proposed method is applicable to various molecules, MQ and its derivatives were examined as the candidate molecules to design the substituents. The application to large chemical space will be the topic of future investigations. For the molecule, the design successfully proposed the optimal derivative whose target state population is the largest in the proximity of the silver spherical NP under the illumination of the electric pulse of the Gaussian sinusoidal wave. It was found that the optimal incident field can achieve the almost perfect population transfer to the target excited state in the molecule near the metal NP. The design of both the molecule and incident electric field of the molecule–NP systems was successfully demonstrated and gave the larger objective function value than those of the design of each component. It was shown that the design and precise control of the molecule–NP systems and the incident field are important to realize the desired photophysical properties. The design method of metal natures of NPs was also examined. The present inverse design approach gives a basis for the design of molecule–NP systems and incident fields and for the manipulation of photochemical events.
Author contributions
T. Shiraogawa: Conceptualization, investigation, methodology, writing-original draft. G. Dall'Osto: investigation, methodology, writing-review & editing. R. Cammi: conceptualization, writing-review & editing. M. Ehara: conceptualization, writing-review & editing, Supervision. S. Corni: conceptualization, methodology, writing-review & editing, supervision.
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgements
ME and TS acknowledge financial support from the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant Numbers (JP20H02718, JP22H05133, JP19J14059, JP21J00210). SC acknowledges financial support from the European Union (EU) under the Horizon 2020 framework programme grant H2020-FET ProID number 964363. The computations were partially performed in the Research Center for Computational Science, Okazaki, Japan (Project: 22-IMS-C185).
Notes and references
- S. Schlucker, Angew. Chem., Int. Ed., 2014, 53, 4756–4795 CrossRef.
- A. B. Zrimsek, N. Chiang, M. Mattei, S. Zaleski, M. O. McAnally, C. T. Chapman, A. I. Henry, G. C. Schatz and R. P. Van Duyne, Chem. Rev., 2017, 117, 7583–7613 CrossRef CAS PubMed.
- E. Dulkeith, M. Ringler, T. A. Klar, J. Feldmann, A. Muñoz Javier and W. J. Parak, Nano. Lett., 2005, 5, 585–589 CrossRef CAS.
- J. F. Li, C. Y. Li and R. F. Aroca, Chem. Soc. Rev., 2017, 46, 3962–3979 RSC.
- S. Linic, U. Aslam, C. Boerigter and M. Morabito, Nat. Mater., 2015, 14, 567–576 CrossRef CAS PubMed.
- C. Zhan, X.-J. Chen, J. Yi, J.-F. Li, D.-Y. Wu and Z.-Q. Tian, Nat. Rev. Chem., 2018, 2, 216–230 CrossRef.
- M. M. Hann and T. I. Oprea, Curr. Opin. Chem. Biol., 2004, 8, 255–263 CrossRef CAS PubMed.
- A. K. Pearce, T. R. Wilks, M. C. Arno and R. K. O’Reilly, Nat. Rev. Chem., 2020, 5, 21–45 CrossRef.
- R. A. Sperling and W. J. Parak, Philos. Trans. R. Soc., A, 2010, 368, 1333–1383 CrossRef CAS PubMed.
- M. Swierczewska, S. Lee and X. Chen, Phys. Chem. Chem. Phys., 2011, 13, 9929–9941 RSC.
- S. M. Risser, D. N. Beratan and S. R. Marder, J. Am. Chem. Soc., 1993, 115, 7719–7728 CrossRef CAS.
- C. Kuhn and D. N. Beratan, J. Phys. Chem., 1996, 100, 10595–10599 CrossRef CAS.
- O. A. von Lilienfeld, R. D. Lins and U. Rothlisberger, Phys. Rev. Lett., 2005, 95, 153002 CrossRef PubMed.
- A. Zunger, Nat. Rev. Chem., 2018, 2, 0121 CrossRef CAS.
- O. A. von Lilienfeld, Int. J. Quantum Chem., 2013, 113, 1676–1689 CrossRef CAS.
- T. Weymuth and M. Reiher, Int. J. Quantum Chem., 2014, 114, 823–837 CrossRef CAS.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- J. G. Freeze, H. R. Kelly and V. S. Batista, Chem. Rev., 2019, 119, 6595–6612 CrossRef CAS PubMed.
- M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354–2377 CrossRef CAS.
- O. A. von Lilienfeld and M. E. Tuckerman, J. Chem. Phys., 2006, 125, 154104 CrossRef PubMed.
- M. Wang, X. Hu, D. N. Beratan and W. Yang, J. Am. Chem. Soc., 2006, 128, 3228–3232 CrossRef CAS.
- D. Xiao, W. Yang and D. N. Beratan, J. Chem. Phys., 2008, 129, 044106 CrossRef.
- T. Shiraogawa and M. Ehara, J. Phys. Chem. C, 2020, 124, 13329–13337 CrossRef CAS.
- C. Brif, R. Chakrabarti and H. Rabitz, New J. Phys., 2010, 12, 075008 CrossRef.
- D. L. Goodwin and I. Kuprov, J. Chem. Phys., 2016, 144, 204107 CrossRef CAS PubMed.
- A. Raza, C. Hong, X. Wang, A. Kumar, C. R. Shelton and B. M. Wong, Comput. Phys. Commun., 2021, 258, 107541 CrossRef CAS.
- S. Malola, L. Lehtovaara, J. Enkovaara and H. Hakkinen, ACS Nano, 2013, 7, 10263–10270 CrossRef CAS PubMed.
- K. Iida, M. Noda, K. Ishimura and K. Nobusada, J. Phys. Chem. A, 2014, 118, 11317–11322 CrossRef CAS PubMed.
- S. Corni and J. Tomasi, J. Chem. Phys., 2001, 114, 3739–3751 CrossRef CAS.
- B. Mennucci and S. Corni, Nat. Rev. Chem., 2019, 3, 315–330 CrossRef.
- E. Coccia, J. Fregoni, C. A. Guido, M. Marsili, S. Pipolo and S. Corni, J. Chem. Phys., 2020, 153, 200901 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- S. Corni, S. Pipolo and R. Cammi, J. Phys. Chem. A, 2015, 119, 5405–5416 CrossRef CAS PubMed.
- S. Pipolo and S. Corni, J. Phys. Chem. C, 2016, 120, 28774–28781 CrossRef CAS PubMed.
- E. Coccia and S. Corni, J. Chem. Phys., 2019, 151, 044703 CrossRef.
- G. Dall'Osto, G. Gil, S. Pipolo and S. Corni, J. Chem. Phys., 2020, 153, 184114 CrossRef PubMed.
- Y. E. Lee, O. D. Miller, M. T. Homer Reid, S. G. Johnson and N. X. Fang, Opt. Express, 2017, 25, 6757–6766 CrossRef PubMed.
- D. Castaldo, M. Rosa and S. Corni, Phys. Rev. A, 2021, 103, 022613 CrossRef CAS.
- W. Zhu, J. Botina and H. Rabitz, J. Chem. Phys., 1998, 108, 1953–1963 CrossRef CAS.
- J. Werschnik and E. K. U. Gross, J. Phys. B: At. Mol. Opt. Phys., 2007, 40, 175–211 CrossRef.
- J. L. Perez Lustres, S. A. Kovalenko, M. Mosquera, T. Senyushkina, W. Flasche and N. P. Ernsting, Angew. Chem., Int. Ed., 2005, 44, 5635–5639 CrossRef.
- T. Klamroth, J. Chem. Phys., 2006, 124, 144310 CrossRef.
- M. Rosa, G. Gil, S. Corni and R. Cammi, J. Chem. Phys., 2019, 151, 194109 CrossRef.
- M. Gerecke, C. Richter, M. Quick, I. N. Ioffe, R. Mahrwald, S. A. Kovalenko and N. P. Ernsting, J. Phys. Chem. B, 2017, 121, 9631–9638 CrossRef CAS.
- E. Heid and C. Schroder, J. Phys. Chem. B, 2017, 121, 9639–9646 CrossRef CAS.
- C. Geuzaine and J.-F. Remacle, Int. J. Numer. Methods Eng., 2009, 79, 1309–1331 CrossRef.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 4370–4379 CrossRef CAS.
- A. D. Rakic, A. B. Djurisic, J. M. Elazar and M. L. Majewski, Appl. Opt., 1998, 37, 5271–5283 CrossRef CAS PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. B.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, Jr., J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
-
M. S. Gordon and M. Schmidt, Theory and Applications of Computational Chemistry: the first forty years, ed. C. Dykstra, G. Frenking, K. Kim, G. E. Scuseria, Elsevier, Amsterdam, 2005, pp 1167–1689 Search PubMed.
- R. H. Byrd, P. H. Lu, J. Nocedal and C. Y. Zhu, SIAM J. Sci. Comput., 1995, 16, 1190–1208 CrossRef.
- C. Zhu, R. H. Byrd and J. Nocedal, ACM Trans. Math. Software, 1997, 23, 550–560 CrossRef.
- J. L. Morales and J. Nocedal, ACM Trans. Math. Software, 2011, 38, 1–4 CrossRef.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article c,
Masahiro
Ehara
c,
Masahiro
Ehara
 *ade and
Stefano
Corni
*bf
*ade and
Stefano
Corni
*bf
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) ·
·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inc(t) + (qref(t) + qpol(t))·
inc(t) + (qref(t) + qpol(t))·![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif)
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) is the electric dipole operator and
is the electric dipole operator and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inc(t) is the time-dependent incident electric field. qref(t) and qpol(t) are polarization charges of the NP due to the external field and molecule, respectively. The molecule–radiation interaction is modeled in the dipole approximation in the length gauge. In the framework of PCM–NP, the metal NP is described as a continuum body characterized by the dielectric function of the metal. The TD–PCM–NP describes the response of the metal NP to the incident field and molecule as the time-dependent polarization charges qref(t) and qpol(t), respectively, located on geometrical centers of each tessera of the discretized NP surface.
inc(t) is the time-dependent incident electric field. qref(t) and qpol(t) are polarization charges of the NP due to the external field and molecule, respectively. The molecule–radiation interaction is modeled in the dipole approximation in the length gauge. In the framework of PCM–NP, the metal NP is described as a continuum body characterized by the dielectric function of the metal. The TD–PCM–NP describes the response of the metal NP to the incident field and molecule as the time-dependent polarization charges qref(t) and qpol(t), respectively, located on geometrical centers of each tessera of the discretized NP surface. ![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) is the electrostatic potential operator acting at the tesserae positions.
is the electrostatic potential operator acting at the tesserae positions.
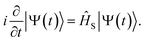
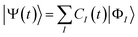
![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) ]|ΦI〉 = EI|ΦI〉
]|ΦI〉 = EI|ΦI〉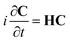
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ·
IJ·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) inc(t) + (qref(t) + Δqpol(t))·VIJ
inc(t) + (qref(t) + Δqpol(t))·VIJ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ = 〈ΦI|
IJ = 〈ΦI|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ΦJ〉,
|ΦJ〉,![[V with combining circumflex]](https://www.rsc.org/images/entities/b_char_0056_0302.gif) |ΦJ〉.
|ΦJ〉.![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ), and molecular potentials on tesserae of the NP (VIJ). Therefore, in the inverse design of the molecule–NP systems with respect to the molecular species and its spatial arrangement, we express these molecular characteristics as
IJ), and molecular potentials on tesserae of the NP (VIJ). Therefore, in the inverse design of the molecule–NP systems with respect to the molecular species and its spatial arrangement, we express these molecular characteristics as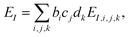
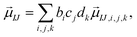
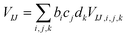
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ,i,j,k, and VIJ,i,j,k are EI,
IJ,i,j,k, and VIJ,i,j,k are EI, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) IJ, and VIJ of the molecule of the ith candidate molecular species with the jth candidate conformation and kth candidate distance with respect to the NP, respectively. bi, cj, and dk are the corresponding participation coefficients, which are treated as optimization variables to tailor the system. The participation coefficients take a value between 0 and 1, and its sum for all the corresponding candidates is 1:
IJ, and VIJ of the molecule of the ith candidate molecular species with the jth candidate conformation and kth candidate distance with respect to the NP, respectively. bi, cj, and dk are the corresponding participation coefficients, which are treated as optimization variables to tailor the system. The participation coefficients take a value between 0 and 1, and its sum for all the corresponding candidates is 1: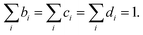
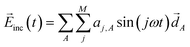
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) A is 1.0 a.u. for all the directions specified by the index A running over the three Cartesian coordinates. The intensity of the field is zero at the start and end of the illumination (t = 0 and T, respectively) and thus more easily obtained in the experiments. The amplitudes {aj,A} of the sine wave components are treated as optimization variables to design the optimal incident field that drives the desired time evolution of the molecule–NP system. In the design of both the incident field and the molecule of the molecule–NP system, the tailored field is further optimized for the designed molecule after rounding-off the participation coefficients.
A is 1.0 a.u. for all the directions specified by the index A running over the three Cartesian coordinates. The intensity of the field is zero at the start and end of the illumination (t = 0 and T, respectively) and thus more easily obtained in the experiments. The amplitudes {aj,A} of the sine wave components are treated as optimization variables to design the optimal incident field that drives the desired time evolution of the molecule–NP system. In the design of both the incident field and the molecule of the molecule–NP system, the tailored field is further optimized for the designed molecule after rounding-off the participation coefficients.
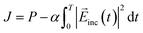
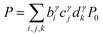

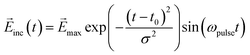
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) max is (1.0 × 10−6, 0.0, 0.0) a.u. ((5.142 × 105, 0.0, 0.0) V m−1) for the (x, y, z) directions. The orientations of the NPs with the Cartesian axes are shown in Fig. S1 and S2 (ESI†). The time profile of this incident field along the x direction is shown in Fig. 3(a). Fig. 3(b) displays the Fourier transform (FT) of the incident field.
max is (1.0 × 10−6, 0.0, 0.0) a.u. ((5.142 × 105, 0.0, 0.0) V m−1) for the (x, y, z) directions. The orientations of the NPs with the Cartesian axes are shown in Fig. S1 and S2 (ESI†). The time profile of this incident field along the x direction is shown in Fig. 3(a). Fig. 3(b) displays the Fourier transform (FT) of the incident field.





