In silico activation of dinitrogen with a light atom molecule

Abstract

The N≡N triple bond can be cleaved in silico with a light atom molecule containing only the earth abundant elements C, H, Si, and P. Extensive density functional theory (DFT) computations on various classes of peri-substituted scaffolds containing Lewis acidic and basic sites in the framework of frustrated Lewis pairs (FLP) indicate that the presence of two silyl cations and two P atoms in a flexible but not too flexible arrangement is essential for energy efficient N₂-activation. The non-bonding lone-pair electrons of the P atoms thereby serve as donors towards N₂, whereas the lone-pairs of N₂ donate into the silyl cations. Newly formed lone-pair basins in the N₂-adducts balance surplus charge. Thereby, the N–N bond distance is increased by astonishing 0.3 Å, from 1.1 Å in N₂ gas to 1.4 Å in the adduct, which makes this bond prone to subsequent addition of hydride ions and protonation, forming two secondary amine sites in the process and eventually breaking the N≡N triple bond. Potential formation of dead-end states, in which the dications (“active states”) aversively form a Lewis acid (LA)–Lewis base (LB) bond, or in which the LA and LB sites are too far away from each other to be able to capture N₂, are problematic but might be circumvented by proper choice of spacer molecules, such as acenaphthalene or biphenylene, and the ligands attached to the LA and LB atoms, such as phenyl or mesityl, and by purging the reaction solutions with gaseous N₂ in the initial reaction steps. Charge redistributions via N₂-activation and splitting were monitored by a variety of real-space bonding indicators (RSBIs) derived from the calculated electron and electron pair densities, which provided valuable insight into the bonding situation within the different reaction steps.

---

Introduction

In the field of biological and chemical catalysis, small molecule activation plays a central role. In millions of years of biological evolution, nature facilitated water oxidation,¹ oxidative hydrogen splitting as well as hydrogen formation via proton reduction,² oxygen reduction,^3,4 carbon dioxide reduction,⁵ and finally splitting of dinitrogen,⁶ – the most inert molecule known – via stepwise reduction, to name the most important ones. The underlying chemical processes are without exception realized by metalloproteins, containing typically 1–6 transition metal atoms such as Mn, Fe, Co, Ni, Cu, and Mo in the active site, since they require complex multi-step redox-reactions, most of which are still under debate so far.^1–6 The resulting biogeochemical cycles of energy and matter are crucial to all forms of life, e.g. without nitrogenases, consuming gaseous N₂, the soil would suffer drastically from deficiency of bio-accessible nitrogen.⁷ In tremendous efforts to understand and mimic nature, scientists are developing and improving crystalline or amorphous solid-state materials (heterogeneous catalysis),^8,9 molecular compounds (homogeneous catalysis),^10–16 and bio-inspired structures (biomimetic catalysis),^17–20 which resulted i.a. in mayor-scale industrial applications in the last century without which the energy and food demands of modern culture couldn’t be maintained. Arguably the most prominent is the Haber–Bosch process for nitrogen fixation and production of ammonia, which was developed and professionalized in the first two decades of the 20th century, giving access to efficient megaton-scale production of fertilizer, and nowadays causes about 1–2% of the global energy demands and about 2–3% of the global CO₂ production.²¹ In the flourishing field of heterogeneous N₂ fixation, a diversity of solid state materials derived from metal–organic frameworks (MOFs),²² covalent organic frameworks (COFs),²³ doped BN,^24,25 BN nanotubes,²⁶ BC nanosheets,²⁷ SiC,²⁸ single metal atoms at graphene²⁹ or BN-graphene sheets,³⁰ nitrogen-rich carbon materials,³¹ boron doped diamond,³² other 2D-networks,³³ and boron carbide nitride nanotube supported single-atom catalysts³⁴ were investigated experimentally and/or computationally. In parallel, recent developments in the field of molecular synthesis proved that N₂ can be cleaved using transition-metal containing compounds,^35–38 and converted to ammonia,^39–41 although in low efficiencies and turn-over numbers so far (Scheme 1). A change in paradigm was introduced shortly after by the first boron-based molecular compounds being capable of nitrogen fixation, proving that transition metal atoms as part of the catalyst are not necessarily essential for nitrogen fixation, not even in homogeneous catalysis (Scheme 1).^42–48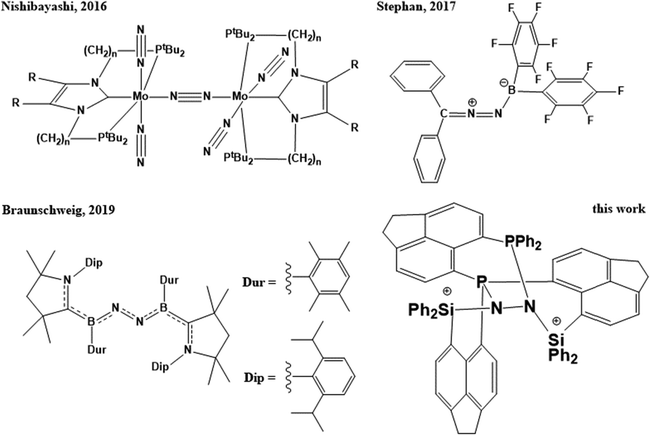

Scheme 1 Activation of N₂ by Mo-pincer dimers, intermolecular frustrated Lewis pairs, hypovalent borylene compounds, and intramolecular frustrated Lewis pairs.

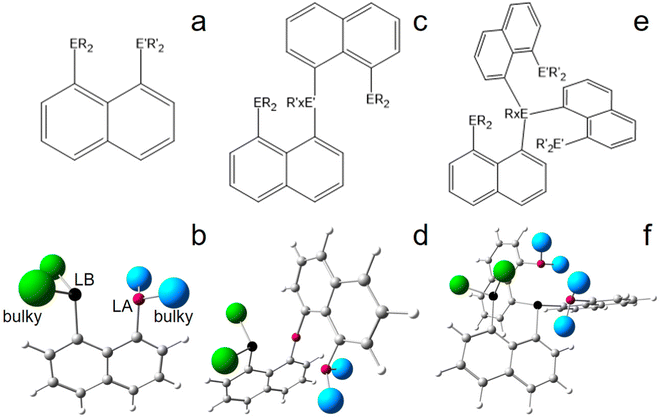
The current study follows that line of evidence, but varies in the conceptual design of the molecular system in order to not only fix and activate the inert N₂ molecule, but to ultimately break the N≡N triple bond. The structures proposed here combine different basic chemical concepts, all of which are hypothesized to be essential for nitrogen uptake, activation, and finally splitting with a light-atom molecule: (1) Uptake & Activation: (a) the active site of the molecule follows the concept of frustrated Lewis pairs (FLPs),^49–55 which combines a Lewis acidic (LA) site like B or Si⁺ with a Lewis basic (LB) site like N or P, fixing and polarizing the target molecule, N₂. FLPs have received tremendous attention in the last decades due to their catalytic capabilities, especially since they are typically constructed of light atoms.^56–60 (b) The catalyst should contain more than one LA and/or LB within one molecule to significantly enhance the gradient of the electrostatic potential in the area between LA and LB. (2) Dynamics: the ideal catalyst molecule offers (limited) rotational degrees of freedom allowing for fine-tuning of the LA–LB distance in the process of N₂ splitting, a requirement for electronic accommodation of the whole system. Metalloproteins undergo series of structural and electronic transitions in catalytic reactions. Other rotations (e.g. ligand motion) should be minimized as they may block the active site or cause entropic contributions to dominate over energetic aspects. (3) Protection: concepts 1 and 2 are seemingly in conflict with each other, because spatially flexible LA/LB-pairs may come close enough to form a direct (and strong) LA–LB-bond, thereby quenching any reactivity towards small non-polarized molecules. In order to keep the LA/LB-pair dynamic but frustrated, the choice of proper spacer groups (e.g. poly-aromatic scaffolds) as well as of ligands attached to the LA/LB-atoms (e.g. phenyl vs. mesityl) is crucial. Ideally, the latter are actively preventing the formation of a direct LA–LB-bond by means of steric ligand-to-ligand repulsion, with the benefit of releasing additional energy via adduct formation.

Typically, it is a matter of months from initial ligand design on the desk to successful bench synthesis in the chemical laboratory. Failures and obstacles cause delays and are not sustainable by means of resources – energy, time, money, and material (any maybe stamina). Computational chemistry nowadays opens large capabilities for screening large numbers of potential candidates, the most promising of which may be synthesized later. In the fields of metal–organic frameworks (MOF), 2D-networks, and solid-state structures, in silico design and screening of hypothetical compounds is already based on algorithmic generation of structural databases.^29,61,62 However, this approach is not easily transferable to molecular design since the variation of parameters, e.g. spacer groups or ligands attached to the active centers, typically results in significant alterations of the structural motifs, many of which are non-unique, e.g. due to rotational isomerism. Moreover, a prerequisite for in situ activation of N₂ with a light-atom molecule is that the catalyst should be principally accessible by (known) synthetic routes, excluding many hypothetic candidates. The compounds chosen in the present density functional theory (DFT) study are thus derived from and related to a variety of published peri-substituted compounds comprising intramolecular interactions.^63–70Peri-substituted compounds were initially synthesized to enforce direct atom–atom contacts and investigate the basic bonding characteristics.⁷¹ The structures typically employ naphthalene or acenaphthalene as spacer groups, but xanthene, dibenzofuran, biphenylene and others are also used to modulate the peri-distance. In the framework of this study only acenaphthalene (ace), and biphenylene (bip) are used with DFT-calculated H⋯H peri-distances of 2.7 and 3.9 Å in the non-substituted species, whereas naphthalene (d_peri = 2.5 Å), xanthene (d_peri = 4.9 Å) and dibenzofuran (d_peri = 5.4 Å) are considered to be detrimental due to their short/large peri-distance and the presence of an oxygen atom in the central part of the spacer molecule in the latter two, the lone-pairs of which might potentially perturb N₂-adduct formation. The focus is directed towards the ace-containing structures as they are potentially most easily available by known synthetic routes.

Limitations of the method: the Gibbs free energy (ΔG) can principally be obtained by vibrational frequency calculations, which was, however, not feasible for the investigated compounds due to their size and the high computational costs at the applied b3pw91-D3/6-311+G(2df,p) level of theory. In order not to be restricted to the electronic energy difference (ΔE) obtained from the DFT optimizations, the DFT optimization were repeated for the most relevant states at the lower b3pw91-D3/6-31+G* level. ΔE (at the higher level) and ΔG (at the lower level) showed the same trends, but considerable differences in the actual numbers. Based on the same grounds, the current study was restricted to the first three reaction steps of N₂ splitting, including N₂ fixation/activation by the ligand system, reduction with hydride (H⁻) and subsequent protonation (H⁺) or second reduction (H⁻). Since a complete transformation of one molecule N₂ into two molecules NH₃ require six reduction and protonation steps in potentially variable order and since both N atoms could be attacked from several topological sites by H⁺ or H⁻ in each step in the systems used here, the potential number of possible reaction paths goes into the hundreds. Thus, the results presented here rather serve as prove of concept for the applicability of the employed chemical concepts than as a definite molecular design and related mechanistic study. Nevertheless, this study may guide synthetic chemists for new ligand designs of light-atom molecules being capable of energy efficient and durable homogeneous splitting of nitrogen.

In the following the molecules investigated for N₂-splitting are denoted as “ligand system” as they may also serve for complexation with metal ions. The (di)cationic states of the ligand system are considered (and thus labeled) as “active” for N₂ uptake and activation if the LA and LB atoms are not closer than 2.5 Å or far off by more than 4.5 Å. The latter two cases accordingly are considered as “dead-end” states. A short LA–LB distance energetically blocks N₂ uptake, whereas a very large distance makes it unlikely by entropic means.

Crucial structures, such as the active ligand system, the different N₂ bound states (N₂-adducts), as well as relevant reaction products with H⁻ or H⁺ were electronically characterized by a set of real-space bonding indicators (RSBIs) in order to monitor charge reorganization events via reduction of N₂. RSBIs comprise the Atoms-In-Molecules (AIM^72–74) and Electron Localizability Indicator (ELI-D⁷⁵) topological approaches, as well as the Non-Covalent Interactions index (NCI⁷⁶). AIM determines atomic basins from the electron density (ED, ρ(r)) providing atomic and fragmental charges and volumes as well as a bond paths motif, which transcends the Lewis picture of chemical bonding, in that it also includes secondary intramolecular chemical contacts in its topological framework. The electronic bond characteristics at the bond critical points (bcps) are indicative of the nature, e.g. degree of covalency, and strength of the interaction. Even more sensitive to the formation of very weak secondary contacts is the NCI, which gives rise to the formation of contact patches also if AIM “overlooks” them.⁷⁷ ELI-D determines basins of paired electrons from the electron pair densities, providing electron populations and volumes for core (C(X)), disynaptic bonding (V₂(X,Y)), and monosynaptic lone-pair (V₁(X)) or protonated (“H atoms”) type of basins. ELI-D and NCI show spatial complementary, as the former is closely related to covalent bonding aspects, whereas the latter is closely related to non-covalent bonding aspects.⁷⁸ The combined use of those RSBIs thus gives a comprehensive picture of chemical bonding in real-space.

DFT calculations

Structural optimizations were conducted for all compounds by density functional theory (DFT) at the b3pw91-D3/6-311+G(2df,p)^79,80 level of theory using Gaussian16⁸¹ at the curta super-computer system of the Freie Universität Berlin. London dispersion was modelled using Grimme's GD3BJ parameters (b3pw91-D3).⁸² The COSMO solvation model was applied to mimic the dichloromethane environment.⁸³ The full ligand systems and corresponding N₂-adducts were too large to afford frequency calculations at this level of theory. Accordingly, the optimizations were repeated at the smaller b3pw91-D3/6-311+G* level for the most relevant states. Subsequent normal mode (or frequency) analysis (at 298.15 K and 1 atm) proved all but one structures to be local minima; for 3a (see below) a negligible phonic band at −5 cm⁻¹ was observed. Peri-interaction energies (α-PIEs) were determined by an isodesmic approach, comparing the energy sum of the di-substituted spacer group and non-substituted spacer group with the two different non-substituted spacer groups, e.g. X-spacer-Y + spacer vs. X-spacer + spacer-Y (X, Y: substituents), disclosing peri-interactions to be either attractive, non-bonding, or repulsive. α-PIEs serve here as reference values to judge the energetic costs of quenching states, see ESI,† for details. Attempts to calculate the transition state (TS) of N₂-adduct formation failed. A potential energy scan (PES) was thus conducted for a series of fixed N–N distances between 1.10 and 1.54 Å. The wavefunction (wfn) files of relevant structures for N₂-activation were used for a topological analysis of the electron density according to the Atoms-In-Molecules (AIM^72–74) space-partitioning scheme using AIM2000,⁸⁴ whereas DGRID-5-1⁸⁵ was used to generate and analyze the Electron-Localizability-Indicator (ELI-D⁷⁵) related real-space bonding descriptors applying a grid step size of 0.075 a.u. using the formatted checkpoint files (fchk). For ELI-D figures, additional grids of 0.15 a.u. step size were computed. NCI⁷⁶ grids were generated with NCIplot⁸⁶ with a grid step-size of 0.12 a.u. Analyses of the reduced density gradient, s(r) = [1/2(3π²)^1/3]|∇ρ|/ρ^4/3, according to the NCI method is used to visualize non-covalent bonding aspects. An estimation of different non-covalent contact types according to steric/repulsive (λ₂ > 0, red-colored), van der Waals-like (λ₂ ≈ 0, green-colored), and attractive (λ₂ < 0, blue-colored) is facilitated by mapping the ED times the sign of the second eigenvalue of the Hessian (sign(λ₂)ρ) on the iso-surfaces of s(r). Structures are displayed with ChemCraft,⁸⁷ bond paths are displayed with AIM2000, NCI figures are displayed with VMD,⁸⁸ and ELI-D figures are displayed with MolIso.⁸⁹

Results and discussion

Structures and energies

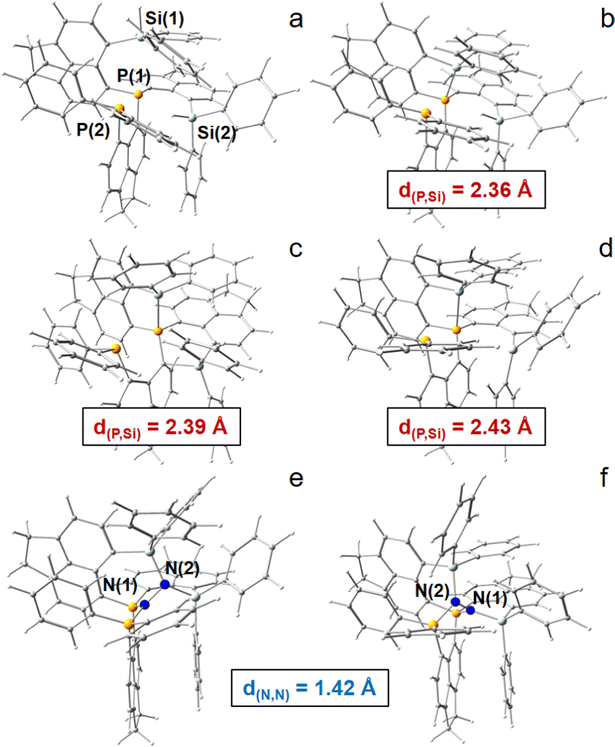
Basic peri-substituted scaffolds are constructed of one spacer group and two peri-substituents, e.g. a LA such as –BF₂ and a LB such as –PPh₂, see Fig. 1a and b for the conceptual design. The fixed peri-distances and limited number of LA and LB atoms, however, restrict their use for small molecule activation. The “best case” obtained by DFT is presented in the ESI.† A more flexible structural composition is given by adding a second spacer group to the LA or LB atom (Fig. 1c and d), but extensive computational studies proved that the high degree of rotational flexibility causes either the LA and LB atoms to be far away from each other or the formation of energetically low-lying quenched states, rendering this design also ineligible for small molecule activation, see the ESI† for the “best case” obtained by DFT. Accordingly, the study was extended to include three spacer groups, linked by a central LB atom (vide infra), see Fig. 1e and f for the conceptual design. One of the three peri-substituents carries another LB, each of the remaining two carries a LA fragment, resulting ideally in a 2LA–2LB active site. The third spacer group not only provides another LA or LB site, but significantly limits molecular rotations, keeping the whole system more rigid, but still flexible. In the course of finding the best candidates for the central atoms of the LA and LB fragments, only the combination of silyl cations and phosphorus atoms was found to be capable for efficient N₂ fixation and activation in silico, see Fig. 2. Replacing P by N or As atoms resulted in significantly lower binding affection and strength towards N₂. However, since the corresponding N-analogues are synthetically hardly accessible and As is toxic, this result is advantageous. Using B atoms as LA generates an additional energetic cost as the initially trigonal-planar R₃B-fragment has to reorganize towards a tetrahedral R₃B-N₂ orientation via N₂-adduct formation, which is unfavorable and causes the tested reactions to be endothermic (not shown). Consequently, only models comprising Si⁺ and P are represented in this study. Besides global abundance and the non-toxicity of the used elements, one appealing advantage of a molecular composition including only C, H, Si, and P atoms and N atoms from the target molecule is that all nuclei are sensitive to NMR, rendering detection of intermediate states and reaction products possible.

Fig. 1 Hypothetical structural design for N₂-activation. peri-Substituted naphthyl compounds based FLPs with one (a and b), two (c and d), or three (e and f) spacer groups, 1–2 E or LA atoms (purple), 1–2 E′ or LB atoms (black), and bulky substituents (R and R′ – x being 0 or 1 – or large blue and green spheres); naphthalene chosen as spacer group only for representative reasons and may be replaced by biphenylene, acenaphthalene, xanthene, dibenzofuran or other spacers.

Fig. 2 3-spacer candidate employing acenaphthyl as spacer group, Si⁺ as LA atoms, P as LB atoms, as well as phenyl rings systems as bulky ligands. (a) Neutral molecule (6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)₂ (1) with two –SiHPh₂ groups. (b) Monocation [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)(-5-ace-6-SiPh₂)]⁺ (2) with one –Ph₂Si⁺ group. (c) Dication [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂]²⁺ (3a); dead-end state. (d) Dication; “active state” (3b). (e) N₂-adduct [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ exhibiting a P₂N–NSi₂ coordination mode (4a). (f) N₂-adduct exhibiting a PSiN–NSiP coordination mode (4b). Si atoms are blusih-grey colored, P atoms orange, N atoms deep blue.

A dicationic ligand system being constructed by a central P atom carrying three acenaphthtyl (ace) spacer groups, a –PPh₂ group as second LB as well as two –Si⁺Ph₂ groups as strong LA in the three peri-positions, finally turned out to be the best candidate for the 3-spacer approach, see Fig. 2. The system is energetically indeed capable to uptake N₂ and extend the N≡N triple bond (d_(N,N) = 1.091 Å for DFT) by 0.327 Å to the unprecedented value of 1.418 Å, corresponding to a N–N single bond, and releasing 161.6 kJ mol⁻¹ of energy in the (in silico) process, see Table S4 (ESI†). Subsequent hydride uptake of the N₂-adduct already breaks the N–N bond, vide infra. However, this inspiring result comes with a major setback, as already the first hydride abstraction from the neutral ligand systems (6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)₂(1) to form the monocation [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)(-5-ace-6-SiPh₂)]⁺ (2) with one –Ph₂SiH and one –Ph₂Si⁺ group results in a quenched state with a short P–Si contact of 2.361 Å, compare Fig. 2a and b. This is already close to the optimized Si–P peri-distance in Ph₂P-ace-Ph₂Si⁺ (d_(P,Si) = 2.324 Å) and hints towards a stabilization (or Si–P bond strength) of larger than 150 kJ mol⁻¹, see Fig. S4 (ESI†). Second hydride abstraction to form the [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂]²⁺ (3a) not only keeps this unfortunate situation (d_(P,Si) = 2.393 Å), but exhibits an additional short contact of 2.105 Å between the second Si cation and an arylic C atom, which is bound to the central P atom, see Fig. 2c. A slightly more “active state” (3b, d_(P,Si) = 2.428 Å, d_(Si,Cπ) = 3.327 Å) in which the LA and LB parts are not interacting that strongly is already 62.2 kJ mol⁻¹ higher in energy, compare Fig. 2c and d. Attempts to solve this problem by introduction of sterically more demanding ligands at the LA site (Mes vs. Ph) couldn’t prevent the formation of an energetically lower-lying dead-end state, although the energetic difference (ΔE = 42.4 kJ mol⁻¹ at the 6-31+G* level) is somewhat smaller, see Fig. S5 (ESI†). Notably, the problem could indeed be solved employing the larger biphenylene (bip) molecule as spacer group for the two LA parts, see Fig. S7 (ESI†). Due to the large peri-distances in the bip parts, the dicationic (“active”) state of this ligand system does not form any direct (intra-spacer) P–Si peri-contacts, but only an indirect (inter-spacer) contact of 2.503 Å, which likely would not hamper N₂-uptake. Moreover, the energetic gain and N–N bond stretching effect is even higher in the bip-variant (ΔE = −210.9 kJ mol⁻¹, d_(N,N) = 1.437 Å), but since this ligand system seems hardly accessible by synthetic means, the focus of this DFT study remains on the ace-variant. Experimentally, formation of energetically lower-lying dead-end state(s) might be avoided also for the ace-variant by bubbling the solution with gaseous N₂ in the crucial (Si)H hydride abstraction steps. If not, the use of larger spacer groups such as bip is unavoidable.

Three different N₂-activation modes were obtained by DFT, see parts e and f of Fig. 2, as well as Fig. S8c (ESI†). Notably, the PSiN–NSiP (Fig. 2f) coordination mode of [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ (4b) is superior to those of P₂N–NSi₂ of 4a (Fig. 2e) or P–N–N–Si₂P of 4c (Fig. S8c, ESI†) modes as it results in significantly lower molecular energies for both investigated structural types (Table S4, ESI†). Apparently, “vertical” through-atom polarization of each N atom within a P–N–Si environment is more effective in weakening the N≡N triple bond than “horizontal” through-bond polarization within a P_2/1–N–N–Si₂P_0/1 environment. In order to investigate this crucial difference in more detail, the electronic bond characteristics of two strongest N₂-adducts (4a, 4b) were investigated computationally applying a set of complementary real-space bonding indicators (RSBI), see the following section.

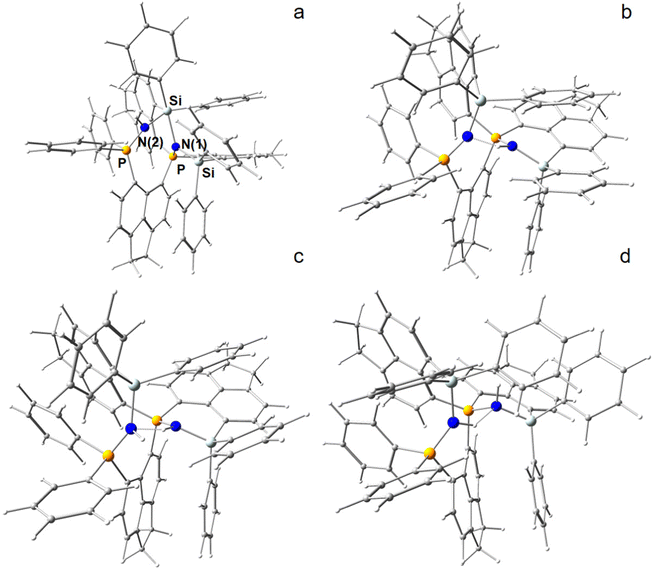
In an attempt to break the strongly activated N–N bond, the most energy efficient N₂-adduct (4b, PSiN–NSiP) of the ace-variant was “exposed” to hydride attack by attaching a H⁻ ion at one of eight potential coordination sites, that is above and below the two (SiP)N(N)-planes at N(1) and N(2), as well as attacking the Si atoms from outside (exo) or inside (endo) within their (Ph₂)Si(N)-tetrahedrons. The hydride attack resulted in two states, in which the N–N bond was ultimately broken to form one Si–N–P and one Si–N(H)–P fragment (Fig. 3a and b). Note that the H⁻ ion formally underwent an Umpolung in that process. In one of those H⁻ reduced N₂-adducts [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂H]⁺ (5a), the electronic bond characteristics of which are also discussed in the RSBI section, a short intramolecular PSiN–H⋯NSiP hydrogen bond is formed, which lowers the molecular energy considerably. To the contrary, although all four models including a Si–H instead of a N–H bond could be optimized to stable structures by DFT, they are not only energetically strongly unfavorable, but the N–N fixation is merely disturbed in those models, even when the Si–H bond is directed towards the inside of the molecule (endo), thereby breaking one of the two Si–N bonds, see Fig. S9 (ESI†).

Fig. 3 (a) Exposing adducts [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺(4b) in silico to H⁻ results in the disruption of the N–N bond [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂H]⁺ (5b). (b) If H⁻ is attached to N(1), a N–H⋯N hydrogen bond is formed further reducing the molecular energy in the isomer (5a). (c) Subsequent in silico exposure to H⁺ provides two R₃Si–N(H)–PR₃ fragments [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·HN₂H]²⁺ (6b). (d) Energetically lowest isomer (6a).

Subsequently, the H⁻ reduced N₂-adduct including the PSiN–H⋯NSiP hydrogen bond was exposed computationally to proton attack at N(1) or N(2), resulting again in two different models, which now formally comprises the dicationic ligand system, one molecule of N₂ and one molecule of H₂, see Fig. 3c and d. The energetically lower model is denoted as [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·HN₂H]²⁺ (6a). Stepwise reduction and protonation is a common reaction motif in biological systems. Notably, second H⁻ attack of the H⁻ reduced N₂-adduct is energetically disfavored and thus not considered further (Table S4, ESI†).

Fig. 4 displays a provisional reaction scheme based on the ΔE values for the so far applied b3pw91-D3/6-311+G(2df,p) level as well as ΔG values for the reoptimized b3pw91-D3/6-31+G* level structures of the “best models”, that is, the energetically lowest lying structural isomers of each electronic state (see also Tables S8–S10, ESI†). Since all but one reactions in that scheme don’t change the number of involved species and rotational movements are rather limited in the sterically crowded ligand systems, entropic effects were expected and found to be rather small: the largest difference between ΔE and ΔG indeed was found for N₂-adduct formation. The neutral ligand system (6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)₂ (1) comprising two –SiHPh₂ fragments already forms (at least) three structural isomers, depending if the Si–H bond is pointing towards the outside (denoted as “exo”) or inside (denoted as “endo”) of the molecule. As the exo–exo- and endo–endo-variants (see Fig. S6a, b and Table S4, ESI†) are higher in energy, they are not considered further and model (6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)₂ (1) thus refers to the exo–endo-state (Fig. 2a). Single hydride abstraction releases considerable amounts of energy (ΔE = −232 kJ mol⁻¹, ΔG = −217 kJ mol⁻¹), because the monocationic model [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂H)(-5-ace-6-SiPh₂)]⁺ (2) forms a short Si–P bond, whereas the second abstraction of the endo-hydride to form the dication [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂]²⁺ (3a) is almost energy neutral (ΔE = −3 kJ mol⁻¹, ΔG = 6 kJ mol⁻¹). Although N₂-adduct formation to form [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ (4b) is energetically strongly favorable, releasing another 162 kJ (ΔE) or 75 (ΔG) mol⁻¹, the (purple colored) 2 and 3a states are considered as dead-end states, which should be circumvented, e.g. by flushing the solution with gaseous N₂via the hydride abstractions, see purple curved arrow in Fig. 4. Conversion of the 1 atm standard state 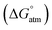to the 1 M standard state 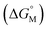is relevant for the N₂-adduct formation step, because the number of moles is changing. Using 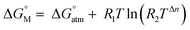with R₁ = 8.31447 J K⁻¹ mol⁻¹, R₂ = 0.08206 L atm K⁻¹ mol⁻¹, T = temperature in K, and n = change in number of moles,⁹⁰ a further free enthalpy expense of 7.9 kJ mol⁻¹ has to be added to the −75 kJ mol⁻¹, leaving −67 kJ mol⁻¹. The basis-set superposition error (BSSE) of 4b was calculated to be 10.1 kJ mol⁻¹, leaving finally −57 kJ mol⁻¹. Once 4b has been formed successfully, it is prone to stepwise attack of adding hydride (ΔE = −243 kJ mol⁻¹, ΔG = −208 kJ mol⁻¹), ultimately splitting the N–N bond [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂H]⁺ (5a), and subsequent protonation (ΔE = −43 kJ mol⁻¹, ΔG = −48 kJ mol⁻¹) to form [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·HN₂H]²⁺ (6a), which formally comprises the ligand system, one molecule N₂ and one molecule H₂, as mentioned above. The energetic cost for the heterolytic splitting of H₂ to form transferable “H⁽⁻⁾” and “H⁽⁺⁾”, according to the reaction scheme: 1/2B₂H₆ + Tf⁽⁻⁾ + H₂ → BH4⁽⁻⁾ + TfH (ΔG = 151.8 kJ mol⁻¹) is overcompensated by the summed up energetic gain of adding hydride and subsequent protonation for the first hydrogen equivalent (ΔG = 255.0 kJ mol⁻¹) forming the diazene structure 6a. Subsequent reduction and protonation steps surely will be much less beneficial. Further reactions with H⁻ and H⁺, however, have not been attempted so far due to the enormous numbers of potential states. The NH₃-poisoned states 3a·NH₃ and 3a·2NH₃ (see Fig. S10, ESI†) were calculated to be 129.2 and 162.2 kJ mol⁻¹ lower in energy (at b3pw91-D3/6-31+G*) than the sum of 3a and one or two NH₃ molecules, making it unlikely that the process can be completed to finally release NH₃ with this ligand system. The reaction 6a + 2BH₄⁻ + 2TfH → 3a·2NH₃ + B₂H₆ + 2Tf⁻ is formally slightly endothermic (ΔG = 27.9 kJ mol⁻¹; b3pw91-D3/6-31+G*).

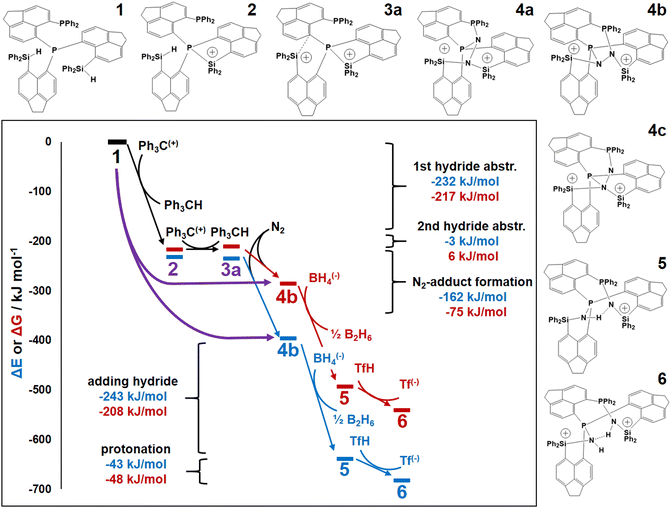Fig. 4 ΔE (b3pw91-D3/6-311+G(2df,p)) and related ΔG (b3pw91-D3/6-31+G*) energy diagrams of the investigated reactions steps. The purple curved arrow indicates a potential shortcut from the neutral ligand system (1, energy value set to zero) to the most stable N₂-adduct (4b) circumventing the formation of dead-end species 2 and 3a (colored in purple) by bubbling the solution with N₂ gas via two-step hydride abstraction. For clarity, all steps and states after adding N₂ are color-coded with respect to the DFT-level (higher level: blue, lower level: red). No transition states included. 1 atm to 1 M and BSSE corrections not included for 4b, see main text. The main difference between ΔE and ΔG stem from thermal corrections, and not from the basis-set level, see Fig. S11 (ESI†) for ΔE at b3pw91-D3/6-31+G*.

Transition-state calculations are not included in the scheme due to the size and complexity of the ligand system, but an attempt was made to evaluate the activation barrier of the N₂ molecule being located within the “active site” of 4b by conducting a potential energy scan with N–N distances fixed to values between 1.10 and 1.55 Å, see Fig. S12 (ESI†) (b3pw91-D3/6-31+G*). The observed continuous rise in energy along shorter bond distances suggests that once N₂ has entered the active site of the ligand system (assuming no blocking P–Si bonds), it will immediately be stretched to about 1.4 Å.

Real-space bonding indicators

The most relevant states, 3a, 4a, 4b, 5a, and 6a, are electronically characterized applying a complementary set of real-space bonding indicators (RSBIs), which were extracted from the calculated electron densities (ED, ρ(r)) and electron pair densities, following the AIM,^72–74 NCI,⁷⁶ and ELI-D⁷⁵ methods. Charge redistributions via N₂-activation and subsequent N–N bond rupture are monitored by means of AIM atomic and fragmental charges (Table 1 and Table S11, ESI†) and electron populations of (non-)bonding ELI-D basins (Table 2 and Tables S12–S13, ESI†). In the investigated systems N₂-uptake is accompanied by tremendous charge accumulation at the N₂-site, as each N atom gains more than 1.4 e. The majority of this charge is delivered by the two adjacent P atoms (together more than 2.5 e), whereas the two Si atoms show minor contributions (together about 0.4 e). For the organic fragments (ace spacer and phenyl rings) charge redistributions never exceed 0.1 e and are thus neglected. In fact, the charge redistributions only happen within the Si₂P₂N₂ fragment, which shows a stable summed up charge in 3a, 4a, and 4b, see Table 1 for details. The results highlight the essential role of the two “hard” Si⁺ ions to drive the activation of the inert N₂ molecule as well as the essential role of the two P atoms to serve as “soft” and flexible electron donors, see Fig. S13 (ESI†) for further details. By reducing the N₂-site and extending the N–N bond in the process to a value above 1.4 Å, which may be considered as an entatic state, the N–N fragment is well prepared for chemical reduction with a hydride atom and subsequent protonation to form two secondary amine sites. In many metalloproteins, Fe₄O₄ cubane clusters serve as reversible electron reservoirs for close-by active sites, the role of which is filled by P atoms in the light atom molecules of this study. This might be related to the observation that the boron atom, which on the one side is electron deficient, but on the other side carries non-bonded ED in the p_z-orbital, is capable to activate N₂ as well.^44–48 Notably, 4a and 4b show similar AIM charges despite the qualitatively different P₂N–NSi₂ and PSiN–NSiP binding modes. Adding a hydride atom to N₂-adduct [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ (4b) thereby splitting the weakened N–N bond and forming a N–H⋯N contact [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂H]⁺ (5a), alters all fragments in a systematical fashion: whereas the P and Si atoms are slightly more positive charged in 5a, all organic fragments are more negative charged, but with one exception those changes never exceed ±0.1 e. Drastic changes, however, are again obtained for the N(H) and N atoms gaining further 0.75 and 0.50 e, which brings both N atomic charges to values of −2 e or larger. It is thus not of surprise that further chemical reduction with another hydride atom is energetically strongly disfavored, see Table S4 (ESI†). In contrast, subsequent protonation of [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂H]⁺ (5a) causes the formation of two secondary amines of the SiPNH-type in [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·HN₂H]²⁺ (6a) and affects the charges accordingly.

Table 1 AIM atomic and fragmental charges (in e)

Q(AIM)	3a	4a	4b	5a	6a	4b–3a	5a–4b	6a–5a
Q AIM(N): 0.00 e (N2), −0.33 e (N2H2), −0.68 e (N2H4), −1.04 e (NH3).
N(1)		−1.51	−1.49	−2.00	−1.87		−0.50	0.13
N(2)		−1.43	−1.43	−2.18	−1.95		−0.75	0.23
H(N)				0.49	0.46		0.49	−0.04
H(N)					0.43			0.43
NxHy		−2.94	−2.93	−3.68	−2.94		−0.76	0.75
P(1)	1.38	2.76	2.70	2.86	2.70	1.31	0.16	−0.16
P(2)	1.52	2.73	2.77	2.81	2.83	1.25	0.04	0.03
Si(1)	2.66	2.89	2.90	2.93	2.92	0.24	0.03	−0.01
Si(2)	2.74	2.90	2.89	2.95	2.91	0.14	0.06	−0.04
Si2P2N2Hx	8.31	8.35	8.33	7.86	8.43	0.02	−0.47	0.57
ace(1)	−0.71	−0.81	−0.76	−0.87	−0.77	−0.05	−0.11	0.10
ace(2)	−1.05	−1.08	−1.00	−1.10	−1.04	0.05	−0.10	0.06
ace(3)	−1.04	−0.98	−1.07	−1.12	−1.08	−0.03	−0.05	0.04
ph(1)	−0.44	−0.40	−0.41	−0.47	−0.41	0.03	−0.06	0.06
ph(2)	−0.44	−0.35	−0.39	−0.46	−0.40	0.05	−0.07	0.06
ph(3)	−0.64	−0.69	−0.68	−0.72	−0.68	−0.04	−0.04	0.04
ph(4)	−0.66	−0.68	−0.66	−0.71	−0.68	0.00	−0.05	0.03
ph(5)	−0.63	−0.68	−0.68	−0.70	−0.68	−0.05	−0.02	0.02
ph(6)	−0.67	−0.67	−0.66	−0.69	−0.66	0.00	−0.03	0.03

---

Table 2 Topological and integrated RSBIs of the N≡N, N=N, and N–N bonds

	d [Å]	ρ(r)bcp [e Å^−3]	∇^2ρ(r)bcp [e Å^−5]	ε	d 1/d	RJI [%]
ρ(r)bcp: ED at the bcp, ∇^2ρ(r)bcp: Laplacian, ε: bond ellipticity d1: distance atom(1)-bcp, RJI: Raub-Jansen Index, G/ρ(r)bcp, H/ρ(r)bcp: kinetic and total energy density over ρ(r)bcp ratios, V: potential energy density, NELI, VELI: electron populations and volumes the ELI-D basin, γELI: ELI-D value at the attractor position.
N2	1.091	4.83	−73.6	0.00	0.50	50.0
N2H2	1.233	3.33	−32.3	0.15	0.50	50.0
4a	1.417	2.02	−8.4	0.02	0.52	60.1
4b	1.418	2.04	−8.7	0.01	0.50	50.6
N2H4	1.428	2.05	−10.1	0.00	0.50	50.0

---

	G/ρ(r)bcp [a.u.]	H/ρ(r)bcp [a.u.]	G/V	N ELI [e]	V ELI [Å^3]	γ ELI
N2	0.88	−1.94	0.31	3.50	6.0	1.46
N2H2	0.63	−1.31	0.32	2.45	5.1	1.52
4a	0.53	−0.82	0.39	1.14	0.8	1.56
4b	0.51	−0.81	0.39	1.15	0.8	1.56
N2H4	0.45	−0.80	0.36	1.33	1.0	1.54

---

The considerably weakened N–N bonds in [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ (4a and 4b) are electronically characterized by topological and integrated bond properties (Table 2) and compared to dinitrogen, diazene and hydrazine. With almost 1.42 Å, the N–N bond distances in 4a and 4b are already very close to the N–N single bond of hydrazine (d_(N,N) = 1.43 Å). Consequently, the ED at the bond critical point (bcp) is reduced from 4.8 e Å⁻³ in N₂ to 2.0 e Å⁻³ in 4a, or 4b, resembling the value of 2.1 e Å⁻³ in hydrazine. This is accompanied by a drastic reduction of the electron populations (N_ELI) of the corresponding ELI-D N–N bonding basins (V₂(N,N)) from 3.5 e in N₂ to 1.1–1.2 e in the N₂-adducts, the latter being already smaller in numbers than the 1.33 e found in the V₂(N,N) basin of hydrazine. Less efficient orbital overlap between the N atoms and thus lower degrees of covalency are reflected by the Laplacian of the ED (∇²ρ(r)_bcp) and the total energy density over ED ratio (H/ρ(r)_bcp), which both drop down considerably (from negative values towards zero). Since the kinetic energy over ED ratio (G/ρ(r)_bcp) is dropping down less “fast” (from positive values towards zero), the ratio between G and the potential energy density (V) increases slightly, hinting towards higher relevance of non-covalent bonding aspects for longer N–N distances. This goes along with slightly increased ELI-D values at the V₂(N,N) attractor position (γ_ELI), suggesting higher localizability (i.e. less electron sharing) of the bonding electron pair. Bond ellipticities (ε) of 0.0 prove the cylindrical symmetry of the N≡N triple bond in N₂ and the N–N single bonds in 4a, 4b, and hydrazine, whereas for the N=N double bond in azene, the symmetry is slightly disturbed (ε = 0.15), as expected. For the small reference models, the N atoms are indistinguishable, which causes the bcp to be located exactly at the middle of the N–N bond, i.e. d₁/d = 0.5. Based on the same grounds, the Raub-Jansen Index (RJI⁹¹), which determines how electron populations with an ELI-D basin are distributed over adjacent AIM atomic basins, is 50%. For the symmetrical 4b (PSiN–NSiP) this is also valid, but slight distortions are observed for the less symmetrical 4a (P₂N–NSi₂), vide infra. The lone-pairs of the N atoms accommodate for charge balancing, but their ELI-D basins show a surprising trend for the investigated ligand systems (Table S12, ESI†): for N₂, N₂H₂, N₂H₄, and NH₃, there is a clear trend of decreasing electron populations with decreasing s-character, e.g. 3.14 e in N₂ (sp-like) to 2.14 e in NH₃ (sp³-like). However, in models 4a, 4b, 5a, and 6a, flatter Si_xP_yNE (E = N, H) planes (more “sp²”-like) cause lower N_ELI values, whereas more tetrahedral shaped planes (more “sp³”-like) cause higher N_ELI-values. An exception is the “azide”-like N(2) atom in 5a, which might be considered as “sp²-like, and the lone-pair basin of which carries 2.9 e.

RSBIs for the Si–N and P–N bonds in 4a, 4b, 5a, and 6a are collected in Table S13 (ESI†). Both bond types become shorter via breaking the N–N bond and forming the secondary amines, accompanied by increased ρ(r)_bcp and N_ELI values. Notably, H/ρ(r)_bcp remains unaffected, whereas the already dominating G/ρ(r)_bcp as well as ∇²ρ(r)_bcp rise to more positive values, indicating essentially increased ionic bond contributions in the Si–N and P–N bonds of 5a and 6a. Whereas the P–N bonds can be considered as polarized-covalent, as indicated by a RJI of about 82%, the Si–N bonds are already at the border of dative bonds (RJI larger than 92%).

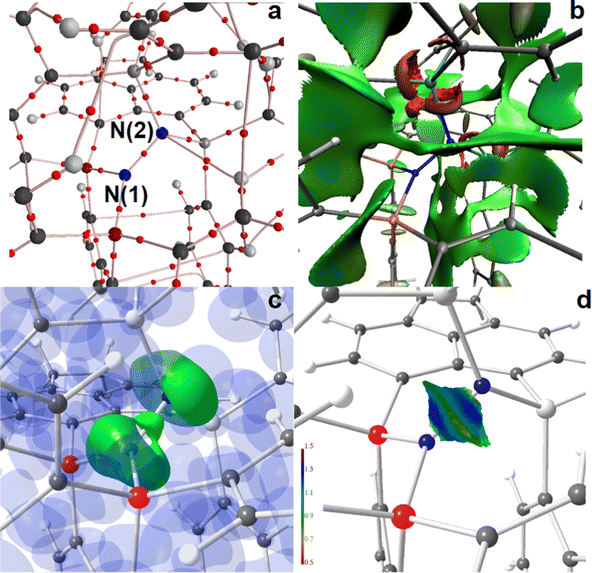
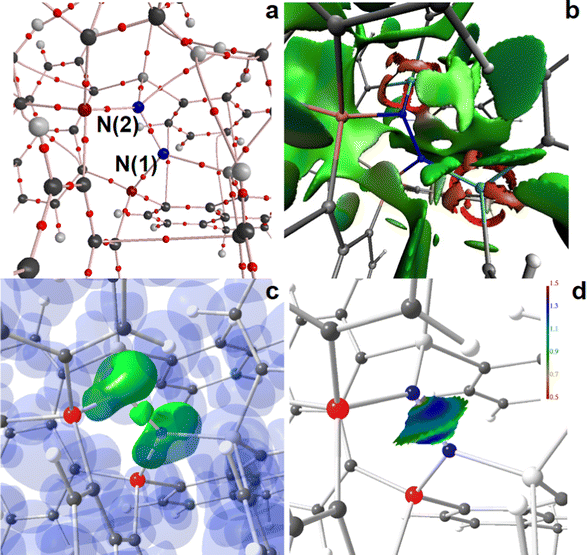
The AIM bond topology as well as NCI and ELI-D basin distributions of the “active site” areas of the two N₂-adducts, 4a and 4b, are displayed in Fig. 5 and 6; full molecule representations and the results for 5a and 6a are comprised in the ESI,† (Fig. S14–S19). For both, 4a and 4b, AIM topology reveals only one long and thus weak secondary C–H⋯N contact at the N₂-site, see parts a of Fig. 5 and 6, suggesting that this site is fully determined by the primary N–N, Si–N, and P–N bonds. Also the NCI, which is even more sensitive to the formation of weak non-covalent interactions, and shows extended flat greenish basins reflecting numerous attractive H⋯H, H⋯C_π, and C_π⋯C_π contacts within the molecules, gives no hint for non-covalent bond contributions within the active site, including the N₂- and P–N-bonds, which are dominated by covalent bond contributions, see parts b of Fig. 5 and 6. Ring-shaped and red-colored NCI-basins around the Si atoms confirm the relevance of non-covalent bonding aspects to the Si–N and Si–C bonds. Parts c and d of Fig. 5 and 6 display color-coded ELI-D iso-surface representations and the ELI-D distribution mapped on the V₂(N,N) basin, respectively. For clarity, V₂(N,N) and V₁(N) (lone-pair basins) are given in solid-green for the iso-surfaces, whereas V₂(Si,N), V₂(P,N), and the remaining basin types are given in transparent-blue (Fig. 5c and 6c). At an iso-value of γ = 1.35, the V₂(N,N) bonding basin is still topologically connected with the two V₁(N(2)) basins of the P₂N-site in 4a, but already separated from the V₁(N(1)) basin of the Si₂N-site. In contrast, V₂(N,N) is well separated from both SiPN-sites in 4b. Apparently, the less symmetric N₂-coordination mode in 4a induces the N–N bonding electron pair to move towards N(1), which results in a RJI of 60% (see above), i.e. 60% of the electron population of V₂(N,N) is located within the AIM atomic basin of N(1)P₂, and 40% in the basin of N(2)Si₂. Nevertheless, since the differences between P₂N–NSi₂ and PSiN–NSiP coordination modes are not tremendous, the size and shape of V₂(N,N) as well as the ELI-D distribution mapped on its surface is very much the same (Fig. 5d and 6d).

Fig. 5 RSBI analysis of [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ (4a) (a) AIM bond paths motif, (b) NCI iso-surface at s(r) = 0.5, (c) ELI-D localization domain representation at iso-value of 1.35, (d) ELI-D distribution mapped on the N–N ELI-D bonding basin. Magnification of the active site. Atom colors: P (red or orange), Si (light gray or light blue), N (blue), C (dark grey).

Fig. 6 RSBI analysis of [(6-Ph₂P-ace-5-)P(-5-ace-6-SiPh₂)₂·N₂]²⁺ (4b) (a) AIM bond paths motif, (b) NCI iso-surface at s(r) = 0.5, (c) ELI-D localization domain representation at iso-value of 1.35, (d) ELI-D distribution mapped on the N–N ELI-D bonding basin. Magnification of the active site. Atom colors: P (red or orange), Si (light gray or light blue), N (blue), C (dark grey).

N–H⋯N bond formation further separates both N atoms in 5a and 6a, see Fig. S16–S19 (ESI†). The new secondary contact within the active site is reflected by an (N)H⋯N bcp as well as by a flat green or bluish NCI basin between the two N atoms, and it leaves a concave impression on V₁(N) with slightly increased ELI-D values in the cavity area (parts d of Fig. S16–S19, ESI†).

Conclusion

The DFT study shows that – at least in silico – the inert N≡N triple bond can be cleaved by molecular compounds containing only the earth abundant elements C, H, Si, and P. The combination of two silyl cations as Lewis acidic sites with the lone-pairs of two phosphorus atoms as Lewis basic sites in a flexible but not too flexible spatial arrangement thereby proved to be essential to energy efficiently drive N₂-uptake, activation and finally splitting. However, the reaction path can’t be proceeded to liberate of NH₃ molecules due to formation of very strong H₃N–Si⁽⁺⁾ bonds in the final steps. Nevertheless, the proposed ligand systems may serve as blueprint for related systems and approaches. Especially the role of the P atoms as “soft” electron donors should be highlighted in this respect. Different modes of N₂-bonding (e.g. P₂N–NSi₂vs. PSiN–NSiP coordination) were encountered and examined by means of real-space bonding indicators derived from the calculated electron and electron pair densities. Minute effects of charge rearrangements via the different reaction steps were monitored by AIM atomic and fragmental charges and by electron populations of bonding and non-bonding ELI-D basins. Via N₂-uptake, the N₂ lone pairs (LP(N)) donate into the LA centers, and electron population is transferred from the N≡N bonding ELI-D basins towards newly formed LP(N) basins. The majority of the electron population within the newly formed P–N bonding basins (stemming from the formerly LP(P) basins of the ligand system) is located within the AIM atomic basins of the N atoms, considerably increasing their charge from zero in gaseous N₂ to ca. −1.5 e in the N₂-adducts. The tremendous weakening of the N–N bond (d_(N,N) = 1.4 Å vs. 1.1 Å in gaseous N₂) makes it prone to subsequent addition of hydride ions and protonation to form two secondary amines. A critical point for this class of peri-substituted compounds remains the potential formation of dead-end states, in which either the LA and LB prematurely form a strong dative bond or the LA and LB sites are too far away from each other to fix N₂. Fine tuning of the relevant distances by combination of suitable spacer molecules, such as (ace)naphthyl, biphenylene, xanthene, or dibenzofuran with (bulky) ligand groups attached to the LA and LB atoms, such as methyl, iso-propyl, tert-butyl, phenyl, or mesityl, as well as bubbling the solution with N₂ gas via hydride abstraction, may solve this problem, but not all combinations might be accessible by synthetic means in the laboratory. Practical work in the laboratory also has to show, if the bulky ligand hamper access of gaseous N₂ to the active site. In silico work is ongoing in order to optimize the ligand system towards energy efficiency and practical accessibility and towards extraction of ΔG and ΔS values of all reaction states to get complete and reliable reaction schemes including transition states.

Author contributions

S. M.: conceptual design, DFT calculations and analysis, manuscript writing. J. B.: conceptual design, critical revision of the article.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

Dr Emanuel Hupf is greatly acknowledged for software support and critically reading the manuscript. The DFG is acknowledged for funding.

References

1. R. E. Blankenship, Molecular mechanisms of photosynthesis, John Wiley & Sons, 3rd edn, 2021.
2. W. Lubitz, H. Ogata, O. Rudiger and E. Reijerse, Hydrogenases, Chem. Rev., 2014, 114(8), 4081–4148.
3. M. Wikstrom, K. Krab and V. Sharma, Oxygen Activation and Energy Conservation by Cytochrome c Oxidase, Chem. Rev., 2018, 118(5), 2469–2490.
4. K. Schroder, NADPH oxidases: Current aspects and tools, Redox Biol., 2020, 34, 101512.
5. A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer and G. L. Waldrop, Frontiers, Opportunities, and Challenges in Biochemical and Chemical Catalysis of CO2 Fixation, Chem. Rev., 2013, 113(8), 6621–6658.
6. B. M. Hoffman, D. Lukoyanov, Z. Y. Yang, D. R. Dean and L. C. Seefeldt, Mechanism of Nitrogen Fixation by Nitrogenase: The Next Stage, Chem. Rev., 2014, 114(8), 4041–4062.
7. N. Gruber and J. N. Galloway, An Earth-system perspective of the global nitrogen cycle, Nature, 2008, 451(7176), 293–296.
8. R. Schlogl, Heterogeneous Catalysis, Angew. Chem., Int. Ed., 2015, 54(11), 3465–3520.
9. V. Kyriakou, I. Garagounis, A. Vourros, E. Vasileiou and M. Stoukides, An Electrochemical Haber–Bosch Process, Joule, 2020, 4(1), 142–158.
10. S. Yadav, S. Saha and S. S. Sen, Compounds with Low-Valent p-Block Elements for Small Molecule Activation and Catalysis, ChemCatChem, 2016, 8(3), 486–501.
11. W. Zhang, W. Z. Lai and R. Cao, Energy-Related Small Molecule Activation Reactions: Oxygen Reduction and Hydrogen and Oxygen Evolution Reactions Catalyzed by Porphyrin- and Corrole-Based Systems, Chem. Rev., 2017, 117(4), 3717–3797.
12. R. Saha and P. K. Chattaraj, Activation of Small Molecules (H-2, CO2, N2O, CH4, and C6H6) by a Porphyrinoid-Based Dimagnesium(I) Complex, an Electride, Acs Omega, 2018, 3(12), 17199–17211.
13. F. Moller, S. Piontek, R. G. Miller and U. P. Apfel, From Enzymes to Functional Materials-Towards Activation of Small Molecules, Chem. – Eur. J., 2018, 24(7), 1471–1493.
14. R. L. Melen, Frontiers in molecular p-block chemistry: From structure to reactivity, Science, 2019, 363(6426), 479–484.
15. L. J. Taylor and D. L. Kays, Low-coordinate first-row transition metal complexes in catalysis and small molecule activation, Dalton Trans., 2019, 48(33), 12365–12381.
16. C. Weetman, A. Porzelt, P. Bag, F. Hanusch and S. Inoue, Dialumenes - aryl vs. silyl stabilisation for small molecule activation and catalysis, Chem. Sci., 2020, 11(18), 4817–4827.
17. H. T. Lei, X. L. Li, J. Meng, H. Q. Zheng, W. Zhang and R. Cao, Structure Effects of Metal Corroles on Energy-Related Small Molecule Activation Reactions, ACS Catal., 2019, 9(5), 4320–4344.
18. E. H. Edwards and K. L. Bren, Light-driven catalysis with engineered enzymes and biomimetic systems, Biotechnol. Appl. Biochem., 2020, 67(4), 463–483.
19. A. C. Ghosh, C. Duboc and M. Gennari, Synergy between metals for small molecule activation: Enzymes and bio-inspired complexes, Coordin. Chem. Rev., 2021, 428, 213606.
20. L. Marchetti and M. Levine, Biomimetic Catalysis, ACS Catal., 2011, 1(9), 1090–1118.
21. IEDT, https://www.iipinetwork.org/wp-content/Ietd/content/ammonia.html.
22. Q. Wang and D. Astruc, State of the Art and Prospects in Metal-Organic Framework (MOF)-Based and MOF-Derived Nanocatalysis, Chem. Rev., 2020, 120(2), 1438–1511.
23. S. S. Liu, M. F. Wang, T. Qian, H. Q. Ji, J. Liu and C. L. Yan, Facilitating nitrogen accessibility to boron-rich covalent organic frameworks via electrochemical excitation for efficient nitrogen fixation, Nat. Commun., 2019, 10, 3898.
24. J. X. Zhao and Z. F. Chen, Single Mo Atom Supported on Defective Boron Nitride Monolayer as an Efficient Electrocatalyst for Nitrogen Fixation: A Computational Study, J. Am. Chem. Soc., 2017, 139(36), 12480–12487.
25. X. Mao, S. Zhou, C. Yan, Z. H. Zhu and A. J. Du, A single boron atom doped boron nitride edge as a metal-free catalyst for N-2 fixation, Phys. Chem. Chem. Phys., 2019, 21(3), 1110–1116.
26. C. V. S. Kumar and V. Subramanian, Can boron antisites of BNNTs be an efficient metal-free catalyst for nitrogen fixation? - A DFT investigation, Phys. Chem. Chem. Phys., 2017, 19(23), 15377–15387.
27. W. B. Qiu, X. Y. Xie, J. D. Qiu, W. H. Fang, R. P. Liang, X. Ren, X. Q. Ji, G. W. Cui, A. M. Asiri, G. L. Cui, B. Tang and X. P. Sun, High-performance artificial nitrogen fixation at ambient conditions using a metal-free electrocatalyst, Nat. Commun., 2018, 9, 3485.
28. M. Zheng, Y. Li, K. N. Ding, Y. F. Zhang, W. K. Chen and W. Lin, Nitrogen fixation on metal-free SiC(111) polar surfaces, J. Mater. Chem. A, 2020, 8(15), 7412–7421.
29. M. Zafari, D. Kumar, M. Umer and K. S. Kim, Machine learning-based high throughput screening for nitrogen fixation on boron-doped single atom catalysts, J. Mater. Chem. A, 2020, 8(10), 5209–5216.
30. S. B. Tang, Q. Dang, T. Y. Liu, S. Y. Zhang, Z. G. Zhou, X. K. Li, X. J. Wang, E. Sharman, Y. Luo and J. Jiang, Realizing a Not-Strong-Not-Weak Polarization Electric Field in Single-Atom Catalysts Sandwiched by Boron Nitride and Graphene Sheets for Efficient Nitrogen Fixation, J. Am. Chem. Soc., 2020, 142(45), 19308–19315.
31. P. Sun, J. Huang, F. Xu, J. J. Xu, T. Q. Lin, W. Zhao, W. J. Dong and F. Q. Huang, Boron-Induced Nitrogen Fixation in 3D Carbon Materials for Supercapacitors, ACS Appl. Mater. Interfaces, 2020, 12(25), 28075–28082.
32. B. Liu, Y. P. Zheng, H. Q. Peng, B. F. Ji, Y. Yang, Y. B. Tang, C. S. Lee and W. J. Zhang, Nanostructured and Boron-Doped Diamond as an Electrocatalyst for Nitrogen Fixation, ACS Energy Lett., 2020, 5(8), 2590–2596.
33. C. W. Liu, Q. Y. Li, C. Z. Wu, J. Zhang, Y. G. Jin, D. R. MacFarlane and C. H. Sun, Single-Boron Catalysts for Nitrogen Reduction Reaction, J. Am. Chem. Soc., 2019, 141(7), 2884–2888.
34. T. Y. Liu, Q. Dang, X. H. Zhou, J. Li, Z. Ge, H. Che, S. B. Tang, Y. Luo and J. Jiang, Synergistic Effect of Boron Nitride and Carbon Domains in Boron Carbide Nitride Nanotube Supported Single-Atom Catalysts for Efficient Nitrogen Fixation, Chem. – Eur. J., 2021, 27(23), 6945–6953.
35. S. F. Ye, E. Bill and F. Neese, Electronic Structures of the [Fe(N-2)(SiP3iPr)](+1/0/-1) Electron Transfer Series: A Counterintuitive Correlation between Isomer Shifts and Oxidation States, Inorg. Chem., 2016, 55(7), 3468–3474.
36. B. D. Matson and J. C. Peters, Fe-Mediated HER vs N2RR: Exploring Factors That Contribute to Selectivity in (P3Fe)-Fe-E(N-2) (E = B, Si, C) Catalyst Model Systems, ACS Catal., 2018, 8(2), 1448–1455.
37. M. P. Shaver and M. D. Fryzuk, Activation of molecular nitrogen: Coordination, cleavage and functionalization of N-2 mediated by metal complexes, Adv. Synth. Catal., 2003, 345(9–10), 1061–1076.
38. J. B. Lu, X. L. Wang, J. Q. Wang, J. C. Liu, H. Xiao and J. Li, Efficient Nitrogen Fixation via a Redox-Flexible Single-Iron Site with Reverse-Dative Iron -> Boron sigma Bonding, J. Phys. Chem. A, 2018, 122(18), 4530–4537.
39. A. Eizawa, K. Arashiba, H. Tanaka, S. Kuriyama, Y. Matsuo, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Remarkable catalytic activity of dinitrogen-bridged dimolybdenum complexes bearing NHC-based PCP-pincer ligands toward nitrogen fixation, Nat. Commun., 2017, 8, 14874.
40. Y. Ashida and Y. Nishibayashi, Catalytic conversion of nitrogen molecule into ammonia using molybdenum complexes under ambient reaction conditions, Chem. Commun., 2021, 57(10), 1176–1189.
41. J. Fajardo and J. C. Peters, Tripodal (P3Fe)-Fe-X-N-2 Complexes (X = B, Al, Ga): Effect of the Apical Atom on Bonding, Electronic Structure, and Catalytic N-2-to-NH3 Conversion, Inorg. Chem., 2021, 60(2), 1221–1228.
42. C. N. Tang, Q. M. Liang, A. R. Jupp, T. C. Johnstone, R. C. Neu, D. T. Song, S. Grimme and D. W. Stephan, 1,1-Hydroboration and a Borane Adduct of Diphenyldiazomethane: A Potential Prelude to FLP-N-2 Chemistry, Angew. Chem., Int. Ed., 2017, 56(52), 16588–16592.
43. R. L. Melen and A. Step, Closer to Metal-Free Dinitrogen Activation: A New Chapter in the Chemistry of Frustrated Lewis Pairs, Angew. Chem., Int. Ed., 2018, 57(4), 880–882.
44. A. J. Ruddy, D. M. C. Ould, P. D. Newman and R. L. Melen, Push and pull: the potential role of boron in N-2 activation, Dalton Trans., 2018, 47(31), 10377–10381.
45. C. Hering-Junghans, Metal-Free Nitrogen Fixation at Boron, Angew. Chem., Int. Ed., 2018, 57(23), 6738–6740.
46. M. A. Legare, G. Belanger-Chabot, R. D. Dewhurst, E. Welz, I. Krummenacher, B. Engels and H. Braunschweig, Nitrogen fixation and reduction at boron, Science, 2018, 359(6378), 896–899.
47. M. A. Legare, C. Pranckevicius and H. Braunschweig, Metallomimetic Chemistry of Boron, Chem. Rev., 2019, 119(14), 8231–8261.
48. M. A. Legare, M. Rang, G. Belanger-Chabot, J. I. Schweizer, I. Krummenacher, R. Bertermann, M. Arrowsmith, M. C. Holthausen and H. Braunschweig, The reductive coupling of dinitrogen, Science, 2019, 363(6433), 1329–1332.
49. D. W. Stephan, Discovery of Frustrated Lewis Pairs: Intermolecular FLPs for Activation of Small Molecules, Top. Curr. Chem., 2013, 332, 1–44.
50. D. W. Stephan, FRUSTRATED LEWIS PAIRS A metal-free landmark, Nat. Chem., 2014, 6(11), 952–953.
51. D. W. Stephan, Frustrated Lewis Pairs, J. Am. Chem. Soc., 2015, 137(32), 10018–10032.
52. D. W. Stephan, Frustrated Lewis Pairs: From Concept to Catalysis, Acc. Chem. Res., 2015, 48(2), 306–316.
53. F. G. Fontaine and D. W. Stephan, On the concept of frustrated Lewis pairs, Philos. T. R. Soc. A, 2017, 375, 20170004.
54. D. W. Stephan and G. Erker, Frustrated Lewis pair chemistry, Philos. T. R. Soc. A, 2017, 375, 20170239.
55. A. R. Jupp and D. W. Stephan, New Directions for Frustrated Lewis Pair Chemistry, Trends Chem., 2019, 1(1), 35–48.
56. G. Menard and D. W. Stephan, Room Temperature Reduction of CO2 to Methanol by Al-Based Frustrated Lewis Pairs and Ammonia Borane, J. Am. Chem. Soc., 2010, 132(6), 1796–1797.
57. D. W. Stephan and G. Erker, Frustrated Lewis Pairs: Metal-free Hydrogen Activation and More, Angew. Chem., Int. Ed., 2010, 49(1), 46–76.
58. L. Greb, P. Ona-Burgos, B. Schirmer, S. Grimme, D. W. Stephan and J. Paradies, Metal-free Catalytic Olefin Hydrogenation: Low-Temperature H2 Activation by Frustrated Lewis Pairs, Angew. Chem., Int. Ed., 2012, 51(40), 10164–10168.
59. S. A. Weicker and D. W. Stephan, Activation of Carbon Dioxide by Silyl Triflate-Based Frustrated Lewis Pairs, Chem. – Eur. J., 2015, 21(37), 13027–13034.
60. A. I. Briceno-Strocchia, T. C. Johnstone and D. W. Stephan, Using frustrated Lewis pairs to explore C-F bond activation, Dalton Trans., 2020, 49(4), 1319–1324.
61. G. Avci, S. Velioglu and S. Keskin, In Silico Design of Metal Organic Frameworks with Enhanced CO2 Separation Performances: Role of Metal Sites, J. Phys. Chem. C, 2019, 123(46), 28255–28265.
62. G. H. Gu, C. Choi, Y. Lee, A. B. Situmorang, J. Noh, Y. H. Kim and Y. Jung, Progress in Computational and Machine-Learning Methods for Heterogeneous Small-Molecule Activation, Adv. Mater., 2020, 32(35), 1907865.
63. J. Beckmann, T. G. Do, S. Grabowsky, E. Hupf, E. Lork and S. Mebs, peri-Interactions in 8-Diphenylphosphino-1-bromonaphthalene, 6-Diphenylphosphino-5-bromoacenaphthene, and Derivatives, Z. Anorg. Allg. Chem., 2013, 639(12-13), 2233–2249.
64. J. Beckmann, E. Hupf, E. Lork and S. Mebs, peri-Substituted (Ace)Naphthylphosphinoboranes. (Frustrated) Lewis Pairs, Inorg. Chem., 2013, 52(20), 11881–11888.
65. E. Hupf, E. Lork, S. Mebs and J. Beckmann, Intramolecularly Coordinated (6-(Diphenylphosphino)acenaphth-5-yl)stannanes. Repulsion vs Attraction of P- and Sn-Containing Substituents in the peri Positions, Organometallics, 2014, 33(10), 2409–2423.
66. E. Hupf, E. Lork, S. Mebs and J. Beckmann, Sterically Congested 5-Diphenylphosphinoacenaphth-6-yl-silanes and -silanols, Organometallics, 2015, 34(15), 3873–3887.
67. S. Furan, E. Hupf, E. Lork, S. Mebs and J. Beckmann, Insights into Frustrated and Regular peri-Substituted (Ace-)Naphthylaminoboranes and (Ace-)Naphthylphosphinoboranes, Eur. J. Inorg. Chem., 2017,(27), 3302–3311.
68. E. Hupf, M. Olaru, C. I. Rat, M. Fugel, C. B. Hubschle, E. Lork, S. Grabowsky, S. Mebs and J. Beckmann, Mapping the Trajectory of Nucleophilic Substitution at Silicon Using a peri-Substituted Acenaphthyl Scaffold, Chem. – Eur. J., 2017, 23(44), 10568–10579.
69. F. Kutter, A. Denhof, E. Lork, S. Mebs and J. Beckmann, 1,8-Bis(diphenylphosphino)biphenylene. A new ligand for late transition metal complexes, Z. Kristallogr. – Cryst. Mater., 2018, 233(9-10), 627–639.
70. F. Kutter, E. Lork, S. Mebs and J. Beckmann, Intramolecular P-H center dot center dot center dot H-Si Dihydrogen Bonding in the 5-Dimethylsily1-9,9-dimethylxanthen-4-yl-diphenylphosphonium Cation, Organometallics, 2018, 37(22), 4287–4296.
71. V. Balasubramaniyan, peri Interaction in Naphthalene Derivatives, Chem. Rev., 1966, 66(6), 567–641.
72. R. F. W. Bader, Subspace Quantum-Mechanics - Quantum Definition of an Atom in a Molecule, Bull. Am. Phys. Soc., 1977, 22(3), 305–306.
73. R. F. W. Bader and T. T. Nguyendang, Quantum-Theory of Atoms in Molecules - Dalton Revisited, Adv. Quantum Chem., 1981, 14, 63–124.
74. R. F. W. Bader, Atoms in Molecules, Acc. Chem. Res., 1985, 18(1), 9–15.
75. M. Kohout, A measure of electron localizability, Int. J. Quantum Chem., 2004, 97(1), 651–658.
76. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132(18), 6498–6506.
77. J. R. Lane, J. Contreras-Garcia, J. P. Piquemal, B. J. Miller and H. G. Kjaergaard, Are Bond Critical Points Really Critical for Hydrogen Bonding?, J. Chem. Theory Comput., 2013, 9(8), 3263–3266.
78. S. Mebs, Complex modes of bonding: NCI/ELI-D vs. DORI surface analyses of hapticities and hydrogen-hydrogen contacts in zincocene related compounds, Chem. Phys. Lett., 2016, 651, 172–177.
79. A. D. Becke, A New Mixing of Hartree-Fock and Local Density-Functional Theories, J. Chem. Phys., 1993, 98(2), 1372–1377.
80. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces - Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671–6687.
81. M. J. T. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Jr. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, C.01, Gaussian, Inc., Wallingford CT, 2016.
82. S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799.
83. S. Miertus, E. Scrocco and J. Tomasi, Electrostatic Interaction of a Solute with a Continuum - a Direct Utilization of Abinitio Molecular Potentials for the Prevision of Solvent Effects, Chem. Phys., 1981, 55(1), 117–129.
84. F. Biegler-Konig, J. Schonbohm and D. Bayles, Software news and updates - AIM2000 - A program to analyze and visualize atoms in molecules, J. Comput. Chem., 2001, 22(5), 545–559.
85. M. Kohout, DGRID, 4.6, 2015.
86. J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, NCIPLOT: A Program for Plotting Noncovalent Interaction Regions, J. Chem. Theory Comput., 2011, 7(3), 625–632.
87. G. A. Andirenko, ChemCraft, 1.8; CrowdStrike: https://www.chemcraftprog.com.
88. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics Modell., 1996, 14(1), 33–38.
89. C. B. Hübschle and P. Luger, MolIso - a program for colour-mapped iso-surfaces, J. Appl. Crystallogr., 2006, 39, 901–904.
90. C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, Wiley & Sons Ltd, 2nd edn, 2004.
91. S. Raub and G. Jansen, A quantitative measure of bond polarity from the electron localization function and the theory of atoms in molecules, Theor. Chem. Acc., 2001, 106(3), 223–232.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp02516g

---