 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Complexity and bifurcations in the motion of a self-propelled rectangle confined in a circular water chamber†
Hiroyuki
Kitahata
 a,
Yuki
Koyano
a,
Yuki
Koyano
 b,
Richard J.G.
Löffler
b,
Richard J.G.
Löffler
 cd and
Jerzy
Górecki
cd and
Jerzy
Górecki
 *d
*d
aDepartment of Physics, Graduate School of Science, Chiba University, Yayoi-cho 1-33, Inage-ku, Chiba 263-8522, Japan. E-mail: kitahata@chiba-u.jp
bGraduate School of Human Development and Environment, Kobe University, 3-11 Tsurukabuto, Nada-ku, Kobe, Hyogo 657-0011, Japan
cLaboratory for Artificial Biology, Department of Cellular, Computational and Integrative Biology (CIBIO), University of Trento, Polo Scientifico e Tecnologico Fabio Ferrari, Polo B, Via Sommarive 9, Povo, 38123, Trentino Alto-Adige, Italy
dInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, Warsaw 01-224, Poland. E-mail: jgorecki@ichf.edu.pl
First published on 11th August 2022
Abstract
We consider the motion of a self-propelled object of rectangular shape inside a circular water chamber. The mathematical model of self-motion includes equations for the orientation and location of the rectangle and reaction–diffusion equation with an effective diffusion coefficient for the time evolution of the surface concentration of active molecules. Numerical simulations of motion were performed for different values of the ratio between the supply rate S and the evaporation rate a of active molecules. Treating S0 = S/a as a control parameter, we found the critical behavior in variables characterizing the trajectory and identified different types of motion. If the value of S0 is small, the rectangle rests at the chamber center. For larger S0, a reciprocal motion during which the rectangle passes through the center is observed. At yet higher supply rates, the star-polygonal motion appears, and the trajectory remains at a distance from the chamber center. In the experiments with a rectangle made of camphor–camphene–polypropylene plastic moving in a Petri dish, we observed the transition from the star-polygonal motion to the reciprocal motion in time. This transition can be understood on the basis of the developed model if we assume that the supply rate decreases in time.
1 Introduction
Complex time evolution of self-propelled objects on a liquid surface has been attracting scientific attention for almost 200 years.1–3 The motion resulting from dissipation of molecules that decrease the surface tension and generate Marangoni flows is an interesting example of the conversion of chemical potential energy into the kinetic energy.4–18 A classical and simple example of the phenomenon is the self-motion of camphor pieces on the water surface.1,2,19–23The origin of self-motion can be explained considering a flux of surface active molecules from the source to the air through the surface layer. The motion occurs because water surface tension is a decreasing function of the surface concentration of active molecules.24–26 The force and torque acting on an object located on the surface are related to the gradient of surface tension integrated over the object (cf.eqn (9) and (10)). Therefore, the surface tension (and equivalently concentration of active molecules) around an object should be inhomogeneous to initiate the motion. Different factors can induce such inhomogeneity. It can appear as the result of an asymmetric release of surface active molecules around the object. For example, in a camphor boat, the surface concentration at the bow is lower than at the stern where the piece of camphor is located.27,28 Inhomogeneity around a symmetric source of surface active molecules can appear as the result of random fluctuations in their local release and dissipation. The positive feedback between displacement and force is important because it leads to a sustained motion. Let us consider a camphor disk resting on the water surface and a symmetric, stationary distribution of camphor molecules around. If, by chance, the disk is slightly shifted from its original position, then the force resulting from non-symmetrical surface camphor concentration drives the disk further away and the asymmetry increases. The disk continuously shifts towards regions with higher inhomogeneity of camphor concentration and the self-propelled motion is supported. Self-propelled motion of symmetric objects was observed in experiments with pills made of camphor,21,29 camphene,30 camphene–camphor waxes31 and camphene–camphor–polypropylene plastics.32
The object motion is observed in a chamber constrained by non-penetrable walls. The active molecules are released to the water surface, therefore the shape and area of the water chamber in which the object moves also play an important role.33–38 A self-propelled object is repelled from the chamber wall due to the higher concentration of the surface active molecules close to the wall, which is induced by Neumann boundary conditions.35,36 A few reports on the influence of the chamber geometry on the character of motion can be found in the literature. The theoretical analysis predicted that if a camphor disk is confined in a circular chamber, the disk stops at the center position or moves along the periphery of the region depending on the friction coefficient and the chamber radius.34 Both experiments and numerical simulations demonstrated that the direction of the rotational motion of a camphor pill in a water chamber made of two half-disks can be controlled by the distance between the half-disk centers.33
The explanation of the relationship between symmetry and geometrical shape of a solid, self-propelled object and the character of its motion is a stimulating problem for the theoretical description.31,32,39–42 It is obvious that shape and motion are correlated in a hydrodynamic fashion. At the same time the dissipation of surface active molecules also depends on the object shape. The force and torque acting on an object also involve information on the shape. For example, an elliptic camphor particle tends to move in the direction of its minor axis,40,41 and a rod-shaped particle moves in the direction perpendicular to its axis.32 However, experiments with solid self-propelled objects of arbitrarily selected shapes that could support theoretical models were usually difficult to design. Camphor, the most frequently used solid material in experiments on self-propelled motion, is a granular solid substance. Pressing camphor granules together in a pill maker works only for small, simple shapes like disks or squares. Other techniques, as saturating an inert porous support material like a paper membrane43 or an agar gel44,45 with a camphor solution produce objects characterized by a few minute-long surface activity. A stationary mode of motion does not appear within such short time. Two recent papers31,32 reported easily shapable self-propelled materials based on the mixture of camphor and camphene. It has been noticed32 that a small amount of polypropylene added to camphene–camphor mixture reduces the material tackiness and makes it perfect for making self-propelled objects of different shapes. The motion of rod-shaped piece made of such plastic in a circular region shows various stable phases, as presented in Fig. 1. All experiments started with the rod randomly located on the surface. The color lines illustrate the rod position and orientation at different times. Time is indicated by the line color and changes from yellow to blue as indicated on the vertical bars next to subfigures. The details on time length of presented trajectory are given in the caption of Fig. 1. The types of characteristic modes of motion for a rod-shaped self-propelled object inside a circular water chamber include (a) a fast rotation at a fixed point, (b) rotation around an axis located at the rod end, (c) rotation along the dish edge, (d) chaotic motion inside a dish, (e) star-polygonal motion and (f) reciprocal motion between the dish edge. All shown modes of motion were stable for more than a minute, which indicates their multistability. Some of these modes were observed for self propelled objects of other shapes. The experiments31,32 and numerical simulations34 indicated that motion along the dish wall was dominating for small objects characterized by a low aspect ratio. It was also observed for soft objects like for example droplets of camphor paraffin solution.46 A few experiments illustrating the motion of self-propelled objects with non-trivial shapes such as a triangle, a rhomboid, a crescent-shaped object, a pointed ellipse, an S-shaped propeller, or a spoon-shaped one were reported in the PhD dissertation of R. Löffler47 (YouTube movies are linked to the Section III. 2.1.1). The S-shaped propeller exhibited anticipated rotation. Fast rotation around the center was also observed for soft objects.48,49 For a pointed ellipse, the transition between polygonal motion and rotation along the dish wall was recorded. A polygonal motion was dominating for a rhomboid, but due to object asymmetry, it also included object rotation. Experiments with a crescent-shaped objects indicated multistability of motion types for a complex shape. For this system, rotation along the dish wall and reciprocal motion were observed.31,47 In the reciprocal motion, the velocity periodically changed its orientation with respect to the crescent geometry. All these experimental systems represent a significant challenge for theoretical studies and simulations. We also investigated a few simpler systems with non-trivial geometries that show a complex motion for which theoretical approach is possible. The critical character of velocity orientation with respect to object size was analyzed in numerical studies on the motion of a circle smoothly deformed to triangle-like shape.50 It was demonstrated that for small objects, the velocity was oriented towards one of the corners and for large ones towards the triangle base. The analysis presented in the recent paper51 illustrates that higher rotational symmetry of an object can increase the stability of the rotational mode with respect to the translational one.
In spite of the number of previous experimental and theoretical studies, the universal mechanism for the choice of the type of motion depending on system parameters is unveiled. In this paper, we concentrate on the motion of a rectangle within a circular chamber and demonstrate that it can be complex and interesting. According to our knowledge this is the first report in which experiments on a freely moving solid object significantly different from a pill are directly compared with simulations. We use the newly reported camphor–camphene–polypropylene plastic to make self-propelled rectangles. We investigate the motion for selected size of the rectangle and the diameter of the water chamber. We focused our attention on two specific types of motion of a self-propelled rectangle: star-polygonal motion and reciprocal motion similar to those illustrated in Fig. 1(e) and (f) respectively. We observed that these types of motion were stable for rectangles with aspect ratio 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 considered below. We present a model of the time evolution of the rectangle based on equation of motion coupled with reaction–diffusion equation for the transport of surface active molecules. There are many parameters that influence the character of such motion including the shape of rectangular particle and the diameter of circular area. Here we fixed their values and considered the ratio between the supply rate S and the evaporation rate a of active molecules as the control parameter of simulations. Numerical results obtained within the model have proven the stability of star-polygonal and reciprocal motion modes. We also investigated the bifurcations that change the character of motion when S/a crosses a critical value. The numerical results are confirmed in experiments with a self-propelled rectangle with the same shape as considered in simulation that moves inside a Petri dish.
1 considered below. We present a model of the time evolution of the rectangle based on equation of motion coupled with reaction–diffusion equation for the transport of surface active molecules. There are many parameters that influence the character of such motion including the shape of rectangular particle and the diameter of circular area. Here we fixed their values and considered the ratio between the supply rate S and the evaporation rate a of active molecules as the control parameter of simulations. Numerical results obtained within the model have proven the stability of star-polygonal and reciprocal motion modes. We also investigated the bifurcations that change the character of motion when S/a crosses a critical value. The numerical results are confirmed in experiments with a self-propelled rectangle with the same shape as considered in simulation that moves inside a Petri dish.
2 Theoretical description of a self-propelled rectangle
We performed numerical simulations for the motion of a self-propelled rectangle characterized by longer and shorter side lengths Ll and Ls, which is confined in a two-dimensional circular region Ω with a radius of R corresponding to the water chamber. The origin of the coordinates is set at the center of Ω. The model comprises the reaction–diffusion equation for the concentration field u(r, t) = u(x, y, t) of surface-active molecules, the equation of motion for the center of mass of the rectangle rc(t) = (xc(t), yc(t)) and that for the direction of its long side θc(t).The evolution equation for u(r, t) is described as
 | (1) |
f(r, rc, θc) = f0(![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (−θc)(r − rc)), (−θc)(r − rc)), | (2) |
 | (3) |
![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (φ) is the rotation matrix
(φ) is the rotation matrix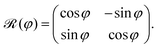 | (4) |
 | (5) |
As the equations of motion, we adopted the Newtonian equation with the overdamped scheme. They are explicitly described as
 | (6) |
 | (7) |
| γ(r, t) = γ0 − Γu(r, t), | (8) |
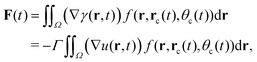 | (9) |
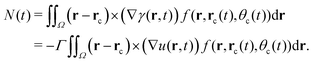 | (10) |
Let us introduce u0 as the unit of the concentration of the surface-active molecule. In order to reduce the number of model parameters, we use the dimensionless equations for the numerical calculations, where the units for the length, time, force and torque are denoted as 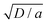 , 1/a,
, 1/a, 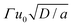 and Γu0D/a, respectively. In these units the model for the rectangular camphor particle motion confined in a circular region is represented by:
and Γu0D/a, respectively. In these units the model for the rectangular camphor particle motion confined in a circular region is represented by:
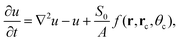 | (11) |
 | (12) |
 | (13) |
f(r, rc, θc) = g(![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) (−θc)(r − rc)), (−θc)(r − rc)), | (14) |
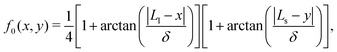 | (15) |
 | (16) |
The Neumann boundary condition was adopted at the boundary of the circular region Ω reflecting the no flux of the surface-active molecules. The initial conditions at t = 0 were set as u(r, t = 0) = 0 and rc = (R − Ll/2 − Δr, 0) and θc = 0. In order to obtain a rapid escape from the initial unstable state that can be a saddle point, we assumed that for times t < 1: rc(t) = (R − Ll/2 − Δr)(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω0t, sin
ω0t, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω0t) and θc(t) = ω0t. Assuming such functional form of rc(t) and θc(t), the dynamics for u in the time interval [0, 1] was calculated using eqn (11). Next, for t ≥ 1 we calculated the dynamics for u, rc and θc using eqn (11)–(16).
ω0t) and θc(t) = ω0t. Assuming such functional form of rc(t) and θc(t), the dynamics for u in the time interval [0, 1] was calculated using eqn (11). Next, for t ≥ 1 we calculated the dynamics for u, rc and θc using eqn (11)–(16).
For the numerical simulation, we selected the parameter values by considering the correspondence to the experiments. In the experiments, the expansion radius of camphor molecules at the water surface is around 3 cm.34,54 Since the inner radius of the Petri dish was 3.5 cm, we set the length unit corresponding to the diffusion length  was 3.5 cm. Thus, in the dimensionless units, the radius R was 1, and the longer and shorter sides of the rectangular camphor particle were set as 1.8/3.5 and 0.6/3.5, respectively. The time unit was set to 1 s considering that characteristic saturation time for the camphor concentration was estimated from the experiments. We previously reported the reciprocating motion in a one-dimensional chamber with a period in the order of 1 s.54 We could not determine the coefficients of the friction for the translational and rotational motion directly from the experimental observation. Therefore, we selected their values as ηt = 10−2 and ηr = 10−4 because for such values the orbits of the camphor particle resemble the ones observed by experiments. The decrease in speed with time was observed in experiments with self propelled pills.32 It indicates that that the supply rate S0 decreased in time. Therefore, in numerical simulations we studied the character of motion treating S0 as a control parameter of the model.
was 3.5 cm. Thus, in the dimensionless units, the radius R was 1, and the longer and shorter sides of the rectangular camphor particle were set as 1.8/3.5 and 0.6/3.5, respectively. The time unit was set to 1 s considering that characteristic saturation time for the camphor concentration was estimated from the experiments. We previously reported the reciprocating motion in a one-dimensional chamber with a period in the order of 1 s.54 We could not determine the coefficients of the friction for the translational and rotational motion directly from the experimental observation. Therefore, we selected their values as ηt = 10−2 and ηr = 10−4 because for such values the orbits of the camphor particle resemble the ones observed by experiments. The decrease in speed with time was observed in experiments with self propelled pills.32 It indicates that that the supply rate S0 decreased in time. Therefore, in numerical simulations we studied the character of motion treating S0 as a control parameter of the model.
Numerical simulations were performed using the explicit method for the diffusion term and Euler method for the time development. The temporal and spatial units were set as Δt = 10−5 and Δx = Δy = 10−2. The smoothing parameter δ was set as δ = 10−2. The parameters for the initial setting were: Δr = 0.3 and ω0 = 1.0. The numerical calculations were performed until t < 1000.
For small S0, the rectangle stopped at the center of the circular region after some time (the rest state). With an increase in S0, it exhibited a reciprocal motion on a certain line passing through the chamber center. For even greater S0, the direction of the reciprocal motion rotated around the center leading to a star-polygonal motion. Fig. 2 illustrates the characteristic trajectory and the concentration field for these three motion types at (a) S0 = 0.6 for the rest state, (b) S0 = 0.9 for the reciprocal motion, and (c) S0 = 1.2 for the star-polygonal motion.
 | ||
| Fig. 2 The characteristic three types of motion of a rectangle confined in a circular region obtained from numerical simulations. The orbits of the center of mass of the rectangle for t ∈ [0, 30] are shown in the upper row. Snapshots of concentration field u of active molecules at t = 30 are shown below the trajectories. The red curves represent the trajectories for: 29.7 ≤ t ≤ 30. (a) S0 = 0.6 for the rest state. (b) S0 = 0.9 for the reciprocal motion. (c) S0 = 1.2 for the star-polygonal motion. Corresponding videos are available in ESI.† | ||
Fig. 3 illustrates the histogram of the probability density p(rc/R) of relative distances rc(t)/R for the star-polygonal motion (S0 = 1.2) (a) and the reciprocal motion (S0 = 0.9) (b). It can be noticed that the characters of the probability for both types of motion are completely different. For the reciprocal motion the support of p(rc/R) is [0, rmax/R] and the function is monotonically increasing in its support. For the star-polygonal motion the support is p(rc/R) is [rmin/R, rmax/R] and the function is bimodal with maxima at the both ends of the interval.
 | ||
| Fig. 3 Histograms on the distance from the center rc/R for (a) star-polygonal (S0 = 1.2), and (b) reciprocal motion (S0 = 0.9). | ||
The previous studies on the motion of ellipse indicated that the velocity is perpendicular to its major axis40,41,46 The same statement applies to the motion of a rectangle. Fig. 4 shows the distribution of the angle between the velocity and the long-axis direction for star-polygonal motion (S0 = 1.2) and for reciprocal motion (S0 = 0.9) calculated for the time interval t ∈ [900, 1000]. For the star-polygonal motion, the orthogonality of these directions dominates and angles ϕ < π/2 are observed at the turnings. In the reciprocal motion, the directions of velocity and long-axis are always perpendicular.
 | ||
| Fig. 4 Histograms on the angle ϕ difference between the direction of the velocity and long-axis direction for (a) star-polygonal motion (S0 = 1.2) and (b) reciprocal motion (S0 = 0.9). | ||
In order to investigate the transitions between modes in detail, we plotted the maximum and minimum distances rmax/R and rmin/R from the chamber center, the maximum speed Vmax, and the rotation angle Δθ as functions of the supply rate S0 in Fig. 5. The rotation angle is defined as follows; we set the polar coordinates whose origin meets the center of the circular region. We detected the reflection point, corresponding to a local maximum in radius, and measured the angle difference between successive reflecting points. This rotation angle should be ∼π for the reciprocal motion, while it is less than π for the star-polygonal motion. Obviously, the rotation angle cannot be defined for the rest state. In order to eliminate the effect of the initial condition, we measured all quantities for t ∈ [900, 1000]. On the basis of the results presented in Fig. 5, we concluded that the transition from the rest state to the reciprocal motion occurs at around S0 = 0.8 since the maximum radius and maximum speed change from zero to finite values at this point. Moreover, the transition from the reciprocal motion to the star-polygonal motion occurs at around S0 = 1.1 since the minimum radius changes from zero to a finite positive value and the rotation angle changes from π to smaller values at this S0. Both the transitions are classified into supercritical bifurcation.
Considering that the supply rate is difficult to measure in the experiment, we plotted rmax/R, rmin/R, and Δθ as functions of Vmax/Vc, where Vc is the speed of the rectangle at the bifurcation point in Fig. 6. In these plots, we can also clearly observe the bifurcation between the reciprocal motion and the star-polygonal motion. The bifurcation from the rest state to the reciprocal motion occurs at Vmax/Vc = 0 and all range of S0 values for which the rest state is observed reduces to this point.
3 Experiments
The experiments were performed for a rectangle made of camphor–camphene–polypropylene plastic prepared as described in ref. 32. All chemicals used were commercially available: (1R)-(+)-camphor (98% purity, CAS: 464-49-3, Sigma-Aldrich), Camphene (95% purity, CAS: 79-92-5, Sigma Aldrich) and polypropylene in the form of pellets (CAS: 9003-07-0, Sigma Aldrich, product number 427861). The chemicals were used without additional purification. A 0.2 cm thick sheet was made of plastic composed of 10% polypropylene, 63% camphene, and 27% camphor weight ratio. Cuboids with the size 1.8 cm × 0.6 cm × 0.2 cm were cut from this plastic sheet. The thickness of considered cuboids was small enough to assume that the model of rectangle motion presented in the previous section can be applied to describe their time evolution. Experiments demonstrating the cuboid motion on the water surface were performed at 23 ± 1 °C in a Petri dish with the radius of 3.5 cm. The dish contained 16 ml water purified using a Millipore ELIX system, which corresponds to 0.4 cm water level. The Petri dish was illuminated from below while recording from above using a Logitech C920 Webcam digital camera.The motion of a rectangle was observed for 1800 seconds. The character of motion changed in time as indicated by the maximum velocity of a rectangle and the other quantities presented in Fig. 9. We relate the observed changes to the decreasing supply rate of surface active substances: camphor and camphene. This decrease can be explained as follows: the molecules of camphor and camphene are distributed throughout the object in a polypropylene scaffold that is a microporous foam.55 At the beginning of experiments the molecules located close to the cuboid surface were dissipated and therefore the supply rate was high. For longer times the dissipated molecules originated from further inside the material and had to migrate through the foam to appear on the water surface. As a result, the rate of dissipation decreased over time. A single experiment with a self-propelled rectangle provides information about the motion of systems characterized by a wide range of supply rate values S0.
The decrease in supply rate during experiments, anticipated on the basis of decreasing velocity, is confirmed by the direct observation of rectangle motion. Fig. 7(a and b) present the two 7 second long fragments of its trajectory. The one in Fig. 7(a), for times [0 s, 7 s] shows the motion at the beginning of experiment, whereas the other in Fig. 7(b), for times [1793 s, 1800 s], corresponds to the end of the observation interval. In the first case the star-polygonal trajectory was observed, whereas in the second we found the reciprocal motion between the dish walls with trajectory passing through the dish center. The character of transition between modes of motion matches the predictions of the model corresponding to the decreasing S0. Fig. 7(c and d) illustrate the probability distribution of distances between the rectangle center and the dish center measured during the first and last 300 seconds of experiment. For the star-polygonal trajectory (cf.Fig. 3(a) and 7(a)) the distribution is bimodal and the probability to find the center of rectangle close to the dish center is null. For reciprocal motion the distribution is unimodal with a pronounced maximum at the maximum distance (cf.Fig. 3(b) and 7(b)). Moreover, as in Fig. 3, the maximum distance in the support of probability distribution is smaller for the reciprocal motion than for the star-polynomial one. Therefore, the results of experiments are in a qualitative agreement with those obtained from numerical simulations.
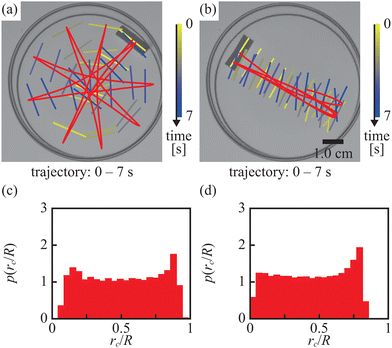 | ||
| Fig. 7 (a and b) The 7 seconds long fragments of the rectangle trajectory observed (a) at the beginning [0 s, 7 s] and (b) at the end [1793 s, 1800 s] of the observation interval. (c and d) The probability distribution of distances between the rectangle center and the dish center. The statistics is done (c) for times [0 s, 300 s] of experiment and (d) for times [1500 s, 1800 s]. Corresponding videos are available in ESI.† | ||
Experiments and simulations predict that for both motion types the angle between the rectangle velocity and the rectangle long axis is close to π/2 (cf.Fig. 4 and 8). The results of numerical simulations indicate the qualitative difference between the star-polygonal and reciprocal types of motion (cf.Fig. 4). For the reciprocal motion q(ϕ) is localized at ϕ = π/2. For the star-polygonal motion the dispersion is wide and q(π/2) = 3.554. The spread of Qq of q(ϕ) defined as:
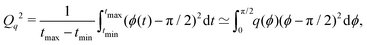 | (17) |
The experimental results show that the spread of angle probability distribution for the star-polygonal motion is smaller than for the reciprocal one. The values of q(π/2) are 3.0565 and 2.4975 and the spreads Qq are 0.2032 and 0.2867 for star-polygonal and the reciprocal one, respectively. There is an agreement between the experiments and simulations for q(π/2) and Qq in star-polygonal motion. However, these values differ significantly for reciprocal motion. We believe that the difference can be explained by spatial inhomogeneities in the value of S0 when active molecules are migrating through the foam from regions deep below the rectangle surface. Experiments with plastics of different camphor–camphene–polypropylene ratio, characterized by a low value of S0 at the beginning of observation should lead to a better match.
The experiments showed that the rectangle never rotates. In one of experiments we tried to force rotational modes of motion like these in Fig. 1(a–c), but they were unstable and, after a few seconds, the rectangle switched back to the reciprocal mode (see movie Stability_check.mp4, ESI†).
We introduced such quantities as Vmax, rmin, rmax and Δθ in order to analyse the rectangle trajectory calculated in numerical simulations (cf.Fig. 5). Fig. 9 shows the time evolution of the same quantities obtained from experiments. The light-colored dots illustrate all obtained results. The dispersion of these results is high. The thick lines show the quantities averaged over 10 consecutive results. The dependence of all investigated quantities on time matches the numerical simulations with decreasing supply rate of surface active molecules. The functions rmax(t) and Δθ(t) suggest that the transition between star-polygonal and reciprocal motion types occurred around t = 600 s.
We believe the main difference between simulations and experiments comes from fluctuations that were not included into the model. Let us notice that rmin is always larger than 0 and Δθ is always less than π. As the result of fluctuations the stable value of rmin(t) is larger than 0 and Δθ(t) stabilizes at angles smaller than π for the reciprocal motion. There is another interesting observation coming from experiments: the values of Δθ(t) for small times do not follow 10-events average but form two branches around it. The branches merge at t = 300 s, still before the bifurcation between the star-polygonal motion and the reciprocal motion. There are many factors that can lead to such dependence including the imperfection of real rectangle. It may suggest yet another, noise induced bifurcation within the star-polygonal type of motion.
Fig. 10 shows the experimental results in the same dimensionless representation as in Fig. 6. To plot the dependence we used the values averaged over 10 consecutive events. The character of functions rmax(Vmax/Vc) and rmin(Vmax/Vc), and Δθ(Vmax/Vc) obtained from the analysis of simulation results is qualitatively confirmed by experiments. The quantitative differences can be related to many factors including the simplicity of the model, unrealistic assumption about the values of ηr and ηt and to the presence of fluctuations strongly influencing rmin(Vmax/Vc)/R, and Δθ(Vmax/Vc).
4 Conclusions and discussion
In the paper, we considered self-propelled motion of a rectangle-shaped object on the water surface inside a circular water chamber. The rectangle is a source of molecules that form a surface layer and decrease the water surface tension. The local inhomogeneities in surface tension generate forces and torques acting on the rectangle and supporting its motion. In experiments with rectangles made of camphor–camphene–polypropylene plastic, we identified two types of motion: reciprocal motion through the dish center and the star-polygonal motion in which the rectangle avoided passing it. The star-polygonal motion was observed at the beginning of an experiment and after a few minutes it changed into the reciprocal one. These modes of motion seem be the only stable ones that appear for the selected experimental conditions.In order to understand the observed behaviour, we performed simulations based on a simple model of self-motion. It describes the evolution of a rectangle configuration together with the surface concentration of active molecules. In numerical simulations we fixed values of such parameters as the chamber radius, the size of rectangle and the friction coefficients for the translational and rotational motions. The supply rate of surface active molecules S0 was considered as the model parameter. We identified a number of variables (Vmax, rmin, rmax, and Δθ) that characterize the rectangle motion. Our simulations show that for small S0 the rectangle rests at the chamber center. At a critical value of S0 the bifurcation in Vmax occurs and the reciprocal motion appears. The amplitude (rmax) increases with S0. At yet larger values of S0 the bifurcation in rmin is observed. Therefore, the simple model leads to correct qualitative description of the character of motion observed in experiments if we consider the supply rate of surface active molecules as a decreasing function of time. This result indicates that the value of S0 can be an important factor determining the choice of type of motion for complex self-propelled objects of arbitrary shapes.
The presented theoretical approach is general and can be applied for future studies on the relationship between the shape of moving object and the character of motion. On the basis of experiments and numerical simulations, we can conclude that a self-propelled rectangle preferably moves in the direction perpendicular to the long axis. Such observation can be important for design of self-moving micro-robots56 propelled by release of surface active molecules that use shape modification to move in a certain direction.
As a natural generalization of our study we plan to consider rectangles with different aspect ratio and water chambers of various sizes to find conditions at which the other types of motion illustrated in Fig. 1 can appear. It seems interesting to verify if the transition between a localised form of rotation (Fig. 1(a and b)) and other motion types can be qualitatively explained within the model. The comparison between experiments and simulations will be a valuable test for its applicability.
The presented results can be the starting point for further studies on self-propelled motion on objects characterized by non trivial shapes. The geometry of water chamber can also have an important influence on the evolution of a self-propelled object, because it defines the limits of spreading the surface active molecules and combined with the value of supply rate defines the profile of surface concentration that translates into forces and torques acting on the object. A few reports on this topic have been published.33,34 However, they all were concerned with the disk-shaped camphor pill. The study on pill motion in a circular chamber34 demonstrated that the dish radius is a critical parameter in transition between the rest state at the dish center and rotation along the dish edge. In the investigation of pill motion in a water chamber formed by a joint half-disks it was found that the distance between half disk centers was a parameters that controlled the probability distribution of local curvatures measured on the pill trajectory.33 It can be expected that the influence between the chamber geometry (shape and size) and the type of observed motion will be more pronounced for objects of complex shapes.
The question if one can engineer a material with a given dissipation of surface active molecules is very interesting and should be considered in future systematic studies. We anticipate it can be done. The polypropylene scaffold of the camphene–camphor–polypropylene plastic becomes denser with the increase in polypropylene concentration.55 The denser scaffold should decrease the diffusion of surface-active molecules and their release, thus decrease the value of S0. However, the character of self-propelled pill motion made of such plastic seems pretty similar for 5%, and 10% polypropylene32 which suggests that the value of S0 does not change a lot. We expect experiments with higher concentrations of polypropylene up to 20% can bring a noticeable decrease in S0. Moreover, for 5% and 10% polypropylene, the character of motion for a pill made of camphene–camphor–polypropylene plastic does not show a quantitative dependence on the camphene/camphor ratio.32 Therefore, in the range of concentrations we have already studied, the value of S0 seems weakly dependent on the composition of the plastic. On the other hand, for the camphene–camphor wax, the velocity of a pill strongly depends on the camphor/camphene ratio.31 Therefore, we can use this wax to make a material with the required release of surface active molecules. However, shaping the wax to a particular geometry is more difficult than for the plastic because of the wax's high tackiness.
Alternatively, the value of S0 can be controlled by changing the parameter a, which describes evaporation and other processes that remove active molecules from the water surface. This can be done by adding other substances to water, but such approach should be carefully planned because the other properties of water can be changed too.
Systems such as those described above can serve as model systems for the study and modeling of hydrodynamic drag of different shapes moving on a water surface. These type of drag fluid dynamics are very difficult to describe and an efficient mathematical model of such may be of interest to the design of shapes of objects moving in liquid media.
Author contributions
The authors contributed to the paper as follows: HK and YK developed the theoretical model, performed numerical simulations and analysed their results, HK prepared ImageJ plug-in used to extract data form the experimental movies, RL performed the experiments, RL and JG performed the analysis of experimental results. All authors contributed to the manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS and PAN under the Japan-Poland Research Cooperative Program (No. JPJSBP120204602). This work was also supported by JSPS KAKENHI Grant No. JP19J00365, JP20K14370, JP20H02712, and JP21H01004, and also the Cooperative Research Program of “Network Joint Research Center for Materials and Devices: Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials” (No. 20211014 and 20214004).References
- C. Tomlinson and W. A. Miller, Proc. R. Soc. Lond., 1862, 11, 575–577 CrossRef.
- R. J. Strutt, Proc. R. Soc. Lond., 1890, 47, 364–367 CrossRef.
- Self-organized Motion, ed. S. Nakata, V. Pimienta, I. Lagzi, H. Kitahata and N. J. Suematsu, The Royal Society of Chemistry, 2019 Search PubMed.
- K. Nagai, Y. Sumino, H. Kitahata and K. Yoshikawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 065301 CrossRef PubMed.
- J. Cejkova, M. Novák, F. Stepanek and M. Hanczyc, Langmuir, 2014, 30, 11937–11944 CrossRef CAS PubMed.
- T. Bánsági, M. Wrobel-Szypula, S. Scott and A. Taylor, J. Phys. Chem. B, 2013, 117, 13572–13577 CrossRef PubMed.
- H. Kitahata and K. Yoshikawa, Phys. D, 2005, 205, 283–291 CrossRef CAS.
- L. Keiser, H. Bense, P. Colinet, J. Bico and E. Reyssat, Phys. Rev. Lett., 2017, 118, 074504 CrossRef CAS PubMed.
- S. Tanaka, Y. Sogabe and S. Nakata, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032406 CrossRef PubMed.
- S. Tanaka, S. Nakata and T. Kano, J. Phys. Soc. Jpn., 2017, 86, 101004 CrossRef.
- F. Wodlei, J. Sebilleau, J. Magnaudet and V. Pimienta, Nat. Commun., 2018, 9, 820 CrossRef CAS PubMed.
- V. S. Akella, D. K. Singh, S. Mandre and M. M. Bandi, Phys. Lett. A, 2017, 382, 1176–1180 CrossRef.
- Y. Matsuda, N. Suematsu and S. Nakata, Phys. Chem. Chem. Phys., 2012, 14, 5988–5991 RSC.
- J. Cejkova, K. Schwarzenberger, K. Eckert and S. Tanaka, Colloids Surf., A, 2019, 566, 141–147 CrossRef CAS.
- Y. Xu, L. Ji, S. Izumi and S. Nakata, Chem. – Asian J., 2021, 16, 1762–1766 CrossRef CAS PubMed.
- E. Lauga and A. M. J. Davis, J. Fluid Mech., 2012, 705, 120–133 CrossRef.
- S. Sur, H. Masoud and J. P. Rothstein, Phys. Fluids, 2019, 31, 102101 CrossRef.
- S. J. Kang, S. Sur, J. P. Rothstein and H. Masoud, Phys. Rev. Fluids, 2020, 5, 084004 CrossRef.
- O. Schulz, J. Phys. Chem. B, 2007, 111, 8175–8178 CrossRef CAS PubMed.
- S. Nakata, Y. Iguchi, S. Ose, M. Kuboyama, T. Ishii and K. Yoshikawa, Langmuir, 1997, 13, 4454–4458 CrossRef CAS.
- S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu and T. Hasegawa, Phys. Chem. Chem. Phys., 2015, 17, 10326–10338 RSC.
- D. Boniface, C. Cottin-Bizonne, R. Kervil, C. Ybert and F. Detcheverry, Phys. Rev. E, 2019, 99, 062605 CrossRef CAS PubMed.
- D. Boniface, C. Cottin-Bizonne, F. Detcheverry and C. Ybert, Phys. Rev. Fluids, 2021, 6, 104006 CrossRef.
- N. J. Suematsu, T. Sasaki, S. Nakata and H. Kitahata, Langmuir, 2014, 30, 8101–8108 CrossRef CAS PubMed.
- Y. Karasawa, S. Oshima, T. Nomoto, T. Toyota and M. Fujinami, Chem. Lett., 2014, 43, 1002–1004 CrossRef CAS.
- Y. Karasawa, T. Nomoto, L. Chiari, T. Toyota and M. Fujinami, J. Colloid Interface Sci., 2018, 511, 184–192 CrossRef CAS PubMed.
- M. Kohira, Y. Hayashima, M. Nagayama and S. Nakata, Langmuir, 2001, 17, 7124–7129 CrossRef CAS.
- M. Shimokawa, M. Oho, K. Tokuda and H. Kitahata, Phys. Rev. E, 2018, 98, 022606 CrossRef CAS PubMed.
- M. Nagayama, S. Nakata, Y. Doi and Y. Hayashima, Phys. D, 2004, 194, 151–165 CrossRef CAS.
- S. Nakata and S.-i Hiromatsu, Colloids Surf., A, 2003, 224, 157–163 CrossRef CAS.
- R. J. G. Löffler, M. M. Hanczyc and J. Gorecki, Phys. Chem. Chem. Phys., 2019, 21, 24852–24856 RSC.
- R. J. G. Löffler, M. M. Hanczyc and J. Gorecki, Molecules, 2021, 26, 3116 CrossRef PubMed.
- S. Nakata, H. Yamamoto, Y. Koyano, O. Yamanaka, Y. Sumino, N. Suematsu, H. Kitahata, P. Skrobanska and J. Gorecki, J. Phys. Chem. B, 2016, 120, 9166–9172 CrossRef CAS PubMed.
- Y. Koyano, N. J. Suematsu and H. Kitahata, Phys. Rev. E, 2019, 99, 022211 CrossRef CAS PubMed.
- M. Mimura, T. Miyaji and I. Ohnishi, Hiroshima Math. J., 2007, 37, 343–384 Search PubMed.
- T. Miyaji, Phys. D, 2017, 340, 14–25 CrossRef.
- T. Ohta, J. Phys. Soc. Jpn., 2017, 86, 072001 CrossRef.
- T. Ohta and T. Ohkuma, Phys. Rev. Lett., 2009, 102, 154101 CrossRef PubMed.
- N. Yoshinaga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012913 CrossRef PubMed.
- H. Kitahata, K. Iida and M. Nagayama, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 010901 CrossRef PubMed.
- K. Iida, H. Kitahata and M. Nagayama, Phys. D, 2014, 272, 39–50 CrossRef.
- S.-I. Ei, H. Kitahata, Y. Koyano and M. Nagayama, Phys. D, 2018, 366, 10–26 CrossRef.
- Y. S. Ikura, E. Heisler, A. Awazu, H. Nishimori and S. Nakata, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012911 CrossRef PubMed.
- S. Soh, K. Bishop and B. Grzybowski, J. Phys. Chem. B, 2008, 112, 10848–10853 CrossRef CAS PubMed.
- S. Soh, M. Branicki and B. Grzybowski, J. Phys. Chem. Lett., 2011, 2, 770–774 CrossRef CAS.
- R. J. Löffler, J. Gorecki and M. Hanczyc, Artificial Life Conference Proceedings, 2018, ALIFE 2018: The 2018 Conference on Artificial Life, pp. 574–579, DOI:10.1162/isal_a_00106.
- R. G. Röffler, PhD Thesis, New materials for studies on nanostructures and spatio-temporal patterns self-organized by surface phenomena, Institute of Physical Chemstry, Polish Academy of Sciences, 2021 Search PubMed.
- V. Pimienta, M. Brost, N. Kovalchuk, S. Bresch and O. Steinbock, Angew. Chem., Int. Ed., 2011, 50, 10728–10731 CrossRef CAS PubMed.
- C. Antoine, J. Irvoas, K. Schwarzenberger, K. Eckert, F. Wodlei and V. Pimienta, J. Phys. Chem. Lett., 2016, 7, 520–524 CrossRef CAS PubMed.
- H. Kitahata and Y. Koyano, J. Phys. Soc. Jpn., 2020, 89, 094001 CrossRef.
- H. Kitahata and Y. Koyano, Front. Phys., 2022, 10, 858791 CrossRef.
- H. Kitahata and N. Yoshinaga, J. Chem. Phys., 2018, 148, 134906 CrossRef PubMed.
- H. Kitahata, Y. Koyano, K. Iida and M. Nagayama, Self-organized Motion: Physicochemical Design based on Nonlinear Dynamics, The Royal Society of Chemistry, 2019, pp. 31–62 Search PubMed.
- Y. Koyano, T. Sakurai and H. Kitahata, Phys. Rev. E, 2016, 94, 042215 CrossRef PubMed.
- R. Löffler, M. Hanczyc and J. Gorecki, Sci. Rep., 2022, 12, 243 CrossRef PubMed.
- L. Soler, V. Magdanz, V. M. Fomin, S. Sanchez and O. G. Schmidt, ACS Nano, 2013, 7, 9611–9620 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: S06_sim.mp4: simulation for the rest state in Fig. 2(a), S09_sim.mp4: simulation for the reciprocal motion in Fig. 2(b), S12_sim.mp4: simulation for the star-polygonal motion in Fig. 2(c), star_polygonal_motion_exp.mp4: experiment showing the star-polygonal motion in Fig. 7(a), reciprocal_motion_exp.mp4: experiment showing the reciprocal motion in Fig. 7(b), stability_check.mp4: experimental test of reciprocal motion stability. See DOI: https://doi.org/10.1039/d2cp02456j |
| This journal is © the Owner Societies 2022 |






