 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A computational tool to accurately and quickly predict 19F NMR chemical shifts of molecules with fluorine–carbon and fluorine–boron bonds
Alexandre S.
Dumon
 a,
Henry S.
Rzepa
a,
Henry S.
Rzepa
 *a,
Carla
Alamillo-Ferrer
b,
Jordi
Bures
*a,
Carla
Alamillo-Ferrer
b,
Jordi
Bures
 b,
Richard
Procter
c,
Tom D.
Sheppard
b,
Richard
Procter
c,
Tom D.
Sheppard
 c and
Andrew
Whiting
c and
Andrew
Whiting
 d
d
aDepartment of Chemistry, Molecular Sciences Research Hub, Imperial College London, White City Campus, Wood Lane, London W12 OBZ, UK. E-mail: rzepa@imperial.ac.uk
bDepartment of Chemistry, The University of Manchester, Manchester M13 9PL, UK
cDepartment of Chemistry, Christopher Ingold Laboratories, University College London, 20 Gordon Street, London, WC1H 0AJ, UK
dCentre for Sustainable Chemical Processes, Department of Chemistry, Science Laboratories, Durham University, South Road, Durham, DH1 3LE, UK
First published on 9th August 2022
Abstract
We report the evaluation of density-functional-theory (DFT) based procedures for predicting 19F NMR chemical shifts at modest computational cost for a range of molecules with fluorine bonds, to be used as a tool for assisting the characterisation of reaction intermediates and products and as an aid to identifying mechanistic pathways. The results for a balanced learning set of molecules were then checked using two further testing sets, resulting in the recommendation of the ωB97XD/aug-cc-pvdz DFT method and basis set as having the best combination of accuracy and computational time, with a RMS error of 3.57 ppm. Cationic molecules calculated without counter-anion showed normal errors, whilst anionic molecules showed somewhat larger errors. The method was applied to the prediction of the conformationally averaged 19F chemical shifts of 2,2,3,3,4,4,5,5-octafluoropentan-1-ol, in which gauche stereoelectronic effects involving fluorine dominate and to determining the position of coordination equilibria of fluorinated boranes as an aid to verifying the relative energies of intermediate species involved in catalytic amidation reactions involving boron catalysts.
1 Introduction
Fluorinated molecules present a vast and important scope of uses, ranging from metallurgy (Hall–Héroult process) to pharmaceuticals.1,2 For example organofluorines represent 10% of pharmaceuticals and up to 30% of agrochemicals.3 Catalysis is one of the uses where the fluorine atom can shine, from helping stereospecificity to obtaining novel and more active catalysts.3–7 As such it becomes important to have powerful and accurate tools in order to identify and characterize fluorinated compounds. Solution phase NMR spectroscopy has proven to be such a tool, especially with the introduction of standard continuous-flow adaptors for high-field instruments equipped with high-sensitivity multi-nuclear probes, which allows transient intermediates to be detected.8–10 The need then is to augment such a tool with one that aids in structural assignments of the measured chemical shifts of all the detected species, including the transients. In addition, new methods have proven to be efficient for the synthesis of molecules using biologically active compounds, such as enzymes engineered to be specific for fluorinated substrates.11 Such an NMR tool would prove useful for the rationalization, verification and improvement of these new strategies.The increasing use of computational modelling based on DFT (density functional) methods (in silico chemistry) for probing catalytic mechanisms and structure is helping to change the approach to the design of new catalysts and such modelling can also play a role in helping to characterise intermediates and products using NMR methods.12–15 An example of such application was the development of a computationally relatively cheap tool for 11B NMR prediction for use in catalytic systems containing boron.16 Previous studies of methods for predicting 19F relative shifts have centred on small learning sets,17–20 proteins21,22 or based on collections of closely related molecules,23–25 or even the influence of the solvation model.26 Three studies stand out. Krivdin18 presented a state-of-the-art review of the computational simulation of 19F NMR. Many molecules are presented in various sets at various levels, but no “one for all” method was recommended, and many of the methods would be too computationally expensive for routine use with relatively large molecules (up to ∼100 atoms). Fedorov17 used two fluorinated molecules containing a total of 14 fluorine atoms for study, but such a model would require considerable extrapolation to the types of catalytic systems we are interested in. The most recent from Benassi is a more complete study, albeit one in which the learning set differs greatly from the testing set and the resulting error is too large (>14 ppm) for the purpose of organofluorine and fluoroboron predictions.27
The present study is an extension to our previous method used for 11B NMR.16 Here we aim to benchmark a selection of methods based on combinations of DFT and other Hamiltonians and basis-sets that could help assignment of 19F chemical shifts, using a carefully selected learning set of compounds appropriate for the study of catalysed reactions and their mechanisms utilizing fluorine as one analytic probe.
2 Computational and experimental details
Starting from the Organic Chemistry Database we identified 29 molecules with 88 unique chemical shifts as recorded in a variety of solvents.28 This was reduced to 83 chemical shifts using Reaxys to corroborate the solvents/experimental conditions of the spectral measurements (see footnotes for excluded values).29 During the selection procedure for what we refer to as the learning set, we noted that even for a simple compound such as PhCF3, significant discrepancies in literature 19F NMR chemical shifts can be observed. These have recently been comprehensively analysed and can be up to Δδ ± 2.5 ppm, albeit more typically Δδ ± 1 ppm, whilst identical samples run at different institutions still had an error of Δδ ± 0.5 ppm.10 These statistics should be borne in mind when analysing the performance of any predictive method.All the calculations presented here were performed using Gaussian 16, revision C.01. The CHAMP portal was used as an electronic notebook for managing the project, enabled with one-click FAIR data publishing to the Imperial College data repository.30,31 All the solvents were modelled at the PCM level using the CPCM implementation.32–34 The density functionals and Hamiltonians that were chosen for evaluation are: B3LYP,35,36 ωB97XD21 and MP2.37–41 The basis sets were: aug-cc-pvdz,42 Def2-svpp43,44 and aug-pcSseq1.45–48 In the case of the B3LYP calculations, the GD3+BJ49 dispersion correction was included for geometry optimisation; the other two methods allow for dispersion either by similar correction or implicitly. NMR shieldings were computed using the Gauge-Independent Atomic Orbital (GIAO) method.50–53 By default, an ultrafine DFT integration grid (99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590) was used, but a superfine grid (175
590) was used, but a superfine grid (175![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974, 2nd row atoms) along with high integral accuracy (10−14 a.u.) was also evaluated. This changed calculated shieldings by <0.04 ppm and fractional Boltzmann populations by <0.017. In the case of MP2 calculations, 2 magnetic tensors can be calculated: the MP2 GIAO method and the SCF GIAO one. Since the SCF GIAO RMSD was bigger than the MP2 one (7.93 ppm versus 5.59 ppm) and its R2 was low (0.982), we discarded this method and only used the MP2 GIAO tensor for the following, under the name MP2/aug-cc-pvdz.
974, 2nd row atoms) along with high integral accuracy (10−14 a.u.) was also evaluated. This changed calculated shieldings by <0.04 ppm and fractional Boltzmann populations by <0.017. In the case of MP2 calculations, 2 magnetic tensors can be calculated: the MP2 GIAO method and the SCF GIAO one. Since the SCF GIAO RMSD was bigger than the MP2 one (7.93 ppm versus 5.59 ppm) and its R2 was low (0.982), we discarded this method and only used the MP2 GIAO tensor for the following, under the name MP2/aug-cc-pvdz.
To predict the chemical shifts the following procedure was followed:
• Full optimisation and NMR calculation for the reference (CFCl3) at each level and in each solvent.
• Full optimisation and NMR calculation for the molecule in the relevant solvents and at each level.
• Comparison for each calculated shift relative to the reference at the same level in the same solvent.
In order to determine the Boltzmann averaged chemical shifts for a species with multiple conformations such as 2,2,3,3,4,4,5,5-octafluoropentan-1-ol, the populations of the possible rotamers were calculated using the formula  with ΔrG being the difference of the Gibbs Free energies between the states, R the perfect gas constant and T the temperature (298.15 K in our case). These populations were used to weight the 19F NMR shift for the fluorine atoms. All mathematical treatment was performed using python.
with ΔrG being the difference of the Gibbs Free energies between the states, R the perfect gas constant and T the temperature (298.15 K in our case). These populations were used to weight the 19F NMR shift for the fluorine atoms. All mathematical treatment was performed using python.
Since according to Roseneau et al.10 the experimental error on the chemical shifts can be typically Δδ ± 1.0 ppm and up to 2.5 ppm, whereas the root mean square error on our calculated values (i.e.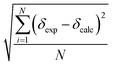 , with N being the number of chemical shifts) can range from 4 ppm to 16 ppm, we chose to perform our regression analysis on the calculated peaks in order to minimize the biggest error and to reveal any systematic errors in the calculated values. The regression analysis equation is therefore:
, with N being the number of chemical shifts) can range from 4 ppm to 16 ppm, we chose to perform our regression analysis on the calculated peaks in order to minimize the biggest error and to reveal any systematic errors in the calculated values. The regression analysis equation is therefore:
| δcalc= slope × δexperimental + intercept | (1) |
2.1 Experimental details
Preparation of the pyridine adduct of difluoro(phenyl)borane: potassium phenyltrifluoroborate (18.4 mg, 0.1 mmol) was suspended in a mixture of anhydrous pyridine (450 μl) and pyridine-d5 (50 μl, with 0.3% v/v TMS) in a J Youngs NMR tube under an atmosphere of argon. Chlorotrimethylsilane (15.3 μl, 1.2 mmol) was added and the tube was sealed. The solid was dissolved by brief sonication and a fine white precipitate of KCl was observed. The sample was analysed by 11B and 19F NMR spectroscopy, using the tetramethylsilane peak as an internal reference. 11B NMR (128 MHz, pyridine) δ = 6.24 ppm (br t). 19F{1H} NMR (376 MHz, pyridine) δ −154.6 (br s, 2H, PhBF2·Py); −156.3 ppm (s, 1H, 29Si satellite JSi–F = 275 Hz, TMSF).2.2 Data availability
All the computational input and output files and experimental NMR primary datasets can be found as a FAIR data repository collection55 and in associated sub-collections.3 Results and discussion
3.1 Entries list and calculated chemical shifts
The list of solvents that were used as well as their calculated reference shielding constant can be found in the data repository collections.55 The list of the molecules we selected, their solvent, as well as their experimental chemical shifts can be found in Table 1:| a Three different values in different solvents are observed. We discuss this further in Section 4.2. b BF3 is reported as a reaction product, but its coordination to this solvent is unknown. c Molecules containing O–F or N–F bonds are considered to be very highly correlated species of a type that DFT theory using small basis sets cannot adequately represent and are not included in the analysis here. For further discussion, see Section 3.3.1. |
|---|

|
Excluding entries 27, 29, 70, 73 and 85 for reasons noted in the footnotes, there are a total of 83 entries for the learning set. The calculated values will be sorted by the method (Hamiltonian) used to calculate the wavefunction. This set of molecules will be called the Learning Set (LS) in the discussion. The results for the ωB97xd, MP2 and B3LYP methods can be found in Tables 2, 3 and 4 respectively.
| Entry | δ ωb97xd/aug-pvdz | δ ωb97xd/pcSseq1 | δ ω97xd/def2svpp | Entry | δ ωb97xd/aug-pvdz | δ ωb97xd/pcSseq1 | δ ωb97xd/def2svpp |
|---|---|---|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 | 46 | −77.46 | −83.82 | −66.87 |
| 2 | −61.35 | −65.31 | −50.90 | 47 | −77.32 | −83.80 | −66.90 |
| 3 | −158.56 | −174.56 | −146.23 | 48 | −77.26 | −83.79 | −66.93 |
| 4 | −159.07 | −175.10 | −146.68 | 49 | −77.25 | −83.78 | −66.92 |
| 5 | −159.11 | −175.19 | −146.85 | 50 | −160.49 | −170.99 | −134.91 |
| 6 | −159.20 | −175.44 | −146.81 | 51 | −116.09 | −122.17 | −92.63 |
| 7 | −159.11 | −175.35 | −146.86 | 52 | −117.72 | −123.96 | −93.95 |
| 8 | −29.10 | −30.33 | −20.04 | 53 | −117.45 | −123.51 | −93.57 |
| 9 | −235.51 | −254.25 | −228.71 | 54 | −117.08 | −123.11 | −93.31 |
| 10 | −66.53 | −70.50 | −61.98 | 55 | −117.55 | −123.56 | −93.82 |
| 11 | −66.70 | −70.52 | −62.12 | 56 | −117.74 | −124.14 | −93.98 |
| 12 | −64.89 | −70.01 | −55.25 | 57 | −115.89 | −121.99 | −92.46 |
| 13 | −65.33 | −69.77 | −54.99 | 58 | −117.77 | −124.19 | −94.01 |
| 14 | −65.20 | −69.55 | −54.95 | 59 | −116.06 | −122.22 | −92.61 |
| 15 | −65.30 | −69.73 | −55.04 | 60 | −81.83 | −83.38 | −66.42 |
| 16 | −65.20 | −69.56 | −54.95 | 61 | −75.53 | −80.46 | −47.78 |
| 17 | −65.36 | −69.82 | −55.13 | 62 | −123.66 | −130.10 | −100.21 |
| 18 | −81.54 | −87.13 | −69.49 | 63 | −122.44 | −128.88 | −99.20 |
| 19 | −81.50 | −87.13 | −69.54 | 64 | −123.49 | −129.92 | −99.97 |
| 20 | −81.53 | −87.13 | −69.53 | 65 | −123.66 | −130.09 | −100.21 |
| 21 | −81.54 | −87.13 | −69.52 | 66 | −123.63 | −130.12 | −100.14 |
| 22 | −81.99 | −87.04 | −69.23 | 67 | −123.37 | −129.66 | −99.80 |
| 23 | −81.67 | −87.11 | −69.44 | 68 | −122.62 | −129.06 | −99.37 |
| 24 | −81.61 | −87.03 | −69.21 | 69 | −122.42 | −128.86 | −99.18 |
| 25 | −81.61 | −87.12 | −69.36 | 71 | −65.27 | −70.58 | −57.81 |
| 26 | −95.87 | −101.36 | −69.15 | 72 | −65.15 | −70.53 | −57.68 |
| 28 | −96.82 | −102.18 | −69.72 | 74 | −146.81 | −155.30 | −148.01 |
| 30 | 18.76 | 18.89 | 36.33 | 75 | −133.97 | −146.36 | −124.36 |
| 31 | −76.55 | −82.98 | −66.72 | 76 | −263.97 | −286.50 | −250.06 |
| 32 | −76.70 | −83.06 | −66.71 | 77 | −55.36 | −60.27 | −47.19 |
| 33 | 18.58 | 18.77 | 36.31 | 78 | −132.05 | −140.23 | −101.56 |
| 34 | −71.53 | −76.86 | −60.58 | 79 | −135.77 | −143.36 | −105.15 |
| 35 | −87.83 | −94.53 | −72.10 | 80 | −213.11 | −229.56 | −206.80 |
| 36 | −102.40 | −107.41 | −83.67 | 81 | −272.60 | −292.94 | −248.15 |
| 37 | −191.54 | −203.31 | −176.87 | 82 | −272.19 | −292.46 | -247.31 |
| 38 | −71.43 | −76.68 | −60.35 | 83 | −272.60 | −292.98 | −248.25 |
| 39 | −87.38 | −93.90 | −71.49 | 84 | −272.60 | −292.76 | −247.79 |
| 40 | −101.97 | −106.79 | −83.05 | 86 | −219.44 | −235.40 | −207.20 |
| 41 | −192.23 | −203.87 | −177.46 | 87 | −219.43 | −235.24 | −206.96 |
| 42 | −55.83 | −76.38 | −60.11 | 88 | −219.43 | −235.27 | −207.00 |
| 43 | −86.52 | −93.24 | −70.86 | ||||
| 44 | −101.14 | −106.15 | −82.41 | ||||
| 45 | −192.54 | −204.45 | −178.04 |
| Entry | MP2/aug-cc-pvdz | Entry | MP2/aug-cc-pvdz | Entry | MP2/aug-cc-pvdz | Entry | MP2/aug-cc-pvdz |
|---|---|---|---|---|---|---|---|
| 1 | 0.00 | 22 | −81.48 | 45 | −199.97 | 66 | −127.82 |
| 2 | −64.13 | 23 | −81.49 | 46 | −77.86 | 67 | −127.36 |
| 3 | −166.29 | 24 | −81.25 | 47 | −77.79 | 68 | −126.73 |
| 4 | −166.98 | 25 | −81.46 | 48 | −77.50 | 69 | −126.44 |
| 5 | −167.12 | 26 | −70.66 | 49 | −77.72 | 71 | −65.51 |
| 6 | −166.87 | 28 | −71.97 | 50 | −160.86 | 72 | −65.42 |
| 7 | −167.13 | 30 | 1.25 | 51 | −120.87 | 74 | −142.98 |
| 8 | −31.25 | 31 | −77.74 | 52 | −122.43 | 75 | −136.38 |
| 9 | −230.67 | 32 | −74.90 | 53 | −122.08 | 76 | −271.01 |
| 10 | −67.66 | 33 | 16.70 | 54 | −121.71 | 77 | −55.62 |
| 11 | −67.66 | 34 | −72.19 | 55 | −122.17 | 78 | −139.05 |
| 12 | −64.53 | 35 | −97.31 | 56 | −122.45 | 79 | −143.41 |
| 13 | −63.39 | 36 | −110.78 | 57 | −120.65 | 80 | −207.91 |
| 14 | −64.11 | 37 | −199.05 | 58 | −122.48 | 81 | −270.47 |
| 15 | −64.36 | 38 | −52.00 | 59 | −120.89 | 82 | −270.07 |
| 16 | −64.11 | 39 | −96.92 | 60 | −78.28 | 83 | −270.46 |
| 17 | −64.43 | 40 | −111.40 | 61 | −82.03 | 84 | −270.29 |
| 18 | −81.46 | 41 | −199.48 | 62 | −127.85 | 86 | −215.99 |
| 19 | −81.41 | 42 | −71.87 | 63 | −126.47 | 87 | −215.72 |
| 20 | −81.44 | 43 | −96.56 | 64 | −127.64 | 88 | −215.78 |
| 21 | −81.18 | 44 | −111.06 | 65 | −127.85 |
| Entry | B3LYP/Def2svpp | B3LYP/aug-cc-pvdz | B3LYP+GD3-BJ/augc-cc-pvdz | B3LYP+GD3-BJ/Def2svpp |
|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | −59.10 | −71.67 | −71.14 | −58.59 |
| 3 | −154.08 | −168.98 | −168.64 | −153.77 |
| 4 | −154.60 | −169.53 | −169.20 | −154.30 |
| 5 | −154.78 | −169.75 | −169.41 | −154.49 |
| 6 | −154.76 | −169.47 | −169.22 | −154.46 |
| 7 | −154.79 | −169.76 | −169.41 | −154.50 |
| 8 | −26.48 | −37.02 | −36.54 | −26.04 |
| 9 | −237.78 | −245.51 | −245.04 | −237.10 |
| 10 | −64.60 | −69.49 | −70.19 | −65.37 |
| 11 | −64.62 | −69.70 | −70.41 | −65.00 |
| 12 | −63.46 | −74.68 | −74.32 | −62.81 |
| 13 | −63.29 | −74.38 | −74.01 | −63.05 |
| 14 | −63.14 | −74.19 | −73.84 | −62.80 |
| 15 | −63.26 | −74.39 | −74.03 | −62.91 |
| 16 | −63.13 | −74.19 | −73.83 | −62.80 |
| 17 | −63.32 | −74.48 | −74.12 | −62.98 |
| 18 | −75.57 | −90.44 | −89.90 | −75.03 |
| 19 | −75.60 | −90.45 | −89.90 | −75.08 |
| 20 | −75.58 | −90.44 | −89.90 | −75.88 |
| 21 | −75.59 | −90.44 | −89.90 | −75.05 |
| 22 | −75.17 | −90.44 | −89.89 | −74.65 |
| 23 | −75.48 | −90.45 | −89.91 | −74.94 |
| 24 | −75.13 | −90.43 | −89.89 | −74.63 |
| 25 | −75.58 | −−90.45 | −89.91 | −75.06 |
| 26 | −78.61 | −110.99 | −110.68 | −78.30 |
| 28 | −79.24 | −111.98 | −111.64 | −78.67 |
| 30 | 31.52 | 10.84 | 11.18 | 31.84 |
| 31 | −74.02 | −85.28 | −84.89 | −73.62 |
| 32 | −74.11 | −85.41 | −85.03 | −73.83 |
| 33 | 31.43 | 10.71 | 11.05 | 31.63 |
| 34 | −68.21 | −80.55 | −80.19 | −67.12 |
| 35 | −79.37 | −97.20 | −96.85 | −78.29 |
| 36 | −90.36 | −111.36 | −110.95 | −89.29 |
| 37 | −183.10 | −199.70 | −199.39 | −182.05 |
| 38 | −67.97 | −80.21 | −79.86 | −67.61 |
| 39 | −78.78 | −96.55 | −96.19 | −78.45 |
| 40 | −89.79 | −110.71 | −110.34 | −89.43 |
| 41 | −183.71 | −200.21 | −199.90 | −183.37 |
| 42 | −67.76 | −79.91 | −79.55 | −67.38 |
| 43 | −78.18 | −95.87 | −95.52 | −77.82 |
| 44 | −89.20 | −110.07 | −109.70 | −88.85 |
| 45 | −184.33 | −200.73 | −200.42 | −183.99 |
| 46 | −74.23 | −86.29 | −85.92 | −73.93 |
| 47 | −74.20 | −86.24 | −85.87 | −73.84 |
| 48 | −74.20 | −86.23 | −85.86 | −73.82 |
| 49 | −74.18 | −86.36 | −85.99 | −73.82 |
| 50 | −146.87 | −177.82 | −176.29 | −146.54 |
| 51 | −98.54 | −126.18 | −125.79 | −98.17 |
| 52 | −100.04 | −128.21 | −127.81 | −99.66 |
| 53 | −99.62 | −127.64 | −127.24 | −99.24 |
| 54 | −99.33 | −127.24 | −126.84 | −98.65 |
| 55 | −99.70 | −127.75 | −127.36 | −99.34 |
| 56 | −100.06 | −128.24 | −127.84 | −99.69 |
| 57 | −98.36 | −125.95 | −125.55 | −97.85 |
| 58 | −100.10 | −128.31 | −127.89 | −99.72 |
| 59 | −97.51 | −126.15 | −125.75 | −98.14 |
| 60 | −74.08 | −86.64 | −86.31 | −73.84 |
| 61 | −55.32 | −88.60 | −87.99 | −54.47 |
| 62 | −106.37 | −133.90 | −133.51 | −105.97 |
| 63 | −105.03 | −132.35 | −131.97 | −104.67 |
| 64 | −106.10 | −133.53 | −133.16 | −105.73 |
| 65 | −106.34 | −133.90 | −133.51 | −106.00 |
| 66 | −106.32 | −133.83 | −133.43 | −105.95 |
| 67 | −105.88 | −133.29 | −132.91 | −105.19 |
| 68 | −104.20 | −132.57 | −132.18 | −104.82 |
| 69 | −105.01 | −132.34 | −131.95 | −104.64 |
| 71 | −66.53 | −74.82 | −74.40 | −66.14 |
| 72 | −66.59 | −74.74 | −74.33 | −66.12 |
| 74 | −154.91 | −154.82 | −154.94 | −155.13 |
| 75 | −133.18 | −142.96 | −143.00 | −132.58 |
| 76 | −263.09 | −280.50 | −279.98 | −262.59 |
| 77 | −53.20 | −62.46 | −62.01 | −52.46 |
| 78 | −107.76 | −142.91 | −142.50 | −107.37 |
| 79 | −111.93 | −146.34 | −145.93 | −142.54 |
| 80 | −213.52 | −220.81 | −220.18 | −212.67 |
| 81 | −257.91 | −286.70 | −286.15 | −257.38 |
| 82 | −256.86 | −286.28 | −285.72 | −256.33 |
| 83 | −257.99 | −286.73 | −286.18 | −257.46 |
| 84 | −257.47 | −286.52 | −285.96 | −256.63 |
| 86 | −213.59 | −229.22 | −228.62 | −213.02 |
| 87 | −213.23 | −229.01 | −228.42 | −212.66 |
| 88 | −213.29 | −229.04 | −228.45 | −212.42 |
Considering that species such as CF3COOH are known for forming stable H-bonded dimers at higher concentrations, we investigated how large the effect on the predicted chemical shift of such self-aggregation or aggregation with explicit solvent molecules would be at the ωB97xd/aug-cc-pvdz level. The results can be found in Table 5:
| System | Solvent | Chemical shift (ppm) | Error (ppm) |
|---|---|---|---|
| Exp. | Acetone | −75.557 | |
| Monomer | −77.32 | 1.82 | |
| Dimer | −78.19 | 2.69 | |
| H-Bond donor 1 | −78.39 | 2.89 | |
| H-Bond donor 2 | −77.28 | 1.78 | |
| Exp. | DCM | −7556 | |
| Monomer | −77.46 | 2.46 | |
| Dimer | −78.33 | 3.33 | |
| Exp. | H2O | −77.761 | |
| Monomer | −77.25 | 0.45 | |
| Dimer | −78.11 | 0.41 | |
| H-Bond donor 1 | −78.27 | 0.57 | |
| H-Bond donor 2 | −76.707 | 1.00 | |
| H-Bond acceptor 1 | −77.11 | 0.59 | |
| H-Bond acceptor 2 | −77.08 | 0.62 | |
| H-Bond acceptor 3 | −76.57 | 1.13 | |
| H-Bond acceptor 4 | −76.41 | 1.29 | |
| Exp. | MeOH | −74.74259 | |
| Monomer | −77.26 | 2.52 | |
| Dimer | −78.15 | 3.41 | |
| H-Bond donor 1 | −78.35 | 3.60 | |
| H-Bond donor 2 | −77.13 | 2.39 | |
| H-Bond acceptor 1 | −77.29 | 2.55 | |
| H-Bond acceptor 2 | −77.10 | 2.36 | |
| H-Bond acceptor 3 | −76.67 | 1.93 | |
| H-Bond acceptor 4 | −76.44 | 1.70 |
The difference between the computed 19F shift for CF3COOH monomer and the various aggregated forms is always less than 1.1 ppm, which is within both experimental and computational error. Furthermore, the relatively low concentrations of substrate used for most NMR measurements would not favour self-aggregations.
A Bland–Altman plot at the ωB97xd/aug-cc-pvdz level for our learning set in Fig. 1 shows more than 95% of the values are contained within the interval mean ±2σ and no obvious linear correlation appears.118 From this, we conclude that the learning Set is well-behaved for our study.
 | ||
| Fig. 1 Bland–Altman plot118 for the learning set. | ||
3.2 Regression analysis
The evaluation of two different DFT functionals applied with various basis sets as well as MP2 method was based on 83 19F NMR peaks, covering a wide range of chemical shifts (−260 ppm to −20 ppm). The regression analysis using eqn (1) obtained by least squares minimisation of the calculated chemical shifts can be found in Table 6. The provided root mean square deviations (RMSD) were obtained using the following equation: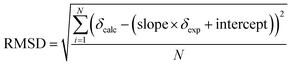 | (2) |
| Slope with std error σ | Intercept with std error σ (ppm) | R 2 | RMSD (ppm) | |
|---|---|---|---|---|
| a This linear regression is for testing set 2 (see Section 3.3.2 for more detail). | ||||
| ωB97xd/aug-cc-pvdz | 1.01 ± 0.01 | −0.25 ± 0.82 | 0.9968 | 3.57 |
| ωB97xd/aug-pcSseq1 | 1.09 ± 0.01 | 0.66 ± 0.85 | 0.9971 | 3.64 |
| ωB97xd/Def2-svpp | 0.98 ± 0.01 | 11.95 ± 1.68 | 0.9861 | 7.23 |
| MP2/aug-cc-pvdz | 1.00 ± 0.01 | −3.56 ± 1.29 | 0.9921 | 5.53 |
| B3LYP/Def2-svpp | 0.99 ± 0.01 | 6.37 ± 1.73 | 0.9856 | 7.45 |
| B3LYP/aug-cc-pvdz | 1.03 ± 0.01 | −7.52 ± 1.08 | 0.9948 | 4.66 |
| B3LYP+GD3BJ/aug-cc-pvdz | 1.03 ± 0.01 | −7.24 ± 1.06 | 0.9950 | 4.55 |
| B3LYP+GD3BJ/Def2-svpp | 0.99 ± 0.01 | 6.45 ± 1.78 | 0.9849 | 7.63 |
| ωB97xd/aug-cc-pvdza | 0.96 ± 0.00 | −6.34 ± 0.40 | 0.9966 | 2.31 |
The ωB97xd/aug-cc-pvdz method shows low RMSD values (Table 6) and an intercept close to zero. The largest RMSD corresponds to 2.64% of the total chemical shift range, while the lowest is 1.24% over the same range. Over this range, the slope tends to be s
The computational cost of the various methods does not correlate well with their accuracy. Thus although the method with the highest R2, ωB97xd/aug-pcSseq1 also has a small RMSD (3.64 ppm), it is approximately 24 times slower to complete than at the ωB97xd/Def2-svpp level. B3LYP/aug-cc-pvdz displays the same features, a good R2, somewhat larger RMSD but clearly non-zero intercepts. The relatively expensive MP2/aug-cc-pvdz combination is not superior to the ωB97xd/aug-cc-pvdz method, but might prove more reliable for molecules with correlated or unusual bonds.
For this type of calculations, based on the parameters, R2, RMSD, slope, intercept and the standard errors, we recommend the ωB97xd/aug-cc-pvdz level, which also has the advantage of being affordable in terms of CPU resources. This is in line with our previous report on 11B NMR16 and gives the advantage that both the 19F and 11B nuclei can be computed at the same level in a single calculation for molecules containing both elements. The regression coefficients (slope ∼ unity, intercept ∼ 0) means the unadjusted calculated value could be used to assign experimental shifts with an average mean error of 3.9 ppm.
| δcalc ≈ δexp | (3) |
Rearranging eqn (1) allows correction for the systematic errors; in eqn (4)δpred indicates the predicted chemical shift.
 | (4) |
 | (5) |
3.3 Testing sets and identification of sources of error
| Molecule | Solvent | Peak (ppm) | ωB97xd/aug-cc-pvdz | ωB97xd/Def2-svpp | ωB97xd/aug-pcSseq1 | MP2/aug-cc-pvdz |
|---|---|---|---|---|---|---|
| 1-Fluoro-2-nitrobenzene | Acetonitrile | −120.5 | −118.37 | −98.27 | −125.23 | −131.85 |
| 2,2,3,3,4,4,5,5-Octafluoropentan-1-ol | Chloroform | −122.5 | −124.36 | −109.32 | −132.06 | −124.26 |
| −125.7 | −127.18 | −112.57 | −135.31 | −126.25 | ||
| −130.2 | −132.24 | −117.22 | −140.79 | −132.53 | ||
| −137.2 | −141.16 | −126.95 | −151.17 | −140.63 | ||
| −137.3 | −141.75 | −127.37 | −151.69 | −141.24 | ||
| Trifluoro(4-fluorophenyl)borate | DMSO | −118.7 | −123.70 | −101.98 | −130.54 | −126.23 |
| −138.9 | −153.62 | −130.32 | −164.45 | −151.40 | ||
| Tris(2,2,2-trifluoroethyl)borate | Chloroform | −76.8 | −80.30 | −78.26 | −86.42 | −80.68 |
| Molecule | Solvent | Peak (ppm) | B3LYP/Def2-svpp | B3LYP/aug-cc-pvdz | B3LYP+GD3BJ/aug-cc-pvdz | B3LYP+GD3BJ/Def2-svpp |
|---|---|---|---|---|---|---|
| 1-Fluoro-2-nitrobenzene | Acetonitrile | −120.5 | −103.11 | −125.62 | −125.37 | −102.90 |
| 2,2,3,3,4,4,5,5-Octafluoropentan-1-ol | Chloroform | −122.5 | −118.86 | −130.40 | −133.75 | −117.95 |
| −125.7 | −120.63 | −137.42 | −137.08 | −120.93 | ||
| −130.2 | −125.10 | −142.06 | −141.48 | −124.87 | ||
| −137.2 | −133.86 | −150.76 | −150.14 | −133.42 | ||
| −137.3 | −134.49 | −151.37 | −150.81 | −133.96 | ||
| Trifluoro(4-fluorophenyl)borate | DMSO | −118.7 | −108.55 | −134.17 | −133.78 | −108.19 |
| −138.9 | −141.90 | −169.80 | −169.38 | −141.50 | ||
| Tris(2,2,2-trifluoroethyl)borate | Chloroform | −76.8 | −78.49 | −89.86 | −89.61 | −77.67 |
| Molecule | Solvent | Peak (ppm) | ωB97xd/aug-cc-pvdz | ωB97xd/Def2-svpp | ωB97xd/aug-pcSseq1 | MP2/aug-cc-pvdz |
|---|---|---|---|---|---|---|
| 1-Fluoro-2-nitrobenzene | Acetonitrile | −120.5 | 3.69 | 8.08 | 4.93 | 7.98 |
| 2,2,3,3,4,4,5,5-Octafluoropentan-1-ol | Chloroform | −122.5 | 0.22 | 1.17 | 0.67 | 1.97 |
| −125.7 | 0.18 | 1.31 | 0.87 | 3.15 | ||
| −130.2 | 0.33 | 1.55 | 0.34 | 1.38 | ||
| −137.2 | 2.14 | 4.47 | 2.19 | 0.30 | ||
| −137.3 | 2.63 | 4.80 | 2.57 | 0.22 | ||
| Trifluoro(4-fluorophenyl)borate | DMSO | −118.7 | 3.37 | 2.50 | 1.75 | 4.22 |
| −138.9 | 12.77 | 6.21 | 12.68 | 8.92 | ||
| Tris(2,2,2-trifluoroethyl)borate | Chloroform | −76.8 | 2.36 | 15.21 | 3.15 | 1.06 |
| RMSD | 4.77 | 6.58 | 4.84 | 98.99 |
| Molecule | Solvent | Peak (ppm) | B3LYP/Def2-svpp | B3LYP/aug-cc-pvdz | B3LYP+GD3BJ/aug-cc-pvdz | B3LYP+GD3BJ/Def2-svpp |
|---|---|---|---|---|---|---|
| 1-Fluoro-2-nitrobenzene | Acetonitrile | −120.5 | 10.22 | 6.05 | 5.92 | 10.40 |
| 2,2,3,3,4,4,5,5-Octafluoropentan-1-ol | Chloroform | −122.5 | 3.63 | 3.44 | 0.19 | 2.74 |
| −125.7 | 2.24 | 0.18 | 0.24 | 2.55 | ||
| −130.2 | 2.23 | 0.17 | 0.01 | 2.02 | ||
| −137.2 | 4.06 | 1.60 | 1.40 | 3.63 | ||
| −137.3 | 4.59 | 2.10 | 1.95 | 4.07 | ||
| Trifluoro(4-fluorophenyl)borate | DMSO | −118.7 | 2.94 | 4.03 | 4.04 | 3.28 |
| −138.9 | 10.46 | 18.35 | 18.37 | 10.07 | ||
| Tris(2,2,2-trifluoroethyl)borate | Chloroform | −76.8 | 8.68 | 2.99 | 3.09 | 7.90 |
| RMSD | 6.31 | 6.81 | 6.70 | 6.06 |
The outlier in this set is the −138.9 ppm measured value for trifluoro(4-fluorophenyl)borate as assigned to the negatively charged trifluoroborate unit. The predicted values show large variation using the computational methods, the errors ranging from 2.60 ppm (B3LYP+GD3BJ/Def2-svpp) to 30.90 ppm (B3LYP/aug-cc-pvdz) using eqn (3), and 6.21 ppm (ωB97xd/Def2-svpp) to 18.37 ppm (B3LYP/aug-cc-pvdz) with eqn (4) (Table 8). To find out whether the effect is general to fluoroborate anions, we searched the CSD (Cambridge Structure Database) for other molecules containing this motif, to determine if any relationship between their predicted solution state 19F chemical shifts and the closest approach of the counter-cation in the solid state might exist. Of the 31 matches, 10 were selected for analysis, having both reported 19F chemical shift values in solution and available for calculation using the calibrated aug-cc-pvdz basis set. The experimental and calculated chemical shifts as well as the CSD reference code and absolute errors can be found in Table 9. For GABCEV120 the values reported in the article for the 19F and 11B NMR (−63.5 ppm and 64.1 ppm respectively) do not match what should be expected experimentally (approximately −140 ppm for the 19F and 5 ppm for the 11B) or by calculation, but those reported in the article ESI do match and are shown in the table. The corresponding plot and structures can be found in Table 9 and Fig. 3 and 4 respectively.
| Compound | Experimental | Calculated | Absolute error | Distance |
|---|---|---|---|---|
| CARKIR | −142121 | −150.64 | 8.64 | 2.62 |
| FUYDOT | −136.58122 | −146.19 | 9.61 | 3.05 |
| OZOJOD | −133.3123 | −144.71 | 11.41 | 3.26 |
| SEGMOJ | −138.6124 | −140.67 | 2.07 | 2.81 |
| SEGMUP | −135.6124 | −141.53 | 5.93 | 2.86 |
| SEGNAW | −137.6124 | −144.51 | 6.91 | 2.97 |
| YOWJIG | −143.33125 | −153.99 | 10.66 | 2.82 |
| ZUCWAY | −142.2126 | −151.76 | 9.56 | 2.97 |
| ZUCZOP | −143.5126 | −154.12 | 10.62 | 2.68 |
| GABCEV | −133.2120 | −141.22 | 8.02 | 2.73 |
 | ||
| Fig. 3 Absolute error (ppm) as a function of the closest approach distance (Å) of the counter-cation for the fluoroborane motif as listed in in Table 9. | ||
Where the cationic component is present intramolecularly, the predicted errors can be no larger than the RMS error, but when omitted as intermolecular components, the errors can be as large as 11.4 ppm. Significantly, there is no relationship between the error and the closest approach of the counter-cation in the solid state. To probe further, we then returned to focus on trifluoro(4-fluorophenyl)borate itself by modelling the shift in solution with various forms of an alkali metal counter-ion present. Since K+ is not defined at the aug-cc-pvdz basis set level, we replaced it with Na+. The errors for the chemical shifts obtained viaeqn (4) are provided in Table 10. The calculated structures for the various complexes of trifluoro(4-fluorophenyl)borate can be found in Fig. 5.
| Experimental | No Na+ | Na+ complexed to F | Na+ complexed to DMSO | Na+ complexed to 6 DMSO |
|---|---|---|---|---|
| −138.9 | −153.62 | −151.39 | −149.88 | −142.23 |
| Absolute error | 12.77 | 10.56 | 9.07 | 3.33 |
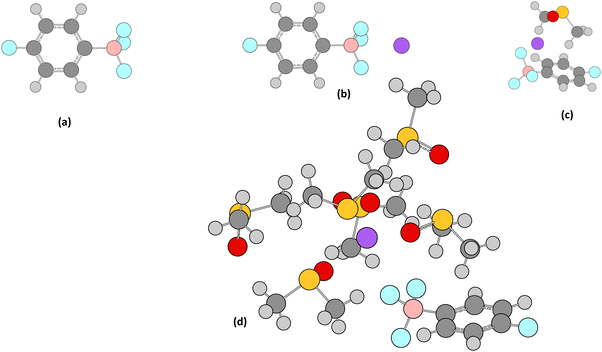 | ||
| Fig. 5 Structures for trifluoro(4-fluorophenyl)borate complexed with Na+ showing (a) no Na+, (b) Na+ complexed, (c) Na+ complexed to DMSO and (d) Na+ complexed to 6 DMSO. | ||
We first tested if inclusion of Na+ alone improved the prediction compared to its absence at the ωB97xd/aug-cc-pvdz level, but the error was only modestly reduced. Next, we complexed the Na+ ion to a DMSO (solvent) molecule. Reasonable agreement with experiment was only obtained with 6DMSO·Na+, suggesting that not only the position but also the explicit solvation of the counter-cation for such fluoroborate anions may be important for more accurate 19F NMR chemical shift predictions. However, such a model increases the size of the system and hence the computational cost significantly. Furthermore optimising the position of the solvated counter-ion can be non-trivial and so this computational tool may no longer be necessarily considered a rapid one, which was one of our objectives in this study.
We concluded our examination of ionic species by investigating seven further solution-phase ionic compounds from Roseneau et al.10 (entries 88, 90–92, 97, 100 and 111 as referenced in the Roseneau tabulation), in this case without including their counter-ions. The experimental chemical shifts, the calculated 19F NMR chemical shifts and the absolute errors for the estimated shifts can be found in Table 11, while their structures can be found in Fig. 6.
| Entry | Experimental shift | Calculated shift | Absolute errors |
|---|---|---|---|
| 88 | 48.16 | 18.05 | 30.11 |
| 90 | 16.03 | −3.29 | 19.32 |
| 91 | 46.98 | 27.04 | 19.94 |
| 92 | −107.51 | −106.52 | 0.99 |
| 97, ax,eq | −95.20 | −121.94 | 26.74 |
| 97, ax,ax | −95.20 | −102.79 | 7.59 |
| 100 | −53.11 | −53.79 | 0.68 |
| 111 | −152.84 | −158.99 | 6.15 |
 | ||
| Fig. 6 Structures of the additional studied ions, with compounds numbered as in the ESI of Roseneau et al.10 | ||
We notice, as have others, that N–F bonds seem to be a significant source of errors, which is not surprising since these types of bonds are very electron rich and hence more highly correlated than e.g. C–F bonds. We do not report the values here but note that O–F bonds were also sources of large errors (sometimes >50 ppm, with a 400 ppm error on the F2O2), for the same reason. B–F bonds tend to occur on anionic components, which appear to have a slightly higher systematic error than neutral and cationic C–F systems (Table 11) and are discussed in more detail below.
Anion 97 contains an Si–F bond for which two isomers were calculated, one with both fluorines axial and one axial and the other equatorial. The match to the experimental value for the diaxial isomer −104 ppm is better than the isomer. The error of 8.8 ppm for the diaxial isomer appears not to be due to the basis set lacking diffuse functions, as often used for anionic species (but ameliorated by the use of an anion-compactifying solvent field). Thus use of the d-aug-cc-pvdz basis (only available for first row elements) on F results in a predicted shift of −104.5 ppm, a slightly larger error than that observed without diffuse functions. A similar error was found for tetrafluoroborate anion itself (Table 9, entry 111) and the error is more probably due to lack of included counter-ion in the calculation as noted above. Cation 100 contains a C–F bond and is predicted well.
Cation 92 also with a C–F bond was calculated as two rotameric orientations for the four isopropyl groups. Of these the conformation with the CH of the isopropyl being anti to the heterocyclic group had an error of 10.2 ppm and the other with the CH group syn was 1.0 ppm, which again shows that conformational analysis using this nucleus may be reliable. In general most cations are predicted accurately, which might suggest that the position and nature of the counter-anion may not be important, whereas anions may be more vulnerable to omission of a cationic counterion.
 | (6) |
 | ||
| Fig. 7 19F NMR predicted chemical shifts for testing set 2 at the ωB97xd/aug-cc-pvdz level, eqn (3). | ||
4 Applications
4.1 Rotamers and stereoelectronic effects
A general problem in regard to predicting chemical shifts is for conformationally mobile systems. We evaluated one example of this, 2,2,3,3,4,4,5,5-octafluoropentan-1-ol in which stereoelectronic (gauche effect) alignments are possible. A search of the CSD (crystal structure database)128 based on the substructure X–O–CH2–CF2–CFR–R′R′′ (X = H, C) was conducted in two parts. The first search was for rotations about bonds 1 and 2 (Fig. 9) for examples that possessed both a primary alcohol or ether function and a fluorinated aliphatic side-chain and the second search for bonds 3 to 5 was for examples with fluorinated side-chains. This reveals a preponderance of syn-periplanar orientations (∼60°) for vicinal heteroatom groups (Fig. 10).129–139 | ||
| Fig. 9 A search of the CSD for molecules similar to 2,2,3,3,4,4,5,5-octafluoropentan-1-ol for values of bond torsions 1-5. | ||
 | ||
| Fig. 10 The two predicted lowest energy conformations of 2,2,3,3,4,4,5,5-octafluoropentan-1-ol exhibiting nine gauche-effect orientations, showing torsion angles. | ||
The five bonds about which three-fold rotations can occur in 2,2,3,3,4,4,5,5-octafluoropentan-1-ol results in 35 = 243 possible rotamers. The crystal structure search (Fig. 9) suggests these could be dominated by gauche effects for all five rotational bonds. Approximate coordinates for these conformers were initially generated using the GMMX conformer dialogue in the Gaussview 6 program and then all were subjected to full energy minimisation and NMR calculation using the recommended ωB97xd/aug-cc-pvdz procedure. Applying eqn (4) leads to prediction errors that are only modestly larger than experimental errors.10 The global free energy minimum emerged as having nine gauche and several antiperiplanar orientations.
We compared 5 different sets: (i) those with all 225 non-duplicated rotamers, (ii) with the 20 (iii) 10 (iv) or 5 highest populated conformations and finally (v) the set with all 28 conformations having a population greater than 1%. The averaged chemical shifts and the populations can be found in the associated FAIR data repository, while the final corresponding RMSDs can be found in Table 12.140 We note that these results are stable toward increasing the DFT quadrature to the more accurate superfine grid; 1.647 ppm for entry i, a potential source of error noted by Wheeler et al.141
| Set of rotamers | (i) | (ii) | (iii) | (iv) | (v) |
|---|---|---|---|---|---|
| RMSD | 3.18 (1.65) | 3.95 (2.34) | 4.49 (2.96) | 4.42 (3.10) | 3.83 (2.22) |
This system is unusual in that selecting the 5 or 10 conformation subsets (iii) and (iv) produces a clearly inferior prediction and even selecting the set with populations >1% (set v) shows a significantly higher error than the full conformer set. In solution intermolecular hydrogen bonds and other effects can influence populations depending on the concentration of the NMR sample. These are not modelled here, but nonetheless the quality of the prediction using rotamer set i suggests that these may be less important than the desirability of including a full conformer space in the calculation.
4.2 Dissociative equilibria between 3- and 4-coordinate boron
The experimental values reported by Oisaki et al.97 as well as Kim et al.98 for difluoro(phenyl)borane (Table 1) in coordinating solvents do not align with these reported by Shmakov et al.95 or Kim et al.98 in non-coordinating chloroform. Tetrahyrofuran (thf) and acetonitrile both might complex with the 3-coordinate boron atom in difluoro(phenyl)borane to form a 4-coordinate species, these being of particular interest in understanding the mechanisms of amidation using boron catalysts. We calculated the 19F NMR spectra in these two solvents at the ωB97xd/aug-cc-pvdz level, for both the complexed and the free forms (Fig. 11 and 12) with values reported in Table 13. | ||
| Fig. 11 Structures for (a) the complexed and (b) free difluoro(phenyl)borane in thf, showing the weak dispersion interactions for the two species treated as a supermolecule. | ||
 | ||
| Fig. 12 Structures for (a) the complexed and (b) free difluoro(phenyl)borane in acetonitrile, showing the weak dispersion interactions for the two species treated as a supermolecule. | ||
| Solvent | Form | 19F chemical shift in ppm (eqn (4)) | Reported value |
|---|---|---|---|
| thf | 4-Coordinate bound | −155.6 | −14295 |
| 3-Coordinate unbound | −95.2 | ||
| Acetonitrile | 4-Coordinate bound | −157.6 | −127.998 |
| 3-Coordinate unbound | −96.2 | ||
| Pyridine | 4-Coordinate bound | −166.8 | −154.6 |
| 3-Coordinate unbound | −95.9 | ||
| Thiophene | 4-Coordinate bound | n/a | — |
| 3-Coordinate unbound | −93.6 | ||
| Sulfolane | 4-Coordinate bound | −144.9 | — |
| 3-Coordinate unbound | −96.1 |
The combined energies of difluoro(phenyl)borane and one molecule of either thf (tetrahydrofurant) or acetonitrile as solvent can be obtained in two ways. Summing the computed free energies of the individual solute and solvent molecules as model (a) or using the free energy of the combined weakly interacting supermolecule as model (b), with both energies obtained with a solvent continuum solvation model applied. The first model corresponds approximately to an infinitely dilute solution of the two components and the second to a 0.041 M equimolar solution (equivalent to a standard state of 1 atm@298 K) in which weak dispersion interactions between the two components can reduce the entropy of separation. Since the solvent is in higher concentration (16 M for thf, 31 M for acetonitrile), this also favours the intermolecular equilibrium towards a greater concentration of the solvent-bound 4-coordinate form. The calculated relative free energy of the 4-coordinate species using acetonitrile as solvent is +3.4 kcal mol−1 using model (a) and −1.2 kcal mol−1 using model (b). Decreasing the free energy of the bound form by −3.9 kcal mol−1 to approximate the effect on the equilibrium of the high molar concentration of acetonitrile via the expression RTLn(31/0.041), T = 298 K and using model (a), indicates that the resulting concentration of unbound 3-coordinate and of solvent-bound 4-coordinate difluoro(phenyl)borane are approximately equal (populations ∼0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.5).
0.5).
The calculated 19F chemical shifts can now be used as limiting values for the 4-coordinate bound and 3-coordinate unbound molecules to get an experimental estimate of the equilibrium. The shift for the 4-coordinate, formally anionic borate form of difluoro(phenyl)borane, may be predicted to be too negative by ∼6 ppm, as shown by the value for BF4− itself (Table 11). Applying this approximate correction suggests that the relative populations of bound/unbound solutes are approximately equal in acetonitrile, deriving from the measured chemical shift of difluoro(phenyl)borane being intermediate between the 3- and 4-coordinate forms in this solvent.
For thf as solvent, combining the calculated corrected limiting chemical shifts for the two forms with the observed value suggests the equilibrium favours 4- over 3-coordinated species by a population ratio of 0.85/0.15. The calculated relative free energy of bound 4-coordinate species for thf as solvent is −0.5 kcal mol−1 using model (a), or −4.0 if approximately corrected for the 16 M concentration of thf. This corresponds qualitatively to the measured 19F chemical shift in this solvent distinctly favouring the 4-coordinated form. These results also hint that model (a) might be better for obtaining free energies for weakly interacting separated components in solution. It remains to be established if model (b) might be better for more concentrated solutions of components interacting more strongly through e.g. one or more strong hydrogen bonds.
In predictive mode, we investigated three further aprotic coordinating solvents, pyridine, thiophene and sulfolane. Thiophene has no minimum for the bound 4-coordinate isomer, dissociating to the unbound form. With pyridine, the 4-coordinate isomer is now significantly more stable in free energy than the unbound form by −11.7 kcal mol−1. We then measured the 19F and 11B shifts in this solvent, finding the former 13 ppm closer to if not actually at the bound limit than with thf as solvent. The calculated 11B shift (+6.8 ppm) is in close agreement with the measured value (6.3 ppm) which supports the inference that the equilibrium for difluoro(phenyl)borane indeed favours the fully 4-coordinated form in pyridine and which is supported by the energy difference of −11.7 kcal mol−1 between it and the unbound 3-coordinate form.
Sulfolane is predicted to be similar to thf, with the bound form 0.34 kcal mol−1 less stable than the unbound separated components, but is favoured if a correction (3.0 kcal mol−1) for the higher molar concentration of the solvent (6.6 M) is applied.
Further insight was obtained by searching for crystal structures containing the sub-structure C–BF–X (X = O, N) and analysing seven such structures, five of which form an intramolecular B–X bond and two of which are sterically inhibited from doing so (Fig. 11 and 12). The former set are examples of potential intramolecular equilibria in which a boron atom could display either a tri- or a four-coordinated form.121,142–146 These seven molecules are shown in Fig. 13 and the chemical shift values in Table 14.
 | ||
| Fig. 13 Structures and Cambridge Refcode identifier of the test set for 4/3-coordinate-boron equilibria. (a) ZICMIJ, (b) CUJSEG, (c) LOCNOJ, (d) CICPEM, (e) UYELAN, (f) NUJQUE and (g) TAKWIO. The crystal structures can be found in the data repository.147 | ||
Of the species shown in Fig. 11, ZICMIJ has no formal stationary point for a 3-coordinate species, but it does appear as an inflexion in the energy surface typical of a “hidden intermediate” and can be estimated to be 13.7 kcal mol−1 higher in free energy than the 4-coordinate isomer. True intramolecular 3-coordinate forms can be located as formal stationary points for CUJSEG (+40.7 kcal mol−1), LOCNOJ (+32.3 kcal mol−1), CICPEM (+23.5 kcal mol−1) and NUJQUE (+19.3 kcal mol−1), with their free energies relative to the 4-coordinate forms shown parentheses. The values suggest that in all cases the 4-coordinate form is the only one with a significant population (1.00) in solution.
The reported 19F shift for the methylamino substituted NUJQUE (and of its octylamino derivative) of −54.5 ppm (compounds 15 and 16 in the article,14819F nmr reference not stated) is anomalous in comparison with the other compounds shown in Fig. 11 and also with the predicted 19F. The 11B shifts for NUJQUE reported as −15 ppm agree well with a calculated value of −13.3 ppm using B(OMe)3 as reference, indicating the molecule probably has the constitution indicated. This in turn suggests the unstated 19F reference for the measured shift148 may not be CFCl3 but CF3H (calc. −57.5) or more probably trifluoroacetic acid (calc. −60.9). Assuming the latter, re-referenced with respect to CFCl3 the measured value for NUJQUE emerges as −131.5 ppm, in reasonable agreement with the predicted value for a 4-coordinate boron species.
UYELAN and TAKWIO are examples of fluoroboranes in which steric hindrance inhibits formation of a 4-coordinate form. For UYELAN, 4-coordination via the oxygen of thf results in a species that is 8.6 kcal mol−1 higher than the individual dissociated components, and so this form is predicted to have no significant population in solution. TAKWIO is also sterically hindered and the 4-coordinate form in thf is 11.1 kcal mol−1 higher in free energy than the non-coordinated form, again unpopulated. The 19F chemical shifts are all well predicted as 3-coordinate for these systems, suggesting that predictive NMR can be used to estimate positions of 3-/4-coordinate dynamic equilibria where they might occur.
5 Conclusions
19F NMR is a powerful tool that can used for the structure determination of fluorinated molecules. We provide herein computational tools to help estimate 19F chemical shifts using reasonable computer resources and with an accuracy of 3–4 ppm or better, providing an additional asset to the synthesis or the study of catalytic mechanisms in which fluorine is exploited as an analytic probe.Author contributions
A. S. Dumon provided methodology, formal analysis, investigation, visualisation, data curation and writing. H. S. Rzepa provided conceptualisation and project administration, data curation and writing. R. Procter provided chemical synthesis and with the other authors analysis, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the EPSRC for grants EP/T030488/1, EP/T030534/1, EP/T030658/1, EP/T030666/1. We thank Dr Chris Edge for invaluable statistical advice.References
- G. E. Totten and D. S. MacKenzie, Handbook of Aluminum, Dekker, 2003, vol. 2 Search PubMed.
- J. Wang, M. Sánchez-Roselló, J. L. Aceña, C. del Pozo, A. E. Sorochinsky, S. Fustero, V. A. Soloshonok and H. Liu, Chem. Rev., 2014, 114, 2432–2506 CrossRef CAS PubMed.
- J. T. Moore and C. C. Lu, J. Am. Chem. Soc., 2020, 142, 11641–11646 CrossRef CAS PubMed.
- L. I. Khusainova, L. O. Khafizova, T. V. Tyumkina and U. M. Dzhemilev, Russ. J. Gen. Chem., 2016, 86, 1438–1441 CrossRef CAS.
- N. Murakami, M. Yoshida, T. Yoshino and S. Matsunaga, Chem. Pharm. Bull., 2018, 66, 51–54 CrossRef CAS PubMed.
- T. Furuya, A. S. Kamlet and T. Ritter, Nature, 2011, 473, 470–477 CrossRef CAS PubMed.
- H. Robatjazi, J. L. Bao, M. Zhang, L. Zhou, P. Christopher, E. A. Carter, P. Nordlander and N. J. Halas, Nat. Catal., 2020, 3, 564–573 CrossRef CAS.
- Y.-C. Ning and R. R. Ernst, Structural Identification of Organic Compounds with Spectroscopic Techniques, Wiley-VCH, 2005 Search PubMed.
- T. D. W. Claridge, High-Resolution NMR Techniques in Organic Chemistry, Elsevier Science, 2016 Search PubMed.
- C. P. Rosenau, B. J. Jelier, A. D. Gossert and A. Togni, Angew. Chem., Int. Ed., 2018, 57, 9528–9533 CrossRef CAS PubMed.
- S. Sirirungruang, O. Ad, T. M. Privalsky, S. Ramesh, J. L. Sax, H. Dong, E. E. K. Baidoo, B. Amer, C. Khosla and M. C. Y. Chang, Nat. Chem. Biol., 2022, 18, 886–893 CrossRef CAS PubMed.
- A. M. Ruppert, M. Jędrzejczyk, O. Sneka-Płšatek, N. Keller, A. S. Dumon, C. Michel, P. Sautet and J. Grams, Green Chem., 2016, 18, 2014–2028 RSC.
- A. S. Dumon, T. Wang, J. Ibañez, A. Tomer, Z. Yan, R. Wischert, P. Sautet, M. Pera-Titus and C. Michel, Catal. Sci. Technol., 2018, 8, 611–621 RSC.
- C.-H. Chan, F. Poignant, M. Beuve, E. Dumont and D. Loffreda, J. Phys. Chem. Lett., 2019, 10, 1092–1098 CrossRef CAS PubMed.
- M. Dhifallah, M. Iachella, A. Dhouib, F. Di Renzo, D. Loffreda and H. Guesmi, J. Phys. Chem. C, 2019, 123, 4892–4902 CrossRef CAS.
- H. S. Rzepa, S. Arkhipenko, E. Wan, M. T. Sabatini, V. Karaluka, A. Whiting and T. D. Sheppard, J. Org. Chem., 2018, 83, 8020–8025 CrossRef CAS PubMed.
- S. V. Fedorov and L. B. Krivdin, J. Fluorine Chem., 2020, 238, 109625 CrossRef CAS.
- L. B. Krivdin, Russian Chem. Rev., 2020, 89, 104 Search PubMed.
- H. Fukaya and T. Ono, J. Comput. Chem., 2004, 25, 51–60 CrossRef CAS PubMed.
- W. Adcock, D. Lünsmann, J. E. Peralta and R. H. Contreras, Magn. Reson. Chem., 1999, 37, 167–172 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- W. C. Isley, A. K. Urick, W. C. K. Pomerantz and C. J. Cramer, Mol. Pharmaceutics, 2016, 13, 2376–2386 CrossRef CAS PubMed.
- H. P. Ebrahimi and M. Tafazzoli, Concepts Magn. Reson., Part A, 2012, 40, 192–204 CrossRef.
- J.-H. Yang, L. A. Clark, G. J. Ray, Y. J. Kim, H. Du and R. Q. Snurr, J. Phys. Chem. B, 2001, 105, 4698–4708 CrossRef CAS.
- J. C. B. Dietschreit, A. Wagner, T. A. Le, P. Klein, H. Schindelin, T. Opatz, B. Engels, U. A. Hellmich and C. Ochsenfeld, Angew. Chem., Int. Ed., 2020, 59, 12669–12673 CrossRef CAS PubMed.
- P. Gao, J. Zhang and H. Chen, Int. J. Quantum Chem., 2021, 121, e26482 CAS.
- E. Benassi, J. Comput. Chem., 2022, 43, 170–183 CrossRef CAS PubMed.
- Organic Chemistry Database, https://organicchemistrydata.org/.
- Reaxys, https://www.reaxys.com/.
- C. Cave-Ayland, M. J. Bearpark, C. Romain and H. S. Rzepa, J. Opensource Software, 2022, 70, 3824 Search PubMed.
- M. J. Harvey, A. Mclean and H. S. Rzepa, J. Cheminformatics, 2017, 9, 4 CrossRef PubMed.
- S. Miertuñ, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- S. Miertus and J. Tomasi, Chem. Phys., 1982, 65, 239–245 CrossRef CAS.
- J. L. Pascual-ahuir, E. Silla and I. Tuñon, J. Comput. Chem., 1994, 15, 1127–1138 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1988, 88, 1053–1062 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- S. Sæbø and J. Almlöf, Chem. Phys. Lett., 1989, 154, 83–89 CrossRef.
- M. Head-Gordon and T. Head-Gordon, Chem. Phys. Lett., 1994, 220, 122–128 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibsom and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- R. McWeeny, Phys. Rev., 1962, 126, 1028–1034 CrossRef.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- M. Klaupp, O. L. Malkina and V. G. Malkin, J. Comput. Chem., 1999, 20, 1304–1313 CrossRef.
- A. Dumon, H. S. Rzepa, C. Alamillo-Ferrer, J. Bures, R. Procter, T. D. Sheppard and A. Whiting, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/8772.
- Z. Cong, T. Kurahashi and H. Fujii, J. Am. Chem. Soc., 2012, 134, 4469–4472 CrossRef CAS PubMed.
- D. Velayutham, K. Jayaraman, K. Kulangiappar, N. Ilayaraja, Y. R. Babu, P. S. Rao, S. N. Reddy, K. V. Babu and M. Noel, J. Fluorine Chem., 2006, 127, 1111–1118 CrossRef CAS.
- H. Schneider, A. Hock, A. D. Jaeger, D. Lentz and U. Radius, Eur. J. Inorg. Chem., 2018, 4031–4043 CrossRef CAS.
- D. A. Ellis, J. W. Martin, D. C. G. Muir and S. A. Mabury, Anal. Chem., 2000, 72, 726–731 CrossRef CAS PubMed.
- N. M. Hein, F. S. Pick and M. D. Fryzuk, Inorg. Chem., 2017, 56, 14513–14523 CrossRef CAS PubMed.
- A. Ribeiro and M. Glen, J. Mag. Res., Ser. A, 1994, 107, 158–166 CrossRef CAS.
- H. Nakai, K. Jeong, T. Matsumoto and S. Ogo, Organometallics, 2014, 33, 4349–4352 CrossRef CAS.
- D. D. L. Jones, I. Douair, L. Maron and C. Jones, Angew. Chem., Int. Ed., 2021, 60, 7087–7092 CrossRef CAS PubMed.
- S. Ando and T. Matsuura, Mag. Reson. Chem., 1995, 33, 639–645 CrossRef CAS.
- P. Xu, P. López-Rojas and T. Ritter, J. Am. Chem. Soc., 2021, 143, 5349–5354 CrossRef CAS PubMed.
- A. Foris, Mag. Reson. Chem., 2004, 42, 534–555 CrossRef CAS PubMed.
- A. Bakhoda, O. E. Okoromoba, C. Greene, M. R. Boroujeni, J. A. Bertke and T. H. Warren, J. Am. Chem. Soc., 2020, 142, 18483–18490 CrossRef CAS PubMed.
- J.-P. Dietz, B. P. Derstine, D. Ferenc, E. T. Crawford, A. J. Arduengo III, B. F. Gupton, D. T. McQuade and T. Opatz, Eur. J. Org. Chem., 2019, 5519–5526 CrossRef CAS.
- F.-L. Zeng, K. Sun, X.-L. Chen, X.-Y. Yuan, S.-Q. He, Y. Liu, Y.-Y. Peng, L.-B. Qu, Q.-Y. Lv and B. Yu, Adv. Synth. Catal., 2019, 361, 5176–5181 CrossRef CAS.
- A. Aydogan, D. J. Coady, S. K. Kim, A. Akar, C. Bielawski, M. Marquez and J. Sessler, Angew. Chem., Int. Ed., 2008, 47, 9648–9652 CrossRef CAS PubMed.
- F. Weigert, J. Fluorine Chem., 1990, 46, 375–384 CrossRef CAS.
- T. Mohy El Dine, O. Sadek, E. Gras and D. M. Perrin, Chem. – Eur. J., 2018, 24, 14933–14937 CrossRef CAS PubMed.
- D. Dunlop, J. Pinkas, M. Horáček, N. Žilková and M. Lamač, Dalton Trans., 2020, 49, 2771–2775 RSC.
- L. P. Press, A. J. Kosanovich, B. J. McCulloch and O. V. Ozerov, J. Am. Chem. Soc., 2016, 138, 9487–9497 CrossRef CAS PubMed.
- M. Baya, D. Joven-Sancho, P. J. Alonso, J. Orduna and B. Menjón, Angew. Chem., Int. Ed., 2019, 58, 9954–9958 CrossRef CAS PubMed.
- A. B. Grommet, J. L. Bolliger, C. Browne and J. R. Nitschke, Angew. Chem., Int. Ed., 2015, 54, 15100–15104 CrossRef CAS PubMed.
- W. Jud, S. Maljuric, C. O. Kappe and D. Cantillo, Org. Lett., 2019, 21, 7970–7975 CrossRef CAS PubMed.
- A. Zweig, R. G. Fischer and J. E. Lancaster, J. Org. Chem., 1980, 45, 3597–3603 CrossRef CAS.
- K. L. Bamford, S. S. Chitnis, Z.-W. Qu and D. W. Stephan, Chem. – Eur. J., 2018, 24, 16014–16018 CrossRef CAS PubMed.
- O. Koleda, T. Broese, J. Noetzel, M. Roemelt, E. Suna and R. Francke, J. Org. Chem., 2017, 82, 11669–11681 CrossRef CAS PubMed.
- C.-P. Zhang, J. Cai, C.-B. Zhou, X.-P. Wang, X. Zheng, Y.-C. Gu and J.-C. Xiao, Chem. Commun., 2011, 47, 9516–9518 RSC.
- S. Y. Erdyakov, A. V. Ignatenko, M. E. Gurskii and Y. N. Bubnov, Mendeleev Commun., 2007, 17, 271–273 CrossRef CAS.
- S. Fantasia, J. M. Welch and A. Togni, J. Org. Chem., 2010, 75, 1779–1782 CrossRef CAS PubMed.
- C. Colomban, E. V. Kudrik, P. Afanasiev and A. B. Sorokin, J. Am. Chem. Soc., 2014, 136, 11321–11330 CrossRef CAS PubMed.
- Z.-Y. Liu and S. P. Cook, Org. Lett., 2021, 23, 808–813 CrossRef CAS PubMed.
- M. E. Zick, J.-H. Lee, M. I. Gonzalez, E. O. Velasquez, A. A. Uliana, J. Kim, J. R. Long and P. J. Milner, J. Am. Chem. Soc., 2021, 143, 1948–1958 CrossRef CAS PubMed.
- T. Yang, H. Lu, Y. Shu, Y. Ou, L. Hong, C.-T. Au and R. Qiu, Org. Lett., 2020, 22, 827–831 CrossRef CAS PubMed.
- F. Le Vaillant, E. J. Reijerse, M. Leutzsch and J. Cornella, J. Am. Chem. Soc., 2020, 142, 19540–19550 CrossRef CAS PubMed.
- N. Ichiishi, A. J. Canty, B. F. Yates and M. S. Sanford, Org. Lett., 2013, 15, 5134–5137 CrossRef CAS PubMed.
- T. Remarchuk and E. Corey, Tetrahedron Lett., 2018, 59, 2256–2259 CrossRef CAS.
- P. Tang, T. Furuya and T. Ritter, J. Am. Chem. Soc., 2010, 132, 12150–12154 CrossRef CAS PubMed.
- M. K. Cybulski, C. J. E. Davies, J. P. Lowe, M. F. Mahon and M. K. Whittlesey, Inorg. Chem., 2018, 57, 13749–13760 CrossRef CAS PubMed.
- G. Meißner, M. Feist, T. Braun and E. Kemnitz, J. Organomet. Chem., 2017, 847, 234–241 CrossRef.
- G. Berionni, H. Kurouchi, L. Eisenburger and H. Mayr, Chem. – Eur. J., 2016, 22, 11196–11200 CrossRef CAS PubMed.
- M. M. Shmakov, S. A. Prikhod'ko, V. V. Bardin and N. Y. Adonin, Mendeleev Commun., 2018, 28, 369–371 CrossRef CAS.
- S. Liu, H. Liu, S. Liu, Z. Lu, C. Lu, X. Leng, Y. Lan and Q. Shen, J. Am. Chem. Soc., 2020, 142, 9785–9791 CAS.
- K. Oisaki, D. Zhao, M. Kanai and M. Shibasaki, J. Am. Chem. Soc., 2006, 128, 7164–7165 CrossRef CAS PubMed.
- B. J. Kim and D. S. Matteson, Angew. Chem., Int. Ed., 2004, 43, 3056–3058 CrossRef CAS PubMed.
- M. Kol, S. Rozen and E. Appelman, J. Am. Chem. Soc., 1991, 113, 2648–2651 CrossRef CAS.
- H. J. Frohn and W. Pahlmann, J. Fluorine Chem., 1984, 24, 219–232 CrossRef CAS.
- N. V. Lebedev, V. V. Berenblit, P. E. Troichanskaya and V. A. Gubanov, Russian J. App. Chem., 2009, 82, 449–455 CrossRef CAS.
- J. Mizukado, Y. Matsukawa, H. dao Quan, M. Tamura and A. Sekiya, J. Fluorine Chem., 2006, 127, 79–84 CrossRef CAS.
- H. Bürger and S. Sommer, J. Chem. Soc., Chem. Commun., 1991, 456–458 RSC.
- H. Frohn and R. Nielinger, J. Fluorine Chem., 1996, 77, 143–146 CrossRef CAS.
- X. Jia, X. Zhou, H. Quan, M. Tamura and A. Sekiya, J. Fluorine Chem., 2011, 132, 1188–1193 CrossRef CAS.
- T. A. Shaler and T. H. Morton, J. Am. Chem. Soc., 1991, 113, 6771–6779 CrossRef CAS.
- N. O. Andrella, N. Xu, B. M. Gabidullin, C. Ehm and R. T. Baker, J. Am. Chem. Soc., 2019, 141, 11506–11521 CrossRef CAS PubMed.
- P. S. Bhadury, M. Pandey and D. K. Jaiswal, J. Fluorine Chem., 1995, 73, 185–187 CrossRef CAS.
- S. Hämmerling, G. Thiele, S. Steinhauer, H. Beckers, C. Müller and S. Riedel, Angew. Chem., Int. Ed., 2019, 58, 9807–9810 CrossRef PubMed.
- M. Ahrens, G. Scholz, T. Braun and E. Kemnitz, Angew. Chem., Int. Ed., 2013, 52, 5328–5332 CrossRef CAS PubMed.
- J. Guang, R. Hopson, P. G. Williard, M. Fujiu, K. Negishi and K. Mikami, J. Org. Chem., 2016, 81, 5922–5928 CrossRef CAS PubMed.
- S. Wilken, M. Treskow, J. Scheers, P. Johansson and P. Jacobsson, RSC Adv., 2013, 3, 16359–16364 RSC.
- S. A. Lermontov, L. L. Ushakova and N. V. Kuryleva, J. Fluorine Chem., 2008, 129, 332–334 CrossRef CAS.
- B. M. Kraft, R. J. Lachicotte and W. D. Jones, J. Am. Chem. Soc., 2001, 123, 10973–10979 CrossRef CAS PubMed.
- M. Talavera, G. Meiner, S. G. Rachor and T. Braun, Chem. Commun., 2020, 56, 4452–4455 RSC.
- L. A. Bischoff, J. Riefer, R. Wirthensohn, T. Bischof, R. Bertermann, N. V. Ignatev and M. Finze, Chem. – Eur. J., 2020, 26, 13615–13620 CrossRef CAS PubMed.
- S. L. Guillot, A. Peña-Hueso, M. L. Usrey and R. J. Hamers, J. Electrochem. Soc., 2017, 164, A1907–A1917 CrossRef CAS.
- D. G. Altman and J. M. Bland, J. R. Stat. Soc. Ser. D, 1983, 32, 307–317 CrossRef.
- A. Dumon, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/9915.
- F. Rauch, S. Fuchs, A. Friedrich, D. Sieh, I. Krummenacher, H. Braunschweig, M. Finze and T. B. Marder, Chem. – Eur. J., 2020, 26, 12794–12808 CrossRef CAS PubMed.
- A. G. Crawford, Z. Liu, I. A. I. Mkhalid, M.-H. Thibault, N. Schwarz, G. Alcaraz, A. Steffen, J. C. Collings, A. S. Batsanov, J. A. K. Howard and T. B. Marder, Chem. – Eur. J., 2012, 18, 5022–5035 CrossRef CAS PubMed.
- C. R. Wade, H. Zhao and F. P. Gabbaï, Chem. Commun., 2010, 46, 6380–6381 RSC.
- A. L. Gott, W. E. Piers, J. L. Dutton, R. McDonald and M. Parvez, Organometallics, 2011, 30, 4236–4249 CrossRef CAS.
- J. Légaré Lavergne, A. Jayaraman, L. C. Misal Castro, E. Rochette and F.-G. Fontaine, J. Am. Chem. Soc., 2017, 139, 14714–14723 CrossRef PubMed.
- K. Durka, M. Urban, M. Dąbrowski, P. Jankowski, T. Klił and S. Luliłžski, ACS Omega, 2019, 4, 2482–2492 CrossRef CAS PubMed.
- S. Jin, H. T. Dang, G. C. Haug, R. He, V. D. Nguyen, V. T. Nguyen, H. D. Arman, K. S. Schanze and O. V. Larionov, J. Am. Chem. Soc., 2020, 142, 1603–1613 CrossRef CAS PubMed.
- A. Dumon, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/9649.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- K. Monde, N. Miura, M. Hashimoto, T. Taniguchi and T. Inabe, J. Am. Chem. Soc., 2006, 128, 6000–6001 CrossRef CAS PubMed.
- Y. S. Sokeirik, H. Mori, M. Omote, K. Sato, A. Tarui, I. Kumadaki and A. Ando, Org. Lett., 2007, 9, 1927–1929 CrossRef CAS PubMed.
- A. Berkessel, S. S. Vormittag, N. E. Schlörer and J.-M. Neudörfl, J. Org. Chem., 2012, 77, 10145–10157 CrossRef CAS PubMed.
- D.-J. Barrios Antùonez, M. D. Greenhalgh, A. C. Brueckner, D. M. Walden, P. Elias-Rodriguez, P. Roberts, B. G. Young, T. H. West, A. M. Z. Slawin, P. Ha-Yeon Cheong and A. D. Smith, Chem. Sci, 2019, 10, 6162–6173 RSC.
- C. Sperandio, J. Rodriguez and A. Quintard, Chem. Sci., 2020, 11, 1629–1635 RSC.
- A. Rudnichenko, V. Timoshenko, A. Chernega, A. Nesterenko and Y. Shermolovich, J. Fluorine Chem., 2004, 125, 1351–1356 CrossRef CAS.
- K. Funabiki, H. Iwata, Y. Yano, Y. Kubota and M. Matsui, Org. Chem. Front., 2015, 2, 369–371 RSC.
- A. Maity, A. Sarkar, B. N. S. Bhaktha and S. K. Patra, New J. Chem., 2020, 44, 14650–14661 RSC.
- D. E. Arkhipov, A. V. Lyubeshkin, A. D. Volodin and A. A. Korlyukov, Mendeleev Commun., 2020, 30, 103–105 CrossRef CAS.
- P. A. Slepukhin, V. I. Filyakova and V. N. Charushin, J. Struct. Chem., 2012, 53, 1011–1012 CrossRef CAS.
- K. I. Pashkevich, D. V. Sevenard, O. G. Khomutov, O. V. Shishkin and E. V. Solomovich, Russ. Chem. Bull., 1999, 48, 359–363 CrossRef CAS.
- A. Dumon, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/10504.
- A. N. Bootsma and S. Wheeler, Popular Integration Grids Can Result in Large Errors in DFT-Computed Free Energies, ChemRxiv, 2019 DOI:10.26434/chemrxiv.8864204.
- J. D. Kirkham, R. J. Butlin and J. P. A. Harrity, Angew. Chem., Int. Ed., 2012, 51, 6402–6405 CrossRef CAS PubMed.
- D. Pla, O. Sadek, S. Cadet, B. Mestre-Voegtl and E. Gras, Dalton Trans., 2015, 44, 18340–18346 RSC.
- K. Yang, G. Zhang and Q. Song, Chem. Sci., 2018, 9, 7666–7672 RSC.
- C. Bonnier, W. E. Piers, A. Al-Sheikh Ali, A. Thompson and M. Parvez, Organometallics, 2009, 28, 4845–4851 CrossRef CAS.
- Z. Wang, C. Cheng, Z. Kang, W. Miao, Q. Liu, H. Wang and E. Hao, J. Org. Chem., 2019, 84, 2732–2740 CrossRef CAS PubMed.
- A. Dumon, Imperial College Research Data Repository, 2021 DOI:10.14469/hpc/10243.
- M. P. Hughes and B. D. Smith, J. Org. Chem., 1997, 62, 4492–4499 CrossRef CAS PubMed.
- T. Murosaki, S. Kaneda, R. Maruhashi, K. Sadamori, Y. Shoji, K. Tamao, D. Hashizume, N. Hayakawa and T. Matsuo, Organometallics, 2016, 35, 3397–3405 CrossRef CAS.
- K. Samigullin, Y. Soltani, H.-W. Lerner, M. Wagner and M. Bolte, Acta Crystallogr., Sect. C: Struct. Chem., 2016, 72, 189–197 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2022 |



