Dehydrogenation of ammonia on free-standing and epitaxial hexagonal boron nitride

Abstract

We report a thermodynamically feasible mechanism for producing H₂ from NH₃ using hBN as a catalyst. 2D catalysts have exceptional surface areas with unique thermal and electronic properties suited for catalysis. Metal-free, 2D catalysts, are highly desirable materials that can be more sustainable than the ubiquitously employed precious and transition metal-based catalysts. Here, using density functional theory (DFT) calculations, we demonstrate that metal-free hexagonal boron nitride (hBN) is a valid alternative to precious metal catalysts for producing H₂via reaction of ammonia with a boron and nitrogen divacancy (V_BN). Our results show that the decomposition of ammonia proceeds on monolayer hBN with an activation energy barrier of 0.52 eV. Furthermore, the reaction of ammonia with epitaxially grown hBN on a Ru(0001) substrate was investigated, and we observed similar NH₃ decomposition energy barriers (0.61 eV), but a much more facile H₂ associative desorption barrier (0.69 eV vs 5.89 eV). H₂ generation from the free-standing monolayer would instead occur through a diffusion process with an energy barrier of 3.36 eV. A detailed analysis of the electron density and charge distribution along the reaction pathways was carried out to rationalise the substrate effects on the catalytic reaction.

---

1 Introduction

Several green energy technologies employing hydrogen to decarbonise transport and industry are of considerable economic interest. However, H₂ has a low energy density by volume (2.4 kWh l⁻¹)¹ and is difficult to store and transport, therefore more effective chemical storage methods are required. Ammonia, which can be stored as a liquid and contains 17.65% H by mass, can provide a convenient source of H₂.² Decomposition of ammonia will only produce H₂ and N₂, the latter a non-toxic, non-greenhouse gas. However, decomposing NH₃ is difficult to achieve, often requiring rare transition metal catalysts such as Ru or Te.³ Furthermore, often further steps are required to purify H₂ before use. Clearly, there is a need to design materials that can simultaneously decompose ammonia and produce pure H₂.

Hydrogenation reactions involve the addition of H₂ to an element or molecule (generally an unsaturated compound) and are widely used in the food,⁴ petrochemical,⁵ and fine chemical industries.⁶ For enabling hydrogenation, a catalyst is employed to activate molecular hydrogen and allow the reaction to proceed. A range of metal-based catalysts make a variety of hydrogenation reactions possible, including: the conversion of alkenes to alkanes using Pt,^7,8 carboxylic acids to alcohols or alkanes using Re/Pd,⁹ and phenols to cyclohexanone/cyclohexanol using Rh.¹⁰ Such catalysis enables new synthesis routes and the production of high-quality feedstocks for fine chemical industries and mass-produced products such as Nylon.

However, the decrease in the availability of metals such as Pt, Pd, and Re, combined with an increase in prices due to high energy demands,¹¹ and local environmental damage,¹² has reduced the appeal of these catalysts. Greener and more sustainable alternative materials with similar catalytic properties need to be found. Hexagonal boron nitride (hBN) nanosheets are of interest for applications including electrical,¹³ optoelectronic¹⁴ and spintronic¹⁵ devices. hBN consists of sp² hybridised N and B atoms forming 2D sheets.¹⁶ Layers of hBN stack in an ABAB pattern held together by van der Waals forces.¹⁷ Charge localisation gives hBN a large experimental band gap of 6 eV.¹⁸ The fabrication techniques used to produce monolayer hBN include chemical vapour deposition,¹⁹ direct reaction,²⁰ and mechanical methods.²¹ Additives can be added during sonication to aid the exfoliation of hBN to nanosheets. Ammonia facilitates hBN exfoliation via a Lewis base mechanism.²² The methods used to produce hBN can result in a range of thicknesses, with the fabrication of monolayer hBN possible.²³

Despite the recent advances in the fabrication process of hBN,²⁴ hBN sheets often contain a range of defects, including impurities, vacancies, edges and grain boundaries.²⁵ These defects have been investigated as metal-free sites for a wide range of reactions, such as; the hydrogenation of alkenes,²⁶ capture of CO₂,²⁷ conversion of methane to methanol,²⁸ and N₂ fixation to NH₃.²⁹ Ball milling has been established as a way of creating additional defect sites.^30,31 Longer milling durations have shown increased activity and selectivity for the nitroaldol reaction at 100 °C.³² Clearly, reactions of hBN defects are possible under achievable conditions.

A range of vacancy defects including boron vacancies (V_B) and nitrogen vacancies (V_N) have been observed using high-resolution transmission electron microscopy.^33,34V_B and V_N have been shown to react with atmospheric components to create catalytically active sites; for example, carbon sites can be introduced by the reaction of V_B with CO₂.³⁵ These sites can then catalyse NO reduction by CO to form N₂ and CO₂.²⁷ These promising results have sparked interest in hBN as a heterogeneous catalyst. Pristine hBN has several properties which are intrinsically suited for a catalyst, including high thermal stability,^16,36 a low coefficient of thermal expansion,³⁷ and high specific surface area.³⁸ The range of active sites available and the physical stability make hBN an excellent candidate for industrial catalysis.

hBN with a boron antisite defect where a nitrogen is replaced with an additional boron atom has been explored as a potential site for hydrogen release from NH₃ using density functional theory (DFT).³⁹ NH₃ is chemisorbed onto the antisite, and H₂ can be released by overcoming a calculated energy barrier of 0.65 eV, leaving behind a NH species which requires an energy of 4.68 eV to remove and regenerate the original site. In this study, we focus on the application of vacancy defects as active sites for the dehydrogenation of ammonia. Each dangling bond on V_B and V_N defects can be hydrogenated to become more stable.⁴⁰ Hydrogenated V_B can behave as H donor sites, able to hydrogenate a range of alkanes at high yields as shown by experiment and supported with DFT.²⁶ However, an efficient way of creating hydrogenated V_B defects has yet to be proposed.

In addition to V_N and V_B defects, larger vacancies such as BN divacancies (V_BN) and triangular (V_N+3B) have been the subject of previous research, with the V_BN defect shown to be more stable under neutral and nitrogen rich conditions.⁴¹ Calculations have shown that V_B vacancies can migrate much more easily than V_N.⁴² Therefore V_B can become trapped when contacting a V_N, forming V_BN through a mutual annihilation process. This process of forming V_BN from V_B and V_N has been used to justify the low concentration of paramagnetic centres measured in irradiated hBN.⁴³V_BN has been investigated for use in H₂ activation and production, requiring an energy barrier of approximately 400 kJ mol⁻¹ to be overcome to release H₂ and regenerate V_BN.⁴⁴ Dehydration of alkanes to alkenes using V_BN sites has also been investigated as a metal-free alternative to commercial production of alkenes.⁴⁵ An activation energy barrier of 112.1 kJ mol⁻¹ (1.16 eV) was found to convert ethane (C₂H₆) to ethene (C₂H₄), resulting in a hydrated V_BN. Given the stability, properties and previous work on V_BN, we expect V_N vacancies to be a source of novel reactivity.

Dehydration of ammonia borane (H₃N–BH₃) by V_N, V_B and V_N+3B has been investigated using DFT as a way of producing H₂.⁴⁶ The results showed low energy barriers to transfer 2H to defects in the hBN sheet followed by further reaction to release a single H₂. However, only 2 of the 6 available hydrogen atoms are released, leaving behind a H₂N–BH₂ species. The incompleteness of the reaction and the limited uses of ammonia borane in industry hinder its practical and widespread adaption as a fuel source. Conversely, ammonia is widely used in industry, most notably in the production of fertilisers and has been shown to decompose completely.⁴⁷ Literature has investigated the use of NO and NO₂ to repair V_N defects, ultimately ‘healing’ the vacancy and producing oxygen.⁴⁸ This process is energetically facile with a rate-limiting barrier of 0.82 eV. Ammonia has the potential to behave similarly and produce hydrogen.

Our computational study shows that the V_BN defects of hBN can provide an excellent site for the reaction of ammonia to form a hydrogenated V_B site or H₂ depending on surface temperature. The hydrogenated V_B can then be used as a source of H₂ for green energy and key hydrogenation reactions such as the hydrogenation of alkenes to alkanes.

2 Computational methodology

First-principles electronic structure calculations were carried out using CASTEP.⁴⁹ The PBE functional⁵⁰ was used to treat exchange and correlation in combination with the Tkatchenko and Scheffler dispersion correction method.⁵¹ The plane wave basis set was expanded to a cut-off energy of 400 eV using Vanderbilt ultrasoft pseudopotentials.⁵² All calculations used a Monkhorst–Pack k-point sampling of the first Brillouin zone⁵³ with a uniform grid of (10 × 10 × 1) or (4 × 4 × 1) for modelling (1 × 1) and (5 × 5) unit cells, respectively. The surface structures were optimised until the maximum force on each atom was less than 0.025 eV Å⁻¹ and the total energy changed by less than 1 × 10⁻⁶ eV. The transition states along the reaction pathways were calculated with the Linear and Quadratic Synchronous Transit (LST/QST) algorithm, with a force tolerance of 0.1 eV Å⁻¹. A (5 × 5) supercell was employed for all defect calculations, with a vacuum region of at least 20 Å to separate the periodically repeated images and avoid spurious interactions.

Adsorption energies E_Ads were calculated using the standard formula:

E_Ads = E_AB − E_A − E_B (1)

where E_AB is the energy of the adsorbed species, E_A and E_B are the energy of the dissociated species.

Formation energies E_f were calculated using the formula:

E_f = E_V − E_hBN + n_NE_N + n_BE_B (2)

where E_V is the energy of a vacancy or system, E_hBN is the energy of the pristine hBN sheet, n_N and n_B are the number of nitrogen and boron atoms removed to create a vacancy respectively, E_N is the energy of an isolated N₂ molecule, and E_B is the reference energy of a boron atom in its α-rhombohedral phase.⁵⁴

3 Results and discussion

3.1 Ammonia decomposition on hBN

Initially, a (1 × 1) cell consisting of a single boron and nitrogen atom was converged with respect to cell size and k-points. When optimised, a bond length of 1.433 Å and lattice parameter of 2.483 Å was achieved, in close agreement with experimental values.²³ It is well established that GGA functionals such as PBE underestimate the band gap; our value of 4.5 eV is in close agreement with other DFT studies.^55,56 Each vacancy was constructed by removing the corresponding atoms, and the energy converged with respect to cell size and k-points.

The two possible mono-vacancies can be seen in Fig. 1. V_N has D_3h symmetry and B–B distances of 2.367 Å around the vacancy site and a magnetic moment of 1 ℏ/2. In contrast, V_B has C_2v symmetry, two N–N distances of 2.786 Å and one of 2.845 Å, with a magnetic moment of 1 ℏ/2, due to Jahn-Teller effects. The geometry and properties of these vacancies is consistent with the literature.^55,57,58 The E_f of V_N and V_B are 8.63 eV and 9.75 eV, respectively. Therefore, V_N is more stable, in agreement with previous works.^59–62V_BN can be formed by removing a pair of adjacent B and N atoms achieving a N–N distance of 2.379 Å, B–B distances of 2.052 Å, B–N distances of 3.099 Å, an overall magnetic moment of 0 ℏ/2, and C_2v symmetry, consistent with previous calculations.⁶³ The B–B distance is shorter due to a weak covalent bond, and there is no overall magnetic moment as the electrons are all able to pair. The E_f of the divacancy has been calculated to be 11.83 eV, approximately 2 eV higher than the mono vacancies consistent with literature.^64,65 The combined formation energy of V_B and V_N is 18.38 eV, much higher than that for a V_BN, thus the probability of forming a V_BN defect is higher than forming separate V_B and V_N defects, as has been previously suggested.⁶⁵

Fig. 1 (a) Pristine hBN sheet. (b) V_BN (E_f = 11.83 eV, spin = 0 ℏ/2) defect. (c) and (d) are V_B (E_f = 9.75 eV, spin = 1 ℏ/2), and V_N (E_f = 8.63 eV, spin = 1 ℏ/2) respectively. Boron atoms are shown in green and nitrogen atoms shown in grey.

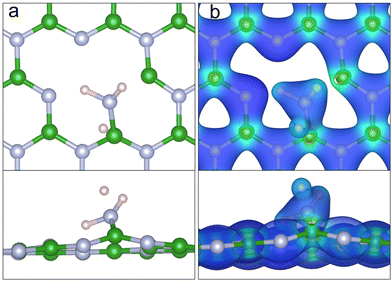
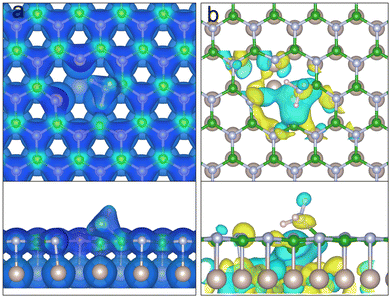
Firstly, the adsorption of ammonia above a pristine hBN monolayer was considered. A range of sites and orientations were investigated. The most stable physisorption site can be seen in Fig. 2a with an E_Ads of −0.172 eV. As in previous work, the most stable site is above the B atom.^56,66–68 However, we found the configuration with hydrogens orientated towards the hBN is preferred by 0.015 eV, with a N distance of 3.34 Å from the surface. In terms of NH₃ orientation upon adsorption, literature results vary depending on the exchange and correlation functional, basis set, and tolerances used, but they generally agree with our results. The barrier to invert the H–H bonds (umbrella inversion) is small and was calculated to be 0.158 eV, similar to values calculated for an isolated ammonia molecule.⁶⁹Fig. 2b and d show the charge accumulation (blue) and charge depletion (red) of ammonia above hBN, with respect to isolated ammonia in the gas phase. The difference in intensity and topology of the charge accumulation reveals a much stronger dispersion interaction when the hydrogen atoms are orientated towards the hBN. The ammonia has a partial charge of 0.13 e and 0.06 e when the hydrogens are orientated towards and away from the hBN, respectively. The greater partial charge is indicative of stronger dispersion interactions, resulting in increased stability when the hydrogen atoms are orientated towards the hBN monolayer.

Fig. 2 (a) The most favourable orientation of ammonia above a pristine hBN sheet has the three N–H bonds pointing towards the surface and an adsorption energy of −0.172 eV at a distance of 3.68 Å from the surface. (c) Inverted ammonia adsorption, with an adsorption energy of −0.157 eV at a distance of 2.92 Å from the surface. These orientations can be inter-converted by overcoming an energy barrier of 0.158 eV. (b) and (d) show charge accumulation (blue) and charge depletion (red) with respect to isolated ammonia (isosurface cutoff 0.001 e Å⁻³).

Several sites and orientations of ammonia above V_BN were considered including on top of B, on top of N, the centre of the vacancy and between N–N, B–B and B–N atoms. Optimised structures gave an E_Ads of −0.25 eV for the most stable adsorption geometry. The nitrogen atom is positioned almost directly above the vacant nitrogen position of the V_BN at a height of 2.76 Å. Contrary to what was observed for NH₃ physisorption on pristine hBN, ammonia adsorbs on top of a divacancy in a slightly tilted configuration to enable the lone pair on the nitrogen to interact with the electron-deficient B–B bond, forming a weak intermolecular bond. Each of the three N–H bonds are consequently pointing away for the vacancy. This geometry is the first step of the deportation reaction which mechanism is illustrated in Fig. 6 and in Fig. S1 of the ESI.†

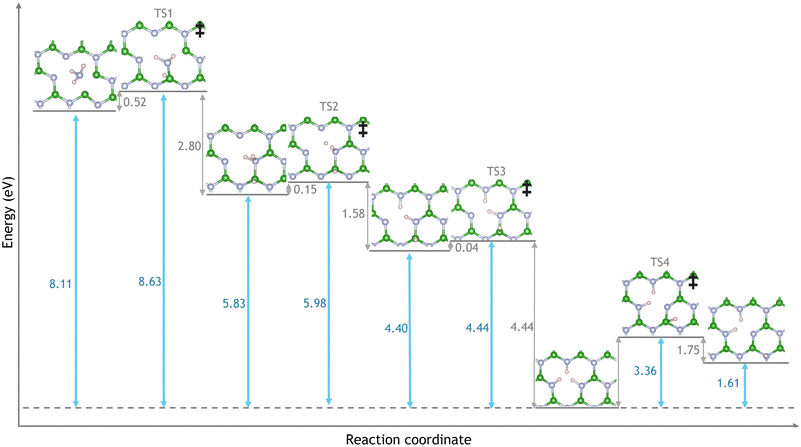
Next, the reaction of NH₃ and V_BN was investigated. A number of pathways, products and intermediates were considered in order to find the minimum energy pathway and the most plausible reaction mechanism. The first intermediate is produced by breaking the strong N–H bond to produce a chemisorbed NH₂ and H species. The surface boron atom plays an active role in stabilising the transition state (TS1) by forming a bond to nitrogen and being ready to accept the deprotonated hydrogen atom as seen in Fig. 3. The resulting energy barrier is 0.52 eV and is the highest barrier to NH₃ dissociation.

Fig. 3 (a) the geometry and (b) the electron density isosurface (0.5 e Å⁻³) of the transition state TS1 for the dissociative chemisorption of ammonia over a hBN V_BN. The energy barrier is 0.52 eV and the limiting step for ammonia disassociation. The geometry of this intermediate shows puckering of the anchoring boron atom 0.4 Å above the plane as the N–B bonds are stretched away from their equilibrium positions. The electron density isosurface shows a weak orbital overlap between the ammonia nitrogen and a hydrogen atom indicative of the first deprotonation step. Once this transition is overcome, the structure collapses to create an adsorbed NH₂ and H.

As the barriers to NH₃ desorption and dissociation are 0.25 eV and 0.52 eV respectively both of these processes are competitive. Therefore the kinetics of the aforementioned reactions we considered to suggest the formation rate of the NH₂ and H species on the surface. Rate coefficients were obtained by means of the Transition State Theory, at the temperatures of 600 K, 800 K, 1000 K and 1200 K which were possible operation temperature values of catalytic H₂ production by methods as described in the ESI.† It was possible to suggest that, at 600 K, the complete convergence of the adsorbed NH₃ into NH₂ and H, was obtained, at roughly 400 seconds (6.6 minutes), whereas, complete convergence was achieved in 0.4 seconds at 1200 K as illustrated in Fig. S2 of the ESI.† Therefore, NH₃ is expected to dissociate into NH₂ and H in a reasonable amount of time.

The second barrier of 0.15 eV over TS2 reflects the migration of a hydrogen atom to satisfy a nitrogen dangling bond. The third transition state (TS3) reflects the migration of two hydrogen atoms to satisfy all the dangling bonds of V_B and form a stable hydrogenated boron vacancy after overcoming a small energy barrier of 0.04 eV. TS3 involves the migration of an H breaking one H–N bond and forming a second N–H bond on the other side of the vacancy with the migration of a second H breaking a B–H bond and forming an H–N bond in place of the original. Both migrations in TS3 are expected to take place in a single step as no relaxed geometry of a single migration was observed. The reaction pathway leads to the formation of a hydrogenated V_B, with a ΔE reaction of −8.11 eV and can be seen in Fig. 6.

Following the creation of a hydrated V_B vacancy, the three remaining hydrogen atoms could diffuse away sequentially; the possible paths are shown in Fig. 4. Considering the first diffusion (Fig. 4a) the hydrogen could either move on top of a nitrogen atom that is adjacent to the vacancy (H_NA) with energy barriers of 3.44 eV (TS5) or move directly away from the vacancy onto a nitrogen that is towards the pristine sheet (H_NP) with energy barriers of 3.36 eV (TS4). No relaxed structures where the hydrogen atom had migrated to the boron atom were observed in geometry optimisations. The boron atom refuses to accept the hydrogen as its p_z orbital is empty. The average bond population of the B–N bond increases from 0.90 e where a N–H bond is present to 1.15 e; this compensates for the loss of connectivity and creation of a dangling bond. The nitrogen atoms surrounding the vacancy have available and occupied p_z orbitals, these bind to the diffusing hydrogen. Therefore, the hydrogen is not accepted by the boron, and moves onto a surrounding nitrogen instead. We found that the H_NP pathway has a lower energy barrier by 0.07 eV (2.10%) and is the dominant route. This slight difference in transition state stability is attributed to a very weak stabilising B–H bond with a population of 0.11 e that is present in TS4 but not TS5. The trend of hydrogen diffusion following the H_NP pathway continues as hydrogen's are removed from the vacancy as TS6 is higher in energy than TS7 by 2.29% and TS8 is higher in energy than TS9 by 1.45%.

Fig. 4 Sequential diffusion of the first (a), second (b) and third (c) hydrogen atoms away from the hydrogenated V_B vacancy to H_NA or H_NP sites. Transition states are identified by ‡. Diffusion to a H_NP site is preferred in each case with an increasing energy barrier increasing with each diffusion event (3.40 eV 3.63 eV and 3.88 eV).

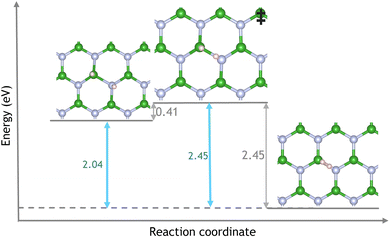
The average energy barrier to diffuse increases as the number of hydrogen atoms increases from 3.40 eV (TS4-5), 3.63 eV (TS6-7) and 3.88 (TS8-9). Hydrogen diffusion creates nitrogen dangling bonds the loss of connectivity destabilises the vacancy resulting in higher barriers hindering further diffusion steps. Diffused hydrogens could then migrate across the surface, where they may find another vacancy or hydrogen. In the latter case, it has been found that two surface hydrogens can desorb from a pristine hBN surface with an energy barrier of 0.41 eV and form H₂ as shown in Fig. 5. This barrier reflects the energy required to break B–H and N–H bonds. The ΔE of the reaction is −2.04 eV; hence it is thermodynamically favourable for surface hydrogen to desorb as H₂. Fig. 6 shows the reaction scheme from ammonia adsorption to diffusion of the first hydrogen via a hydrogenated V_B vacancy.

Fig. 5 Combination of two H_ads to create H₂ and desorb from a pristine hBN surface following diffusion from a hydrogenated V_B vacancies. Transition states are identified by ‡. The ΔE of the reaction is −2.04 eV.

Fig. 6 The reaction pathway of ammonia with a V_BN to produce a hydrogenated V_B defect in monolayer hBN. Transition states are identified by ‡ and labelled TS1-4. The activation energy for the reaction is 0.52 eV reflecting the energy required to deprotonate a hydrogen atom from ammonia. Subsequent steps occur with a negligible energy barrier to produce a hydrogenated boron vacancy with a ΔE reaction of −8.11 eV. A hydrogen atom can then diffuse away from the vacancy after overcoming an energy barrier of 3.36 eV.

Our results show that dehydration of ammonia followed by the insertion of a nitrogen atom into the V_BN to form a hydrogenated V_B is energetically facile as N becomes part of the lattice. Subsequent removal of H₂ from V_B is more challenging to achieve and requires higher temperatures.

3.2 Ammonia decomposition on hBN/Ru(0001)

So far, the hBN system studied is that of an isolated “freestanding” monolayer. However, this does not represent the only or the most probable case for technological applications in catalysis. In practice, epitaxial single-layer hBN is typically grown and employed as a catalytic material on a metal substrate. Currently, high-quality hBN surfaces can be epitaxially grown by CVD on a Ru(0001) surface.⁷⁰ Therefore we expanded our investigations to include vacancies over a Ru(0001) substrate.

Ru(0001) has a hexagonal-close-packed hcp crystal structure. It has been found that the most stable hBN over Ru(0001) configuration occurs when boron atoms continue the hcp stacking arrangement and nitrogen atoms sit on the adjacent top site directly above the Ru in the layer below.^71–73 Charge transfer between hBN and Ru(0001) leads to repulsive/attractive forces acting on the nitrogen/boron of the hBN overlayer.⁷³ Consequently, the boron atoms are marginally closer to the surface than the nitrogen. It is important to note that larger cells of hBN/Ru(0001) lead to the formation of a 12 × 12 nanomesh, however, experimentally the nanomesh consists of large pores 2.2 Å above the Ru(0001) surface,⁷¹ a similar distance to our calculated value of 2.17 Å and where vacancies would have adequate space to form.

The Ru(0001) lattice is 8.5% larger than that of hBN. This lattice mismatch stretches the hBN N–B bonds to match those of the Ru(0001) surface below in order to create N–Ru bonds. The Mulliken atomic charge distributions in boron and nitrogen atoms change from 2.18 to 2.63 e (+20%) and from 5.82 to 5.64 e (−3%) respectively, when comparing pristine hBN to pristine hBN/Ru(0001), showing that the B–N bond becomes more polarised as a consequence of the substrate interaction. The difference in populations reflects the reduction in B–N bond strength when above a Ru(0001) surface due to the additional strain caused by the substrate. The Mulliken charges on the boron and nitrogen atoms change dramatically (from 0.82 to 0.37 e for boron and from −0.82 to −0.64 for nitrogen). The atomic partial charges indicate that the nature of hBN interlayer bonding has changed due to the Ru(0001) layer below. As with the isolated monolayer, vacancy defects can be introduced when above a Ru(0001) surface with E_f of 2.37 eV, 3.45 eV and 5.38 eV for V_B, V_N, and V_BN defects, respectively. These energies are lower than for a monolayer (−63% on average), owing to the added stability provided by the Ru layer below.

The calculated pathway for the reaction of NH₃ with a hBN V_BN on a Ru(0001) surface can be seen in Fig. 7 showing intermediates and transition states.

Fig. 7 The reaction pathway of ammonia with a V_BN hBN defect above a Ru(0001) substrate. Transition states are identified by ‡ and labelled TS10-14. The ammonia is readily chemisorbed onto the surface after overcoming a low energy barrier of 0.02 eV. A hydrogenated V_B defect is produced by sequential deprotonation steps. The highest energy barrier is 0.61 eV and reflects the energy to deprotonate the final hydrogen atom. The ΔE of the reaction is −3.21 eV. H₂ can then associativity desorb by overcoming an energy barrier of 0.69 eV.

As with the monolayer, several adsorption sites and orientations of ammonia on a hBN/Ru(0001) surface were considered. Optimised structures gave an E_Ads of −0.52 eV for the most stable adsorption geometry. This is indicative of strong physisorption with NH₃ being adsorbed more strongly onto hBN/Ru(0001) than a hBN monolayer with an E_Ads of −0.25 eV. This difference in adsorption energy is attributed to the increased polarisation of the B–N bonds; thus, the interaction between the ammonia lone pair and the electron-deficient boron atoms of the vacancy is stronger.⁷⁴ Similar to the monolayer, ammonia is physisorbed onto the hBN/Ru(0001) surface with a slightly tilted orientation allowing the nitrogen lone pair to point towards the B–B bond at a height of 1.90 Å above the surface, as can be seen in Fig. 8.

Fig. 8 NH₃ over a hBN/Ru(0001) surface. (a) and (b) physisorption and chemisorption of NH₃ respectively. (c) A hydrogenated V_B hBN monolayer above a Ru(0001) substrate. The reaction proceeds via physisorption and chemisorption followed by a series of deprotonations to (c).

Unlike adsorption onto an isolated monolayer, NH₃ chemisorbed state with an adsorption energy of −1.57 eV was also observed as shown in Fig. 8b. The chemisorbed state has the ammonia's nitrogen bonded with one of the vacancy's boron atoms at a height of 1.07 Å and an average H–N–B bond angle of 110.3°. This chemisorption step is easily achieved by overcoming a very low energy barrier of 0.02 eV as only inter-molecular repulsion needs to be overcome in TS10. The existence of a chemisorbed NH₃ species can be explained by the overall weaker N–B bonding in the hBN lattice due to stretching to fit the Ru(0001) surface unit cell, resulting in average N–B distances of 1.57 Å (9.8% longer compared to the optimum bond length of 1.43 Å, which makes the B atoms more electrophilic, binding to the ammonia more readily. Additionally, the N–Ru bond reduces the electron density available to the nitrogen for binding with boron atoms. Subsequent deprotonation of a H atom to a chemisorbed NH₂ species occurs with a barrier of 0.21 eV (TS11) to saturate a dangling bond on the nitrogen occurs. This results in a B–NH₂ and a N–H satisfying half of the dangling bonds in the vacancy. Next, the NH₂ rotates around the B–N bond and binds to the baron atom on the other side of the vacancy after overcoming an energy barrier of 0.36 eV (TS12). The next step involves breaking a second N–H bond to satisfy the final dangling bond and hydrogenate the vacancy in TS13. For the decomposition of NH₃ on hBN/Ru(0001) TS13 has the highest barrier of 0.61 eV due to the stability of the final intermediate and change from sp³ to sp². The product of the reaction is similar to that of the previous mechanism investigated for the monolayer (Fig. 6), with hydrogen atoms satisfying the dangling bonds of the V_B pointing away from the Ru as shown in Fig. 8c. The final structure has an E_Ads of −3.73 eV. The difference in pathway and energy barriers reflect the impact of the substrate. The small lattice mismatch between hBN and Ru(0001) allows the hBN monolayer to map onto the Ru(0001) lattice. Consequently, the B–N bonds stretch away from the ideal free-standing hBN lattice vectors causing, an overall weakening of the B–N bonds, affecting the band structure and electron density in the epitaxial layer in agreement with previously reported by experimental measurement.⁷⁵ The change in electronic structure stabilises key intermediates for the reaction making a chemisorbed state possible which was not observed for the isolated monolayer. Despite these differences in mechanism, the product of NH₃ decomposition on suspended hBN and hBN/Ru(0001) is similar and correspond to the creation of a hydrogenated V_B vacancy.

Fig. 9 NH₃ over a hBN/Ru(0001) surface. (a) and (b) physisorption and chemisorption of NH₃ respectively. (c) A hydrogenated V_B hBN monolayer above a Ru(0001) substrate. The reaction proceeds via physisorption and chemisorption followed by a series of deprotonations to (c).

Hydrogen desorption from a hydrogenated V_BN over a Ru(0001) surface was considered. The three surface hydrogen atoms are orientated away from the Ru(0001) substrate below (Fig. 8c). Two of the hydrogens were then found to desorb from the surface as H₂ after overcoming a low energy barrier of 0.69 eV in TS14, producing H₂. As with the monolayer, the remaining hydrogen atom could migrate across the surface and combine with a second hydrogen adatom, form H₂, and desorb. The H₂ desorption barrier from a pristine hBN/Ru(0001) surface was calculated to be 0.91 eV as shown in Fig. 6. The barrier for hydrogen to combine and desorb from the surface is higher than that for hBN/Ru(0001) than for the monolayer due to greater filling of the B p_z orbital.

Alternatively, sequential diffusion of the final three hydrogen atoms was also considered. Unlike the monolayer where only H_NA and H_NP arrangements were found to be stable, the Boron atom adjacent to the vacancy has been found to accept a hydrogen atom H_BA. Both of these routes are shown in Fig. 10 with the transition state of the H_BA route lower in energy by 0.31 (6.5%) eV. This change in boron activity is due to B–Ru bonding which populates the B p_z orbital. As this orbital is now populated, it can be used to bond with a diffusing hydrogen. After leaving the vacancy, the hydrogen atom would then diffuse over hBN and combine with another diffusing hydrogen after overcoming an energy barrier of 0.91 eV as shown in Fig. 9. Here unlike the monolayer, direct desorption of H₂ is preferred with a low energy barrier of 0.69 eV compared to the diffusion process with barriers of 2.28 eV and 0.91 eV.

Fig. 10 Diffusion of hydrogen from a hydrated V_B vacancy via H_BA and H_NA pathways. Transition states are identified by ‡. The H_NA pathway has an activation energy of 2.59 eV and a ΔE reaction of 0.99 eV. The H_BA pathway proceeds with an activation energy of 2.28 eV and a ΔE reaction of 0.37 eV.

Attempting the associative desorption of H₂ from the hydrogenated V_B hBN monolayer results in a very high energy barrier of 5.98 eV. In this case, the adsorbed hydrogens rearrange to bring two adjacent hydrogens within 1.45 Å of each other, overcoming minimal activation energy of 0.07 eV as seen in Fig. S3 of the ESI.† The two hydrogen atoms associatively desorb by overcoming an energy barrier of 5.98 eV, leaving behind a boron vacancy containing a single hydrogen atom. The transition state barrier is much higher for associative desorption (5.98 eV) than diffusion (3.36 eV). Therefore, hydrogens are more likely released from the vacancy by diffusion from the isolated monolayer, in contrast to hBN/Ru(0001), where H₂ associatively desorbs.

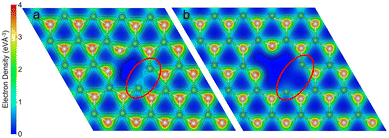
In order to explain the different reactivity of hBN/Ru(0001) compared to the free-standing hBN, we analysed the electron density of the pristine vacancy for the two systems. Fig. 11 shows the electron density slice of V_BN. By comparing the two isosurfaces, we can see that when over Ru(0001), the hBN monolayer has a much lower electron density between localised the boron atoms and can therefore bind more readily with the incoming NH₃. Additionally, the approaching ammonia experiences less repulsion from the reduced electron density in the vacancy. The lattice mismatch and consequent changes in B–N bonding have a profound effect on the reaction pathway. The reduced B–B bonding character and larger space provided by the lattice miss-match allows for the ammonia to chemisorb onto one of the boron atoms as seen in Fig. 8. The chemisorbed NH₃ species is not stable for the isolated monolayer, instead, direct dissociative chemisorption occurs after the ammonia physisorption step. After the initial deprotonation, the effects of the substrate are evident for all remaining steps, with drastically different barrier heights and intermediates. The reduced electron density on the boron atoms caused by Ru(0001) increases the strength of the dipole–dipole bond between the surface and ammonia. Correspondingly the E_Ads for NH₃ are −0.25 and −0.52 eV for the isolated monolayer and the monolayer above a Ru(0001) substrate, respectively.

Fig. 11 An electron density contour map from 0 to 4 e Å⁻³ of the hBN V_BN monolayer (a) and the V_BN monolayer over Ru(0001) (b). We can see that the electron density of the B–B bond in the vacancy (circled in red) is much higher for the isolated hBN monolayer than with a Ru(0001) substrate below. B–B distances are 2.05 Å and 2.98 Å for isolated hBN and hBN/Ru(0001).

Fig. 12 shows the Highest Occupied Molecular Orbital (HOMO) for the physisorbed ammonia above the V_BN and V_BN over Ru(0001). Both plots show the electron density accumulation stretching from the physisorbed ammonia's nitrogen towards the surface boron atoms. The HOMO comprises of contributions from both the NH₃ and the B–B atoms of the vacancy immediately underneath the adsorbate. The HOMO of the hBN/Ru(0001) system includes mixing of the boron sp² orbitals with those of the Ru, which shifts the HOMO towards the centre of the vacancy. It follows that the reaction happens at the B–B site in order to minimise the energy of the HOMO orbital.

Fig. 12 The HOMO of physisorbed NH₃ over (a) V_BN and (b) V_BN over Ru(0001) with an isosurface value of 0.02 e Å⁻³. In both cases, the HOMO consists of ammonia and boron orbitals, however in (b) the HOMO is situated towards the centre of the vacancy. Showing where the ammonia reacts to lower the energy of these orbitals. Orbitals far from the vacancy have been omitted for clarity.

Fig. 13a shows the electron density isosurface of NH₃ chemisorbed onto a hBN V_BN defect with a Ru(0001) substrate. Here we can see bond formation between the NH₃ nitrogen and a surface boron atom in the vacancy. The tetragonally bonded nitrogen has a Mulliken charge of −0.85 e, and the B–N bond has a population of 0.62 e, showing more ionic character than a B–N hBN bond (typically 0.87 e). The result of electron donation from the substrate is that the B–B bond of the divacantcy is incredibly weak having been stretched to a length of 3.12 Å.

Fig. 13 (a) the electron density isosurface (0.5 e Å⁻³) and (b) the HOMO (0.02 e Å⁻³) for chemisorbed ammonia above a hBN/Ru(0001) V_BN defect. The isosurface shows N–Ru bonding and the ammonia bonded to the surface boron atom, indicative of a chemisorbed state. The HOMO still contains significant B and Ru character, the energy of which can be minimalised by subsequent deprotonation of ammonia hydrogens. Orbitals far from the vacancy have been omitted for clarity.

Observing ammonia in a similar position above an isolated monolayer, the nitrogen has a charge of −1.00 e and a reduced bond population of 0.39 e in the B–N bond. Yet, the B–B bond is strongly covalent with a population of 0.67 e. The existing B–B bond is therefore favoured over forming the new B–NH₃. Furthermore, the ammonia's hydrogens are closer to the nitrogen dangling bonds on the other side of the vacancy. For the reaction to proceed, a hydrogen must deprotonate from the ammonia to form a stable surface intermediate as seen in Fig. 6. Fig. 13b shows the HOMO of chemisorbed NH₃ above hBN/Ru(0001). The HOMO consists of mixed Ru and B atomic orbital characters, similar to that of the physisorbed of NH₃Fig. 12b.

The second key difference between the monolayer hBN and hBN/Ru(0001) is the height of energy barrier for associative desorption of H₂ from the hydrogenated V_B. The latter system only requires an energy of 0.69 eV, while the former requires an energy of 5.98 eV. Clearly, the Ru(0001) has a significant role to play in aiding the desorption of H₂. The N–Ru bonding stabilises the V_B defect by partially satisfying the nitrogen dangling bonds as evidenced by the average Mulliken charge on the N–H bonded nitrogen staying around −0.74 e as the desorption proceeds. In contrast, the free-standing hBN monolayer values vary from −0.88 to −0.90 e. The differences in bonding contributes to dramatically reduce the H₂ desorption energy barrier between the two hBN systems. Fig. 14 shows the change in energy of a V_BN as a function of the number of hydrogens adsorbed on the divacancy. As the number of hydrogen atoms increases, so does the stability of the V_BN. The defect stabilisation effect is much more pronounced for the monolayer than hBN/Ru(0001).

Fig. 14 The change in energy with the number of hydrogen atoms chemisorbed in a V_B for both a hBN monolayer and hBN/Ru(0001). There is a trend where with decreasing number of hydrogen atoms, the energy of the site increases. The effect is more pronounced for the monolayer than for hBN/Ru(0001) due to stabilisation from the Ru and steric effects of neighbouring hydrogen atoms.

To reduce steric clashes, the hydrogenated monovacancy positions hydrogen atoms above and below the hBN honeycomb maintaining an average H–H distance of 1.88 Å. When the Ru(0001) substrate is included in the calculations, the hydrogen atoms can only adsorb above the hBN plane (see Fig. 8), resulting in an average H–H distance of 1.74 Å. The increased H–H distance reduces the dipole–dipole interaction of the hydrogen atoms and the overall energy of the monolayer structure. In contrast, despite the larger hBN/Ru(0001) unit cell, the H–H distance is shorter, resulting in greater steric hindrance and reducing the change in binding energy. Overall, the energy of the system decreases by a smaller amount as hydrogens are added for V_B hBN/Ru(0001) compared to the V_B monolayer. The combination of electronic and steric effects allows H₂ to desorb from a hydrogenated V_B with a lower energy barrier in the hBN/Ru(0001) system than for the monolayer.

To determine if stretching of hBN affects the reactivity and lowers the H₂ desorption energy of the hBN/Ru(0001) system a cell with the Ru(0001) removed but maintaining the B–N bond length of 1.57 Å was used. Geometry optimisations with a fixed cell size showed a difference in energy between the hydrated vacancy and the H₂ desorbed state of 4.91 eV similar to that of the monolayer (4.77 eV). Furthermore, a hBN bilayer and a hBN monolayer with a graphene monolayer substrate was considered to compare the effect of different substrates. These showed a difference in energy between the hydrated vacancy and the H₂ desorbed state of 4.65 eV and 4.60 eV respectively, similar to the monolayer. As the difference between the hydrated V_B and desorbed H₂ states are similar to that of the monolayer, it is presumed that the transition state energies would also be similar. Given the similarity of the results when considering stretching and different substrates it is clear that the Ru(0001) has a significant impact on the reactivity of hBN.

As NH₃ can readily decompose into a V_BN defect overcoming an achievable barrier of 0.52 eV and 0.61 eV, for the monolayer and hBN/Ru(0001) respectively. Both materials are excellent precursors for forming hydrogenated V_B sites of catalytic interest. The high hydrogen diffusion energy of 3.36 eV limits the use of the monolayer as a source of H₂. However, when a Ru(0001) substrate is placed below the monolayer H₂ desorption energy reduces to 0.69 eV, demonstrating that substrate effects can change the catalytic activity of hBN/Ru(0001) vacancies, making hBN a promising candidate for NH₃ decomposition to H₂. In fact, the energy barrier of dehydrogenation on hBN is lower than that which has been reported for TiO₂⁷⁶ and Molybdenum Nitrides⁷⁷ with the H₂, and is similar to that of metal complexes.^78,79 Furthermore, as the nitrogen is incorporated into the hBN a pure product is expected.

4 Conclusions

In conclusion, using DFT calculations, we have investigated the reaction of ammonia with a V_BN vacancy in both a “free-standing” hBN monolayer and a hBN monolayer above a Ru(0001) substrate. A stable hydrogenated V_B is created in each case before desorption of H₂. The atomistic mechanism describing NH₃ dehydrogenation and H₂ desorption has been described in detail before discussing the key differences due to substrate-effects, hBN bonding and geometry which result in differing reaction pathways. The activation energy barrier for the dehydrogenation of ammonia was found to be 0.52 eV for the free-standing monolayer and 0.61 eV for hBN/Ru(0001). Subsequent associative desorption of H₂ is facile for hBN/Ru(0001) compared to the monolayer with barriers of 0.69 eV and 5.89 eV, respectively. H₂ generation from the free-standing monolayer would instead occur through a diffusion process with an energy barrier of 3.36 eV. This huge difference in the recombinative desorption barrier between the system can be rationalised by analysing the widely differing electronic structure and bonding of the hydrogenated V_B structures. This work shows that hBN could be an excellent candidate for generating H₂ from NH₃ for fuel as part of the emerging hydrogen economy and as a catalyst for hydrogenation reactions.

Author contributions

A. P. conceived the presented idea, performed the DFT simulations and wrote the manuscript under the guidance of M. S. N. X. and G. B. performed kinetics calculations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work made use of ARCHER2, the UK's national high performance computing service, via the UK's HPC Materials Chemistry Consortium, which is funded by EPSRC (EP/R029431). A. P. acknowledges the University of Surrey for access to the Eureka High Performance Computing facility and funding in the form of a PhD studentship. M. S. acknowledge the Royal Society for personal funding through a Royal Society University Research Fellowship URF\R\191029. Thanks to Robert Lawrence and Louie Slocombe for their help and conversation. Supplemental data for this article can be found at https://doi.org/10.15126/900374.

Notes and references

1. A. F. D. Center, US Department of Energy, 2014.
2. G. Thomas, P. George, Potential Roles of Ammonia in a Hydrogen Economy, U.S. Department of Energy, 2006, 1–23.
3. K. E. Lamb, M. D. Dolan and D. F. Kennedy, Int. J. Hydrogen Energy, 2019, 44, 3580–3593.
4. A. J. Wright, A. Wong and L. L. Diosady, Food Res. Int., 2003, 36, 1069–1072.
5. N. López, B. Bridier and J. Pérez-Ramírez, J. Phys. Chem. C, 2008, 112, 9346–9350.
6. Á. Molnár, A. Sárkány and M. Varga, J. Mol. Catal. A: Chem., 2001, 173, 185–221.
7. O. Guselnikova, A. Olshtrem, Y. Kalachyova, I. Panov, P. Postnikov, V. Svorcik and O. Lyutakov, J. Phys. Chem. C, 2018, 122, 26613–26622.
8. M. Peer, A. Qajar, R. Rajagopalan and H. C. Foley, Carbon, 2014, 66, 459–466.
9. J. Ullrich and B. Breit, ., ACS Catal., 2018, 8, 785–789.
10. S. I. Fujita, T. Yamada, Y. Akiyama, H. Cheng, F. Zhao and M. Arai, J. Supercrit. Fluids, 2010, 54, 190–201.
11. T. Bossi and J. Gediga, Johnson Matthey Technol. Rev., 2017, 61, 111–121.
12. D. M. Díaz-Morales, J. H. Erasmus, S. Bosch, M. Nachev, N. J. Smit, S. Zimmermann, V. Wepener and B. Sures, Environ. Pollut., 2021, 286, 117284.
13. S. A. Tawfik, S. Ali, M. Fronzi, M. Kianinia, T. T. Tran, C. Stampfl, I. Aharonovich, M. Toth and M. J. Ford, Nanoscale, 2017, 9, 13575–13582.
14. X. Lü, S. He, H. Lian, S. Lv, Y. Shen, W. Dong and Q. Duan, Appl. Surf. Sci., 2020, 531, 147262.
15. F. Zheng, G. Zhou, Z. Liu, J. Wu, W. Duan, B. L. Gu and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 1–5.
16. S. N. Perevislov, Refract. Ind. Ceram., 2019, 60, 291–295.
17. C. R. Hsing, C. Cheng, J. P. Chou, C. M. Chang and C. M. Wei, New J. Phys., 2014, 16, 113015.
18. G. Cassabois, P. Valvin and B. Gil, Nat. Photonics, 2016, 10, 262–266.
19. X. Song, Q. Li, J. Ji, Z. Yan, Y. Gu, C. Huo and Y. Zou, 2D Mater., 2016, 3, 035007.
20. R. T. Paine and C. K. Narulat, Chem. Rev., 1990, 90, 73–91.
21. K. Zhang, Y. Feng, F. Wang, Z. Yang and J. Wang, J. Mater. Chem. C, 2017, 5, 11992–12022.
22. L. Cao, S. Emami and K. Lafdi, Mater. Express, 2014, 4, 165–171.
23. C. Jin, F. Lin, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 1–4.
24. C. Maestre, B. Toury, P. Steyer, V. Garnier and C. Journet, J. Phys. Mater., 2021, 4, 044018.
25. M. Jana and R. N. Singh, Int. Mater. Rev., 2018, 63, 162–203.
26. D. J. Nash, D. T. Restrepo, N. S. Parra, K. E. Giesler, R. A. Penabade, M. Aminpour, D. Le, Z. Li, O. K. Farha, J. K. Harper, T. S. Rahman and R. G. Blair, ACS Omega, 2016, 1, 1343–1354.
27. M. D. Esrafili, S. Heydari and L. Dinparast, Struct. Chem., 2019, 30, 1647–1657.
28. A. Akça, Comput. Theor. Chem., 2021, 1202, 113291.
29. Y. Zhang, H. Du, Y. Ma, L. Ji, H. Guo, Z. Tian, H. Chen, H. Huang, G. Cui, A. M. Asiri, F. Qu, L. Chen and X. Sun, Nano Res., 2019, 12(4), 919–924.
30. Y. Ding, F. Torres-Davila, A. Khater, D. Nash, R. Blair and L. Tetard, MRS Commun., 2018, 8(3), 1236–1243.
31. L. H. Li, Y. Chen, B. Behan, H. Zhang, M. Petravic and A. M. Glushenkov, J. Mater. Chem., 2011, 21(32), 11862–11866.
32. S. Torii, K. Jimura, S. Hayashi, R. Kikuchi and A. Takagaki, J. Catal., 2017, 355, 176–184.
33. C. Jin, F. Lin, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 3–6.
34. J. C. Meyer, A. Chuvilin, G. Algara-Siller, J. Biskupek and U. Kaiser, Nano Lett., 2009, 9, 2683–2689.
35. Y. Jiao, A. Du, Z. Zhu, V. Rudolph, G. Q. Lu and S. C. Smith, Catal. Today, 2011, 175, 271–275.
36. D. R. Lide and G. Baysinger, CRC Handbook of Chemistry and Physics, 2019.
37. Q. Cai, D. Scullion, W. Gan, A. Falin, S. Zhang, K. Watanabe, T. Taniguchi, Y. Chen, E. J. Santos and L. H. Li, arXiv, 2019, 1–9.
38. L. Xue, B. Lu, Z. S. Wu, C. Ge, P. Wang, R. Zhang and X. D. Zhang, Chem. Eng. J., 2014, 243, 494–499.
39. A. A. Peyghan, J. Mex. Chem. Soc., 2015, 59(1), 67–73.
40. N. L. McDougall, J. G. Partridge, R. J. Nicholls, S. P. Russo and D. G. McCulloch, Phys. Rev. B, 2017, 96, 1–9.
41. S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 161404.
42. A. Zobelli, C. P. Ewels, A. Gloter and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 75(9), 1–7.
43. M. Fanciulli, Philos. Mag. B, 1997, 76(3), 363–381.
44. R. Cortese and D. Campisi, Mol. Catal., 2020, 493, 110891.
45. R. Cortese, D. Campisi, A. Prestianni and D. Duca, Mol. Catal., 2020, 493, 110891.
46. A. Kuang, T. Zhou, G. Wang, Y. Li, G. Wu, H. Yuan, H. Chen and X. Yang, Appl. Surf. Sci., 2016, 362, 562–571.
47. I. Lucentini, X. Garcia, X. Vendrell and J. Llorca, Ind. Eng. Chem. Res., 2021, 60, 18560–18611.
48. B. Xiao, X. F. Yu and Y. H. Ding, RSC Adv., 2014, 4, 22688–22696.
49. M. K. Agusta and I. Prasetiyo, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
51. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 6–9.
52. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
53. J. D. Monkhorst, J. Hendrik and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
54. K. Shirai, H. Dekura, Y. Mori, Y. Fujii, H. Hyodo and K. Kimura, J. Phys. Soc. Jpn., 2011, 80, 084601.
55. B. Huang and H. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 1–8.
56. Y. J. Liu, B. Gao, D. Xu, H. M. Wang and J. X. Zhao, Phys. Lett. A, 2014, 378, 2989.
57. J. Strand, L. Larcher and A. L. Shluger, J. Phys.: Condens. Matter, 2020, 32, 055706.
58. K. Watanabe and T. Taniguchi, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–4.
59. M. S. Si and D. S. Xue, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–4.
60. M. D. Esrafili and P. Mousavian, Appl. Surf. Sci., 2018, 440, 580–585.
61. O. L. Malkina, Phys. Chem. Chem. Phys., 2002, 4, 5467–5474.
62. W. Amalia, P. Nurwantoro and Sholihun, Comput. Condens. Matter, 2019, 18, e00354.
63. D.-H. Kim, H.-S. Kim, M. W. Song, S. Lee and S. Y. Lee, Nano Convergence, 2017, 4, 1–8.
64. T. B. Ngwenya, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245425.
65. M. S. Si, J. Y. Li, H. G. Shi, X. N. Niu and D. S. Xue, EPL, 2009, 86, 46002.
66. A. A. Peyghan, H. Soleymanabadi and Z. Bagheri, J. Mex. Chem. Soc., 2015, 59, 67–73.
67. H. Li, Z. Chen, X. Fang and D. Tie, Superlattices Microstruct., 2015, 88, 371–376.
68. M. Pashangpour, Int. Proc. Chem., Biol. Environ. Eng., 2011, 2, 113–116.
69. D. C. Ghosh, J. Jana and R. Biswas, Int. J. Quantum Chem., 2000, 80, 1–26.
70. Q. Zhang, Y. Chen, C. Zhang, C. R. Pan, M. Y. Chou, C. Zeng and C. K. Shih, Nat. Commun., 2016, 7, 1–7.
71. T. Brugger, S. Günther, B. Wang, J. H. Dil, M. L. Bocquet, J. Osterwalder, J. Wintterlin and T. Greber, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–6.
72. A. Kutana, A. Goriachko, Z. Hu, H. Sachdev, H. Over and B. I. Yakobson, Adv. Mater. Interfaces, 2015, 2, 1–8.
73. H. Li, H. Zhu and R. Zhao, New J. Chem., 2022, 46, 11035–11043.
74. Á. Logadóttir and J. K. Nørskov, J. Catal., 2003, 220, 273–279.
75. A. B. Preobrajenski, M. A. Nesterov, M. L. Ng, A. S. Vinogradov and N. Mårtensson, Chem. Phys. Lett., 2007, 446, 119–123.
76. D. Cheng, J. Lan, D. Cao and W. Wang, Appl. Catal., B, 2011, 106, 510–519.
77. J. Zhao, C. Cui, H. Wang, J. Han, X. Zhu and Q. Ge, J. Phys. Chem. C, 2019, 123, 554–564.
78. C. H. Christensen, T. Johannessen, R. Z. Sørensen and J. K. Nørskov, Catal. Today, 2006, 111, 140–144.
79. I. Lucentini, X. Garcia, X. Vendrell and J. Llorca, Ind. Eng. Chem. Res., 2021, 60, 18560–18611.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01392d

---