Open Access Article
Open Access ArticleUnveiling the structure of aqueous magnesium nitrate solutions by combining X-ray diffraction and theoretical calculations†
Yunxia
Wang
ab,
Guangguo
Wang
ab,
Daniel T.
Bowron
 c,
Fayan
Zhu
c,
Fayan
Zhu
 *ac,
Alex C.
Hannon
*ac,
Alex C.
Hannon
 *c,
Yongquan
Zhou
*c,
Yongquan
Zhou
 a,
Xing
Liu
d and
Guosheng
Shi
a,
Xing
Liu
d and
Guosheng
Shi
 ade
ade
aKey Laboratory of Comprehensive and Highly Efficient Utilization of Salt Lake Resources, Qinghai Provincial Key Laboratory of Resources Chemistry of Salt Lakes, Qinghai Institute of Salt Lakes, Chinese Academy of Sciences, Xining 81008, China. E-mail: zhufayan@126.com
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
cISIS Facility, STFC, Rutherford Appleton Laboratory, Chilton, Didcot, Oxon OX11 0QX, UK. E-mail: alex.hannon@stfc.ac.uk
dShanghai Applied Radiation Institute, Shanghai University, Shanghai 200444, China
eWenzhou Institute, University of Chinese Academy of Sciences, Wenzhou 325001, China
First published on 8th September 2022
Abstract
The structure of aqueous magnesium nitrate solution is gaining significant interest among researchers, especially whether contact ion pairs exist in concentrated solutions. Here, combining X-ray diffraction experiments, quantum chemical calculations and ab initio molecular dynamics simulations, we report that the [Mg(NO3)2] molecular structure in solution from the coexistence of a free [Mg(H2O)6]2+ octahedral supramolecular structure with a free [NO3(H2O)n]− (n = 11–13) supramolecular structure to an [Mg2+(H2O)n(NO3−)m] (n = 3, 4, 5; m = 3, 2, 1) associated structure with increasing concentration. Interestingly, two hydration modes of NO3−—the nearest neighbor hydration with a hydration distance less than 3.9 Å and the next nearest neighbor hydration with hydration distance ranging from 3.9 to 4.3 Å—were distinguished. With an increase in the solution concentration, the hydrated NO3− ions lost outer layer water molecules, and the hexagonal octahedral hydration structure of [Mg(H2O)62+] was destroyed, resulting in direct contact between Mg2+ and NO3− ions in a monodentate way. As the concentration of the solution further increased, NO3− ions replaced water molecules in the hydration layer of Mg2+ to form three-ion clusters and even more complex chains or linear ion clusters.
1. Introduction
Magnesium ions (Mg2+) and nitrate ions (NO3−) are important members of the Hofmeister series1 and display ion-specific effects.2 They are present in chloride-type salt lakes and magnesium sulfate sub-type salt lakes and become concentrated by wind evaporation. The solution structure is an important basis for establishing the phase equilibrium and metastable phase equilibrium models of multi-element water–salt systems to construct macroscopic thermodynamic models of solutions, especially for the accurate acquisition of Pitzer parameters at high concentrations. An accurate understanding of the structure of magnesium nitrate solutions is important to promote the green development and utilization of salt lake resources and refine the theory of electrolyte solutions.Researchers carried out extensive studies on the structure of magnesium nitrate solutions; however, this research has focused on whether contact ion pairs (CIP) exist in concentrated magnesium nitrate solutions and the hydration structure of NO3−. In the crystal structure of magnesium nitrate hexahydrate Mg(NO3)2·6H2O,3–5 a solvent-shared ion pair (SIP) [Mg(H2O)62+](NO3−) forms between magnesium hexahydrate and NO3− without the formation of CIPs. Many researchers also believe that no CIPs exist in concentrated magnesium nitrate solutions. Xu et al. reported that Pb2+ more easily forms ion pairs than Sr2+, Ca2+, and Mg2+.6,7 They also pointed out that due to the high energy barrier of hydrated Mg2+, it is difficult to remove the water molecules in the first hydration layer of Mg2+ from the hydration sphere. However, some researchers take an opposite view. Using Raman spectroscopy, Peleg et al.8 reported that CIPs formed when the water–salt ratio (WSR) was less than 6. For example, a CIP was present in the molten salt of Mg(NO3)2·2H2O and Mg(NO3)2·1.35NaNO3. Irish et al.9 suggested that Mg2+, NH4+, and NO3− had very weak abilities to form CIPs in solution, but upon increasing the divalent metal ion radius, the possibility of forming a CIP between Pb2+ and NO3− increased. Chang et al.10 found that no CIPs were present in a saturated magnesium nitrate solution at 25 °C, while monodentate contact ion pairs (MCIPs) and bidentate contact ion pairs (BCIPs) formed as the concentration gradually increased. Minofar et al.11 noted that the tendency to form CIPs in magnesium acetate solution was stronger than that in magnesium nitrate solution. Zhang et al.12 employed Raman spectroscopy and electrodynamic balance to study magnesium nitrate solution and found that CIPs formed when the water salt ratio (WSR) was 6.
Many researchers believe that it is difficult to form CIPs in magnesium nitrate solutions,6,7 while MCIPs/BCIPs are formed in molten hydrated magnesium nitrate;8,12 however, most of the above conclusions are drawn from Raman/infrared spectroscopy, and there is a lack of supporting evidence from other characterization techniques. Moreover, Raman spectroscopy meets the problem of whether it has a particular sensitivity to certain motifs. Other structural probes such as X-ray spectroscopy suffer from how the electronic similarities between water molecules and the atomic species of the counter ions make chemical disambiguation difficult. Although it is difficult to see the presence of ion pairs because the weightings of strongly specific pair correlation terms contribute to the measured structure factors, the sensitivity of X-ray diffraction and neutron diffraction techniques to structural contributions is linear. Moreover, we can use atomistic modelling techniques such as the empirical potential structure refinement method to simulate, subject to known bulk and atomic/molecular scale physical and chemical constraints, the differential scattering cross section F(Q) and the total pair distribution function G(r) to extract the partial pair distribution functions of key importance. Therefore, X-ray diffraction is a good way to study the solution structure of Mg(NO3)2, which can provide information about short-range ordered structures in this system. To date few studies have investigated magnesium nitrate solutions using this method, although X-ray diffraction has been used to study aqueous systems of nitric acid (Ca2+, Cr3+, Cd2+, NH4+, Zn2+, and Al3+) to obtain information about the hydration structure of anions and cations in the solution, as well as structural information of CIPs.13–18
The hydration structure of NO3− has also been investigated. NO3− is a planar polyatomic ion with two hydration modes—planar and non-planar.19,20 Many methods such as neutron diffraction, X-ray diffraction, quantitative calculations, and molecular dynamics simulations have been used to study the hydration structure of NO3−.13–18,20–22 For example, Caminiti et al.15 used X-ray diffraction to study an ammonium nitrate solution and found that each oxygen atom in NO3− interacted with three water molecules to form a tetrahedral structure, so that the hydration number was 9 in the first hydration layer of NO3− with an rN–O(W) of 3.4 Å, while Bowron et al.23 investigated 1 M Cr(NO3)3 solution using neutron diffraction and found that when the radial distance of the first hydration layer rN–O(W) was 5.1, there were almost 12 water molecules within it. Using ab initio calculations, Wang and Salvador20,21 studied the structure of [NO3−(H2O)n] hydrate clusters and found that three water molecules directly interacted with NO3−. They also suggested that indirect hydrated water molecules existed in the first hydration layer. Based on the above, although the hydration number and hydration distance of NO3− have been determined, the details of the hydration structure of NO3− are still unclear in magnesium nitrate solutions.
In the present work, the CIPs and hydration structure of NO3− in magnesium nitrate solution were investigated. X-Ray diffraction was used to obtain scattering data, which was analyzed using empirical potential structure refinement (EPSR) modeling24,25 to obtain the distribution function of atom pairs. Important structural information such as the distance between atoms and the coordination number were also obtained. Moreover, EPSR resolved the structural details of hydrated Mg–O(W) and associated Mg–O(NO3−) to accurately analyze the structure of the magnesium nitrate solution. Based on this, quantitative calculation methods were used to further verify the structural details of ion pairs in the solution. This work is expected to provide a new understanding of the structure of magnesium nitrate aqueous solutions and offer guidance for developing and utilizing magnesium nitrate resources in salt lakes.
2. Experimental and theoretical methods
2.1. X-Ray diffraction experiment and data analysis
Analytical grade magnesium nitrate hexahydrate was purchased from Sigma Aldrich. Weight was used to confirm the compositions of aqueous magnesium nitrate solutions with WSR of 100, 60, 30, and 15, and these compositions are shown in the ESI† (Table S1). A quartz glass capillary with a diameter of 2 mm and a wall thickness of 0.1 mm was used to encapsulate the magnesium nitrate solution. The data were collected at room temperature (21 ± 1 °C) using an X’pert Pro diffractometer (Panalytical) taking Kα radiation from an Rh-filtered Ag-anode (λ = 0.5609 Å) operating at 60 kV. Air background and empty capillary scattering were also measured to correct the diffraction data. After polarization, Bremsstrahlung component of the X-ray beam, absorption, multiple scattering, fluorescence and Compton scattering from the sample, and air background and empty capillary scattering corrections, the reduced data are scaled to oscillate around the self-scattering from the sample and normalized to the single atom scattering F(Q).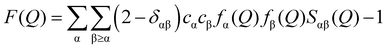 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ; λ is the X-ray wavelength; θ is the half-scattering angle; cα and cβ are the concentration of α and β atoms; fα(Q) and fβ(Q) are the atomic scattering factors; ρ is the density of the sample; δij is the Kronecker function; Sαβ(Q) is the Faber–Ziman partial structure factor, its expression is as follows:
θ/λ; λ is the X-ray wavelength; θ is the half-scattering angle; cα and cβ are the concentration of α and β atoms; fα(Q) and fβ(Q) are the atomic scattering factors; ρ is the density of the sample; δij is the Kronecker function; Sαβ(Q) is the Faber–Ziman partial structure factor, its expression is as follows: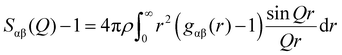 | (2) |
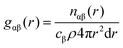 | (3) |
The F(Q) obtained by the experiment is Fourier transformed to obtain the total pair distribution function G(r):
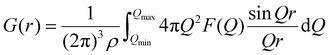 | (4) |
In the following step the X-ray scattering data were analyzed using the EPSR method.24,25 The EPSR program is designed for extracting structural information from neutron or X-ray diffraction data. EPSR first performs a standard Monte Carlo simulation of a system using the intramolecular structure, the bulk atomic density, and a set of Lennard-Jones atomic reference potentials, followed by a model refinement process driven by a comparison between simulated and experimental scattering data. The details of the structural models and simulation box are shown in Tables S2, S3 and Fig. S1 (ESI†). Fig. 1 shows the experimentally-determined and EPSR simulated F(Q) and G(r) values for Mg(NO3)2 solutions. In the intermolecular range of primary structural interest, there is a good agreement between the experimental and the EPSR simulated data (the difference between experimental and simulated F(Q) is shown in Fig. S1d, ESI†), which indicates that the refined structures are close to the real structures. There is a discrepancy at low r. The low r at 0.98 Å is the distance of OH, but X-ray is not sensitive to the light atom such as H. Therefore, this is the main reason for the discrepancy. However, in this work we mainly focus on longer r from 2 to 5 Å, so this discrepancy has little effect on our results. To compare the effect of the ion charge on the polarization effect, a full charge and scaled charges28,29 1.5, 1.7 and 1.9 for Mg2+ ions and −0.75, −0.85 and −0.95 for NO3− ions were used to perform EPSR simulations. It shows that the result from full charge is better than that using scaled charges (Tables S2, S4, S5 and Fig. S2, S3, ESI†). Therefore, we mainly use the EPSR simulation result with full charge for discussion in this work.
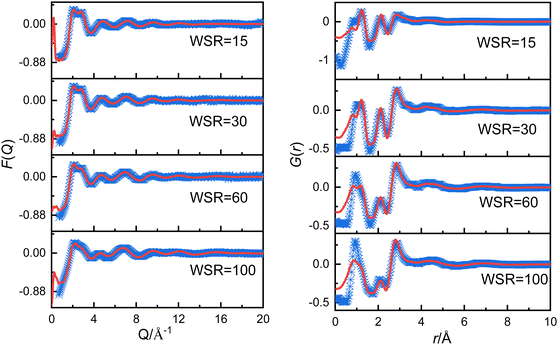 | ||
| Fig. 1 Experimentally obtained (blue points) and EPSR simulated (red solid line) F(Q) (left panel) and G(r) (right panel) for magnesium nitrate solutions. | ||
2.2. Computational modelling of hydrated ion structures
The equilibrium optimized geometry parameters of the [Mg2+m(NO3)−n(H2O)q] clusters were obtained by means of “geometry optimization” type of calculations performed by using the ωB97XD method,30 based on density functional theory (DFT), and the def2-TZVP31,32 basis set. The vibrational harmonic wavenumbers of the investigated clusters were also obtained by means of “frequency calculations” at the ωB97XD/def2-TZVP level of theory and then they were used in examining whether the model used in the calculation corresponds to a local minimum on the potential energy surface of the investigated cluster. The zero-point vibrational energies (ZPE) and basis set superposition error (BSSE) were also used to correct the energy of the hydrated clusters. To assess the uncertainty related to the choice of different functionals, the structures of [Mg2+m(NO3)−n(H2O)q] clusters were also optimized using other methods/basis (M06-2X33/6-311++G(d,p),34 B3LYP35/def2-TZVP) (see the Fig. S4 and Tables S6, S7, ESI†). All of the calculations were carried out using the Gaussion16 package.362.3. Ab initio molecular dynamics (AIMD) simulations
AIMD simulations were performed with the CP2K package.37 We used a hybrid Gaussian and augmented plane waves (GAPW)38 scheme, in which the electronic density is expanded in the form of plane waves with a cutoff of 280 Ry. In addition, Grimme's empirical dispersion corrections are also included.39 The revised Perdew–Burke–Ernzerhof40 was chosen as the exchange and correlation functional. Goedecker–Teter–Hutter pseudopotentials41 were used to treat the core electrons. Double-zeta split valence basis sets were used for all atomic kinds. The motion of nuclei follows Newton's equation of motion and was propagated based on the velocity Verlet algorithm with a time step of 1 fs. At each time step, the wavefunction was optimized based on the orbital transformation method, and the self-consistent field convergence criterion was set to 1.0 × 10−5 a.u. All systems are first equilibrated with the TIP3P water model42 and OPLS-AA force field43 for the ions for periods of at least 1 ns carried out with the Gromacs package.44 The last snapshot of the equilibration phase from empirical simulations was chosen as the initial structure in the AIMD simulations. Generally in each AIMD run, the system was equilibrated in the canonical ensemble (NVT) using a Nosé–Hoover thermostat at 298 K for at least 100 ps. Experimental densities (ρ) were used for Mg(NO3)2 solutions at 298 K (see Table S1, ESI†). The side length of cubic boxes and the number of water molecules and ions are shown in Table S1 (ESI†), which are consistent with the atom number density of EPSR. The calculation parameters of AIMD in this work are close to that of other researchers.45–473. Results and discussion
3.1. Mg2+ hydration structure
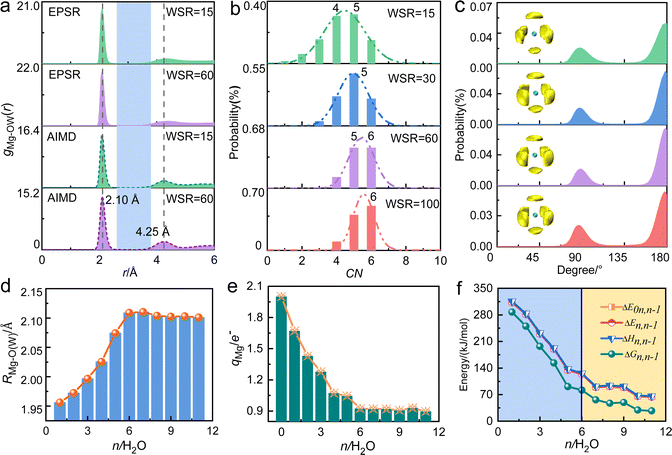
Table 1 and Fig. 2a show that the Mg2+–O(W) hydration distance (rMg–O(W)) remained 2.10 Å and did not change with the concentration. Fig. S2a (ESI†) shows the pair distribution functions of Mg2+–O(W) obtained from EPSR and AIMD are similar, which increases the credibility of the results. This distance equals the value in MgCl2 solution reported by Waluyo et al.48 The hydration number of the first hydration layer gradually decreased from 5.40 ± 0.66 at WSR = 100 to 4.30 ± 1.16 at WSR = 15, indicating that increasing amounts of NO3− enter the first hydration layer of Mg2+ to form a CIP as the solution concentration increased. Fig. 2b shows the coordination number (CN) distributions of the first hydration layer of Mg2+. The CNs of the first hydration layer of Mg2+ were 6 and 5 when WSR = 100. Their distribution probabilities were 50% and 40%, respectively, and the distribution probability of other structures was less than 10%. When WSR = 60, the distribution probabilities of hydration numbers 5 and 6 were about 45%, and the distribution probability of other structures was less than 15%. When WSR = 30, the first hydration layer of Mg2+ was dominated by a coordination number of 5, with a probability of approximately 48%, while the probability of coordination numbers of 4 and 6 was close to 26% respectively. These results suggest that when WSR = 30, structures with hydration numbers of 4, 5, and 6 all existed in the solution, which produced a solution with a complex structure. When the solution concentration was further increased to WSR = 15, Mg2+ existed mainly as tetrahydrate and pentahydrate, which accounted for about 30% each. These results indicate that in agreement with literature studies of dilute solutions, Mg2+ mainly existed in the hexahydrate form in lower concentration solutions but also as tetrahydrate and pentahydrate structures in concentrated solution. Using Monte Carlo simulations, researchers have previously found that rMg–O(W) was 2.12 Å with CN = 6.49 [Mg(H2O)6]2+ existed as an octahedral supramolecular structure because of the strong hydration ability of Mg2+. Waluyo et al.48 also pointed out that Mg2+ formed stable, highly-ordered, high-density hydration shells; therefore, the saturated hydration number of Mg2+ is 6, which decreases to 5 or 4 in concentrated solutions.| Atom pair | WSR | c (mol L−1) | EPSR | AIMD | Atom pair | EPSR | AIMD | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r (I,peak)/Å | CNI | r (I,peak)/Å | CNI | r (I,peak)/Å | CNI | r (I,peak)/Å | CNI | ||||
| MgO(W) | 100 | 0.54 | 2.10 | 5.4 | 2.11 | 6.0 | N–O(W) | 3.59 | 12.4 | 3.47 | 15.7 |
| 60 | 0.89 | 2.10 | 5.3 | 2.09 | 5.5 | 3.58 | 12.8 | 3.47 | 14.9 | ||
| 30 | 1.71 | 2.10 | 4.9 | 2.11 | 4.8 | 3.59 | 12.4 | 3.47 | 14.8 | ||
| 15 | 3.15 | 2.15 | 4.3 | 2.09 | 4.6 | 3.56 | 11.4 | 3.49 | 14.0 | ||
| Mg–O(N) | 100 | 0.54 | 2.10 | 0.6 | — | — | Mg–N | 3.27 | 0.6 | — | — |
| 60 | 0.89 | 2.10 | 0.7 | 2.17 | 0.5 | 3.30 | 0.7 | 3.15 | 0.5 | ||
| 30 | 1.71 | 2.09 | 1.1 | 2.17 | 1.3 | 3.28 | 1.1 | 3.13 | 1.2 | ||
| 15 | 3.15 | 2.07 | 1.7 | 2.17 | 1.4 | 3.21 | 1.7 | 3.15 | 1.4 | ||
From the O(W)–Mg–O(W) angular distribution diagram (Fig. 2c) and spatial density function (SDF) diagram (Fig. 2c and Fig. S5, ESI†), the O(W)–Mg–O(W) angles of Mg2+ in the investigated concentration range were 90° and 180°. This indicates that when there are six water molecules around Mg2+, the first hydration layer of Mg2+ favors the adoption of a stable octahedral hydration configuration, and this geometry is favored even in a highly concentrated nitrate solution. This is consistent with the conclusion that the hydrated Mg2+ forms a six-coordinate supramolecular structure.49,50 As shown in Fig. 2a, there is an obvious gap between the first hydration layer and the second hydration layer of Mg2+. Therefore, it can be inferred that the water molecules on the second hydration layer have little influence on the inner hydration layer, and the first hydration layer of Mg2+ forms a stable six-coordinated octahedral “supramolecular” hydrated structure. The formation of this supramolecular hydration layer makes NO3− mainly exchange with water molecules in the second hydration layer, and hardly enter the inner hydration layer. But there is no obvious gap in gCa–O(W) of calcium nitrate solutions,51 which further confirms the stronger hydration ability of Mg2+.
Density functional theory was then used to study the structures and related energies of [Mg(H2O)n=1–11]2+ to further verify the hydration ability of Mg2+. Within the assumptions and approximations involved in the adopted theory, the structure and associated energy of “isolated” [Mg(H2O)n=1–11]2+ are shown in Fig. S6 and Table S8 (ESI†). As shown in Fig. 2d, rMg–O(W) increased from 1.96 Å at n = 1 to 2.11 Å at n = 6, and then remained constant at a value close to that obtained from X-ray scattering experiments and molecular dynamics simulations.48,49,52,53 From the curve showing the relationship between the charge q of Mg2+ and the hydration number n (Fig. 2e and Table S9, ESI†), the water molecules in the outer hydration layer have little effect on the charge of Mg2+. The successive hydration energy ΔE0n,n−1 was 310 kJ mol−1 when a water molecule hydrated the first hydration layer of Mg2+ (Fig. 2f), which is close to values calculated at the B3LYP/aVDZ level.54 The hydration capacity decreased upon increasing the metal ion radius with the same charge. In addition, the hydration capacity of alkaline earth metal ions is generally stronger than that of monovalent alkali metal ions. The lifetime of water molecules in the first hydration layer of Mg2+ was microseconds, while that of Ca2+, K+, and Na+ was only a few picoseconds.55 Researchers also reported that the free energy of hydration of Mg2+ is greater than that of Ca2+.56 These studies show the strong hydration capacity of Mg2+, which has a six-coordinate octahedral hydration structure.
3.2. NO3− hydration structure
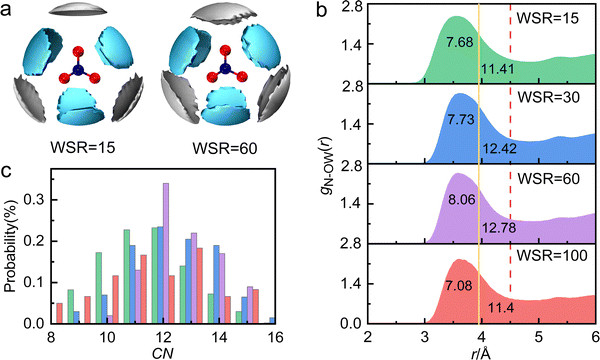
Table 1 shows that the experimental hydration distance of NO3− (rN–O(W)) ranged from 2.7 to 4.6 Å, and the hydration peak was at 3.58 Å, almost 0.1 Å larger than our AIMD result. This error may be caused by different calculation ways of the two methods, but the overall trend of rN–O(W) and coordination number obtained by these two methods is the same. The hydration parameters of NO3− are similar to those obtained from other methods, such as MD simulations57 and neutron diffraction58 experiments. Metal cations also affect the hydration distance and hydration number of NO3−.13,15–18,22,57 For example, due to strong interactions between Cr3+ and water molecules, there is only a weak peak at 3.35 Å in the radial distribution function (RDF) of aqueous Cr(NO3)3 solution.16 Further investigation of the hydration structure of NO3− in 1 M Cr(NO3)3 solution by neutron diffraction, found that the hydration number CNN–O(W) was 12 when the integral radius rN–O(W) was 5.1 Å.23 Due to the broad hydration peak of gN–O(W), there are many hydration forms of water molecules in hydrated NO3− (2.7–4.85 Å); however, we are still unclear about the hydration details.Fig. 3a shows the SDFs of hydrated water molecules in the range of 2.7–4.6 Å around the central NO3− with the fractional isosurface value of 0.15 (the detailed information is shown in Fig. S7 and S8, ESI†). It displays that water molecules tend to hydrate in the planar direction of NO3−, while the probability of hydration at the axial position is relatively small. There are mainly two kinds of hydrated water molecules around NO3−. One is the nearest neighbor (NN) hydrated water molecule represented by the cyan region, with rN–O(W) of 2.7–3.9 Å. In addition, when WSR = 100, the first hydration layer of NO3− ends at 3.95 Å, obtained from AIMD (Fig. S2d, ESI†). The other is the next nearest neighbor (NNN) hydrated water molecule represented by the silver region. Bowron et al.23 investigated chromium nitrate solution by neutron diffraction and found that the rN–O(W) of the first hydration layer was 5.1 Å. This is mainly due to the overlay of the first and second hydration layers of NO3−.
Since the partial pair distribution function gN–O(W)(r) is an asymmetric wide peak, the coordination number calculation of N–O(W) (CNN–O(W)) is difficult. In this work, the CNN–O(W) is discussed in detail by the following methods. (1) As shown in Fig. 3b, taking the maximum N–O(W) interatomic distance in monoclinic Mg(NO3)2·6H2O (rmaxN–OW = 3.952 Å)59 as a cutoff, the N–O(W) coordination number appears to be CNN–O(W) = 6–8. SDF shows that the maximum hydration distance of the first hydration layer is also 3.9 Å (the yellow solid line), which indicates that the number of hydrated water molecules in the NN hydration layer is ∼6. (2) Taking the maximum in calculating SDF at 4.60 Å as a cutoff (Fig. 3b, the red dash line), results in a CNN–O(W) of 11–13. It can be speculated that the hydration number of the NNN hydration layer is about 5–7. A wide distribution of the local N–O(W) coordination numbers, corresponding to a cutoff distance of 4.5 Å and a 〈CNN–O(W)〉 of 12, is shown in Fig. 3c. We note that CNN–O(W) of 12 accounted for the largest proportion, followed by 11- and 13-fold hydration nitrate. Therefore, the coordination number obtained by method 1 is relatively small, because the number of water molecules in the NNN hydration layer is not taken into account. The result obtained by method 2 is consistent with the conclusion obtained in Fig. 3c. The total hydration number of NO3− (CNN–O(W)) in solution is less than 13, which is consistent with the results of neutron scattering experimental result CNN–O(W) = 12.23 Based on the above, previous researchers did not distinguish the NN and NNN hydration layers of NO3−. In the present work, it is demonstrated that the NN hydration distance is less than 3.9 Å with a hydration number of ∼6 and the NNN hydration distance is 4.12 Å with a hydration number of 5–7.
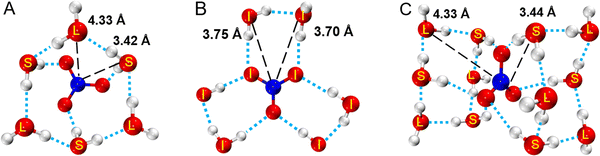
According to the above research, the structural model of hydrated NO3− was constructed and optimized with DFT to obtain three lower energy structures (A, B and C) as shown in Fig. 4, and more detailed information and other structures are shown Fig. S9 (ESI†). In structure A, 3 water molecules (S) directly hydrate on NO3−, where the distance between water molecule, S and NO3−rN–O(W) is 3.42 Å. 3 water molecules (L) indirectly hydrate on NO3−, where the distance between water molecule L and NO3−rN–O(W) is 4.33 Å. The hydration distance of these water molecules is consistent with the hydration regions in SDF. In structure B, all six water molecules hydrate at the plane equatorial position of the nitrate ion, eventually forming a structure that resembles a “three-petaled flower” shape. The hydration distance of rN–O(W) ranges from 3.70 to 3.75 Å. In structure C, 12 water molecules hydrate on both sides parallel to the NO3− plane, presenting a centrosymmetric distribution. These hydration water molecules are also divided into two types, including the inner 6 water molecules S directly hydrate on NO3− with an rN–O(W) of about 3.44 Å, and the rN–O(W) of the outer 6 water molecules L are about 4.33 Å. X-ray diffraction results show that the hydration number of NO3− is about 11–13, which is close to the number of water molecules in structure C. Therefore, structure C can represent a real hydration structure of NO3− in the solution. Fig. 4 also shows that 6 water molecules directly form hydrogen bonds with NO3−, and these water molecules are in the first hydration layer, while the remaining outer 6 water molecules indirectly interact with NO3−, located in the second hydration layer. Salvador and Simeon18,60 also reported that NO3− had two hydration structures, but did not provide specific hydration structures. Triolo et al.61 studied the hydration number of the nitrate ion in lithium nitrate solution and found that 5 water molecules hydrated NO3−, of which three hydrated at the equatorial position, and the other two hydrated at the axial position. Many researchers support that the N–O(W) distance is in the range of 3.45 ± 0.05 Å,11,16,18,62,63 but they did not report hydration distances of 3.7 Å and 4.3 Å. Herein, both kinds of hydration details were studied in this work. According to the hydration distance, the hydration interaction is the strongest at rN–O(W) = 3.4 Å in the first hydration layer, while rN–O(W) = 4.3 Å has a weaker interaction in the second hydration zone. As the solution concentration increases, more water molecules at 4.3 Å are replaced by Mg2+, forming solvent-shared ion pairs (SIPs) or contact ion pairs (CIPs).
3.3. Ion association
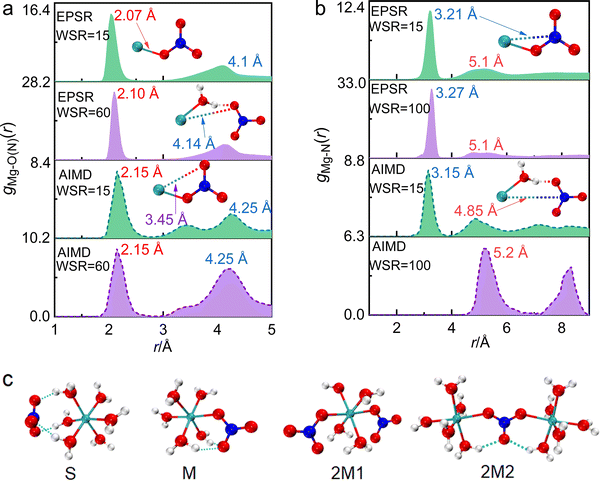
The structure of ion pairs in magnesium nitrate solution was represented by the Mg–O(N) bond between Mg2+ and oxygen atoms in NO3−, and the Mg–N bond between Mg2+ and N atoms in NO3− (Fig. 5a, b and Fig. S2b, e, ESI†). The first RDF peak obtained by EPSR and AIMD simulation overlaps well in the short distance. The first peaks of gMg–O(N)(r) at ∼2.1 Å and gMg–N(r) at ∼3.2 Å denote to the distance between Mg2+ and the nearest O atoms and N atoms from NO3− in CIPs, respectively (Fig. 5a and b). While, there are some differences of gMg–O(N)(r) in medium and long distance obtained by these two methods. The second peak of gMg–O(N)(r) at 3.0–5.0 Å from EPSR is broad without splitting, while there are two split peaks in the same r range from AIMD (Fig. 5a). The peak at ∼3.45 Å denotes the distance between Mg2+ and the second nearest O(NO3−) in CIPs. The other one at ∼4.25 Å denotes the distance between Mg2+ and the nearest O(NO3−) in SIPs. The reason for this discrepancy is that the two simulation methods are based on different principles. AIMD simulation is time consuming. Considering the calculation cost and accuracy of results, the atomic number of AIMD simulation box is ∼1/30 of the EPSR simulation box at the same concentration (Table S1, ESI†). Therefore, the EPSR result represents the statistical average, but AIMD result hardly represents the average value because of the little number of ions. What needs illustration is that when WSR = 100, only one Mg2+ and two NO3− are placed in the AIMD simulation box, which makes it almost impossible to form CIP, so there is no peak at around 2.1 Å.
Table 1 shows that rMg–O(N) = 2.1 Å, which is almost equal to rMg–O(W). The CN increased from 0.6 to 1.6 as the concentration increased, which indicates that CIPs were present in the investigated concentration range. In particular, the ion association phenomenon plays a significant role in highly concentrated solutions where WSR = 15. rMg–N remained at 3.3 Å as the concentration changed (Fig. 5b and Fig. S2e, ESI†), but CNMg–N increased from 0.63 to 1.68 as the concentration increased, which is consistent with the trend (0–1.7) calculated by AIMD (Table 1). If Mg2+ and NO3− existed as a monodentate coordination complex, the coordination number of Mg–O(N) and Mg–N were equal; if they exist in the form of a bidentate coordination complex, the ratio of CNMg–O/CNMg–N is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Table 1 shows that this ratio is 1; therefore, Mg2+ and NO3− existed as a monodentate coordination complex. When WSR = 15, the CN of both Mg–O(N) and Mg–N was 1.68, which does not fit the values of the bidentate/monodentate coordination complexes. This suggests that there are two NO3− ions around each Mg2+ ion, i.e., CIPs gradually transformed into triple ion clusters (TICs) or multiple ion clusters (MICs). Using Raman and infrared spectroscopy, Chang et al.10 reported that NO3− first forms a SIP with Mg2+, and then the SIPs gradually change to MCIPs and BCIPs. Many researchers believe that the CIP formation probability in magnesium nitrate solutions is low, or that CIPs may form when the WSR < 6
1. Table 1 shows that this ratio is 1; therefore, Mg2+ and NO3− existed as a monodentate coordination complex. When WSR = 15, the CN of both Mg–O(N) and Mg–N was 1.68, which does not fit the values of the bidentate/monodentate coordination complexes. This suggests that there are two NO3− ions around each Mg2+ ion, i.e., CIPs gradually transformed into triple ion clusters (TICs) or multiple ion clusters (MICs). Using Raman and infrared spectroscopy, Chang et al.10 reported that NO3− first forms a SIP with Mg2+, and then the SIPs gradually change to MCIPs and BCIPs. Many researchers believe that the CIP formation probability in magnesium nitrate solutions is low, or that CIPs may form when the WSR < 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 This conclusion disagrees with our present study. We also verified the existence of CIPs in Mg(NO3)2 droplets at WSR < 35 using Raman spectroscopy in our previous work.64 The latest research manifests that ions have an effect on the water structure of the hydration sphere, but have little effect on the water structure of bulk water.65 Therefore, when the solution concentration increases, the electrostatic interaction between Mg2+ and NO3− dominates to form direct CIPs because the influence of Mg2+ and NO3− on the water structure of the inner hydration layer decreases. Besides, NO3− is the water structure breaker,66 which also has a strong influence on the form of CIP, especially in concentrated solution.
6 This conclusion disagrees with our present study. We also verified the existence of CIPs in Mg(NO3)2 droplets at WSR < 35 using Raman spectroscopy in our previous work.64 The latest research manifests that ions have an effect on the water structure of the hydration sphere, but have little effect on the water structure of bulk water.65 Therefore, when the solution concentration increases, the electrostatic interaction between Mg2+ and NO3− dominates to form direct CIPs because the influence of Mg2+ and NO3− on the water structure of the inner hydration layer decreases. Besides, NO3− is the water structure breaker,66 which also has a strong influence on the form of CIP, especially in concentrated solution.
DFT was used to further study the structural details of ion pairs in this solution. According to the X-ray diffraction experiment results, ion-pair/cluster models are as follows: one SIP model (S, Fig. 5c) and two solvent-shared ion clusters (2S1 and 2S2, Fig. S4, ESI†) were suggested, and their detailed structure parameters are shown in the ESI† (Tables S6 and S7). When Mg2+ and NO3− formed an MCIP, the rMg–O(N) of 2.05 Å in structure M is very close to the X-ray diffraction value of 2.10 Å, and the calculated value of rMg–N 2.99 Å was 0.3 Å less than the X-ray diffraction experimental value of 3.3 Å. When Mg2+ and NO3− formed a BCIP, rMg–O(N) = 2.03 Å in structure B, which is close to the X-ray scattering value, but the value of rMg–N = 2.43 Å is nearly 1 Å less than the X-ray scattering value; therefore, Mg2+ mainly interacts with NO3− in the monodentate form in the investigated concentration range. The X-ray diffraction results show that a TIC or MIC formed in solution when WSR = 15. In structure 2M2, rMg–N = 3.2 Å, which is only 0.1 Å less than the experimental value, and the rMg–Mg value of 6.4 Å is close to the peak value of 6.0 Å in gMg–Mg (Fig. S2f, ESI†). Note that, the CN of both Mg–O(N) and Mg–N was 1.68, which imply that structures 2M1 or 3M exist in concentrated solution. Therefore, this shows that Mg2+ and NO3− mainly exist in the monodentate form in MIC. Other TIC structures and their structural parameters are shown in Fig. S4 and Tables S6, S7 (ESI†), but these values do not match the experimental ones, so there is a low probability that they exist in solution.
Fig. 6 shows snapshots of the ion pair structures at WSR = 15 and 30 extracted from EPSR simulation boxes and AIMD, respectively. The other snapshots are shown in Fig. S10 (ESI†). Most NO3− ions in dilute solution formed free hydrated ions, and fewer ion-pairs were formed; however, in the concentrated solution, especially when WSR = 15, most Mg2+ and NO3− ions formed triple-ion clusters, and even more complex cyclic and chain-like structures. Fig. 6 also shows that Mg2+ and NO3− exist in the monodentate form in CIPs and MICs. Therefore, it can be seen that SIPs or free hydrated ions mainly exist in dilute magnesium nitrate solutions. NO3− enters the first hydration layer of Mg2+ to form a MCIP [Mg2+(H2O)5NO3−] at higher concentrations. TICs [Mg2+(H2O)4(NO3−)2], MICs and even more complex chain ion clusters [(Mg2+)n(NO3−)m(H2O)6n−m], formed when the solution concentration continued to increase. This trend is consistent with Zhang's research on magnesium nitrate droplets using electrodynamic balance combined with Raman spectroscopy.12 However, Mg2+ and NO3− exist in the form of SIPs in Mg(NO3)2·6H2O crystals, rather than CIPs. This mystery will be further solved in our future work.
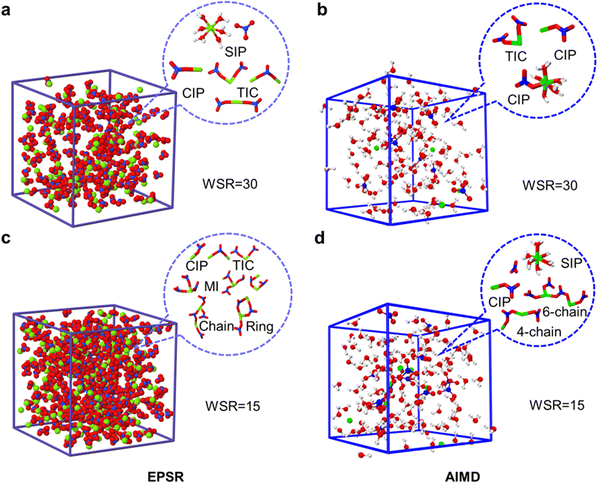 | ||
| Fig. 6 EPSR and AIMD simulation boxes of magnesium nitrate solutions at WSR = 30 (a and b) and WSR = 15 (c and d), and main microscopic species in each box. | ||
4. Conclusions
In this work, the ion hydration and association in aqueous magnesium nitrate solutions were studied and the formation of direct contact ion pairs in solutions was discovered using multitechnique. The results show that the first hydration layer of magnesium ions in dilute solutions existed as hexahydrate octahedra, whose boundary with the second hydration layer was obvious. The nearest neighbor hydration layer of NO3− is shorter than 3.9 Å with ∼6 water molecules in this hydration layer, where the water molecules can be divided into two hydration modes and their hydration distance is 3.4 and 3.7 Å. The next nearest neighbor hydration layer of NO3− ranges from 3.9 to 4.3 Å with a hydration number of ∼6. When WSR > 60 solvent-sharing ion pairs and/or freely-hydrated ions are the main species in the solution. When the solution concentration increases, nitrate ions enter the first hydration layer of magnesium ions and a monodentate contact ion pair [Mg2+(H2O)5NO3−] is formed. As the concentration of the solution further increased, nitrate ions replaced water molecules in the magnesium ion hydration layer to form monodentate triple-ion clusters, as well as more complex chains or linear ion clusters. Our findings provide a basic molecular picture of magnesium nitrate in aqueous solution, and help to understand its related physical, chemical and biological properties in solution.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (U1607106) and the Innovation Platform Construction Project of Key Laboratory of Salt Lake Resource Chemistry of Qinghai Province (2022-ZJ-Y06). We thank the UKRI-STFC (UK Research and Innovation – Science and Technology Facilities Council) for funding support. We also thank Dr Thomas F. Headen from the Disordered Materials Group at the ISIS Neutron and Muon Source for his help at X-ray diffraction experiment.References
- M. G. Cacace, E. M. Landau and J. J. Ramsden, Q. Rev. Biophys., 1997, 30, 241–277 CrossRef CAS PubMed.
- J. Song, T. H. Kang, M. W. Kim and S. Han, Phys. Chem. Chem. Phys., 2015, 17, 8306–8322 RSC.
- A. Braibanti, A. Tiripicchio, M. T. Camellini, A. M. M. Lanfredi and F. Bigoli, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 354–361 CrossRef CAS.
- R. L. Mozzi and W. R. Bekebrede, Acta Crystallogr., 1961, 14, 1296–1297 CrossRef CAS.
- T. G. Chang and D. E. Irish, Can. J. Chem., 1973, 51, 118–125 CrossRef CAS.
- M. Xu, J. P. Larentzos, M. Roshdy, L. J. Criscenti and H. C. Allen, Phys. Chem. Chem. Phys., 2008, 10, 4793–4801 RSC.
- M. Xu, C. Y. Tang, A. M. Jubb, X. Chen and H. C. Allen, J. Phys. Chem. C, 2009, 113, 2082–2087 CrossRef CAS.
- M. Peleg, J. Phys. Chem., 1972, 76, 1019–1025 CrossRef CAS.
- D. E. Irish, T. G. Chang, S. Y. Tang and S. Petrucci, J. Phys. Chem., 1981, 85, 1686–1692 CrossRef CAS.
- T. G. Chang and D. E. Irish, J. Phys. Chem., 1973, 77, 52–57 CrossRef CAS.
- B. Minofar, R. Vácha, A. Wahab, S. Mahiuddin, W. Kunz and P. Jungwirth, J. Phys. Chem. B, 2006, 110, 15939–15944 CrossRef CAS.
- Y. H. Zhang, M. Y. Choi and C. K. Chan, J. Phys. Chem. A, 2004, 108, 1712–1718 CrossRef CAS.
- R. Caminiti and T. Radnai, Z. Naturforsch., 1980, 35, 1368–1372 CrossRef.
- S. P. Dagnall, D. N. Hague and A. D. C. Towl, J. Chem. Soc., Faraday Trans. 2, 1982, 78, 2161–2167 RSC.
- R. Caminiti, G. Licheri, G. Piccaluga and G. Pinna, J. Chem. Phys., 1978, 68, 1967–1970 CrossRef CAS.
- R. Caminiti, P. Cucca and T. Radnai, J. Phys. Chem., 1984, 88, 2382–2386 CrossRef CAS.
- R. Caminiti, G. Licheri, G. Piccaluga and G. Pinna, Chem. Phys., 1977, 19, 371–376 CrossRef CAS.
- P. Smirnov, M. Yamagami, H. Wakita and T. Yamaguchi, J. Mol. Liq., 1997, 73–74, 305–316 CrossRef.
- A. Tongraar, P. Tangkawanwanit and B. M. Rode, J. Phys. Chem. A, 2006, 110, 12918–12926 CrossRef CAS PubMed.
- P. Salvador, J. E. Curtis, D. J. Tobias and P. Jungwirth, Phys. Chem. Chem. Phys., 2003, 5, 3752–3757 RSC.
- X. B. Wang, X. Yang, L. S. Wang and J. B. Nicholas, J. Chem. Phys., 2002, 116, 561–570 CrossRef CAS.
- L. X. Dang, T. M. Chang, M. Roeselova, B. C. Garrett and D. J. Tobias, J. Chem. Phys., 2006, 124, 066101 CrossRef.
- D. T. Bowron and S. DíAz-Moreno, J. Phys. Chem. B, 2009, 113, 11858–11864 CrossRef CAS.
- A. K. Soper, Chem. Phys., 1996, 202, 295–306 CrossRef CAS.
- A. K. Soper, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 104204 CrossRef.
- A. K. Soper and E. R. Barney, J. Appl. Crystallogr., 2011, 44, 714–726 CrossRef CAS.
- A. K. Soper, Rutherford Appleton Laboratory Technical Report.
- M. Kohagen, P. E. Mason and P. Jungwirth, J. Phys. Chem. B, 2014, 118(28), 7902–7909 CrossRef CAS PubMed.
- I. M. Zeron, J. L. F. Abascal and C. Vega, J. Chem. Phys., 2019, 151(13), 134504 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Chem. Phys., 1994, 98, 11623–11627 CrossRef CAS.
- M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, G. Petersson and H. Nakatsuji, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- T. Laino, F. Mohamed, A. Laio and M. Parrinello, J. Chem. Theory Comput., 2006, 2(5), 1370–1378 CrossRef CAS PubMed.
- M. Iannuzzi and J. Hutter, Phys. Chem. Chem. Phys., 2007, 9(13), 1599–1610 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104 CrossRef PubMed.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80(4), 890 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(3), 1703–1710 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105(28), 6474–6487 CrossRef CAS.
- D. V. D. Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26(16), 1701–1718 CrossRef PubMed.
- Y. Ding, A. Hassanali and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(9), 3310–3315 CrossRef CAS.
- Y. Crespo and A. Hassanali, J. Chem. Phys., 2016, 144(7), 074304 CrossRef PubMed.
- J. C. C. Santos, F. R. Negreiros, L. S. Pedroza, G. M. Dalpian and P. B. Miranda, J. Am. Chem. Soc., 2018, 140(49), 17141–17152 CrossRef CAS PubMed.
- I. Waluyo, C. Huang, D. Nordlund, U. Bergmann, T. M. Weiss, L. G. Pettersson and A. Nilsson, J. Chem. Phys., 2011, 134, 064513 CrossRef PubMed.
- M. Bernal-Uruchurtu and I. Ortega-Blake, J. Chem. Phys., 1995, 103, 1588–1598 CrossRef CAS.
- D. T. Richens, The chemistry of aqua ions: synthesis, structure, and reactivity: a tour through the periodic table of the elements, Wiley, New York, 1997 Search PubMed.
- Y. Wang, F. Zhu, T. Yamaguchi, K. Yoshida, G. Wang, R. Liu, L. Song, Y. Zhou and H. Liu, J. Mol. Liq., 2022, 356, 119010 CrossRef CAS.
- C. I. León-Pimentel, J. I. Amaro-Estrada, J. Hernández-Cobos, H. Saint-Martin and A. Ramírez-Solís, J. Chem. Phys., 2018, 148(14), 144307 CrossRef PubMed.
- J. M. Martínez, R. R. Pappalardo and E. S. Marcos, J. Am. Chem. Soc., 1999, 121(13), 3175–3184 CrossRef.
- G. Bai, H. B. Yi, H. J. Li and J. J. Xu, Mol. Phys., 2013, 111, 553–568 CrossRef CAS.
- H. Ohtaki and T. Radnai, Chem. Rev., 1993, 93, 1157–1204 CrossRef CAS.
- B. Jayaram and D. Beveridge, J. Phys. Chem., 1990, 94, 7288–7293 CrossRef CAS.
- J. W. Smith, R. K. Lam, O. Shih, A. M. Rizzuto, D. Prendergast and R. J. Saykally, J. Chem. Phys., 2015, 143, 084503 CrossRef.
- G. W. Neilson and J. E. Enderby, J. Phys. C: Solid State Phys., 1982, 15, 2347 CrossRef CAS.
- J. Schefer and M. Grube, Mater. Res. Bull., 1995, 30, 1235–1241 CrossRef.
- V. Simeon, V. Butorac, V. Tomišić and N. Kallay, Phys. Chem. Chem. Phys., 2003, 5, 2015–2019 RSC.
- R. Triolo, A. H. Narten and G. Johansson, Communication presented at the meeting of the Italian Chemical Society, Sicilian section, Palermo, Italy, 1976.
- X. L. Lei and B. Pan, J. Phys. Chem. A, 2010, 114, 7595–7603 CrossRef CAS PubMed.
- H. S. Frank and M. W. Evans, J. Chem. Phys., 1945, 13, 507–532 CrossRef CAS.
- Y. Wang, L. Song, G. Wang, H. Liu, Z. Jing, Y. Zhou, F. Zhu and Y. Zhang, Spectrochim. Acta, Part A, 2022, 267, 120478 CrossRef CAS.
- C. Zhang, S. Yue, A. Z. Panagiotopoulos, M. L. Klein and X. Wu, Nat. Commun., 2022, 13(1), 822 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 2009, 109(3), 1346–1370 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01828d |
| This journal is © the Owner Societies 2022 |