 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single ion free energy calculation in ASIC1: the importance of the HG loop
Cédric
Vallée
 *abc,
Brendan J.
Howlin
*abc,
Brendan J.
Howlin
 *ab and
Rebecca
Lewis
ac
*ab and
Rebecca
Lewis
ac
aLeverhulme Quantum Biology Doctoral Training Centre, University of Surrey, Guildford GU2 5XH, UK. E-mail: c.vallee@surrey.ac.uk; b.howlin@surrey.ac.uk
bDepartment of Chemistry, Faculty of Engineering and Physical Sciences, University of Surrey, Guildford GU2 7XH, UK
cSchool of Veterinary Medicine, Faculty of Health and Medical Sciences, University of Surrey, Guildford GU2 7AL, UK
First published on 17th May 2022
Abstract
Acid Sensing Ion Channels (ASICs) are one of the most studied channels of the Epithelial Sodium Channel/Degenerin (ENaC/DEG) superfamily. They are responsible for excitatory responses following acidification of the extracellular medium and are involved in several important physiological roles. The ASIC1 subunit can form a functional homotrimeric channel and its structure is currently the most characterised of the whole ENaC/DEG family. Here we computed the free energy profiles for single ion permeation in two different structures of ASIC1 using both Na+ and Cl− as permeating ions. The first structure is the open structure of the channel from the PDB entry 4NTW, and the second structure is the closed structure with the re-entrant loop which contains the highly conserved ‘HG’ motif form PDB entry 6VTK. Both structures show cation selective free energy profiles, however the profiles of the permeating Na+ differ significantly between the two structures. Indeed, whereas there is only a small energetically favorable (−0.5 kcal mol−1) location for Na+ in the open channel (4NTW) near the end of the pore, we observed a clear ion binding site (−7.8 kcal mol−1) located in between the ‘GAS’ belt and the ‘HG’ loop for the channel containing the re-entrant loop (6VTK). Knowing that the ‘GAS’ motif was determined as the selectivity filter, our results support previous observations while addressing the importance of the ‘HG’ motif for the interactions between the pore and the permeating cations.
Acid-Sensing Ion Channels (ASICs) are proton-gated trimeric cation channels mainly permeable to sodium (Na+) and, to a lesser extent, calcium (Ca2+) as well.1 They are members of the amiloride-sensitive ion channels superfamily ENaC/DEG. In mammals, ASICs are encoded by four genes from which at least two of them (ASIC1 and ASIC2) exist as splice variants leading to different isoforms.2,3 They are widely expressed in the nervous system where they play several different roles. They are involved in pain, synaptic plasticity, neurodegenerative diseases, ischemia, and cancer.3–7 The mammalian ASIC1a subunit and its avian ortholog chicken ASIC1 are the most studied of the family. They can be functional as either homotrimers or heterotrimers. The structure of cASIC1 homotrimers has been thoroughly characterized in several different conformations.8–11
For decades, the selectivity filter of the ENaC/DEG superfamily was determined as the ‘G/SxS motif’, where ‘x’ is a non-conserved residue, which constitutes a constriction belt inside the pore of the channel.10,12 However, the last published structure of ASIC1 shows a pre-TM1 re-entrant loop near the ‘GAS’ belt, suggesting new insights regarding the selectivity filter.11 This re-entrant loop constitutes the ‘HG’ motif, conserved in all channels of the ENaC/DEG superfamily. Loss-of-function mutations located at these two residues in the Epithelial Sodium Channel (ENaC) are known to be responsible for pseudohypoaldosteronism type 1 (PHA-I).2 The role of pre-TM1 and TM1 residues in ion selectivity have recently been shown, supporting the structural observations.13
Here, in order to study the impact of the re-entrant ‘HG’ loop on ion permeation, we calculated single ion free energy profiles of two ions, Na+ and chloride (Cl−), using two different ASIC1 structures. The first structure used is the open structure of ASIC1 stabilised with a snake toxin (PDB entry 4NTW, method X-ray diffraction, resolution 2.0710). The second structure used is the closed structure of ASIC1 solubilised by styrene maleic acid with the re-entrant ‘HG’ loop (PDB entry 6VTK, method cryogenic electron microscopy, resolution 2.8211). There are differences between the two structures, yet the main differences seem to be found at the transmembrane region, with a different structure of the gate (open or closed) and the absence or presence of a re-entrant loop containing the conserved ‘HG’ motif. The free energy calculations have been widely used to study ion permeation and ion selectivity in ion channels.14–17 Our results suggest that the ‘HG’ loop is a key element for binding cations and, together with the ‘GAS’ belt, constitute an ion binding site, which most likely represents the actual selectivity filter of the channel.
1 Materials and methods
1.1 Systems construction and comparison
The 3D structures of the channel were obtained from the protein data bank (PDB entries 4NTW and 6VTK).10,11 Both structures were embedded in a heterogeneous lipid bilayer membrane constituted of dipalmitoylphosphatidylcholine (DPPC) lipids and palmitoyloleoylphosphatidylcholine (POPC) lipids in a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 ratio (648 lipid molecules for 4NTW, and 642 lipid molecules for 6VTK) using the CHARMM-GUI Membrane Builder input generator.18–22 Then, systems were solvated in water (156
50 ratio (648 lipid molecules for 4NTW, and 642 lipid molecules for 6VTK) using the CHARMM-GUI Membrane Builder input generator.18–22 Then, systems were solvated in water (156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 304 molecules for 4NTW, and 196
304 molecules for 4NTW, and 196![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 833 molecules for 6VTK) and neutralised with 120 mM NaCl (410 Na+ and 353 Cl− for 4NTW, and 415 Na+ and 364 Cl− for 6VTK). The water model used is the TIP3P model,23 and the force field used is the all atom CHARMM36 force field with specific parameters for tryptophan, tyrosine and phenylalanine (WYF) π–cation interactions available on CHARMM-GUI.24,25 Systems were minimised for 15
833 molecules for 6VTK) and neutralised with 120 mM NaCl (410 Na+ and 353 Cl− for 4NTW, and 415 Na+ and 364 Cl− for 6VTK). The water model used is the TIP3P model,23 and the force field used is the all atom CHARMM36 force field with specific parameters for tryptophan, tyrosine and phenylalanine (WYF) π–cation interactions available on CHARMM-GUI.24,25 Systems were minimised for 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps using the steepest decents algorithm with position restraints of 4000 kJ mol−1 nm−2 for the backbones, 2000 kJ mol−1 nm−2 for the side chains, and 1000 kJ mol−1 nm−2 for lipids and dihedral angle restraints of 1000 kJ mol−1 rad−2 for the lipids' head (C2) and unsaturations (carbon–carbon double bond for POPC). Following the minimisation, systems were equilibrated by 6 equilibration steps for a total of 1.875 ns. Systems were first set in a canonical ensemble (NVT) by using the Berendsen thermostat to keep the system at a constant temperature of 310.15 K with the same restraints as the minimisation. Then, the restraints were slightly released before setting the systems into isothermal–isobaric ensembles (NPT) by using the Berendsen barostat in addition to the Berendsen thermostat to keep the systems at a constant pressure of 1 bar as well. Finally, the restraints were further released until a production run of 1 ns without any restraints with a Nose-Hoover thermostat and a Parrinello-Rahman barostat. The timestep used was 1 fs until the systems were set up in NPT ensembles, then it was increased to 2 fs for all the following molecular dynamics (MD) simulations. All simulations were run using the LINCS algorithm for the covalent hydrogen bonds, the Particle Mesh Ewald (PME) method for the electrostatic interactions, and a cut-off of 1.2 nm for the van der Waals (vdW) radius with a switching radius of 1 nm. Simulations were run using GROMACS (GROningen MAchine for Chemical Simulations) version 2020.3.26
000 steps using the steepest decents algorithm with position restraints of 4000 kJ mol−1 nm−2 for the backbones, 2000 kJ mol−1 nm−2 for the side chains, and 1000 kJ mol−1 nm−2 for lipids and dihedral angle restraints of 1000 kJ mol−1 rad−2 for the lipids' head (C2) and unsaturations (carbon–carbon double bond for POPC). Following the minimisation, systems were equilibrated by 6 equilibration steps for a total of 1.875 ns. Systems were first set in a canonical ensemble (NVT) by using the Berendsen thermostat to keep the system at a constant temperature of 310.15 K with the same restraints as the minimisation. Then, the restraints were slightly released before setting the systems into isothermal–isobaric ensembles (NPT) by using the Berendsen barostat in addition to the Berendsen thermostat to keep the systems at a constant pressure of 1 bar as well. Finally, the restraints were further released until a production run of 1 ns without any restraints with a Nose-Hoover thermostat and a Parrinello-Rahman barostat. The timestep used was 1 fs until the systems were set up in NPT ensembles, then it was increased to 2 fs for all the following molecular dynamics (MD) simulations. All simulations were run using the LINCS algorithm for the covalent hydrogen bonds, the Particle Mesh Ewald (PME) method for the electrostatic interactions, and a cut-off of 1.2 nm for the van der Waals (vdW) radius with a switching radius of 1 nm. Simulations were run using GROMACS (GROningen MAchine for Chemical Simulations) version 2020.3.26
Equilibrated structures were converted from GRO format to PDB format using gmx trjconv command. Original and equilibrated PDB files were used for comparison of the structures. Comparison of the different structures were realised by calculating the root mean squared difference (RMSD) of ‘Aligned’ and ‘Superposed’ structures using MOE 2020.09 (Molecular Operating Environment).27 Overall structures were compared, then extracellular domain, transmembrane domain and ‘GAS’ motif were compared separately to scale the differences for different regions of the channel. The radius of the pores of the different systems was computed using the HOLE program.28 The visualisation of the systems was performed using both MOE and VMD 1.9.4a51 softwares.27,29
1.2 Steered molecular dynamics
From equilibrated systems, the closest ion of interest (Na+ or Cl−) to the pore was moved toward the top of the pore using a position restraint on the ion with a short MD simulation of 2 ps. Then, the ion of interest was pulled through the pore (i.e. in the Z-axis) using a harmonic spring constant of 1000 kJ mol−1 nm−2 at a rate of 0.01 nm ps−1 for 400 ps (pulled by 4 nm). The harmonic spring constant chosen here is almost similar to the force constant used by Lynagh T. et al., (2017)15 of 2.5 kcal mol−1 Å−2. To pull a single Cl− through the closed pore of ASIC1 (6VTK), a harmonic spring constant of 4000 kJ mol−1 nm−2 needed to be used. The center of mass of both transmembrane domains (TM1 and TM2) of the channel for both structures was used as reference for the pulling steered molecular dynamics (SMD) to ensure that the ion was permeating through the pore. The trajectories generated from the SMD provided the reaction coordinates for the free energy calculations of single ion permeation. SMD simulations were run using GROMACS version 2020.3.261.3 Free energy calculations
To compute free energy of single ion permeation, the umbrella sampling (US) method was used.30 Windows were generated using snapshots from the pulling SMD every 10 ps for both ions (Na+ and Cl−) and both structures (4NTW and 6VTK), for a spacing of approximately 1 Å. For the open structure of ASIC1 (4NTW) every single window was used for a total of 40 windows. For the closed structure (6VTK), only windows starting from the bottom of the gate were used for a total of 28 windows. The permeating ion was restrained inside the pore near its Z-axis position using the same force constant used for the pulling SMD. Each window was equilibrated first for 2 ns, then were sampled for 10 ns, for a total of 1632 ns for US simulations. Potential of mean force (PMF) profiles were computed using WHAM with bootstrap analysis for statistical errors.31–33 US simulations and WHAM analyses were run using GROMACS version 2021.3.261.4 Radial distribution function
Analysis of the coordination number of the ion was performed by using the radial distribution function (rdf) calculated by GROMACS version 2021.3.26 The coordination number of the single permeating Na+ was obtained for each window by integrating (1) the radial density function using the ion of interest as reference and either water molecules, oxygen atoms from the carbonyl group of the backbones, oxygen atoms from hydroxyl or carboxyl group of the side chains and specific carbon atoms from the ring of aromatic residues (with specific atom name in the topology) as selected atoms.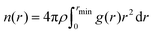 | (1) |
2 Results and discussion
2.1 Comparison of ASIC1 structures
The different structures of ASIC1 have been compared before running umbrella sampling simulations (Fig. 1). First, the RMSD between the original structure and the equilibrated system have been calculated. For 4NTW, the RMSD between the original structure and the equilibrated system is 1.66 Å. For 6VTK, the RMSD between the original structure and the equilibrated system is 1.54 Å, showing that both structures have been well equilibrated and are stable. Secondly, the structure of the PDB entry 4NTW and its equilibrated system have been compared to the structure of the PDB entry 6VTK and its equilibrated system. The RMSD between the overall original structures and between the overall equilibrated structures were 3.39 Å and 2.88 Å respectively. To get a complete comparison of the two structures and understand where the differences are located, RMSD of the different structures have been calculated for the extracellular domain and for the transmembrane domain only. For the extracellular domain only, the RMSD between both original structures and equilibrated structures decreased considerably and were 1.49 Å and 1.96 Å respectively. However, for the transmembrane domain only, the RMSD were 8.05 Å and 5.83 Å respectively. These results support that the main differences between both structures are located at the transmembrane region and thus could impact free energy calculations of ion permeation. In order to further describe where the differences are located within the transmembrane domain, RMSD of the gate only and of the ‘GAS’ motif only have been calculated. For the gate, the RMSD are 4.43 Å and 3.55 Å between the original and equilibrated structures respectively. For the ‘GAS’ motif only, the RMSD are 4.23 Å and 2.85 Å respectively. These results and the superposition of the structures show that the gate, as well as the re-entrant ‘HG’ loop (for which the RMSD could not be calculated as it is lacking in the PDB entry 4NTW), are the main differences contrary to the flexible ‘GAS’ belt (Fig. 1). | ||
| Fig. 1 Comparison of ASIC1 structures. Both ASIC1 structures (PDB entry 4NTW in red and PDB entry 6VTK in blue) are represented by Ribbons. On the left panel, the overall superposition of both equilibrated structures. RMSD between equilibrated 4NTW and equilibrated 6VTK is 2.88 Å. On the inset, the superposition of the equilibrated transmembrane domain with dotted lines showing the location of the gate, the ‘GAS’ motif and the ‘HG’ motif respectively. RMSD between equilibrated transmembrane domain of 4NTW and equilibrated transmembrane domain of 6VTK is 5.83 Å (3.55 Å for the gate only and 2.85 Å for the ‘GAS’ motif only). Structures were rendered using MOE. | ||
2.2 Na+ and Cl− free energy profile in PDB 4NTW
The PMF of single ion permeation has been computed for Na+, the naturally permeating cation, and Cl−, a non-permeating anion. For both energy calculations, the same equilibrated system was used (Fig. 2A). The chosen structure of ASIC1 was the open structure from PDB 4NTW. This structure allows a full permeation of both ions through the open pore without using large forces as the narrowest part of the pore is 2 Å. The pore of the channel did not change after the equilibration process, showing a stable system (Fig. 2B and C). | ||
| Fig. 2 Single ion free energy profile in a open structure of ASIC1 (PDB 4NTW). (A) Simulation box of the system with the channel represented with ‘ribbons’ (α-helices in red, β-sheets in yellow, turns in blue and coils in white), the heterogeneous membrane constituted of DPPC and POPC lipids represented in ‘dynamics bonds’ with ‘glass’ materials for transparency, ions are represented in purple and cyan spheres for Na+ and Cl− respectively, and water molecules represented by red ‘points’. (B) Pore structures of ASIC1 with the two transmembrane domains of each subunit. The scatter plot was generated using the HOLE program. (C) Graph plot of the radius of the pore of ASIC1 generated by the HOLE program. The 0 coordinate in the Z-axis correspond to the Z-coordinate of the ‘GAS’ belt. (D) PMF of the permeation of two different ions (Na+ in purple and Cl− in cyan). The reaction coordinate of the PMF matches to the Z-coordinate of the pore plot. Structures and HOLE scatter plot were rendered using VMD. | ||
The PMF obtained for both ions is quite different (Fig. 2D). First, for Cl−, the free energy of permeation consists of an almost symmetrical barrier of +8.77 kcal mol−1, with a maximum located around the ‘GAS’ belt, thus around the narrowest part of the pore. This result was expected for a cation-selective channel. Secondly, for Na+, the permeation profile in the open structure of ASIC1 has already been computed (Lynagh T., et al.),15 using different parameters (different force field, different temperature, different sampling time and homogeneous lipid membrane). Here, the free energy profile of Na+ in the open channel using the CHARMM36 WYF force field at 310.15 K in a system constituted of a heterogeneous lipid membrane for 10 ns is shown. Despite the differences between the two set ups, the PMF of Na+ obtained here display some similarities with the one from Lynagh T., et al.15 Indeed, both profiles are quite similar as they both possess a succession of three small barriers, where the gate and the ‘GAS’ belt are located, and a well lower down in the pore, where there are negatively charged residues located. Moreover, the overall reaction asymmetry for the permeation of Na+ is −3.3 kcal mol−1, which is quite close to the published profile too.15 Globally, the profiles obtained strongly demonstrate an easier permeation for Na+ compared to Cl−, which supports the experimental observations of ASIC1 as a cation selective channel.
2.3 Na+ and Cl− free energy profile in PDB 6VTK
Secondly, the closed channel with the re-entrant loop (6VTK) has been studied. This structures can only allow an analysis of ion permeation from the bottom of the gate to the end of the pore. There is not enough free space to restrain the ion in place at the gate coordinate without involving large forces, even after solvation and equilibration of the channel (Fig. 2B and C). Indeed, in order to pull a Cl− ion through this close channel, the pulling force needed to be 4 times stronger than the force used for Na+ or for both ions through the open channel (4NTW). With smaller force, the Cl− would rather cross the lipid bilayer than the closed channel itself (data not shown).The most important difference between both structures is the presence of the re-entrant loop containing the highly conserved ‘HG’ motif. This loop is located bellow the ‘GAS’ belt, and thus bellow the gate, which makes it possible to analyse with umbrella sampling. The difference of PMF between Cl− and Na+ for 6VTK (Fig. 3D) is relatively similar to the one for 4NTW (Fig. 2D). For Cl−, the free energy consists of a huge barrier (+16.7 kcal mol−1). This barrier is more important than the open structure (4NTW) and this could be explained by size exclusion around the gate. However, by looking at the coordinates around the ‘HG’ motif (−5 Å), the barrier for Cl− is still high (around +14.2 kcal mol−1) which could imply that the ‘HG’ motif further enhances anions exclusion in this cation-selective channel. Then, for Na+, the PMF shows an energetically favorable permeation of Na+ with a well of −7.77 kcal mol−1 located below the ‘GAS’ motif and near the ‘HG’ motif (around −5 Å). These results suggest that, like for the 4NTW, the 6VTK structure of ASIC1 represents a cation selective structure which can be correlated with experimental observations.
 | ||
| Fig. 3 Single ion free energy profile in ASIC1 with ‘HG’ loop (PDB 6VTK). (A) Simulation box of the system with the channel represented with ‘ribbons’ (α-helices in red, β-sheets in yellow, turns in blue and coils in white), the heterogeneous membrane constituted of DPPC and POPC lipids represented in ‘dynamics bonds’ with ‘glass’ materials for transparency, ions are represented in purple and cyan spheres for Na+ and Cl− respectively, and water molecules represented by red ‘points’. (B) Pore structures of ASIC1 with the two transmembrane domains and the re-entrant loop of each subunit. The scatter plot was generated using the HOLE program. (C) Graph plot of the radius of the pore of ASIC1 generated by the HOLE program. The 0 coordinate in the Z-axis correspond to the Z-coordinate of the center of ‘GAS’ belt. (D) PMF of the permeation of two different ions (Na+ in magenta and Cl− in turquoise). The reaction coordinate of the PMF matches to the Z-coordinate of the pore plot. Structures and HOLE scatter plot were rendered using VMD. | ||
2.4 Comparison of free energy profiles: the ‘HG’ loop is crucial for binding the permeating cation
Now that it has been shown that different structures of ASIC1 are good representations of the channel for cation selectivity over anion, comparison of the PMF regarding Na+, the naturally permeating ion, is described here. First, by looking at the pore size from the bottom of the gate until the end of the pore, some differences can be observed. In fact, even after the gate, the pore of the channel with the re-entrant loop (6VTK) is globally narrower than the pore of the open structure (4NTW) (Fig. 4A). The presence of the re-entrant loop decreases considerably the size of the pore with, for example, a pore radius of about 4 Å in 6VTK compared to about 8 Å in 4NTW at −15 Å in the Z-axis. However, this does not change the minimum radius of the pore below the ‘GAS’ motif for both channels (around 2 Å). These observations are in agreement with previous studies of pore structures (open and closed) containing the re-entrant loop.11,34 Both structures can then be compared from the gate to the end of the pore, which represents the last 28 windows of the umbrella sampling for 4NTW, and every window for 6VTK. | ||
| Fig. 4 Single Na+ free energy profile in two different structures of ASIC1. (A) Graph plot of the radius of the pore of ASIC1 generated by the HOLE program (4NTW in red, 6VTK in blue). The 0 coordinate in the Z-axis correspond to the Z-coordinate of the centre of ‘GAS’ belt. (B) PMF of the permeation of Na+ in the open structure 4NTW (purple) and in the close structure with the re-entrant loop 6VTK (magenta). The reaction coordinate of the PMF matches to the Z-coordinate of the pore plot. (C) Pore structure of a snapshot of the window corresponding to the well of the PMF in 6VTK. The pore is represented with ‘ribbons’ (α-helices in red and coils in white), residues of the ‘GAS’ (glycine, alanine and serine) and ‘HG’ (histidine and glycine) motifs are represented with ‘licorice’ (carbons in cyan, hydrogens in white, oxygens in red and nitrogen in blue), permeating Na+ is represented in purple sphere. Structure was rendered using VMD. | ||
As described before, the PMF for Na+ permeation in 4NTW consists of a succession of small barriers followed by a well at the location of negatively charged residues. Two of the three barriers correspond to the coordinates of residues of the gate, and the last barrier corresponds to the coordinates of the residues of the ‘GAS’ motif. The well describes an energetically favorable position of the ion of −0.54 kcal mol−1. Contrarily, the Na+ permeation after the gate for 6VTK, consists mainly of a wide well located just below the ‘GAS’ motif and just above the ‘HG’ motif coordinates. The well described an energetically favorable position of the ion of −7.77 kcal mol−1, which is about 8 times bigger than the well observed for 4NTW (Fig. 4B). This well describes a potential cation binding site inside the pore of ASIC1 involving both the ‘GAS’ and the ‘HG’ motifs. By looking at the structure corresponding at this reaction coordinate, Na+ seems to be coordinated by the side chain of one of the three histidine of the ‘HG’ motif and by the carbonyl of the backbone of one of the three glycine of the ‘GAS’ motif (Fig. 4C).
To validate if Na+ is indeed coordinated by these atoms, the coordination number of the ion has been calculated for each window (Fig. 5A and B). For both structures, Na+ has a coordination number of 6 throughout its permeation, which is consistent with coordination studies of Na+,35–37 and is mainly coordinated by water. These observations are in agreement with the hypothesis about a hydrated permeation of Na+ through ASIC1.15,38,39 For 4NTW, the ion is mostly coordinated by water and does not really interact with the channel, except from windows 19 until 25 for which the ion is interacting with water molecules and oxygen atoms from carbonyl groups and/or hydroxyl groups of residues of the ‘GAS’ motif (Fig. 5A). Conversely, for 6VTK, Na+ is mainly interacting with water molecules but is also interacting with at least one atom from the channel (Fig. 5B). From windows 5 to 9, Na+ is coordinated with 4 water molecules, 1 oxygen from the carbonyl group of the glycine of the ‘GAS’ belt and 1 aromatic ring from the side chain of the histidine of the ‘HG’ motif. Histidine can coordinate Na+ with its aromatic ring via π–cation interaction, but it can also coordinate the ion via the basic nitrogen of the ring.40,41 The strength of the interaction between histidine and Na+ are dependent on the protonated state of the histidine, which can be interesting to investigate in this case as ASICs are activated by protons. In term of ion transport, while the hydrated ion is approaching the narrowest part of the pore, two water molecules need to be substituted by the oxygen of the carbonyl group of one glycine of the ‘GAS’ belt as well as the ring or the basic nitrogen of one histidine of the ‘HG’ loop. This loss of part of the hydration shell in favour of residues of the pore is energetically favourable for Na+. These results support the structural observation from the snapshot of MD in Fig. 4C, and highlight the importance of the ‘HG’ re-entrant loop for the cation binding site of ASIC1 pore.
 | ||
| Fig. 5 Coordination number of Na+ during umbrella sampling simulation in ASIC1. (A) Coordination number of the permeating Na+ for the last 28 windows in 4NTW. (B) Coordination number of the permeating Na+ in 6VTK. | ||
3 Conclusions
Many different structures corresponding to different configurations of the homotrimeric channel ASIC1 has been determined. Here, the only open structure and the only structure with the conserved ‘HG’ loop (PDB entries 4NTW and 6VTK respectively) has been used to investigate the free energy of single ion permeation. Even if the ‘HG’ containing structure is closed, partial permeation of ion from the gate until the end of the pore can be computed. Both structures show cation selective profiles which is in agreement to experimental observations. However, the PMF profile for Na+ differ significantly between both structures. Indeed, there is no clear interactions between the ion and the protein in the open channel (4NTW), whereas there is an evident ion binding site in the channel with the re-entrant ‘HG’ loop (6VTK). These results suggest, not only that the ‘HG’ motif plays a crucial role for ion permeation, but also that the selectivity filter of ASICs can be redefined as the combination of the ‘GAS’ motif and the ‘HG’ motif.Author contributions
C. V.: Conceptualization, formal analysis, computing resources acquisition, investigation, methodology, validation, visualization, writing – original draft, writing – review & editing. B. J. H.: conceptualization, computing resources acquisition, funding acquisition, project administration, supervision, validation, writing – review & editing. R. L.: funding acquisition, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work used the High Performance Computer cluster EUREKA of the University of Surrey and the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk). This research was funded by Leverhulme Trust, grant number DS-2017-079.References
- R. Waldmann, G. Champigny, F. Bassilana, C. Heurteaux and M. Lazdunski, Nature, 1997, 386, 173–177 CrossRef CAS PubMed.
- S. Kellenberger and L. Schild, Physiol. Rev., 2002, 82, 735–767 CrossRef CAS PubMed.
- E. Deval, X. Gasull, J. Noël, M. Salinas, A. Baron, S. Diochot and E. Lingueglia, Pharmacol. Ther., 2010, 128, 549–558 CrossRef CAS PubMed.
- S. Diochot, A. Baron, M. Salinas, D. Douguet, S. Scarzello, A.-S. Dabert-Gay, D. Debayle, V. Friend, A. Alloui and M. Lazdunski, et al. , Nature, 2012, 490, 552–555 CrossRef CAS PubMed.
- J. A. Wemmie, J. Chen, C. C. Askwith, A. M. Hruska-Hageman, M. P. Price, B. C. Nolan, P. G. Yoder, E. Lamani, T. Hoshi and J. H. Freeman Jr, et al. , Neuron, 2002, 34, 463–477 CrossRef CAS PubMed.
- Z.-G. Xiong, X.-M. Zhu, X.-P. Chu, M. Minami, J. Hey, W.-L. Wei, J. F. MacDonald, J. A. Wemmie, M. P. Price and M. J. Welsh, et al. , Cell, 2004, 118, 687–698 CrossRef CAS PubMed.
- C. Liu, L.-L. Zhu, S.-G. Xu, H.-L. Ji and X.-M. Li, J. Cancer, 2016, 7, 1888–1891 CrossRef CAS PubMed.
- J. Jasti, H. Furukawa, E. B. Gonzales and E. Gouaux, Nature, 2007, 449, 316–323 CrossRef CAS PubMed.
- E. B. Gonzales, T. Kawate and E. Gouaux, Nature, 2009, 460, 599–604 CrossRef CAS PubMed.
- I. Baconguis, C. J. Bohlen, A. Goehring, D. Julius and E. Gouaux, Cell, 2014, 156, 717–729 CrossRef CAS PubMed.
- N. Yoder and E. Gouaux, eLife, 2020, 9, e56527 CrossRef CAS PubMed.
- S. Kellenberger, M. Auberson, I. Gautschi, E. Schneeberger and L. Schild, J. Gen. Physiol., 2001, 118, 679–692 CrossRef CAS PubMed.
- Z. P. Sheikh, M. Wulf, S. Friis, M. Althaus, T. Lynagh and S. A. Pless, J. Gen. Physiol., 2021, 153, e202112899 CrossRef CAS PubMed.
- B. Egwolf and B. Roux, J. Mol. Biol., 2010, 401, 831–842 CrossRef CAS PubMed.
- T. Lynagh, E. Flood, C. Boiteux, M. Wulf, V. V. Komnatnyy, J. M. Colding, T. W. Allen and S. A. Pless, eLife, 2017, 6, e24630 CrossRef PubMed.
- E. Flood, C. Boiteux, B. Lev, I. Vorobyov and T. W. Allen, Chem. Rev., 2019, 119, 7737–7832 CrossRef CAS PubMed.
- P. Musunuru, S. Padhi and U. D. Priyakumar, J. Phys. Chem. B, 2021, 125, 8028–8037 CrossRef CAS PubMed.
- S. Jo, T. Kim and W. Im, PLoS One, 2007, 2, 1–9 CrossRef PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- S. Jo, J. B. Lim, J. B. Klauda and W. Im, Biophys. J., 2009, 97, 50–58 CrossRef CAS PubMed.
- E. L. Wu, X. Cheng, S. Jo, H. Rui, K. C. Song, E. M. Dávila-Contreras, Y. Qi, J. Lee, V. Monje-Galvan, R. M. Venable, J. B. Klauda and W. Im, J. Comput. Chem., 2014, 35, 1997–2004 CrossRef CAS PubMed.
- J. Lee, D. S. Patel, J. StÅhle, S.-J. Park, N. R. Kern, S. Kim, J. Lee, X. Cheng, M. A. Valvano, O. Holst, Y. A. Knirel, Y. Qi, S. Jo, J. B. Klauda, G. Widmalm and W. Im, J. Chem. Theory Comput., 2019, 15, 775–786 CrossRef CAS PubMed.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- J. Huang and A. D. MacKerell Jr, J. Comput. Chem., 2013, 34, 2135–2145 CrossRef CAS PubMed.
- J. Lee, X. Cheng, J. M. Swails, M. S. Yeom, P. K. Eastman, J. A. Lemkul, S. Wei, J. Buckner, J. C. Jeong, Y. Qi, S. Jo, V. S. Pande, D. A. Case, C. L. Brooks, A. D. MacKerell, J. B. Klauda and W. Im, J. Chem. Theory Comput., 2016, 12, 405–413 CrossRef CAS PubMed.
- H. Bekker, H. Berendsen, E. Dijkstra, S. Achterop, R. Vondrumen, D. Vanderspoel, A. Sijbers, H. Keegstra and M. Renardus, PHYSICS COMPUTING’92, 1993, pp. 252–256 Search PubMed.
- Chemical Computing Group ULC, Molecular Operating Environment (MOE), 2020.09, 2021.
- O. S. Smart, J. G. Neduvelil, X. Wang, B. Wallace and M. S. Sansom, J. Mol. Graphics, 1996, 14, 354–360 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942 Search PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- M. Souaille and B. Roux, Comput. Phys. Commun., 2001, 135, 40–57 CrossRef CAS.
- J. S. Hub, B. L. De Groot and D. Van Der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- Z. Chen, S. Lin, T. Xie, J.-M. Lin and C. M. Canessa, J. Gen. Physiol., 2021, 154, 1–19 Search PubMed.
- H. Ohtaki and T. Radnai, Chem. Rev., 1993, 93, 1157–1204 CrossRef CAS.
- H. Ohtaki, Highlights in Solute-Solvent Interactions, 2002, 1–32 Search PubMed.
- A. Grossfield, P. Ren and J. W. Ponder, J. Am. Chem. Soc., 2003, 125, 15671–15682 CrossRef CAS PubMed.
- T. Dudev and C. Lim, Acc. Chem. Res., 2014, 47, 3580–3587 CrossRef CAS PubMed.
- T. Dudev and C. Lim, Sci. Rep., 2015, 5, 1–7 Search PubMed.
- S. Hashemian, Russ. J. Inorg. Chem., 2011, 56, 397–401 CrossRef CAS.
- S.-M. Liao, Q.-S. Du, J.-Z. Meng, Z.-W. Pang and R.-B. Huang, Chem. Cent. J., 2013, 7, 1–12 CrossRef PubMed.
| This journal is © the Owner Societies 2022 |
