Lower degree of dissociation of pyruvic acid at water surfaces than in bulk

Abstract

Understanding the acid/base behavior of environmentally relevant organic acids is of key relevance for accurate climate modelling. Here we investigate the effect of pH on the (de)protonation state of pyruvic acid at the air–water interface and in bulk by using the analytical techniques surface-specific vibrational sum frequency generation and attenuated total reflection spectroscopy. To provide a molecular interpretation of the observed behavior, simulations are carried out using a free energy perturbation approach in combination with electronic structure-based molecular dynamics. In both the experimental and theoretical results we observe that the protonated form of pyruvic acid is preferred at the air–water interface. The increased proton affinity is the result of the specific microsolvation at the interface.

---

Pyruvic acid (CH₃COCOOH, Fig. 1a) is an important intermediate in several metabolic and environmental processes.¹ For instance, in the gas and aqueous phase of an aerosol, pyruvic acid can influence the composition of the atmosphere by contributing to the formation of secondary organic aerosols, which have an effect on the radiation balance in the atmosphere.²

Understanding the behavior of organic acids, like pyruvic acid, at aqueous interfaces is thus very relevant for predicting its influence on atmospheric reactions which are needed for climate modelling. Reaction rates and product distribution of organic matter, i.e. acidic or basic form, in atmospheric aerosols and oceans depend on the pH of the aqueous phase. However, it is not a priori clear if the pH dependence of the molecule in the bulk is the same as at the interface. The degree of dissociation, i.e. (de)protonation, is a key parameter to understand the reactivity and potential catalytic role at different surfaces.^3,4 Due to its atmospheric relevance, the (photo)chemistry of pyruvic acid in solution,^5–12 as well as the adsorption¹³ and chemistry at oxide surfaces¹⁴ has been extensively studied. A recent study, using online electrospray ionization mass spectrometry, reports that gas phase pyruvic acid molecules colliding with a water–air interface transfers a proton at 1.8 pH units lower than in the bulk, referred to by the authors as enhanced acidity at the interface.¹⁵ This is a surprising result as in general the neutral form of an acid/base pair is favored over the conjugated base at the air/water interface.^16–23 The increased proton affinity of carboxylate groups at the water surface compared to bulk has been explained as a consequence of the difference in the local solvation: the carboxylic acids anion can be better solvated in bulk than at the surface.²² Here, we report on a combined experimental and computational effort to estimate and explain the acidity constant of pyruvic acid at the water surface. Sum Frequency Generation spectra at the water–air interface and ATR spectra in bulk of pyruvic acid solutions are recorded as a function of pH and interpreted with the help of ab initio molecular dynamics simulations.

In the last few decades second harmonic generation (SHG)¹⁷ and surface specific vibrational sum frequency²² generation (VSFG) have provided the means to measure the fraction of protonated and deprotonated carboxylic acids groups at interfaces, selectively probing the interface and overcoming the difficulty of an overwhelming signal originating from bulk molecules obtained in classical techniques such as potentiometric titration, voltammetry or electrophoresis.²⁴ From the simulations, the acidity constants are computed using the reversible proton insertion/deletion method^25,26 providing a detailed microscopic understanding of the interface apparent pK_a variations. We find that pyruvic acid has a lower degree of dissociation, i.e. deprotonation, at the interface compared to bulk at a given pH. This can be explained in terms of the local solvation of the protonated and deprotonated forms of pyruvic acid.

In Fig. 1, the ATR (b) and VSFG (c) spectra of 1.4 M aqueous solutions in the carbonyl stretch region at different bulk pH-values are depicted. We use a relatively high concentration of 1.4 M to have enough sensitivity for the surface experiments. The ATR spectra report on the bulk response, as the probing depth is around 1 μm, while the VSFG spectra originate from the interfacial molecules. As the H₂O bending mode gives a response in the same spectral region, the samples were prepared in D₂O. The pH values were determined by rescaling the values obtained with a pH meter (see ESI† for details). As both the bulk and surface spectra are measured in D₂O, the difference in hydrogen bonding strength between hydrogen and deuterium should not influence the results. The ATR spectrum, reflecting the bulk response, is at low pH dominated by a signal at 1729 cm⁻¹ assigned to the carbonyl stretch vibration of the carboxylic acid group (ν_COOD), while at high pH the asymmetric stretch vibration of the deprotonated carboxyl group (ν_AS,COO⁻) at 1614 cm⁻¹ is the most prevailing feature in the spectrum.²² The signal at 1710 cm⁻¹ (ν_CO) originates from the carbonyl group of pyruvic acid. The VSFG spectrum (Fig. 1c), featuring the surface vibrational response, shows the same spectral features at roughly the same frequencies. Both methods, as seen in Fig. 1b and c, clearly illustrate a decrease in the ν_COOD peak with increasing pH, while at the same time the asymmetric ν_AS,COO⁻ peak increases, reflecting the shift in the acid–base equilibrium.

Fig. 1 Spectra of (a) pyruvic acid in the frequency region of the carbonyl and carboxylate anion vibrations (b) ATR and (c) VSFG spectra at different pH values. The dashed lines represent the fits.

To quantify the observed changes of the peak intensities in bulk and at the air–water interface in the ν_AS,COO⁻, ν_COOD and ν_CO vibrational bands, we fit the ATR and VSFG spectra at each measured pH value. The ATR spectra were fitted with five Lorentzian functions in the frequency region from 1500 to 1800 cm⁻¹ with constant central frequencies and widths of each Lorentzian peak (for more information see ESI†). Besides the three bands mentioned above, we included a band at 1589 and 1767 cm⁻¹, i.e. the shoulders at the low and high frequency side in the ATR spectrum, tentatively assigned to dimer formation or other conversion products with increasing pH. The VSFG spectra were fitted with a nonresonant (NR) signal and 3 Lorentzian line shapes for the resonances of ν_AS,COO⁻, ν_CO and ν_COOD at 1620, 1708.5 and 1740.5 cm⁻¹ respectively, with fixed parameters for the NR phase, the frequency and linewidth (see ESI†). The amplitudes normalized to the maximum of the ν_COOD and ν_AS,COO⁻, representing the acid and conjugated base form of pyruvic acid, obtained from the fits of the ATR and VSFG spectrum are depicted in Fig. 2.

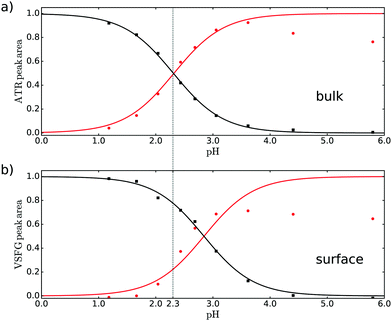Fig. 2 Normalized areas of the bands associated with the ν_AS,COO⁻ (red, circles) and ν_COOD (black, squares) vibrations obtained from fitting (a) ATR and (b) VSFG spectra.

By comparing Fig. 2a and b it can directly be concluded that at the surface the protonated form is more stable compared to the bulk: a higher bulk pH is needed to deprotonate the surface molecules. The quantification of the difference between bulk and apparent surface pK_a is potentially complicated by adsorption/desorption, dimer and oligomer formation, electrostatics, and the presence of counterions in the solution. The intensity of the carbonyl band at 1708 cm⁻¹ provides indirectly information on the surface coverage and thus the effect of adsorption/desorption. As discussed in the ESI,† the deprotonated form of pyruvic acid desorbs partly from the surface at higher pH. Moreover, electrostatic interaction between the deprotonated species could also potentially reduce the surface coverage upon increasing pH. As discussed in the ESI,† the deprotonated base form of pyruvic acid desorbs partly from the surface at higher pH. Also dimer and oligomer formation seems to become a problem at higher pH as reflected in the intensity of the [COO⁻] amplitude. The decrease of the [COO⁻] amplitude in Fig. 2a at high pH potentially originates from dimer formation and/or conversion of pyruvic acid into other forms like zymonic acid,^27,28 apparent from the increase of the shoulder at lower frequency as mentioned above. For the VSFG data the decrease of the [COO⁻] amplitude at high pH is most likely dominated by a lower surface coverage at higher pH. Screening effects from sodium, as NaOD has been used to adjust the pH, or hydronium counter ions are not expected to change the observed results, as the bulk result matches literature values with lower concentration (see below).

A fit through the amplitudes for the acid/base pair with the Henderson–Hasselbalch equation results in a bulk pK_a of 2.3 ± 0.05, very similar to literature.¹⁵ As our result obtained in D₂O for relatively high concentration matches the literature result at low concentration in H₂O, we conclude that both possible dimer formation and the use of D₂O do not significantly influence the result. For the surface case, we only fit the acid curve (black curve in Fig. 2) to determine the apparent pK_a and use this value for the base curve, as the base curve might be less reliable due to the issues mentioned above. The resulting apparent pK_a is 2.9 ± 0.15 for the interface. We thus find that the degree of deprotonation of pyruvic acid at a given pH is lower at the surface than in the bulk.

We compare the experimental results with those obtained from ab initio molecular dynamics simulations to find an explanation of the observed behavior. Molecular dynamics simulations can provide the atomistic picture of the pyruvic acid solution at the water/vapor interface. For the calculations of the pK_a we use the same method which we used for our previous study of pyruvic acid at the quartz/water interface²⁹ (see ESI† for details). To compute the difference in pK_a's for pyruvic acid in bulk water and at the water–air interface, we used a free energy perturbation approach where we start with the protonated pyruvic acid at the surface and deprotonated pyruvic acid in the bulk. We gradually transform the protonated form into the deprotonated one and vice versa. This allows us to estimate the difference in the deprotonation free energy between surface and bulk and therefore the corresponding difference in pK_a.

Using such an approach we found that pyruvic acid has a 4 units larger pK_a at the water/vapor interface than in the bulk, (ΔpK_a = 3.9) which is larger than the experimental difference but still pointing to the same direction.

The microscopic origin of such pK_a difference can be understood if we analyze the local solvation as obtained from the molecular dynamics simulations. In particular, the solvation of the pyruvic acid (both at the air/water and in bulk) can be analyzed using the radial distribution functions, which are reported in Fig. 3. In the protonated form the solvation structure around the OH group is similar for bulk and interface (Fig. 3a). In both cases the OH group donates a relatively strong hydrogen bond, which, however, is slightly shorter at the interface (red line, position of the first peak at 1.55 Å) than in the bulk (black line, position of the first peak at 1.65 Å). On the other hand, the conjugated base is stabilized accepting hydrogen bonds from surrounding water molecules with an average coordination number in the first shell of 3.0 in bulk and of only 2.4 at the interface (Fig. 3b). Here the difference between bulk and interface is larger than for the protonated form. The lower coordination number at the water surface is a consequence of the interrupted H-bond network. The deprotonated form is better stabilized in the bulk, where a higher number of water molecules can crowd in the first solvation shell favoring the deprotonated form over the protonated one, explaining the lower acidity at the water surface.

Fig. 3 Radial distribution functions (rdf) between (a) the hydrogen atom of the protonated pyruvic acid (H_AH) and the oxygen atoms of the water solvent (O_w) (acid in bulk in black, acid at the interface in red), (b) the oxygen atom of the deprotonated pyruvic acid (O_A⁻) and the hydrogen atoms of the water solvent (H_w) (conjugated base in bulk in black, at the interface in red). The dashed lines represent the associated coordination number.

The larger difference in pK_a found in the calculation is possibly due to the simplified model, which does not take into account some complications such as adsorption/desorption processes, dimerization and/or polymerization. Although the simulated concentration is also lower with respect to that of the experiments, we do not believe that this is the reason behind the difference. Indeed, for bulk the pK_a measurements seem to show that the pK_a is insensitive to the concentration, at least in the explored range. On the other hand, the desorption of pyruvate (deprotonated base) from the surface could have an impact. In our simulation timescales we do not observe such a diffusion of pyruvate towards the bulk, however this may still happen on longer times. We do expect that diffusion would reduce the calculated pK_a and bring the calculated value closer to the experimental one. In fact, bulk solvation would favour the deprotonated form of the acid with respect to the protonated one, yielding therefore a lower pK_a. Despite the simplification, the computational model is providing the microscopic/molecular picture which is not straightforward to obtain in the experiments. In particular, the simulation can provide the details of the microsolvation around the acid and estimate its impact on the deprotonation free energies.

This combined experimental and theoretical study thus shows that the degree of deprotonation of pyruvic acid at the water–vapor interface is lower than in the bulk, as the neutral form is preferred at the interface, which is in line with observations for carboxylic acids and primary amines with long alkyl chains,^{16–18,20–22} but seems to contradict the online electrospray ionization mass spectrometry (OESI-MS) study.¹⁵ However, the OESI-MS experiment involves gas phase pyruvic acid molecules colliding with a water interface that has a certain pH value. During the collision a proton from pyruvic acid could be transferred to OH⁻ present in the aqueous medium. With the VSFG method, we consider the pyruvic acid molecules in the bulk and their adsorption/desorption at the interface. This allows an equilibrium to be established between the surface and the bulk of the solution and between the protonated and the deprotonated form depending on the pH. In our opinion the two methods probe thus different things possibly explaining the different results.

The reduced solvation at the interface makes the protonated form more stable than the conjugated base at pH values at which, in bulk, the deprotonated state is already preferred. This observation can have an impact on the conformation and functioning of molecules on the aqueous surface and an influence on the environment and reaction processes in the atmosphere.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Max Planck Institute for Polymer Research for use of the laboratories and Grazia Gonella for fruitful discussions. The calculations were performed on the supercomputer of the High Performance Computing Center (HLRS) of Stuttgart (grant 2DSFG) and on the supercomputer Mogon at the Johannes Gutenberg University Mainz (http://hpc.uni-mainz.de). This project has received funding from the Deutsche Forschungsgemeinschaft under the TRR146 project (project A4). M. S. acknowledges funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germanys Excellence Strategy-EXC 2033-390677874-RESOLV.

References

1. R. S. Andino, et al. , J. Phys. Chem. A, 2020, 124, 3064–3076.
2. A. G. Carlton, B. J. Turpin, H.-J. Lim, K. E. Altieri and S. Seitzinger, Geophys. Res. Lett., 2006, 33, L06822.
3. A. M. Jubb and H. C. Allen, J. Phys. Chem. C, 2012, 116, 13161–13168.
4. J. S. Hub, M. G. Wolf, C. Caleman, P. J. van Maaren, G. Groenhof and D. van der Spoel, Chem. Sci., 2014, 5, 1745–1749.
5. K. L. Plath, K. Takahashi, R. T. Skodje and V. Vaida, J. Phys. Chem. A, 2009, 113, 7294–7303.
6. E. C. Griffith, R. K. Shoemaker and V. Vaida, Orig. Life Evol., 2014, 43, 341–352.
7. A. E. Reed Harris, B. Ervens, R. K. Shoemaker, J. A. Kroll, R. J. Rapf, E. C. Griffith, A. Monod and V. Vaida, J. Phys. Chem. A, 2014, 118, 8505–8516.
8. R. J. Rapf, M. R. Dooley, K. Kappes, R. J. Perkins and V. Vaida, J. Phys. Chem. A, 2017, 121, 8368–8379.
9. A. E. Reed Harris, A. Pajunoja, M. Cazaunau, A. Gratien, E. Pangui, A. Monod, E. C. Griffith, A. Virtanen, J.-F. Doussin and V. Vaida, J. Phys. Chem. A, 2017, 121, 3327–3339.
10. K. J. Kappes, A. M. Deal, M. F. Jespersen, S. L. Blair, J.-F. Doussin, M. Cazaunau, E. Pangui, B. N. Hopper, M. S. Johnson and V. Vaida, J. Phys. Chem. A, 2021, 125, 1036–1049.
11. Y. Pocker, J. E. Meany, B. J. Nist and C. Zadorojny, J. Phys. Chem., 1969, 73, 2879–2882.
12. D. Grosjean, Atmos. Environ., 1983, 17, 2379–2382.
13. Y. Fang, D. Lesnicki, K. J. Wall, M.-P. Gaigeot, M. Sulpizi, V. Vaida and V. H. Grassian, J. Phys. Chem. A, 2019, 123, 983–991.
14. M. R. Alves, Y. Fang, K. J. Wall, V. Vaida and V. H. Grassian, J. Phys. Chem. A, 2019, 123, 7661–7671.
15. A. J. Eugene, E. A. Pillar, A. J. Colussi and M. I. Guzman, Langmuir, 2018, 34, 9307–9313.
16. K. Eisenthal, Chem. Rev., 1996, 96, 1343–1360.
17. X. Zhao, S. Ong, H. Wang and K. B. Eisenthal, Chem. Phys. Lett., 1993, 214, 203–207.
18. P. Miranda, Q. Du and Y. Shen, Chem. Phys. Lett., 1998, 286, 1–8.
19. Y. Rao, M. Subir, E. A. McArthur, N. J. Turro and K. B. Eisenthal, Chem. Phys. Lett., 2009, 477, 241–244.
20. H. Wang, X. Zhao and K. B. Eisenthal, J. Phys. Chem. B, 2000, 104, 8855–8861.
21. C. Y. Tang, Z. Huang and H. C. Allen, J. Phys. Chem. B, 2010, 114, 17068–17076.
22. S. Strazdaite, K. Meister and H. J. Bakker, J. Am. Chem. Soc., 2017, 139, 3716–3720.
23. M. Luo, N. A. Wauer, K. J. Angle, A. C. Dommer, M. Song, C. M. Nowak, R. E. Amaro and V. H. Grassian, Chem. Sci., 2020, 11, 10647–10656.
24. J. Reijenga, A. van Hoof, A. van Loon and B. Teunissen, Anal. Chem. Insights, 2013, 8, ACI.S12304.
25. M. Sulpizi and M. Sprik, Phys. Chem. Chem. Phys., 2008, 10, 5238–5249.
26. M. Sulpizi and M. Sprik, J. Condens. Matter Phys., 2010, 22, 284116.
27. R. J. Perkins, R. K. Shoemaker, B. K. Carpenter and V. Vaida, J. Phys. Chem. A, 2016, 120, 10096–10107.
28. R. J. Perkins, PhD thesis, University of Colorado at Boulder, 2017.
29. S. Parashar, D. Lesnicki and M. Sulpizi, J. Phys. Chem. Lett., 2018, 9, 2186–2189.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental procedures, simulation details and theory on the pK_a calculation using thermodynamics integration. See DOI: https://doi.org/10.1039/d2cp01293f

‡ Present address: Sorbonne Université, CNRS, Physico-Chimie des électrolytes et Nanosystèmes Interfaciaux, F-75005 Paris, France.

§ These authors contributed equally to this work.

---