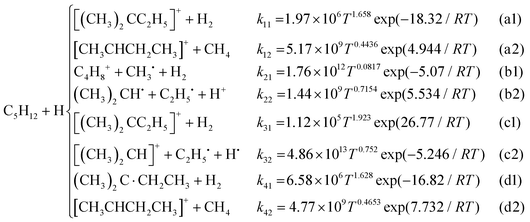Comparison of the hydrogen extraction reactions of isopentane molecules and ions

Abstract

In plasma-assisted combustion, excited species, ions, radicals, and other active intermediates can be produced by the excitation, ionization, and dissociation processes, which are conducive to steady combustion under the conditions of low temperature and pressure. Positive ions are reported to play an important role in electron impact ionization of fuels, but the associated kinetic processes are rarely discussed owing to the lack of experimental data and uncertain reaction pathways in the model. As they are the smallest geometric structures with primary, secondary, and tertiary hydrogen atoms, a study is presented to discuss the hydrogen abstraction potential energy surfaces of isopentane molecules and positive ions by hydrogen radicals at the DLPNO-CCSD(T)/aug-cc-pVTZ//B3LYP-D3(BJ)/6-311G(2df,2p) and DLPNO-CCSD(T)/aug-cc-pVTZ//M06-2x-D3/ma-def2-TZVP levels. The strengths of C–C and C–H bonds were characterized by bond order analyses to predict changes in the active sites of isopentane molecules and positive ions. Molecular orbitals were analyzed to identify simple feature patterns for establishing forming rules, showing consistency with the potential energy surface (PES) analysis. Structure selectivity of different reactions was discussed based on the predicted rate constant calculations in the temperature range of 300–2000 K, and the mechanisms were compared based on the isopentane pyrolysis model constructed with the combination of Reaction Mechanism Generator (RMG) and updated rate constants determined in this work.

---

1. Introduction

Ignition and combustion stability covering a wide range of operating conditions has remained a hotspot issue in modern energy systems. The optimization and improvement of energy-conversion combustion systems still present great challenges, especially under extreme conditions.¹ The application of a plasma-assisted approach seems promising to overcome the limits of region of ultra-lean fuel–air mixtures in high speed flows, low temperatures, low pressure of high-altitude flights^2–5 and so on.

In a plasma-assisted system, high-energy electrons, ions, excited species, and radicals are generated through excitation, ionization, and dissociation processes.⁶ Therefore, it is a key challenge to quantitatively examine the contributions of different species to combustion enhancement at the fundamental response level.⁷ The crucial step is to detect the critical species during the plasma-assisted combustion (PAC) kinetic process. In the air, oxygen-containing species such as O, O₃, and O(¹D) and nitrogen-containing species, including N, NO, and NO₂, as well as excited states, ions, etc. have been identified.^8,9 Mintoussov et al.¹⁰ investigated the influence of a pulsed nanosecond atmospheric pressure barrier discharge based on the OH, CH, and C₂ emission profiles by using emission spectroscopy. Ombrello et al. isolated ozone or trioxygen (O₃) produced by dielectric barrier plasma discharge from C₃H₈/O₂/N₂ laminar lifted flames¹¹ and O₂(a¹Δ_g) produced in a microwave discharge plasma from ethylene (C₂H₄)-lifted flames.¹² Quantitative measurements were performed by using absorption spectroscopy, and the flame propagation speed was determined to be increased by several percentage points. Wang et al.¹³ reported a novel microwave PAC system with emission spectroscopy and pulsed cavity ring-down spectroscopy (CRDS) and hypothesized that OH(X) radicals play a more prominent role in flame stabilization, but OH(A) radicals play a more dominant role in the ignition enhancement. Although the dominant species can be identified in experiment, the role of species produced by a plasma discharge of the fuel has not been discussed in an elementary reaction.

A validated kinetic model is required to understand the PAC reaction at the microscopic level. However, even in homogeneous plasma reactors, current kinetic models are likely to introduce large errors to predict time-dependent primary species histories.¹⁴ Zhang et al.¹⁵ coupled a dielectric barrier discharge flow reactor with a molecular beam mass spectrometer for conducting detailed species diagnostics in a CH₄/O₂/Ar system and detected hydrocarbons ranging between C₂ and C₅. The uncertainty factor for quantification is estimated to be 20% for major species and 50% for intermediates. Sun et al.¹⁶ performed path flux analysis in the non-equilibrium plasma-assisted methane (CH₄) oxidation mechanism and proposed that the fuel was dissociated primarily by H abstraction with OH, O, and H or via collisions with an electron, Ar⁺ and Ar* before further oxidation. They predicted the formation of O and CH₂O reasonably, overestimated the concentrations of CO, H₂O, and H₂, and underestimated the concentration of CO₂. In addition, several studies on PCA have focused on small molecule fuels, such as methane,^17–20 which is the main component in natural gas and has a simple structure both numerically and experimentally. Compared with steady combustion, there has been relatively little discussion of C₂–C₅ fuels and their structure selectivity in PAC. On the other hand, many of the reactions are difficult to study experimentally due to the relative complexity of separating reactions and/or species and the sometimes very slow time scales involved.²¹ Therefore, theoretical calculations would provide the necessary useful tools for predicting reaction pathways and estimating rate parameters.

Herein, as isopentane (i-C₅H₁₂) being the smallest alkane with primary, secondary, and tertiary hydrogen atoms, i-C₅H₁₂ molecules (C₅H₁₂), ions (C₅H₁₂⁺) and their hydrogen extraction reactions by H atoms were evaluated and compared at DLPNO-CCSD(T)/aug-cc-pVTZ//B3LYP-D3(BJ)/6-311G(2df,2p) and DLPNO-CCSD(T)/aug-cc-pVTZ//M06-2x-D3/ma-def2-TZVP levels. Then PESs were discussed at the same level with explanation by wave function analysis. Finally, the structure selectivity of hydrogen extraction reactions by H atoms was discussed depending on the combination of the isopentane pyrolysis model constructed using RMG and calculated rate constants to compare the kinetics and products between PAC and steady combustion.

2. Method

The conformational space of isopentane (i-C₅H₁₂) molecules and ions was studied with the MM+ force field in the HyperChem²² package. The Gaussian 16 program²³ was used to perform ab initio calculations. The equilibrium geometries of the i-C₅H₁₂ local minima were optimized at superfine grids for the dispersion-corrected density functionals^24–26 B3LYP-D3(BJ) with Becke–Johnson damping²⁷ with the triple-ζ basis set 6-311G(2df,2p) and M06-2x-D3 with the minimally augmented polarized triple zeta basis set ma-def2-TZVP.^28,29 This methodology helped to suppress the basis set superposition error (BSSE) to afford a better description for weakly bonded complexes.^30,31 The potential energy surfaces of the i-C₅H₁₂ global minimum were also explored. Vibrational characteristics with hindered internal rotor correction of stationary points (isomers, reactants, and product complexes, and transition states (TSs)) were determined at B3LYP-D3(BJ)/6-311G(2df,2p) and M06-2x-D3/ma-def2-TZVP levels. The single point energies of PESs were refined using the DLPNO-CCSD(T) method (default setting, TightPNO, TightSCF and Grid = 6) with the aug-cc-pVTZ basis sets and ORCA³² software which enabled this to approach the results of the coupled-cluster CCSD(T) method within 1 kJ mol⁻¹.^33,34

The rate constants were calculated based on the transition-state theory (TST) for the abstraction processes in the temperature range of 300–2000 K with the Mesmer program.³⁵ The Eckart,^36,37 Wigner³⁸ and zero-curvature tunneling (ZCT)³⁹ approximations were applied with the Polyrate program.⁴⁰ Wave function analyses were performed using the Multiwfn program.⁴¹ The chemical kinetics mechanisms of i-C₅H₁₂ were constructed through the combination of automated methods Reaction Mechanism Generator (RMG)⁴² and updated rate constants determined in this work for analyses using CHEMKIN-PRO software.⁴³

3. Results and discussion

3.1 Geometric parameters of i-C₅H₁₂ and i-C₅H₁₂⁺

As shown by the geometries and Fischer formula shown in Fig. 1(a) and (b), two local minima with C₁ and C_s symmetry were optimized at B3LYP-D3(BJ)/6-311G(2df,2p) and M06-2x-D3/ma-def2-TZVP levels after relaxed PES scan of the C1–C2–C3–C4 dihedral angles by 360 degrees in steps of 10 degrees at the same level. C₁ symmetry was found to be a global minimum (at both CCSD(T)/cc-pVTZ//M06-2x-D3/ma-def2-TZVP and CCSD(T)/cc-pVTZ//B3LYP-D3(BJ)/6-311G(2df,2p) levels for C₅H₁₂ and C₅H₁₂⁺) because the steric hindrance effect caused by three-branched methyl groups in C_s symmetry led to a larger dipole moment, as marked by yellow arrows in the given figure. Ionization results in a significant contraction in the electron cloud density of C₁, C₄, and C₅, as the lighter color of C₂ and C₃ indicates the loss of an electron of pentane (C₅H₁₂) and C₅H₁₂⁺ determined by the ADCH⁴⁴ population. A compliance matrix⁴⁵ predicted that, when compared with C₅H₁₂, the strength of the C–C ([2]–[3]) bond in C₅H₁₂⁺ decreased distinctly, while the strength of other C–C ([1]–[2], [3]–[4] and [4]–[5]) bonds slightly increased in lower compliance constants. Fig. 1(c) shows that the energies of the highest occupied molecular orbital (E_HOMO) of the C_s symmetry in both C₅H₁₂ and C₅H₁₂⁺ were higher than those of C₁ symmetry, while the energies of the lowest unoccupied molecular orbital (E_LUMO) were lower in C₅H₁₂ and C₅H₁₂⁺. Compared with C₅H₁₂, C₅H₁₂⁺ with larger dipole moments had more discrete but lower energy levels. Populations of two conformations⁴⁶ at B3LYP-D3(BJ)/6-311G(2df,2p) and M06-2X-D3/ma-def2-TZVP Gibbs free energies (ΔG) were calculated using eqn (1) and (2).Fig. 1(d) shows that the population difference between the two conformations of C₅H₁₂⁺ was smaller than that of C₅H₁₂, especially at lower temperatures below 1600 K. Since recent studies in the field of combustion have paid less attention to the effects of conformation, the following discussion only took the global minimum, the C₁ symmetry, into consideration.

Fig. 1 Comparison of two conformers of isopentane molecules and ions. (a1) C₁ conformer of C₅H₁₂; (a2) C_s conformer of C₅H₁; (b1) C₁ conformer of C₅H₁₂⁺; (b2) C_s conformer of C₅H₁₂⁺; (c) molecular orbital diagram of C₅H₁₂ and C₅H₁₂⁺; (d) conformation populations with temperature of C₅H₁₂ and C₅H₁₂⁺.

The strength of bonds was reported to be closely related to the activity and selectivity.⁴⁷ Laplacian bond order (LBO),⁴⁸ fuzzy bond order (FBO),⁴⁹ and Wiberg bond order (WBO),⁵⁰ which revealed a direct correlation with the bond dissociation energy (BDE) of C₅H₁₂ in Fig. 2(b), were listed to characterize C–C and C–H bonds as shown in Fig. 2(a). Both bond order analysis and BDE results showed that the C–C bond sequence of C₅H₁₂ was: secondary–tertiary ([2]–[3]) < branched primary–tertiary ([3]–[4] and [3]–[5]) < primary–secondary ([2]–[3]). The sequence of C–H bond strength in C₅H₁₂ was: secondary ([2]) < tertiary ([3]) < primary ([1]) ≈ branched primary ([4]). The green rectangles in Fig. 2(b) show that the differences between CBS-QB3 and CBS-APNO were within 1 kcal mol⁻¹ and could become larger with lower bond dissociation energies (BDEs). Furthermore, FBO and WBO displayed better differentiation between secondary and tertiary hydrogen atoms than LBO, while CBS-APNO performed better than the CBS-QB3 method. Bonds of C₅H₁₂⁺ were predicted by the bond order analysis using the CBS-APNO method. A significant decline in secondary–tertiary ([2]–[3]) and a slight increase in primary–tertiary ([3]–[4] and [3]–[5]) and primary–secondary ([2]–[3]) could be noticed. Smaller differences could be observed in the C–H bonds of C₅H₁₂⁺ than those of C₅H₁₂; these differences are caused by atomic composition and electron density, as shown in Fig. 1(a). An increase of C and H atom composition in primary ([1]) and secondary ([2]) environments, and a decrease of C and H in tertiary ([3]) and primary ([4] and [5]) environments tended to balance the effect of ionization on carbon atoms, so hydrogen bonds became weaker but more average.

Fig. 2 Bond comparison of C₅H₁₂ and C₅H₁₂⁺C₁ conformers. (a) Composition of carbon and hydrogen atoms to valence electron density. (b) LBO, FBO, WBO, and BDE of the C–C and C–H bonds of C₅H₁₂ showed a direct correlation at CBS-QB3 and CBS-APNO. (c) C–C and C–H bonds of C₅H₁₂⁺ characterized by LBO, FBO, and WBO at CBS-APNO.

3.2 Mechanism of the abstraction reaction by the H atoms of isopentane molecules and ions

In this study, four abstraction reaction paths for the H atoms of C₅H₁₂ and eight C₅H₁₂⁺ were obtained. Fig. 3 shows the transition states (TS) and the corresponding products (PR). Each geometry in the same reaction path was marked with the same double-digit, such as 01_ts. The first digit 0 represents the reactant isomer C₅H₁₂ and 1 represents C₅H₁₂⁺. The second digit corresponds to the reactive sites marked in pink, as shown in Fig. 2(a) (CH₃)₂CHCH₂CH₂ + H₂ (01_PR), (CH₃)₂CHCH˙CH₃ + H₂ (02_PR), CH₃(CH₂˙)CHCH₂CH₃ + H₂ (03_PR) and CH₃(CH₃)C˙CH₂CH₃ + H₂ (04_PR) could be obtained when the H atom reacts with C₅H₁₂. In addition to the product H₂ by a H atom reacting with another H atom at the reactive site of the reactant isomer C₅H₁₂, the reaction paths of C₅H₁₂⁺ showed more abundant products. The abstraction reactions of the H atom in the C₅H₁₂⁺ ion can also be combined with the cleavage of the C–C bond to perform alkyl extraction, so small molecular structures of CH₄, C₂, and C₃ may be found in the products.

Fig. 3 Optimized geometries of transition states and the corresponding products (marked with the same number): (a) C₅H₁₂ and (b) C₅H₁₂⁺.

Fig. 4 shows a pictorial representation of the calculated potential energy surface at the DLPNO-CCSD(T)/aug-cc-pVTZ//B3LYP-D3(BJ)/6-311G(2df,2p) (in parentheses) and DLPNO-CCSD(T)/aug-cc-pVTZ//M06-2X-D3/ma-def2-TZVP levels, for some possible abstraction reactions of C₅H₁₂ and C₅H₁₂⁺ by H atoms. Fig. 4(a) shows reaction paths 01 and 04, abstraction of primary H by a H atom, showing higher strength of the C–H bond. The energy barrier of the C–C bond in Fig. 2 is the highest, about 10 kcal mol⁻¹. Followed by reaction paths 02 and 03, the abstraction of secondary H and tertiary H in C₅H₁₂ is about 7 kcal mol⁻¹ higher than the reactant isomer. So the sequence of reactivity may be: 03 > 02 > 01 > 04. For the products of C₅H₁₂ + H, the sequence of stability was 04 > 03 ≈ 02 > 01.

Fig. 4 Schematic diagrams of the potential energy surfaces refined at the DLPNO-CCSD(T)/aug-cc-pVTZ level and optimized at B3LYP-D3(BJ)/6-311G(2df,2p) (in parentheses) and M06-2X-D3/ma-def2-TZVP levels: (a) C₅H₁₂ and (b) C₅H₁₂⁺.

Because bond strength dropped with the decrease of electron cloud density after ionization, the abstraction reaction paths of C₅H₁₂⁺ + H in Fig. 4(b) could be presented in two ways: the first way was formed by breaking the C–H bond similar to that of C₅H₁₂ + H as shown in Fig. 4(a); the second was formed by C–C bond cleavage. For the first way (abstraction products), although the overall energy barrier is lowered compared to C₅H₁₂ + H, the sequence of reactivity seems to remain as 13 > 12 > 11 > 14. As illustrated in Fig. 2(a), the apparent increase in the activity of 12 and 13 (abstraction products) might be due to the rise of carbon and hydrogen atom composition to valence electron density in secondary and tertiary carbon. For the products of C₅H₁₂⁺ + H (abstraction products), the sequence of stability was 11 > 13 > 14 > 12. The improved product stability of the primary reaction path (11 and 14) may be caused by the trend of the electron density average of the three primary groups (CH₃–). For the second way of C₅H₁₂⁺ + H (cleavage products), the sequence of reactivity was 14 ≈ 11 > 12 > 13, which seems to be opposite in polarity to the first way (abstraction products), depending on the strength of the nearby C–C bonds being abstracted. For the products (cleavage products), the sequence of stability was 14 > 11 > 12 > 13. The cleavage of the primary groups (CH₃) to form CH₄ seemed to possess lower energy barriers and more stable products. Because the cleavage products, H₂ and CH₄, were neutral molecules without charge, the C₄ ions had a unit positive charge. The charged C₂ and C₃ were complex and may be verified experimentally.

The molecular orbital (MO) of TSs could be seen as a mixture of the MO of potential products. The orbital interaction diagram analyses shown in Fig. 5 were used to understand the frontier MOs of TSs in C₅H₁₂ + H and C₅H₁₂⁺ + H reaction paths. Similarly, each geometry was marked with a double-digit, with 0 indicating C₅H₁₂ + H and 1 representing C₅H₁₂⁺ + H. The second digit of C₅H₁₂⁺ + H was used to classify reaction types: 1 represents reaction paths that possessed H₂ as the abstraction product and 2 represents reaction paths to obtain the cleavage products. Fig. 6 shows that, for the reaction path with the abstraction product H₂, the HOMOs of TSs were all mixed with those of two H atom (H atom as the reactant isomer and H atom at the reactive site) fragments and hydrocarbon fragments. The LUMOs of TSs in the C₅H₁₂⁺ + H reaction path were mainly composed of LUMOs of two H atom fragments, while those in the C₅H₁₂ + H reaction path were almost entirely LUMOs of hydrocarbon fragments. This probably makes the C₅H₁₂⁺ + H reaction path much easier to generate H₂. For the C₅H₁₂⁺ + H reaction path with cleavage products, the LUMOs of TSs were mixed by the HOMOs of two H atom fragments and hydrocarbon fragments, which might predict the cleavage of C–C and C–H bonds to form smaller fragments.

Fig. 5 Orbital interaction diagram of TSs (marked in black lines) in C₅H₁₂ + H and C₅H₁₂⁺ + H abstraction reaction paths. The blue lines represent the HOMO and LUMO of the fragments formed by the H atom as the reactant isomer and the H atom at the reactive site. The HOMO and LUMO composited with other atoms in the system are marked with purple lines. The numbers marked beside the lines indicate the contribution (those smaller than 10% are not highlighted) from the fragmental MO to the corresponding TSs.

Fig. 6 The results of the calculated rate constants of C₅H₁₂ + H in this study (full lines in blue and purple) were compared to previous experimental data (-Baktwin et al.⁵¹) and theoretical calculations (-Truong et al.;⁵² ▲-Xin Hong et al.⁷).

3.3 Kinetics of the abstraction reaction by the H atoms of isopentane molecules and ions

For the PESs optimized at B3LYP-D3(BJ)/6-311G(2df,2p) (marked as B3L) and M06-2X-D3/ma-def-TZVP (marked as M06) levels and refined at the DLPNO-CCSD(T)/aug-cc-pVTZ level, the calculated values of rate constants with the tunneling effect corrected by the Eckart (E), Wigner (W) and zero-curvature tunneling (ZCT) methods for the hydrogen abstraction of C₅H₁₂ by the H atom were compared with the literature values.^9–11Fig. 6 shows that the rate constants calculated using the PESs optimized with the M06-2X functional were generally higher than those calculated using the B3LYP functional. Rate constants corrected by the Wigner and the ZCT tunneling revealed a better agreement than those corrected using the Eckart model. The results of M06/E were relatively close to those obtained by Hong et al. at a temperature above 500 K compared to the other methods in this study. Three-parameter Arrhenius expressions for the high-pressure-limit rate constants (cm³ mol⁻¹ s⁻¹) from 500 K to 2000 K at the DLPNO-CCSD(T)/aug-cc-pVTZ//M06-2X-D3/ma-def2-TZVP level were fitted as follows:
The sequence of the calculated rate constants was k₀₃ > k₀₂ > k₀₄ > k₀₁. In other words, the hydrogen abstraction reactivity of different reactive sites was tertiary > secondary > branched primary > primary, which was consistent with the abovementioned results of energy barriers and bond strengths.

The rate constants of C₅H₁₂⁺ + H were calculated at B3L and M06 levels and corrected using the Wigner and ZCT tunneling models, which showed good agreement with each other in the above discussion. The results of two reaction paths (abstraction products labeled 1 in blue lines and cleavage products labeled 2 in purple lines) are presented in Fig. 7. Tunneling appeared to have a smaller effect on primary and branched primary sites than on secondary and tertiary sites, and it deserved more consideration when the M06 method was used below 1000 K.

Fig. 7 The results of the calculated rate constants of C₅H₁₂⁺ + H in this work. Those marked with blue lines stand for reaction paths with abstraction products.

The primary and branched primary sites are more prone to abstraction products than to cleavage products, especially at low temperatures <1000 K, because higher C–C bond strengths make C–C bonds harder to be broken, and lower abstraction energy barriers facilitate abstraction as discussed above. Secondary and tertiary sites with weaker C–C bonds had advantages in formalizing cleavage products. High-pressure-limit rate constants (cm³ mol⁻¹ s⁻¹) at the DLPNO-CCSD(T)/aug-cc-pVTZ level//M06-2X-D3/ma-def2-TZVP level, as the highest accuracy achieved in this study, were fitted to a three-parameter Arrhenius expression over the temperature range from 500 K to 2000 K as follows:

The sequence of the calculated rate constants <1000 K was k₃₁ > k₂₁ > k₂₂ > k₄₂ > k₁₂ > k₄₁ > k₁₁ > k₃₂. The hydrogen abstraction reactivity to generate abstraction products was tertiary > secondary > branched primary > primary, the same as C₅H₁₂; the sequence to generate cleavage products was secondary > branched primary > primary > tertiary.

To further discuss the potential influence of fuel ions on the reaction system, a basic model containing 204 species and 4682 reactions was built using RMG for the steam cracking of C₅H₁₂. Then the 12 calculated reaction rate constants were incorporated into the basic model. The updated model includes 210 species and 4690 reactions. Fig. 8 demonstrates the reaction path for the dissociation of C₅H₁₂ and C₅H₁₂⁺ at different temperatures. The normalized contributions to destruction were determined by rate-of-production (ROP) analysis with CHEMKIN-PRO, marked along with the reaction path arrows in Fig. 8. The final product showed a significant difference at different temperatures. Both C₅H₁₂ and C₅H₁₂⁺ tend to form methane (CH₄) at low temperature (∼1000 K) and H₂ at high temperature (∼2000 K). The result indicates that the C–H bond may dissociate at a higher temperature than the C–C bond, which is in good agreement with the dissociation energy of the C–C and C–H bonds shown in Fig. 2. To compare the reaction path of C₅H₁₂ and C₅H₁₂⁺, the dissociation intermediates differ in the number of carbon atoms. C₅H₁₂ tends to dissociate into large molecules, and C₅H₁₂⁺ dissociates more into small molecules, indicating that ionization improves the bond dissociation and makes the reaction easier.

Fig. 8 Reaction path of (a) C₅H₁₂ at 1000 K; (b) C₅H₁₂⁺ at 1000 K; (c) C₅H₁₂ at 2000 K; and (d) C₅H₁₂⁺ at 2000 K.

Fig. 9 shows the sensitivity of CH₄ and H₂ in the top 15 related reactions. The reaction type means the role of the reaction in the reaction path, including direct reactions, i.e., abstraction, and indirect reactions, such as activation, addition, or isomerization of other reactants involved in abstraction reactions. The same reactants followed by different numbers indicate different activation sites or conformations. The same reaction shows a greater sensitivity of H₂ at 2000 K and a higher sensitivity of CH₄ at 1000 K, which matches the trend of final product formation in the reaction path.

Fig. 9 Sensitivity of (a) CH₄ at 1000 K; (b) H₂ at 1000 K; (c) CH₄ at 2000 K; and (d) H₂ at 2000 K in top 15 most related reactions.

4. Conclusions

In conclusion, the minimum energy paths on the PESs for hydrogen abstraction of i-C₅H₁₂ molecules and positive ions (C₅H₁₂ and C₅H₁₂⁺) were optimized using DFT methods (B3LYP-D3(BJ)/6-311G(2df,2p) and M06-2X-D3/ma-def2-TZVP) and refined at the DLPNO-CCSD(T)/aug-cc-pVTZ level. Bond order analysis showed good agreement with the BDE results of C₅H₁₂ at CBS-QB3 and CBS-APNO levels and revealed that the bond strength sequence did not change after ionization. The C–C bond sequence was secondary–tertiary < branched primary–tertiary < primary–secondary, and the C–H bond strength was secondary < tertiary < primary ≈ branched primary. The sequence of structure selectivity of H abstraction of both C₅H₁₂ + H and C₅H₁₂⁺ + H to generate the abstraction product H₂ was tertiary > secondary > branched primary > primary. For the decline in bond strengths caused by the decrease of electron density after ionization, C₅H₁₂⁺ + H possessed another way of abstraction reaction by cleavage of C–C bonds to generate small molecules such as CH₄, C₂, and C₃ products, which showed activity towards the formation of final products, such as H₂ at high temperature and CH₄ at low temperature. The dominant cleavage products of C₅H₁₂ + H and C₅H₁₂⁺ + H reactions were obtained based on the pyrolysis model constructed using RMG and explained by the different components of their TS molecular orbitals using frontier orbital theory.

Author contributions

Yi Gao: methodology, investigation, writing – original draft. Bin Yang: writing – review & editing. Yang Zhao: investigation, writing – original draft. All authors jointly analyzed and interpreted the data.

Conflicts of interest

The authors declare no conflict of interest.

References

1. Y. Ju and W. Sun, Prog. Energy Combust. Sci., 2015, 48, 21–83.
2. J. A. T. Gray and D. Lacoste, Combust. Flame, 2018, 199, 258–266.
3. Y. Ju, J. K. Lefkowitz, C. B. Reuter, S. H. Won, X. Yang, S. Yang, W. Sun, Z. Jiang and Q. Chen, Plasma Chem. Plasma Process., 2016, 36, 85–105.
4. T. Shiraishi, SAE Int. J. Engines, 2019, 12, 101–113.
5. S. J. Barkley, K. Zhu, J. E. Lynch, J. Michael and T. Sippel, Combust. Flame, 2019, 199, 14–23.
6. C. Gong, L. Yi, K. Wang, K. Huang and F. Liu, Energy, 2020, 192, 116598.
7. X. Hong, H. Sun and C. K. Law, Comput. Theor. Chem., 2011, 963, 357–364.
8. A. Starikovskiy and N. Aleksandrov, Prog. Energy Combust. Sci., 2013, 39, 61–110.
9. Z. H. Wang, L. Yang, B. Li, Z. S. Li, Z. W. Sun, M. Aldén, K. F. Cen and A. A. Konnov, Combust. Flame, 2012, 159, 120–129.
10. E. Mintoussov, S. Pancheshnyi and A. Starikovskii, 42nd AIAA Aerospace Sciences Meeting and Exhibit, 2004 DOI:10.2514/6.2004-1013.
11. T. Ombrello, S. H. Won, Y. Ju and S. Williams, Combust. Flame, 2010, 157, 1906–1915.
12. T. Ombrello, S. H. Won, Y. Ju and S. Williams, Combust. Flame, 2010, 157, 1916–1928.
13. C. Wang and W. Wu, Combust. Flame, 2014, 161, 2073–2084.
14. A. Rousso, S. Yang, J. Lefkowitz, W. Sun and Y. Ju, Proc. Combust. Inst., 2017, 36, 4105–4112.
15. R. Zhang, H. Liao, J. Yang, X. Fan and B. Yang, Proc. Combust. Inst., 2019, 37, 5577–5586.
16. W. Sun, M. Uddi, S. H. Won, T. Ombrello, C. Carter and Y. Ju, Combust. Flame, 2012, 159, 221–229.
17. N. L. Aleksandrov, S. V. Kindysheva, E. N. Kukaev, S. M. Starikovskaya and A. Y. Starikovskii, Plasma Phys. Rep., 2009, 35, 867.
18. W. Wang, R. Snoeckx, X. Zhang, M. S. Cha and A. Bogaerts, J. Phys. Chem. C, 2018, 122, 8704–8723.
19. X. Mao, A. Rousso, Q. Chen and Y. Ju, Proc. Combust. Inst., 2019, 37, 5545–5552.
20. T. Y. Chen, A. C. Rousso, S. Wu, B. M. Goldberg, H. van der Meiden, Y. Ju and E. Kolemen, J. Phys. D: Appl. Phys., 2019, 52, 18LT02.
21. R. Gilbert and S. Smith, Theory of Unimolecular Recombination Reactions, 1990.
22. HyperChem(TM) Professional 7.51, Hypercube, Inc.: 1115 NW 4th Street, Gainesville, Florida 32601, USA, 2011.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Rev. A.03), Wallingford CT, 2016.
24. A. R. Hajipour, M. Karimzadeh Younjali, S. Jalilvand, H. Farrokhpour and A. Chermahini, Comput. Theor. Chem., 2014, 1045, 10.
25. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
26. S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964.
27. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305.
30. E. Papajak and D. Truhlar, J. Chem. Theory Comput., 2010, 7, 10–18.
31. Y. Gao, Y. Zhao, Q. Guan and F. Wang, Chem. Phys. Lett., 2020, 759, 138035.
32. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
33. D. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063.
34. J. Martin, F. Neese, D. Liakos, M. Kesharwani and M. Sparta, J. Chem. Theory Comput., 2015, 11, 1525–1539.
35. D. Glowacki, C.-H. Liang, C. Morley, M. Pilling and S. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
36. C. Eckart, Phys. Rev., 1930, 35, 1303–1309.
37. S. H. Lipoff and D. R. Herschbach, Mol. Phys., 2010, 108, 1133–1143.
38. C. A. Gonzalez, T. C. Allison and F. Louis, J. Phys. Chem. A, 2001, 105, 11034–11040.
39. Y. Wang and J. M. Bowman, J. Chem. Phys., 2008, 129, 121103.
40. R. Steckler, W.-P. Hu, Y.-P. Liu, G. C. Lynch, B. C. Garrett, A. D. Isaacson, V. S. Melissas, D.-h Lu, T. N. Truong, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1995, 88, 341–343.
41. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
42. C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225.
43. S. An and J. C. Jung, Case Stud. Therm. Eng., 2020, 21, 100694.
44. T. Lu and F. Chen, J. Theor. Comput. Chem., 2012, 11, 163–183.
45. G. von Frantzius, R. Streubel, K. Brandhorst and J. Grunenberg, Organometallics, 2006, 25, 118–121.
46. T. Lu and S. Manzetti, Struct. Chem., 2014, 25, 1521–1533.
47. V. Gomonaj and H. Toulhoat, ACS Catal., 2018, 8, 8263–8272.
48. T. Lu and F. Chen, J. Phys. Chem. A, 2013, 117, 3100–3108.
49. I. Mayer and P. Salvador, Chem. Phys. Lett., 2004, 383, 368–375.
50. A. Michalak, R. L. DeKock and T. Ziegler, J. Phys. Chem. A, 2008, 112, 7256–7263.
51. R. R. Baldwin and R. W. Walker, J. Chem. Soc., Faraday Trans. 1, 1979, 75, 140–154.
52. S. Zhang and T. N. Truong, J. Phys. Chem. A, 2003, 107, 1138–1147.

---