A computational study of direct CO₂ hydrogenation to methanol on Pd surfaces

Abstract

The reaction mechanism of direct CO₂ hydrogenation to methanol is investigated in detail on Pd (111), (100) and (110) surfaces using density functional theory (DFT), supporting investigations into emergent Pd-based catalysts. Hydrogen adsorption and surface mobility are firstly considered, with high-coordination surface sites having the largest adsorption energy and being connected by diffusion channels with low energy barriers. Surface chemisorption of CO₂, forming a partially charged CO₂^δ−, is weakly endothermic on a Pd (111) whilst slightly exothermic on Pd (100) and (110), with adsorption enthalpies of 0.09, −0.09 and −0.19 eV, respectively; the low stability of CO₂^δ− on the Pd (111) surface is attributed to negative charge accumulating on the surface Pd atoms that interact directly with the CO₂^δ− adsorbate. Detailed consideration for sequential hydrogenation of the CO₂ shows that HCOOH hydrogenation to H₂COOH would be the rate determining step in the conversion to methanol, for all surfaces, with activation barriers of 1.41, 1.51, and 0.84 eV on Pd (111), (100) and (110) facets, respectively. The Pd (110) surface exhibits overall lower activation energies than the most studied Pd (111) and (100) surfaces, and therefore should be considered in more detail in future Pd catalytic studies.

---

1. Introduction

Methanol synthesis by direct hydrogenation of CO₂ has been recognised as a potential route towards sustainable fuels for transport and a circular fuel economy.¹ The industrial synthesis of methanol involves syngas, which is a mixture of CO/CO₂/H₂ commonly produced from coal gasification. Whilst methanol synthesis from fossil fuels is efficient and profitable, environmental pressures are urging the chemical industry to transfer from a linearoil economy to net zero emissions by 2050.² Bussche et al. built a steady-state kinetic model that revealed CO₂, and not CO, is likely to be the main source of carbon in methanol synthesised from syngas;^2–4 such knowledge encourages consideration of direct CO₂ hydrogenation to methanol, using anthropogenic CO₂ from the atmosphere. However, a better understanding of the interaction of CO₂ with transition metal catalysts is required for the design of novel and effective catalytic systems. Many factors, such as the source of H₂, affect the extent to which the process of direct methanol synthesis from CO₂ can be “green”; however, the idea of using an atmospheric pollutant such as CO₂ for fuel synthesis, and/or also generating feedstock for further synthesis of chemical compounds, such as formic acid, is broadly appealing.⁵

A crucial step in the direct hydrogenation of CO₂ to methanol is the initial CO₂ activation. On a heterogeneous catalyst, the reverse water-gas shift (RWGS) reaction needs to be inhibited while maintaining a strong interaction between CO₂ and the catalytic surface.^5,6 Pd alone exhibits poor selectivity to methanol for direct CO₂ hydrogenation, but the selectivity is greatly enhanced when it is alloyed with other transition metals, such as Zn.^5,7–11 In order to understand fully the Pd-based alloy reactivity, it is necessary first to know the nature of the interactions between CO₂ and Pd. The available experimental data for the interaction of CO₂ with Pd facets are limited, but computation using density functional theory (DFT) is providing insight into the processes.^12–15 Burghaus et al. reported that CO₂ reactivity on clean Pd surfaces is weak, not favouring dissociation to CO unless an alkali metal species is coadsorbed.¹⁵ The weak interaction is considered to be predominantly a van der Waals physisorption, based on the theoretical and experimental observations at the Pd (111) surface.^14,16,17 CO₂ adsorption on Pd has been studied in the context of the RWGS reaction and utilisation of syngas, and desorption of CO₂ from the Pd (111) surface is reported as requiring 0.26 eV of energy.¹⁴ Solymosi et al. reported that CO₂ desorption from the Pd (100) surface also has a relatively low energy of 0.35 eV, which was, in contrast, associated with a chemisorption, involving a metal to empty CO₂ π* orbital electron transfer.¹² Evidence of CO₂ chemisorption on Pd (110) in the presence of water was also reported by Brosseau et al.¹⁸ Therefore, the character of the CO₂ interaction with Pd surfaces seems to depend on the surface structure. The differing adsorption energies can be correlated with surface energies, given physisorption was exclusively observed on the lowest energy (111) surface, and experimental evidence of chemisorption was observed for CO₂ on the higher energy Pd (100) and (110) surfaces, though the latter is noted as being in the presence of water.^12–14,18

Complementary to these observations, the rate of catalytic hydrogenation of CO₂ on Pd increases greatly when the active species is paired with suitable metal oxide supports, such as TiO₂ and ZnO, as they facilitate CO₂ adsorption and activation.^9,19,20 Ko et al. computed the adsorption of CO₂ on transition metal surfaces, using the dispersion-corrected PBE-D2 density functional, and reported two types of CO₂ adsorption on Pd (111): an exothermic physisorption (−0.33 eV) of undistorted CO₂, parallel to the surface; and a less exothermic chemisorption (−0.18 eV) with CO₂ in a bent geometry, and having a partial negative charge.²¹ In contrast, Zhang et al. recently calculated the CO₂ chemisorption on Pd (111) to be endothermic (0.06 eV) using the PBE density functional, in agreement with Habas et al., who reported the adsorption energy of CO₂ to be 0.22 eV above the dissociation limit, using DFT with the B3LYP density functional.²² Liu et al. have also shown that, when using the PBE density functional, the inclusion of the DFT-D2 correction dramatically changes the adsorption energy of chemisorbed species on the Pd (111) surface, from 0.30 eV to −0.18 eV.¹⁷ Although there is no consensus on the matter of the endo- or exothermicity of CO₂ chemisorption on Pd surfaces, the reported values are generally small, which agrees with the experimental reports of a weak interaction between CO₂ and Pd surfaces.

Direct CO₂ hydrogenation to methanol is proposed to proceed via a surface formate intermediate (HCOO*, where * indicates an adsorbed species), with Medford et al. having shown that HCOO* could act as a poison for other reaction pathways due to its high thermodynamic stability on the catalyst surface.²³ Variations of the mechanism proposed by Grabow, which progresses via formic acid (HCOOH) as shown in Fig. 1, have been presented, such as an initial Eley–Rideal type mechanism on Cu-based catalytic systems, where CO₂ in the gas phase reacts with surface-bound hydrogen to yield formate.²⁴ Recently, Huš et al. concluded that dioxymethylene (H₂COO*) should be preferably considered over formic acid (HCOOH*) on Cu-based catalysts as the former is more strongly bound to the metallic surface and the activation energy towards hydroxymethoxy (H₂COOH*) is lower.²⁵

Fig. 1 Formate pathway of direct CO₂ hydrogenation to methanol on metallic surfaces, as proposed by Grabow et al. (via HCOOH*, blue) and Huš et al. (via H₂COO*, orange). * indicates a surface-bound species and δ-indicates that CO₂ is partially charged (i.e. activated).^25,26

Pd-based catalysts supported on ZnO are potent alternative catalysts for this reaction, with their reactivity attributed to the Pd-Zn binary metallic phases and their stabilisation of the HCOO* intermediate, similar to the Cu-based catalyst.^9,20 Zhang et al. have reported DFT studies of an alternative CO₂ formate mechanism that involves dissociation of HCOOH to HCO and OH, and subsequent hydrogenations of HCO to produce CH₃OH.²⁷ Furthermore, Brix et al. have recently considered the initial CO₂ hydrogenation on Pd (111) to proceed via carboxylic acid (COOH), instead of formate, in a DFT study using the dispersion-corrected PBE-D3 density functional, and they observed a high energy barrier of 2.23 eV for CO₂ hydrogenation to formate on Pd (111), in contrast to the barrier of 0.85 eV reported by Zhang et al.^23,24

Whilst binary metallic alloy catalysts may offer more desirable selectivity, stability, and tunability than their monometallic counterparts, the lack of basic understanding of the behaviour of monometallic materials hinders the design of emergent multi-component materials. To achieve the required insight in the context of CO₂ hydrogenation over Pd, we need to understand reactivity across all the prominent surface facets. Thus, we present here an in-depth investigation of CO₂ interaction with low energy Pd (111), (110) and (100) surfaces using DFT calculations, followed by investigation of the direct CO₂ hydrogenation to CH₃OH, via the Grabow mechanism, on the Pd (111), (110) and (100) surfaces, in the context of rationalising CO₂ reactivity on Pd-based catalysts.

2. Methodology

The Fritz Haber Institute ab initio molecular simulations (FHI-aims) software package has been used for full potential all-electron DFT calculations, with the Pythonic Atomic Simulation Environment (ASE) used for management of calculation geometries.^28,29 The default convergence criteria within FHI-aims for self-consistent field (SCF) calculations were used, i.e. the changes between the current and previous SCF iterations in charge density, sum of eigenvalues, and total energy were below N × 1.67 × 10⁻⁵ e a₀⁻³, 10⁻³ eV, and 10⁻⁶ eV, respectively, where N is the number of atoms in the model. Scalar relativistic treatment of kinetic energy for all elements was achieved by the atomic zero-order regular approximation (ZORA), and a Gaussian-type broadening with width of 0.01 eV was applied to the occupation of electronic states. The Perdew–Burke–Ernzerhof exchange correlation (XC) density functional has been used unless explicitly stated otherwise, paired with the Tkatchenko-Scheffler van der Waals dispersion correction (PBE + vdW). A default “light” basis set (version: 2010) has been used for geometry optimisations, providing structural accuracy;^28,30,31 energy calculations were then performed with a “tight” basis set (version: 2010) on the optimised geometries, providing greater electronic accuracy and mitigation of basis set superposition error.²⁸ For geometry optimisations, convergence was deemed complete when forces on all unconstrained atoms were less than 0.01 eV Å⁻¹.

Due to the closed-shell electronic configuration of Pd ([Kr] 4d¹⁰), spin-paired calculations were used in periodic calculations; gas-phase adsorbate structures were calculated both spin-paired and spin-unpaired, and the energy of the more stable configuration considered for reference in subsequent periodic calculations. The effect of the spin-paired approximation has been assessed towards the activation energies in relevant surface hydrogenation reactions in Section S3 of the ESI,† with a spin-paired treatment shown to introduce small error bars of ±0.05 eV.

2.1 Bulk models

For sampling the Brillouin zone of face-centred cubic (FCC) Pd in a primitive unit cell, a (9 × 9 × 9) Monkhorst–Pack k-grid provides converged accuracy, as detailed in Section S1 of the ESI.†³² The lattice constant (a₀ = 3.91 Å), bulk modulus (B₀ = 183.37 GPa), and cohesive energy (E_coh = 4.00 eV) calculated for bulk FCC Pd match closely with the experimental observations of 3.88 Å, 180.40 GPa, and 3.89 eV, respectively.^33,34

2.2 Surface models

Using the optimised model of bulk FCC Pd, a surface supercell was created with dimensions of (3 × 3 × n), where n is the number of atomic layers in the z-direction perpendicular to the material surface. The x- and y-dimensions were chosen such that the adsorbates are significantly separated (7.5 Å), and a vacuum layer of 40 Å was added in the z-direction. The k-grid sampling was reduced appropriately for altered cell dimensions, with a k-grid of (3 × 3 × 1) applied. Due to the one-sided nature of the slab models considered, a dipole-correction was used in all calculations.

The energy penalty for breaking chemical bonds at the surface of a material (E_cleave) is calculated as:

where the DFT total energy of an unrelaxed surface slab model (E^Unrelaxed_Slab), the bulk energy per atom (E_bulk), the number of atoms in the model (N), and the surface area (A), are needed. E_cleave converges for the Pd (111), (100) and (110) facets when E_cleave ceases to fluctuate as a function of slab thickness, as can be seen for n ≥ 5 in Fig. 2; thus, 5 layer models are used for all subsequent calculations.

Fig. 2 E _cleave calculated for Pd FCC (111), (110) and (100) surfaces as a function of increasing model thickness, n. A key is provided to identify the symbols and linear fits; the average cleave energy (solid horizontal line) was taken from n ≥ 5, to avoid bias from inaccurate thin slabs (dashed lines).

To calculate the surface energy (E_surf), the energy of stabilisation provided by geometry relaxation (E_relax) needs to be obtained from the difference in total DFT energy of the optimised slab (E^Relaxed_Slab) and E^Unrelaxed_Slab:

where a single-sided model of the surface is considered, hence the denominator is A only. Constraints were used to maintain the bulk structure for Pd atoms distant from the adsorption site, i.e. the bottom layers of the slab model. E^Relaxed_Slab was calculated for all three surface facets with one, two or three layers of surface atoms unconstrained, with E_relax converging only when the top three surface layers are unconstrained.

In summary, accurate results have been achieved herein with a 3 × 3 × 5 supercell surface model, with the bottom two layers constrained to their bulk positions and the three top surface layers unconstrained. The surface energies (E_surf) can subsequently be calculated as follows:

E_surf = E_cleave + E_relax. (3)

with these settings, and are presented in Table 1. The calculated Pd (111), (100) and (110) E_surf match previous computation and experiments, thus supporting the validity of our approach.

Table 1 Pd FCC (111), (100) and (110) surface energies calculated using the outlined settings. Literature and experiment are provided for comparison

Ref.	XC	E surf/(J m^−2)
		Pd (111)	Pd (100)	Pd (110)
This work	PBE + vdW	1.72	1.91	1.99
Methfessel et al.^35	LDA	1.64	1.86	1.97
Vitos et al.^36	GGA	1.92	2.33	2.23
Patra et al.^37	LDA	1.88	2.43	2.25
	PBE	1.36	1.79	1.61
	PBEsol	1.63	2.15	1.93
	SCAN	1.54	2.03	1.83
	SCAN + rVV10	1.77	2.29	2.05
Singh-Miller et al.^38	PBE	1.31	1.49	1.55
Da Silva et al.^39	LDA	1.87	—	—
	PBE	1.33	—	—
Skriver et al.^40	LDA	1.88	—	—
Tyson et al.^41	Experiment	2.00	—	—
Boer et al.^42	Experiment	2.01	—	—

---

2.3 Surface adsorption

For catalytic surface reactions, the adsorption energy (E_ads) measures the interaction between a surface and reactant, and is deduced from comparison of the energies of the optimised gas-phase adsorbate (E_A), optimised surface (E_S) and the combined system (E_A–S).

E_ads = E_A–S − (E_A + E_S). (4)

where a negative value indicates favourable adsorption. Due to basis set incompleteness when using an atom centred basis, a Boys-Bernardi counterpoise correction is necessary for surface-adsorbate interactions to account for the basis set superposition error (BSSE).⁴³ In our work, the BSSE for CO₂ adsorbed on Pd (111) was assessed on an aperiodic model with all Pd atoms within 7.0 Å of the adsorbed CO₂ molecule included (i.e. all atoms within the distance of the atom-centred basis cut-off, including those in neighbour cells). The energy of the CO₂ in the presence and absence of Pd basis functions (E_A(A–S) and E_A(A), respectively) were compared, and the equivalent comparison of the energy of the slab model in the presence and absence of the basis functions of the CO₂ adsorbate (E_S(A–S) and E_S(S), respectively) was also performed.⁴³ The BSSE energy (E_BSSE) was then calculated as:⁴³

E_BSSE = [E_A(A–S) − E_A(A)] + [E_S(A–S) − E_S(S)]. (5)

A more negative E_BSSE indicates a greater overbinding error; however, by subtracting E_BSSE from E_ads, the counterpoise corrected adsorption energy can be established (E^CP_ads) as:

E^CP_ads = E_ads − E_BSSE. (6)

With the “light” basis set, E_BSSE is −0.08 eV for CO₂ on Pd (111), but E_BSSE was reduced to −0.02 eV with the “tight” basis set. Considering the low BSSE with the “tight” basis, which is used subsequently throughout this work, the E_BSSE contribution to E_ads was deemed negligible and was not subsequently calculated for species other than CO₂.

2.4 Transition state structures

For kinetic studies, we have used a machine learning nudged elastic band (MLNEB) method to identify saddle points and minimum energy paths (MEPs).^44,45 A spring constant of 0.05 eV Å⁻¹ has been used throughout; the convergence criterion of forces on all unconstrained atoms of below 0.05 eV Å⁻¹, with energy uncertainty below 0.03 eV, was deemed sufficiently accurate for CO₂ adsorption. Comparison with a more stringent force criterion of 0.01 eV Å⁻¹ altered the activation energy for CO₂ adsorption on FCC (111) surface by 5 meV only (Section S2, ESI†).

2.5 Vibrations and Thermodynamics

Vibration frequency calculations have been performed for structures in the reaction pathway using the ASE Vibrations module and the Frederiksen method.⁴⁶ To reduce the computational cost, the number of vibrating Pd atoms in the structures was tested as a function of distance from the adsorbate, from the nearest Pd neighbours outwards. The vibrational energy converged at first Pd neighbours of the adsorbate, and this approximation has been applied throughout. The vibration frequencies were also calculated for transition state structures, and the saddle points were confirmed by the presence of an imaginary frequency vibration. Due to the use of a finite difference approach, occasional additional imaginary frequencies did occur due to numerical noise, but were always below 10i meV and thus did not impact on the results. Free energies of gas components were calculated using an ideal gas-phase approximation, whereas the energies of periodic surface structures with adsorbates were calculated using a harmonic approximation. Once the zero-point energy (ZPE) was established, the contribution of ZPE was added to E_ads yielding enthalpy of adsorption, H_ads.

3. Results and discussions

3.1 Hydrogen adsorption

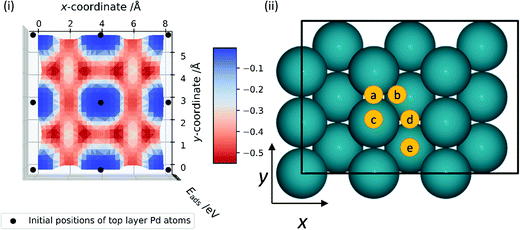
Prior to investigating the reaction steps in CO₂ hydrogenation, an understanding of hydrogen behaviour on Pd is crucial as the interaction of H with CO₂ is integral to the reaction profile. Thus, a survey was conducted of E_ads for H, E_ads(H), on the Pd surfaces; the H atom was positioned at various locations on the surface and optimised, with constraints in the xy-plane. E_ads(H) on the Pd (111), (100), and (110) surfaces was calculated with respect to the gas-phase diatomic hydrogen molecule and is plotted across the xy-plane in Fig. 3(i), 4(i), and 5(i), respectively. The ZPE-correction was not applied in these scans and all energies presented in this section are based on differences in total electronic energy. The most stable adsorption site for H on the Pd (111) surface is the HCP hollow position, which is site B in Fig. 3(ii), with E_ads(H) of −0.67 eV; similar stability over high coordination sites is observed on the (100) surface, where the hollow site (Fig. 4(ii), site C) has lower energy with E_ads(H) of −0.54 eV, and the “FCC” site (Fig. 5(ii), site B) is of lower energy in the case of the (110) surface, with E_ads(H) of −0.56 eV. The least stable adsorption site for H on all surfaces is atop, with E_ads(H) of −0.12, −0.08 and 0.00 eV on the (111), (100) and (110) Pd surfaces, respectively. The typical reactant feed for CO₂ hydrogenation is between 1 : 3 to 1 : 9 molar ratio of CO₂ and H₂, and thus dissociated hydrogen would be readily available on the catalyst surface.^9,20 High hydrogen mobility can be deduced from Fig. 3(i), 4(i) and 5(i), as differences in favourable E_ads are low along specific channels, highlighted in red. The adsorption energies for H on the Pd (111) surface (−0.67 eV) and the (110) surface (−0.56 eV) compare reasonably with the experimental work of Conrad et al., who report initial heats of adsorption for ½H₂ of 0.45 and 0.53 eV for Pd (111) and (110) surfaces, respectively.⁴⁷ There is also good agreement with previous theoretical research, as Herron et al. calculated atomic hydrogen adsorption energies on Pd (111) using PW91 and reported them to be −0.59, −0.56, and 0.00 eV on FCC hollow, HCP hollow, and atop positions, respectively.⁴⁸ Similarly, Fonseca et al. used PBE in their DFT study of hydrogen adsorption on Pd (111) and observed −0.66, −0.61, and −0.50 eV adsorption energies of hydrogen atom on FCC hollow, HCP hollow, and bridge position, respectively.⁴⁹

Fig. 3 (i) Adsorption energy (E_ads) of a hydrogen atom on Pd (111) surface, calculated as a function of x- and y-coordinate; the H atom remained constrained in the xy-plane during each geometry optimisation. A key is provided for the adsorption energies, in units of eV. (ii) Top-down view of the FCC Pd (111) surface with a 3 × 3 × 5 atoms simulation cell. Blue spheres represent Pd atoms and yellow circles represent unique adsorption sites: (a) hollow-FCC, (b) hollow-HCP, (c) bridge, (d) atop. Black lines represent the x- and y-direction cell boundaries.

Fig. 4 (i) Adsorption energy (E_ads) of hydrogen atom on Pd (100) surface calculated as a function of x- and y-coordinate; the H atom remained constrained in the xy-plane during each geometry optimisation. A key is provided for the adsorption energies, in units of eV. (ii) Top-down view of the FCC Pd (100) surface with a 3 × 3 × 5 atoms simulation cell. Blue spheres represent Pd atoms and yellow circles represent unique adsorption sites: (a) atop, (b) bridge (c) hollow. Black lines represent the x- and y-direction cell boundaries.

Fig. 5 (i) Adsorption energy (E_ads) of hydrogen atom on Pd (110) surface calculated as a function of x- and y-coordinate; the H atom remained constrained in the xy-plane during each geometry optimisation. A key is provided for the adsorption energies, in units of eV. (ii) Top-down view of the FCC Pd (110) surface with a 3 × 3 × 5 atoms simulation cell. Blue spheres represent Pd atoms and yellow circles represent unique adsorption sites: (a) short bridge, (b) “FCC” (c) atop, (d) long bridge, (e) hollow. Black lines represent the x- and y-direction cell boundaries.

3.2 CO₂ adsorption

The adsorption energies and structures for CO₂ on the Pd (111), (100) and (110) surfaces are reported in Table 2. The undistorted CO₂ is most stable with a C–Pd bond distance, d(C–Pd), of 3.454 Å, which agrees with the physisorbed species observed by Habas et al.²²H_ads(CO₂) is strongest on the close-packed (111) surface, and is found to relate linearly with the number of Pd atoms that neighbour the surface adsorption site; when H_ads(CO₂) is plotted as a function of surface atom coordination number, which are 9, 8, and 7 for the Pd (111), (100), and (110) surfaces, respectively, a linear fit returns R² = 0.998.

Table 2 Geometric and energetic observations for CO₂ and CO₂^δ− physisorbed and chemisorbed species on low-index Pd surfaces, respectively; CO^TS₂ is the transition state geometry between these stable local minima. H_ads is the ZPE-corrected species adsorption energy, given in eV; d_(C–Pd¹) is the distance between the carbon and the nearest neighbouring Pd given in Å, and ∠_O–C–O is the angle between the oxygen, carbon, and oxygen, given in °

Species	Pd surface
	111			100			110
	H ads	d (C–Pd^1)	∠O–C–O	H ads	d (C–Pd^1)	∠O–C–O	H ads	d (C–Pd^1)	∠O–C–O
CO2	−0.21	3.45	179.5	−0.18	3.28	179.1	−0.16	3.26	179.2
CO2^TS	0.12	2.37	154.8	0.00	2.45	160.6	No energy barrier
CO2^δ−	0.09	2.10	140.3	−0.09	2.06	140.6	−0.19	2.06	140.2

---

The stronger physisorption, rather than chemisorption, observed for CO₂ on the Pd (111) surface (E_ads(CO₂) = −0.21 eV) was reported previously by Ko et al.²² (−0.33 eV); they also identify a chemisorbed state CO₂^δ− with E_ads = −0.16 eV,¹⁷ which compares with our observation of H_ads(CO₂^δ−) = 0.09 eV. Similarly, Huš et al. observed that on Cu catalysts, CO₂ binds to the metal surface in a bent geometry, where one of the oxygens binds to a secondary metal atom and the carbon binds to a metal atom underneath.²⁵ Higham et al. observed an endothermic CO₂ chemisorption on Cu (100) and (110) surfaces, similarly to our result on Pd (111).⁵⁰ Energy differences between our results and those of Ko et al. are probably due to the choice of van der Waals correction;²¹ never-the-less, the observed trends are very similar, and the stability of the physisorbed CO₂ implies that there is an energy barrier on the Pd (111) surface for the activation of CO₂.

H _ads(CO₂^δ−) is endothermic (0.09 eV) on the Pd (111) surface, matching the work of Zhang et al.,²⁷ and exothermic (−0.09 and −0.19 eV) on the Pd (100) and (110) surfaces, respectively.²⁷ Reduction of the size of the model surface, such that 1/4 monolayer (ML) coverage of CO₂ is achieved on Pd (111), (100) and (110) surfaces, results in H_ads(CO₂^δ−) of 0.12 eV, −0.03 eV and −0.16 eV, respectively. The higher (less favourable) H_ads(CO₂^δ−) values for 1/4 ML coverage, when compared to the 1/9 ML coverage presented in Table 2, are intuitively linked to unfavourable interactions between neighbouring adsorbates. H_ads(CO₂^δ−) is noted as increasingly negative (i.e. strengthens) with increasing E_surf for the Pd facets, and the energy difference between surface-bound CO₂ and CO₂^δ− also decreases; these observations agree with experimental data that show an absence of chemisorption on the Pd (111) surface, and both physisorption and chemisorption on the Pd (100) surface.^12–14 Despite differences in H_ads(CO₂^δ−) on the surfaces examined, the adsorbed geometries of CO₂ and CO₂^δ− are consistent across all surfaces (Table 2); only a small difference in angles (0.4°) is calculated for either the physisorbed or chemisorbed geometries when compared across the three facets. The impact of steric interactions for adsorbed CO₂ can be quantified via the distortion energy, i.e., the gas-phase energy of the adsorbed bent CO₂ geometry relative to the preferred linear CO₂ configuration, which is 1.35, 1.33 and 1.33 eV for Pd (111), Pd (110), and (100) facets, respectively. Given that the overall adsorption energies are exothermic on Pd (100) and (110) surface facets, it can be concluded that the binding energy between surface Pd atoms and the CO₂ must be significant to negate the distortion energy arising from the unfavourable bent CO₂ geometry.

Mulliken charge analysis of the CO₂ and CO₂^δ− species adsorbed on the Pd (111), (110), and (100) facets provides insight into the electronic charge of the surface species, and the data acquired are reported in Table 3. The notation used for describing charges on atoms of interest is shown in Fig. 6: O¹ and O² are oxygen atoms on CO₂ molecule; the two closest Pd atoms interacting with CO₂ are labelled Pd¹ and Pd², where Pd¹ is closest to O¹ and Pd² is closest to O²; and Pd_surf, Pd_sublayer, and Pd_slab refer to the first, second and all layers of Pd atoms in the model, respectively.

Table 3 Net Mulliken charges, in units of e, on relevant atoms for CO₂ physisorption and chemisorption on the Pd (111), (110) and (100) surfaces; the charges (q) over Pd atoms have been averaged in the first surface layer surface (Pd_surf) and sublayer (Pd_sublayer), and summated over the whole slab (Pd_slab)

	Pristine surfaces			CO2				CO2^δ−
	Pd (111)	Pd (110)	Pd (100)	Gas	Pd (111)	Pd (110)	Pd (100)	Pd (111)	Pd (110)	Pd (100)
q c	—	—	—	+0.48	+0.47	+0.45	+0.44	+0.39	+0.38	+0.38
q O ^1	—	—	—	−0.24	−0.22	−0.22	−0.22	−0.19	−0.26	−0.23
q O ^2	—	—	—	−0.24	−0.23	−0.22	−0.22	−0.23	−0.24	−0.25
q Pd ^1	—	—	—	—	−0.02	−0.05	−0.05	−0.32	−0.10	−0.15
q Pd ^2	—	—	—	—	−0.01	−0.02	0.00	−0.30	+0.04	−0.07
q Pdsublayer	+0.03	+0.02	+0.02	—	+0.02	+0.05	0.00	−0.02	+0.03	0.00
q Pdsurf	−0.03	−0.03	−0.02	—	0.00	−0.01	0.00	−0.07	0.00	−0.02
q Pdslab	0.00	0.00	0.00	—	−0.02	−0.01	0.00	+0.04	+0.11	+0.10

---

Fig. 6 Side- and top-view of CO₂ chemisorbed on the FCC Pd (100) surface, illustrating notations used for Mulliken analysis. Blue, red, and grey spheres represent Pd, O, and C atoms, respectively. Black crosses mark constrained bulk Pd layers.

For CO₂ physisorption on the Pd (111) surface (Fig. 7a), the charge of the carbon (q_C) is +0.47 e, very similar to the gas phase CO₂ (q_C = +0.48 e), and only small changes are observed on the surface Pd. For CO₂^δ− on the Pd (111) surface (Fig. 7b), negatively charged Pd atoms bond to an oxygen and carbon (q_Pd¹ = −0.30 e, q_Pd² = −0.32 e). The distance d(C–Pd²) is 2.85 Å, and there is a direct electronic interaction between Pd² and the carbon atom of CO₂. The average charge on the second layer of Pd atoms, q_Pdsublayer, decreases from +0.03 to +0.02 e upon physisorption and decreases further to −0.02 e upon chemisorption. The average charge on the first surface atomic layer of Pd, q_Pdsurf, is −0.03 e, 0.00 e and −0.07 e for pristine Pd (111) surface, Pd (111) slab with CO₂, and Pd (111) slab with CO₂^δ−, respectively, suggesting that the electron density has been pulled to the first two layers of Pd, and to the CO₂^δ− adsorbate via Pd¹ and Pd². q_C has decreased from +0.47 e to +0.39 e, indicating some metal (Pd¹) to empty CO₂ π* orbital electron transfer.¹² The negatively charged oxygen close to the negative q_Pd¹ and q_Pd² will result in electrostatic repulsion, and thus are likely to contribute in the decreased stability of CO₂^δ− on the Pd (111) surface.^22,51

Fig. 7 A red-white-blue (negative-neutral-positive charges) color-coded visualisation of the net Mulliken charge on atoms for (a) CO₂ physisorbed and (b) CO₂^δ− chemisorbed on the Pd (111) surface.

In contrast, for CO₂^δ− on Pd (110) the q_C reduction is by 0.07 e upon chemisorption, with higher electron density on the oxygens and much less charge redistribution on the surface Pd atoms compared to the Pd (111) surface (q_Pd¹ of −0.10 e and −0.30 e, respectively), which all contribute to the overall stability (i.e. lower H_ads). For CO₂^δ− on a Pd (100) facet, the charges calculated are intermediary between the results on the Pd (111) and (110) surfaces, and H_ads also falls between the values observed for Pd (111) and (110) surfaces.

The overall charge transfer from the metal to CO₂^δ− is −0.04, −0.10 and −0.11 e on Pd (111), (100), and (110) surfaces, respectively, which is small but correlates directly with adsorption strength. In the previous literature, Bader charge analysis has been considered for CO₂ chemisorption on Pd (111) surfaces, and the transfer to CO₂^δ− reported as −0.28 and −0.43 e by Tang et al. and Habas et al., respectively;^22,52 the direction of charge transfer is consistent with our own observations, with the quantitative difference attributed to methodological differences, i.e. Mulliken charge analysis has a stronger basis set dependency than Bader analysis.^53,54 Importantly, we show qualitatively that the charge transfer to CO₂^δ− increases over Pd (111), (100), and (110) surfaces, indicating that Pd (100) and (110) surfaces are more suitable for CO₂ activation than the most stable Pd (111) surface.

3.3 Interactions of intermediates with Pd surfaces.

Reaction intermediates from the Grabow mechanism, as introduced in Section 1.2, have been optimised on the pristine Pd (111), (100) and (110) surfaces, in each case starting from an atop position, which ensured that adsorbates were starting at a proximity allowing metal-adsorbate bond formation during the geometry optimisation process. For example, in the case of CO₂, the chemisorbed species could easily be missed starting from the gas phase due to an energy barrier for the chemisorption of CO₂ on Pd (111) and (100) surfaces. The calculated values of H_ads are presented in Fig. 8 and tabulated in Section S4 of the ESI.†

Fig. 8 H _ads of the intermediates in the direct CO₂ hydrogenation to methanol, as studied on the low-index Pd surfaces, presented in order of increasing E_surf: (111), (100) and (110),²⁶ in blue, orange and grey, respectively. Error bars of ±0.05 eV are provided to account for the spin-paired approximation applied to the adsorbed species, as described in Section 2.3.

For the intermediates considered, the average difference between the highest and lowest H_ads across the three surfaces is 0.22 eV; the smallest difference is for the CO₂ molecule (0.05 eV), and the largest for H₂CO, H₂COOH, and CO₂^δ− (0.36, 0.33, and 0.29 eV, respectively). Plotting the surface energy (E_surf) of the low-index Pd surfaces against the adsorption enthalpy (H_ads) of these intermediates on the corresponding surfaces (Fig. 9) illustrates where surface properties associate with these observations. In particular, H_ads of CO₂, CO₂^δ−, H₂COOH, and H₂CO present clear linear correlations with the stability of the surface facets, giving R² of 0.988, 0.997, 0.987, and 1.000, respectively. HCOO, HCOOH, H₃CO, and CH₃OH give a poor linear fit, which indicates that other factors, such as steric effects, should be considered for rationalising the strength of these adsorbate interactions with the Pd surfaces. For example, due to additional space on the long-bridge site on the Pd (110) surface, the HCOOH can be accommodated in a different orientation from that on the Pd (111) and (100) surfaces (i.e. C–H atoms facing down, rather than up), which makes the resulting structures more difficult to compare directly.

Fig. 9 E _surf of the Pd (111), (100) and (110) surfaces plotted against H_ads of intermediates in the mechanism of CO₂ hydrogenation to methanol. The red dashed line is the linear fit of the data points, and R² is the linear coefficient of determination showing the quality of the fit.

3.4 Transition states and reaction profile

To gain further insight into reaction mechanisms, activation energies were calculated. Here, for each reaction step that involved a hydrogenation, it was necessary to set the transition state (TS) starting geometry such that a hydrogen atom was positioned near to the intermediate; optimisation of these starting models with proximal hydrogen in some instances led to instability of the intermediate adsorption structures, which, however, did not cause problems when directly applied to the TS calculations. Once a transition state structure was confirmed, the ZPE-corrected activation energy (H_act) was calculated for each reaction step as:

H_act = H_TS (species) − H_ads (species). (7)

The reference initial state for the calculation of H_act is the species adsorbed on the surface, and for hydrogenation steps a hydrogen atom is also adsorbed, but the two adsorbates have a very limited interaction between them. The resulting H_act are presented in Fig. 10 and structures tabulated in Section S6 in the ESI.† Here, CO₂^δ− was considered as the starting point, i.e. proceeding via a Langmuir–Hinshelwood mechanism, and not a physisorbed CO₂.²⁶ As part of the reaction pathway via formate, the decomposition of H₂COOH* into H₂CO* and OH* was included, as previously considered for metal catalysts containing Cu, Pd and Zn.^24–26,55 All TS have also been validated by vibrational analysis, displaying only one imaginary frequency each. The elementary step towards which each energy barrier refers are presented in Table 4.

Fig. 10 The ZPE-corrected activation energies (H_act, eV) of reaction steps in the pathway for CO₂ hydrogenation to methanol, presented for Pd surfaces in order of increasing E_surf, i.e. (111), (100), and (110), given in blue, orange, and grey, respectively. In each case, the label refers to the initial reaction species, and the activation energies are also tabulated.

Table 4 Detailed reaction steps towards which the H_act(species) abbreviations refer to in Fig. 10

H act(CO2^δ−)	2.5H2 + H* + CO2*chem → TS1 + 2.5H2	H act(H2COOH)	1.5H2 + H2COOH* → TS4 + 1.5H2
H act(HCOO)	2H2 + HCOO* + H* → TS2 + 2H2	H act(H2CO)	0.5H2 + H2CO* + H* + H2O → TS5 + 0.5H2 + H2O
H act(HCOOH)	1.5H2 + HCOOH* + H* → TS3 + 1.5H2	H act(H3CO)	CH3O* + H* + H2O → TS6 + H2O

---

The activation energy for CO₂^δ− hydrogenation, H_act(CO₂^δ−), is 1.13 eV, 1.10 eV and 0.81 eV on the Pd (111), (100) and (110) surfaces, respectively. The observation that H_act(CO₂^δ−) is lowest on the Pd (110) surface can be attributed to the additional space underneath the CO₂^δ− on the preferred long-bridge site, which facilitates the hydrogen atom binding to the carbon. The H_act(CO₂^δ−) on the Pd (111) surface (1.13 eV) matches the work of Zhang et al. (0.85 eV), though differs somewhat from the results of Brix et al. (2.23 eV); we believe that this difference stems from the use of a physisorbed CO₂ geometry in their calculations, with a chemisorbed structure considered in our work and the calculations by Zhang et al.^27,55

H _act(HCOOH) is observed to follow the trend (100) > (111) > (110), i.e. different from the E_surf trend. The H_act(HCOOH) of 1.41 eV evaluated for the most commonly studied Pd (111) surface is larger than the 1.13 eV reported by Brix et al. Given that the adsorption energy of HCOOH on the Pd (111) surface is calculated as −0.58 eV, and desorption is considered as the reverse process, the high H_act(HCOOH) observed (1.41 eV) for the Pd (111) surface suggests that HCOOH is more likely to desorb than react further. The high activation barrier for HCOOH hydrogenation agrees with work by Huš et al. on Cu-based catalysts; however, formic acid is not amongst the product stream observed when using Pd catalysts experimentally, with CH₃OH, CO and trace to significant amounts of CH₄ reported.^5,9,20,25,56 Thus, another intermediate, such as H₂COO, might be of importance in leading to the experimental products, as was determined for Cu-based catalysts.²⁵ In our work, the H_act(HCOOH) on the Pd (110) surface is about 40% lower than on Pd (111) and almost 45% lower than on the Pd (100). The reduction of H_act(HCOOH) might stem from lower stability of the HCOOH, and reduced stability of the hydrogen atom on Pd (110), which translates into a more accessible transition state.

The activation enthalpy for dissociation of H₂COOH species, H_act(H₂COOH), is highest on the Pd (100) surface, where the H₂COOH intermediate is stabilised. Brix et al. reported a high H_act(H₂COOH) of 2.01 eV on Pd (111), while we calculate H_act(H₂COOH) to be only 0.40 eV; the significant discrepancy of 1.61 eV arises from a considerable difference in the transition state geometry, i.e., our transition state involves breaking of a single C–O bond, whereas both C–O bonds were broken in the transition state found by Brix et al. For hydrogenation of formaldehyde, H_act(H₂CO) is similarly low (0.67–0.74 eV) on the three surfaces; however, on the (111) surface it is higher than H_ads of H₂CO (−0.58 eV), whilst on Pd (100) and (110) surfaces, H₂CO is stabilised more (−0.83 and −0.94 eV) than on Pd (111). The stronger H_ads on (100) and (110) surfaces means that H₂CO desorption is less likely, and reactivity favoured, whilst desorption would be a competitive process on the (111) surface. Desorption of H₂CO during CO₂ hydrogenation to methanol on Pd catalysts is a major concern in experiment,⁵ and thus the Pd (100) and (110) surfaces may be preferable in catalyst design.

In most hydrogenation steps examined on the three Pd surfaces, the reaction pathway favoured migration of the hydrogen atom towards the least stable on-top site before bonding to the intermediate. Therefore, the relative stability of the hydrogen adsorption sites, as shown in Section 3.1, has a major impact on the H_act for most hydrogenation reactions on the Pd (111), (100) and (110) surfaces. Reducing the difference in stability for hydrogen atoms on the possible surface sites might be an important factor in the design of catalysts for CO₂ hydrogenation to methanol, as it could lead to reduction of H_act for species reacting on a Pd-based catalyst.

A reaction profile based on the energy of initial, TS and final geometries, relative to the energy of isolated Pd (111), (100) and (110) surfaces and gas-phase reactants, is plotted in Fig. 11, with each individual step balanced stoichiometrically by energies of gas-phase molecules.

Fig. 11 The ZPE-corrected energy profile of CO₂ hydrogenation to methanol, via the formate pathway, on Pd (111), (100), and (110) surfaces, plotted in blue, orange, and grey, respectively, relative to the energy of pristine surface and gas phase reactants.²⁶ Energies of intermediate structures and transition state geometries have been stoichiometrically balanced with energies of gas phase reactants; * indicates surface bound species.

Based on total electronic energy for all the surfaces, which is presented in the ESI,† the reaction energy for the conversion of CO₂ to methanol is exothermic (−1.05 eV) relative to gas phase reactants, which agrees with reaction energy (−1.17 eV) derived from atomization energies.^5,57,58 The gas-phase reaction enthalpy presented above (−0.26 eV) is underestimated by 0.26 eV with respect to experimental values reported in literature,⁵ and the magnitude of the error in gas-phase energies of molecules is typical for gradient corrected functionals, such as PBE.⁵⁹ The highest H_act in the CO₂ hydrogenation reaction across the Pd (100), (111) and (110) surfaces is H_act(HCOOH), with values of 1.51, 1.41, and 0.84 eV, respectively, which is therefore a likely rate determining step (RDS) for the reaction. However, in an experimental study by Aas et al., the decomposition of HCOOH on Pd (110) was shown to require 0.42 eV, which is only 50% of the H_act(HCOOH) on Pd (110), and therefore much more likely.⁶⁰ An important feature of the reaction energy profile is that TS1 remains endothermic on all three surfaces, with respect to the gas phase reactants, which would inevitably influence the rate of the reaction. All transition states on Pd (110) remain either below net zero energy of the reaction or significantly lower than Pd (111) and Pd (100) when above, which indicates that Pd (110) is the most active among the surfaces investigated here. As highlighted in Section 3.1, the hydrogen atoms are stabilised strongly on the Pd (111), (100), and (110) surfaces; the binding energies of intermediates with a neighbouring hydrogen atom do not vary significantly from the sum of binding energies of the adsorbates calculated separately, which suggests that the presence of hydrogen neither stabilises nor destabilises the intermediates at the low 1/9 ML coverage of hydrogen considered.²⁶ However, presence of a hydrogen atom at the nearest neighbouring site to chemisorbed CO₂ was observed to result in CO₂ desorption during geometry optimisation, to form a linear physisorbed species, which may indicate a lower stability of chemisorbed CO₂ with increasing hydrogen ML coverage. Experimentally, the presence of H₂ appears to induce a larger CO₂ intake both at increased temperature and/or pressure, but this phenomenon has been linked to CO₂ dissociation.⁶¹

3.5 Gibbs free energy analysis

Gibbs free energy changes (ΔG, eV) between the reaction steps a–v in Table 5 across Pd (111), (110) and (100) were calculated and are shown in Fig. 12 and 13. The pressure (p) used was 1 atm (1013125 Pa), which was applied to gas components. The temperatures (T) considered were 0 K (i.e., enthalpy), 300 K for ambient conditions, and 500 K as typical experimental conditions for CO₂ hydrogenation over Pd catalysts.²⁰ Graphs of the effect of temperature are shown for Pd (111) in Fig. 12, with other surfaces presented in Section S7 in the ESI.† A comparison of results for 500 K presented in Fig. 13.

Table 5 Calculated reaction steps in CO₂ hydrogenation reaction via formate on Pd

(a) 3H2 + CO2*phys → TS0 + 3H2	(b) 3H2 + TS0 → CO2*chem + 3H2
(c) 3H2 + CO2*chem → CO2*chem+ H* +2.5H2	(d) 2.5H2 + H* + CO2*chem → TS1 + 2.5H2
(e) 2.5H2 + TS1 → HCOO* + 2.5H2	(f) 2.5H2 + HCOO* → HCOO* + H* + 2H2
(g) 2H2 + HCOO* + H* → TS2 + H2	(h) 2H2 + TS2 → HCOOH* +2H2
(i) 2H2 + HCOOH* → HCOOH* + H* + 1.5H2	(j) 1.5H2 + HCOOH* + H* → TS3 + 1.5H2
(k) 1.5H2 + TS3 → H2COOH* + 1.5H2	(l) 1.5H2 + H2COOH* → H2COOH*rotated + 1.5H2
(m) 1.5H2 + H2COOH*rotated → TS4 + 1.5H2	(n) 1.5H2 + TS4 → H2CO* + OH* + 1.5H2
(o) 1.5H2 + H2CO* + OH* → H2CO* + H2O* +H2	(p) H2 + H2CO* + H2O* → H2CO* + H2 + H2O
(q) H2 +H2CO* + H2O → H2CO* + H* + 0.5 H2 + H2O	(r) 0.5H2 + H2CO* + H* + H2O → TS5 + 0.5H2 + H2O
(s) 0.5H2 + TS5 + H2O → CH3O* + 0.5H2 + H2O	(t) CH3O* + 0.5H2 + H2O → CH3O* + H* + H2O
(u) CH3O* + H* + H2O → TS6 + H2O	(v) H2O + TS6 → CH3OH* + H2O

---

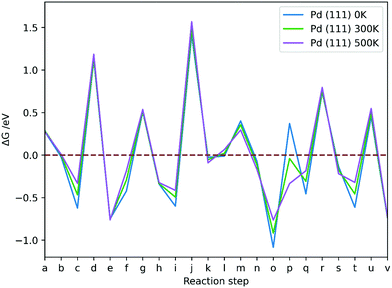Fig. 12 The Gibbs free energy changes between reaction steps in CO₂ hydrogenation reaction via formate on Pd (111) at p of 1 atm and T of 0 K, 300 K and 500 K; reaction steps a–v are explained in Table 5.

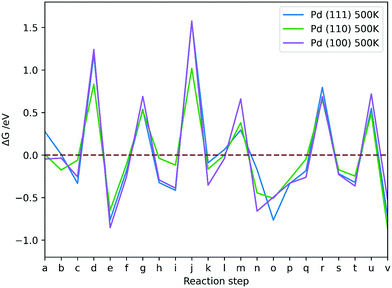Fig. 13 The Gibbs free energy changes between reaction steps in CO₂ hydrogenation reaction via formate on Pd (111), (110), and (100) at p of 1 atm and T of 500 K; reaction steps a–v are explained in Table 5.

As T increases (Fig. 12), formation of species on Pd (111) from respective TS structure shows more negative (favourable) ΔG for formation of H₂COOH (k), H₂CO* (n) and H₃CO* (s), and less negative for CO₂^δ− (b) and HCOOH* (h), while HCOO* (e) and CH₃OH* (v) are not significantly affected. On Pd (100), formation of species from respective TS structure shows similar trends to Pd (111) with an increase of T, but formation of H₂CO* (n) and CH₃OH* (v) is increasingly more favourable also. On Pd (110), elevated T facilitates formation of CO₂^δ− (b), HCOO* (e), H₂COOH (k) and CH₃OH* (v), but formation of HCOOH* (h) shows a ΔG increase, while H₂CO (n) and H₃CO* (s) are not significantly affected. Overall, the changes are subtle and are most prominent for processes involving H adsorption, which becomes less favourable as T increases, and for H₂O desorption, which is more favourable as T increases.

Large positive ΔG is observed for all reaction steps involving breaking of Pd–H bonds and attaching of the hydrogen to the adsorbates, i.e. formation of TS1 (d), TS2 (g), TS3 (j), TS5 (r) and TS6 (u), which indicates that the very strong Pd–H interaction at 1/9 ML hydrogen coverage impedes the reaction on Pd (111), (100) and (110) surfaces even at the first hydrogenation step to formate.

The Pd (110) surface has the lowest ΔG values for TS formations, except for dissociation of H₂COOH (m), which is more favourable on the Pd (111) surface. The ΔG associated with TS formation are not strongly affected by T, which suggests that the flat low-index surfaces of Pd are not the likely source of methanol formation in supported metallic Pd catalysts. The conclusion is in agreement with experiment, showing that pure unsupported Pd does not produce methanol at 463 K and atmospheric pressure.⁹ Moreover, changing T was shown to have a very limited effect on formation of intermediates in CO₂ hydrogenation on Pd catalysts. Adsorbing hydrogen on Pd surfaces is less favourable at higher T, but formation of TS structures remains unaffected, thus rendering the process less feasible at high T; however, elevated T is necessary to activate CO₂ on Pd (100), showing that low T CO₂ activation is key for CO₂ hydrogenation to be kinetically viable.

4. Summary and conclusions

Direct hydrogenation of CO₂ to methanol on transition metal catalysts is a promising approach for green energy storage, and new and more efficient catalysts need to be designed to make the technology viable; here, we have investigated the CO₂ hydrogenation reaction via the formate pathway on Pd (111), (100), and (110) surfaces to support this endeavour.

Firstly, we investigated the stability of H on the Pd surfaces, showing that high coordination sites have the largest adsorption energy, and these high stability sites are interlinked via channels with low diffusion barriers; we also show for CO₂ adsorption that the preference of physical or chemical adsorption is dependent on the stability of the Pd surface facet. For the CO₂ hydrogenation reaction, the transition state for CO₂^δ− hydrogenation (TS1), to form formate, is endothermic, which will influence the overall rate of the reaction. H_act(HCOOH) is the highest energy step in the reaction profile on the Pd (111), (100), and (110) surfaces (TS3), and it can be considered as the likely rate determining step of this reaction on the surfaces examined. Based on thermodynamical analysis, the formation of TS1 has a high barrier that is not significantly influenced by reaction conditions, which indicates that flat surfaces of metallic Pd are unlikely to be the source of formate, and subsequently, methanol in product streams of reactions using supported monometallic Pd catalysts. Increased temperature was found to facilitate CO₂ chemisorption on Pd (100) and (110), but has an adverse effect on multiple other reaction steps, including the free energy of hydrogen adsorption. Novel Pd-based polymetallic nanoparticle catalysts for direct CO₂ hydrogenation to methanol could be designed to lower the barrier to initial CO₂ hydrogenation, TS1, and lower the barrier for formic acid hydrogenation (TS3) or facilitate a mechanism that proceeds via an alternative intermediate, such as H₂COO. Importantly, a Pd-based CO₂ hydrogenation catalyst should have lower Pd-H binding strength to facilitate the reaction.

Overall, we show that the most stable geometry of CO₂ adsorbed on Pd surface varies across (111), (100) and (110) facets and future studies should not be limited to consideration of the lowest energy (111) surface facet. Inclusion of zero-point energy has shown the Pd (100) surface to be unsuitable for CO₂ hydrogenation, highlighting that consideration of enthalpy is important for accuracy in computational catalysis. Low-index Pd surfaces are therefore unlikely to be the source of methanol formation on supported monometallic Pd catalysts, which indicates the potential importance of low-coordination metallic sites and metal-support interfacial sites. The H₂COO intermediate could be alternatively considered as part of the formate pathway, and future work will entail modelling of the reaction with this intermediate also considered on multi-component Pd-based catalytic systems, which have been shown to manifest great selectivity to CH₃OH in direct CO₂ hydrogenation.^20,62–64

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors are grateful for funding by the EPSRC Centre-to Centre Project (Grant reference: EP/S030468/1). IK acknowledges the Cardiff School of Chemistry for a PhD studentship award. We are grateful to Matthias Scheffler, Yuanyuan Zhou, Herzain Rivera, Graham Hutchings, Mike Bowker and David Willock for useful discussions. AJL acknowledges funding by the UKRI Future Leaders Fellowship program (MR/T018372/1). The authors acknowledge computational resources and support from: the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via the Welsh Government; the UK National Supercomputing Services ARCHER and ARCHER2, accessed via membership of the Materials Chemistry Consortium, which is funded by Engineering and Physical Sciences Research Council (EP/L000202/1, EP/R029431/1, EP/T022213/1); and the Isambard UK National Tier-2 HPC Service operated by GW4 and the UK Met Office, and funded by EPSRC (EP/P020224/1).

References

1. G. Hutchings, M. Davidson, P. Atkins, P. Collier, N. Jackson, A. Morton, M. Muskett, M. Rosseinsky, P. Styring, P. Thornley and C. Williams, Sustainable synthetic carbon based fuels for transport: Policy Briefing, The Royal Society, 2019.
2. S. Roy, A. Cherevotan and S. C. Peter, ACS Energy Lett., 2018, 3, 1938–1966.
3. K. M. V. Bussche and G. F. Froment, J. Catal., 1996, 161, 1–10.
4. M. Bowker, R. A. Hadden, H. Houghton, J. N. K. Hyland and K. C. Waugh, J. Catal., 1988, 109, 263–273.
5. M. Bowker, ChemCatChem, 2019, 11, 4238–4246.
6. J. Ko, B.-K. Kim and J. W. Han, J. Phys. Chem. C, 2016, 120, 3438–3447.
7. J. Xu, X. Su, X. Liu, X. Pan, G. Pei, Y. Huang, X. Wang, T. Zhang and H. Geng, Appl. Catal. Gen., 2016, 514, 51–59.
8. I. Melián-Cabrera, M. L. Granados and J. L. G. Fierro, J. Catal., 2002, 210, 285–294.
9. N. Iwasa, H. Suzuki, M. Terashita, M. Arai and N. Takezawa, Catal. Lett., 2004, 96, 75–78.
10. N. Iwasa, T. Mayanagi, N. Ogawa, K. Sakata and N. Takezawa, Catal. Lett., 1998, 54, 119–123.
11. R. Manrique, R. Jiménez, J. Rodríguez-Pereira, V. G. Baldovino-Medrano and A. Karelovic, Int. J. Hydrogen Energy, 2019, 44, 16526–16536.
12. F. Solymosi and A. Berkó, J. Catal., 1986, 101, 458–472.
13. F. Solymosi, J. Mol. Catal., 1991, 65, 337–358.
14. T. Matsushima and H. Asada, J. Chem. Phys., 1986, 85, 1658–1668.
15. U. Burghaus, Prog. Surf. Sci., 2014, 89, 161–217.
16. C.-L. Kao, A. Carlsson and R. J. Madix, Surf. Sci., 2002, 497, 356–372.
17. X. Liu, L. Sun and W.-Q. Deng, J. Phys. Chem. C, 2018, 122, 8306–8314.
18. R. Brosseau, T. H. Ellis and H. Wang, Chem. Phys. Lett., 1991, 177, 118–122.
19. A. Erdöhelyi, M. Pásztor and F. Solymosi, J. Catal., 1986, 98, 166–177.
20. H. Bahruji, M. Bowker, G. Hutchings, N. Dimitratos, P. Wells, E. Gibson, W. Jones, C. Brookes, D. Morgan and G. Lalev, J. Catal., 2016, 343, 133–146.
21. J. Ko, B.-K. Kim and J. W. Han, J. Phys. Chem. C, 2016, 120, 3438–3447.
22. M.-P. Habas, F. Mele, M. Sodupe and F. Illas, Surf. Sci., 1999, 431, 208–219.
23. A. J. Medford, J. Sehested, J. Rossmeisl, I. Chorkendorff, F. Studt, J. K. Nørskov and P. G. Moses, J. Catal., 2014, 309, 397–407.
24. S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299.
25. M. Huš, D. Kopač, N. S. Štefančič, D. L. Jurković, V. D. B. C. Dasireddy and B. Likozar, Catal. Sci. Technol., 2017, 7, 5900–5913.
26. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
27. M. Zhang, Y. Wu, M. Dou and Y. Yu, Catal. Lett., 2018, 148, 2935–2944.
28. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
29. A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dulak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
30. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
31. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
32. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
33. J. W. Arblaster, Platinum Met. Rev., 2012, 56, 181–189.
34. P. Janthon, S. (Andy) Luo, S. M. Kozlov, F. Viñes, J. Limtrakul, D. G. Truhlar and F. Illas, J. Chem. Theory Comput., 2014, 10, 3832–3839.
35. M. Methfessel, D. Hennig and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4816–4829.
36. L. Vitos, A. V. Ruban, H. L. Skriver and J. Kollár, Surf. Sci., 1998, 411, 186–202.
37. A. Patra, J. E. Bates, J. Sun and J. P. Perdew, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E9188–E9196.
38. N. E. Singh-Miller and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 235407.
39. J. L. F. Da Silva, C. Stampfl and M. Scheffler, Surf. Sci., 2006, 600, 703–715.
40. H. L. Skriver and N. M. Rosengaard, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 7157–7168.
41. W. R. Tyson and W. A. Miller, Surf. Sci., 1977, 62, 267–276.
42. F. R. de Boer, W. C. M. Mattens, R. Boom, A. R. Miedema and A. K. Niessen.
43. S. S. Xantheas, J. Chem. Phys., 1996, 104, 8821–8824.
44. M. H. Hansen, J. A. G. Torres, P. C. Jennings, Z. Wang, J. R. Boes, O. G. Mamun and T. Bligaard, ArXiv190400904 Phys.
45. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
46. T. Frederiksen, M. Paulsson, M. Brandbyge and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205413.
47. H. Conrad, G. Ertl and E. E. Latta, Surf. Sci., 1974, 41, 435–446.
48. J. A. Herron, S. Tonelli and M. Mavrikakis, Surf. Sci., 2012, 606, 1670–1679.
49. S. Fonseca, G. Maia and L. M. C. Pinto, Electrochem. Commun., 2018, 93, 100–103.
50. M. D. Higham, M. G. Quesne and C. R. A. Catlow, Dalton Trans., 2020, 49, 8478–8497.
51. P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 10th edn, 2014.
52. Q. Tang, F. Shi, K. Li, W. Ji, J. Leszczynski, A. G. Russell, E. G. Eddings, Z. Shen and M. Fan, Fuel, 2020, 280, 118446.
53. J. S. Gómez-Jeria, J. Chil. Chem. Soc., 2009, 54, 482–485.
54. J. Dobado, H. Martinez, J. Molina and M. Sundberg, Quantum Systems in Chemistry and Physics, 2000, vol. 2, pp. 337–353.
55. F. Brix, V. Desbuis, L. Piccolo and É. Gaudry, J. Phys. Chem. Lett., 2020, 11, 7672–7678.
56. T. Fujitani, M. Saito, Y. Kanai, T. Watanabe, J. Nakamura and T. Uchijima, Appl. Catal. Gen., 1995, 125, L199–L202.
57. R. Haunschild and W. Klopper, J. Chem. Phys., 2012, 136, 164102.
58. J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen and T. Bligaard, J. Chem. Phys., 2014, 140, 144107.
59. A. Posada-Borbón and H. Grönbeck, ACS Catal., 2021, 11, 9996–10006.
60. N. Aas, Y. Li and M. Bowker, J. Phys.: Condens. Matter, 1991, 3, S281.
61. F. Solymosi, A. Erdöhelyi and M. Lancz, J. Catal., 1985, 95, 567–577.
62. J. Díez-Ramírez, J. L. Valverde, P. Sánchez and F. Dorado, Catal. Lett., 2016, 146, 373–382.
63. J. Díez-Ramírez, J. A. Díaz, P. Sánchez and F. Dorado, J. CO₂ Util., 2017, 22, 71–80.
64. H. Bahruji, M. Bowker, W. Jones, J. Hayward, J. Ruiz Esquius, D. J. Morgan and G. J. Hutchings, Faraday Discuss., 2017, 197, 309–324 (i) (ii).

---

Footnote

† Electronic supplementary information (ESI) available: The accompanying supporting information contains details of the calculation methods, and detailed energetics for all steps in the reaction profiles. All structures associated with the presented work are available from the NOMAD repository at DOI: 10.17172/NOMAD/2021.05.24-1 (all data) and 10.17172/NOMAD/2021.05.25-1 (optimised structures). All underpinning energetic data is available at DOI: 10.17035/d.2022.0164034480. See DOI: 10.1039/d2cp01019d

---