Spectroscopic signatures of nonpolarons: the case of diamond†
Joao C.
de Abreu
 *a,
Jean Paul
Nery
b,
Matteo
Giantomassi
*a,
Jean Paul
Nery
b,
Matteo
Giantomassi
 c,
Xavier
Gonze
cd and
Matthieu J.
Verstraete
c,
Xavier
Gonze
cd and
Matthieu J.
Verstraete
 a
a
ananomat/Q-MAT/CESAM and European Theoretical Spectroscopy Facility, Université de Liège, B-4000, Belgium. E-mail: jcabreu@uliege.be
bDipartimento di Fisica, Università di Roma La Sapienza, I-00185 Roma, Italy
cUCLouvain, Institute of Condensed Matter and Nanosciences (IMCN), Chemin des Étoiles 8, B-1348 Louvain-la-Neuve, Belgium
dSkolkovo Institute of Science and Technology, Moscow, Russia
First published on 9th May 2022
Abstract
Polarons are quasi-particles made from electrons interacting with vibrations in crystal lattices. They derive their name from the strong electron-vibration polar interactions in ionic systems, that induce spectroscopic and optical signatures of such quasi-particles. In this paper, we focus on diamond, a non-polar crystal with inversion symmetry which nevertheless shows interesting signatures stemming from electron-vibration interactions, better denoted “nonpolaron” signatures in this case. The (non)polaronic effects are produced by short-range crystal fields, while long-range quadrupoles only have a small influence. The corresponding many-body spectral function has a characteristic energy dependence, showing a plateau structure that is similar to but distinct from the satellites observed in the polar Fröhlich case. We determine the temperature-dependent spectral function of diamond by two methods: the standard Dyson–Migdal approach, which calculates electron–phonon interactions within the lowest-order expansion of the self-energy, and the cumulant expansion, which includes higher orders of electron–phonon interactions. The latter corrects the nonpolaron energies and broadening, providing a more realistic spectral function, which we examine in detail for both conduction and valence band edges.
1 Introduction
Interactions between electrons and vibrational modes of solids (phonons) create composite bound states known as polarons. Most of the attention in the field has quite naturally been focused in systems where these effects are expected to be strong, e.g. polar materials,1 their vacancies,2 molecular crystals3 or 2D-materials.4 In these systems the electrons interact among others with long-range (LR) dipole fields induced by displaced ions. Although covalent materials have no dipole moments, one could expect long-range quadrupole fields to contribute to the formation of polarons, as inferred from their significant impact on the carrier mobility in Si.5,6Some covalent systems with strong electron–phonon (e–ph) interactions show conductivity induced by hopping of small polarons, e.g.: disordered systems such as chalcogenide glasses,7 molecular crystals such as S8,8 rare gas solids such as Xe,9 or 2D phosphorene and arsenene,10 where the polaron is localized in lone-pair orbitals. Large polarons in covalent materials have been historically neglected, and were dubbed “nonpolarons” by Emin.11 We note that polaronic signatures were found in doped diamond with a hydrogen-terminated surface having a negative electron affinity.12 In the present paper we study polaronic effects in intrinsic diamond, to find whether the long- or short-range (SR) potential binds phonons to electrons, and to quantify from first-principles the binding and spectral signatures of polarons in non-polar materials.
The detection of polarons in a crystal often relies on angle-resolved photoemission spectroscopy (ARPES), which measures the kinetic energy and angular distribution of electrons excited by incident light. These quantities are directly related to the number of states available, as a function of energy and momentum. Signatures of polarons in ARPES experiments can be found in cuprate superconductors,13 ionic 3D14–17 and 2D15,18 crystals, ferromagnetic materials,19 and interfaces.20 In the simplest model, neglecting surface effects, ARPES can be related to the one-electron spectral function, which is the central property of interest here.
Besides (non)polaron binding and the renormalization of the direct electronic band gap,21 the effects of phonons in non-polar materials can also be seen in the optical excitation of carriers in indirect band gap semiconductors.22 The scattering of carriers by phonons dominates transport mechanisms at high temperature, hence an appropriate description of the spectral function is essential to calculate transport properties including many-body effects. Important experimental observables are the thermoelectric conductivity,23 the charge carrier mobility/conductivity,24 or superconductivity.25
First-principles calculations of the spectral function at the valence band maximum (VBM) and conduction band minimum (CBM) for (polar) LiF and MgO were examined by Nery et al.26 within a zero temperature formalism. In this paper, we expand their approach by studying a non-polar material, diamond, and including finite temperature effects. We will focus on the renormalization of electronic energies at T = 0 K (the zero point renormalization, or ZPR), their temperature dependence, and the emergence of nonpolaronic signatures. Vibrational properties and e–ph matrix elements are obtained using density functional perturbation theory (DFPT)27,28 while the interaction between electrons and phonons, which leads to the formation of a quasi-particle (QP), is treated using many-body perturbation theory (MBPT).29
The article is organized as follows. Section 2 summarizes the most important theoretical aspects of the e–ph problem with particular emphasis on the different approaches that can be used to compute spectral functions and QP energies. More specifically, we compare the standard Dyson equation in the Migdal approximation (DM)30,31 with the cumulant-expansion (CE) method,32–34 which includes higher order diagrams in the self-energy. The CE was previously shown to provide accurate results for e–e interactions35 and also to improve plasmonic polaron satellite energies.36,37 In Section 3, we describe spectral signatures in diamond and show that the CE gives better results relative to DM. In addition, we show that LR quadrupole fields do not contribute strongly to the spectral signals; the latter are mostly created by local crystal fields. We also include an ESI† which summarizes the basic equations of density functional theory (DFT) (used for ground-state calculations) and DFPT. ESI† also includes analyses and clarifies important aspects of numerical convergence, analytical transformations for the cumulant expansion, and finite temperature effects. Atomic units are used everywhere unless explicitly noted.
2 Methods
We study the interaction between bare electrons and bare phonons by assuming that it can be treated with MBPT techniques. It is important to note that for polarons this is not always possible. In strongly interacting cases, small localized polarons can be formed, which cannot be treated perturbatively.In ESI† S1, we summarize the DFT and DFPT methods. In this section, we detail the MBPT formalism and explain how to split the LR and the SR from the total DFPT potential.
2.1 Self-energy
Following ref. 26, we refer to the lowest order e–ph self-energy (second order in the atomic displacements) as the Fan–Migdal (FM) self-energy.31 It includes two terms, the static Debye–Waller (DW)38 and the dynamic Fan39 term,| Σnk(ω) = ΣDWnk + ΣFannk(ω). | (1) |
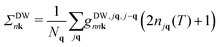 | (2) |
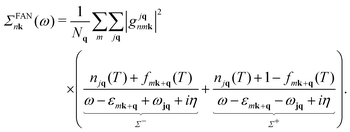 | (3) |
In principle, the DW matrix element gDW should be computed as the second-order derivative of the self-consistent potential with respect to the phonon displacement. In practice, we use the acoustic sum rule, together with the rigid-ion approximation,41 to express gDW in terms of the first order e–ph matrix elements.40,42 Inside the parentheses of eqn (3), there are two terms with the Bose Einstein factors n and n + 1, which we label Σ− and Σ+. Each term represents in turn two separate scattering events, into and out of state nk, which correspond to absorption and emission of phonons, pairing with the appropriate electron or hole state.
2.2 Dyson–Migdal approach
The interacting Green's function G can be expressed in terms of the initial bare propagator G0 and the exact self-energy via the Dyson equation.43 In the diagonal approximation,44 the off-diagonal matrix-elements of Σ in the Bloch basis set are assumed to be negligible, and the Dyson equation reduces to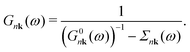 | (4) |
Finally, the spectral function A is given by
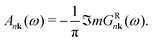 | (5) |
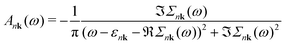 | (6) |
2.3 Cumulant expansion
The Green's function in the time domain can be rewritten in an exponential form (cumulant expansion) using Kubo's formula32| Gnk(t) = G0nk(t)eCnk(t), | (7) |
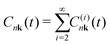 | (8) |
The cumulant functions can be determined by expanding the exponential in eqn (7) and comparing powers with the standard Feynman expansion of the Green's function.35 Using the Fan–Migdal self-energy (Fan and DW terms), one obtains
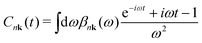 | (9) |
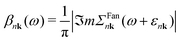 | (10) |
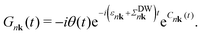 | (11) |
The spectral function is obtained by applying the Fourier transform to the Green's Function in the time domain, eqn (11), and inserting it into eqn (5). It can be shown that the CE Green's function is exact to second order, and all higher order terms are included, though in an approximate way, while DM only includes the exact second order terms.48,49 In the long time limit, the cumulant has an affine asymptotic behaviour which contains its contributions to the lifetime and lineshape of the QP state,
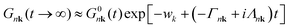 | (12) |
2.4 Energy renormalization
In this section, we summarize three commonly used approximations to compute the QP energy from the e–ph self-energy. If we ignore the frequency dependence of the imaginary part of the self-energy, one obtains that the main peak of the DM spectral function (eqn (6)) is located at the energy εNLnk that solves the non-linear (NL) QP equation| εNLnk = ε0nk + ℜeΣnk(ω = εNLnk). | (13) |
| εlinearnk = ε0nk + ZnkℜeΣnk(ω = ε0nk) | (14) |
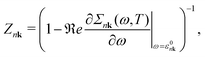 | (15) |
| εOMSnk = ε0nk + ℜeΣnk (ω =ε0nk). | (16) |
The evaluation of the energy correction is also carried out for the CE approach. The effective CE self-energy is determined by inverting eqn (4) after inserting the CE and non-interacting Green's functions. Then the NL equation is used to obtain eigenenergies. Further details over the effective CE self-energy are described in S5 (ESI†).
In Section 3.1, we will check the results of the different approaches for the band edges of diamond, showing that the OMS approximation using DM produces QP shifts very close to the CE-NL (as already observed for polar materials26).
2.5 Long-range and short-range potentials
Converging e–ph calculations requires very dense q-grids that are prohibitively expensive for DFPT. For this reason, we employ the Fourier-based interpolation scheme, initially proposed by Eiguren,50 to interpolate the e–ph scattering potentials on arbitrarily dense q-meshes. The potential interpolation scheme has an important advantage for the e–ph matrix elements of high unoccupied states, which are very delicate to access accurately with Wannier Function based interpolation methods.51The e–ph scattering potential presents a non-analytical behaviour52 in the long wave-length limit (q → 0) associated to a LR behaviour in real-space, which requires a specialized numerical treatment. Over the past decade, this problem has been subject to several investigations that lead to a well established procedure: the dipole fields for q → 0 are treated using a Fröhlich-like potential,53,54 which depends on the Born effective charges and diverges as 1/q. Recently,5,55,56 the treatment of LR contributions has been generalized to include contributions generated by dynamical quadrupoles.57 As the Born effective charges of diamond are zero, in what follows we focus on the treatment of the quadrupole interaction.
In non-polar materials, the Fourier interpolation of the e–ph potentials proceeds by first removing the non-analytical long-range contribution induced by the displacement of the κ-th atom along the Cartesian direction α using the generalized quadrupole model
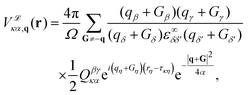 | (17) |
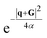 , is a Gaussian filter55 with a variance of
, is a Gaussian filter55 with a variance of 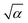 . The resulting short-range potentials, which are smooth and analytic in q space, are then used to build the scattering potential Wκ,α(r, R) in the real-space supercell (see, e.g., eqn (12) in Brunin et al.55). The short-range W is Fourier-interpolated on a much denser q-grid and the non-analytic LR terms are finally added back to get the total scattering potential. Interestingly, one can use this interpolation technique to compute e–ph matrix elements in which only the LR (SR) part of the scattering potential is included. In Section 3.2, we will analyze the separate contributions from the SR and LR potential and their effect on self energies and spectral functions.
. The resulting short-range potentials, which are smooth and analytic in q space, are then used to build the scattering potential Wκ,α(r, R) in the real-space supercell (see, e.g., eqn (12) in Brunin et al.55). The short-range W is Fourier-interpolated on a much denser q-grid and the non-analytic LR terms are finally added back to get the total scattering potential. Interestingly, one can use this interpolation technique to compute e–ph matrix elements in which only the LR (SR) part of the scattering potential is included. In Section 3.2, we will analyze the separate contributions from the SR and LR potential and their effect on self energies and spectral functions.
3 Results
All calculations in this work are performed using the ABINIT58,59 software. Convergence studies are presented in this section, followed by an analysis of spectral functions and ARPES spectra. All calculations use the full DFPT potential, albeit at the end of this section, we split the scattering potential into LR and SR contributions and check their respective effects on the QP. Further details on ground-state and DFPT calculations, such as the lattice constant, band gap and phonon band structure, can be found in ESI† S2.3.0 Convergence studies
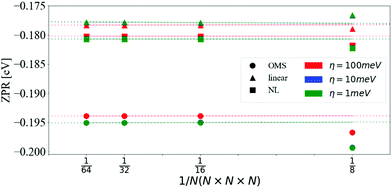 | ||
| Fig. 1 ZPR for the CBM as a function of the number of divisions in the q-mesh and different values of η. The data was fitted with a linear model and extrapolated for 1/N → 0. Calculations were done with the OMS approach eqn (16) (circles), the linear approximation eqn (14) (triangles) and the non-linear approach eqn (13) (squares). The values obtained with η = 10 meV and η = 1 meV are indistinguishable on the scale of the graph. | ||
| CBM | VBM | Band gap | |
|---|---|---|---|
| OMS | −0.196 | 0.130 | −0.325 |
| Linear | −0.177 | 0.118 | −0.295 |
| NL | −0.180 | 0.119 | −0.299 |
The ZPR of polar materials, such as LiF and MgO, is largely dominated by the Fröhlich interaction.26 In diamond, there are no dipole contributions, yet the ZPR is similar to that of LiF and MgO in relative terms. The Fröhlich ZPR of MgO26,60 and LiF26,61 for the CBM is approximately 4% and 1%, respectively, of the experimental band gap. Similarly, the ZPR of diamond62 is about 4%. This shows that accurate computations of band gaps require the inclusion of e–ph interaction even in homo-polar crystals. It should be noted, however, that electron–electron interactions beyond the KS-DFT mean-field approximation are absent in our calculations. These corrections may vary depending on the wave-vector, e.g., for the indirect band gap of diamond the GW correction is around 0.02 eV while it is about 0.2 eV for the direct band gap.21,63 We also ignored thermal expansion, zero-point lattice expansion,64,65 and further anharmonic effects. Other calculations including these phenomena are detailed in Table 2.
| ZPR (meV) | Calc./exp. | DF(P)T/MC | SC/AHC | (Non-)A | EE | TE | (An)Ha |
|---|---|---|---|---|---|---|---|
| −36470 | Exp | ||||||
| −325 | FP (This work) | DFPT | AHC | Non-A | No | No | Ha |
| −31563 | FP | MC | SC | A | No | Yes | ? |
| −32044 | FP | DFT | SC | A | No | No | AnHa |
| −33042 | FP | DFPT | AHC | Non-A | No | No | Ha |
| −33763 | FP | MC | SC | A | G 0 W 0 | Yes | ? |
| −36644 | FP | DFPT | AHC | Non-A | No | No | Ha |
| −37244 | FP | DFPT | AHC | A | No | No | Ha |
| −38042 | FP | DFPT | AHC | A | No | No | Ha |
| −43644 | FP | DFPT | SC | A | No | No | Ha |
| −43944 | FP | DFT | SC | A | No | No | Ha |
| −46271 | FP | DFT | SC | A | No | No | Ha |
| −61972 | Semi-Emp* | DFPT | AHC | A | No | Yes | Ha |
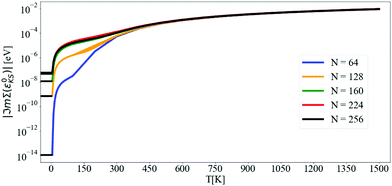
Fig. 2 shows the convergence of the imaginary part of Σ at the CBM using the tetrahedron scheme. Above 5 K, ℑmΣ(ε0CBM) converges at N = 160, and from 5 K to 60 K, there is a steep increase of ℑmΣ(ε0CBM) from 6 × 10−8 eV to 10−5 eV, respectively. At 300 K, ℑmΣCBM(ε0CBM) reaches 10−4 eV and at 1500 K it is almost 10−2 eV. In Fig. 3 and 4, we compare finite η results with the converged tetrahedron values.
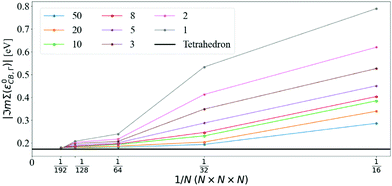
Fig. 3 shows that ℑmΣcΓ(ε0cΓ), where cΓ means bottom of the conduction band at Γ, converges towards the tetrahedron value for large N and small η. Using N = 128, ℑmΣcΓ(ε0cΓ) differs from the tetrahedron method by values in the 34 meV to 6 meV interval when varying η from 50 meV to 1 meV, respectively. Increasing the q-mesh density to N = 192, the interval is even smaller, going from 6 meV to 1 meV when varying η from 50 meV to 1 meV.
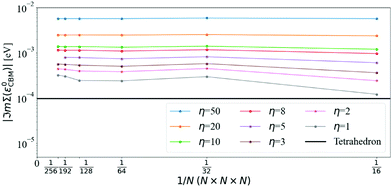
The convergence of the imaginary part at the CBM is more problematic (see Fig. 4): the value of ℑmΣCBM(ε0CBM) at T = 300 K with the tetrahedron method is very small, around 10−4 eV, i.e. smaller than the values of η. Further convergence would require η ≤ 10−4 and even denser grids, which are not practical or indeed necessary. Selecting η = 5 meV and N = 128 (values that will be used later on), ℑmΣCBM(ε0CBM) is within an order of magnitude of the very small tetrahedron value. Lowering η systematically decreases ℑmΣCBM(ε0CBM), but it also increases numerical noise as detailed below.
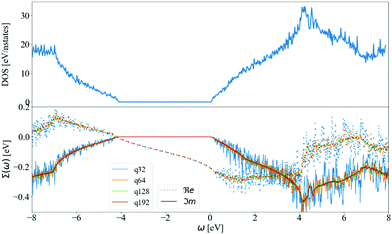
The effect of increasing the density of the q-mesh in the imaginary part of the dynamical self-energy can be observed in Fig. 5: as the q-mesh increases, the noise decreases. We choose a q-mesh of N = 128 for all the following calculations, which produces low computational noise and a convergence error of 0.6% on the value of the self energy at the CBM.
In Fig. 5, we also display the density of states (DOS). The imaginary part of the self-energy can be seen as a similar sum over accessible electronic states at m, k + q, but weighted by finite e–ph matrix elements, Bose–Einstein factors at finite T, and shifted by phonon frequencies. Another observation is a linear departure of ℑmΣCBM(ω) at ωLO from the value ℑmΣCBM(ε0CBM). The DOS shows a similar behavior. This is at variance with the case of Fröhlich model and polar materials,26 in which the e–ph matrix elements diverge at small q. This results in a peak in the self-energy at the LO phonon frequency, which is not present in the corresponding DOS.
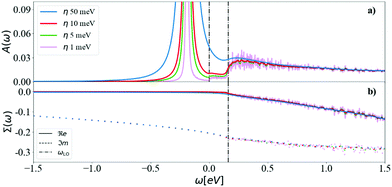
For a fixed, accurate, q-mesh size (N = 128), we show the effect of η in Fig. 6. At very low η = 1 meV, there are strong oscillations in the satellite features of the spectral function. The width of the QP peak also increases with η, such that a numerical compromise must be found. Above the CBM QP energy of −0.180 eV, there are two plateaus in the spectral function: a small one starting at zero frequency, and a more important one starting at the highest phonon frequency, ωLO, (dot-dashed line), analogous to the peak observed in the Frölich self energy form for polar materials. To avoid computational noise, and very dense q-meshes, we select for the rest of the paper a N = 128 q-mesh and η = 5 meV. Analysis of the plateaus and the spectral function will be detailed in Section 3.1.
Other convergence to consider in the self-energy is the sum over m bands in eqn (3), which includes unoccupied states and its numerical convergence over empty bands becomes burdensome. An alternative is to replace high-energy bands with the solution of a non-self-consistent Sternheimer equation.67 Study of this convergence can be found in Section S4 (ESI†).
The calculation of the cumulant function at low temperatures is complicated by the very small value of ℑmΣCBM(ε0CBM). ℑmΣCBM(ε0CBM) is related to the decay of the QP and its lifetime: the smaller it is, the longer it takes the QP to decay. The range of the time mesh can be estimated through eqn (12), which is an envelope of the Green's function, which can be used to determine the time at which the QP decays and reaches a given tolerance tol, tmax = − (ln(tol) + w)/Γ.
At low temperatures, e.g. 40 K, ℑmΣCBM(ε0CBM) is −4.95 × 10−6 eV and the number of frequency points required is huge. The grid size can be estimated as Δω/δω, where Δω is the frequency range, and δω is the spacing between points, which can be otained as δω = 2π/tmax. We get tmax ≈ 918 ps for a tol of 10−3, and for a range Δω of 20 eV (the convergence of Δω is explained in S3, ESI†), we obtain 5.3 × 106 points. Therefore, we limit the calculations to room temperature and above, where considerably fewer frequency points are required.
At T = 300 K, ℑmΣCBM(ε0CBM) = −1.51 × 10−4 eV gives a tmax ≈ 20 ps with a tolerance of 10−3, leading to 174.7 × 103 frequency points. Increasing the temperature, ℑmΣCBM(ε0CBM) increases, which means shorter QP lifetimes and a lower number of frequency points.
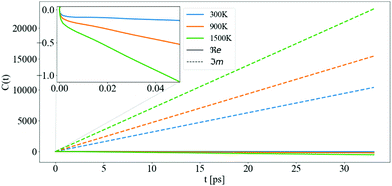
In Fig. 7, the cumulant function is shown for T = 300, 900, and 1500 K. The linear behavior of the cumulant at infinite time is present both in the real and imaginary parts. The large time slope of the real part is ℑmΣCBM(ε0CBM) and the slope of the imaginary part is ℜeΣCBM(ε0CBM). The intercept of ℜeC(t), wk, originates from the asymmetry46 of the denominator of Σ when summing over all jq states, both elements described in eqn (12) and its convergence is examined in more detail in the S3 (ESI†). The increase of the ℜeC(t) at t → ∞ accelerates the decay of the QP and determines its lifetime τ = 1/2Γ.
3.1 Spectral function and ARPES at finite temperature
After converging the self-energy, we can evaluate the spectral function at finite temperatures using the DM and the CE approaches. In Fig. 8, the ZPR can be observed by following the shift of the renormalized band gap to T = 0 K (the bare band gap is set to zero). The ZPR can be determined experimentally by extrapolating the linear regime at high temperatures to 0 K. Using a Pässler fit68 to the measurements of Clark et al.69 gives a ZPR of −0.259 eV. Using also the difference in renormalization for isotopes 12C and 13C, the obtained ZPR is −0.364 eV.70Table 2 shows a range of calculated ZPR that go from −315 meV to −619 meV.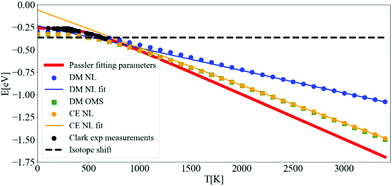 | ||
| Fig. 8 Variation of the indirect band gap of diamond with respect to temperature. The bare band gap was set to zero. The calculations of the band gap using DM-NL (blue points) do not produce a strictly linear behaviour, and the DM-OMS (green squares) produces the same values as the CE using the NL approach (yellow points). Pässler fit68 (solid red line) to the experimental points by Clark et al.69 (black points) and measured ZPR by isotope shift70 (black dashed line). The calculations were done with N = 64 and η = 10 meV. | ||
The fast convergence of the real part of the self-energy allows to determine the renormalization of the band gap in Fig. 8 at a coarse N = 64 q-mesh and at a η of 10 meV. The slope of the DM-OMS energy is very close to the CE-NL slope, −0.409 meV K−1, giving an extrapolated ZPR from high temperatures of −0.281 eV. This value differs from the CE-NL calculated at T = 0 K by −0.066 eV. This discrepancy emerges from two factors: the linear extrapolation should be made above diamond's high Debye temperature (2246 K),73 and the non-adiabatic self-energy, eqn (3), includes a plus and minus term of the phonon energy that is not present in the adiabatic self-energy (an adiabatic self-energy yields the same ZPR when calculated at T = 0 K and when extrapolated from high temperatures). The very similar behaviour with temperature for DM-OMS and CE-NL derives from the cancellation of errors of the former between the exclusion of higher order e–ph interactions and the evaluation of the self-energy at the KS energy. The behavior of DM-NL is erratic, since it is not linear at high temperatures, as opposed to CE-NL and DM-OMS. If one attemps a linear extrapolation for temperatures above 2500 K, where it becomes almost linear, the ZPR gives −0.092 eV with a discrepancy of −0.207 eV from the ZPR calculated at T = 0 K, three fold the CE-NL discrepancy. Note that in the NL approach we use the value of the highest point of the main peak in the spectral function (as it will be seen later on) and should be the one taken into account. The fortuitous coincidence with DM-OMS has been found in other works.26
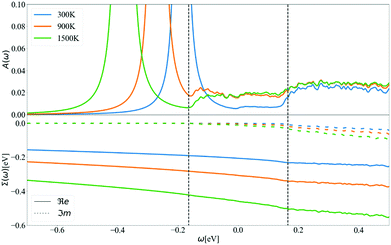
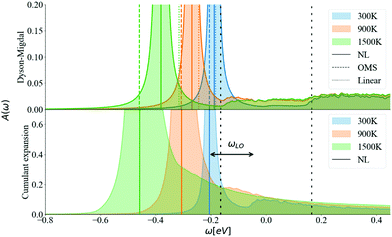
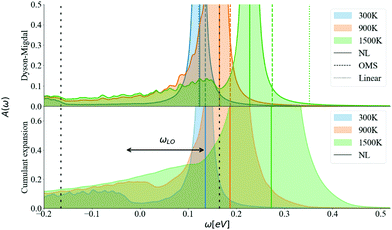
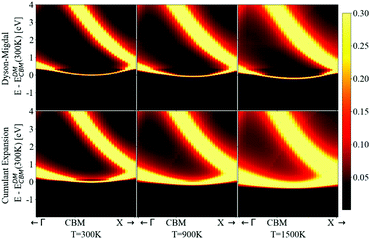
Going further by evaluating the dynamical part of the spectral function at the CBM in Fig. 9 for T = 300, 900, and 1500 K, one can observe a temperature-dependent offset in the QP peak (the KS energy is ω = 0) which corresponds to the DM-NL energy. Unlike the Fröhlich polaron in simple polar materials, where there are well defined satellite peaks, here the signature of a nonpolaron is a plateau. As the temperature increases, more states become available; in particular, Σ− starts to contribute to the presence of another plateau with states below the KS energy. Similar to polar materials, the DM approach overestimates the energy distance between the main QP and the high plateau, giving 2.4 ωLO at T = 300 K.
The energy shift of the QP relative to the KS energy at both the CBM and VBM reduces the band gap, as shown in Fig. 10 and 11, respectively (the KS energy is set at 0 eV in each case). Taken together, they determine the band gap shift in Fig. 8. The QP peaks are located at the εNL energy. The DM-NL energy differs from the CE-NL more noticeably at higher temperatures. Since the latter contains higher orders of e–ph interactions, the CE approach is more appropriate to determine the QP energy. These energies are very close to the DM-OMS approximation, as also observed in Fig. 8.
At the DM level, the frequencies of both plateaus are disconnected from the QP energy, as discussed in the ESI† S6.2. As the temperature increases, the nonpolaron plateau seems to get closer to the QP peak. However, this is an artifact of DM, as new states become accessible through Σ−. In DM, Σ+ gives contributions that start at +ωLO counting from the KS energy, independently of the temperature or position of the QP peak. At higher temperatures, Σ− becomes larger and contributes to the spectral function at −ωLO. Since the band renormalization is larger than −ωLO, the −ωLO plateau still appears to the right of the QP peak, giving the impression that the plateau is shifting with temperature, while it actually corresponds to another plateau. Also, there is an un-intuitive behaviour with DM at the VBM, where the broadening of the QP at 900 K seems wider than at 1500 K. This is due to the overlap between the states created by Σ+ at +ωLO (counting from ω = 0) and the QP peak. More detailed analysis is deferred to S6.2 (ESI†).
For the CE approach, let us focus first on the CBM. At low temperatures, Σ+ produces a plateau at the right energy distance, +ωLO, from the QP peak. When increasing the temperature, the main QP becomes wider. It is easier to identify features in the DM spectral function, because the self-energy consists only of two terms, Σ+ and Σ−. In the CE instead, as it consists of an exponential representation, higher order terms mix the contributions from the QP peak with satellite features in the spectral function. This smooths out the plateau, which is no longer separate from the QP at higher temperatures, although a weak peak is visible at 900 K, and a long tail is still present at 900 K and 1500 K. Results are similar for the VBM (Fig. 11). Unlike polar insulators, such as LiF and MgO,26 or the Fröhlich model in the CE approach, there is no visible signature at +2ωLO.
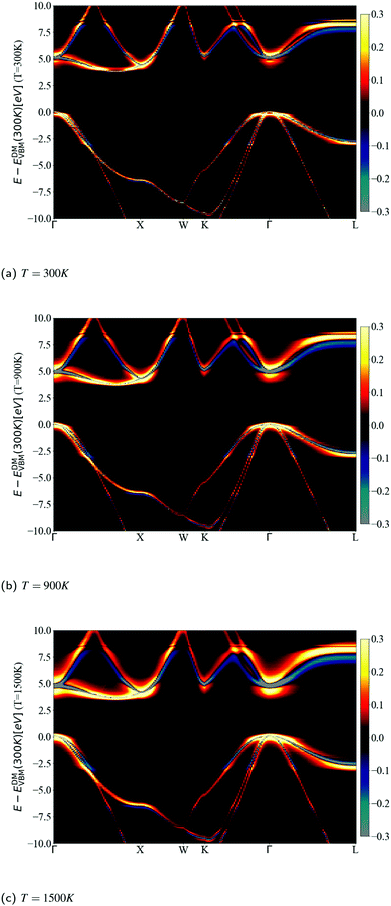
The spectral function close to the band edges was calculated along a path between high-symmetry points in reciprocal space (as commonly done in ARPES experiments). This allows us to visualize the effects of phonons, and to compare the DM and CE approaches in reciprocal space (see Fig. 12). For both approaches we can perceive at 300 K a light red color just above the yellow band at the CBM, which represents the nonpolaronic signature. In DM, the plateau is located at 2.4ωLO above the CBM quasi-particle peak, and as the temperature increases, the plateau shifts down about 0.32 eV, which seems constant in this energy interval (the same shift can be seen in the top plot of Fig. 10 with the shift of the plateau to lower energy from 300 K to 900 K). The QP peak shifts down from −0.179 eV to −0.367 eV when the temperature increases from 300 K to 1500 K, respectively. See Table S6.1 (ESI†). In the CE, the satellite band is located ωLO away from the CBM QP peak at 300 K. As temperature increases the QP mixes with the nonpolaronic signature and increases the broadening. There is also a huge broadening increase at the degenerate bands close to the high-symmetry point X. The changes with temperature and absolute energy resolution mean these features should be visible experimentally, and we hope to stimulate more detailed ARPES studies on intrinsic diamond as a model for nonpolarons.
To compare more quantitatively, the DM calculated ARPES was subtracted from the CE calculations in Fig. 13. The intensity range is limited between −0.3 and 0.3 to detail the view of the nonpolaronic signatures. For positive values the CE has a higher spectral function, while the opposite occurs for negative values. One can observe a broadening or/and shift effect when transiting from DM (a thin line green or grey) to CE, which surrounds the green or grey line by a yellow or red area. In some parts of the band structure, such as the bottom of the conduction band close to the high symmetry point L, one can observe a tail to higher energies and an asymmetry close to the QP peak, as the weight at the QP energy using DM (blue), is spread to the tail within CE (yellow). As the temperature increases from 300 K in Fig. 13a, 900 K in Fig. 13b, to 1500 K in Fig. 13c, the broadening increases, especially for states close to the Fermi level. The shift of the QP peak from DM to CE as seen in Fig. 10 and 11 is not visible in the full band structure, as the scale of the energy in the calculated ARPES spectra is much wider than the energy shift.
Individual ARPES images for CE and DM can be found in Fig. S6.4 (ESI†). The dispersion of bands is noticeable and qualitatively comparable with measured ARPES images in boron-doped diamond.74–76 However, doping lifts the degeneracy and lowers the Fermi energy below the VBM, making it difficult to observe polaronic features, the plateau or even the QP peak at the VBM. The only observation we have found of experimental polaronic signatures in ARPES is in surface hydrogen-terminated on diamond,12 showing several satellite signatures offset by multiples of ωLO from the QP.
3.2 Contribution due to long-range and short-range fields
In this section, we employ the Fourier-based interpolation technique discussed in Section 2.5 to analyze the contribution given by the SR and LR quadrupolar fields to the e–ph scattering potentials. More specifically, we compare the unit cell average of the (local part) of the e–ph scattering potential55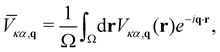 | (18) |
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) . In the first one, the LR contribution is given by
. In the first one, the LR contribution is given by  , the potential of the model in eqn (17). Dynamical quadrupoles are given by
, the potential of the model in eqn (17). Dynamical quadrupoles are given by| Qβγκα = (−1)κ+1Qκ|εβγα|, | (19) |
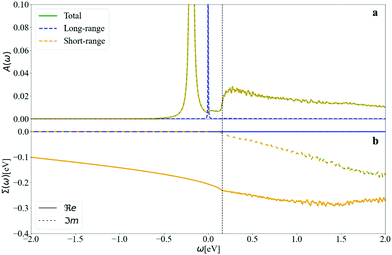
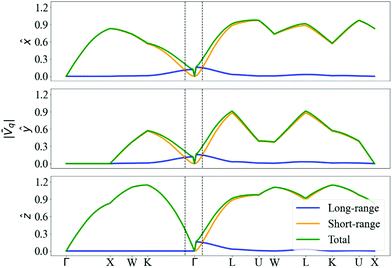
Even if a quadrupole long-range field is present, it can be noticed from Fig. S6.3 (ESI†) that its importance disappears when calculating the scattering matrix elements, and there is thus negligible contribution from long-range fields to the nonpolaron spectral function. The maximum value of |gjqnmk| is of 0.97, close to the effective coupling constant found experimentally in surface hydrogen-terminated on diamond of 1.1.12
The negligible contribution of long-range fields can also be observed in the spectral function and the self-energy in Fig. 15. The self-energy of the long-range is almost zero, meaning that there is no interaction between the electrons and the phonons that could produce long-range fields, leading to a single peak at the KS energy of the non-interacting system. The short-range field results are almost identical to those of the full DFPT potential.
4 Conclusion
First-principles e–ph calculations for diamond reveal spectroscopic signatures that originate from a quasiparticle that can be called nonpolaron: a bound electron state dressed with phonons in a non-polar system. We expect such signatures to be generic and occur in other covalent crystals.In diamond, unexpectedly, the contribution to the formation of the nonpolaron from the long-range quadrupole fields is negligible and the binding is mainly generated by the short-range fields.
The calculations were done using both the standard Dyson–Migdal approach and the cumulant expansion. According to the CE, the signature of a nonpolaron is a plateau in the spectral function, starting one phonon energy (corresponding to the highest frequency mode) above the main QP peak. The plateau shape is at variance with the satellite peaks seen in polar systems, each separated from the QP peak or the previous replica by the LO phonon energy.
As in polar materials, we find that the QP is not properly captured in one shot NL-DM (although it might be improved by self-consistency in G). It yields an incorrect temperature dependence of the DM QP peak, which is not linear at high temperatures. The DM approximation also yields a wrong position for the plateau structure, which is located at ±ωLO relative to the KS value, independently of the position of the QP.
Calculations of the ZPR within CE and using the DM on-the-mass-shell approximation give similar results, and are in good agreement with experimental values of the ZPR. In addition, the cumulant expansion method delivers a physically correct nonpolaron energy, and the inclusion of the higher order terms in the e–ph interaction provides a more “realistic” view of the spectral function. The calculated ARPES spectrum of diamond around the band gap shows a broader dispersion within CE compared to Dyson–Migdal.
Finally, in order to obtain the spectral functions, self-energies, ZPR and temperature dependence of the band gap, convergence with respect to the q-mesh and the broadening parameter η were carefully studied. The real part of the QP self-energy converges quickly in opposition to the imaginary part. The narrow QP broadening at the VBM and CBM implies a very strong sensitivity of the imaginary part of the self-energy to convergence, and the imaginary η introduced in the Green's function should be chosen carefully. Our study showcases the combination of convergence techniques to reduce computational cost, in particular: the Sternheimer equation, which substitutes empty bands by a linear response equation, and the Kramers–Kronig relation, which replaces a difficult frequency integration by the use of a pre-calculated complex self-energy.
This paper motivates further research, both experimental and theoretical, on the topic of non-polar phonon modes in interacting electron–phonon systems.
Author contributions
J. C. A. prepared the manuscript, carried out calculations, prepared all graphical material and implemented the cumulant expansion, with help from M. G., J. P. N. and M. J. V. J. P. N. contributed by including supplementary information, discussions, editing and reviewing. M. G. and X. G. contributed with discussions, editing and reviewing. M. J. V. and X. G. acquired the main funding for the project. M. J. V. supervised the project and calculations, and edited and reviewed the manuscript.Conflicts of interest
The authors have no conflicts of interest to declare.Acknowledgements
This work has been supported by the Fonds de la Recherche Scientifique (FRS-FNRS Belgium) through the PdR Grant No. T.0103.19 – ALPS. Computational resources have been provided by CECI funded by the FRS-FNRS Belgium under Grant No. 2.5020.11, as well as the Tier-1 supercomputer of the Fédération Wallonie-Bruxelles, infrastructure funded by the Walloon Region under grant agreement no. 1117545. We acknowledge a PRACE award granting access to MareNostrum4 at Barcelona Supercomputing Center (BSC), Spain (OptoSpin project id. 2020225411).References
- M. Meevasana, et al. , New J. Phys., 2010, 12, 023004 CrossRef.
- A. Janotti, J. B. Varley, M. Choi and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085202 CrossRef CAS.
- P. M. Chaikin, A. F. Garito and A. J. Heeger, Phys. Rev. B: Solid State, 1972, 5, 4966 CrossRef.
- K. P. McKenna, M. J. Wolf, A. L. Shluger, S. Lany and A. Zunger, Phys. Rev. Lett., 2012, 108, 116403 CrossRef PubMed.
- G. Brunin, H. P.-C. Miranda, M. Giantomassi, M. Royo, M. Stengel, M. J. Verstraete, X. Gonze, G.-M. Rignanese and G. Hautier, Phys. Rev. Lett., 2020, 125, 136601 CrossRef CAS PubMed.
- J. Park, J.-J. Zhou, V. A. Jhalani, C. E. Dreyer and M. Bernardi, Phys. Rev. Lett., 2020, 102, 125203 CAS.
- D. Emin, C. H. Seager and R. K. Quinn, Phys. Rev. Lett., 1982, 28, 813 CrossRef.
- D. J. Gibbons and W. E. Spear, J. Phys. Chem. Solids, 1966, 27, 1917 CrossRef CAS.
- S. H. Howe, P. G. Le Comber and W. E. Spear, Solid State Commun., 1971, 9, 65 CrossRef CAS.
- V. Vasilchenko, S. Levchenko, V. Perebeinos and A. Zhugayevych, J. Phys. Chem. Lett., 2021, 12, 4674 CrossRef CAS PubMed.
- D. Emin and M.-N. Bussac, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14290 CrossRef CAS PubMed.
- J. D. Rameau, J. Smedley, E. M. Muller, T. E. Kidd and P. D. Johnson, Phys. Rev. Lett., 2011, 106, 137602 CrossRef CAS PubMed.
- K. M. Shen, et al. , Phys. Rev. Lett., 2004, 93, 267002 CrossRef CAS PubMed.
- M. Mohamed, M. M. May, M. Kanis, M. Brützam, R. Uecker, R. van de Krol, C. Janowitz and M. Mulazzi, RSC Adv., 15606 Search PubMed.
- C. Chen, J. Avila, E. Frantzeskakis, A. Levy and M. C. Asensio, Nat. Commun., 2015, 6, 8585 CrossRef CAS PubMed.
- M. Emori, A. Sakino, K. Ozawa and H. Sakama, Solid State Commun., 2014, 188, 15 CrossRef CAS.
- S. Moser, et al. , Phys. Rev. Lett., 2013, 110, 196403 CrossRef CAS PubMed.
- M. Kang, et al. , Nat. Mater., 2018, 17, 676 CrossRef CAS PubMed.
- J. M. Riley, F. Caruso, C. Verdi, L. B. Duffy, M. D. Watson, L. Bawden, K. Volckaert, G. van der Laan, T. Hesjedal, M. Hoesch, F. Giustino and P. D.-C. King, Nat. Commun., 2018, 9, 2305 CrossRef CAS PubMed.
- C. Cancellieri and V. N. Strocov, Spectroscopy of Complex Oxide Interfaces: Photoemission and Related Spectroscopies, Springer, Cham, 2018, pp. 107–151 Search PubMed.
- G. Antonius, S. Poncé, P. Boulanger, M. Côté and X. Gonze, Phys. Rev. Lett., 2014, 112, 215501 CrossRef.
- P. B. Lautenschlager, P. Allen and M. Cardona, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 5501 CrossRef CAS PubMed.
- Z. Tong, S. Li, X. Ruan and H. Bao, Phys. Rev. B, 2019, 100, 144306 CrossRef CAS.
- J. M. Ziman, Electrons and Phonons: The theory of transport phenomena in solids, Oxford University Press, 1960 Search PubMed.
- F. Marsiglio and J. P. Carbotte, in Electron-Phonon Superconductivity, ed. K. H. Bennemann and J. B. Ketterson, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 73–162 Search PubMed.
- J. P. Nery, P. B. Allen, G. Antonius, L. Reining, A. Miglio and X. Gonze, Phys. Rev. B, 2018, 97, 115145 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355 CrossRef CAS.
- S. Baroni, S. Gironcoli and A. Dal Corso, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- R. M. Martin, L. Reining and D. M. Ceperley, Interacting Electrons: Theory and Computational Approaches, Cambridge University Press, 2016 Search PubMed.
- F. J. Dyson, Phys. Rev., 1949, 75, 1736 CrossRef.
- A. B. Migdal, Zh. Eksp. Teor. Fiz., 1958, 34, 1438 CAS.
- R. Kubo, J. Phys. Soc. Jpn., 1962, 17, 1100 CrossRef.
- O. Gunnarsson, V. Meden and Schönhammer, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 10462 CrossRef CAS PubMed.
- J. J. Kas, J. J. Rehr and L. Reining, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085112 CrossRef CAS.
- F. Aryasetiawan, L. Hedin and K. Karlsson, Phys. Rev. Lett., 1996, 77, 2268 CrossRef CAS PubMed.
- M. Guzzo, J. Kas, F. Sottile, M. Silly, F. Sirotti, J. Rehr and L. Reining, Eur. Phys. J. B, 2012, 85, 324 CrossRef.
- F. Caruso and F. Giustino, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045123 CrossRef.
- E. Antoncik, Czech. J. Phys., 1955, 5, 449 CrossRef CAS.
- H. Y. Fan, Phys. Rev., 1951, 82, 900 CrossRef CAS.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- P. B. Allen and V. Heine, J. Phys. C: Solid State Phys., 1976, 9, 2305 CrossRef CAS.
- S. Poncé, Y. Gillet, J. Laflamme Janssen, A. Marini, M. Verstraete and X. Gonze, J. Chem. Phys., 2015, 143, 102813 CrossRef PubMed.
- G. D. Mahan, Many-Particle Physics, Springer, Boston, 2000 Search PubMed.
- G. Antonius, S. Poncé, E. Lantagne-Hurtubise, G. Auclair, X. Gonze and M. Côté, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085137 CrossRef.
- A. Mishchenko, N. Prokof'ev, A. Sakamoto and B. Svistunov, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 6317–6336 CrossRef CAS.
- B. Gumhalter, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165406 CrossRef.
- D. C. Langreth, Phys. Rev. B: Solid State, 1970, 1, 471 CrossRef.
- M. Guzzo, G. Lani, F. Sottile, P. Romaniello, M. Gatti, J. J. Kas, J. J. Rehr, M. G. Silly, F. Sirotti and L. Reining, Phys. Rev. Lett., 2011, 107, 166401 CrossRef PubMed.
- L. Hedin, Phys. Scr., 1980, 21, 477 CrossRef CAS.
- A. Eiguren and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045124 CrossRef.
- F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108 CrossRef.
- P. Vogl, Phys. Rev. B: Solid State, 1976, 13, 694 CrossRef.
- C. Verdi and F. Giustion, Phys. Rev. Lett., 2015, 115, 176401 CrossRef PubMed.
- J. Sjakste, N. Vast, M. Calandra and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 054307 CrossRef.
- G. Brunin, H. P.-C. Miranda, M. Giantomassi, M. Royo, M. Stengel, M. J. Verstraete, X. Gonze, G.-M. Rignanese and G. Hautier, Phys. Rev. B, 2020, 102, 094308 CrossRef CAS.
- V. A. Jhalani, J.-J. Zhou, J. Park, C. E. Dreyer and M. Bernardi, Phys. Rev. Lett., 2020, 125, 136602 CrossRef CAS PubMed.
- M. Royo and M. Stengel, Phys. Rev. X, 2019, 9, 021050 CAS.
- X. Gonze, et al. , Comput. Phys. Commun., 2020, 248, 107042 CrossRef CAS.
- A. H. Romero, et al. , J. Chem. Phys., 2020, 152, 124102 CrossRef CAS PubMed.
- D. M. Roessler and W. C. Walker, Phys. Rev., 1967, 159, 733 CrossRef CAS.
- D. Roessler and W. C. Walker, J. Phys. Chem. Solids, 1967, 28, 1507 CrossRef CAS.
- O. Madelung, Semiconductors: Data Handbook, Springer, London, 2004 Search PubMed.
- F. Karsai, M. Engel, E. Flage-Larsen and G. Kresse, New J. Phys., 2018, 20, 123008 CrossRef CAS.
- A. Miglio, V. Brousseau-Couture, E. Godbout, G. Antonius, Y.-H. Chan, S. G. Louie, M. Côté, M. Giantomassi and X. Gonze, npj Comput. Mater., 2020, 6, 167 CrossRef.
- V. Brousseau-Couture, E. Godbout, M. Côté and X. Gonze, Phys. Rev. B Search PubMed , submitted.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef PubMed.
- X. Gonze, P. Boulanger and M. Côté, Ann. Phys., 2010, 523, 168–178 CrossRef.
- R. Pässler, Phys. Status Solidi B, 1999, 216, 975 CrossRef.
- C. D. Clark, P. J. Dean and P. V. Harris, Proc. R. Soc. A, 1964, 277, 312 CAS.
- M. Cardona, Solid State Commun., 2005, 133, 3 CrossRef CAS.
- B. Monserrat, G. J. Conduit and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 184302 CrossRef.
- S. Zollner, M. Cardona and S. Gopalan, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 3376 CrossRef CAS PubMed.
- D. L. Burk and S. L. Friedberg, Phys. Rev., 1958, 111, 1275 CrossRef CAS.
- T. Yokoya, T. Nakamura, T. Matsushita, T. Muro, Y. Takano, M. Nagao, T. Takenouchi and H. T.-O. Kawarada, Nature, 2005, 438, 647 CrossRef CAS PubMed.
- A. C.-t Pakpour-Tabrizi, Nanoscale Adv., 2020, 2, 1358 RSC.
- H.-t Okazaki, J. Phys. Chem. Solids, 2008, 69, 2978 CrossRef CAS.
- F. M. Peeters and J. T. Devreese, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 4890 CrossRef PubMed.
- W. H. Sio, C. Verdi, S. Ponce and F. Giustino, Phys. Rev. B, 2019, 99, 235139 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp01012g |
| This journal is © the Owner Societies 2022 |

![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)