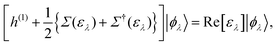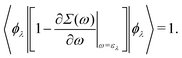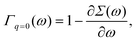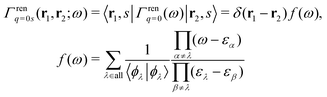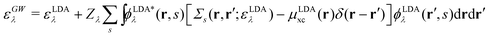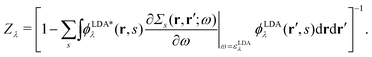Extended quasiparticle approach to non-resonant and resonant X-ray emission spectroscopy
Received
28th February 2022
, Accepted 20th June 2022
First published on 21st June 2022
Abstract
The initial states of the secondary processes of X-ray emission spectroscopy (XES) and resonant inelastic X-ray scattering (RIXS) are highly excited eigenstates with a deep core hole after a X-ray photoelectron spectroscopy (XPS) process and a X-ray photoabsorption spectroscopy (XAS) process, respectively, so that the XES and RIXS calculation offers a good example of extended quasiparticle theory (EQPT) (K. Ohno, S. Ono and T. Isobe, J. Chem. Phys., 2017, 146, 084108) which is applicable to any initial exited eigenstate. We apply the standard one-shot GW + Bethe–Salpeter equation (BSE) approach in MBPT to this problem on the basis of EQPT and analyze XES and RIXS spectra for CH4, NH3, H2O, and CH3OH molecules. We also suggest a simpler approach only using the GW calculation without solving the BSE to compute the XES and RIXS energies, although it cannot give the spectral intensity. Moreover, according to extended Kohn–Sham theory (T. Nakashima, H. Raebiger and K. Ohno, Phys. Rev. B, 2021, 104, L201116), we give a justification and comment of applying the method relying on time-dependent density functional theory as well as the one-shot GW + BSE approach to this problem.
1 Introduction
Recent advances in synchrotron1 and in-house2 X-ray sources have accelerated the use of powerful analytical tools involving an excitation of a core electron.3,4 While X-ray photoelectron spectroscopy (XPS) and X-ray photoabsorption spectroscopy (XAS) use the primary process of exciting one electron from a core level up to, respectively, above and below the vacuum level, (non-resonant) X-ray emission spectroscopy (XES) and resonant inelastic X-ray scattering (RIXS) involve the secondary processes, where X-ray radiative recombination of a valence electron and a core hole takes place after the XPS core-level ionization and the XAS core-electron excitation, respectively. XES and RIXS have been recognized as new experimental techniques for chemical analyses which can give important information of valence electrons in the presence of a deep core hole.5,6 However, since the initial states in the secondary processes of XES and RIXS are highly excited eigenstates with a deep core hole, which is created in the preceding XPS and XAS processes, a first-principle calculation using the GW + Bethe–Salpeter equation (BSE) method7 in many-body perturbation theory (MBPT) or time-dependent density functional theory (TDDFT)8 for XES and RIXS is a big challenge. This situation is different from XPS and XAS, whose initial states are the ground state. Below, we confine our discussion to XES and RIXS only.
In order to obtain the transition energies and the intensities of XES spectra, Besley et al.9 applied configuration interaction singles (CIS), TDDFT, and equation of motion – coupled cluster singles & doubles (EOM-CCSD) methods. Concerning the X-ray fluorescence photon energies, the TDDFT results with BLYP and B3LYP exchange–correlation functionals showed large deviations from the experimental data due to the self-interaction error, but the use of a short-range-corrected functional improved the results. Their CIS, TDDFT(B3LYP), and EOM-CCSD results with the 6-3111G** basis set for the carbon K-edge XES spectrum of a CH3OH molecule showed, however, three peaks only in contrast to the experimental spectrum10 showing five peaks. Recently, Besley refined the TDDFT result and obtained five peaks using B3LYP11 or CAM-B3LYP12 with the cc-pCVQZ basis set, but still an empirical shift by −6.3 eV or −5.7 eV was required to fit to the experimental XES spectrum. (A larger shift by +10.9 eV was required for a direct comparison between the Kohn–Sham eigenvalues and the experimental XES spectrum.12) In the present paper, we focus this problem from a different point of view on the basis of exact theories, i.e., extended quasiparticle theory (EQP) by Ohno et al.13 and extended Kohn–Sham (EKS) theory which was quite recently established by Nakashima et al.14 There are also several other reports on XES using TDDFT.15–18 Recently, Cruz et al.19,20 used TDDFT for the RIXS analysis.
On the other hand, in order to treat XES or RIXS with the Green's function method in MBPT, Vinson et al.21,22 performed a standard one-shot GW (G0W0) calculation and solve the BSE for valence excitations only. Their initial state for XES is the neutral N electron ground state, not the true N − 1 electron state. Therefore, they had to introduce an empirical parameter to compare their results with experiments. However, according to EQP theory,13 one can start calculation of the GW + BSE method of MBPT from an arbitrary excited eigenstate. That is, EQP theory allows us to set the initial state to be the N − 1 (or N) electron excited state with a deep core hole, where one electron is emitted from the core level to the vacuum (empty) level. This theory can remove the difficulty to compute XES and RIXS spectra with MBPT, which is a clear novelty. Indeed, we have recently succeeded in calculating the XES spectra of several small molecules (CH4, NH3, H2O, CH3OH) using the G0W0 + BSE method of MBPT without introducing any empirical parameter.23 In our approach, the initial state of the GW + BSE method is the core-excited state.
The purpose of the present paper is to give a justification of using MBPT and TDDFT for XES and RIXS and discuss the problem lying in the existing methodologies. Here, we apply the G0W0 + BSE method to the XES and RIXS analysis of CH4, NH3, H2O, and CH3OH molecules and discuss the accuracy of the resulting spectra. Moreover, according to extended Kohn–Sham theory,14 we give a justification and comment of applying the method relying on TDDFT as well as the one-shot GW + BSE approach to this problem. Based on this theory, we discuss the proper problem of the XES and RIXS calculations.
In what follows, we assume, as usual, that the initial state of the XES and RIXS secondary processes is an excited eigenstate of the total Hamiltonian. However, some non-equilibrium effect may occur in the experimental situation. For example, we have totally ignored the effect of molecular vibration, which is sometimes experimentally observed in the XES and RIXS spectra.24 So, we have to say that we use a time-independent approximation and totally ignore dynamical effect. However, for the dynamics, we have successfully performed a TDGW molecular dynamics simulation for the excited state CO* + H → HCO reaction25 on the basis of EQP theory. Another research using the non-equilibrium Green's function technique26,27 has been performed by Spataru et al.28 and by Perfetto and Stefanucci.29 Such studies should be extended to the X-ray related dynamics30 in the future.
The rest of this paper is organized as follows. First, we will briefly review EQP and EKS theories in Section 2. Computational details and results of our RIXS calculation based on EQP theory are given, respectively, in Sections 3 and 4. Discussions are given in Section 5, where a simpler approach only using the GW calculation without solving the BSE is suggested, and finally Section 6 concludes the paper.
2 Theory
2.1 EQP theory
Here we briefly review the keypoint of extended quasiparticle (EQP) theory.13 First, let us derive the equation satisfied by the EQP wave functions and the EQP energies. The Hamiltonian H is given by H = H(1) + H(2) with the one-body part| | 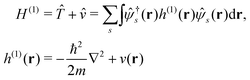 | (1) |
and the two-body part| | 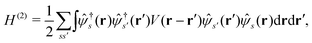 | (2) |
where ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r),
(r), ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) †s(r) are annihilation and creation operators at position and spin coordinates (r, s), V(r − r′) = e2/4πε0|r − r′| is the Coulomb interaction, and
†s(r) are annihilation and creation operators at position and spin coordinates (r, s), V(r − r′) = e2/4πε0|r − r′| is the Coulomb interaction, and 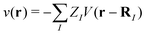 is the nuclear potential. The commutation relation between
is the nuclear potential. The commutation relation between ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r) and H is given by
(r) and H is given by| | 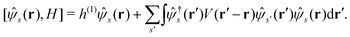 | (3) |
Let |ΨM±1λ〉 and |ΨMγ〉 be the (M ± 1)- and M-electron eigenstates of the Hamiltonian H, and EM±1λ and EMγ be the corresponding energy eigenvalues. Then, by sandwiching eqn (3) with 〈ΨM−1μ| and |ΨMγ〉 or with 〈ΨMγ| and |ΨM+1ν〉, we derive| | 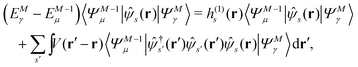 | (4a) |
| | 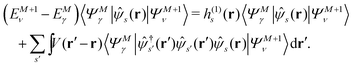 | (4b) |
Here, the second term in the right-hand side (r.h.s.) of eqn (4) is conventionally rewritten as| | 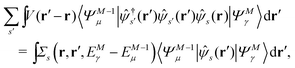 | (5a) |
| | 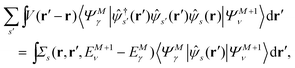 | (5b) |
by introducing the energy-dependent self-energy 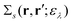 . Since both identities (5a) and (5b) hold simultaneously, they should be an equivalent identity. In fact, if we replace M, μ and γ with M + 1, γ and ν in eqn (5a), we obtain eqn (5b). This means that both equations should hold for arbitrary M, γ, μ and ν. This is the reason that MBPT can be applicable to an arbitrary excited eigenstate as an initial state. Indeed the full Green's function formulation of MBPT can be reproduced by using the Brillouin–Winger perturbation theory,13 which is certainly applicable to any excited eigenstate without doubt. Now, defining EQP energies as
. Since both identities (5a) and (5b) hold simultaneously, they should be an equivalent identity. In fact, if we replace M, μ and γ with M + 1, γ and ν in eqn (5a), we obtain eqn (5b). This means that both equations should hold for arbitrary M, γ, μ and ν. This is the reason that MBPT can be applicable to an arbitrary excited eigenstate as an initial state. Indeed the full Green's function formulation of MBPT can be reproduced by using the Brillouin–Winger perturbation theory,13 which is certainly applicable to any excited eigenstate without doubt. Now, defining EQP energies as| | | εμ =EMγ − EM−1μ, εν =EM+1ν − EMγ, | (6) |
and EQP wave functions as| | ϕμ(r, s) = 〈ΨM−1μ|![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r)|ΨMγ〉, ϕν(r, s) = 〈ΨMγ| (r)|ΨMγ〉, ϕν(r, s) = 〈ΨMγ|![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r)|ΨM+1ν〉, (r)|ΨM+1ν〉, | (7) |
we successfully derive EQP equations| | 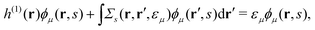 | (8a) |
| | 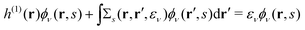 | (8b) |
from eqn (5a) and (5b).
EQP energies defined by eqn (6) directly correspond to the photoemission (PE) and inverse photoemission (IPE) energies associated with the initial excited eigenstate |ΨMγ〉, and EQP wave functions defined by eqn (11) describe the created hole and electron (particle) distribution in the corresponding PE/IPE process. However, EQP wave functions are not orthogonal to each other and their norm is less than one.31–33 They are even not linearly independent.34 Therefore, there are, in principle, infinite number of occupied (occ) EQP wave functions ϕμ(r, s) even for the finite M-electron system, as there are infinite number of (M − 1)-electron states |ΨM−1μ〉. This implies that the electron spin density
| | 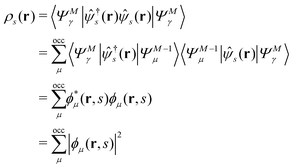 | (9) |
must be expressed with an infinite sum of occupied EQP wave functions even in the finite
M-electron system, and makes the rigorous analysis such as in highly correlated systems difficult. This problem was, however, solved quite recently by extended Kohn–Sham theory explained in Section 2.2.
2.2 EKS theory
Extended Kohn–Sham (EKS) theory14 solves this problem on the normalization of EQP wave functions. Multiplying both sides of eqn (8) by e−iελt1 and using the original definition 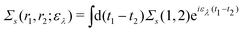 (numbers are abbreviations for position and time coordinates, i.e., i = (ri, ti)), one readily obtains the time-dependent EQP equation35,36
(numbers are abbreviations for position and time coordinates, i.e., i = (ri, ti)), one readily obtains the time-dependent EQP equation35,36| | 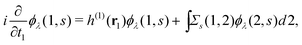 | (10) |
where time-dependent EQP wave functions, ϕλ(1, s), are defined by| | ϕμ(1, s) = 〈ΨM−1μ|![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (1)|ΨMγ〉, ϕν(1, s) = 〈ΨMγ| (1)|ΨMγ〉, ϕν(1, s) = 〈ΨMγ|![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (1)|ΨM+1ν〉 (1)|ΨM+1ν〉 | (11) |
using the Heisenberg operator ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (1) = eiHt1
(1) = eiHt1![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r1)e−iHt1. Then, the two-time spin density matrix ρs(1, 2) is introduced as
(r1)e−iHt1. Then, the two-time spin density matrix ρs(1, 2) is introduced as| | 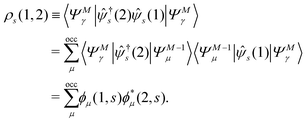 | (12) |
This ρs(1, 2) coincides with the Green's function −iGs(1, 2) for t1 < t2 and satisfies| | 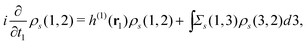 | (13) |
which is readily derived from eqn (10) by multiplying 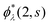 and summing with λ
and summing with λ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (=μ) over all occupied EQP states. Next, let us assume that ρs(1, 2) is expressed by M normalized EKS wave functions
(=μ) over all occupied EQP states. Next, let us assume that ρs(1, 2) is expressed by M normalized EKS wave functions ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i(1, s) (i = 1, 2,…,M) as
i(1, s) (i = 1, 2,…,M) as| | 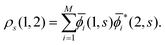 | (14) |
It certainly satisfies the necessary condition for the electron spin density 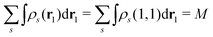 . (Note that the original ϕλ had norm less than 1 and infinite number of ϕλ were required to satisfy this necessary condition.) At each time t1, we can introduce the dual orbitals
. (Note that the original ϕλ had norm less than 1 and infinite number of ϕλ were required to satisfy this necessary condition.) At each time t1, we can introduce the dual orbitals ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) j(1, s) (j = 1, 2,…,M), which satisfy the biorthogonality condition
j(1, s) (j = 1, 2,…,M), which satisfy the biorthogonality condition| | 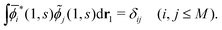 | (15) |
Note that ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) i(1, s) can be made from
i(1, s) can be made from ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i(1, s) by using the the Gram–Schmidt orthogonalization to all the other M − 1 orbitals
i(1, s) by using the the Gram–Schmidt orthogonalization to all the other M − 1 orbitals 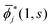 (j ≠ i). Then, we have
(j ≠ i). Then, we have 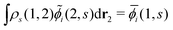 for i ≤ M. Then, eqn (13) yields the equation14
for i ≤ M. Then, eqn (13) yields the equation14| | 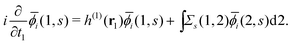 | (16) |
Eqn (10) and (16) have exactly the same form, and thus we know that ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i(1, s) is equivalent to the EQP wave function ϕμ(1, s) except for a normalization factor. Therefore, the electron spin density ρs(r1) =ρs(1, 1) is expressed by M normalized EQP wave functions except for normalization. Those functions are not necessarily mutually orthogonal. So far, we discussed the occupied EQP wave functions only, but a similar discussion is possible also for the empty EQP wave functions.14
i(1, s) is equivalent to the EQP wave function ϕμ(1, s) except for a normalization factor. Therefore, the electron spin density ρs(r1) =ρs(1, 1) is expressed by M normalized EQP wave functions except for normalization. Those functions are not necessarily mutually orthogonal. So far, we discussed the occupied EQP wave functions only, but a similar discussion is possible also for the empty EQP wave functions.14
Although there are a lot of independent excitations that are not directly associated with the PE and IPE processes in the (M ± 1)-electron states |ΨM±1λ〉, they can be eliminated in the summation over all occupied (and empty) EQP states, and instead we have to accept that the EQP energies have an imaginary part, which represents the peak width and the inverse of the QP lifetime. However, according to Baym–Kadanoff's conservation laws,37,38 we can derive the hermitized equation14
| | 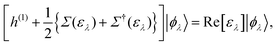 | (17) |
which can be regarded as the EKS equation. Moreover, we derive
32,33| | 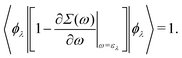 | (18) |
Thus the operator 1 − ∂
Σ(
ω)/∂
ω|
ω=ελ normalizes the EQP states. This normalization procedure is closely related to the Ward identity
38,39| | 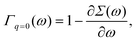 | (19) |
which is the
q → 0 limit of the Ward–Takahashi identity, where
q ≡ (
q,
ω′ −
ω) denotes the momentum-energy transfer
via the Coulomb interaction. In
eqn (19),
Γq=0(
ω) is the vertex operator in the
q → 0 limit. Comparing
(19) with
(18), we have
14| | | 〈ϕλ|Γq=0(ελ)|ϕλ〉 = 1. | (20) |
The vertex function, which connects the dynamical interaction to a pair of Green's functions, has an effect to make the system gauge invariant by the Ward–Takahashi identity, and guarantees the local charge conservation by the continuity equation.
38,40 However, in the limit
q → 0, no multiple excitation is possible. Therefore, the vertex function in this limit counts the (
M ± 1)-electron states |
ΨM±1λ〉 with purely one electron or hole only, and has an effect to normalize the corresponding EQP wave functions to unity, ignoring all the other EQP wave functions involving multiple excitations. This is the physical meaning of
eqn (20).
A simple way to normalize EQP wave functions is to multiply the Green's function by14
| | 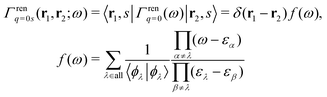 | (21) |
and introduce the normalized Green's function
Ḡ(
ω) as
| | | Ḡ(ω) = Γren1/2q=0(ω)G(ω)Γren1/2q=0(ω) = G(ω)f(ω). | (22) |
It is proved
14 in Hedin's exact
GWΓ formulation that the frequency integrals at each order of the expansion in terms of skeleton-diagrams equally give rise to all contributions from the poles of all Green's functions in the series, and therefore
f(
ω) →
f(
ελ) normalizes all EQP wave functions appearing inside all Green's functions in the expansion. Therefore, one can simply normalize the EQP wave functions to unity. The only difference from the traditional DFT is that the EQP wave functions are not necessarily orthogonal to each other, because the self-energy is energy dependent. A non-orthogonality actually implies that the EQP wave functions are interacting, or correlated, in contrast to the fictitious non-interacting KS orbitals. This EKS theory is applicable to the excited states,
i.e. the problem of the XES and RIXS studies, by relying on EQP theory explained in Section 2.1. However, the very important message here is that one has to use an accurate nonlocal self-energy in order to obtain a good result.
3 Computational details
There is also a problem of basis functions to represent the wave functions for the XES and RIXS studies. The electronic structure calculations in quantum chemistry usually use the Gaussian basis functions which are not always suited to represent highly extended states. To overcome the basis set incompleteness, we apply the all-electron mixed basis approach,41 in which both plane waves (PWs) and numerical atomic orbitals (AOs) are used as basis functions. We have successfully applied this approach in our previous XPS42,43 and XES23 studies. A similar XPS study has been performed by Golze et al.44 Here, we select CH4, NH3, H2O, and CH3OH molecules as target systems. There are experimental XES data for these molecules.10,45–47 There are also experimental RIXS data for NH3,48 H2O,49 and CH3OH.50 We take the input coordinates of these target molecules from the PubChem3D data.51 First, we perform the DFT calculation for the spin-polarized electron configuration for the XES and RIXS excited states with a core hole. We use the local density approximation (LDA) of Perdew–Zunger's interpolation formula52 for the exchange–correlation functional. Second, using the resulting Kohn–Sham (KS) eigenvalues and KS orbitals, we calculate the EQP energies using the one-shot GW approach. In this approach, the EQP wave functions are replaced by the LDA Kohn–Sham orbitals ϕLDAλ(r, s), and the GW EQP energies εGWλ are estimated from the LDA energy eigenvalues εLDAλ as| | 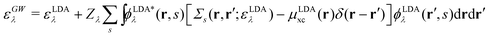 | (23) |
with a renormalization factor| | 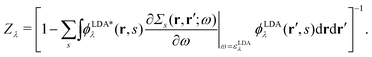 | (24) |
Finally, the BSE is solved within the Tamm–Dancoff approximation.53 In order to avoid quite heavy numerical ω integrations, the generalized plasmon pole (GPP) model54 is applied to the dynamical screened Coulomb interaction in the correlation term of the GW self-energy54 and the direct term of BSE Hamiltonian.7 The computational conditions such as unit cell parameters, cutoff energies for PWs, the Fock exchange Σx and the correlation term Σc(ω) (here, the self-energy Σ(ω) is decomposed as Σ(ω) = Σx + Σc(ω)), and the number of levels are listed in Table 1. For AOs, we use minimal basis, i.e., 1s, 2px, 2py, 2pz for C, N, O and 1s for H. (AOs are confined inside nonoverlapping atomic spheres.) All calculations in this paper use periodic boundary conditions. So, in order to treat the isolated systems, we use the spherical cut technique for the Coulombic interactions.55 The radius of Coulomb truncation is the half of the side length of the simple cubic unit-cell, and the molecular size should be smaller than this radius.
Table 1 Molecules, unit cell parameters (simple cubic), cutoff energies for plane waves (EcutoffPW), exchange (Ecutoffx) and correlation (Ecutoffc), and the number of levels used in the GW + BSE calculations
| Molecule |
Cell parameter (Å) |
E
cutoffPW PW (Ry) |
E
cutoffx exchange (Ry) |
E
cutoffc correlation (Ry) |
Number of levels |
| CH4 |
a = b = c = 12.0 |
44.2 |
122.8 |
11.1 |
2000 |
| NH3 |
a = b = c = 10.0 |
63.7 |
223.9 |
15.9 |
2000 |
| H2O |
a = b = c = 10.0 |
63.7 |
223.9 |
15.9 |
2500 |
| CH3OH |
a = b = c = 14.0 |
38.1 |
114.2 |
11.1 |
2500 |
4 Results
First we show the one-shot GW (G0W0) results. Initial state has a core hole at C1s for CH4 and CH3OH, N1s for NH3, and O1s for H2O, corresponding to the K-edge XES/RIXS spectra of carbon, nitrogen, and oxygen atoms. The other electron configuration is the same as the neutral ground state in XES (X). In contrast, in RIXS (R), one electron, which has the same spin as the removed core electron, is added to the LUMO level. This corresponds to the lowest-energy singlet exciton with a core hole induced by the X-ray absorption. These states are generated within the LDA. Contributions to the one-shot GW calculation are listed in Tables 2–5. In these tables, asterisk (*) attached onto εGW values indicates occupied levels, and εGW values without asterisk are empty levels. Note that the GW energy εGW is not the simple addition of Σx + Σc − μLDAxc because of the existence of the prefactor, i.e. the renormalization factor Zλ in eqn (23). We see from these tables that, for all molecules, there are interesting correlations between the up spin and down spin EQP states and between the XES (Xn) and RIXS (Rn). For example, εLDA and εGW have similar values between up and down spins at the same level, when both spin states are simultaneously occupied or empty, while they have quite different values when up spin is occupied and down spin is empty or vice versa. Moreover, we notice that the expectation values of the LDA exchange–correlation potential (μLDAxc) and the exchange and correlation parts of the self-energy (Σx and Σc) are almost the same (at most 2 eV difference) between Xn and Rn. This means that the main difference between Xn and Rn in the GW energy εGW comes from the LDA energy eigenvalue εLDA. We will discuss this point later in Section 5.
Table 2 Contributions to the one-shot GW calculation for XES (X) and RIXS (R) of CH4. εLDA and μLDAxc are the LDA eigenvalue and the expectation value of the LDA exchange–correlation potential; Σx and Σc are, respectively, the exchange and correlation parts of the self-energy; and εGW is the GW extended quasiparticle energy. Asterisk (*) attached onto εGW values indicates occupied levels. This table lists the data for single-particle levels (Xn, Rn) only
| Process/level |
Up spin (eV) |
Down spin (eV) |
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
| X1 (C1s) |
−331.6 |
−60.9 |
−103.5 |
10.4 |
−359.1* |
−300.6 |
−28.9 |
−3.2 |
−10.5 |
−287.8 |
| R1 (C1s) |
−325.7 |
−60.8 |
−103.5 |
12.4 |
−348.3* |
−295.2 |
−29.4 |
−3.4 |
−12.6 |
−285.8 |
| X2 |
−29.3 |
−17.5 |
−27.5 |
3.1 |
−35.5* |
−28.2 |
−15.9 |
−25.0 |
2.8 |
−33.8* |
| R2 |
−23.6 |
−17.4 |
−27.3 |
4.5 |
−29.7* |
−22.6 |
−16.0 |
−25.3 |
6.9 |
−23.7* |
| X3–5 |
−21.0 |
−16.5 |
−22.5 |
0.8 |
−25.9* |
−20.4 |
−15.3 |
−21.1 |
0.6 |
−25.2* |
| R3–5 |
−15.3 |
−16.4 |
−22.3 |
2.3 |
−18.2* |
−14.8 |
−15.3 |
−21.1 |
2.2 |
−17.5* |
| X6 |
−6.6 |
−6.3 |
−2.8 |
−0.9 |
−4.0 |
−6.3 |
−5.6 |
−2.1 |
−0.8 |
−3.6 |
| R6 |
−2.5 |
−4.7 |
−1.6 |
−2.0 |
−1.5 |
−2.8 |
−4.7 |
−5.6 |
−1.2 |
−4.6* |
| X7–9 |
−5.5 |
−9.0 |
−4.0 |
−1.1 |
−1.7 |
−5.2 |
−8.4 |
−3.6 |
−1.0 |
−1.5 |
| R7–9 |
−1.2 |
−4.7 |
−1.4 |
−1.8 |
0.2 |
−1.5 |
−4.3 |
−2.0 |
−1.1 |
−0.6 |
Table 3 Contributions to the one-shot GW calculation for XES (X) and RIXS (R) of NH3. εLDA and μLDAxc are the LDA eigenvalue and the expectation value of the LDA exchange–correlation potential; Σx and Σc are, respectively, the exchange and correlation parts of the self-energy; and εGW is the GW extended quasiparticle energy. Asterisk (*) attached onto εGW values indicates occupied levels. This table lists the data for single-particle levels (Xn, Rn) only
| Process/level |
Up spin (eV) |
Down spin (eV) |
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
| X1 (N1s) |
−453.1 |
−71.3 |
−121.3 |
12.0 |
−485.8* |
−417.3 |
−34.6 |
−4.3 |
−12.2 |
−401.8 |
| R1 (N1s) |
−446.1 |
−71.2 |
−121.2 |
14.4 |
−473.5* |
−410.8 |
−35.1 |
−4.5 |
−14.6 |
−399.1 |
| X2 |
−34.7 |
−20.4 |
−32.0 |
3.7 |
−41.9* |
−33.4 |
−18.5 |
−29.1 |
3.3 |
−40.0* |
| R2 |
−27.9 |
−20.3 |
−31.9 |
5.6 |
−33.7* |
−26.7 |
−18.6 |
−29.6 |
6.8 |
−29.3* |
| X3–4 |
−24.0 |
−19.0 |
−26.0 |
0.9 |
−29.7* |
−23.3 |
−17.6 |
−24.2 |
0.7 |
−28.7* |
| R3–4 |
−17.3 |
−18.9 |
−25.8 |
2.6 |
−20.9* |
−16.7 |
−17.6 |
−24.1 |
2.3 |
−20.4* |
| X5 |
−19.9 |
−20.2 |
−28.1 |
1.5 |
−25.8* |
−18.7 |
−18.3 |
−25.5 |
1.2 |
−24.3* |
| R5 |
−13.4 |
−20.0 |
−27.6 |
3.1 |
−17.2* |
−12.4 |
−18.2 |
−25.2 |
2.8 |
−16.9* |
| X6 |
−8.0 |
−7.7 |
−3.5 |
−1.0 |
−4.8 |
−7.7 |
−7.1 |
−2.8 |
−0.9 |
−4.5 |
| R6 |
−2.9 |
−5.7 |
−2.0 |
−2.1 |
−1.5 |
−3.4 |
−5.9 |
−7.1 |
−1.0 |
−5.4* |
| X7–8 |
−6.4 |
−9.6 |
−4.5 |
−1.0 |
−2.5 |
−6.1 |
−9.0 |
−4.0 |
−1.0 |
−2.2 |
| R7–8 |
−1.3 |
−5.7 |
−2.1 |
−2.0 |
0.1 |
−1.8 |
−5.9 |
−3.1 |
−1.2 |
−0.4 |
| X9 |
−3.7 |
−3.0 |
−1.0 |
−0.5 |
−1.6 |
−3.6 |
−2.9 |
−1.0 |
−0.4 |
−2.1 |
| R9 |
−0.5 |
−2.4 |
−0.5 |
−1.2 |
−0.0 |
−0.9 |
−2.8 |
−1.1 |
−1.0 |
−0.3 |
Table 4 Contributions to the one-shot GW calculation for XES (X) and RIXS (R) of H2O. εLDA and μLDAxc are the LDA eigenvalue and the expectation value of the LDA exchange–correlation potential; Σx and Σc are, respectively, the exchange and correlation parts of the self-energy; and εGW is the GW extended quasiparticle energy. Asterisk (*) attached onto εGW values indicates occupied levels. This table lists the data for single-particle levels (Xn, Rn) only
| Process/level |
Up spin (eV) |
Down spin (eV) |
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
| X1 (O1s) |
−594.1 |
−82.0 |
−139.7 |
12.0 |
−634.6* |
−553.9 |
−41.0 |
−5.8 |
−12.1 |
−533.6 |
| R1 (O1s) |
−585.9 |
−81.9 |
−139.7 |
14.5 |
−620.5* |
−546.2 |
−41.5 |
−6.0 |
−14.6 |
−530.0 |
| X2 |
−40.9 |
−23.9 |
−37.7 |
4.3 |
−49.7* |
−39.7 |
−21.6 |
−34.2 |
3.9 |
−47.2* |
| R2 |
−32.9 |
−23.8 |
−37.6 |
7.5 |
−37.7* |
−31.5 |
−21.7 |
−34.8 |
6.8 |
−37.1* |
| X3 |
−27.8 |
−22.2 |
−30.0 |
1.3 |
−34.3* |
−26.9 |
−20.4 |
−28.0 |
1.0 |
−33.0* |
| R3 |
−19.8 |
−22.1 |
−30.1 |
3.1 |
−24.0* |
−19.2 |
−20.5 |
−28.0 |
2.6 |
−24.5* |
| X4 |
−25.4 |
−23.5 |
−32.7 |
1.8 |
−32.4* |
−24.1 |
−21.4 |
−30.0 |
1.5 |
−30.7* |
| R4 |
−17.6 |
−23.2 |
−32.2 |
3.6 |
−22.3* |
−16.6 |
−21.4 |
−29.9 |
3.5 |
−20.8* |
| X5 |
−23.7 |
−24.2 |
−33.7 |
2.2 |
−30.6* |
−22.4 |
−22.0 |
−30.8 |
1.8 |
−28.9* |
| R5 |
−16.0 |
−23.9 |
−33.2 |
3.9 |
−20.6* |
−14.8 |
−21.9 |
−30.5 |
3.6 |
−19.1* |
| X6 |
−9.1 |
−8.8 |
−4.1 |
−0.9 |
−5.3 |
−8.8 |
−8.2 |
−3.5 |
−0.8 |
−4.9 |
| R6 |
−2.8 |
−6.3 |
−2.3 |
−2.0 |
−1.0 |
−3.5 |
−7.1 |
−9.0 |
−0.7 |
−5.8* |
| X7 |
−7.5 |
−10.3 |
−4.9 |
−0.9 |
−5.3 |
−7.2 |
−9.8 |
−4.5 |
−0.8 |
−2.8 |
| R7 |
−1.2 |
−6.3 |
−2.4 |
−1.9 |
0.5 |
−1.9 |
−7.3 |
−4.2 |
−1.0 |
0.0 |
| X8 |
−4.0 |
−2.9 |
−1.0 |
−0.3 |
−2.4 |
−3.9 |
−2.8 |
−1.0 |
−0.3 |
−2.3 |
| R8 |
−0.6 |
−2.6 |
−0.8 |
−1.0 |
0.1 |
−0.9 |
−2.7 |
−1.2 |
−0.8 |
−0.2 |
| X9 |
−3.9 |
−2.9 |
−1.0 |
−0.3 |
−2.3 |
−3.8 |
−2.7 |
−0.9 |
−0.3 |
−2.3 |
| R9 |
−0.3 |
−2.0 |
−0.3 |
−0.9 |
−0.4 |
−0.7 |
−2.7 |
−1.0 |
−0.7 |
0.1 |
Table 5 Contributions to the one-shot GW calculation for XES (X) and RIXS (R) of CH3OH. εLDA and μLDAxc are the LDA eigenvalue and the expectation value of the LDA exchange–correlation potential; Σx and Σc are, respectively, the exchange and correlation parts of the self-energy; and εGW is the GW extended quasiparticle energy. Asterisk (*) attached onto εGW values indicates occupied levels. This table lists the data for single-particle levels (Xn, Rn) only
| Process/level |
Up spin (eV) |
Down spin (eV) |
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
| X1 (O1s) |
−515.2 |
−78.8 |
−132.1 |
11.1 |
−551.4* |
−515.3 |
−78.8 |
−132.1 |
11.1 |
−551.4* |
| R1 (O1s) |
−509.4 |
−78.8 |
−132.1 |
13.0 |
−540.9* |
−509.4 |
−78.9 |
−132.2 |
13.0 |
−541.0* |
| X2 (C1s) |
−333.1 |
−60.8 |
−103.6 |
10.7 |
−360.5* |
−301.9 |
−28.8 |
−3.2 |
−10.9 |
−289.4 |
| R2 (C1s) |
−326.7 |
−60.8 |
−103.5 |
12.6 |
−350.3* |
−295.9 |
−29.1 |
−3.3 |
−12.8 |
−286.1 |
| X3 |
−34.2 |
−20.7 |
−32.5 |
5.0 |
−40.1* |
−33.9 |
−20.6 |
−32.3 |
5.1 |
−39.7* |
| R3 |
−28.3 |
−20.7 |
−32.5 |
6.7 |
−32.7* |
−28.0 |
−20.7 |
−32.6 |
6.9 |
−32.7* |
| X4 |
−27.8 |
−18.5 |
−28.2 |
3.1 |
−33.8* |
−26.9 |
−17.1 |
−26.1 |
2.8 |
−32.5* |
| R4 |
−21.7 |
−18.4 |
−28.0 |
4.8 |
−25.8* |
−21.0 |
−17.2 |
−26.3 |
5.0 |
−24.3* |
| X5 |
−22.2 |
−17.5 |
−23.8 |
1.4 |
−26.8* |
−21.8 |
−16.9 |
−23.2 |
1.3 |
−26.3* |
| R5 |
−16.2 |
−17.5 |
−23.7 |
2.9 |
−19.1* |
−15.9 |
−17.1 |
−23.4 |
3.0 |
−18.7* |
| X6 |
−21.7 |
−16.7 |
−23.2 |
1.4 |
−26.5* |
−21.1 |
−15.7 |
−21.9 |
1.2 |
−25.8* |
| R6 |
−15.6 |
−16.7 |
−23.0 |
2.8 |
−18.7* |
−15.7 |
−15.2 |
−21.9 |
2.6 |
−18.2* |
| X7 |
−21.0 |
−18.6 |
−24.1 |
1.1 |
−25.2* |
−20.5 |
−17.6 |
−23.1 |
1.0 |
−24.7* |
| R7 |
−15.0 |
−18.4 |
−23.9 |
2.5 |
−17.6* |
−14.7 |
−17.5 |
−23.1 |
2.5 |
−17.3* |
| X8 |
−16.8 |
−19.4 |
−26.1 |
1.7 |
−21.5* |
−16.7 |
−19.1 |
−25.8 |
1.7 |
−21.4* |
| R8 |
−11.1 |
−19.2 |
−25.8 |
3.0 |
−14.1* |
−11.1 |
−19.0 |
−25.5 |
3.0 |
−14.1* |
| X9 |
−14.6 |
−19.7 |
−26.7 |
2.2 |
−19.1* |
−14.6 |
−19.6 |
−26.6 |
2.1 |
−19.1* |
| R9 |
−8.9 |
−19.5 |
−26.4 |
3.5 |
−11.7* |
−9.0 |
−19.5 |
−26.9 |
3.5 |
−11.8* |
| X10 |
−7.4 |
−13.7 |
−7.5 |
−1.5 |
−2.9 |
−7.1 |
−11.4 |
−5.8 |
−1.4 |
−3.0 |
| R10 |
−2.3 |
−6.6 |
−2.7 |
−2.1 |
−0.7 |
−2.6 |
−6.3 |
−7.4 |
−1.0 |
−4.4* |
| X11 |
−6.5 |
−9.9 |
−5.2 |
−1.2 |
−3.1 |
−6.1 |
−9.0 |
−4.4 |
−1.1 |
−2.7 |
| R11 |
−1.8 |
−9.3 |
−4.8 |
−2.1 |
0.3 |
−1.8 |
−6.4 |
−3.3 |
−1.4 |
−0.3 |
| X12 |
−5.8 |
−9.0 |
−4.1 |
−1.1 |
−2.3 |
−5.5 |
−8.3 |
−3.5 |
−1.1 |
−1.9 |
| R12 |
−5.6 |
−1.2 |
−2.2 |
−1.7 |
0.2 |
−1.4 |
−4.6 |
−2.1 |
−1.0 |
−0.1 |
| X13 |
−5.7 |
−9.1 |
−4.1 |
−1.1 |
−2.1 |
−5.4 |
−8.5 |
−3.6 |
−1.1 |
−1.8 |
| R13 |
−1.1 |
−4.6 |
−1.6 |
−1.5 |
0.2 |
−1.4 |
−5.3 |
−2.5 |
−1.3 |
−0.0 |
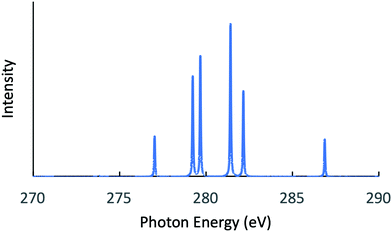
Next, the RIXS spectra obtained by solving the BSE are shown in Fig. 1 and in Fig. 2, respectively, for NH3 and CH3OH. The calculated XES and RIXS fluorescence photon energies are listed in Table 6 together with the experimental data.10,45–50 There are three excitonic states S1–S3 for XES and four excitonic states S1–S4 for RIXS in the case of CH4, NH3, and H2O molecules, while there are six excitonic states for XES and seven excitonic states for RIXS in the case of a CH3OH molecule. The XES results are slightly different from those of our previous report23 due to the choice of different computational conditions given in Table 1. For the present XES results, the agreement with the experimental values is better than our previous report23 for CH4, NH3 and H2O (the difference between the present results and the experimental data45–47 is 1–1.5 eV), but a bit worse for CH3OH (the difference from the experimental data10 is 2–4 eV). Similarly, the RIXS results well reproduce the overall experimental tendencies. In particular, the result for NH3 (Fig. 1) reproduces the shoulder peak observed experimentally;48 the shoulder peak D1 of Fig. 5 in ref. 48 corresponds to the calculated peak at 398.2 eV in Fig. 1. However, our RIXS results are systematically larger by 2–3 eV from our XES results, in contrast to the experimental XES and RIXS data showing the difference at most 1.5 eV. Accordingly, our RIXS results are systematically overestimated by 2–4 eV from the available experimental data for NH3 and H2O.48,49 A possible reason of this systematic deviation is discussed in the following section. Nevertheless, it is worthwhile to note that, our RIXS result for CH3OH (Fig. 2 and Table 6) well coincides with the experimental data.50
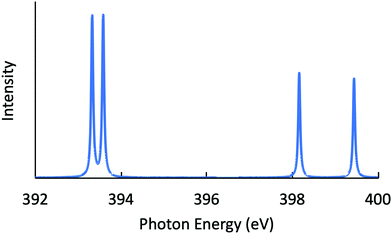 |
| | Fig. 1 Calculated RIXS spectrum for NH3. | |
 |
| | Fig. 2 Calculated RIXS spectrum for CH3OH. | |
Table 6 XES and RIXS fluorescence photon energies obtained by solving the BSE after the GW calculation for the EQP energies, which are listed in Tables 2–5. Available experimental values10,45–50 are listed together
| Molecule |
State |
XES (eV) |
RIXS (eV) |
| Calc. |
Exp. |
Calc. |
Exp. |
|
Ref. 45.
Ref. 46.
Ref. 47.
Ref. 10.
Ref. 48.
Ref. 49.
Ref. 50.
|
| CH4 |
S1 |
277.5 |
276.4a |
280.8 |
— |
| S2 |
277.5 |
276.4a |
280.8 |
— |
| S3 |
277.5 |
276.4a |
280.8 |
— |
| S4 |
— |
— |
285.3 |
— |
| NH3 |
S1 |
390.5 |
388.6b |
393.4 |
389.0e |
| S2 |
390.5 |
388.6b |
393.4 |
389.0e |
| S3 |
396.1 |
395.0b |
398.2 |
392.5e |
| S4 |
— |
— |
399.4 |
394.3e |
| H2O |
S1 |
521.8 |
520.8c |
524.4 |
522.3f |
| S2 |
525.7 |
524.8c |
528.5 |
524.3f |
| S3 |
528.1 |
526.6c |
531.4 |
526.3f |
| S4 |
— |
— |
532.5 |
526.5f |
| CH3OH |
S1 |
270.8 |
275.2d |
273.8 |
274.3g |
| S2 |
274.6 |
277.0d |
277.0 |
276.7g |
| S3 |
277.1 |
279.4d |
279.2 |
279.0g |
| S4 |
277.8 |
281.2d |
279.7 |
279.3g |
| S5 |
279.5 |
282.5d |
281.4 |
281.0g |
| S6 |
280.2 |
282.8d |
282.2 |
281.4g |
| S7 |
— |
— |
286.9 |
287.0g |
5 Discussion
The EQP energy of the C1s core hole created by a XPS process, −287.8 eV, which is given in Table 2 as X1 (C1s) εGW for down spin, should coincide with the C1s XPS energy of a neutral system. So, we performed the GW calculation of a neutral CH4 molecule at the ground state and obtained εGWC1s for the 1 (C1s) XPS level as shown in Table 7. The resulting C1s XPS energy εGWC1s = −289.4 eV is fairly close to the EQP energy −287.8 eV of the X1 C1s core hole (Table 2) with a 1.6 eV difference, which is an error caused by the approximations used and some insufficiency of the parameter set (including the supercell size), etc. Anyway, the error of 1.6 eV is relatively small compared to the absolute value 288 eV and acceptable. This strongly supports the validity of the present methodology.
Table 7 Contributions to the one-shot GW calculation for neutral CH4 at the ground state. εLDA and μLDAxc are the LDA eigenvalue and the expectation value of the LDA exchange–correlation potential; Σx and Σc are, respectively, the exchange and correlation parts of the self-energy; and εGW is the GW quasiparticle energy. Asterisk (*) attached onto εGW values indicates occupied levels
| Level |
(eV) |
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
| 1 |
(C1s) |
−265.6 |
−58.0 |
−96.2 |
10.0 |
−289.4* |
| 2 |
|
−17.1 |
−15.5 |
−24.2 |
2.8 |
−22.3* |
| 3–5 |
(HOMO) |
−9.5 |
−14.0 |
−19.3 |
0.5 |
−13.8* |
| 6 |
|
−0.6 |
−1.8 |
−0.6 |
−0.3 |
0.3 |
Moreover, using an idea to calculate the photoabsorption energy only by performing the GW calculation for the cation of the target molecule without solving the BSE,56 we can estimate the XES energies only from the result given in Table 7 of a neutral GW calculation as εGWC1s − εGWHOMO = −289.4 + 13.8 eV = 275.6 eV, which is different from the experimental XES value −276.4 eV by 0.8 eV only. This again strongly supports the validity of the present theory, although this type of calculation (as well as the above-mentioned paper56) does not allow us to calculate the spectral intensity. It can be used at least for the purpose of error estimation, but we think the ability is more than that. We can more positively expect that the accuracy of the involved calculation becomes better, because this is simply a standard GW calculation for a neutral molecule. In fact, there was a similar advantage in the spin-unpolarized calculation in cationic systems of Al, B, Na3, and Li3 treated in the above-mentioned paper.56
Similarly, for RIXS, we performed GW calculation for an ammonia anion NH3−1 and obtained Table 8. From down spin levels, we can estimate the RIXS energies as εGWN1s − εGWn = −397.3 eV − εGWn(n = 3–6) as −385.9 eV, −385.9 eV, −390.9 eV, and −396.0 eV, which can be compared with the experimental values in Table 6: −389.0 eV, −389.0 eV, −392.5 eV, and −394.3 eV. The differences between theory and experiment are, respectively, 3.1 eV, 3.1 eV, 1.6 eV, and 1.7 eV. The larger differences compared to the CH4 XES case discussed above are probably due to the GW calculation for an anion, not for a neutral molecule.
Table 8 Contributions to the one-shot GW calculation for NH3− anion. εLDA and μLDAxc are the LDA eigenvalue and the expectation value of the LDA exchange-correlation potential; Σx and Σc are, respectively, the exchange and correlation parts of the self-energy; and εGW is the GW quasiparticle energy. Asterisk (*) attached onto εGW values indicates occupied levels
| Level |
Up spin (eV) |
Down spin (eV) |
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
ε
LDA
|
μ
LDAxc
|
Σ
x
|
Σ
c
|
ε
GW
|
| 1 (N1s) |
−373.9 |
−68.3 |
−114.0 |
13.8 |
−397.3* |
−373.9 |
−68.3 |
−114.0 |
13.8 |
−397.3* |
| 2 |
−18.1 |
−18.1 |
−28.1 |
5.0 |
−20.2* |
−18.1 |
−18.1 |
−28.2 |
5.1 |
−20.3* |
| 3–4 |
−8.3 |
−15.9 |
−21.7 |
2.1 |
−11.3* |
−8.3 |
−15.9 |
−21.7 |
2.1 |
−11.4* |
| 5 |
−3.5 |
−15.7 |
−21.1 |
1.9 |
−6.4* |
−3.5 |
−15.7 |
−21.0 |
1.9 |
−6.4* |
| 6 |
0.5 |
−2.3 |
−0.3 |
−1.6 |
0.7 |
0.0 |
−2.7 |
−2.8 |
−1.5 |
−1.3* |
As seen in the previous section, there is a systematic deviation between our XES and RIXS results. The most probable reason is the approximation used in the present calculation. The validity of the linearization of the QP equation, i.e., the so-called renormalization of the one-shot GW approximation, is not obvious in particular for the deep core level. So, we tried to use the X1 (C1s) εGW(EQP)C1s(↑, ↓) values listed in Table 2 in the argument of the self-energy Σc(εGW(EQP)), and reperformed a GW + BSE calculation for the CH4 XES case. The resulting εGW(EQP)C1s(↑, ↓) values, however, did not change at all up to one decimal place written in Table 2 even if we used the correct EQP energy in the argument of the self-energy. The difference is about 0.01 eV. So, we think the linearization does not cause any significant problem at least in the present case. In this sense, there is no oscillatory behavior in the self-energy as discussed by Mejuto-Zaera et al.57 at least in the present case. In the present and previous calculations, we have used the GPP model.54 It is known that sometimes the GPP model gives a worse result compared with the numerical ω integration. However, unfortunately, it is quite heavy to perform the numerical ω integration for the XES and RIXS studies. From a tentative calculation, we found that there is a possibility to lower the XES and RIXS energies by using the full numerical ω integration up to 1000 points corresponding to about 200 eV. Moreover, we used the Tamm–Dancoff approximation53 in solving the BSE.
On the other hand, as seen in Tables 2–5, the main difference between XES and RIXS in the GW energy εGW comes from the LDA energy eigenvalue εLDA, since the expectation values of the LDA exchange–correlation potential (μLDAxc) and the exchange and correlation parts of the self-energy (Σx and Σc) are almost the same between the XES and RIXS calculations. Therefore, another reason for the difference between the resulting XES and RIXS energies may lie in the LDA energy eigenvalues εLDA. The use of LDA is an approximation in particular for excited states, even though EQP theory is the exact theory and the usual way to calculate the self-energy is justified for excited states. For example, we have to be careful for a treatment of the charge neutrality in the unit cell for a cation system required in the XES calculation. In order to exclude the interaction between the unit cells, we have introduced the spherical cut technique for the Coulombic interaction.55 In particular, in the XES calculation of + charged molecule with a deep core hole, the effect of Coulomb spherical cut and the unit-cell size may become more serious. So, we performed a LDA calculation with a slightly larger unit cell (14 Å) for the CH4 XES case with the same cutoff energy for plane waves as listed in Table 1. Then, we obtained −331.7 eV (up spin) and −300.6 eV (down spin) for the X1 (C1s) level, which is different from the εLDA values in Table 2 by only 0.1 eV. As well, to investigate the effect of the electric dipole, we performed a similar LDA calculation with a slightly larger unit-cell (12 Å) for the NH3 and H2O RIXS (charge neutral) case with the same cutoff energy for plane waves as listed in Table 1. In this case, we obtained −445.8 eV (up spin) and −410.5 eV (down spin) for the R1 (N1s) level of NH3 and −585.7 eV (up spin) and −546.0 eV (down spin) for the R1 (O1s) level of H2O. The difference from the εLDA values in Tables 3 and 4 is 0.3 eV for NH3 and 0.2 eV for H2O. Therefore, the unit-cell size listed in Table 1 is almost sufficient.
Finally, we want to give a justification and comment of applying TDDFT to the XES and RIXS studies. As demonstrated in Sections 2.1 and 2.2, Kohn–Sham equation is applicable to excited states. However, as is well known, the condition to apply TDDFT for an initially excited state is that one should use the exchange–correlation kernel constructed by including the information of the wave function of the initial excited state.8 This should not be the simple LDA kernel. From EKS theory,14 the true kernel should be the hermitized self-energy in MBPT, and, from EQP theory,13 it is applicable to any excited eigenstate of the many-body Hamiltonian. This means that, even with hybrid functional such as B3LYP, the difference between the correct self-energy and the hybrid functional may cause a systematic error in the XES and RIXS calculations. It would be important to use a more elaborate functional, which imitates the important characteristic of the true self-energy.
6 Conclusion
In this paper, we have demonstrated the validity of applying the Green's function method based on many-body perturbation theory (MBPT) to the XES and RIXS studies. The important point is that one can rely on extended quasiparticle (EQP) theory13 and extended Kohn–Sham theory,14 which enable one to treat an arbitrary excited eigenstate as an initial state. From this point of view, we have given a justification and comment of applying TDDFT to the XES and RIXS studies. Though Kohn–Sham equation is applicable to excited states, the exchange–correlation kernel must be dependent on the initial state according to TDDFT.8 From EKS theory,14 the true kernel should be the hermitized self-energy in MBPT, and, from EQP theory,13 it is applicable to any excited eigenstate of the many-body Hamiltonian. This means that, even with hybrid functional such as B3LYP, the difference between the correct self-energy and the hybrid functional may cause a systematic error in the XES and RIXS calculations. It would be important to use a more elaborate functional, which imitates the important characteristic of the true self-energy. This is, however, left for a future study.
We have explicitly applied the one-shot GW + Bethe–Salpeter equation (BSE) method to the XES and RIXS calculations of CH4, NH3, H2O, and CH3OH molecules, which include the chemically important K-edge XES/RIXS spectra of carbon, nitrogen, and oxygen atoms in the soft X-ray regime. Our results give the fluorescence photon energies of XES and RIXS in reasonable agreement with the experimental data, although there appear some deviations between our XES and RIXS results. We infer these errors from several approximations, such as the plasmon-pole model,54 the Tamm–Dancoff approximation53 or one-shot methods. So, the numerical ω integration and the self-consistent GW calculations will be desirable for more accurate investigations.
In Section 5, we have also presented a convenient method to calculate the XES or RIXS energies just by performing a GW calculation of a neutral ground state or of an anion without solving the Bethe–Salpeter equation, although it does not allow us to calculate the spectral intensity. The results obtained in this approach are also in good agreement with the experimental values of the XES and RIXS energies. In particular, in the case of the XES analysis, the approach treating a neutral molecule can give better results compared to the full GW + BSE calculation for a cation molecule with a deep core hole.
In terms of the computational scalability, the GW + BSE method is advantageous compared to the EOM-CCSD method if we use the generalized plasmon pole model54 instead of doing the numerical ω integration. The EOM-CCSD calculation with the localized basis scales as N6. On the other hand, the GW + BSE calculation using the reciprocal lattice space representation scales as N4. For more precise discussion, the atomic vibration effect24 is also important, although this is beyond the scope of the present study.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Grant-in-Aid Scientific Research B (Grant No. 21H01877) from Japan Society for the Promotion of Science (JSPS). In this research we used supercomputers at Institute for Materials Research, Tohoku University (Project No. 202012-SCKXX-0512), at Institute for Solid State Physics, University of Tokyo, and at Kyushu University (HPCI Project ID. hp210131).
References
- H. Asakura and T. Tanaka, Chem. Lett., 2021, 50, 1075–1085 CrossRef CAS.
- P. Zimmermann, S. Peredkov, P. M. Abdala, S. DeBeer, M. Tromp, C. Müller and J. A. van Bokhoven, Coordination Chem. Rev., 2020, 423, 213466 CrossRef CAS.
-
K. Siegbahn, C. Nordling, R. Fahlman, R. Nordberg, K. Hamrin, K. Hedman, G. Johansson, T. Bergmark, S. E. Karlsson, I. Lindgren and B. Lingberg, ESCA, Atomic, Molecular and Solid State Structure Studies by Means of Electron Spectroscopy, Nova Acta Regiae Soc. Sci. Ups., Uppsala, 1967 Search PubMed.
-
K. Siegbahn, C. Nordling, G. Johansson, J. Hedman, P. F. Heden, K. Hamrin, U. Gelius, T. Bergmark, L. O. Werme, R. Manne and Y. Baer, ESCA, Applied to Free Molecules, North-Holland, Amsterdam, 1969 Search PubMed.
- F. de Groot, Chem. Rev., 2001, 101, 1779–1808 CrossRef CAS PubMed.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Phys. Rev. B, 2000, 62, 4927–4944 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- J. E. Rubensson, N. Wassdahl, R. Brammer and J. Nordgren, J. Electron Spectrosc. Relat. Phenom., 1988, 47, 131–145 CrossRef CAS.
- N. A. Besley, Acc. Chem. Res., 2020, 53, 1306–1315 CrossRef CAS PubMed.
- N. A. Besley, Comput. Mol. Sci., 2021, 11, e1527 CAS.
- K. Ohno, S. Ono and T. Isobe, J. Chem. Phys., 2017, 146, 084108 CrossRef PubMed.
- T. Nakashima, H. Raebiger and K. Ohno, Phys. Rev. B, 2021, 104, L201116 CrossRef CAS.
- Y. Zhang, S. Mukamel, M. Khalil and N. Govind, J. Chem. Theory Comput., 2015, 11, 5804 CrossRef CAS PubMed.
- I. P. E. Roper and N. A. Besley, J. Chem. Phys., 2016, 144, 114104 CrossRef PubMed.
- D. R. Mortensen, G. T. Seidler, J. J. Kas, N. Govind, C. P. Schwartz, S. Pemmaraju and D. G. Prendergast, Phys. Rev. B, 2017, 96, 125136 CrossRef.
- A. E. A. Fouda and N. A. Besley, Theor. Chem. Acc., 2018, 137, 6 Search PubMed.
- V. V. da Cruz, N. Ignatova, R. C. Couto, D. A. Fedotov, D. R. Rehn, V. Savchenko, P. Norman, H. Ågren, S. Polyutov, J. Nishkanen, S. Eckert, R. M. Jay, M. Fondell, T. Schmitt, A. Pietzsch, A. Föhlisch, F. Gel'mukhanov, M. Odelius and V. Kimberg, J. Chem. Phys., 2019, 150, 234301 CrossRef PubMed.
- V. V. da Cruz, S. Eckert and A. Föhlisch, Phys. Chem. Chem. Phys., 2021, 23, 1835–1848 RSC.
- J. Vinson, T. Jach, W. T. Elam and J. D. Denlinger, Phys. Rev. B, 2014, 90, 205207 CrossRef.
- J. Vinson, T. Jach, M. Müller, R. Unterumsberger and B. Beckhoff, Phys. Rev. B, 2016, 94, 035163 CrossRef PubMed.
- T. Aoki and K. Ohno, Phys. Rev. B, 2019, 100, 075149 CrossRef CAS.
- R. C. Couto, V. V. Cruz, E. Ertan, S. Eckert, M. Fondell, M. Dantz, B. Kennedy, T. Schmitt, A. Pietzsch, F. F. Guimaraes, H. Ågren, F. Gel'mukhanov, M. Odelius, V. Kimberg and A. Föhlisch, Nat. Commun., 2017, 8, 14165 CrossRef CAS PubMed.
- T. N. Pham, S. Ono and K. Ohno, J. Chem. Phys., 2016, 144, 144309 CrossRef PubMed.
-
L. P. Kadanoff and G. Baym, Quantum Statistical Mechanics: Green's function Methods in Equilibrium and Nonequilibrium Problems, Addison-Wesley, Redwood City, California, 1962, 1989 Search PubMed.
- L. V. Keldysh, J. Exp. Theor. Phys., 1964, 47, 1515–1527 Search PubMed (Sov. Phys. JETP, 1965, 20, 1018–1026).
- C. D. Spataru, L. X. Benedict and S. G. Louie, Phys. Rev. B, 2004, 69, 205204 CrossRef.
- E. Perfetto and G. Stefanucci, J. Phys.: Cond. Mat., 2018, 30, 465901 CrossRef CAS PubMed.
- T. S. Tan, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2021, 104, 035144 CrossRef CAS.
- A. B. Migdal, J. Exp. Theor. Phys., 1957, 32, 399–400 CAS (Sov. Phys. JETP, 1957, 5, 333–334).
- A. J. Layzer, Phys. Rev., 1963, 129, 897–907 CrossRef.
- F. Hüser, T. Olsen and K. S. Thygesen, Phys. Rev. B, 2013, 87, 235132 CrossRef.
- G. Csanak, H. S. Taylor and R. Yaris, Adv. At. Mol. Phys., 1971, 7, 287–361 Search PubMed.
- A. Klein and R. Prange, Phys. Rev., 1958, 112, 994–1007 CrossRef CAS.
-
L. Hedin and S. Lundqvist, in Solid State Physics Vol. 23, ed. F. Seitz, D. Turnbull and H. Ehrenreich, Academic Press, New York, 1969, pp. 1–180 Search PubMed.
- G. Baym and L. P. Kadanoff, Phys. Rev., 1961, 124, 287–299 CrossRef.
- G. Strinati, Nuovo Cimento, 1988, 11, 1–86 CrossRef CAS.
-
P. Nozières, Theory of Interacting Fermi Systems, Westview Press, 1964, CRC Press, FL, 2018 Search PubMed.
-
J. R. Schrieffer, Theory of Superconductivity, Westview Press, 1964, CRC Press, FL, 2018 Search PubMed.
- S. Ono, Y. Noguchi, R. Sahara, Y. Kawazoe and K. Ohno, Comput. Phys. Commun., 2015, 189, 20–30 CrossRef CAS.
- S. Ishii, S. Iwata and K. Ohno, Mater. Trans., 2010, 51, 2150–2156 CrossRef CAS.
- T. Aoki and K. Ohno, J. Phys.: Condens. Matter, 2018, 30, 21LT01 CrossRef PubMed.
- D. Golze, J. Wilhelm, M. J. van Setten and P. Rinke, J. Chem. Theory Comput., 2018, 14, 4856–4869 CrossRef CAS PubMed.
- P. Glans, R. E. La Villa, Y. Luo, H. Ågren and J. Nordgren, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 3399–3414 CrossRef CAS.
- J. Nordgren, H. Ågren, L. O. Werme, C. Nordling and K. Siegbahn, J. Phys. B: Atom. Mol. Phys., 1976, 9, 295–302 CrossRef CAS.
- S. Kashtanov, A. Augustsson, Y. Luo, J. H. Guo, C. Sathe, J. E. Rubensson, H. Siegbahn, J. Nordgren and H. Ågren, Phys. Rev. B, 2004, 69, 024201 CrossRef.
- L. Weinhardt, M. Blum, O. Fuchs, A. Benkert, F. Meyer, M. Bär, J. D. Denlinger, W. Yang, F. Reinert and C. Heske, J. Electron. Spectrosc. Relat. Phenom., 2013, 188, 111–120 CrossRef CAS.
- L. Weinhardt, A. Benkert, F. Meyer, M. Blum, R. G. Wilks, W. Yang, M. Bär and F. Reinert, J. Chem. Phys., 2012, 136, 144311 CrossRef PubMed.
- A. Benkert, F. Meyer, D. Hauschild, M. Blum, W. Yang, R. G. Wilks, M. Bär, F. Reinert, C. Heske and L. Weinhardt, J. Phys. Chem. A, 2016, 120, 2260 CrossRef CAS PubMed.
- E. E. Bolton, J. Chen, S. Kim, L. Han, S. He, W. Shi, V. Simonyan, Y. Sun, P. A. Thiessen, J. Wang, B. Yu, J. Zhang and S. H. Bryant, J. Cheminformat., 2011, 3, 32 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B, 1981, 23, 5048–5079 CrossRef CAS.
- S. M. Dancoff, Phys. Rev., 1950, 78, 382–385 CrossRef.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B, 1986, 34, 5390–5413 CrossRef CAS PubMed.
- G. Onda, L. Reining, R. W. Godby, R. Del Sole and W. Andreoni, Phys. Rev. Lett., 1985, 75, 818–821 CrossRef PubMed.
- T. Isobe, R. Kuwahara and K. Ohno, Phys. Rev. A, 2018, 97, 060502(R) CrossRef.
- C. Mejuto-Zaera, C. Weng, M. Romanova, S. J. Cotton, K. B. Whaley, N. M. Tubman and V. Vlcek, J. Chem. Phys., 2021, 154, 121101 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  * and
Tsubasa
Aoki
* and
Tsubasa
Aoki
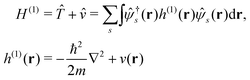
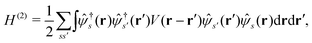
![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r),
(r), ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) †s(r) are annihilation and creation operators at position and spin coordinates (r, s), V(r − r′) = e2/4πε0|r − r′| is the Coulomb interaction, and
†s(r) are annihilation and creation operators at position and spin coordinates (r, s), V(r − r′) = e2/4πε0|r − r′| is the Coulomb interaction, and 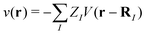 is the nuclear potential. The commutation relation between
is the nuclear potential. The commutation relation between ![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r) and H is given by
(r) and H is given by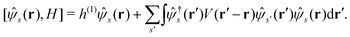
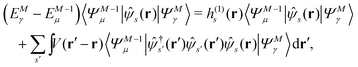
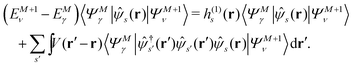
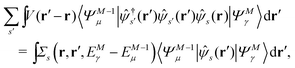
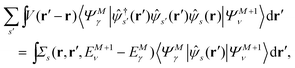
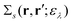 . Since both identities (5a) and (5b) hold simultaneously, they should be an equivalent identity. In fact, if we replace M, μ and γ with M + 1, γ and ν in eqn (5a), we obtain eqn (5b). This means that both equations should hold for arbitrary M, γ, μ and ν. This is the reason that MBPT can be applicable to an arbitrary excited eigenstate as an initial state. Indeed the full Green's function formulation of MBPT can be reproduced by using the Brillouin–Winger perturbation theory,13 which is certainly applicable to any excited eigenstate without doubt. Now, defining EQP energies as
. Since both identities (5a) and (5b) hold simultaneously, they should be an equivalent identity. In fact, if we replace M, μ and γ with M + 1, γ and ν in eqn (5a), we obtain eqn (5b). This means that both equations should hold for arbitrary M, γ, μ and ν. This is the reason that MBPT can be applicable to an arbitrary excited eigenstate as an initial state. Indeed the full Green's function formulation of MBPT can be reproduced by using the Brillouin–Winger perturbation theory,13 which is certainly applicable to any excited eigenstate without doubt. Now, defining EQP energies as![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r)|ΨMγ〉, ϕν(r, s) = 〈ΨMγ|
(r)|ΨMγ〉, ϕν(r, s) = 〈ΨMγ|![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r)|ΨM+1ν〉,
(r)|ΨM+1ν〉,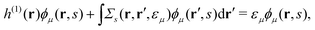
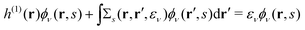
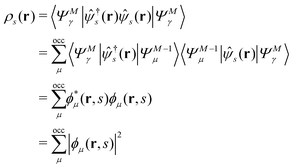
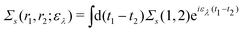 (numbers are abbreviations for position and time coordinates, i.e., i = (ri, ti)), one readily obtains the time-dependent EQP equation35,36
(numbers are abbreviations for position and time coordinates, i.e., i = (ri, ti)), one readily obtains the time-dependent EQP equation35,36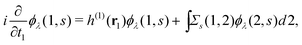
![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (1)|ΨMγ〉, ϕν(1, s) = 〈ΨMγ|
(1)|ΨMγ〉, ϕν(1, s) = 〈ΨMγ|![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (1)|ΨM+1ν〉
(1)|ΨM+1ν〉![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (1) = eiHt1
(1) = eiHt1![[small psi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b6.gif) (r1)e−iHt1. Then, the two-time spin density matrix ρs(1, 2) is introduced as
(r1)e−iHt1. Then, the two-time spin density matrix ρs(1, 2) is introduced as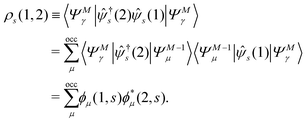
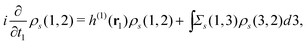
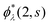 and summing with λ
and summing with λ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (=μ) over all occupied EQP states. Next, let us assume that ρs(1, 2) is expressed by M normalized EKS wave functions
(=μ) over all occupied EQP states. Next, let us assume that ρs(1, 2) is expressed by M normalized EKS wave functions ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i(1, s) (i = 1, 2,…,M) as
i(1, s) (i = 1, 2,…,M) as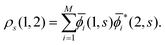
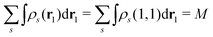 . (Note that the original ϕλ had norm less than 1 and infinite number of ϕλ were required to satisfy this necessary condition.) At each time t1, we can introduce the dual orbitals
. (Note that the original ϕλ had norm less than 1 and infinite number of ϕλ were required to satisfy this necessary condition.) At each time t1, we can introduce the dual orbitals ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) j(1, s) (j = 1, 2,…,M), which satisfy the biorthogonality condition
j(1, s) (j = 1, 2,…,M), which satisfy the biorthogonality condition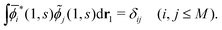
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) i(1, s) can be made from
i(1, s) can be made from ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i(1, s) by using the the Gram–Schmidt orthogonalization to all the other M − 1 orbitals
i(1, s) by using the the Gram–Schmidt orthogonalization to all the other M − 1 orbitals 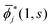 (j ≠ i). Then, we have
(j ≠ i). Then, we have 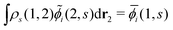 for i ≤ M. Then, eqn (13) yields the equation14
for i ≤ M. Then, eqn (13) yields the equation14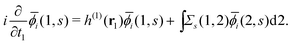
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) i(1, s) is equivalent to the EQP wave function ϕμ(1, s) except for a normalization factor. Therefore, the electron spin density ρs(r1) =ρs(1, 1) is expressed by M normalized EQP wave functions except for normalization. Those functions are not necessarily mutually orthogonal. So far, we discussed the occupied EQP wave functions only, but a similar discussion is possible also for the empty EQP wave functions.14
i(1, s) is equivalent to the EQP wave function ϕμ(1, s) except for a normalization factor. Therefore, the electron spin density ρs(r1) =ρs(1, 1) is expressed by M normalized EQP wave functions except for normalization. Those functions are not necessarily mutually orthogonal. So far, we discussed the occupied EQP wave functions only, but a similar discussion is possible also for the empty EQP wave functions.14