A reduced electrophilicity for simple Lewis acids A involved in non-covalent interactions with Lewis bases B

Abstract

Dissociation energies D_e for B⋯A = B + A can be written D_e = c′N_BE_A, where N_B and E_A are the nucleophilicities and electrophilicities of the Lewis base B and the Lewis acid A, respectively. A reduced electrophilicity is defined Ξ_A = E_A/σ_max, where σ_max is the maximum electrostatic surface potential on iso-surface of A, the atom directly involved in the non-covalent interaction. This definition is tested for halogen-bonded complexes B⋯YX, with Lewis bases B = N₂, CO, C₂H₂, C₂H₄, H₂S, HCN H₂O or NH₃. D_e plotted against N_B for several series B⋯YX yields straight lines of gradient E_A. When D_e/σ_max is the ordinate, the straight lines conflate to a single line, gradient Ξ_IX = E_IX/σ_max. Hydrogen-bonded complexes B⋯HX (X = F, Cl, Br, I), coinage-metal complexes B⋯MX (M = Cu, Ag, Au; X = F, Cl, Br, I), and alkali-metal bonded complexes B⋯MX (M = Li, Na: X = F, H, CH₃) behave similarly. Ξ_A is an intrinsic property of the atom immediately involved in the non-covalent bond.

---

1. Introduction

The use of reduced quantities in chemistry/physics to identify or focus attention on relationships among properties of otherwise disparate substances/topics is not uncommon. For example, in connection with the well-known Law of Corresponding States, if the reduced densities ρ/ρ^c of liquids (where ρ^c is the density at the critical temperature T^c), are plotted against T/T^c, a single curve results onto which a number of liquid substances fit very well. Reduced potential energy functions that apply to a range of related diatomic molecules are a second example and provide useful generalisations that provoke questions about what is common to molecules that can be so described. Quantities such as reduced mass and reduced energies feature as simplifying and unifying tools in the theory of rotational spectroscopy. In this article, we shall show that, for a wide range of non-covalent interactions B⋯A of Lewis bases B with Lewis acids A (namely, interactions through hydrogen, halogen, coinage-metal and alkali-metal bonds), we can define a reduced electrophilicity of A. We shall show that the reduced electrophilicity is an interesting general property of complexes B⋯YX in which the non-covalent interaction is one of several different types. It is independent of the atom X in the molecule YX involved in the non-covalent interaction. Thus, the reduced electrophilicity is a property that describes the propensity of Y to form the appropriate non-covalent bond, independently of X.

The terms nucleophile and electrophile were introduced by Ingold¹ in 1933. In his book “Structure and Mechanism in Organic Chemistry”,² Ingold gave the following definitions: “Reagents which act by donating their electrons to, or sharing them with, a foreign atomic nucleus will be called nucleophilic reagents or sometimes nucleophiles” and “Reagents which act by acquiring electrons, or a share in electrons, which previously belonged exclusively to a foreign molecule will be called electrophilic reagents, or sometimes electrophiles.’ Since 1933, there has been an extensive literature on the subject of nucleophilicity and electrophilicity. For example, using both words ‘nucleophilicity and electrophilicity’ together as a search topic in the Web Of Science returns 694 publications with an average citation of 30 per article. The great majority of the work is concerned with scales of nucleophilicity and electrophilicity based on rates of reaction, mainly involving organic molecules, as reviewed, for example, by Mayr and Patz³ in an article entitled: ‘Scales of Nucleophilicity and Electrophilicity: A System for Ordering Polar Organic and Organometallic Reactions.’ The definitions employed here, on the other hand, are based on the energy D_e of the (usually weak) non-covalent interaction of a pair of (initially isolated) molecules (a Lewis base B and a Lewis acid A) when they come together to form the isolated complex B⋯A without chemical reaction. Although these definitions are also consistent with those of Ingold quoted earlier, the subjects of the present article might be more correctly called, gas-phase nucleophilicities and electrophilicities of molecules involved in non-covalent interactions.

Some years ago,⁴ a method was proposed for reproducing the intermolecular stretching force constants k_σ of simple hydrogen-bonded complexes B⋯HX by assigning dimensionless nucleophilicities N_B and electrophilicities E_HX to the Lewis base B and to the Lewis acids HX, respectively, according to eqn (1):

k_σ = cN_BE_HX, (1)

in which c is a constant. The series for which X = F, Cl, Br and CN and B = N₂, OC, PH₃, H₂S, HCN, CH₃CN, H₂O and NH₃ was the main focus initially⁴ but this group was soon extended to include the π- and pseudo-π-Lewis bases acetylene, ethylene and cyclopropane.⁵ Later, it was shown that the approach could also be applied to several series of halogen-bonded complexes B⋯XY, where XY is one of the Lewis acids F₂, ClF, Cl₂, BrCl, Br₂^6,7 and ICl.⁸ In all these cases, the k_σ were experimental, zero-point state values, as determined from the centrifugal distortion constants⁹ available from analyses of the rotational spectra of such complexes. A detailed analysis^10,11 of ab initio calculated, equilibrium dissociation energies D_e showed that experimental k_σ values are directly proportional to D_e through the simple equation:

D_e = C_σk_σ, (2)

and that the constant C_σ = 1.50(3) × 10³ m² mol⁻¹ was appropriate to the whole series B⋯HX (B = N₂, CO, C₂H₂, C₂H₄, H₂S, H₃P, HCN, H₂O or NH₃ and X = F, Cl, Br or I) and B⋯XY (with XY as listed earlier). This relationship was shown to hold also when both D_e and k_σ were equilibrium values, as calculated ab initio at the CCSD(T)CBS level (CBS = complete basis set extrapolation) for the restricted series B⋯HF, B⋯HCl, B⋯F₂, B⋯Cl₂ and B⋯ClF but involving the same set of Lewis bases B.¹² Plots of D_eversus k_σ yielded good straight lines having gradients in agreement with those established in ref. 10 and 11 for these series. In a further, more wide-ranging analysis,¹³ the ab initio calculated values of D_e for 250 complexes were considered. The complexes were formed from 11 Lewis bases B and 23 Lewis acids A, chosen to include several types of non-covalent interaction (hydrogen, halogen, tetrel, pnictogen and chalcogen bonds). The D_e values were fitted by a least-squares method to eqn (3) (with c′ set as 1.00 kJ mol⁻¹ for convenience) to yield N_B and E_A values.

D_e = c′N_BE_A (3)

There was evidence that each of the five types of non-covalent interaction was fitted equally well and therefore it was concluded that eqn (3) is valid for all those interaction types. Thus the determined values of N_B and E_A were established as properties of the individual molecules.

Further investigations of complexes B⋯MX, (M = Cu, Ag or Au, X = F or Cl) involving the coinage-metal bond¹⁴ and of alkali-metal bonded complexes B⋯LiX and B⋯NaX (X = F, H or CH₃)¹⁵ have revealed that the ab initio calculated values of D_e for the complexes involving these two types of non-covalent interaction can also be represented by eqn (3). However, when eqn (3) was fitted to D_e values by using the least-squares method described in ref. 13 although the fits were good, somewhat different N_B values from those obtained in ref. 13 resulted, perhaps not surprisingly in view of the much more polar character of the LiX, NaX and CuX, AgX and AuX diatomic molecules than of HX, XY, etc. For the B⋯MX coinage metal series¹⁴ it was discovered that graphs of D_eversus N_B were good straight lines through the origin and led to the following order of electrophilicities E_AuF > E_AuCl > E_CuF > E_CuCl > E_AgF ≈ E_AgCl. It was also noted that, to good approximation, plots of D_e/σ_maxversus N_B, where σ_max is the maximum positive value of the molecular electrostatic surface potential (MESP) on the 0.001 e bohr⁻³ electron density iso-surface, fall on the same straight line for both MF and MCl for a given M. This suggests that a reduced electrophilicity might be defined as (E_MX/σ_max).

In the present article, we examine whether this definition of reduced electrophilicity is generally valid. To do so we present ab initio calculations of the equilibrium dissociation energy D_e accompanying the process B⋯IX = B + IX for the series of halogen-bonded complexes B⋯IX in which the Lewis base B is N₂, CO, C₂H₂, C₂H₄, H₂S, HCN H₂O or NH₃ and IX is variously IF, ICl, IBr or I₂. The corresponding series B⋯BrX (X = Br, Cl or F) and B⋯ClX (X = Cl or F) are also investigated. The calculations of D_e were conducted at the CCSD(T)(F12c)/cc-pVDZ-F12 level of theory. A least-squares fit of the D_e values to eqn (3) was carried out using the set of known N_B values¹³ for the Lewis bases to determine the E_YX (Y = I, Br, Cl) for the Lewis acids involved. Not only can eqn (3) be tested for this extended series, but also we shall investigate whether the graph of D_e/σ_maxversus N_B is a single straight line for the full set of iodine-bonded complexes B⋯IX (X = F, Cl, Br and I), and also for several other series. Put another way, we ask the question: Does E_IX/σ_max provide a reduced electrophilicity for the set of Lewis acids IF, ICl, IBr and I₂, i.e. one independent of the atom attached to I? Some previously published D_e values for the series of hydrogen-bonded complexes B⋯HX (X = F, Cl, Br and I)^10,11 and the series of alkali-metal-bonded complexes B⋯NaX and B⋯LiX (X = F, H and CH₃)¹⁵ will be treated in the same way to test whether the concept of reduced electrophilicity is generally applicable.

2. Theoretical methods

The geometry optimizations of the isolated monomers and complexes were carried out using the CCSD(T)(F12c) explicitly correlated, coupled-cluster method.^16,17 The cc-pVDZ-F12 basis sets, which are optimised for use with the CCSD(T)-F12 method,¹⁸ were used for all of the first and second row atoms. Pseudo-potential (PP) basis sets were employed for the atoms Br and I in combination with the ECP-10-MDF¹⁹ and ECP-28-MDF²⁰ effective core potentials to account for scalar relativistic effects. The frozen-core approximation was used in all the calculations, which employed the MOLPRO package.^21,22 Dissociation energies, so computed at the CCSD(T)(F12c)/cc-pVDZ-F12 level, were corrected for basis set superposition error (BSSE)²³ by means of the counterpoise keyword in MOLPRO. D_e values for 132 new complexes and 12 monomers were calculated specifically for this article. The remaining D_e values employed here are from earlier publications: the data for coinage-metals complexes are from ref. 14, those for the alkali-metal complexes are from ref. 15 and some of the B⋯HX (X = F, Cl, Br, I) and B⋯XY (X and Y are halogen atoms) are from ref. 10 and 11.

Molecular electrostatic surface potentials (MESP) were calculated by using the MP2/aug-cc-pVTZ wavefunction in the GAUSSIAN program²⁴ and represented at the 0.001 e bohr⁻³ electron density iso-surface with the Jmol program²⁵ (an open-source Java viewer for chemical structures in 3D. available at http://www.jmol.org/). The extreme values (maxima and minima) on the iso-surface were calculated with the multiwfn program.²⁶

The results for 132 new complexes and 12 monomers are presented in this article for the first time and are recorded in the ESI.† Those for complexes involving the Li and Na non-covalent bonds were published previously in ref. 15) and those involving Cu, Ag and Au with X = F and Cl were first published in ref. 14 but results for CuBr and CuI are new. All values of D_e for the coinage-metal complexes were calculated at the CCSD(T)/aug-cc-pVTZ, aug-cc-pVTZ-PP levels as appropriate and the binding energy D_e was obtained by using the CBS extrapolation method.^27,28 In excess of 300 complexes are discussed.

3. Results

3.1 The iodine-bonded series B⋯IX (X = F, Cl, Br, I)

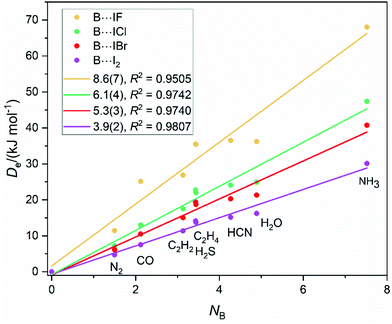
Fig. 1 shows a graph in which the equilibrium dissociation energies D_e of the iodine-bonded complexes B⋯IX (X = F, Cl, Br and I) are plotted against the nucleophilicity N_B of the series of Lewis bases B = N₂, CO, C₂H₂, C₂H₄, H₂S, HCN H₂O or NH₃, the latter quantities as determined in ref. 13. D_e is the energy required to move the components of B⋯IX from their equilibrium distance in the complex to become infinitely separated molecules B and IX relaxed to their hypothetical equilibrium states. The Lewis base PH₃ has been omitted from the list because it was shown previously that complexes such as H₃P⋯ICl²⁹ and H₃P⋯ClF³⁰ are of a different type from the remainder and have significant electric charge redistribution on complex formation. The linear-regression fits to the points (with the origin taken as a point under the assumption that the nucleophilicity N_B = 0 when D_e = 0) are shown as solid straight lines. The R² values shown in Fig. 1 indicate that the fits are satisfactory, with that for B⋯IF the worst at 0.95. Clearly, eqn (3) is obeyed by each of the B⋯IX series. The gradient of each straight line corresponds to the electrophilicity of the Lewis acid according to eqn (3) given that c′ = 1.00 kJ mol⁻¹ was used in the determination of the N_B values by the least squares fit to 250D_e values in ref. 13. The conclusion is therefore that E_IF = 8.6(7) > E_ICl = 6.1(4) > E_IBr = 5.3(3) > E_I2 = 3.9(2), which order is consistent with electron withdrawing power of the X atom in the order F > Cl > Br > I.

Fig. 1 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for the four series of iodine bonded complexes B⋯IX (X = F, Cl, Br and I). The continuous straight lines are linear regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit, as measured by R².

The concept of reduced electrophilicity discussed in the Introduction can now be tested for the B⋯IX series. Dividing eqn (3) by the value of σ_max (the maximum positive value of the MESP on the 0.001 e bohr⁻³ electron density iso-surface near to the I atom along the axis of the IX diatomic molecule), we have

D_e/σ_max = c′N_B(E_A/σ_max) = N_BΞ_A, (4)

in which Ξ_A = c′E_A/σ_max defines the reduced electrophilicity of the Lewis acid A and is dimensionless given that c′ = 1.0 kJ mol⁻¹, σ_max is in kJ mol⁻¹, and E_A is dimensionless. Thus, a plot of D_e/σ_maxversus N_B should be a straight line through the origin and have gradient Ξ_A. Values of σ_max calculated at the MP2/aug-cc-pVTZ level are available from Table 1. Fig. 2 displays these plots for the series B⋯IX, when X = F, Cl, Br and I.

Table 1 Maximum molecular electrostatic potentials σ_max/(kJ mol⁻¹) on the 0.001 e bohr⁻³ electron-density iso-surface of various Lewis acids YX (on the axis at the Y end of the molecule)^a

Lewis acid YX	X = I	X = Br	X = Cl	X = F	X = CN	X = CP	X = CCH	X = H	X = CH3
a Calculated at the MP2/aug-cc-pVTZ level of theory.
IX	125.7	158.4	180.1	241.3	201.3	—	142.0	—	—
BrX	—	118.8	141.3	205.6	—	—	—	—	—
ClX	—	—	107.0	172.1	—	—	—	—	—
HX	119.4	160.1	190.2	287.9	216.9	126.3	134.8
CuX	342.8	366.1	379.8	405.1	—	—	—	—	—
AgX	296.0	305.1	308.0	294.5	—	—	—	—	—
AuX	270.1	314.6	346.7	404.8	—	—	—	—	—
LiX	—	—	—	764.2	—	—	—	809.5	793.1
NaX	—	—	—	566.8	—	—	—	510.0	471.0

---

Fig. 2 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the four series of iodine-bonded complexes B⋯IX (X = F, Cl, Br and I). The continuous straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line and the quality of the fit as measured by R².

Fig. 2 confirms that there is indeed a reduced electrophilicity Ξ_A having the value 0.034(2) for the iodine atom in the four diatomic molecules IF, ICl, IBr and I₂. The scatter and R² are rather larger for IF, but the gradients of the four straight lines are identical within their quoted errors. In fact, some points are obscured by superposition of others. It is of interest to examine, in the same way, the situation when the Lewis acids are the pseudo-halogens ICN and ICCH. The graph of D_eversus N_B is shown in Fig. 3 while that when the ordinate is D_e/σ_max is in Fig. 4. The latter diagram shows that the gradients in Fig. 4 are equal within the fitting error and hence both ICN and ICCH can be described by a reduced electrophilicity Ξ = 0.0229(4). We note, however, that this value is different from that for the IX (X = F, Cl, Br, I) given in Fig. 2.

Fig. 3 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for the two series of iodine-bonded complexes B⋯IX (X = CN and CCH). The continuous straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

Fig. 4 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the two series of iodine-bonded complexes B⋯IX (X = CN and CCH). The continuous straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line and the quality of the fit as measured by R².

3.2 The bromine-bonded series B⋯BrX (X = F, Cl, Br)

Fig. 5 shows the graphs of D_eversus N_B for the three series B⋯BrX (X = F, Cl, Br). The same pattern as observed for the B⋯IX series is evident, with the largest scatter from its regression line again when X = F. Values of D_e are not given in ref. 10 and 11 for N₂⋯Br₂ and HCN⋯Br₂ and these were calculated for the present work. Evidently, eqn (3) is obeyed by each series, as indicated by R² values close to unity. The electrophilicities of the BrX are in the order X = F > Cl ≥ Br.

Fig. 5 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for the three series of bromine-bonded complexes B⋯BrX (X = F, Cl and Br). The continuous straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

The corresponding graphs of D_e/σ_maxversus N_B for the series B⋯BrF, B⋯BrCl and B⋯Br₂ are set out in Fig. 6. Note again that the gradients, which yield the reduced electrophilicity Ξ_A for the molecules BrX, are almost equal within the errors of the fits and suggest that, as for the B⋯IX series, the definition of reduced electrophilicity used here is reasonable.

Fig. 6 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the three series of bromine-bonded complexes B⋯BrX (X = F, Cl and Br). The continuous straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line and the quality of the fit as measured by R².

3.3 The chlorine-bonded series B⋯ClX (X = F, Cl)

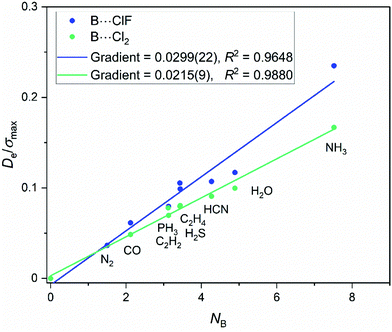
There are only two members of this series. Fig. 7 shows the graph of D_eversus N_B for both the B⋯ClF and B⋯Cl₂ series. Eqn (3) appears to be obeyed by both. The D_e/σ_maxversus N_B plots shown in Fig. 8 have gradients = 0.030(2) and 0.022(1) for the B⋯ClF and B⋯Cl₂ series, respectively. Hence, we cannot unambiguously assign a reduced electrophilicity to the ClF and Cl₂ molecules for their interactions with the Lewis bases B, as was the case for the B⋯BrX and B⋯IX series. Nevertheless these values are much closer together than the gradients of 5.2(4) and 2.3(1) kJ mol⁻¹ of the fitted points in the graphs of D_eversus N_B for the B⋯ClF and B⋯Cl₂ series, respectively.

Fig. 7 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for the two series of chlorine-bonded complexes B⋯ClX (X = F and Cl). The continuous straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

Fig. 8 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the two series of chlorine-bonded complexes B⋯ClX (X = F and Cl). The straight lines are regression fits to the points (solid dots) for each series, (origin as a point). The inset gives the gradient of each fitted line and the quality of the fit, as measured by R².

3.4 Is there a reduced electrophilicity Ξ_A appropriate to the hydrogen halides HX?

The evidence presented in Sections 3.1–3.3 indicates that the quantity Ξ_A defined by means of eqn (3) and (4) might be used as a reduced electrophilicity for the Lewis acids A involved in series of halogen-bonded complexes. A reduced electrophilicity so defined is a measure of the propensity of, e.g. IX to form B⋯IX halogen bonds independently of the halogen atom X attached to it. It is of interest to investigate whether this concept has generality. In this section, hydrogen-bonded complexes B⋯HX having X = F, Cl, Br and I will be discussed first and then X = CN, CP and CCH will be considered.

Dissociation energies D_e for the series B⋯HX (now including B = PH₃), calculated at the explicitly-correlated level CCSD(T)(F12c)/cc-pVDZ-F12 and corrected for basis set superposition error (BSSE), have been published elsewhere.^10,11 Using again N_B values determined in ref. 13, Fig. 9 was constructed. It shows clearly that the B⋯HX series obey eqn (3) with well-determined gradients and R² values, the latter close to 1. The gradients provide measures of the electrophilicities E_HX of the hydrogen halides, which have the values 7.0(4), 4.5(2), 3.9(2) and 2.8(1) for X = F, Cl, Br and I, respectively, an order consistent with chemical intuition (the greater the slope the stronger the hydrogen bonds). Fig. 10 shows the corresponding set of graphs in which D_e/σ_max is now the ordinate. The gradients determined by linear regression fits are closely bunched and have the mean value of 0.0239(7), which is, according to eqn (4), the reduced electrophilicity Ξ_HX of the hydrogen halides. The narrow spread of values indicates that the reduced electrophilicity of the hydrogen halides appears to be a well-defined quantity.

Fig. 9 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for the four series of hydrogen-bonded complexes B⋯HX (X = F, Cl, Br and I). The straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

Fig. 10 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the four series of hydrogen-bonded complexes-B⋯HX (X = F, Cl, Br and I)). The straight lines are regression fits of the points (solid dots) for each series, (origin as a point). The inset gives the gradient of each fit and the quality of the fit as measured by R².

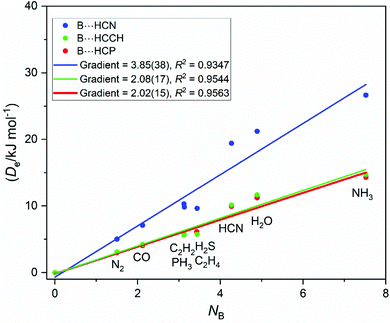
Given the results for the hydrogen halides, it is of interest to consider hydrogen acids of the type HCX in which H is now directly attached to a carbon atom. D_e values for B⋯HCN, B⋯HCP and B⋯HCCH complexed with the same set of Lewis bases B were calculated at the CCSD(T)(F12c)/cc-pVTZ-F12 level of theory and corrected for BSSE. The graphs of D_e plotted against N_B for these three series are in Fig. 11. Note that the points for B⋯HCCH and B⋯HCP are close to coincident. Convergence in the geometry optimisation for H₂S⋯HCN and H₂S⋯HCCH was not achieved and so points for these are missing.

Fig. 11 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for three series of hydrogen-bonded complexes B⋯HX (X = CN, CP and CCH). The straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

Although the scatter of the points is rather large for the HCN series, eqn (3) is obeyed by all three Lewis acids HCN, HCP and HCCH. Moreover, as can be seen in Fig. 12, the plots of D_e/σ_max against N_B for all three series lead to the same gradient within the fitting error. Thus, the reduced electrophilicity appears to be a property that can be assigned to these three Lewis acids also. We note, however, that Ξ_HCX = E_HCX/σ_max is different from the value obtained for the hydrogen halides.

Fig. 12 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the three series of hydrogen-bonded complexes B⋯HX (X = CN, CP, and CCH). The straight lines are regression fits to the points (solid dots) for each series, (origin as a point). The inset gives the gradient of each fit and the quality of the fit as measured by R².

3.5 Reduced electrophilicity and the coinage-metal halides MX (M = Cu, Ag, Au; X = F, Cl, Br, I)

Complexes of the type B⋯MX, where M = Cu, Ag, Au, X = F, Cl were discussed in ref. 14, where the possibility of a reduced electrophilicity was first raised. The Lewis bases B are again the nine simple molecules B = N₂, CO, C₂H₂, C₂H₄, H₂S, PH₃, HCN, H₂O, and NH₃. For the present article, calculations have been extended to include X = Br and I. The graphs of D_eversus N_B for the series B⋯AuX (X = F, Cl, Br and I) are displayed in Fig. 13, while the plots with D_e/σ_max as the ordinate are in Fig. 14. The corresponding pairs of diagrams for M = Cu are available as Fig. S1 and S2 of the ESI,† while for M = Ag Fig. S3 and S4 (ESI†) are appropriate. The magnitude and order of the D_e values for the B⋯MX complexes (and therefore the values of the N_B of the Lewis bases when involved in such complexes, as published in ref. 14) are both quite different from those used¹³ for the hydrogen- or halogen-bonded series. Nevertheless, it is clear from Fig. 13 and Fig. S1, S3 (ESI†) that eqn (3) is valid for coinage-metal bonds as well as hydrogen- and halogen bonds. Moreover, the order of the electrophilicities of the aurous halides is E_AuF > E_AuCl > E_AuBr > E_AuI. The order for the argentous and cuprous halides is the same.

Fig. 13 Dissociation energy D_e plotted against the nucleophilicity of the Lewis base B for the four series of coinage-metal-bonded complexes B⋯AuX (X = F, Cl, Br, I). The straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

Fig. 14 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the four series of coinage-metal-bonded -bonded complexes- B⋯AuX (X = F, Cl, Br, I). The straight lines are regression fits to the points (solid dots) for each series, (origin as a point). The inset gives the gradient of each fit and the quality of the fit as measured by R².

Fig. 14 illustrates how division of the D_e value by σ_max reduces the four straight lines in Fig. 13 to a single line. Thus, the gradients of the four lines in Fig. 14 are identical within the fitting error, with the mean value 0.0442(18). This is the dimensionless reduced electrophilicity Ξ_AuX of the AuX diatomic molecules. Fig. S2 and S4 (ESI†) indicate that Ξ_CuX = 0.0283(18) and Ξ_AgX = 0.0287(22).

The coinage-metal diatomic molecules are much more polar than the Lewis acids considered in earlier sections. For example, the electric dipole moments of CuCl and AgCl are 5.74 D³¹ and 6.076(6) D,³² respectively, while those of BrCl, ICl and HBr are 0.519(4) D,³³ 1.24(2) D³⁴ and 0.8280(6) D,³⁵ respectively. CuCl and AgCl (and presumably AuCl) also have large ionicities i_c. The ionicity of a diatomic molecule is a measure of the fractional contribution of the structure M⁺Cl⁻ to the valence-bond description of the molecule. It can be calculated³⁶ from the nuclear quadrupole coupling constant χ_z(X) of the halogen atom X in the appropriate diatomic molecule by using eqn (5), in which eQq_n,1,0 is the quadrupole coupling constant arising from a single electron in a np_z orbital.

i_c = 1 + {χ_z(X)/(eQq_n,1,0)} (5)

The i_c values for CuCl and AgCl are 0.71 and 0.67,³⁷ while those for BrCl, ICl and HBr are 0.06, 0.25 and 0.30.³⁶ Despite their greater ionicity, the concepts of electrophilicity and reduced electrophilicity introduced by eqn (3) and (4), respectively, appear to apply at least as well to the coinage-metal complexes B⋯MX as they do to the hydrogen-bonded B⋯HX and halogen-bonded B⋯YX discussed here.

3.6 Reduced electrophilicity of the alkali-metal compounds LiX and NaX (X = F, H, CH₃)

Application of eqn (5) to alkali-metal halides such as NaCl and LiCl shows values of i_c that are close to 1, indicating that these molecules are essentially ion pairs in the gas phase.³⁶ The question that then arises is: Does the concept of reduced electrophilicity apply as well to alkali-metal bonded complexes such as B⋯NaX and B⋯LiX as it does to hydrogen-bonded, halogen-bonded and coinage-metal-bonded complexes? D_e and N_B values for B⋯MF, B⋯MH, B⋯MCH₃ were recently published¹⁵ for M = Na and Li, with Lewis bases B = CO, HCN, H₂O, NH₃, H₂S and PH₃. A set of N_B, E_LiX and E_NaX were derived by the least-squares method from 34 values of D_e for complexes that could be identified as isostructural with their hydrogen- and halogen-bonded counterparts. As for the coinage-metal bond series, the N_B scale had some significant differences from that used for the hydrogen- and halogen-bonded series. The variation of D_e with N_B for the alkali-metal bonded complexes (first published in ref. 15) is set out again in Fig. 15 (redrawn). Each series leads to an excellent straight line, which indicates eqn (3) is appropriate here also. The electrophilicities have the order E_LiH > E_LiF ≈ E_LiCH3 > E_NaF > E_NaH > E_NaCH3, as previously established.¹⁵

Fig. 15 Dissociation energy D_e plotted against the nucleophilicity N_B of the Lewis base B for the six series of alkali-metal-bonded complexes B⋯LiX and B⋯NaX (X = F, H, CH₃). The straight lines are regression fits to the points (solid dots) for each series, with the origin taken as a point. The inset gives the gradient of each fitted line in kJ mol⁻¹ and the quality of the fit as measured by R².

The corresponding graphs of D_e/σ_maxversus N_B are set out in Fig. 16. The gradients of the three straight lines for the B⋯LiX complexes in Fig. 16 are very nearly equal. However, a separate linear regression fit of all the B⋯LiX points alone gives Ξ_LiX = E_LiX/σ_max = 0.01114(2) for the reduced electrophilicity of the LiX molecules, while for the B⋯NaX complexes alone the value is 0.01007(10). It appears that the reduced electrophilicities of the LiX and NaX molecules are very similar, but not equal.

Fig. 16 D _e/σ_max plotted against the nucleophilicity N_B of the Lewis base B for the six series of alkali-metal-bonded complexes B⋯LiX and B⋯NaX (X = H, F, CH₃). The six straight lines are regression fits to the points (solid dots) for each series, (origin as a point). The inset gives the gradient of each fit and the quality of the fit as measured by R².

4. Conclusions and discussion

The main conclusion of this work is that it is possible to define a reduced electrophilicity Ξ_A for a Lewis acid A when involved in non-covalent complexes B⋯A formed with Lewis bases B. This is found to be true for a range of non-covalent interaction types. A summary of the values of Ξ_A determined here is available in Table 2.

Table 2 Values of the reduced electrophilicity Ξ_A determined for various Lewis acids A^a

Lewis acid A	Reduced electrophilicity ΞA
a The reduced electrophilicity of a given Lewis acid A is defined as EA/σmax and is the gradient of the straight line obtained by plotting De/σmax against NB for a series of complexes B⋯A, where the NB and EA are the nucleophilicity and electrophilicity of the Lewis bases B and the Lewis acid A, respectively. σmax is the maximum positive value of the MESP of A on the 0.001 e bohr^−3 iso-surface along its symmetry axis and near to the atom that is directly involved in the non-covalent interaction of A with B.
IX (X = F, Cl, Br, I)	0.033(2)
IX (X = CN, CCH)	0.0229(4)
BrX (X = F, Cl, Br)	0.033(3)
ClX (X = F, Cl)	∼0.026(4)
HX (X = F, Cl, Br, I)	0.0239(7)
HX (X = CN, CP, CCH)	0.0164(13)
CuX (X = F, Cl Br, I)	0.0283(18)
AgX (X = F, Cl, Br, I)	0.0287(22)
AuX (X = F, Cl, Br, I)	0.0442(18)
LiX (X = H, F, CH3)	0.01114(2)
NaX (X = H, F, CH3)	0.01007(10)

---

Graphs of the equilibrium dissociation energy D_e for complexes B⋯IX plotted against the nucleophilicity N_B of the Lewis bases B = N₂, CO, C₂H₂, C₂H₄, H₂S, HCN, H₂O, and NH₃ for the four series X = I, Br, Cl, F have been used to show that eqn (3), D_e = c′N_BE_A, is obeyed by each of these series of iodine-bonded complexes. It is thereby established that the order of the gas-phase non-covalent electrophilicities E_IX of these dihalogen molecules is E_IF > E_ICl > E_IBr > E_I2. Moreover, when D_e is divided by σ_max, (i.e. the value of the molecular electrostatic potential on the 0.001 e bohr⁻³ electron density iso-surface on the molecular axis near to I), the plot of D_e/σ_maxversus N_B reveals that the four distinct straight lines of different gradient in the D_eversus N_B plots have become conflated to give a single straight line to a good level of approximation. The gradient of the single straight line is referred to as the reduced electrophilicity Ξ_IX = D_e/σ_max of the IX molecules (X = I, Br, Cl and F). The same procedure followed for the series B⋯BrX and (less certainly) the series B⋯ClX allows similar conclusions and leads to the order of the reduced electrophilicities Ξ_IX = Ξ_BrX > Ξ_ClX. The series B⋯ICX (X = N, CH) also behaved in the same manner as the B⋯IX series, but the conflation of the two straight lines when D_e/σ_max is plotted against N_B yields an Ξ_ICX value smaller than that of the B⋯IX series.

It has also been possible to show that a similar conflation of four straight lines to a single straight line results when D_e/σ_max is plotted against N_B for the hydrogen-bonded series B⋯HX (X = F, Cl, Br, I) and hence provides a reduced electrophilicity Ξ_HX for the hydrogen halides. When HX is replaced by HCX, where X = CN. CP and CCH, a value of Ξ_HCX is again established but, as for the corresponding IX and ICX series, it is found that Ξ_HX > Ξ_HCX.

When the Lewis acid is more polar, as for AuX, AgX and CuX in the three series of coinage-metal bonded complexes B⋯MX (M = Cu, Ag, Au; X = F, Cl, Br, I), it is still possible to establish well-determined reduced electrophilicities for the Lewis acids in the order Ξ_AuX > Ξ_AgX ≈ Ξ_CuX. Even when the Lewis acid is close to being an ion pair, as in LiX and NaX (X = F, H, CH₃), the approach is again successful and leads to well-determined reduced electrophilicities in the order Ξ_NaX ≈ Ξ_LiX.

It is important to discuss the significance of the newly-defined quantity referred to as reduced electrophilicity. Eqn (3) in Section 3.1 has been established to hold for a wide range of non-covalent interactions involved in axially symmetric complexes B⋯YX, where Y is the atom of the Lewis acid directly involved in that interaction. An important quantity in this context is the most positive electrostatic potential σ_max at the 0.001 e bohr⁻³ iso-surface on the symmetry axis in the vicinity of the atom Y of the Lewis acid (0.001 e bohr⁻³ is the conventional choice of electron density for such surfaces). It was shown in Section 3.1 that division of eqn (3) by σ_max to give eqn (4) and then a plot of D_e/σ_maxversus N_B leads in all cases considered here to a straight line through the origin. According to eqn (4), the gradient of this line is E_YX/σ_max, that is the electrophilicity of the molecule YX per unit maximum positive electrostatic potential on the symmetry axis at Y. We have shown (by consideration of four different types of non-covalent interaction and a range of axially symmetric Lewis acids YX) that the quantity E_YX/σ_max is an intrinsic property of the atom Y involved in the non-covalent interaction with the nucleophilic region of the Lewis base B. Thus, it is the same for all diatomic Lewis acids when the same atom Y is that involved in the non-covalent interaction with B. This result is made clear, for example, by Fig. 10, which involves the four hydrogen halides. When YX is a triatomic (or higher) molecule, as in Fig. 12 (which deals with the axially symmetric polyatomic Lewis acids HCN, HCP and HCCH), E_YX/σ_max is again an intrinsic property of the atom Y = H for the group, but has a slightly different value from that of the hydrogen halides (Fig. 10). Therefore it seems justified to give the quantity E_YX/σ_max the name reduced electrophilicity and the special symbol Ξ_YX. This new reduced quantity clearly points to systematic family relationships among groups of Lewis acids involving different types of non-covalent interaction. Further investigation might reveal further aspects the relationship.

Thus, we conclude that the reduced electrophilicity of a Lewis acid YX is an intrinsic property of the atom Y and its axial electrostatic surface potential directly involved in the non-covalent interaction. It appears to be independent of the nature of the remainder of YX, certainly so when YX is a diatomic molecule and nearly so for more complex YX. It therefore provides a measure of the propensity of atom Y to participate in a wide range of hydrogen bonds (if Y = H), halogen bonds (if Y is a halogen atom), coinage-metal bonds (if Y is a Group 11 atom), alkali-metal bonds (if Y is an alkali-metal atom).

The vast majority of data on nucleophilicities and electrophilicities involves quantities that are derived from the rate constants of chemical reaction in solution between more complex molecules than those discussed here (see ref. 3, for example). The electrophilicities and their reduced values presented in the Results section refer to the limiting, gas-phase interactions between pairs of molecules otherwise isolated and therefore comparison of the two scales is unlikely to be useful. Two papers have been published,^38,39 however, that make a theoretical interpretation of the gas-phase N and E values set out initially in ref. 4.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

ACL thanks the University of Bristol for the award of a University Senior Research Fellowship. IA thanks the Ministerio de Ciencia e Innovación of Spain (PGC2018-094644-B-C22 and 5931125495-125495-4-21) and Comunidad de Madrid (P2018/EMT-4329 AIRTEC-CM) for financial support.

References

1. C. K. Ingold, J. Chem. Soc., 1933, 1120–1127.
2. C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell University Press, Ithaca, New York, 1953, pp. 200–201.
3. H. Mayr and M. Patz, Angew. Chem., Int. Ed. Engl., 1994, 33, 938–957.
4. A. C. Legon and D. J. Millen, J. Am. Chem. Soc., 1987, 109, 356–358.
5. A. C. Legon and D. J. Millen, J. Chem. Soc., Chem. Commun., 1987, 986–987.
6. A. C. Legon, J. Chem. Soc., Chem. Commun., 1998, 2585–2586.
7. A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714.
8. A. C. Legon, in Halogen Bonding: Fundamentals and Applications, ed. P. Metrangolo and G. ResnatiStructure and Bonding, Springer-Verlag, Berlin, 2008, ch. 2, vol. 126, pp. 17–64.
9. D. J. Millen, Can. J. Chem., 1985, 63, 1477–1479.
10. A. C. Legon, Phys. Chem. Chem. Phys., 2014, 16, 12415–12421.
11. A. C. Legon, Phys. Chem. Chem. Phys., 2014, 16, 25199.
12. I. Alkorta and A. C. Legon, New J. Chem., 2018, 42, 10548–10554.
13. I. Alkorta and A. C. Legon, Molecules, 2017, 22, 1786–1799.
14. I. Alkorta, N. R. Walker and A. C. Legon, Inorganics, 2021, 9, 13.
15. I. Alkorta, J. G. Hill and A. C. Legon, Phys. Chem. Chem. Phys., 2020, 22, 16421–16430.
16. C. Hättig, D. P. Tew and A. Köhn, J. Chem. Phys., 2010, 132, 231102.
17. C. Hättig, W. Klopper, A. Köhn and D. P. Tew, Chem. Rev., 2012, 112, 4–74.
18. J. G. Hill and K. A. Peterson, J. Chem. Phys., 2014, 141, 094106 . See http://bit.ly/ccBasis for a repository of basis functions, including cc-pVDZ-F12 for Br and I, constructed by J. G. Hill.
19. M. Doig, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
20. I. S. Lin, H. Stoll and P. Schwertfeger, J. Chem. Phys., 2006, 124, 034107.
21. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, ‘Molpro: a general-purpose quantum chemistry program package’, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
22. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, MOLPRO 2019.2, a package of ab initio programs, 2019.
23. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al., Gaussian 16; Revision, A.03, Gaussian, Inc., Wallingford, CT, USA, 2016.
25. Jmol: An Open-Source Java Viewer for Chemical Structures in 3D. Available online at: http://www.jmol.org/.
26. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
27. D. Feller, J. Chem. Phys., 1993, 98, 7059–7071.
28. A. Halkier, T. Helgaker, P. Jorgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446.
29. A. C. Legon, Chem. Phys. Lett., 1999, 314, 472–480.
30. R. A. Shaw, J. G. Hill and A. C. Legon, J. Phys. Chem. A, 2016, 120, 8461–8468.
31. S. Hau and P. F. Bernath, J. Phys. Chem. A, 2015, 119, 1435–1438.
32. K. P. R. Nair and J. Hoeft, J. Phys. B: At. Mol. Phys., 1984, 17, 735–738.
33. K. P. R. Nair, J. Hoeft and E. Tiemann, Chem. Phys. Lett., 1978, 58, 153–156.
34. E. Herbst and W. Steinmetz, J. Chem. Phys., 1978, 56, 5342–5347.
35. F. A. van Dijk and A. Dymanus, Chem. Phys. Lett., 1970, 5, 387–389.
36. W. Gordy and R. L. Cook, Microwave Molecular Spectra, John Wiley and sons, New York, 2nd edn, 1984, ch. 14, p. 752.
37. A. C. Legon and N. R. Walker, Phys. Chem. Chem. Phys., 2018, 20, 19332–19338.
38. A. Ebrahimi, H. Roohi, M. Habibi and M. Hasannejad, Chem. Phys. Lett., 2006, 327, 368–372.
39. A. Cedillo, R. Contreras, M. Galván, A. Aizman, J. Andrés and V. S. Safont, J. Phys. Chem. A, 2007, 111, 2442–2447.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d2cp00779g

---