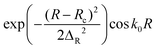Representing globally accurate reactive potential energy surfaces with complex topography by combining Gaussian process regression and neural networks
Zijiang
Yang
 ,
Hanghang
Chen
and
Maodu
Chen
,
Hanghang
Chen
and
Maodu
Chen
 *
*
Key Laboratory of Materials Modification by Laser, Electron, and Ion Beams (Ministry of Education), School of Physics, Dalian University of Technology, Dalian 116024, P. R. China. E-mail: mdchen@dlut.edu.cn
First published on 12th April 2022
Abstract
There has been increasing attention in using machine learning technologies, such as neural networks (NNs) and Gaussian process regression (GPR), to model multi-dimensional potential energy surfaces (PESs). A PES constructed using NNs features high accuracy and generalization capability, but a single NN cannot actively select training points as GPR does, resulting in expensive ab initio calculations as the molecular complexity increases. However, a PES constructed using GPR has a slow speed of evaluation and it is difficult to accurately describe a fast-changing potential. Herein, an efficient scheme for representing globally accurate reactive PESs with complex topography based on as few points as possible by incorporating active data selection of GPR into NN fitting is proposed. The validity of this strategy is tested using the BeH2+ system, and only 1270 points are automatically sampled. The generalization performance and speed of evaluation of the generated PES are much better than those of the GPR PES constructed using the same dataset. Moreover, an accurate NN PES is fitted by 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 points as a benchmark for comparison to further test the global accuracy of the PES obtained using this scheme, and the corresponding results present extremely consistent topography characteristics and calculated Be+(2S) + H2 reaction probabilities.
122 points as a benchmark for comparison to further test the global accuracy of the PES obtained using this scheme, and the corresponding results present extremely consistent topography characteristics and calculated Be+(2S) + H2 reaction probabilities.
1. Introduction
Potential energy surface (PES), as a crucial concept in physical chemistry, was introduced by the separation of nuclear and electronic motions, which gives rise to molecular spectroscopies and chemical reactivity dynamics simulations. Since the quality of dynamical calculations is determined directly by the accuracy of potential energy, numerous numerical methods1–9 for generating PESs have been developed over the past few decades to avoid excessive computational cost. Constructing an applicable PES of a molecular system generally requires two steps, namely, the calculations of energy points in the selected coordinate range and representing the mathematical relationship between the nuclear configurations and the corresponding potential energies from a mass of discrete data. The developments in the electronic structure theory and computing power have enabled high-precision ab initio energies for small systems. However, establishing a global PES of a system with multiple dimensions is still a challenge. This is particularly true for reactive PESs with complex topography in which all the reactant and product channels and the regions where reaction can access need to be included for accurately characterizing the classical trajectory or quantum scattering calculations. For example, it usually takes tens of thousands of points to build complex-forming reactive PESs dominated by a well even for the simplest triatomic systems.10–12 Therefore, it is a key issue to efficiently sample data points in the nuclear configuration space to make the construction of polyatomic or complex structured PESs truly possible.In recent years, there has been increasing attention in representing high-dimensional PESs using machine learning algorithms.13–18 Among these methods, it is worth mentioning that the artificial neural network (NN)19 is a powerful and robust tool for fitting high-quality PESs of reactive systems in the gas phase and the interaction of molecules with surfaces.20–37 NNs can give an analytic form about the nuclear coordinates and energies by minimizing the cost function to obtain the optimal parameters of every neuron. However, the implementation of the NN approach is essentially based on the ab initio points selected in advance, and it becomes exponentially difficult to perform electronic structure calculations in enormous configurations as the complexity of the system increases. There have been widespread studies on how to saturate the energy points in a large configuration space based on the NN fitting. Raff et al. developed the use of trajectories and distance between ab initio points to choose new configurations.38 Behler proposed the sampled scheme of the configuration space by the large discrepancy between two different NN fits.39 Lin et al. put forward an uncertainty-driven strategy to automatically construct multidimensional NN PESs.40,41 They used the weighted negative squared difference surface between two independent NN structures as the uncertainty metric to search and add new data at the less reliable region of PES. These ways in generating an optimal dataset automatically amount to active learning, a machine learning algorithm with an efficient decision on the selection of training data.
Another popular machine learning method in modeling PESs is the kernel-based Gaussian process regression (GPR).42 Unlike NNs, GPR is a nonparametric model without a specific functional form, and it provides a statistical estimate of the energy value at an unknown configuration based on the pre-existing ab initio points. Benefiting from the Bayesian modeling, GPR can construct accurate PESs with fewer data points, and it has been successfully applied in multiple molecular systems.43–56 An important advantage of the GPR model is that it can explicitly provide the predictive uncertainty at an unknown configuration via variance, providing a straightforward active learning scheme to sample data points. Guan et al. utilized this unique feature to reproduce the H + H2O ↔ H2 + OH and H + CH4 ↔ H2 + CH3 reactive PESs by continually adding new energy points with the maximum of variance,57 and the two reliable PESs were obtained only by assembling 920 and 4000 points, respectively. Uteva et al. used three active learning strategies to determine the training sets of GPR in generating intermolecular PESs for CO2–Ne, CO2–H2, and Ar3 systems,58 and their studies further demonstrate the high efficiency of GPR in sampling data. Therefore, using the GPR method to represent PESs can save a mass of ab initio calculations, and it is more convenient and efficient for data acquisition than the NN model.
On the other hand, the speed of evaluation is also a very important factor for the assessment of constructed PESs. Reactive PESs obtained by the GPR approach are much slower to evaluate than the NN fitting because the product of two vectors with the size of the number of training points n needs to be evaluated numerically, scaling as O(n), which restrains the subsequent dynamics calculations to a great extent when the value of n is relatively large. In contrast, the numerical evaluation of NN PESs only depends on the number of layers and neurons of the network, thus it is very fast to access the energy values of the arbitrary configurations. Moreover, there exists the risk of ill-conditioned covariance matrices when the training set contains very close points or rapidly varying energy values, indicating that the GPR model is not suitable for constructing reactive PESs with obvious well or barrier structures owing to the requirement of dense points in these regions.
To sum up, a pure NN model can represent accurate PESs, but it cannot actively select training points as GPR does, thus the corresponding electronic structure calculations become much too expensive as the molecular complexity increases. PESs generated by the GPR method can significantly save the number of ab initio points compared with the NN fitting, but the speed of evaluation is slow and the regions with fast-changing energy cannot be accurately reproduced, thus the GPR model is usually used to construct PESs near the equilibrium geometry rather than global reactive PESs. Therefore, constructing globally accurate multi-dimensional PESs with a rapid speed of evaluation remains a challenge by using a single model. Combining the advantages of the above two machine learning algorithms could be a good idea to overcome this difficulty. In this work, we propose a new scheme for representing reactive PESs with complex topography by incorporating the active data selection of GPR into the NN fitting, which can generate accurate analytic PESs with a rapid speed of evaluation by sampling as few ab initio points as possible. First, a small initial dataset is selected to produce a rough GPR PES; and then the new ab initio data are added to the training set by searching the maximum in the variance space, and this procedure is automatically repeated until obtaining the convergent value of the highest predictive variance; finally, the NN method is used to construct the analytical PES based on the finally determined training points. We test the validity of this scheme in a simple triatomic Be+(2S) + H2 reactive system. The main reason is that accurate ab initio data can be obtained due to the relatively small number of electrons of this system, which is critical for testing a new approach for constructing PESs. Moreover, compared to H3, LiH2, or other simpler systems, the ground state BeH2+ PES features more complex topography characteristics, including wells, barriers, cusps formed by the avoided crossing, and rapidly changing energies in some regions. Therefore, the Be+(2S) + H2 system is a suitable candidate for examining the feasibility and universal applicability of this new strategy. The remainder of this paper is as follows: Section 2 gives the detailed methodology, including the ab initio calculations, searching points in GPR and NN fitting. In Section 3, the results and discussion are presented, which prove the effectiveness of this scheme in representing reactive PESs with few points. Section 4 concludes this article.
2. Methods
In this work, the ab initio calculations are performed using Molpro 2012 software.59 The energy points of the ground state (12A′) BeH2+ are calculated at the internally contracted multi-reference configuration interaction60,61 levels with the Davidson correction (MRCI + Q), and the augmented Dunning-type correlation consistent polarized quadruple basis set62 is adopted for H and Be atoms. Ab initio energy calculations for this system are carried out in a wide configuration space, and the data points are sampled in the Jacobi coordinates (r, R, and θ). The reactive region of Be+(2S) + H2 is defined as 0.4 Å ≤ r ≤ 9.6 Å, 0.1 Å ≤ R ≤ 13.2 Å, 0° ≤ θ/degree ≤ 90°, and the product region of BeH+ + H is defined as 1.0 Å ≤ r ≤ 9.6 Å, 0.1 Å ≤ R ≤ 13.2 Å, 0° ≤ θ/degree ≤ 180°. A total of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 energy points covering the whole configuration region are selected as the reference set, which provides the candidate points added to the training database and serves as the test data to examine the generalization ability of the trained model.
040 energy points covering the whole configuration region are selected as the reference set, which provides the candidate points added to the training database and serves as the test data to examine the generalization ability of the trained model.
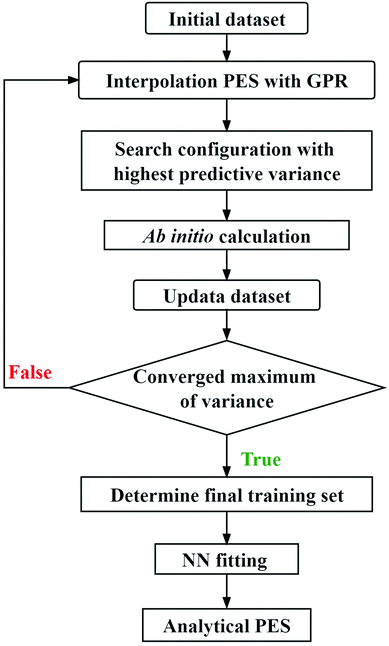
This new scheme that combines the actively selecting points of GPR and the NN fitting is a universal approach for the construction of multidimensional reactive PESs, and the basic procedure of this strategy is illustrated in Fig. 1. For the triatomic system, the initial configurations can be sampled in the Jacobi coordinates by using the Latin hypercube sampling (LHS) approach,63 which can avoid clustering and the samples cover the whole coordinate region in each degree of freedom. It is important to note that using the Jacobi coordinates to sample is not suitable for polyatomic reactive systems due to the significantly increasing complexity. In addition, a previous study58 suggests that the LHS has limitations for large systems. As the system's dimensions increase, the initial configurations can be sampled along each reaction pathway with the other coordinates fixed at the corresponding transition states, which are determined by relatively low-level ab initio calculations, ensuring that the dynamically relevant configuration space is covered. A preliminary GPR PES is constructed based on the initial energy points. Next, the new ab initio data are added to the training set by searching the configuration with the highest predictive variance by this GPR PES in a large coordinate space, and then a new GPR PES is constructed using the updated training dataset. This process is repeated automatically until obtaining the convergent maximum of predictive variance, and the training set is eventually determined. In the final step, the analytical PES is represented by the NN fitting based on this training set. To ensure the important permutation symmetry of the generated PES, the permutation invariant polynomial (PIP)9 is adopted as the input of GPR and NN models, namely, the PIP-GPR53 and PIP-NN21,24 methods are used in the process of constructing PES.
Next, the basic theory and important equations involved in this strategy are described. The Gaussian process is a kernel-based non-parametric supervised machine learning algorithm, which can be regarded as a limit of the Bayesian network with an infinite number of nodes. The detailed description of GPR can be found in the relevant literature,42 and here we only give a brief introduction about its application in active data selection for representing PESs. Supporting the initial dataset containing n configurations X = [x1,…, xn], where the inputs of xi are the PIPs constructed by the interatomic distance, and the outputs y = [y1,…, yn] of the GPR model are the corresponding normalized potential energies. The joint multivariate Gaussian distribution can be expressed as follows:
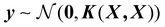 | (1) |
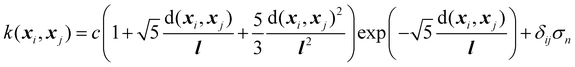 | (2) |
The goal of training a GPR is to obtain the parameters of kernel function by maximizing the following logarithm of the marginal likelihood,
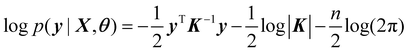 | (3) |
A new data point (x*, y*) to be predicted also follows the prior distribution of eqn (1),
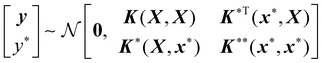 | (4) |
| μ(x*) = [K*K + σn2I]−1y | (5) |
| σ2(x*) = K** − K*T[K + σn2I]−1K* | (6) |
NNs consist of layers of interconnected mathematical function simulating biological neurons, and it can present a flexible form with arbitrary precision. There has been increasing interest in generating multi-dimensional PESs with NNs, and for more details please refer to the relevant reviews.14,15 For the studied system, the NN structure contains two hidden layers with 11 neurons. The analytical form in expressing the relationship between inputs and outputs is written as follows:
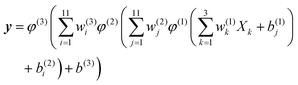 | (7) |
3. Results and discussion
To begin with, a total of 40 ab initio data are selected by the LHS strategy as the initial training set, and then the new data in the test dataset are added based on PIP-GPR interpolation. The highest predictive variance as a function of the number of training points is described in Fig. 2(a). As can be seen, the value of the highest variance decreases rapidly at first and then tends to be flat. The highest variance is convergent to 3.45 eV2 when the number of training points reaches 1270, and these actively sampling energy points are used in the next PIP-NN fitting. Fig. 2(b) gives the test error calculated on PIP-GPR PES as a function of the number of training data. The test error refers to the root mean square error (RMSE) of all the test data points. The RMSE value is very large when the model is trained with a small number of points, which is different from H357 or Ar358 PESs constructed using the GPR model. In these systems, the RMES can be decreased to the meV level merely by using dozens of samples. This is because the ground state BeH2+ PES contains abundant wells and barriers and the energy values change rapidly in some configurations; more points are required for accurately describing its structural characteristics even adopting the GPR method that greatly saves the electronic structure calculations. The test RMSE of the PIP-GPR PES trained by 1270 points is 6.12 meV.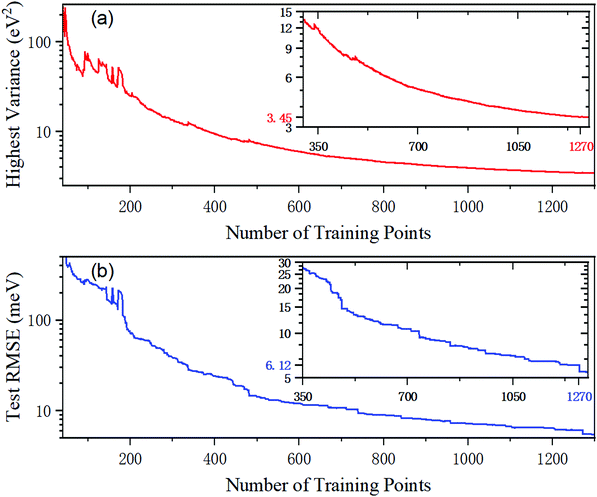 | ||
| Fig. 2 The highest predictive variance and the RMSE of the test database as a function of the number of training points in the GPR training for the BeH2+ system. | ||
Fig. 3 shows the difference between the predicted energies and the ab initio results in the test database, and the values of predictive energy are obtained on the PESs constructed using the PIP-GPR model and the proposed new approach with 1270 training data. The energy values of the abscissa axis are relative to the dissociation limit of triatomic Be+–H–H. The test RMSEs of the PES represented by the pure PIP-GPR model and this new method are 6.12 meV and 1.80 meV, respectively, implying the accuracy of the PES is remarkably improved by using an additional NN fitting after actively selecting points with the GPR model. In the new method, the final analytic PES is fitted by the PIP-NN scheme, which can yield extremely accurate PESs, such as the recently reported ultracold reactive system of KRb + KRb → K2 + Rb2,65 which presented an RMSE of only 1.86 cm−1. The Be+(2S) + H2 reactive PES features multiple wells, barriers, and cusps formed by the avoided crossing effect of the first excited state,66 which go against the fitting accuracy, and too small RMSE can also increase the risk of long-range potential for the tested system. Although the fitting RMSE does not reach the order of spectroscopic accuracy, the accuracy of the obtained PES is sufficient for dynamics studies on the endothermic reaction of Be+(2S) + H2. It can be seen from the distributions of the test errors that both the methods can give accurate predictions in the energy region below −4 eV. However, the PIP-GPR PES presents large predictive errors in the region of relatively high energy. On the contrary, the PES generated by the new strategy keeps a very small predictive error in the whole energy region. The absolute highest error values in the test dataset for the PIP-GPR method and the new model are 179.6 meV and 11.3 meV, respectively, suggesting that the generalization performance of the new approach is much better than that of the pure GPR model for the construction of PESs with complex topography.
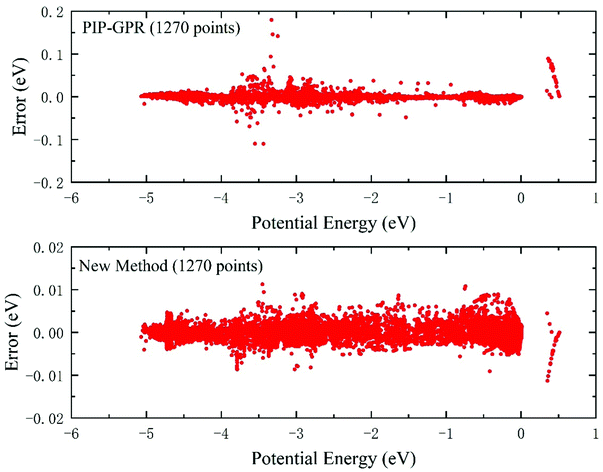 | ||
| Fig. 3 Predictive error distributions in the test database of the PESs constructed by the PIP-GPR model (1270 points) and the new method (1270 points) for the BeH2+ system. | ||
The speed of evaluation is also a very important aspect to assess PESs, and it directly affects the efficiency of the subsequent quantum scattering calculations. The evaluation of NN PESs depends on the number of neurons, and any two layers are linked by a simple function; thus, the speed of evaluating a NN PES is very fast. For the GPR model, as shown in eqn (5), it requires to calculate the covariance matrixes between the predicted configurations and all of the training data and the product of vector–vector with n dimensions, so the efficiency of predicting a new data point is very low when the number of training data is relatively large. We use a single core on a single compute node (Intel(R) Core(TM) i5-1035G1 CPU@1.00 GHz) to evaluate 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 potential values on the PESs modeled using different schemes, and the evaluation times for the PIP-GPR PES and the PES constructed by the new method are 25.41 s and 7.37 s, respectively. The time cost is saved around three times than the pure GPR method, and this ratio will increase remarkably when the training set contains more data points.
000 potential values on the PESs modeled using different schemes, and the evaluation times for the PIP-GPR PES and the PES constructed by the new method are 25.41 s and 7.37 s, respectively. The time cost is saved around three times than the pure GPR method, and this ratio will increase remarkably when the training set contains more data points.
Three-dimensional BeH2+ PESs constructed using the new scheme at four different Be+–H–H angles (45°, 90°, 135°, and 180°) are plotted in Fig. 4. The PES is smooth in the whole coordination space and no non-physical structures are present for every angle, demonstrating that there is no overfitting during PIP-NN training. The right valley and left valley on the PES correspond to the Be+(2S) + H2 channel and BeH+ + H channel, respectively. It can be seen that there exist a well and a barrier on the PES for each Be+–H–H angle, and the two structures become less obvious with the increase of the Be+–HH angle. The topography characteristics of BeH2+ PES imply the complicated changes between the nuclear configuration and energy.
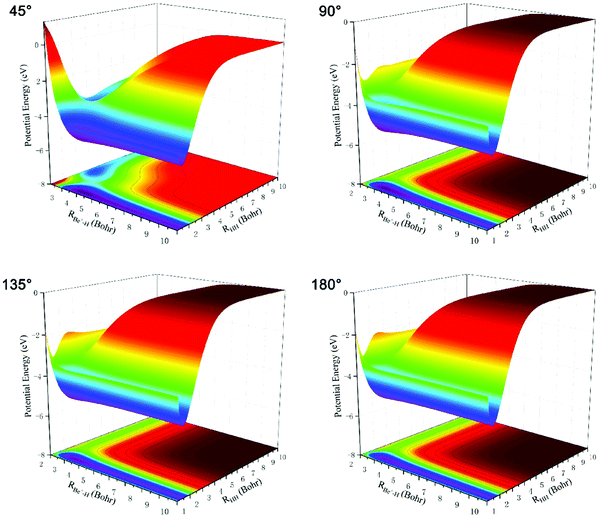 | ||
| Fig. 4 Three-dimensional BeH2+ PESs constructed by the new method at four different Be+–H–H angles (45°, 90°, 135°, and 180°). | ||
The molecular constants of diatomic species H2(X1Σg+) and BeH+(X1Σ+) are listed in Table 1. The values of bond length Re, dissociation energy De, vibrational frequencies ωe, and anharmonicity constants ωexe calculated on the PES generated by the new method coincide with the experimental values well,67 indicating that the new PES can accurately describe the distributions of the rovibrational states of the reactant and product when the dynamics calculations of the Be+(2S) + H2 → BeH+ + H reaction are implemented. Table 2 gives the geometries and energy values of stationary points for the ground state BeH2+, compared with the previous MRCI + Q results.68 The energy values are relative to the Be+ + H2 dissociation limit. It can be seen that the equilibrium structure and saddle points obtained on the PES constructed using this new scheme are in good agreement with the high-level ab initio calculations.
| This work | Experimental data67 | ||
|---|---|---|---|
| H2(X1Σg+) | R e (bohr) | 1.400 | 1.401 |
| D e (eV) | 4.743 | 4.747 | |
| ω e (cm−1) | 4402.7 | 4401.2 | |
| ω e x e (cm−1) | 104.90 | 121.33 | |
| BeH+(X1Σ+) | R e (bohr) | 2.489 | 2.480 |
| D e (eV) | 3.163 | 3.280 | |
| ω e (cm−1) | 2220.5 | 2221.7 | |
| ω e x e (cm−1) | 40.74 | 39.79 | |
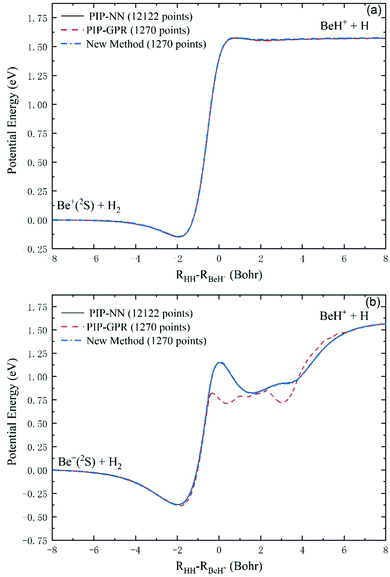
To further verify the reliability of this scheme in representing global reactive PESs, we use all the test data and additional 82 points on the minimum energy path to fit an accurate PIP-NN PES as the benchmark for comparison, and the fitting RMSE is only 0.91 meV. Fig. 5(a and b) show the collinear and global minimum energy paths of the Be+(2S) + H2 → BeH+ + H reaction, respectively. For the collinear collision, there are a shallow well and a low barrier, and the reactive paths calculated on the PESs generated by the three approaches are indistinguishable. Compared to the collinear path, the global minimum energy path includes a more obvious well and barrier, and there exists a small hump behind the barrier. It can be seen that the path obtained on the PES generated by the new method is completely consistent with the PIP-NN PES constructed with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 points, but the PIP-GPR PES produced by the same database cannot well reproduce the barrier and the complex shape of the product region. These results indicate that the GPR model only can produce sufficiently accurate results at the smooth parts of the PES, whereas the regions with fast-changing energy values cannot be described correctly for this system.
122 points, but the PIP-GPR PES produced by the same database cannot well reproduce the barrier and the complex shape of the product region. These results indicate that the GPR model only can produce sufficiently accurate results at the smooth parts of the PES, whereas the regions with fast-changing energy values cannot be described correctly for this system.
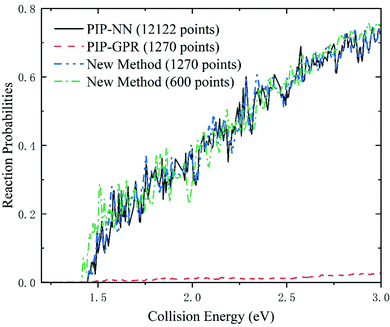
In addition to the assessments of the error, speed of evaluation, and topography characteristics, quantifying the quality of reactive PESs by quantum scattering is also very important. To prove that the new scheme can accurately character the dynamically relevant regions of PES, we perform the reactant coordinate based time-dependent wave packet69,70 calculations on the Be+(2S) + H2 → BeH+ + H reaction based on the PESs produced by different strategies. The time evolution of the wave function is based on the second-order split operator method.71 The main parameters used in the dynamical calculations are given in Table 3. In Fig. 6, the total reaction probabilities of the Be+(2S) + H2 → BeH+ + H reaction with the total angular momentum number J = 0 are displayed. The energy threshold value is 1.45 eV, which corresponds to the endothermicity of this reaction. The results obtained on PIP-NN PES with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 points save as the benchmark for comparison. It is clear that the reaction probabilities calculated on PIP-GPR PES have substantial errors, and the key resonance characteristics formed by the intermediate complex on the wells are not presented. This suggests that BeH2+ PES modeled by the GPR method is extremely unreliable for dynamics studies even though the number of training points has reached thousands. The main reason for the almost negligible probabilities calculated on PIP-GPR PES is that the collision of J = 0 partial wave is dominated by the global minimum energy path, as shown in Fig. 5(b), and this PES does not reproduce the key activated barrier, which corresponds to the transition state of this reaction, thus the calculated reaction probabilities are significantly weakened. To prove that the strategy can quickly converge to an error range necessary to run dynamics, we represent a PES with only 600 points based on this new scheme, and the corresponding reaction probabilities are also presented in Fig. 6. For the new PES with 600 points, the reaction probabilities agree with the results calculated on PIP-NN PES generated with 12
122 points save as the benchmark for comparison. It is clear that the reaction probabilities calculated on PIP-GPR PES have substantial errors, and the key resonance characteristics formed by the intermediate complex on the wells are not presented. This suggests that BeH2+ PES modeled by the GPR method is extremely unreliable for dynamics studies even though the number of training points has reached thousands. The main reason for the almost negligible probabilities calculated on PIP-GPR PES is that the collision of J = 0 partial wave is dominated by the global minimum energy path, as shown in Fig. 5(b), and this PES does not reproduce the key activated barrier, which corresponds to the transition state of this reaction, thus the calculated reaction probabilities are significantly weakened. To prove that the strategy can quickly converge to an error range necessary to run dynamics, we represent a PES with only 600 points based on this new scheme, and the corresponding reaction probabilities are also presented in Fig. 6. For the new PES with 600 points, the reaction probabilities agree with the results calculated on PIP-NN PES generated with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 points, indicating the high efficiency of the presented strategy in obtaining reliable PESs that can be used in dynamics studies. When the number of training data increases to 1270, the corresponding results are almost identical to those of the NN PES, suggesting that the PES obtained by this new scheme can accurately describe the dynamically relevant regions.
122 points, indicating the high efficiency of the presented strategy in obtaining reliable PESs that can be used in dynamics studies. When the number of training data increases to 1270, the corresponding results are almost identical to those of the NN PES, suggesting that the PES obtained by this new scheme can accurately describe the dynamically relevant regions.
Our calculation results of the ground BeH2+ PES suggest that the standard GPR method could not correctly represent the reactive PESs with complex topography characteristics based on a small number of points. One important reason is that the GPR model inherently cannot give accurate prediction for the rapidly changing value, and the ill-conditioned covariance matrix may appear when the data distribution is relatively dense, resulting in numerical instability in those regions. But the GPR model is a very convenient and reliable tool for sampling data by giving the uncertainties of the predicted points. NNs have excellent generalization ability, but the performance of NNs in constructing PESs depends strongly on the distribution of training data. Incorporating the actively selecting data of GPR into the NN fitting can produce globally accurate reactive PESs with a rapid speed of evaluation based on as few ab initio points as possible.
4. Conclusions and prospects
There has been fast developing interest in constructing multi-dimensional PESs using modern machine learning technologies, and most of them are implemented by the NN and GPR algorithms. NN is a powerful tool to generate accurate PESs, but the NN fitting is based on the points selected in advance, resulting in expensive electron structure calculations as the molecular complexity increases. Although GPR provides a direct approach in actively sampling data, the constructed PESs have a low speed of evaluation and the rapidly changing potential cannot be accurately characterized. Therefore, combining the advantages of the above two methods could be a good idea to obtain accurate PESs with highly efficient evaluation based on as few ab initio points as possible. In this work, an efficient scheme for representing globally accurate reactive PESs with complex topography by incorporating the actively selecting points of GPR into the NN fitting is proposed. This strategy is verified by the triatomic example of the BeH2+ system, and only 1270 points are assembled to construct the global PES. The accuracy, generalization performance, and speed of evaluation of the PES constructed by this new scheme are much better than those of the PES produced by the pure GPR with the same training data. To further test the global accuracy of the PES, an accurate PIP-NN PES is constructed with 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 122 points as the benchmark for comparison. The topography characteristics of the PES generated by this scheme and the calculated quantum reaction probabilities of the Be+(2S) + H2 reaction are in good agreement with the corresponding results obtained on this PIP-NN PES.
122 points as the benchmark for comparison. The topography characteristics of the PES generated by this scheme and the calculated quantum reaction probabilities of the Be+(2S) + H2 reaction are in good agreement with the corresponding results obtained on this PIP-NN PES.
The proposed scheme is an all-purpose method for representing global reactive PESs, characterized by high accuracy and rapid speed of evaluation, and its advantages are particularly prominent for systems with complex topography. For instance, the long-lived complex-forming reactive systems usually require a mass of ab initio points to model PESs and abundant energy grids to character the quantum dynamics. This method can greatly save the cost of electronic structure calculations and the generated PES can accelerate the quantum scattering calculations. The presented scheme seems to be very promising for constructing reactive PESs with more dimensionality. On the other hand, this scheme also has some limitations for particularly large systems. The inverse of the covariance matrix needs to be calculated in each GPR iteration, and the training complexity scales as O(n3), so the speed of actively selecting points dramatically decreases with the increase of dimension. This speed can be effectively improved by decreasing the number of training data at the cost of reducing the accuracy.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11774043).References
- M. A. Collins, Theor. Chem. Acc., 2002, 108, 313–324 Search PubMed.
- T. Hollebeek, T. S. Ho and H. Rabitz, Annu. Rev. Phys. Chem., 1999, 50, 537–570 CrossRef CAS PubMed.
- C. Qu, Q. Yu and J. M. Bowman, Annu. Rev. Phys. Chem., 2018, 69, 151–175 CrossRef CAS PubMed.
- G. C. Schatz, Rev. Mod. Phys., 1989, 61, 669–688 CrossRef CAS.
- J. Ischtwan and M. A. Collins, J. Chem. Phys., 1994, 100, 8080–8088 CrossRef CAS.
- A. Aguado and M. Paniagua, J. Chem. Phys., 1992, 96, 1265–1275 CrossRef CAS.
- K. S. Sorbie and J. N. Murrell, Mol. Phys., 1975, 29, 1387–1407 CrossRef CAS.
- A. J. C. Varandas, Adv. Chem. Phys., 1988, 74, 255–338 CAS.
- B. J. Braams and J. M. Bowman, Int. Rev. Phys. Chem., 2009, 28, 577–606 Search PubMed.
- W. T. Li, J. C. Yuan, M. L. Yuan, Y. Zhang, M. H. Yao and Z. G. Sun, Phys. Chem. Chem. Phys., 2018, 20, 1039–1050 RSC.
- Z. J. Yang, S. F. Wang, J. C. Yuan and M. D. Chen, Phys. Chem. Chem. Phys., 2019, 21, 22203–22214 RSC.
- J. C. Yuan, D. He and M. D. Chen, Sci. Rep., 2015, 5, 14594 CrossRef CAS PubMed.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, J. Phys. Chem. Lett., 2020, 11, 5120–5131 CrossRef CAS PubMed.
- S. Manzhos and T. Carrington, Chem. Rev., 2021, 121, 10187–10217 CrossRef CAS PubMed.
- G. Schmitz, I. H. Godtliebsen and O. Christiansen, J. Chem. Phys., 2019, 150, 244113 CrossRef PubMed.
- T. T. Nguyen, E. Szekely, G. Imbalzano, J. Behler, G. Csanyi, M. Ceriotti, A. W. Gotz and F. Paesani, J. Chem. Phys., 2018, 148, 241725 CrossRef PubMed.
- V. Vassilev-Galindo, G. Fonseca, I. Poltavsky and A. Tkatchenko, J. Chem. Phys., 2021, 154, 094119 CrossRef CAS PubMed.
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, Nature, 1986, 323, 533–536 CrossRef.
- S. Manzhos, X. G. Wang, R. Dawes and T. Carrington, J. Phys. Chem. A, 2006, 110, 5295–5304 CrossRef CAS PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2013, 139, 054112 CrossRef PubMed.
- C. J. Xie, X. L. Zhu, D. R. Yarkony and H. Guo, J. Chem. Phys., 2018, 149, 144107 CrossRef PubMed.
- B. Jiang and H. Guo, J. Chem. Phys., 2014, 141, 034109 CrossRef PubMed.
- B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506 Search PubMed.
- J. C. Yuan, D. He and M. D. Chen, Phys. Chem. Chem. Phys., 2015, 17, 11732–11739 RSC.
- K. J. Shao, J. Chen, Z. Q. Zhao and D. H. Zhang, J. Chem. Phys., 2016, 145, 071101 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- B. Kolb, B. Zhao, J. Li, B. Jiang and H. Guo, J. Chem. Phys., 2016, 144, 224103 CrossRef PubMed.
- T. G. Yang, A. Y. Li, G. K. Chen, C. J. Xie, A. G. Suits, W. C. Campbell, H. Guo and E. R. Hudson, J. Phys. Chem. Lett., 2018, 9, 3555–3560 CrossRef CAS PubMed.
- X. R. Zhang, L. L. Li, J. Chen, S. Liu and D. H. Zhang, Nat. Commun., 2020, 11, 223 CrossRef CAS PubMed.
- I. Miyazato, S. Nishimura, L. Takahashi, J. Ohyama and K. Takahashi, J. Phys. Chem. Lett., 2020, 11, 787–795 CrossRef CAS PubMed.
- Y. Y. Hong, Z. X. Yin, Y. F. Guan, Z. J. Zhang, B. N. Fu and D. H. Zhang, J. Phys. Chem. Lett., 2020, 11, 7552–7558 CrossRef CAS PubMed.
- X. X. Hu, Y. P. Zhou, B. Jiang, H. Guo and D. Q. Xie, Phys. Chem. Chem. Phys., 2017, 19, 12826–12837 RSC.
- J. L. Chen, X. Y. Zhou, Y. L. Zhang and B. Jiang, Nat. Commun., 2018, 9, 4039 CrossRef PubMed.
- J. Q. Han, L. F. Zhang, R. Car and E. Weinan, Commun. Comput. Phys., 2018, 23, 629–639 Search PubMed.
- K. T. Schutt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Muller, J. Chem. Phys., 2018, 148, 241722 CrossRef CAS PubMed.
- Z. X. Yin, B. J. Braams, Y. F. Guan, B. N. Fu and D. H. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 1082–1091 RSC.
- L. M. Raff, M. Malshe, M. Hagan, D. I. Doughan, M. G. Rockley and R. Komanduri, J. Chem. Phys., 2005, 122, 084104 CrossRef CAS PubMed.
- J. Behler, Phys. Chem. Chem. Phys., 2011, 13, 17930–17955 RSC.
- Q. D. Lin, Y. L. Zhang, B. Zhao and B. Jiang, J. Chem. Phys., 2020, 152, 154104 CrossRef CAS PubMed.
- Q. D. Lin, L. Zhang, Y. L. Zhang and B. Jiang, J. Chem. Theory Comput., 2021, 17, 2691–2701 CrossRef CAS PubMed.
- C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, MIT Press, Cambridge, Mass., 2006, vol. 1 Search PubMed.
- A. Christianen, T. Karman, R. A. Vargas-Hernandez, G. C. Groenenboom and R. V. Krems, J. Chem. Phys., 2019, 150, 064106 CrossRef PubMed.
- Q. Liu, L. Liu, F. An, J. Huang, Y. Z. Zhou and D. Q. Xie, J. Chem. Phys., 2021, 155, 084302 CrossRef CAS PubMed.
- B. Kolb, P. Marshall, B. Zhao, B. Jiang and H. Guo, J. Phys. Chem. A, 2017, 121, 2552–2557 CrossRef CAS PubMed.
- J. Cui and R. V. Krems, Phys. Rev. Lett., 2015, 115, 073202 CrossRef PubMed.
- A. Kamath, R. A. Vargas-Hernandez, R. V. Krems, T. Carrington and S. Manzhos, J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
- E. Uteva, R. S. Graham, R. D. Wilkinson and R. J. Wheatley, J. Chem. Phys., 2017, 147, 161706 CrossRef PubMed.
- V. L. Deringer, A. P. Bartok, N. Bernstein, D. M. Wilkins, M. Ceriotti and G. Csanyi, Chem. Rev., 2021, 121, 10073–10141 CrossRef CAS PubMed.
- J. Cui and R. V. Krems, J. Phys. B: At., Mol. Opt., 2016, 49, 224001 CrossRef.
- R. V. Krems, Phys. Chem. Chem. Phys., 2019, 21, 13392–13410 RSC.
- S. Venturi, R. L. Jaffe and M. Panesi, J. Phys. Chem. A, 2020, 124, 5129–5146 CrossRef CAS PubMed.
- C. Qu, Q. Yu, B. L. Van Hoozen, J. M. Bowman and R. A. Vargas-Hernandez, J. Chem. Theory Comput., 2018, 14, 3381–3396 CrossRef CAS PubMed.
- J. Dai and R. V. Krems, J. Chem. Theory Comput., 2020, 16, 1386–1395 CrossRef CAS PubMed.
- H. Sugisawa, T. Ida and R. V. Krems, J. Chem. Phys., 2020, 153, 114101 CrossRef CAS PubMed.
- Q. F. Song, Q. Y. Zhang and Q. Y. Meng, J. Chem. Phys., 2020, 152, 134309 CrossRef CAS PubMed.
- Y. F. Guan, S. Yang and D. H. Zhang, Mol. Phys., 2018, 116, 823–834 CrossRef CAS.
- E. Uteva, R. S. Graham, R. D. Wilkinson and R. J. Wheatley, J. Chem. Phys., 2018, 149, 174114 CrossRef PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- M. Stein, Technometrics, 1987, 29, 143–151 CrossRef.
- M. T. Hagan and M. B. Menhaj, IEEE Trans. Neural Netw., 1994, 5, 989–993 CrossRef CAS PubMed.
- D. Z. Yang, J. X. Zuo, J. Huang, X. X. Hu, R. Dawes, D. Q. Xie and H. Guo, J. Phys. Chem. Lett., 2020, 11, 2605–2610 CrossRef CAS PubMed.
- Z. J. Yang, J. C. Yuan, S. F. Wang and M. D. Chen, RSC Adv., 2018, 8, 22823–22834 RSC.
- K. P. Huber and G. Herzberf, Constants of Diatomic Molecules, Springer, 1979 Search PubMed.
- A. J. Page, D. J. D. Wilson and E. I. von Nagy-Felsobuki, Phys. Chem. Chem. Phys., 2010, 12, 13788–13797 RSC.
- S. Gómez-Carrasco and O. Roncero, J. Chem. Phys., 2006, 125, 054102 CrossRef PubMed.
- Z. G. Sun, X. Lin, S. Y. Lee and D. H. Zhang, J. Phys. Chem. A, 2009, 113, 4145–4154 CrossRef CAS PubMed.
- M. D. Feit, J. A. Fleck and A. Steiger, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS.
| This journal is © the Owner Societies 2022 |