Bandgaps of atomically precise graphene nanoribbons and Occam's razor

Abstract

Rationalization of the “bulk” (ΔE_ac) or “zigzag-end” (ΔE_zz) energy gaps of atomically precise armchair graphene nanoribbons (AGNRs), which are directly related to fundamental applications in nanoelectronics, could be challenging and largely controversial with respect to their magnitude, origin, substrate influence (ΔE_sb), and spin-polarization, among others. Hereby a simple self-consistent and “economical” interpretation is presented, in full accordance with Occam's simplicity principle, which is highly successful (within less than 1%) in predicting all energy gaps of the 5-, 7-, and 9-AGNRs, in contrast to other complicated and/or contradicting prevailing views in the literature for ΔE_ac, ΔE_zz, and ΔE_sb. The present approach is based on “appropriate” DFT (TDDFT) calculations, general symmetry principles, and plausibility arguments. The excellent agreement with experiments and the new insight gained is achieved by invoking the approximate equivalence of Coulomb correlation energy with the staggered sublattice potential. Breaking established stereotypes, we suggest that the measured STS gaps are virtually independent of the substrate, essentially equal to their free-standing values, and that the “true” lowest energy state is a closed singlet with no conventional magnetism. The primary source of discrepancies is the finite length of AGNRs together with inversion/reflection symmetry conflict and the resulting topological end/edge states. Such states invariably mix with other “bulk” states making their unambiguous detection/distinction difficult. This can be further tested by eliminating end-states (and ΔE_zz), by eliminating “empty” zigzag rings.

---

1. Introduction

Edge or end states in graphene nanoribbons (GNRs), and in particular armchair GNRs (AGNRs), have attracted much interest recently,^1–8 due to their anticipated magnetic properties,^9,10 although their presence in finite nanographenes (NGRs) was predicted a long time ago.¹¹ However, the significance and importance of end states for AGNRs was recognized only recently,^1–8 after the pioneering bottom-up synthesis of atomically precise AGNRs of finite lengths L with short zigzag ends, and their characterization by scanning tunnelling microscopy (STM) and spectroscopy (STS).^3–16 Clearly no end states appear in the common infinite AGNRs fabricated via the usual top-bottom techniques, which are theoretically described by periodic boundary conditions at their two ends.¹ The new developments have brought to the forefront new concepts and properties such as the “bulk band gaps” ΔE_ac (or Δ_ac^1,6) i.e., the energy gaps between delocalized states, and the energy separation of the zigzag-end-localized “end-states”, denoted here by (ΔE_zz) (or Δ_zz^6–8), thus increasing both the quantity and quality of the key properties to be rationalized, understood, or interrelated at the atomic scale. At the same time, despite the increased complexity, such advances have also allowed the study of the L-dependence of key-quantities such as the bandgaps^4–7 (both, ΔE_ac and ΔE_zz), conductivity, aromaticity,^1,3,4 and even Raman spectra.¹⁷ The L-dependence studies^4,5 revealed that the changes in such properties versus length are not always gradual (or smooth). The presence of a metal-insulator-like phase transition at a critical length L_c was advocated by two different recent studies, Lawrence et al.⁸ and Zdetsis et al.,⁴ almost simultaneously. However, these two studies have offered different assessments and interpretations on the nature of the transition and magnetism, as well as the value of L_c.^4,8 This is not something new or unusual in a rapidly grown pioneering field like this,¹ and this is not the only existing “discrepancy”. Other conflicting (or conflicting-looking) results (experimental and theoretical) include the magnitude and nature of the bandgaps,^1,6,7,12,13 the existence and nature of magnetism in the edge states,^1,3–7 and the magnitude of the substrate's influence on these properties.^1,5–7 For example, the magnitude of the bandgap for the 5-AGNRs has been measured by (at least) three different groups^8,12,13 to be 0.85 eV,⁸ 2.8 eV,¹² and 0.1 eV¹³ respectively, while the theoretical values vary from 0.1 eV¹ to 1.7 eV.¹⁴ For the 7-AGNRs the measured values of ΔE_zz vary between 1.9 eV⁶ and 2.5 eV,⁷ whereas the measured ΔE_ac values range from 2.3 eV to 3.2 eV,^6,7,9,15 overlapping significantly with the range of ΔE_zz. Thus, the unambiguous distinction between ΔE_ac and ΔE_zz is another subtle point together with the bridging of the measured and calculated ΔE_ac values, which also vary widely from 2.3 eV to 3.7 eV.^1,6,7,14 Some of the (different) measured or calculated values correspond to AGNRs of different lengths, but in the literature the quoted values are usually given without reference to the actual length which is, thus, treated as a hidden variable. However, the biggest problem seems to be the large difference between the measured values of the gap(s) in relation to the “official” theoretical values obtained by the GW method,¹⁴ which are widely recognized as an almost universal point of reference. For example, the measured STS gap value(s) for the 7-AGNRs is between 2.3 eV and 2.8 eV,^6,7,9,15 whereas the theoretical GW value¹⁴ is 3.7 eV (i.e. about 1.5 eV higher). Thus, one possible interpretation is that the real STS gap is indeed 3.7 eV, and the difference of ∼1.5 eV is due to screening from the metallic substrate (usually Au), which remains to be seen. On the other hand, the simpler interpretation suggested here (in accordance with Occam's principle) consistent with our results, is that the real (theoretical and experimental) STS gap is in reality ∼2.5 ± 0.3 eV and the reference GW results¹⁴ are overestimated by about 1.5 eV. This claim (see Section 2.4) is supported by both theoretical⁶ and experimental^6,7 evidence:

(1) The theoretical reference GW results¹⁴ have been obtained for AGNRs of infinite length, not for finite atomically precise AGNRs. Recent GW results by Wang et al.⁶ for the finite length (7, 24) AGNRs showed a gap of 2.8 eV in full support of the present results. Moreover,

(2) experimental measurements^6,7 for 7-AGNRs supported on non-metallic substrates, such as NaCl and MgO (without metallic screening) found an STS gap of ∼2.5 eV, in full agreement with the present interpretation. As a result, it appears that there are several conflicting results and interpretations (or highbrow “solutions”) about the STS gaps, although the real solution seems to be much simpler (but not always obvious), as could be possibly argued on the basis of Occam's principle. Thus, there seem to be several subtle points behind the controversy for the energy gaps of atomically precise AGNRs, which include:

(1) The finite length of the AGNRs.

(2) The overestimation of the reference theoretical values.

(3) The magnitude of the substrate interaction.

(4) The topological end-states.

(5) The inversion/reflection symmetry conflict.

(6) The “exact” exchange in the DFT functionals.

(7) The mixing of zigzag-end localized topological end-states with other delocalized “bulk” states, which leads to.

(8) Difficulties in distinguishing between ΔE_ac, ΔE_zz gaps, and in part Δε_ζζ, which is the real energy separation between the end-states.

Along these lines the present work aims at deciphering all these subtle points, which are clearly interrelated. Thus, the present work can be considered as a touchstone or a positive synthesis of various conflicting views. Based on previous experience,^1,3,19 it is expected that such synthesis should be proven successful and constructive, facilitating the successful and accurate functionalization of AGNRs for realistic applications. We can fully rationalize all known experimental data for the 5-, 7-, and 9-AGNRs within less than 1% accuracy, predict non-measured gaps, and pinpoint at the same time the sources of discrepancies.

2. Theoretical framework

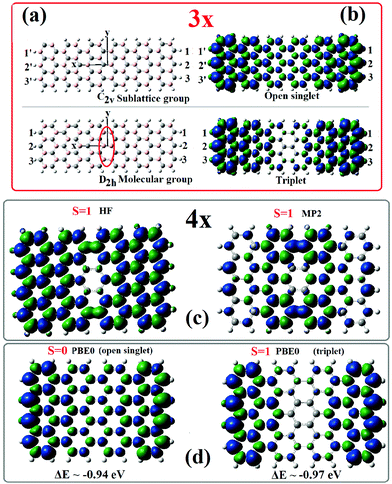
For a consistent and transparent understanding and interpretation of the origin and magnitude of ΔE_ac, ΔE_zz as well as the factors that influence their size, it is important to realize that practically all these quantities are dominated by the influence of the (“many-body”) Coulomb correlation energy combined with sublattice frustration, which gives rise to the staggered sublattice potential²⁰ across the zigzag ends of finite length AGNRs. In fact, the sublattice frustration, which is equivalent to the inversion/reflection symmetry conflict, is the driving force for the generation of the end/edge states and, as we have illustrated earlier,^2–4 constitutes the largest contribution to the Coulomb correlation energy. Such symmetry conflict is clearly illustrated in Fig. 1 and in particular in Fig. 1(a). As we can see in Fig. 1(a), the sublattice symmetry group, which is characterized by a horizontal C₂ rotation symmetry axis and a vertical S₂ rotation-reflection axis, lacks a center of inversion. As a result, end-atoms at the two zigzag ends belong to different sublattices. However, the molecular symmetry group, which reflects the symmetry of the Hamiltonian, is of D_2h symmetry with a center of inversion and two (horizontal and vertical) C₂ axes. Therefore, if we try to build the sublattice structure preserving the full D_2h symmetry, we end up with a region in the middle, designated by a vertical ellipse in Fig. 1a, where there is a sublattice conflict with neighboring (pink in the figure) carbon atoms across the y-axis belonging to the same sublattice. This is actually the reason for the generation of topological end-states which do not penetrate in the symmetry-forbidden central region of the AGNRs.³

Fig. 1 Molecular and sublattice symmetry of the 3 × 6 (7, 12) AGNR (a), reflected in the spin densities (b). Isovalue = 0.004. The vertical elliptic curve indicates the region of sublattice imbalance (and frustration). Comparison of the corresponding spin densities for the 4 × 4 (9, 8) AGNR at the HF, MP2 and DFT/PBE0 level is given in (c and d).

Thus, the understanding that most (or all) of the Coulomb correlation energy is devoted to counterbalancing the topological frustration between sublattice and molecular symmetry-groups is the starting (and key) point of the present investigation. This principle together with the established^2–5 (hidden) strong contributions of aromaticity and shell structure^2–5 constitute the basis for a deeper understanding of all these quantities (ΔE_ac, ΔE_zz, Δε_ζζ, and ΔE_s). Hence, if we can properly alleviate the sublattice-molecular group symmetry frustration (which is equivalent to inversion/reflection symmetry conflict^3–5), under the natural constrains of shell structure and aromaticity,^2,5 we could effectively account for the (largest part of) Coulomb correlation energy. This would also explain why the open shell states (singlet or triplet) are not the real lower energy states, but rather “pseudo-states”.²¹

2.1 A synopsis of the aromatic/topological shell model

The “shell model” was initially invoked by the present author²² as a molecular bridge from benzene to graphene through a sequence (termed the “main sequence”) of hexagonal (D_6h symmetry) polycyclic hydrocarbons (PAHs) of the general form C_6n²H_6n, n = 1, 2,…, containing n hexagonal monocyclic rings surrounding each other. The integer n is also called the shell number since, if we consider the nth PAH of the sequence, we can uncover a shell structure with a benzene nucleus (n = 1) surrounded by n − 1 annulene layers or “shells”, as is shown in Fig. 2. This shell structure has been shown to be a realistic concept, with characteristic peaks and dips in the aromaticity indices, which is analogous to the electronic atomic shell model, responsible for the periodic table of the elements. In the current aromatic shell model, the shell number n corresponds to the principal quantum number n, and the number of layers (around the benzene nucleus) l = n − 1 is analogous to the angular momentum quantum number L. The role of the ±M_L values is played by the number of the u and g parity MOs in the given shell.²² Moreover the shell model (shell structure) is not merely an abstract concept, but it has been used as a very useful and powerful tool in rationalizing the exotic properties of graphene at the molecular level,² and for understanding the key properties of AGNRs (such as the triple periodicity in terms of width),³ as well as the aromaticity and stability of various NGRs.⁵

Fig. 2 The shell model and the “main sequence of PAHs (shown up to n = 6), illustrating the aromaticity patterns (with red dots at the centers of the aromatic or “full” rings), and the structure and symmetry of the HOMO and LUMO orbitals (top). The bottom part illustrates the analogy with corresponding rectangular NGRs or AGNRs with an equal number of armchair and zigzag rings (see the text).

The shell model is responsible^2,22 for the double periodicity in the aromaticity patterns, and the structure/symmetry of the HOMOs and LUMOs (E_1g and E_2u) of hexagonal PAHs seen in Fig. 2. The even parity E_1g HOMOs (and odd parity E_2u LUMOs) are associated with a triangular Clar-type aromaticity pattern and odd shell number, like n = 3 circumcoronene (CIRCO), whereas E_2u HOMOs (and E_1g LUMOs) are connected with hexagonal non-Clar-type aromaticity and an even shell number like n = 2 coronene (CO).^2,5,22 As we can see in the figure, the HOMO of the nth PAHs is similar to the LUMO of the (n − 1)th and vice versa. Likewise, for rectangular NGRs and AGNRs we have a three-member periodicity specified by their shorter dimension, i.e. the width defined by the number of zigzag rings, Z, which (due to the shell structure) has the form:³Z = 3n, 3n + 1, or Z = 3n − 1, n = 1, 2,…. This is the well-known 3n, 3n ± 1 rule of AGNRs. The first two types correspond to PAHs with CIRCO and CO aromaticity patterns with effective HOMOs* of odd (b_3u) and even (b_2g) parities respectively; where “effective” means effective “bulk” MOs, defined by neglecting the frontier end-state MOs.³ Obviously the LUMOs* follow the exactly opposite trend. Therefore, the shell structure (or shell model) is both a conceptual and efficient tool for graphene-based structures, such as AGNRs.

2.2 Calculation of ΔE_zz and ΔE_ac from the one-body DFT calculations

Within the 1-electron approximation underlining the DFT and Hartree–Fock (HF) self-consistent fields, the symmetry frustration between molecular (D_2h) and sublattice (C_2V) symmetry groups can be alleviated by effectively breaking (or redefining) the symmetry of the additional degrees of freedom (besides spatial coordinates) i.e., the spin and/or pseudospin (for real-space calculations). In the first case we can introduce non-zero spin values preserving the molecular symmetry,³ whereas in the second case we are forced to break molecular symmetry, by introducing open-shell singlet states, which when optimized geometrically converge normally to C_2v symmetric geometries compatible with sublattice symmetry, thus breaking the inversion/reflection symmetry. This occurs because the HOMO (and LUMO) orbitals of the open singlet are obtained, by construction, by mixing the HOMO and LUMO orbitals of the closed singlet. These orbitals have opposite parities, u, or g, (and opposite behaviour under the σ_y or σ_xz reflection plane^2,3). Thus, by losing the σ_y (or σ_xz) reflection plane of the D_2h symmetry group, as is illustrated in Fig. 1(a), we can get sublattice distribution with opposite sublattice points at the two ends. This facilitates frontier molecular orbitals (HOMO, LUMO) localized only at one end (left or right) of the AGNR, producing an antisymmetric (pseudo)spin density, as is shown in Fig. 1(b), reflecting the sublattice symmetry and structure. Obviously, the reverse picture with the pseudospins interchanged is equally valid. On the other hand, the molecular D_2h symmetry demands the same type (same sublattice) of atoms at the two ends, as shown in the lower part of Fig. 1(a), thus producing a symmetric, with respect to the y-axis, (pseudo)spin distribution (bottom of Fig. 1(b)). In both cases the (pseudo)spin distribution is almost zero at the middle part of the AGNR. This is reproduced in the corresponding “spin” densities (b). Such spin densities, in Fig. 1(b–d), which are generated self consistently (through the DFT convergence process) are in fact pseudospin densities. The open singlet reflects the sublattice symmetry (with different types of atoms at the two ends) with an equal number of up and down (pseudo) spins, or A and B sublattice points. This results in a balanced (nearly zero spin distribution in the middle). The triplet state on the other hand has also a region of zero spin in the middle, exactly where the sublattice imbalance occurs. In contrast to the band description (in k-space), in the real-space (“molecular”) calculations the sublattice degree of freedom does not enter in the spatial Hamiltonian and can only be introduced as (pseudo)spin. Then, due to the better account of Coulomb interaction, open shell states (triplet or singlet) appear energetically lower than the closed singlet state. This is because the additional degree of freedom of “pseudospin”, introduced to take care of the sublattice topology (and the staggered potential), facilitates the optimization of Coulomb interaction by keeping away each of the other electrons of different spin (for which Pauli repulsion is not operative), but of identical pseudospins. Moreover, as was illustrated in Section 2.1 (and Fig. 2), based on the shell model,^2,3 the unoccupied states of the “previous” (shell number smaller by 1) PAH are the occupied ones of the current PAH. In AGNRs this is responsible for the interplay between odd and even parity HOMOs as the width of AGNRs is growing (3n AGNRs have an odd HOMO and even LUMO, whereas 3n + 1 AGNRs are characterized by an even HOMO and odd LUMO).^2,3 This is also responsible for the well-known 3n, 3n ± 1 width rule for AGNRs.³ Note that the (pseudo)spin densities invariably reflect the sublattice (pseudospin) structure within the frustrated molecular (D_2h) symmetry³ in the first case, or the sublattice symmetry (C_2v) in the latter, where opposite end sites have opposite spins. It should be emphasized at this point that for wider AGNRs (where n > 1 in the above rule for width³), higher spin states are required³ to lower the total energy (within the molecular D_2h symmetry group). Such larger (pseudo)spin-polarized states optimize better the sublattice distribution (within the D_2h molecular group),³ whereas the open-shell singlets lie higher in energy and revert to the closed singlet state. This illustrates emphatically that the open-singlet state is not the true ground (lowest energy) state of AGNRs (and, consequently, no conventional magnetism is truly present). Nevertheless, the open singlet state is still a very useful and efficient concept for the description of end-states. It should be emphasized that in both cases of Fig. 1, when correlation is introduced even at the MP2 level, the energetical ordering is reversed and the lowest energy structure is a closed singlet.⁴ In addition, the MP2 correlated “spin” density of the triplet, as we can see in Fig. 1(c), is rather correcting the HF failure (having the opposite sign) than reflecting the full sublattice structure. Note also in Fig. 1(c and d) that the triplet state is slightly lower than the open singlet, and that the energy difference of the open shell singlet and triplet states (which are practically isoenergetic) from the closed singlet is about 0.95 eV. This should be a good estimate of the “missing” Coulomb energy in this case and based on the (approximate) electron–hole symmetry, the expected (HOMO–LUMO) separation of the open singlet (or the triplet) should be about twice as large (∼2 eV). Indeed, the calculated open-singlet HOMO–LUMO gap for the 9-AGNRS (or 4x) is 2.2 eV, and so is ΔE_zz (vide infra). Even more important is the fact that the corresponding value for the 3 × 6 or (7, 12) AGNR is also about 0.93 eV, suggesting an open-singlet gap of about 1.9 which is in excellent agreement with both the measured value⁶ of ΔE_zz (1.90 eV), and the calculated open singlet gap. It is important to observe also that the open-singlet value “ΔE_zz” = 1.2 eV for the 5-AGNRs and the 1.9 eV open singlet gap for the 7-AGNRs are practically equal to the correlation improved GW-LDA bandgap differences,¹⁴ which is highly suggestive for the essential correctness of our claim. Thus, within the one-electron approximation we have established the correct basis for discussion and analysis of both ΔE_zz and ΔE_ac. ΔE_zz is identified as the open-singlet HOMO–LUMO gap, whereas ΔE_ac can be identified as the difference |(HOMO−1)-(LUMO+1)|, with the understanding that both HOMO and LUMO are end-states. Nevertheless, similar values of gaps and analogous estimates can be found in the triplet state as well. Furthermore, it should be emphasized that the central meaning of ΔE_zz is only valid for lengths L longer than the critical length (L ≥ L_c), although the open-singlet HOMO–LUMO is defined for almost all lengths and is practically constant, as was also verified by Wang et al.⁶

2.3 Introducing many-body corrections to the gaps

For both gaps (ΔE_ac and ΔE_zz) we can further correct if we wish their (one-body) values by considering additional many body contributions through time-dependent DFT (TDDFT), which has been shown¹ to provide very good (“many-body”) estimates of the gaps, so that the STS spectrum overall looks very much like the (luminous) optical spectrum, because both are dominated by molecular overlaps between transition states. This is further illustrated and “verified” from the results below. Furthermore, the use of TDDFT allows the clear and unambiguous identification of the energy separation of the end/edge states, which according to the present investigation is not given by ΔE_zz, as Wang et al.⁶ have suggested, but by another type of gap which here is denoted as Δε_ζζ. In the usual one-body approximation Δε_ζζ corresponds to the HOMO–LUMO separation of the closed singlet true ground state for L ≥ L_c, which is always only a few 0.1 eV (∼0.1 eV, for L → ∝) in accord with the association of the end states with the Dirac points^3,4 (and charge neutrality points⁴) located “very close” to the Fermi level. TDDFT indeed verifies that in contrast to Δε_ζζ which involves transition from one purely end-localized HOMO state to an opposite-parity end-localized LUMO state, the ΔE_zz gap always involves transitions from a mixture (∼60% to ∼40%) of “surface”-“bulk” states to another state of about equal amount of mixing. Thus, although ΔE_zz involves a large number of localized end-states, it should not be associated with the energy separation of the end-states. Another way, besides TDDFT, to distinguish between “bulk” and “surface” energy gaps is by comparing to the corresponding “edge-modified” AGNRs,⁵ obtained by eliminating “empty” (i.e., non-aromatic) end-rings, which also eliminates topological end-states (and, therefore, ΔE_zz and Δε_ζζ).

2.4 The substrate influence on the measured STS gaps

As we have mentioned above, the main crucial property under possible dispute is the magnitude of the substrate influence (screening) ΔE_sb on the measured STS gap. According to our earlier estimates¹ ΔE_sb should be of the order of a few 0.1 eV. However, almost in all cases ΔE_sb larger than 1 eV is needed to bridge the experimental STS measurements for AGNRs deposited on metal surfaces (usually Au) and the theoretical values for free standing AGNRs. The theoretical values widely recognized as an almost universal point of reference are the GW results of Yang et al.,¹⁴ which among the theoretical values reported earlier are clearly the largest (and many times, by far). As a result, ΔE_sb which is defined as the difference of the STS measurements and the theoretical reference values are unrealistically large. For example, for the 7-AGNRs the theoretical GW gap¹⁴ is 3.7 eV, whereas the experimental STS gap value obtained by various groups^6,7,9,15 is 2.5 ± 0.2 eV. Thus, ΔE_sb should be at least 1.2 eV. However, the STS value of 2.5 eV was also obtained for 7-AGNRs deposited on non-metallic substrates, such as NaCl⁶ and MgO,⁷ for which such a large ΔE_sb value is clearly unrealistic. On the basis of their STS measurements on samples grown on MgO, Kolmer et al.⁷ concluded that ΔE_sb should be marginal, which is in full agreement with our present results. However, the general consensus, with few exceptions^1,7,18 is largely different (up to now). In this work we are led to conclude that the GW results¹⁴ overestimate the bandgaps mainly due to the size effect, since the GW results of Yang et al.¹⁴ were obtained for infinite AGNRs, whereas the atomically precise AGNRs have finite length (and topological end-states). This could be sufficient to explain the resulting unrealistically large ΔE_sb values. Yet, besides the infinite size (and the corresponding periodic boundary conditions) the lack of exact exchange in the LGA wavefunctions building the Green's function could also be important since exchange interaction is very sensitive to inversion symmetry frustration. Nevertheless, judging from our TDDFT results, it is more reasonable to attribute the gap difference between the infinite and the finite size AGNRs (size effect) to the mixing of edge/end states with the infinite “bulk” states (and the scattering at the zigzag edges) which can drastically reduce the gap. This is corroborated by the GW results⁶ of Wang et al.⁶ for the finite (7, 24) AGNR (and slightly longer), who obtained a gap of 2.8 eV clearly closer to the measured (by several groups) gap, and substantially smaller compared to the 3.7 eV (G₀W₀) value¹⁴ for the infinite 7-AGNR. Parenthetically, it should be mentioned at this point that even in the worst-case scenario where the substrate interaction is strong (especially when the distance of the STS tip from the surface is small), this leads to mixed substrate-AGNR states¹ which can be easily recognized (and excluded) from the measurements by comparing the two separate STS spectra. Moreover, such states would be expected to have low overlap with the pure AGNR-excited-states, and consequently the corresponding transition(s) would have very low intensity and would be difficult to detect. Thus, we assert here that ΔE_sb should indeed be marginal, in full agreement with the experimental results (for 7-AGNRs grown directly on the MgO substrate) and conclusions of Kolmer et al.⁷

2.5 Computational details

The theoretical and computational details of the present investigation are described in ref. 1–5. The computations, as before, have been performed with the Gaussian²³ program package using DFT and TDDFT employing the PBE0 functional²⁴ (which includes “exact” exchange, in contrast to PBE) and the 6-G31(d) basis set. The same computational package was used for the Møller–Plesset many-body perturbation theory of 2nd order (MP2) calculations, with the same basis set. The PBE0 functional and the 6-31G(d) basis set²³ have been constantly, consistently, and successfully used over the last 7–8 years^1–5,22,25 by the present author for all graphene-based structures (PAHs, NGRS, AGNRs), small, medium, and large (up to ∼1440 atoms, 8190 electrons).²⁵ This functional (PBE0) and basis set have been consistently used for all types of calculations (geometry optimizations, energies, and/or vibrational frequencies) which is very important for the broad range of structures and comparisons used. For smaller structures the results have been successfully compared with the results obtained with larger basis sets. However, the best test for the PBE0/6-31g(d) approach is the excellent agreement obtained with measured quantities such as the STS gaps (e.g., the measured open singlet gap of 1.90 eV for the 3 × 6 AGNR,⁶ or the optical gap of perylene¹) and other properties, including cohesive energies,²⁵ even for non-graphene-like structures (finite or infinite). For example, the calculated band gap and cohesive energy of diamond was calculated using this PBE0/6-31g(d) theoretical level with almost chemical accuracy.²⁵ Thus, this level of calculation is clearly adequate for our purposes. The convergence criterion for SCF was set to tight, which corresponds to 10⁻⁸ change in the RMS density matrix, whereas the RMS force criterion for the geometry optimization was set to 1 × 10⁻⁵ atomic units (tight) for the “key structures” and 3 × 10⁻⁴ for the rest of the calculations. Finally, the visualization of the results was accomplished using GaussView software.²⁶

2.6 Synopsis of the theoretical approach

For the atomically precise AGNRs examined here it has been illustrated that although the closed singlet is the correct lowest energy state, due to (inversion) symmetry frustration (which is also a sublattice frustration), open shell states, such as open shell singlet and triplet appear energetically lower due to better account of the Coulomb correlation energy (within the 1-electron approximation).³ Thus, such open shell states should be considered as “pseudo-states”, and their resulting spin distribution within the one-electron DFT framework should be characterized as the “pseudospin” distribution. The full amount (or most of it) of the Coulomb correlation energy can be estimated from the total energy difference of the closed singlet and the open singlet or triplet states. Thus, using standard DFT calculations (with functionals including exact exchange, such as the PBE0²³) for the closed and open singlet, and/or triplet states we can have a very good estimate of all (“surface” and “bulk”) energy gaps, measured by STS as follows:

(1) The HOMO–LUMO gap of the closed singlet corresponds to the real energy separation of the end-states localized at the zigzag ends, Δε_ζζ. This is true for long enough AGNRs for which both HOMO and LUMO are zigzag-end-localized.

(2) In this case the (HOMO−1)–(LUMO+1) difference corresponds to the “bulk” bandgap ΔE_ac between states delocalized over the entire AGNR.

(3) ΔE_ac can be further verified, if desired, by comparing to the HOMO–LUMO gap of the edge modified AGNRs,^4,5 which contain no zigzag end bonds, and no end-states.

(4) On the other hand, the zigzag-end-localized HOMO–LUMO gaps of the open-shell singlet or the triplet states provide a very good estimate of the “mixed” ΔE_zz gap.

(5) Further refinement of all these three gaps (“bulk”, “surface”) can be obtained, if needed, by the analysis of the orbital composition of the main peaks of the excitation spectrum obtained by TDDFT. This can also help the correct identification (and nature) of the gaps.

3. Results and discussion

3.1 5-AGNRs

Fig. 3 summarizes the present results for the 5-AGNRs (or 2 × AGNRs) which have also been studied by several groups.^{1,4,8,12,13,16}

Fig. 3 (a) Variation of the open singlet, ΔE_zz, and the “bulk” |(HOMO−1)-(LUMO+1)| = ΔE_ac gaps (in eV) in terms of length L (in Å) for the 5-AGNRs (2×). (b) Variation in the ΔE_ac gap (in eV) as a function of length for the edge modified 5-AGNRs together with the usual polynomial fit (see text). (c) Excitation spectrum of the 2 × 22 and 2 × 23 AGNRs. Intensity(I) is in arbitrary units and excitation energy (ΔE) in eV. (d) Variation with length of the HOMO–LUMO, and ΔE_zz, Δε_ζζ gaps, calculated by TDDFT as “first” and “second” optical gaps respectively, including the corresponding experimental values from ref. 8 and 13 (see text).

3.1.1 Open singlet and closed singlet results. In Fig. 3(a) the open singlet HOMO–LUMO gap, ΔE_zz, and the “bulk” gap ΔE_ac are plotted versus length L. Following the discussion in section 2.2 for the open singlet gap and its relation to ΔE_zz, we have defined ΔE_zz as the HOMO–LUMO gap of the open singlet state, contrary to the original definition of Wang et al.⁶ as the energy separation of the end states. Obviously, for an open singlet ground state both definitions are equivalent, but this is not the case. As we can see in Fig. 3(a), the “one-body” ΔE_ac = |(HOMO−1)–(LUMO+1)| gap after the discontinuity (or transition) at L ≈ 100 Å, which we have discussed in detail in a previous work,⁴ starts opening up at L_c, contrary to the “one-body” ΔE_zz (i.e., the open singlet HOMO–LUMO gap) which varies slowly and smoothly over the entire range of lengths. This is very strange indeed, if ΔE_zz is going to represent the real separation of the edge states, since ΔE_zz first appears at and after the transition at L_c. This behaviour (smooth variation) should be better suited for ΔE_ac. This is indeed verified in Fig. 3(b), which shows the HOMO–LUMO gap of the “edge modified AGNRs”, which seems to saturate to the value of 1.22 eV, very close to the value of 1.25 eV, suggested from the behavior of the “normal” AGNRs in Fig. 3(a). The edge modified AGNRs by construction have no edge states and their HOMOs and LUMOs are delocalized over their entire length,⁴ and therefore their fundamental gap corresponds to ΔE_ac. Such edge-modified AGNRs are obtained by eliminating the empty (non-aromatic) end-rings⁵ of the standard AGNRs, which also eliminates end-states and zigzag end-bonds.⁵ This is a clear manifestation of the importance of aromaticity for AGNRs (and graphene itself).^2,3 Comparing the behavior of the “bulk gap” in Fig. 3(a and b), we can see that due to quantum confinement (both lateral and longitudinal) the (HOMO−1) and (LUMO+1) states defining the “one-body” ΔE_ac are also affected by the abrupt appearance of the edge states, in sharp contrast to the (“one-body”) open singlet gap which seems to be practically insensitive to the appearance of the end-states, contrary to what is expected from its original definition. This in fact emphasizes the “many-body” nature of the end states through their connection with inversion symmetry conflict, which is further supported by Fig. 3(c) and Fig. S1 (ESI†). The “correct” behavior (with length variation) of the “one-body” ΔE_ac is given by the (delocalized) HOMO–LUMO gap of the edge-modified AGNRs in Fig. 3(b). As we can see in Fig. 3(b) the value of ΔE_ac (HOMO–LUMO gap of the edge-modified AGNRs) as a function of length, as L → ∝, seems to saturate to the value of 1.22 eV. This could be misleading since only lengths up to about 140 Å have been considered. To remedy this problem we have recently suggested²⁵ fitting the calculated ΔE_ac as a function of L efficiently and transparently^1,25 to a polynomial of the form ΔE_ac(L) = A + B × L^−C, where the value A corresponds to the gap at infinity, ΔE_ac(∝) = A, and the constant C to some short of effective (“fractal”) dimensionality (here equal to 1.20).^1,25 As we can see in the inset in Fig. 3(b), the projected ΔE_ac value is 1.07 eV.

3.1.2 TDDFT Corrections. The ΔE_ac value of 1.07 eV obtained above is also verified by the TDDFT result ΔE_ac = 1.01 eV (see Fig. S1, ESI†). The TDDFT value (1.01 eV) is clearly closer to the value of 0.85 eV measured by Lawrence et al.,⁸ assuming a very reasonable substrate screening (of about 0.15 eV), as we have suggested recently.⁴ However, further correct information is given in Fig. 3(c), showing the spectra of the 2 × 22 and 2 × 23 AGNRs immediately before and after transition, respectively (see Fig. 3(d) too). As is illustrated in Fig. 2(c), in the 2 × 23 AGNR (immediately after the transition) there is a strong peak value at 0.87 eV, very close to the recently measured⁸ STS gap of 0.85 eV. Detailed analysis of the TDDFT results shows that this peak includes transitions involving end-states to a large percentage (about 60%). Thus, the calculated value of 0.87 eV and the measured⁸ gap should be assigned to ΔE_zz. This, contrary to the “one-body” gap obtained by the open singlet state, restores the expected correct behavior of ΔE_zz at (and after) L_c. Even more interesting is the fact that extrapolating to longer AGNRs gives a gap of 0.85 eV (exactly), which is in unexpected full agreement with the experiment, as is shown in Fig. 3(d). Fig. 3(d) also shows that, contrary to the “one-body” (open-singlet) ΔE_zz gap of Fig. 3(a), both “many-body” gaps, ΔE_zz, and Δε_ζζ (the latter corresponding to the “real energetical separation of the end-states), change discontinuously at the critical length (∼100 Å). However, in contrast to Δε_ζζ and the HOMO–LUMO gaps which drop at L_c, the ΔE_zz increases. Thus, the observed⁸ gap opening (of about 0.30 eV) is due to the increased aromaticity at the critical length, and the mixing of bulk and end-states at an almost equal amount. Lawrence et al.⁸ have attributed such gap opening to the different electrostatic potential felt by valence electrons at different regions of the ribbon due to the positive partial charge on the hydrogen atoms along the sides of the AGNR. However, the paradigm of edge-modified AGNRs contradicts this interpretation.⁴ Our present work reveals that the gap opening is a many-body effect related with the aromatic transition and the change from bulk-like (ΔE_ac) to coupled “surface-bulk” end-states (ΔE_zz). On the other hand, the calculated Δε_ζζ gap of 0.1 eV in Fig. 3(d) is in full agreement with the results of Kimouche et al.¹³ Thus, Kimouche et al.,¹³ and Lawrence et al.,⁸ have apparently (“correctly”) measured different kinds of gaps. Moreover, the same could be true for the value of 2.8 eV measured by Zhang et al.,¹² which could be assigned as a tentative ΔE_ac value, either for very short AGNRs (without end-states), or for longer AGNRs with a strong “bulk” transition from deep occupied states (well below the HOMO−1 orbital) to higher unoccupied states (well above the LUMO+1), and thus much larger than the real ΔE_ac (which is technically determined by the HOMO−1, LUMO+1 difference). We can also observe in the 5-AGNRs that differences between the “one-body” and “many-body” (TDDFT) methods for assigning ΔE_ac, ΔE_zz, and Δε_ζζ are relatively large compared to the 7- and 9-AGNRS, where the corresponding differences are of the order of 0.1–0.2 eV. This could be related to the fact that the 5-AGNRs (contrary to 7- and 9-AGNRs) are topological and aromatic mixtures.³ Thus, the three seemingly conflicting measurements^8,12,13 for the 5-AGNRs could be attributed to different length samples (and/or different positions of the STS tip). Yet, alternatively, one could claim, based on the GW results,¹⁴ that there is a substrate interaction of equal magnitude (0.85 eV) and the “real gap” is 1.7 eV. This conclusion is clearly considered here as highly improbable, in view of equally good (in fact better) agreement for the 7- and 9-AGNRs, not to mention Occam's principle. Moreover, if this is indeed a general trend, it clearly illustrates that elaborate correlation calculations (e.g., GW) could be avoided (see also ref. 23) if topological frustration can be taken into account appropriately by simple DFT (one particle) calculations, provided that the DFT functionals include “exact” exchange which is sensitive to inversion symmetry conflict.⁴

3.2 7-AGNRs

Fig. 4 summarizes the results for the 7-AGNRs, represented by the 3 × 6 or (7, 12) AGNR, for which there are detailed experimental STS data.⁶ Results for all three spin states (closed singlet, open singlet, and triplet) are shown.

Fig. 4 Spin states of the 3 × 6 (7, 12) AGNR: (a) triplet, (b) closed singlet, and (c) open singlet states, showing frontier MOs, and gaps, together with charge density and spin density (see text). (d) Excitation spectrum for the standard (black line) and edge-modified (red line on line) AGNRs. Intensity is given in arbitrary units, and excitation energy in eV. Boxes (rectangular and elliptical) emphasize the calculated values in agreement with the experimental measurements. Question marks indicate alternative possibilities and/or identifications of the corresponding gaps (see text).

3.2.1 Three spin-states: closed/open singlet and triplet. First of all, we can comment on the significance of the exact exchange in the DFT functional, which was discussed in Section 2.1. The calculated DFT/PBE0 open singlet ΔE_zz gap is 1.9 eV in full agreement with the measured⁶ ΔE_zz gap for the 3 × 6 (7, 12) AGNR. In contrast the ΔE_zz gap calculated with the PBE functional, which does not include “exact exchange”, is less than half this value (∼0.5 eV, in agreement with the PBE calculations of Wang et al.⁶). As we can see in Fig. 4(a–c), which show the one-body DFT picture for the triplet, closed singlet, and open singlet, respectively, there are gaps in all of them between the HOMO (or HOMO−1) and LUMO, which are equal or very nearly equal to the measured ΔE_zz value of 1.9 eV. We must remember also that this value is practically equal to the correlation energy obtained from the difference between the GW and LDA values¹⁴ for these AGNRs. Let us first focus on the open singlet, which is commonly accepted as the “ground state”. Fig. 4(d) is practically identical with Fig. 2(b and c) of Wang et al.⁶ where the definitions of ΔE_zz and ΔE_ac (which are designated as Δ_zz and Δ_ac, respectively) are illustrated. Moreover, the calculated DFT/PBE0 ΔE_zz and ΔE_ac values (contrary to those of DFT/PBE, with no “exact exchange”, used by Wang et al.⁶) are practically identical to the measured values for the 3 × 6 (7, 12) AGNR deposited on a non-metallic NaCl substrate (in full analogy to similar results for the 5-AGNRs, described above).

The end states, which are localized at the two zigzag ends, can be clearly seen in Fig. 4(b) illustrating the frontier MOs of the closed singlet. These end states, which comprise the HOMO and LUMO orbitals (labeled 267 and 268 respectively) have clearly zero density in the interior of the AGNR, in contrast to the MOs above and below them, which are (de)localized in the interior “bulk” region. However, although the end states in the closed singlet description appear in both ends, in the open shell case of Fig. 4(c) the end states appear only on one zigzag end at a time. Based on the closed singlet ground state, it becomes clear that the “real” energy separation of the end states is the HOMO–LUMO gap of the closed singlet state which is (almost always) about 0.1–0.3 eV (depending on the length). This is corroborated by the TDDFT results, giving rise to the Δε_ζζ gap, which was discussed earlier for the 5-AGNRs, and is consistent with the appearance of Dirac points close and around the Fermi level, whereas ΔE_zz is due to mixed transitions involving both “end” and “bulk” states.

3.2.2 TDDFT results. Fig. 4(d) shows the excitation spectrum of the closed singlet state for the normal 3 × 6 (7, 12) AGNR. We can clearly see two characteristic maxima at 1.9 eV and 3.2 eV, which practically coincide with the measured ΔE_zz, and ΔE_ac values respectively for this AGNR.⁶ As we can see in Fig. 4(d), ΔE_ac involves transitions between (mixtures of) “bulk states” (from HOMO−1 and HOMO−2, to LUMO+1 and LUMO+2); whereas ΔE_zz corresponds to transitions from mixtures of “bulk” + “surface” states (such as HOMO−3 + HOMO) to mixtures of “bulk” + “surface” (e.g. LUMO+3 + LUMO) states. Thus, ΔE_zz, although not equal to the energy separation of the end states, is clearly associated with the first (lowest energy) transition involving end and bulk states, corresponding to the measured ΔE_zz value of 1.9 eV and the magnitude of the open singlet gap. This is also verified by the TDDFT results in Fig. 4(d) for the edge-modified closed singlet, in which the peak of 1.9 eV is totally absent, whereas the peak of the “bulk” gap ΔE_ac is present and identical to the 3.2 eV peak of the normal (7, 12) AGNR. The position of the ΔE_ac peak, contrary to ΔE_zz, changes (decreases) as the length increases. Thus, for the 3 × 14 (7, 28) AGNR we found a ΔE_ac value of 2.8 eV, as is shown in Fig. S2(a) (ESI†). This value of 2.8 eV, as could be expected, is in perfect agreement with the calculated GW value⁶ and the experimental measurements for the (7, 24–28) AGNR(s) on an insulating NaCl substrate.⁶

3.3 9-AGNRs

We can observe in Fig. S2(c) (ESI†) that the overall spectrum of the 4 × 6 AGNR which has the same length with the 3 × 6 AGNR, except for a suppression of the Δε_ζζ peak, looks at first sight very much like the one for the 3 × 6 AGNR. Clearly a (deep) “bulk” gap could be expected not to vary very much or be so sensitive to the exact AGNR's width; but for the peak around 2.0 eV, which up to now was associated with the ΔE_zz gap of the 3×- AGNRs, further investigation is needed, which is described in Fig. 5. Fig. 5(a–c) are the corresponding analogues of Fig. 4(a–c) respectively. However, contrary to the 7-AGNRs, the experimental data for the 9-AGNRs are very limited.¹⁶ Therefore most of the results shown in Fig. 5 should be considered as predictions of the present work. As we can see in Fig. 5(c) for the open singlet the two fundamental gaps ΔE_zz and ΔE_ac are very close together (2.2 eV and 2.4 eV respectively) and not exactly equal to the corresponding 3 × 6 gaps This is also true for the almost equal values of ΔE_zz and ΔE_ac obtained from triplet (and closed singlet). Thus, the peak around 2.0 eV in Fig. 5(d) is the result of the overlap of the ΔE_zz and ΔE_ac gaps, whereas the peak around 3.2 eV in the same figure, Fig. 5(d), although of “bulk” type (similarly to the 3 × 6 AGNR) is not the smallest “bulk” gap, and the real ΔE_ac for the 4 × 6 (9, 12) AGNR should be around 2.0 eV. This is verified in Fig. 5(d), which shows that the 2.1 eV “bulk” peak (together with the “deeper” 3.2 eV “bulk” peak) survives the elimination (total and partial) of the empty (non-aromatic) end-rings which generates the edge modified AGNRs (without end states, and ΔE_zz). As is well known, this “bulk” peak value decreases as the length of the AGNR increases. For the 4 × 13 AGNR we find ΔE_ac = 1.6 eV, but for the longer 4 × 18 (9, 36) and 4 × 24 (9, 48) AGNRs of lengths L ≈ 78 Å and L ≈ 104 Å respectively, we obtain (by TDDFT) for both of them ΔE_ac = 1.45 eV. This value is in very good agreement with the recently measured gap of 1.4 eV by Talirz et al.,¹⁶ as is illustrated in Fig. S3 (ESI†). We can also clearly see in Fig. S3(b and c) (ESI†) the “surface” ΔE_zz gap at about 2.1–2.2 eV. Thus, for the 9-AGNRs the predicted values for the gaps are ΔE_ac = 1.45 ± 0.1 eV, and ΔE_zz = 2.1 ± 0.1 eV.

Fig. 5 Spin states of the 4 × 6 (9, 12) AGNR: (a) triplet, (b) closed singlet, and (c) open singlet, showing frontier MOs, gaps, and spin densities. (d) Excitation spectrum for the standard (black line), partially edge-modified (blue line on line), and fully edge modified AGNRs (red line on line). Intensity is given in arbitrary units, and excitation energy in eV. The frontier orbitals and aromaticity patterns of partially and fully edge modified AGNRs are shown in the right and left portions of the figure. The peak at 1.45 eV is further verified by Fig. S4 (ESI†) which shows the spectrum of the edge-modified 4 × 24 AGNR.

4. Conclusions

We have achieved excellent agreement (within 1% or less) with the measured STS gaps (“bulk” and “surface”) for the known 5-, 7- and 9-AGNRs, although with the “surface” gaps, as illustrated in Table 1, namely:

Table 1 Calculated and measured gaps for the 5-, 7-, and 9-AGNRs (in eV). Numbers with an asterisk denote the present values, while numbers in the parenthesis indicate the reference numbers of the original studies. Numbers in bold emphasize the agreement between theoretical and experimental results, whereas the underlined numbers in italics indicated the results of GW calculations.¹⁴

AGNR	Δεζζ Calculated	Δεζζ Measured	ΔEzz Calculated	ΔEzz Measured	ΔEac Calculated	ΔEac Measured
a Values obtained in the present work.
5-	0.1^(1)	0.1^(13)	0.85	0.85^(8)	1.1^a, 1̲.7̲^(14)	—
7-	0.1^(1)^a	—	1.9^a	1.9^(6), 2.5^(7)	2.5 , 2.8^a, 2.8^(6), 3̲.7̲^(14)	2.8 ^(6), 2.5 ± 0.2^(6,7,9,15)
9-	0.1^(1)^a	—	2.2^a	—	1.45 , 1.6^(1), 2̲.0̲^(14)	1.4 ^(16)

---

(a) For the 5-AGNRs the measured⁸ gap value is 0.85 eV. The gap calculated here with DFT/PBE0 is 1.07, whereas the TDDFT/PBE0 value is exactly 0.85 eV, also indicating that this is a ΔE_zz gap.

(b) Moreover, the measured¹³ 0.1 eV gap is recognized to fully coincide with the Δε_ζζ gap calculated here (by both DFT-TDDFT/PBE0).

(c) For the 7-AGNRs the measured^6,7,9,10,15 ΔE_ac gap of 2.3 ± 0.2 eV coincides with the ΔE_ac gap calculated here (with both DFT-TDDFT/PBE).

(d) Furthermore, for the (7, 28) AGNR the measured⁶ and GW-calculated⁶ 2.8 eV gap fully coincides with the ΔE_ac gap calculated here (with both DFT-TDDFT/PBE0), whereas for the (7, 12) AGNR the measured⁶ and calculated⁶ ΔE_ac gap is ∼3.2 eV.

(e) The measured⁶ ΔE_zz gap of 1.9 eV for the 7-AGNRs, (7, 12), and longer, is clearly identical to the ΔE_zz gap calculated here of 1.9 eV (with both DFT-TDDFT/PBE0).

(f) For the 9-AGNRs the only known (to the present author) measurement¹⁶ for the gap is 1.4 eV. The present calculations (TDDFT/PBE0) yield a ΔE_ac value of 1.45 eV, and also predict ΔE_zz = 2.1 ± 01 eV, quite close to the corresponding gap for the 7-AGNRs.

Note that for the 5- and 9-AGNRs the ΔE_zz gaps are theoretical predictions of the present work, due to the lack of analogous experimental data.

At the same time the present work has provided a simple physical understanding/rationalization of the origin and properties of these gaps. We have shown that such excellent agreement can be obtained using a transparent approach, using a minimum of computational resources, avoiding high level many-body methods, such as the advanced GW approach.¹⁴ This is accomplished by recognizing (and suitably exploiting) the fact that most (or all) of the Coulomb correlation energy is devoted to offset the (inversion) symmetry conflict. This is an added insight. Thus, simple DFT calculations with or without “fictitious” open shell states (such as open shell singlets or triplets) can give accurate results, especially when augmented by TDDFT calculations which can further refine the results, provided that the chosen DFT functional includes the “exact” exchange (such as the PBE0 functional²³ used here, proven to provide excellent results^1–5,24), and the finite length of the AGNRs is taken into account (recall the synopsis of the theoretical approach in Section 2.5). Under the same provisions (a finite size of AGNRs and “exact exchange”) the GW approach would also give the correct results, as is illustrated in ref. 6, where taking into account the finite size of the 7-AGNRs has lowered the GW gap by about 1 eV, in very good agreement with the measured STS value. As a result, a similarly large overestimation of the expected substrate screening would be avoided, since the GW results¹⁴ are widely used as reference values for the free standing AGNRs. This is corroborated by STS measurements of AGNRs on non-metallic substrates.^6,7 Thus, the measured STS gaps are practically independent of the substrate and virtually equal to the free-standing values, obtained by any of the three computational methods: DFT, TDDFT, and GW (from the simplest to the more complex), provided the finite size and the “exact” exchange are taken into account. Obviously, the simplest (and computationally most economical) approach should be normally preferred, in accordance also with Occam's principle. A combination of DFT and TDDFT, as is used here, should be considered ideal.

Additional supplementary material with more details and comparisons for the spectra of 5-, 7-, and 9-AGNRs are given in the ESI.†

Conflicts of interest

There are no conflicts to declare.

References

1. A. D. Zdetsis and E. N. Economou, Rationalizing and Reconciling Energy Gaps and Quantum Confinement in Narrow Atomically Precise Armchair Graphene Nanoribbons, Carbon, 2017, 116, 422–434.
2. A. D. Zdetsis, Bridging the Physics and Chemistry of Graphene(s): From Hückel's Aromaticity to Dirac's Cones and Topological Insulators, J. Phys. Chem. A, 2020, 124, 976–986.
3. A. D. Zdetsis, Do We Really Understand Graphene Nanoribbons? A New Understanding of the 3n, 3n ± 1 Rule, Edge “Magnetism” and Much More, J. Phys. Chem. C, 2020, 124, 7578–7584.
4. A. D. Zdetsis and E. N. Economou, Topological Metal-Insulator Transition in Narrow Graphene Nanoribbons?, Carbon, 2021, 176, 548–557.
5. A. D. Zdetsis, 4n + 2 = 6n? A Geometrical Approach to Aromaticity?, J. Phys. Chem. A, 2021, 125, 6064–6074.
6. S. Wang, et al., Giant edge state splitting at atomically precise graphene zigzag edges, Nat. Commun., 2016, 7, 1150,  DOI:10.1038/ncomms115077.
7. M. Kolmer, et al., Rational synthesis of atomically precise graphene nanoribbons directly on metal oxide surfaces, Science, 2020, 369, 571–575,  DOI:10.1126/science.abb8880.
8. J. Lawrence, et al., Probing the Magnetism of Topological End States in 5-Armchair Graphene Nanoribbons, ACS Nano, 2020, 14, 4499–4508.
9. Y.-C. Chen, D. G. Oteyza, Z. Pedramrazi, C. Chen, F. R. Fischer and M. F. Crommie, Tuning the Band Gap of Graphene Nanoribbons Synthesized from Molecular Precursors, ACS Nano, 2013, 6123–6128.
10. S. Song, et al., On-surface synthesis of graphene nanostructures with π-magnetism, Chem. Soc. Rev., 2021, 50, 3238–3262.
11. K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Edge state in graphene ribbons: Nanometer size effect and edge shape dependence, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954.
12. H. Zhang, H. Lin and K. Sun, et al., On-surface synthesis of rylene-type graphene nanoribbons, J. Am. Chem. Soc., 2015, 137, 4022–4025.
13. A. Kimouche, M. M. Ervasti, R. Drost, S. Halonen, A. Harju, P. M. Joensuu, J. Sainio and P. Liljeroth, Ultra-narrow metallic armchair graphene nanoribbons, Nat. Commun., 2015, 6(10177), 1–6.
14. L. Yang, C.-H. Park, Y.-W. Son, M. L. Cohen and S. G. Louie, Quasiparticle energies and band gaps in graphene nanoribbons, Phys. Rev. Lett., 2007, 99, 186801.
15. P. Ruffieux, J. Cai, N. C. Plumb, L. Patthey, D. Prezzi, A. Ferretti, E. Molinari, X. Feng, K. Müllen and C. A. Pignedoli, et al., Electronic Structure of Atomically Precise Graphene Nanoribbons, ACS Nano, 2012, 6, 6930–6935.
16. L. Talirz, H. Söde and T. Dumslaff, et al., On-Surface Synthesis and Characterization of 9-Atom Wide Armchair Graphene Nanoribbons, ACS Nano, 2017, 11, 1380–1388.
17. J. Overbeck, et al., A Universal Length-Dependent Vibrational Mode in Graphene Nanoribbons, ACS Nano, 2019, 13, 13083–13091.
18. A. Varykhalov, J. Sánchez-Barriga, A. M. Shikin, C. Biswas, E. Vescovo, A. Rybkin, D. Marchenko and O. Rader, Electronic and Magnetic Properties of Quasifreestanding Graphene on Ni, Phys. Rev. Lett., 2008, 101, 157601.
19. A. D. Zdetsis, The real structure of the Si₆ cluster, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 23202.
20. Y.-W. Son, M. L. Cohen and S. G. Louie, Energy Gaps in Graphene Nanoribbons, Phys. Rev. Lett., 2006, 97, 216803.
21. M. Huzak, M. S. Deleuze and B. Hajgató, Half-metallicity and spin-contamination of the electronic ground state of graphene nanoribbons and related systems: An impossible compromise?, J. Chem. Phys., 2011, 135, 104704.
22. A. D. Zdetsis, Classics Illustrated: Clar's Sextet and Hückel's (4n + 2) π Electron Rules, J. Phys. Chem. C, 2018, 122, 17526–17536.
23. M. J. Frisch, et al., Gaussian 09, revision C.01, Gaussian, Inc., Wallingford, CT, 2009.
24. C. Adamo and V. Barone, Toward Reliable Density Functional Methods Without Adjustable Parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6169.
25. R. Dennington; T. Keith and J. Millam, GaussView, version 5.09, Semichem Inc., Shawnee Mission, KS, 2016.
26. A. D. Zdetsis and S. Niaz, From Zero to Infinity: Customized Atomistic Calculations for Crystalline Solids —Applications to Graphene and Diamond, Adv. Mater. Lett., 2021, 12(9), 21091659,  DOI:10.5185/amlett.2021.091659.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00650b

---