A theoretical study on spontaneous dipole orientation in ice structures

Abstract

Spontaneous dipole orientation is studied for a set of simulated porous ASW ice films on a substrate held at temperatures ranging from 10 K to 140 K. It is found that the water dipoles in the films obtained at the lower temperatures are oriented such that a negative electric field with a magnitude of 10⁸–10⁹ V m⁻¹ is obtained. The magnitude of the field increases approximately linearly with height above the substrate, akin to experimental observations, although the magnitude of our field increases faster. A strong temperature dependence of the surface potential resulting from the spontelectric field is found, where the surface potential decreases when the substrate temperature increases. The surface potential finally becomes close to zero for temperatures around and above 110 K.

---

1 Introduction

Amorphous solid water (ASW) is the most abundant form of water in the Universe. ASW has attracted a significant amount of attention in order to understand its properties in astrophysical environments.^2,3 It has been shown that porous ASW films made by vapour deposition of water molecules onto cold surfaces (temperatures below ∼ 110 K) create a powerful electric field, owing to spontaneous dipole orientation of the molecules in the film.^4–6 Unlike ASW, crystalline ice does not show an overall polarization, which can be explained by the full hydrogen bond network leading to a balance of dipoles.^5,7

The effect where the dipole orientation leads to an ordering through the film and consequently a strong electric field (the strength can be around 10⁸ V m⁻¹), has been seen by Field and co-workers in a broad range of organic and inorganic materials where the individual molecules have a permanent dipole moment.^1,8,9 These solid materials are called spontelectrics and the phenomenon is referred to as the spontelectric effect. The spontelectric effect has also been shown to have implications for star formation.¹⁰ Furthermore, spontelectric behavior (i) may have implications in determining the lifetime of organic thin film electronics as the presence of an internal electric field may present a barrier to current passage; (ii) may have important implications in terms of the stability of amorphous materials; (iii) could enable us to engineer surfaces with embedded high electric fields to mimic the effects of such fields in the active pockets of enzymes. The present work represents the first molecular dynamics study of deposition resulting in a spontelectric material.‡ We however note that Kexel and Solov’yov¹¹ have done simulations of spontelectric field in cis-methyl formate structures.

Field and co-workers did not detect spontaneous dipole orientation in water ice films (at T ≥ 40 K)⁷ using the same experimental technique as applied in their successful observations on N₂O films.¹² This lack of detection is explained by the ordering dictated by the hydrogen bonding which outcompetes spontaneous dipole orientation.^12,13 However, a negative surface potential, caused by the intrinsic electric field in ASW films has been reported by Bu et al.⁵ They used a Kelvin probe to measure the surface potentials in the vapour-deposited ice films grown at temperatures between 10 K and 110 K. The values of the surface potential show no dependence on the nature of the substrates on which the films are grown. A linear increase of the surface potential with film thickness is seen for a given temperature. The other property demonstrated is that the higher the deposition temperature, the smaller the surface potential. Thus, as temperature rises the surface potential reduces so as to vanish at deposition temperatures over a limit. Bu et al. concluded that the polarization for porous ASW structures results from the molecules not being completely coordinated.⁵ A more recent study, done by Sagi et al.,⁶ qualitatively confirmed the conclusion of Bu et al.,⁵ and associated the spontaneous polarization observed in ASW films with the spontelectric effect.

In the present study, we have performed detailed molecular dynamics simulations to investigate the presence of the spontelectric phenomenon in porous ASW ice films.

2 Theoretical details

Molecular dynamics simulations are useful for depositing water vapour molecules onto a cold substrate, thereby forming a condensed ice film. Here, 400 porous low-density amorphous solid water films are created by dropping water molecules onto a silica substrate at substrate temperatures (T_s) between 10 K and 140 K and two distinct incoming gas temperatures (T_g) of 150 K and 300 K. Fig. 1 illustrates two of the studied structures from different viewpoints. Next, we briefly describe the most relevant points of the MD simulations.

Fig. 1 Example ice structures obtained at (T_s, T_g) of (30 K, 150 K) (upper images) and (140 K, 150 K) (lower images) from top and side viewpoints.

The substrate is modeled as a coarse-grained silica surface using the parameters in the Essmann and Geiger paper.¹⁴ The substrate grains (SiO₂ units) with the mass of 60.1 a.u. interact via a Lennard-Jones (LJ) potential, where the ε and σ parameters are 5.7632 kJ mol⁻¹ and 2.800 Å, respectively.¹⁴ The TIP4P/2005 potential model¹⁵ is employed for water. This model treats water molecules as rigid bodies having four interaction centers: one LJ site located on the atomic oxygen, two positive coulomb charges (q₊ = 0.5564) centered on the atomic hydrogens, and a negative charge (q₋ = −1.1128) on the bisector of the angle 0.15 Å away from the oxygen atom. The corresponding LJ parameters are ε = 0.7799 kJ mol⁻¹ and σ = 3.159 Å. The LJ parameters for the water–silica interactions are set to be ε = 2.1133 kJ mol⁻¹ (the geometric mean of ε_H2O and ε_SiO2) and σ = 2.979 Å (the arithmetic mean of σ_H2O and σ_SiO2). All the interactions are truncated at a cut-off of 14 Å.

The simulation box is 31 Å × 31 Å and periodic in the x- and y-directions. It is not periodic in the z-direction. The xy-plane is defined as the plane of the substrate onto which water molecules are dropped. The z-direction is perpendicular to this plane. The box contains three layers of SiO₂ particles (FCC lattice). Each individual layer consists of 100 particles. The bottom layer is fixed during the simulation, while the particles in the other two layers can move. The temperature of the simulation is controlled by the Berendsen thermostat. The simulations are done using the DL–POLY molecular dynamics program.¹⁶

For a distinct pair of (T_s, T_g), each structure containing 500 water molecules is obtained in a simulation in which one molecule at a time is dropped onto the surface. 400 such structures are obtained and classified in distinct (T_s, T_g) pairs. Typically, 10 different structures are provided for each temperature pair, though there are some cases with 30 structures. After a water molecule has been deposited, a simulation time of 3 ps is applied to allow the deposited water molecule to relax. Thereafter the next water molecule is deposited. The orientation of a newly deposited water molecule may be affected by the previously deposited molecules, i.e. there is feedback in the deposition procedure. When all 500 molecules have been deposited, the simulation is continued for 12.5 ps. Thus, the relaxation time is substantial in order to let the molecules settle and redistribute their energy over the structure. The current paper investigates the spontelectric phenomenon in these simulated structures.

3 Results and discussion

The final geometries of the ASW structures are used to calculate the average x, y,z-components of the dipole moment (〈μ_x〉,〈μ_y〉 and 〈μ_z〉), the average degree of dipole orientation (〈μ_z〉/μ), the ice thickness (d), the electric field (E_cal) and the surface potential (V_s). The average quantities refer to structures with the same pair of temperatures (T_s, T_g). For instance, to calculate 〈μ_z〉, the mean value of μ_z is obtained for the 10 or 30 structures available for each temperature pair. The standard error of the mean (SEM) is also calculated. We note that for very large ice structures 〈μ_x〉 and 〈μ_y〉 would be zero due to symmetry.

Given the coordinates for each water molecule, the cartesian components of its dipole moment are straightforward to compute. To calculate the average dipole orientation (〈μ_z〉/μ), μ should be the dipole moment of the water molecule in its environment in the amorphous ice. In the TIP4P/2005 water potential model, μ is particularly easy to calculate as each molecule is rigid, so the value of μ is fixed at 0.479931 eÅ.

The ice thickness (d) is defined as the difference in height between the lowest water molecule and the top one in the ice film. The calculation of the electric field within the ice film is, based on the review of Field et al.,¹E_cal= 〈μ_z〉/Ωε₀. ε₀ and Ω are respectively the vacuum permittivity and the volume of the water molecule, which we set to 31.82 ų. This value is computed using the equation Ω = m/ρ, in which m is the mass of the water molecule and ρ is the density of compact (non-porous) low-density amorphous solid water (0.94 g per molecule).¹⁷ The surface potential (V_s) equals the electric field (E_cal) multiplied by the ice film thickness.

The average cartesian components of the dipole moments for T_g 150 K and 300 K are presented in Tables S1 and S2 (ESI†) respectively. As expected, 〈μ_x〉 and 〈μ_y〉 appear random due to symmetry, and the SEM values exceed the corresponding means in 64% and 71% of the 400 cases, respectively. This is fully in line with the 68% that is on average expected from a standard deviation, and is thus a sign that the simulations are correctly performed. The z-component however averages to a non-zero negative value, except for the highest temperatures. There is a general decrease in the value of 〈μ_z〉 with increase in substrate temperature. This behavior is expected due to the relation between temperature and orientation of dipoles. The higher the temperature, the smaller the dipole orientation. This trend is in line with the trend of the standard model for spontelectrics.¹Tables 1 and 2 focus on the quantities related to the spontaneous dipole orientations in the ice films at different temperature combinations (the corresponding SEM values are presented in the more comprehensive Tables S3 and S4, ESI†). At all (T_s, T_g) but (130 K, 150 K) and (140 K, 150 K), the spontelectric characteristics are negative but their magnitudes seem to decrease with increase in T_s such that there are even positive values at higher substrate temperatures for T_g = 150 K.

Table 1 〈μ_z〉/μ, E_cal, d and V_s at T_g = 150 K and T_s between 10 K and 140 K. There are 30 obtained structures for the bold T_ss

T s/K	〈μz〉/μ	E cal/10^+8 V m^−1	d/Å	V s/V
10	−0.025	−6.89	43.72	−3.06
20	−0.028	−7.79	41.53	−3.22
30	−0.025	−6.93	40.94	−2.76
40	−0.025	−6.78	39.97	−2.59
50	−0.031	−8.44	41.76	−3.42
60	−0.030	−8.23	38.91	−3.06
70	−0.015	−4.04	34.62	−1.37
80	−0.017	−4.61	37.04	−1.77
90	−0.005	−1.44	37.16	−0.41
100	−0.016	−4.47	37.13	−1.60
110	−0.012	−3.30	35.46	−1.37
120	−0.004	−1.08	35.03	−0.37
130	0.006	1.57	32.29	0.67
140	0.014	3.81	29.88	1.26

---

Table 2 〈μ_z〉/μ, E_cal, d and V_s at T_g = 300 K and T_s between 10 K and 140 K. There are 30 obtained structures for the bold T_ss

T s/K	〈μz〉/μ	E cal/10^+8 V m^−1	d/Å	V s/V
10	−0.045	−12.39	39.38	−4.97
20	−0.029	−7.90	39.09	−3.09
30	−0.030	−8.20	34.67	−2.83
40	−0.026	−7.02	35.15	−2.57
50	−0.018	−4.84	33.82	−1.50
60	−0.021	−5.67	33.25	−1.92
70	−0.016	−4.30	32.37	−1.33
80	−0.010	−2.89	33.77	−1.01
90	−0.011	−2.91	30.27	−0.83
100	−0.014	−3.78	31.26	−1.00
110	−0.008	−2.15	30.05	−0.67
120	0.000	−0.01	30.66	−0.33
130	−0.002	−0.69	30.17	−0.24
140	−0.003	−0.73	29.53	−0.23

---

The calculated field is considerably larger (roughly an order of magnitude) than the field obtained by Bu et al.,⁵ which may suggest that in the simulated ice structures the dipoles are more oriented than in the experimentally studied ASW. There may be several reasons for this, including difference in molecule deposition technique between the experiments and the simulations. The choice of water model could also affect the spontelectric field. The TIP4P/2005 model is neither flexible nor polarizable, and does not account for vibrations. Since part of the energy redistribution after a molecule has been deposited on a surface is vibrationally mediated, perhaps this could matter. Furthermore, there may be quantum mechanical effects which are not considered in the classical MD simulations. Still the model appears to give results in qualitative agreement with the observations.

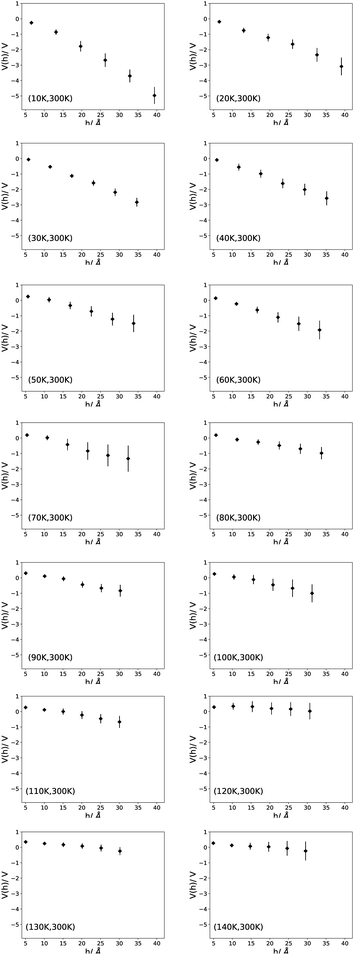
Bu et al. found a sudden change in the magnitude of the surface potential after the first few deposited monolayers. V_s then continues to increase linearly with film thickness, but slower than for the first few monolayers. We do not find the abrupt change that Bu et al. observe, but we do see the linear increase in V_s, see Tables S5–S16 (ESI†) where each of our structures is divided into six layers of equal height, not necessarily containing the same number of water molecules. For each layer,〈μ_z〉,〈μ_z〉/μ, E_cal, the average thickness of each layer (d_l), the average number of water molecules in the layer and V (d_l) = E_cald_l are tabulated. Fig. 2 presents the change of V (h) =E_calh with the height (h) above the lowest water molecule in the ice structures simulated at T_g = 300 K and substrate temperatures ranging from 10 K to 140 K. Looking at the plots, it is seen that the thickness of the ice films is reduced as T_s rises so that the height is about 40 Å at the lower temperatures and becomes about 30 Å at the higher temperatures. A roughly linear relation between h and V (h) is seen at all temperatures. Layer by layer, a regular change in V (h) is seen, in general confirming the results reported by Bu et al.⁵V (h) depends strongly on the substrate temperature. When T_s increases, the magnitude of V (h) decreases and begins to fluctuate around zero at T_s ≥ 110 K. Although there are some differences at higher substrate temperatures for T_g = 150 K compared to T_g = 300 K, the same general behavior can be observed for both cases, see Fig. S1 in ESI.†

Fig. 2 The height dependence of the potential V (h) at T_s between 10 K and 140 K and T_g = 300 K.

4 Conclusion

This is the first theoretical deposition study where spontaneous dipole orientation is observed. We conclude that for our model the simulated ASW films show a negative spontaneous electric field as high as 10⁸–10⁹ V m⁻¹, and consequently a negative surface potential, V (h), is found which grows approximately linearly with height in the film (h). The calculated field becomes smaller as the substrate temperature rises and finally falls to zero at T_s ≥ 110 K, which is in agreement with the experimental observations.^5,6 Still, there is certainly room for much improvement. For instance, we have used a simple model of the water potential where the molecular dipole moment is fixed. Therefore, non-linear effects arising from changes in the molecular dipole moment on condensation are neglected.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has in part been funded by the European Community FP7-ITN Marie-Curie Programme (LASSIE project, grant agreement no. 238258) and in part by the Swedish Research Council grant number 2020-05293. This article/publication is based upon work from COST Action CM1401 “Our Astrochemical History”, supported by COST (European Cooperation in Science and Technology). The computations involved the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through Grant No. 2018-05973.

References

1. D. Field, O. Plekan, A. Cassidy, R. Balog, N. C. Jones and J. Dunger, Int. Rev. Phys. Chem., 2013, 32, 345–392.
2. R. A. Baragiola, Planet. Space Sci., 2003, 51, 953–961.
3. A. Tielens, Rev. Mod. Phys., 2013, 85, 1021.
4. M. Iedema, M. Dresser, D. Doering, J. Rowland, W. Hess, A. Tsekouras and J. Cowin, J. Phys. Chem. B, 1998, 102, 9203–9214.
5. C. Bu, J. Shi, U. Raut, E. H. Mitchell and R. A. Baragiola, J. Chem. Phys., 2015, 142, 134702.
6. R. Sagi, M. Akerman, S. Ramakrishnan and M. Asscher, J. Chem. Phys., 2020, 153, 144702.
7. R. Balog, P. Cicman, D. Field, L. Feketeová, K. Hoydalsvik, N. C. Jones, T. A. Field and J.-P. Ziesel, J. Phys. Chem. A, 2011, 115, 6820–6824.
8. J. Lasne, A. Rosu-Finsen, A. Cassidy, M. R. McCoustra and D. Field, Phys. Chem. Chem. Phys., 2015, 17, 30177–30187.
9. A. Cassidy, R. L. James, A. Dawes and D. Field, ChemistryOpen, 2020, 9, 983.
10. A. Rosu-Finsen, J. Lasne, A. Cassidy, M. R. McCoustra and D. Field, Astrophys. J., 2016, 832, 1.
11. C. Kexel and A. V. Solov’yov, Eur. Phys. J. D, 2021, 75, 1–12.
12. R. Balog, P. Cicman, N. Jones and D. Field, Phys. Rev. Lett., 2009, 102, 073003.
13. M. Roman, A. Dunn, S. Taj, Z. G. Keolopile, A. Rosu-Finsen, M. Gutowski, M. R. McCoustra, A. M. Cassidy and D. Field, Phys. Chem. Chem. Phys., 2018, 20, 29038–29044.
14. U. Essmann and A. Geiger, J. Chem. Phys., 1995, 103, 4678–4692.
15. J. L. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505.
16. I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911–1918.
17. T. Loerting and N. Giovambattista, J. Phys.: Condens. Matter, 2006, 18, R919.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00360k

‡ In the standard model of spontelectrics, the field is constant in the film with respect to the height above the substrate¹, while in our case it varies somewhat in magnitude but we still refer to this as a spontelectric effect.

---