Theoretical study of the NO₃ radical reaction with CH₂ClBr, CH₂ICl, CH₂BrI, CHCl₂Br, and CHClBr₂

Abstract

The potential reaction of the nitrate radical (NO₃), the main nighttime atmospheric oxidant, with five alkyl halides, halons (CH₂ClBr, CH₂ICl, CH₂BrI, CHCl₂Br, and CHClBr₂) has been studied theoretically. The most favorable reaction corresponds to a hydrogen atom transfer. The stationary points on the potential energy surfaces of these reactions have been characterized. The reactions can be classified into two groups based on the number of hydrogen atoms in the halon molecules (1 or 2). The reactions with halons with only one hydrogen atom show more exothermic profiles than those with two hydrogen atoms. In addition, the kinetics of the reaction of NO₃ + CH₂BrI was studied in much higher detail using a multi-well Master Equation solver as a representative example of the nitrate radical reactivity against these halocarbons. These results indicate that the chemical lifetime of the alkyl halides would not be substantially affected by nitrate radical reactions, even in the case of NO₃-polluted atmospheric conditions.

---

1. Introduction

While the hydroxyl radical (OH) is the main oxidant in the sunlit atmosphere, the nitrate radical (NO₃), which rapidly photolyzes during daytime, is the dominant atmospheric oxidant at night.¹ The importance of the nitrate radical in the chemistry of the nocturnal atmosphere has led to many studies of its gas-phase reaction and mechanisms with hundreds of inorganic and organic species^1–6 (and references therein).

The emission of halogen-containing organic compounds from the ocean into the atmosphere, and their subsequent chemistry, has for decades been of interest due to the role of these species in atmospheric ozone destruction.^7,8 The main atmospheric removal processes of alkyl halides include their reaction with OH and photolysis^3,9 while the nighttime chemistry of many of these organohalogens is less well understood. Assessment of the atmospheric impact of these species requires knowledge of the reaction rates and mechanisms of their degradation chemistry during both the day and at night. Here, the reactivity of NO₃ with five alkyl halides, halons (CH₂ClBr, CH₂ICl, CH₂BrI, CHCl₂Br, and CHClBr₂), is studied using ab initio computational methods. These halons have atmospheric lifetimes ranging from hours to days. Their atmospheric degradation leads to the release of very reactive halogen atoms, which initiate catalytic ozone destruction cycles both in the troposphere and the stratosphere.

The three potential reactions indicated in Scheme 1 are considered for the five alkyl halides. In the first reaction (I), there is a hydrogen transfer from the alkyl halide towards the NO₃ radical with the formation of nitric acid (HNO₃). In the second reaction (II), a halogen atom is transferred with the formation of halo-nitrate derivatives. In the last equation process (III), a S_N2 type reaction happens with formation of a methyl nitrate derivative and a halogen radical.

Scheme 1 Potential reactions of the halons with NO₃. In this study, X and Y atoms are halogens (Cl, Br and I) and Z can be a halogen or a hydrogen atom.

2. Computational methods

The geometry of the minima and transition states (TS) has been obtained at the UM08HX/6-311+G(2df,2p) computational level^10,11 with the Gaussian-16 package.¹² For the iodine atom, the effective core potential Def2-TZVP basis set has been used.¹³ Frequency calculations at the same level were performed to confirm that the structures found correspond either to a minimum (no imaginary frequencies) or a true TS (only one imaginary frequency), and to compute the thermodynamic corrections to the electronic energy at room temperature (298.15 K). For all the TSs, intrinsic reaction coordinate (IRC) calculations were carried out to confirm the two minima connected along the TS.

The UM08HX/6-311+G(2df,2p) computational level has been shown to provide excellent performance when compared to the balanced multicoefficient method based on coupled cluster theory with single and double excitations (BMD-CCSD) computational level in the description of TSs and radical reactions.^14,15 In addition, we have compared the results obtained by Bai et al.¹⁶ at the CCSD(T)//B3LYP level of theory for the pathways yielding CH₂I + HNO₃ with those obtained at M08HX and DLPNO-CCSD(T)/M08HX levels used here, showing that in the last case a better agreement with the experimental data would be attained [see Table S1 of the ESI†].

The potential complexes formed by the pre-reactive molecules and the products were explored using a combination of meta-dynamics, molecular mechanism and optimizations with the CREST program.¹⁷ The unique minima provided by the CREST method were then used as a starting point for additional optimization with the UM08HX/6-311+G(2df,2p) computational level. The resulting geometries were compared in order to remove repeated minima and ranked based on their energy.

The binding energy of the complexes has been calculated as the electronic energy difference between the complexes and the isolated optimized monomers. No zero point energy correction has been taken into account for the computation of this parameter and the potential energy surfaces.

The molecular electrostatic potential (MESP) was calculated with Gaussian-16. The Multiwfn program¹⁸ has been used to locate the extreme (maxima and minima) of the MESP function on the 0.001 a.u. electron density isosurface. The MESP and the extreme values have been represented with the Jmol program.¹⁹

The electron density of the systems was analyzed within the quantum theory of atoms in molecules (QTAIM)^20,21 theory with the AIMAll program.²² The analysis of the electron density shows points of null gradient that can be classified based on the sign of their curvature in nuclear attractors (3, −3), bond critical (3, −1), ring critical (3, +1) and cage critical points (3, +3). The value of the second derivative (i.e., the Laplacian), of the bond critical points provides important information regarding the nature of the interaction i.e. covalent or weak interaction.

The kinetics of each pathway and the rate coefficient of the NO₃ + CH₂BrI reaction were calculated using the Master Equation Solver for Multi-Energy well Reactions (MESMER) program.²³ Each intermediate species formed during the reaction was assumed to dissociate back to the reactants or forward to the products, or be stabilized by collision with the N₂ third body. The internal energy of each intermediate was divided into a contiguous set of grains (width = 70 cm⁻¹) containing a bundle of rovibrational states. The density of these states was calculated using the theoretical vibrational frequencies and rotational constants, without making a correction for anharmonicity and using a classical treatment for the rotational modes.²⁴ Reaction across the barrier between the pre- and post-reaction complexes involves an H-atom transfer, and so an Eckart tunneling correction (with an asymmetric barrier) was applied to the rate calculated using Rice–Ramsperger–Kassel–Markus (RRKM) theory.²³

Each grain was then assigned a set of microcanonical rate coefficients for dissociation to reactants or products (as appropriate), which were determined using inverse Laplace transformation to link them directly to the corresponding capture rate coefficients.²³ The capture rate coefficient for NO₃ + CH₂BrI was calculated using long-range transition state theory.²⁵ In this case the dispersion force dominates over the dipole–dipole and dipole-induced dipole forces; the C₆ coefficient was estimated using the London formula with theoretical ionization energies [IE(NO₃) = 13.7 eV; IE(CH₂BrI) = 9.25 eV] and volume polarizabilities [α(NO₃) = 5.15 × 10⁻³⁰ m³; α(CH₂BrI) = 12.5 × 10⁻³⁰ m³] determined in the present study. The resulting capture rate coefficient, increased by a factor of 1.3 to account for the less significant forces,²⁵ is 8.1 × 10⁻¹⁰ exp(−400/T) cm³ molecule⁻¹ s⁻¹. The capture rate coefficient of HNO₃ + CHBrI (which is required to compute the dissociation rates of the post-reaction complexes to the products) was set to 7.0 × 10⁻¹⁰ exp(−400/T) cm³ molecule⁻¹ s⁻¹.

The probability of collisional transfer between grains was estimated using the exponential down model.²⁴ The average energy for downward transitions, 〈ΔE〉_down, was set to 300 cm⁻¹ for N₂ with a slight positive temperature dependence.²⁴ The probabilities for upward transitions were determined by detailed balance.^24,26 The Master Equation, which describes the evolution with time of the adduct grain populations, was then expressed in matrix form and solved to yield the rate coefficients for bimolecular reaction to HNO₃ + CHBrI, and/or recombination to the pre- or post-reaction complexes, at a specified pressure (1 bar) and temperature (230–400 K).

3. Results and discussion

This section is divided into six parts. The first one presents and analyzes the results of the entrance and exit channels of all the potential reactions between NO₃ and the five alkyl halides molecules (hydrogen and halogen transfer and S_N2 reaction). The next three parts are devoted to the hydrogen transfer, detailing the results of the pre-reactive complexes, the post-reaction complexes and finally the TS structures. The fifth part deals with the S_N2 reaction and the last part will consider the kinetics of the representative reaction, NO₃ + CH₂BrI, as is further discussed below.

3.1. Entrance and exit channel energies

In the first step of this study, the energies of the entrance and exit channels were computed as the sum of the energies of the isolated reactant (or product) molecules. In Table 1, the electronic energies to the three exit channels for each reaction are listed with respect to the energy of the entrance channel. The analogous ΔG values are listed in Table S2 (ESI†).

Table 1 Relative electronic energy of the exit channel energy (kJ mol⁻¹)

Reaction^a	CH2ClBr:NO3	CH2ClI:NO3	CH2BrI:NO3	CHCl2Br:NO3	CHClBr2:NO3
a See Scheme 1. b The X halogen that forms the NO3X molecule is the lighter of the halogens in the molecule. c The X halogen that forms the NO3X molecule is the heaviest of the halogens in the molecule. d The X (radical) formed corresponds to the lighter halogen in the molecule. e The X (radical) formed corresponds to the heaviest halogen in the molecule.
I	−58.2	−57.1	−53.6	−74.0	−73.4
II^b	140.5	140.2	121.7	113.7	114.7
II′^c	118.5	60.0	63.7	91.4	92.4
III^d	−39.6	−37.2	−80.9	−37.5	−32.8
III′^e	−84.4	−151.6	−150.4	−84.9	−84.4

---

From the values listed in Table 1 and Table S5 (ESI†), it is clear that the hydrogen transfer from the alkyl halides towards NO₃ (Reaction I, Scheme 1) and the S_N2 attack of NO₃ to the halon (Reaction III, Scheme 1) are favorable exothermic processes while the halogen transfer (Reaction II, Scheme 1) is endothermic in all cases. These results are a consequence of the balance between the strength of the bonds that are broken and formed. It is clear that the NO₃–H bond is much stronger than the C–H in the halons while the opposite is the case between the NO₃–X and C–X bonds, in agreement with the available experimental bond dissociation energies (Table S3, ESI†). In the same way, the CH bond of those halons with three halogen atoms (CHCl₂Br and CHClBr₂) is more acid than the CH bond of those with only two halogens (CH₂ClBr, CH₂ClI and CH₂BrI); consequently, the hydrogen transfer is more favorable in the former case than the latter one. The relative energy of the exit channel in Reaction III depends on the leaving halogen atom. Values around −37 kJ mol⁻¹ are found when chlorine is the leaving halogen, −84 when it is bromine and −150 when it is iodine. Based on these results, the rest of the present work will be focused on the study in detail of the species involved in the hydrogen transfer and on the S_N2 attack of NO₃ to the halon.

3.2. Pre-reactive complexes

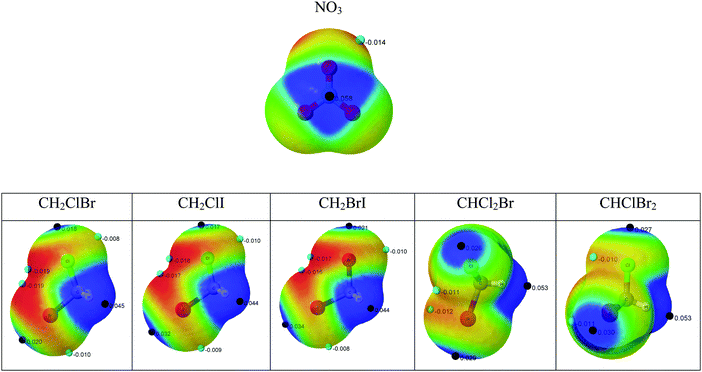
The formation of non-covalent complexes is driven initially by the electrostatic potential of the molecules involved. The complexes formed usually correspond to the closed contact of complementary charged regions in the molecules. For this reason, the molecular electrostatic potential has been calculated for all the reactants and plotted on the 0.001 a.u. electron density surface, which corresponds to an approximated van der Waals volume description of the molecules (Fig. 1).

Fig. 1 Molecular electrostatic potential (MESP) on the 0.001 a.u. electron density surface. The blue and red colors indicate values of MESP > +0.015 and < −0.015 au, respectively. The location of the MESP maxima and minima are identified with black and light blue dots, respectively, and their values are indicated in a.u.

The molecular electrostatic potential (MESP) results in the NO₃ (radical) present positive regions above and below the nitrogen atom with a maximum value of 0.058 a.u. and negative regions corresponding to the lone pairs of the oxygen atoms (−0.014 a.u.). The halon molecules show positive values associated to the hydrogen atoms and in the extension of the C–X bonds (σ-hole).²⁷ In all cases, the positive values associated with the hydrogen atoms are larger than those associated with the halogen σ-hole. The two systems with three halogen atoms show more positive values around the H atoms (0.053 au) than those with only two halogens (0.045 au), in agreement with previous reports indicating the increasing acidity of the C–H bond with the number of halogen atoms in the methane derivatives.²⁸ Negative regions are found associated with the lone pairs of the halogen atoms.

The CREST method provides between 7 and 18 conformers for each of the pre-reactive complexes. The number of unique conformers is reduced to 6 when they are re-optimized using the M08-HX method. The molecular graphs of the most stable conformation for each complex are shown in Fig. 2, and all of them are listed in Table S4 (ESI†).

Fig. 2 Molecular graph of the most stable conformation of the pre-reactive complexes studied for each reaction. The locations of the bond (BCP), ring (RCP) and cage critical points (CCP) are indicated with small green, red and blue spheres, respectively. The calculated electronic binding energy with respect to the reactants for each complex is also shown.

The pre-reactive complexes show modest binding energies, the most stable complexes for each case yield binding energies between −33 and −20 kJ mol⁻¹ (Table 2). In the case of the relative free energies, the values obtained are positive (approximately +54 kJ mol⁻¹ at 298 K) (Table S5, ESI†) due to the effect of the entropy. The presence of iodine enhances the capability of the systems to form complexes with NO₃. Thus, the strongest complexes of CH₂ClI and CH₂BrI yield binding energies of −33 kJ mol⁻¹, while for the other halocarbons they are between −21 and −20 kJ mol⁻¹.

Table 2 Number of conformers using the CREST method and reoptimization with M08-HX. The binding energy (kJ mol⁻¹) of the most stable for each complex is indicated

	CH2ClBr:NO3	CH2ClI:NO3	CH2BrI:NO3	CHCl2Br:NO3	CHClBr2:NO3
a Most stable conformer in each complex.
# Conformers CREST	18	9	7	7	8
# Conformers M08-HX	6	6	6	6	6
E b	−21.7	−32.6	−32.7	−20.3	−20.3

---

The disposition of the molecules in the pre-reactive complex minima and the AIM analysis (Table S4, ESI†) indicate that in the most stable conformation the two molecules are mainly attracted by the interaction between the oxygen atoms of NO₃ and the halogen and hydrogen atoms of the halons. In general, a large variety of interactions are observed in the minima found as tetrel bonds^29–32 between the lone pair of the oxygen atoms of NO₃ and the carbon atom of the halons, and pnicogen bonds^33–35 between the lone pairs of the halogens and the nitrogen of NO₃. It is interesting that in the complexes with iodine, all the minima show intermolecular bond critical points between the iodine atom and one of the oxygen atoms of NO₃.

3.3. Hydrogen transfer TS

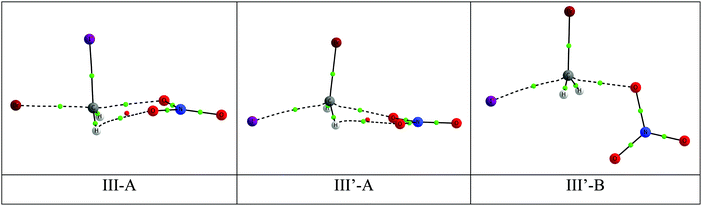
For each halon, two or three TS conformers of the hydrogen transfer have been characterized depending on the variety of substituents on the halon molecule. The three TS conformers of the NO₃:CH₂BrI systems are shown in Fig. 3 and for all the systems in Table S6 of the ESI.† The geometries of the TS are characterized by a C–H⋯O disposition that is close to linear, with angles between 171 and 177°. There is a near-linear inverse correlation between the C–H and the O⋯H distances in the TS structures (Fig. S1, ESI†).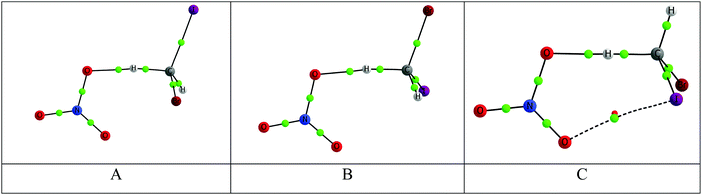

Fig. 3 Molecular graph of the three TS conformers of the hydrogen transfer NO₃ + CH₂BrI reaction. The location of the BCPs and RCPs are indicated with small green and red dots, respectively.

The relative energies of these TSs are given in Table 3 and Table S5 (ESI†). In general, the relative electronic energies are between +12 and +17 kJ mol⁻¹ with respect to the entrance channel. In the case of the relative free energies, the values obtained are around +55 kJ mol⁻¹ at 298 K.

Table 3 Relative electronic energy (kJ mol⁻¹) of the hydrogen transfer TS with respect to the entrance channel

Conformer	NO3:CH2ClBr	NO3:CH2ClI	NO3:CH2BrI	NO3:CHCl2Br	NO3:CHClBr2
A	17.3	16.0	14.8	13.8	11.7
B	17.2	15.2	14.2	13.7	11.7
C	16.7	14.7	13.3

---

More detailed analysis shows that the relative electronic energy of the TS (Table 3) decreases as the number and size of the halogen atoms increases. Thus, in the halons with two halogen atoms the lowest barriers are 16.7 > 14.7 > 13.3 for CH₂ClBr, CH₂ClI and CH₂BrI, respectively, compared with 13.7 and 11.7 for CHCl₂Br and CHClBr₂, respectively. In those cases where the halon molecule has two hydrogen atoms, the most stable TS conformer has an H-atom in anti disposition (conformation C in Fig. 3). In addition, for each system the longest C–H distance in the TS corresponds with the smallest barrier.

3.4. Post-reaction complexes of the hydrogen transfer

As in the case of the pre-reactive complexes, the MESP of the isolated components of the products has been analyzed (Fig. S2, ESI†). The NO₃H molecule shows the most positive region associated with the hydrogen atom (0.117 au) and the negative regions correspond to the lone pairs of the oxygen atoms (between −0.018 and −0.032 au). In the case of the halons radical derivatives, the MESP is flatter than the closed shell halons shown in Fig. 1, with smaller maxima and minima. The maxima are associated with the extension of the C–X and C–H bonds opposite to the location of the single electron carbon radical (single electron hole in analogy to the lone pair hole).^36–38 The minima correspond to the lone pairs of the halogen atoms and the single electron carbon radical.

The number of configurations obtained with CREST and further re-optimized with the M08 DFT method is larger than in the case of the pre-reactive complexes (see Table 4). The binding energies of the most stable complex for each halon with NO₃H are very similar, ranging between −22.2 to −23.5 kJ mol⁻¹. Thus, the energy of the complexes formed is almost independent of the halogen atoms present in the halons.

Table 4 Number of conformers using the CREST method followed by re-optimization with M08-HX. The binding energy and relative energy with respect to the entrance channel (kJ mol⁻¹) of the most stable for each complex is indicated

	CHClBr:NO3H	CHClI:NO3H	CHBrI:NO3H	CCl2Br:NO3H	CClBr2:NO3H
a Most stable conformer of each complex.
# Conform CREST	15	39	72	24	20
# Conform M08-HX	12	20	35	20	13
E b	−23.0	−22.4	−23.5	−22.2	−22.8
E rel entrance channel^a	−81.3	−79.5	−77.4	−96.2	−96.2

---

The molecular graphs of the most stable configurations of each conformer are shown in Fig. 4, and their molecular parameters are listed in Table S7 (ESI†). In the two most stable minima for each complex, three common features are observed: an OH⋯X hydrogen bond, an oxygen–X interaction and a tetrel bond with the single electron hole (O⋯C interaction). In the rest of the conformations, other interactions such as weak CH⋯O hydrogen bonds, pnicogen O⋯N and OH⋯C bonds are observed.

Fig. 4 Molecular graph of the most stable conformation of each complex upon hydrogen transfer. The binding energies with respect to the isolated monomers are indicated.

The potential and free energies of these complexes are negative with respect to the entrance channel (Table 4, Table S5 (ESI†) and Fig. 5). In general, the systems can be divided in two groups, those with a hydrogen atom in the resulting radical of the halon and those without it. In the former, the energies are smaller in absolute value than in the latter ones. Thus, the relative electronic energies of the most stable conformers of NO₃H:CHClBr, NO₃H:CHClI and NO₃H:CHBrI complexes are between −77 and −81 kJ mol⁻¹ while those of NO₃H:CCl₂Br and NO₃H:CClBr₂ are −96 kJ mol⁻¹. Something similar occurs with the free energies that are around −33 and −45 kJ mol⁻¹ at 298 K, for the two families of complexes mentioned before.

Fig. 5 Profiles of the relative electronic energy (left-hand panel) and Gibbs energy (right-hand panel) for the NO₃ + CH₂BrI (black) and NO₃ + CHCl₂Br (blue) reactions.

3.5. S_N2 reaction

For each halogen atom in the halon, two TS conformers of the S_N2 reaction have been characterized, except for NO₃:CH₂ClI and NO₃:CH₂BrI reactions where the leaving halogen is the lightest one (Cl and Br, respectively) where the different conformers tried converged to a single one (Table 5). The three TSs located in the NO₃:CH₂BrI reaction are gathered in Fig. 6 and for the rest of the systems in Table S8 (ESI†).

Table 5 Relative electronic energy (kJ mol⁻¹) of the S_N2 TS with respect to the entrance channel

Reaction/conformer	NO3:CH2ClBr	NO3:CH2ClI	NO3:CH2BrI	NO3:CHCl2Br	NO3:CHClBr2
a The X (radical) formed corresponds to the lighter halogen in the molecule. b The X (radical) formed corresponds to the heaviest halogen in the molecule.
III-A^a	170.0	120.3	96.4	182.2	185.7
III-B^a	145.8	—	—	175.4	179.0
III′-A^b	150.5	69.5	74.1	161.1	164.6
III′-B^b	108.3	118.6	70.8	153.3	139.2

---

Fig. 6 Molecular graph of the three TS conformers of the S_N2 reaction between NO₃ and CH₂BrI.

In all cases, the reactions where the leaving group is the largest halogen atom show smaller barriers than when it is the smaller halogen atom. In any case, the calculated barriers for these reactions are much larger than the corresponding for the hydrogen transfer previously mentioned. The smaller differences are for the NO₃:CH₂ClI and NO₃:CH₂BrI reactions where the S_N2 reaction barriers that produce iodine radical atom are 55 and 58 kJ mol⁻¹ larger than the corresponding hydrogen transfer. Thus, even though the product of these reactions (Table S9, ESI†) is more stable than in the hydrogen transfer process, the larger difference in the barrier should favor the hydrogen transfer path in kinetic conditions as those found in the atmosphere.

3.6. Kinetics of the NO₃ + CH₂BrI reaction

We selected the NO₃ + CH₂BrI reaction as a representative example for a detailed kinetic study for two reasons: (i) From an atmospheric point of view, there is no shortage of Cl or Br from heterogeneous reactions involving sea-salt particles, but iodine has more limited sources.³⁹ So if this reaction is fast enough, the CHBrI radical that is produced could be a significant source of atmospheric reactive iodine. (ii) The barriers of the hydrogen transfer reaction are relatively low (Table 3).

The hydrogen-atom transfer reaction between NO₃ and CH₂BrI presents three pathways associated with different transition states (A, B and C), as shown in Fig. 3. These involve the formation of a NO₃–CH₂BrI pre-reaction complex, H-atom transfer over a barrier to form a post-reaction complex, followed by dissociation into HNO₃ and CHBrI (Fig. 5). The conformation of the pre-reactive complexes corresponds to those ranked as #1, #5 and #6 in the conformational search detailed in Section 3.2. In the same way, the post-reaction complexes associated with the three pathways are those ranked as #8, #7 and #10 in Section 3.4. The rotational constants and vibrational frequencies of the stationary points on the potential energy surface (i.e. reactants, products and intermediates) used in the MESMER calculation are listed in Table S10 (ESI†).

At a pressure of 1 bar (i.e. at the Earth's surface), recombination to the intermediate complexes does not compete with reaction, even at the lowest temperature of 230 K (−43 °C). This is because the pre-reaction complexes are relatively weakly bound with respect to the reactants (Fig. 5); furthermore, if the reaction does pass over the barrier then the post-reaction complex is unbound with respect to the products, because of the significant exothermicity of the overall reaction. Fig. 7 is an Arrhenius plot of the overall reaction. This shows that pathway C, which has the lowest barrier, contributes 48% to the total reaction rate at the lowest temperature of 230 K. However, at 400 K the contributions from the three pathways are very similar.

Fig. 7 Arrhenius plot of the overall reaction between NO₃ and CH₃BrI at a pressure of 1 bar N₂ and temperatures between 230 and 400 K, illustrating the overall reaction and the contribution from each of the pathways A, B and C.

The overall reaction rate coefficient is given by k (230–400 K) = 1.79 × 10⁻¹³ exp(−1516/T) cm³ molecule⁻¹ s⁻¹. The relatively small pre-exponential factor results from the relatively tight transition states of the three pathways. At 298 K, k = 1.1 × 10⁻¹⁵ cm³ molecule⁻¹ s⁻¹. In a relatively polluted environment where the NO₃ mixing ratio was 50 ppt (i.e. a concentration of 1.2 × 10⁹ cm⁻³),⁴⁰ the lifetime of CH₂BrI due to NO₃ reaction would be 209 hours. This is much longer than the annually averaged tropospheric lifetime (∼4 hours) of this alkyl halide against photolysis lifetime.⁹

4. Concluding remarks

Three potential reactions between NO₃ and a series of halons (CH₂ClBr, CH₂ICl, CH₂BrI, CHCl₂Br, and CHClBr₂) have been studied theoretically. The halogen transfer from the halon to NO₃ is a highly endothermic process. The S_N2 attack of NO₃ to the halon with liberation of a halogen atom is an exothermic process but with high activation barriers. The hydrogen transfer is an exothermic process with low activation barriers yielding HNO₃ and the corresponding halide-radical.

The hydrogen transfer reaction profiles present five generic stationary points:

1. The entrance channel (isolated NO₃ and halon molecule), which we use here as the reference energy level.

2. Several pre-reaction NO₃:Halon complexes which have binding energies for the most stable conformer between −20 and −33 kJ mol⁻¹. Due to the entropic factor these complexes have positive free energies (between +20 and +26 kJ mol⁻¹ at 298 K) with respect to the reactants.

3. Two or three hydrogen transfer TS structures, depending on the substituents of the halons. The electronic barriers with respect to the entrance channel are between +12 and +17 kJ mol⁻¹ while the relative free energies are aproximatively +55 kJ mol⁻¹ at 298 K.

4. Between 12 and 35 conformers of the NO₃H:Halon radical post reaction hydrogen transfer complexes have been characterized. Both, electronic and free energies are negative relative to the entrance channel. The electronic energies are around either −80 or −96 kJ mol⁻¹, depending on whether the resulting halon radical molecules have one or no hydrogen atoms, respectively. The corresponding free energies are around −33 or −45 kJ mol⁻¹ at 298 K.

5. The exit channel (isolated HNO₃ and halon radical) also show negative values of electronic and free energy with respect to the entrance channel. The electronic energies are about 23 kJ mol⁻¹ lower than the post-reaction complexes: around −57 or −74 kJ mol⁻¹ for the halons with two or one H atoms, respectively, and the relative free energies are around −52 or −68 kJ mol⁻¹ at 298 K.

Our results show that NO₃-mediated oxidation of CH₂ClBr, CH₂ICl, CH₂BrI, CHCl₂Br, and CHClBr₂ in the atmosphere will not compete with other atmospheric removal processes, predominately photolysis and reaction with OH.

Author contributions

A. S.-L. and I. A. devised research. I. A. performed the calculations. J. M. C. P. carried out the MESMER calculations. I. A., J. M. C. P., J. E., J. Z. D., A. U. A., and A. S.-L. analysed data. I. A. wrote the paper with contributions from all authors.

Conflicts of interest

The authors declare that they have no conflict of interest.

Acknowledgements

IA: This work was carried out with financial support from the Ministerio de Ciencia, Innovación y Universidades (PGC2018-094644-B-C22) and Comunidad de Madrid (P2018/EMT-4329 AIRTEC-CM). Thanks are also given to the CTI (CSIC) for their continued computational support. This study received funding from the European Research Council Executive Agency under the European Union's Horizon 2020 Research and Innovation Programme (Project ERC-2016-COG 726349 CLIMAHAL).

References

1. R. P. Wayne, I. Barnes, P. Biggs, J. P. Burrows, C. E. Canosa-Mas, J. Hjorth, G. Le Bras, G. K. Moortgat, D. Perner, G. Poulet, G. Restelli and H. Sidebottom, Atmos. Environ., Part A, 1991, 25, 1–203.
2. S. W. North, Nat. Chem., 2011, 3, 504–505.
3. J. B. Burkholder, S. P. Sander, J. Abbatt, J. R. Barker, C. Cappa, J. D. Crounse, T. S. Dibble, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, C. J. Percival, D. M. Wilmouth and P. H. Wine, JPL Publication 19-5, Jet Propulsion Laboratory, Pasadena, 2019 http://jpldataeval.jpl.nasa.gov, 2019.
4. Q. Li, R. Borge, G. Sarwar, D. de la Paz, B. Gantt, J. Domingo, C. A. Cuevas and A. Saiz-Lopez, Atmos. Chem. Phys., 2019, 19, 15321–15337.
5. A. S. Mahajan, H. Oetjen, A. Saiz-Lopez, J. D. Lee, G. B. McFiggans and J. M.-C. Plane, Geophys. Res. Lett., 2009, 36, L16803.
6. A. Saiz-Lopez, R. P. Fernandez, C. Ordóñez, D. E. Kinnison, J. C. Gómez Martín, J. F. Lamarque and S. Tilmes, Atmos. Chem. Phys., 2014, 14, 13119–13143.
7. WMO (World Meteorological Organization), Scientific Assessment of Ozone Depletion: 2014, Geneva, Switzerland, 2014.
8. A. Saiz-Lopez, J. F. Lamarque, D. E. Kinnison, S. Tilmes, C. Ordóñez, J. J. Orlando, A. J. Conley, J. M.-C. Plane, A. S. Mahajan, G. Sousa Santos, E. L. Atlas, D. R. Blake, S. P. Sander, S. Schauffler, A. M. Thompson and G. Brasseur, Atmos. Chem. Phys., 2012, 12, 3939–3949.
9. C. Ordóñez, J. F. Lamarque, S. Tilmes, D. E. Kinnison, E. L. Atlas, D. R. Blake, G. Sousa Santos, G. Brasseur and A. Saiz-Lopez, Atmos. Chem. Phys., 2012, 12, 1423–1447.
10. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868.
11. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
12. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Journal, 2016.
13. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
14. X. Xu, I. M. Alecu and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 1667–1676.
15. L. G. Gao, J. Zheng, A. Fernández-Ramos, D. G. Truhlar and X. Xu, J. Am. Chem. Soc., 2018, 140, 2906–2918.
16. F.-Y. Bai, X. Wang, Y.-Q. Sun and X.-M. Pan, RSC Adv., 2015, 5, 88087–88095.
17. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
18. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
19. Jmol: An Open-Source Java Viewer for Chemical Structures in 3D, available online at: http://www.jmol.org/.
20. R. F.-W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990.
21. P. L.-A. Popelier, Atoms In Molecules. An introduction, Prentice Hall, Harlow, England, 2000.
22. T. A. Keith, Journal, 2019 Version (aim.tkgristmill.com).
23. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
24. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell, Oxford, 1990.
25. Y. Georgievskii and S. J. Klippenstein, J. Chem. Phys., 2005, 122, 194103.
26. D. R. Glowacki, C.-H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
27. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
28. I. Alkorta and S. Maluendes, J. Phys. Chem., 1995, 99, 6457–6460.
29. I. Alkorta, I. Rozas and J. Elguero, J. Phys. Chem. A, 2001, 105, 743–749.
30. A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321.
31. S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 1824–1834.
32. S. Scheiner, Phys. Chem. Chem. Phys., 2021, 23, 5702–5717.
33. S. Scheiner, J. Chem. Phys., 2011, 134, 164313.
34. S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem. – Eur. J., 2011, 17, 6034–6038.
35. J. E. Del Bene, I. Alkorta and J. Elguero, in Noncovalent Forces, ed. S. Scheiner, Springer International Publishing, Cham, 2015 DOI:10.1007/978-3-319-14163-3_8, pp. 191–263.
36. F. Blanco, I. Alkorta, I. Rozas, M. Solimannejad and J. Elguero, Phys. Chem. Chem. Phys., 2011, 13, 674–683.
37. A. Bauzá, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2016, 17, 1608–1614.
38. M. A.-A. Ibrahim and E. M.-Z. Telb, ACS Omega, 2020, 5, 21631–21640.
39. A. Saiz-Lopez, J. M.-C. Plane, A. R. Baker, L. J. Carpenter, R. von Glasow, J. C. Gómez Martín, G. McFiggans and R. W. Saunders, Chem. Rev., 2012, 112, 1773–1804.
40. S. S. Brown and J. Stutz, Chem. Soc. Rev., 2012, 41, 6405–6447.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00021k

---