Pyridine interaction with γ-CuI: synergy between molecular dynamics and molecular orbital approaches to molecule/surface interactions

Abstract

We have used a synergistic computational approach merging Molecular Dynamics (MD) simulations with density functional theory (DFT) to investigate the mechanistic aspects of chemisorption of pyridine (Py) molecules on copper iodide. The presence of both positive and negative ions at the metal halide surface presents a chemical environment in which pyridine molecules may act as charge donors and/or acceptors. Computational results reveal that Py molecules interact with the γ-CuI(111) surface owing to a combination of noncovalent Cu⋯N, Cu/I⋯π/π*, and hydrogen bonding interactions as determined via Natural Bonding Orbitals (NBO). Introduction of surface defect sites alters the interaction dynamics, resulting in a “localizing effect” in which the Py molecules clump together within the defect site. Significant enhancement of hydrogen bonding between C–H σ* and I 6p orbitals results in more tightly surface-bound Py molecules. Our findings provide a platform for understanding the interaction between Py and Py-derivative vapors and metal-based surfaces that contain both electron acceptor and donor atoms.

---

Introduction

Next-generation smart materials exhibit observable and rapid responses to target compounds or classes of compounds in the environment. The response of such sensor materials may arise due to either physical or chemical interaction, ranging from chemisorption, to solventochromism, to reversible or irreversible bonding.^1–3 The response may be electrochemical, such as a change in voltage or conductivity, or it may be spectral, such as a visible color change, or either the enabling or quenching of luminescence behavior.

Transition metal d¹⁰ centers offer a particularly wide range of chemical and photophysical behaviors that can potentially be leveraged for use as smart materials in chemical detection. Chemically speaking, d¹⁰ ions such as Cu(I), Ag(I), and Au(I) exhibit flexible coordination spheres ranging from 2- to 4-coordination with no crystal field preferences. They readily form metal–organic polymers and other networks with bridging ligands, leading to a diverse family of materials.^4–8 They also exhibit strong chemical bonding preferences for soft ligands such as aromatic nitrogen, sulfur and phosphorus nucleophiles which constitute a wide range of industrial, military, and medically relevant compounds. In terms of their photophysical characteristics, d¹⁰ complexes tend to be photoemissive and are known to exhibit metal-centered (e.g. d → p), cluster-centered (e.g. in halometallates), metal-to-ligand charge transfer, and halide-to-ligand charge transfer transitions.^9,10 In many instances, a single chromophore will show more than one of these behaviors, with observed intensity and/or wavelength depending upon solvent, temperature, or exposure to chemical agents resulting in a unique spectroscopic signature. The foregoing chemical and photophysical diversity and flexibility has spurred investigations of d¹⁰ systems as biosensors, chemical sensors and optical sensors.^11–13

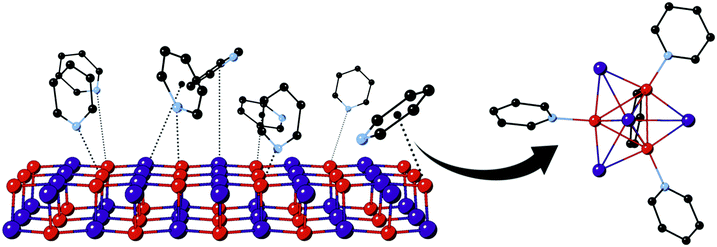
We have previously reported on the conversion of solid γ-CuI upon exposure to gaseous pyridine (Py) to emissive [CuI]₄Py₄ and are currently studying the applications of this reaction for chemical sensors.¹⁴ The solid transformation of zinc blende lattice γ-CuI into discrete [CuI]₄Py₄ clusters involves substantial chemical reorganization, as illustrated in Scheme 1; nevertheless, it appears to occur relatively quickly – on the minutes time scale. Surface bonding of Py is almost certainly involved in the process, as suggested in the scheme. Nevertheless, the nature of that bonding is unclear, and questions remain surrounding the involvement of the nitrogen lone pair as well as aromatic π-electron systems, especially given the soft character of both Cu(I) and iodide ions. Many reports have focused on nucleophilic molecule interactions with elemental Cu, Ag, and Au surfaces or nanoclusters.^15–20 Consideration of metal halides, such as CuI, introduces the possibility of additional interactions associated with the potentially electron-accepting, yet relatively electron-rich, metal ions as well as electron-donating halide centers. For example, a previous density functional theory (DFT) study of Py (along with benzene and thiophene) adsorption to Cu(111) surface confirmed the experimental result that Py molecules lie flat along the metal surface,^21,22 rather than upright as suggested in Scheme 1. Importantly, no experimental or computational studies have yet addressed the chemisorption behavior of Py on the more electronically complex CuI surfaces.

Scheme 1 Envisioned reaction of Py (g) with γ-CuI (s) to form [CuI]₄Py₄ (s).

Our recent computational study on the interaction of dimethyl sulfide (Me₂S) vapor with γ-CuI demonstrated that this nucleophile was able not only to adsorb to the Ag(I)-doped CuI surface, but ultimately to embed itself into the solid.²³ Nevertheless, the relatively simple Lewis base Me₂S is distinctly different from Py, which offers additional reactivity through its π-electrons, including possible acceptor behavior. Interestingly, in the case of Me₂S, Ag(I) doping was shown to open up the CuI lattice, making it more subject to nucleophile embedding. As part of that study, we highlighted the value of “atomistic” molecular dynamics studies to produce small molecule-surface ensemble models at relatively little computational expense. These rather large models can include hundreds of vapor molecules interacting on CuI slabs >5 nm in thickness. Specific interactions uncovered by MD may then be examined in detail by trimming the ensemble and then re-examining it in molecular orbital studies using DFT.

In this contribution we expand on the synergism between these complimentary computational techniques, this time studying a more complex system wherein the orientation of the nucleophile (Py) is chemically non-trivial. We show that the atomistic approach, which considers only dipole–dipole interactions, offers computationally inexpensive models that can be used in computationally demanding single-point DFT orbital calculations. DFT modeling allowed us to examine CuI–Py interactions according to electrostatic potentials (ESPs) between polarized species and charge-transfer perspectives via natural bond orbitals (NBO). The Py plane-to-surface bonding angle is investigated and optimized according to bonding strength and distance. Additionally, using a feed-back loop between atomistic and DFT models, we have constructed a comprehensive model for the behavior of Py at the γ-CuI (111) surface. Our findings show that, while the charge transfer from the N lone electron pair to the empty Cu 4s are the strongest interactions, they are not the sole driving force in the geometric orientation of the Py molecule with respect to the surface. Instead a combination of π/π* orbitals interacting with Cu 4s and I 6p atomic orbitals, as well as hydrogen bonding with I 6p orbitals, give rise to strong adsorption of Py molecules to the surface. Using Py as a model molecule, this study represents a milestone in terms of the comprehensiveness and rigor in the analysis of supramolecular assembly and tuning of CuI-based photoemissive materials.

Computational methods

Molecular dynamics simulations

Molecular Dynamics (MD) calculations were performed with the NANIM simulation program.²⁴ MD simulations were performed in the NVT ensemble with a time step of 2 fs and an equilibration period of 100 ps. The temperature was set to 298 K via the velocity-rescaling thermostat (coefficient = 0.01 ps).²⁵ Surface slab generation was performed with the zinc blende structure for copper iodide (assuming a cubic lattice parameter of 0.620 nm). The slab had two-dimensional periodicity with dimensions of 5.2609 × 5.3127 nm. The slab depth was ∼5.1 nm, with the top surface layer being a (111) face made up of cations and the bottom surface layer being a (111) face made up of anions. The surface described thus far was used in the simulations of a pyridine monolayer interacting with an ideal surface. Additionally, simulations were performed for a kinked surface, as well as a surface containing a variably sized “crater.” To create a kinked surface from an ideal surface, first a terrace was generated along the cation-terminated surface by removing one ∼2.3 nm wide layer of metal-iodide pairs (see Fig. 1). Second, half of the metal-iodide pairs located along the upper part of the surface steps were removed in order to create kink sites. To alternatively create a one-layer deep crater on an ideal surface, one, two, four, or eight metal-iodide pairs were removed from the center of both the top surface layer and the bottom surface layer. After surface construction was completed, seventy Py molecules were distributed along the top surface layer. Two stationary walls confine this system along the non-periodic dimension. One wall (wall A) was placed well above the Py monolayer, and a second wall (wall B) was placed well underneath the (111) anion-terminated surface of the slab. The atomic interaction model consists of Coulombic, Lennard-Jones, and Vashishta-Rahman interactions for the intermolecular potential and harmonic stretching/bending terms for the intramolecular potential.^26–32 Details of the interaction potential were largely described in our previous work.²³ Additionally, the effective atomic charges assigned to carbon, nitrogen, and hydrogen (which we derived from DFT calculations of APT charges for a Py molecule interacting with a CuI cluster, via the LANL2dz basis set) were +0.0129, −0.3166, and +0.0632, respectively. System walls were assigned the following Lennard-Jones potential parameters: A = 90.415 eV Å⁻⁹ and B = 0.39459 eV Å⁻³ for wall A; A = 90.415 eV Å⁻⁹ and B = 3.9459 eV Å⁻³ for wall B.

Fig. 1 Atomistic model for the kinked (111) copper iodide surface. This surface model is used to assess the interaction of the pyridine monolayer with copper(I) iodide substrate. Image made with VMD.³³

Density functional theory

Density functional theory (DFT) calculations were performed using the Gaussian16 software program.³⁴ Method validation was performed utilizing the well-known CuI cubane compound [CuI]₄Py₄ and the M06³⁵ or B3LYP^36,37 functionals paired with the cep-121G(d),^38–41 LANL2dz,^42,43 def2tzvp/6-311+g(d,p),^44–47 or aug-cc-pvdz^48–51 basis sets (Fig. S1 and Table S1, ESI†). Validation results demonstrate the B3LYP and lanl2dz functional and basis set pairing as the best match with experimentally determined crystallographic parameters⁵² and were utilized for following calculations. The agreement of the B3LYP/lanl2dz computational results with experimental values show that the use of van der Waals corrections (i.e., Grimme style, D3 or D4) are unnecessary and as such were not utilized in this study. Atomic force tensors (Table S2, ESI†) were determined as part of the DFT calculations and used for Molecular Dynamics simulation input variables. DFT adsorption energies (E_ads) were calculated by the equation:

E_ads = E^Py/CuI − (E^Py + E^CuI)

where E^Py/CuI is the free energy of the optimized system where the Py ring is in contact with the surface and E^Py and E^CuI are the free energies of the Py molecule and CuI slab alone, respectively.⁵³ Positive values indicate adsorption and negative values indicate repulsion. These adsorption energies are a combination of noncovalent interaction strength, van der Waals repulsion, as well as electronic (Coulombic) attraction and have been used by us and others to probe the interaction between organic and inorganic molecular components.^54,55

Electrostatic potential surfaces

The donor/acceptor regions of Py molecules were investigated via electrostatic potential (ESP) analysis. Calculations were performed within the Gaussian16 program on an optimized Py molecule using the basis set described above. Electrostatic potentials were generated on an electron density surface at 0.002 ε bohr⁻¹ where areas of positive/negative potential indicate electron-rich/deficient regions. Electrostatic potentials generated at this isodensity value have been determined by previous studies to be an accurate indicator for supramolecular assembly.^56,57

Natural bonding orbitals (NBO) and quantum theory of atoms in molecules (QTAIM)

NBO calculations were performed using the NBO7 software suite utilizing the individual components constructed from the Molecular Dynamic outputs. NBO second order perturbation theory was applied to parse out the donor–acceptor interaction between the Py electron donor and the Cu or I electron acceptor including deconvoluting the sub-noncovalent interaction types, i.e. halogen, hydrogen bonding, as well as identify the atomic or molecular orbitals involved. Orbitals were rendered using the Jmol (v.14.30.1) java applet.^58,59 Models generated and used for NBO calculations can be found in Fig. S2 and S3 (ESI†).

Results and discussion

Electrostatic potential surface of pyridine

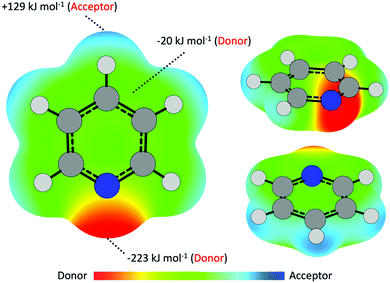
Previous work on the interaction of nucleophilic volatile organic compound (VOC) vapors with metal-based surfaces have largely focused on elemental metallic systems, wherein noncovalent interactions between species give rise to regium bonding.^15,18,19,21 These interactions are thus an important component in understanding adsorption and catalytic mechanisms of metallic compounds.^{16,17,20,60,61} Simply described, interactions occur between electron acceptor–donor pairs, and in metallic cases metal centers act as acceptors while the VOC donor may contribute through either a lone electron pair or π aromatic system.^20,62–64 Pyridine, as a simple N-heteroaromatic, is capable of electron donation via either the N lone pair (n-interactions) or the π cloud (π-interactions), giving rise to a potential competition between σ- and π-interactions. This was noted by Atodiresei et al., who reported that Py is capable of adsorbing onto Cu(110) and Ag(110) surfaces in either a parallel (π-interaction) or perpendicular (n-interaction) geometry.²² In this example only the metal center, acting as an electron acceptor, is capable of interacting with the incoming electron-donating VOC molecule. This dynamic changes in metal halide systems, wherein the halide may act as an electron donor to empty (electron-accepting) antibonding molecular orbitals of the VOC. As such, a number of other noncovalent interactions are possible, including X⋯H and X⋯π* bonding.

The interaction of vapor-phase molecules and CuI surfaces can first be partially described as a coulombic attraction between polarized regions along either CuI surface or the Py molecule. As such, electron density surfaces are useful in identifying regions of relative electron richness (V_s,min) and depletion (V_s,max) that may serve as electron donors or acceptors, respectively, in facilitating supramolecular assembly, catalytic reactions, and surface adsorption.^16,65,66 For Py (Fig. 2) polarization about the molecule results in a region of electron richness adjacent the N atom owing to the presence of lone pair electrons. This region has an electrostatic potential value of −223 kJ mol⁻¹. As the most negative region (V_s,min), this site is the strongest potential electron donor for formation of noncovalent interactions with the CuI surface, thus indicating a stronger propensity to interact via σ-interaction. Turning towards π-interactions, regions of electron richness are also located directly above and below the ring plane adjacent the C atoms. Here the electrostatic potential is slightly negative at −20 kJ mol⁻¹ and indicates significantly poorer electron-donor behavior compared to the N lone pair. Less obviously, the Py molecule features a region of positive electrostatic potential, and thus may also act as an electron acceptor. This region of positive potential (V_s,max) is located about the terminal end of the para and meta C–H bond and has a potential value of +129 kJ mol⁻¹.

Fig. 2 Electrostatic potentials of a pyridine molecule mapped onto a 0.002 ε bohr⁻¹ isodensity surface highlighting regions which may act as electron donors (negative potentials) or acceptors (positive potentials).

As previously discussed, the iodide is an electron donor within the CuI surface and thus may interact with this electron-acceptor region on the Py molecules. The large positive potential value (+129 kJ mol⁻¹vs. −20 kJ mol⁻¹) indicates that this region might potentially out-compete interactions with the π cloud. Given the dual electron-donating/-accepting capacity of the Py molecule, the question of how competition between these sites results in preferred bonding geometries about CuI remains unclear based on ESP surfaces alone and thus warrants detailed investigation.

Ideal copper(I) iodide surface

Surfaces that do not contain terminal atoms or defect sites, termed ‘ideal’, are historically used in DFT modelling to understand the chemisorption mechanism of small molecules to metal-based surfaces. These models typically are limited to elemental metals or metal oxides and exclude families of metal halides such as perovskites. While less realistic owing to the lack of defect sites or terminal atoms, these models are nevertheless important as a first step in understanding some basic principles as to how small molecules may interact with metal-based surfaces. As such, we have opted to start with an ideal CuI surface in which Py molecules are free to interact along the (111) plane in order to determine (i) the prediction of the Py geometry along the surface, (ii) the Py–CuI adsorption energy, and (iii) identify and quantify the atomic and molecular orbitals involved in the charge transfer process.

Molecular dynamics simulations. Molecular Dynamics (MD) calculations were performed for an ideal (111) cation-terminated γ-CuI surface coated with a Py monolayer (see Fig. 3). These MD simulations provided a detailed structural description (i.e. set of atomic coordinates) that served as starting point in the quantum mechanical calculations. In general, this approach improves the accuracy of quantum analysis while reducing the computational workload required since the simulations only consider dipole–dipole interactions between atoms and/or molecules. These calculations are performed on exceptionally large models which include 70 Py molecules along the CuI surface and are outside the capabilities of DFT calculations. As such, these MD simulations provide statistical insights into the overall behavior of the Py monolayer. Fig. 3 displays the tilting angle distribution of the Py molecules at the γ-CuI surface. It is discovered that Py molecules have a general preference for either a flat orientation of 1° or near-flat orientation of ∼15°. Along an ideal surface, nonetheless, about one-third of the Py molecules have a tilting angle greater than 40°. The preference for flat orientation by the Py molecules can be attributed to dipole–dipole interactions between Py molecules as indicated by the general positioning of the nitrogen atoms apart from each other as well as potential dispersion interactions with the γ-CuI surface.

Fig. 3 Molecular Dynamics simulations (left) for the Py monolayer at an ideal surface and (right) angular distribution of Py molecules (i.e. flat orientation = 0°; upright orientation = 90°). Image made with VMD.³³

Potential energy mapping and ground state geometry. In comparison to DFT methods, molecular dynamics (MD) calculations are particularly advantageous in their ability to calculate the ‘ideal’ or minimum energy position of a large number of molecules in a relatively short amount of computational time. The resulting atomic positions, derived from strictly electrostatic parameters, however, lack finer considerations such as polarization and orbital-orbital interactions. As such, MD calculations represent an ideal synergistic methodology for coupling to higher order calculations such as DFT since MD can provide a rough but useful starting point for exploration of energy mapping. As such, we have selected a single Py molecule from the MD simulations described above and explored in detail its interaction with a CuI(111) surface. Using these coordinates, we have mapped the potential energy of the Py/CuI ensemble using DFT.

The N atom resides almost directly above a positively charged Cu metal center (Fig. S4, ESI†). Fig. 4 shows the potential energies for a series of calculations wherein the Py molecule is removed from the CuI surface in a step-wise manner while being held at a plane-to-surface angle of 90°. The results of this study reveal a minimum energy value at a surface⋯N distance of 2.65 Å. Fitting a Morse potential, we are able to determine an adsorption energy of 0.528 eV, a value consistent with other studies on adsorption of heterocyclic aromatic molecules to metallic (Cu/Ag/Au) surfaces.^19,21,22 This adsorption energy value is significantly lower than the calculated value of 0.714 eV for the removal of a formally coordinated Py from the known cubane [CuI]₄Py₄ complex. Absorption of a Py molecule on a CuI surface can conceivably produce an orientation of the molecular plane anywhere from perpendicular to parallel to the surface.

Fig. 4 Interaction energy between pyridine and a CuI surface as a function of (top) surface⋯N distance and (bottom) pyridine tilting angle.

Starting at the optimized bond distance, the interaction energy was calculated as a function of tilt angle of the Py ring in relation to the CuI surface (Fig. 4). Tilting of the Py molecule reveals a ground state in which the molecular plane is canted at an angle of 90° with respect to the CuI surface. This position is lower in energy by 1.75 eV and 3.53 eV for the two parallel orientations 0° and 180°, respectively. Orientation of the Py molecule at angles other than 90°, however, undoubtedly facilitates interaction of the CuI surface with both the N lone pair and the aromatic π cloud on the face of the Py plane. Importantly, the ground state calculations reveal that the Py molecules preferentially adsorb perpendicular to the CuI surface, as we might expect if only the N lone pair were involved in the interaction.

Charge transfer orbital interactions. The donor and acceptor orbitals responsible for the interaction between Py molecules and the CuI surface were investigated via Natural Bonding Orbital (NBO) theory. Previously it has been reported that Py interacts with Cu and Ag surfaces via a combination of the N lone pair and the Py π system.²² Our potential energy calculations initially support this conclusion insofar as for the ground state the Py plane is perpendicular and thus dominated by the N lone pair. NBO calculations reveal four principal donor/acceptor orbital pairs involved in the interaction of Py with CuI. We present representative models in Fig. 5. The first two donor orbitals (Fig. 5a and b) are, unsurprisingly, the N lone pair and the π system which donate charge to acceptor Cu 4s atomic orbitals. The third interaction (Fig. 5c) arises from donor iodide lone pairs with the Py π* orbitals acting as charge acceptors. These findings highlight the ability of the π system to act not only as a charge donor when interacting with positively charged metal atoms, but also as an acceptor (π*) in the presence of electron-rich species. Notably, the fourth interaction type (Fig. 5d) can be classified as hydrogen bonding and involves C–H σ or σ* orbitals interacting with the adjacent vacant Cu 4s or I 6p atomic orbitals, respectively. The diversity in the donor and acceptor orbital pairs illustrated in Fig. 5 highlights the complex nature in which Py molecules may interact with metal halide surfaces.

Fig. 5 Orbitals involved in the noncovalent interaction between Py and the CuI surface in the ground state. The Py tilt angle is 90° in relation to the CuI surface. Arrows denote the direction of the electron charge transfer.

To better understand their directing role and to relate the strength of these interactions to one another, we have calculated their respective stabilization energies (Table 1). The total stabilization energy at a tilt angle of 90° is 12.64 kcal mol⁻¹. As expected, when Py is oriented perpendicular to the CuI surface (90°–120°), the N lone pair interaction with Cu is strongest, contributing 37% (4.64 kcal mol⁻¹) of the total stabilization energy. Interestingly, despite the geometry, interaction via the π and π* is nearly as strong, contributing 35% toward the total stabilization energy. Of this amount, the major portion is due to Py charge donor behavior involving the Py π orbitals at 2.89 kcal mol⁻¹, while the remainder (1.48 kcal mol⁻¹) is associated with charge acceptor behavior involving the Py π*. In its interaction via the C–H orbitals the Py molecule acts as either a charge donor or acceptor. As described above, in cases where the Py acts as a charge donor the C–H (σ) orbitals interact with the Cu 4s orbitals, contributing 1.29 kcal mol⁻¹, while in cases where the Py molecule acts as a charge acceptor the C–H (σ*) orbitals interact with the I 6p orbitals, contributing 2.34 kcal mol⁻¹. The sum of the stabilization energies for the C–H interactions is 3.63 kcal mol⁻¹, representing a 29% contribution. These findings highlight three important factors with regard to the interactions of Py with CuI: (i) interaction with the N lone pair, while the strongest, still represents a minority of the overall interaction strength, (ii) the interaction energies are stronger for the Py π and C–H σ orbitals than for the Py π* and C–H σ* orbitals, indicating that Py charge donor behavior is more important than its acceptor behavior, and (iii) hydrogen bonding interactions are non-negligible and contribute significantly to the overall interaction.

Table 1 Summary of NBO stabilization energies for a Py molecule perpendicular along an ideal CuI surface. The interaction types are grouped by the role of the Py molecule, acting as either a charge donor (π and σ) or charge acceptor (π* and σ*)

Interaction type	Pyridine role
	Donor (kcal mol^−1)	Acceptor (kcal mol^−1)	Donor + acceptor (kcal mol^−1)
N–CuI	4.64	0.00	4.64
π/π*-CuI	2.89	1.48	4.37
C–H (σ/σ*)-CuI	1.29	2.34	3.63
Total stabilization energy			12.64

---

We note that there is a divergence of MD- and DFT-determined geometric orientation preference of the Py molecule with respect to the CuI surface for the ground state. As we have previously noted, MD simulations consider only dipole–dipole interactions between molecules, making them computationally inexpensive even for large models. This is evident in our results which show maximization of N⋯N distances between Py molecules. Furthermore, MD simulations contain multiple Py molecules which invariably influence the overall statistical Py geometric orientation as they interact with one another. DFT calculations, on the other hand, consider many more properties that influence the Py–CuI geometry including polarization and orbital interactions. These additional considerations provide a much more detailed understanding of the Py–CuI ensemble. However, DFT calculations require sizeable computational resources and thus can only be performed on models containing a fraction of the atoms in MD simulations. Our findings expose a critically important flaw in current modelling techniques that may rely on solely ideal surfaces or a lone computational methodology. While further exploration of the divergence of MD- and DFT-determined geometric orientation preference is outside the scope of this study, we bring attention to it as a point for future research.

Defect copper(I) iodide surfaces

While commonly used and well accepted in MD-based calculations, the use of defect surfaces is rarer for DFT-based modelling owing to the necessary increase in computational expense. Defective surfaces, however, represent a more realistic approximation of actual surfaces, which invariably suffer from defect or kink sites, and thus computations involving defect sites must lead to more meaningful predictions of chemical behavior. These sites, additionally, are critically important in the prediction and understanding of chemical activity. For example, in catalysis a defective region is more apt to give rise to a ‘localizing’ effect and may help hold molecules in close proximity to one another or increase their exposure to surface atoms. As such, we have included MD and DFT calculations using a simple defect CuI surface in which we have systematically removed atoms while maintaining a neutral charge balance. Our aims are to determine: (i) the change in preferred Py orientation, (ii) the difference in adsorption energy compared to the ideal surface model, and (iii) shifts in charge transfer dynamics between donor and acceptor orbitals.

Molecular dynamic simulations. Defect sites along the CuI surface are expected to influence molecular tilting angles; we have explored this notion. Fig. 6 and Fig. S5 (ESI†) display the results for MD simulations that include surface defects where pairs of CuI atoms were systematically removed. This removal results in the formation of a ‘crater’ in the surface while maintaining an overall neutral charge. Notably, removal of CuI atoms results in clustering of Py molecules within the site at nearly perpendicular angles to the surface (Fig. 6). This behavior is strictly localized to the defect site and becomes more pronounced as the defect site size is increased. The presence of a sixteen-atom-sized crater site, for example, is seen to cause alignment of six Py molecules at high tilting angle, while for the four- and eight atom sized craters we observed the alignment of two and three Py molecules, respectively. This kind of alignment effect was commonly observed for the crater sites, although it should be noted that Py molecules are not necessarily held rigidly in place; some Py molecules inside crater sites occasionally lie flat. The placement of Py molecules within the crater site offers new opportunities to form additional noncovalent interactions, specifically π stacking between Py molecules, while at the same time altering the primary interactions modes observed for the ideal surface. In cases where π stacking is occurring we expect, for example, these orbitals to become less available for participation in donor–acceptor charge transfer with Cu or I surface atoms.

Fig. 6 Molecular Dynamics simulations for the Py monolayer at a cratered surface (circled in red). The crater site ranges in size from (left to right) four to eight to sixteen Cu–I pairs removed from the top layer of the ideal surface. In general, the crater causes Py molecules to group inside the defect and exhibit higher tilting angles. Image made with VMD.³³

Charge transfer orbital interactions. To determine how the defect site and subsequent localizing effect alters the chemisorption of Py molecules to the CuI surface, we first determined the ground state geometry of a Py molecule within a 16-atom defect site derived from the MD calculations (Fig. 7). We note that for this model the MD calculations indicate that the Py molecules are almost entirely upright and are oriented parallel to one another within the defect site. Focusing on the central Py molecule, DFT calculations determined an ideal angle of 100° with a much tighter range compared to that of a single Py molecule placed on a defect-free surface, owing to constriction and van der Waals repulsion by adjacent Py molecules. The adsorption energy of the Py molecule within the defect site was determined to be 0.306 eV, which initially indicates than that the Py is less energetically bound to the defective CuI surface compared to the ideal surface (0.528 eV). NBO calculations reveal six distinct orbital interaction pairs involved in the adsorption of Py within the defect site. These interaction pairs are shown in Fig. 8. In addition to the four previously described pairings observed for the ideal surface model, the additional two arise from Py⋯Py interactions between VOC molecules. In one case the π system, acting as a charge donor, interacts with the π* of an adjacent Py molecule forming a classic π–π noncovalent interaction. This type of behavior is typical of aromatic systems which display π stacking behavior with even larger offset and parallel or near parallel stacking in the solid state.^67–69 The second Py⋯Py interaction can be more accurately described as a n⋯π noncovalent interaction. Here, the central Py π* acts as a charge acceptor, while the lone pair of an adjacent Py molecule acts as a charge donor. This type of interaction is generally considered less stabilizing, and therefore weaker, than π–π interactions.⁷⁰

Fig. 7 Interaction energy between pyridine and a defective CuI surface as a function of pyridine tilting angle.

Fig. 8 Orbitals involved in the noncovalent interaction between pyridine and the defect CuI surface in the ground state. The pyridine tilt angle is 90° in relation to the CuI surface. Noninteracting CuI atoms are colored light gray for clarity.

To compare the relative strengths of the noncovalent interactions and reconcile the lower adsorption energy of the defect surface to the ideal surface, we have tallied the NBO determined stabilization energies for each donor/acceptor pairing in Table 2. At this optimized angle the N–CuI orbital pairs (N lone pair donor and Cu acceptor) dominate, contributing a total of 6.45 kcal mol⁻¹ (44%). Notably, significant hydrogen bonding between Py and the CuI surface contribute the second largest stabilization energy of 4.86 kcal mol⁻¹. Of this stabilization, 69% arises from the C–H σ* orbitals acting as charge acceptors from I donors, while the remaining 31% results from the C–H σ orbitals acting as charge donors. In comparison, π interactions with the CuI surface account for only 2.20 kcal mol⁻¹ of the total stabilization energy, of which 73% is from Py π orbitals acting as charge donors. The Py⋯Py interactions are weakest, including both π–π and n–π interactions, and contribute only ∼8% to the total stabilization.

Table 2 Summary of NBO stabilization energies for a Py molecule within a CuI 16-atom defect site. The interaction types are grouped by the role of the Py molecule, acting either as a charge donor or charge acceptor

Interaction type	Molecular pair	Pyridine role
		Donor (kcal mol^−1)	Acceptor (kcal mol^−1)	Donor + acceptor (kcal mol^−1)
N–CuI	Py/CuI	6.45	0.00	6.45
H–CuI	Py/CuI	1.52	3.34	4.86
π/π*-CuI	Py/CuI	1.61	0.59	2.20
π–π*	Py/Py	0.53	0.09	0.62
π*-N	Py/Py	0.00	0.63	0.63
Total Stabilization energy				14.76

---

The stabilization energies highlight two points: (i) Py⋯Py interactions do not significantly stabilize Py molecules within the defect site, and (ii) the inclusion of I atoms as charge donors significantly enhances the overall stabilization energy. The latter finding demonstrates the importance of having an electron donor embedded within the surface for capture and subsequent bonding with Py vapor molecules, since only the I atoms are able to participate meaningfully with the C–H σ/σ* bonds. In the absence of these atoms the C–H orbitals would otherwise go unutilized or potentially lead to competitive Py⋯Py interactions, leading to weaker noncovalent interactions with the metallic surface. With respect to the weak Py⋯Py interactions, it becomes clear that the perpendicular geometric orientation is most likely the result of destabilizing steric repulsion rather than positive charge transfer attraction and that these interactions do not contribute significantly to the Py adsorption process. Repulsion is also credited with the lower DFT-determined adsorption energy which is excluded from the NBO determined stabilization energies. Interestingly, the results indicate that while the Py molecule interacts more strongly with the defective CuI surface, the repulsion amongst adjacent Py molecules results in an overall less stable configuration within the well. This sets up an intriguing competition wherein Py molecules are more readily able to interact with the surface but must balance this with the available space within the defect site. This simple, yet critical, point provides a rationalization to the observed localizing effect whereby the Py molecules almost exclusively prefer an upright orientation within the crater site. This geometry is best suited to maximize the number of Py molecules within the available space, while simultaneously minimizing Py–Py contacts.

The agreement of MD and DFT modeling results highlights two important points: (i) ideal surfaces and those with defects produce entirely different results with regard to the geometric orientation and (ii) defect sites enhance the ability for electron donor I atoms to interact with electron acceptor C–H sites. With respect to the first point, we highlight this observation to draw attention to the need of DFT modelling to include defect models in addition to ideal surfaces. It is clear from our findings that the behavior of small molecules along a surface varies significantly when a defect site is present. Herein, we show that defect sites are important in enhancing adsorption and expanding the modes of interaction between the Py molecule and the CuI surface. These effects arise primarily from an enhancement of hydrogen bonding with terminal I atoms which are only present within the defect site.

Conclusion

We have investigated the interaction of nucleophilic pyridine molecules with copper(I) iodine surfaces utilizing a synergistic computational approach with Molecular Dynamic (MD) and density functional theory (DFT) modelling. Our findings feature the rarely reported CuI surface, which unlike historically investigated metallic surfaces, contains both cationic metal centers as well as anionic halides. Molecular Dynamic calculations were performed over several nanoseconds using a single layer of pyridine (Py) molecules to initially provide geometric information on the Py–CuI interaction. Electrostatic potentials along an isodensity surface of pyridine were used to achieve a molecular-level understanding of adsorption and to characterize the donor and acceptor sites of the neutral Py molecule in which polarization gives rise to regions of variable acceptor/donor strengths. The ESP values demonstrate the ability of Py to act as either an electron donor or acceptor, resulting in interactions with both Cu and I atoms. Natural bonding orbital (NBO) calculations show that the charge transfer from the N lone electron pair to the empty Cu 4s are the strongest interactions, but do not dominate as the most significant driving force in the geometric orientation of the Py molecule along the surface. Instead, a combination of π/π* orbitals interacting with Cu 4s and I 6p atomic orbitals alongside hydrogen bonding with I 6p orbitals give rise to strong adsorption of Py molecules to the surface. Introduction of defect sites along the CuI surface not only introduces Py⋯Py interactions via π stacking, but also significantly enhances the ability to form hydrogen bonds with terminal I atoms within the defect site. The result is a localizing effect within the defect site whereby Py molecules are tightly held close to the surface yet are oriented in such a way to minimize Py–Py contacts due to steric repulsion. Our findings provide a first-principle understanding on how orbital pair interactions and changes in metal halide surface leads to shifts in adsorption and noncovalent interactions utilizing a hybrid Molecular Dynamic-density functional theory methodology.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

We thank Prof. Christopher L. Cahill at The George Washington University for access and allocation of computational resources. The authors acknowledge William & Mary Research Computing for providing computational resources and/or technical support that have contributed to the results reported within this paper. URL: https://www.wm.edu/it/rc.

References

1. K. Dashtian, S. Shahbazi, M. Tayebi and Z. Masoumi, Coord. Chem. Rev., 2021, 445, 214097.
2. G. A. Leith, C. R. Martin, A. Mathur, P. Kittikhunnatham, K. C. Park and N. B. Shustova, Adv. Energy Mater., 2021, 2100441.
3. W. Luo and G. Wang, Adv. Opt. Mater., 2020, 8, 2001362.
4. A. Schlachter and P. D. Harvey, J. Mater. Chem. C, 2021, 9, 6648–6685.
5. O. Veselska and A. Demessence, Coord. Chem. Rev., 2018, 355, 240–270.
6. S.-Y. Liu, J.-P. Zhang and X.-M. Chen, Cryst. Growth Des., 2017, 17, 1441–1449.
7. M. Shao, M.-X. Li, Z.-X. Wang, X. He and H.-H. Zhang, Cryst. Growth Des., 2017, 17, 6281–6290.
8. H. Fei, D. L. Rogow and S. R. J. Oliver, J. Am. Chem. Soc., 2010, 132, 7202–7209.
9. M. W. Mara, K. A. Fransted and L. X. Chen, Coord. Chem. Rev., 2015, 282–283, 2–18.
10. N. Armaroli, G. Accorsi, F. Cardinali and A. Listorti, Photochemistry and Photophysics of Coordination Compounds I, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 69–115.
11. Y. C. López, H. Viltres, N. K. Gupta, P. Acevedo-Peña, C. Leyva, Y. Ghaffari, A. Gupta, S. Kim, J. Bae and K. S. Kim, Environ. Chem. Lett., 2021, 19, 1295–1334.
12. G. Evtugyn, S. Belyakova, A. Porfireva and T. Hianik, Sensors, 2020, 20, 6963.
13. J. Dong, D. Zhao, Y. Lu and W.-Y. Sun, J. Mater. Chem. A, 2019, 7, 22744–22767.
14. J. P. Killarney, M. McKinnon, C. Murphy, K. M. Henline, C. Wang, R. D. Pike and H. H. Patterson, Inorg. Chem. Commun., 2014, 40, 18–21.
15. C. Deng, J. Chen and Q. Tang, J. Phys. Chem. C, 2021, 125, 4489–4497.
16. G. Li, J. H. Stenlid, M. S. G. Ahlquist and T. Brinck, J. Phys. Chem. C, 2020, 124, 14696–14705.
17. M. de las, N. Piña, A. Frontera and A. Bauzá, J. Phys. Chem. Lett., 2020, 11, 8259–8263.
18. R. L. H. Freire, D. Guedes-Sobrinho, A. Kiejna and J. L. F. Da Silva, J. Phys. Chem. C, 2018, 122, 1577–1588.
19. X. Jia and W. An, J. Phys. Chem. C, 2018, 122, 21897–21909.
20. J. Halldin Stenlid, A. J. Johansson and T. Brinck, Phys. Chem. Chem. Phys., 2018, 20, 2676–2692.
21. K. Tonigold and A. Groß, J. Chem. Phys., 2010, 132, 224701.
22. N. Atodiresei, V. Caciuc, J.-H. Franke and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045411.
23. A. D. Nicholas, F. H. Barnes, D. R. Adams, M. S. Webber, M. A. Sturner, M. D. Kessler, D. A. Welch, R. D. Pike and H. H. Patterson, Phys. Chem. Chem. Phys., 2020, 22, 11296–11306.
24. D. A. Welch, T. J. Woehl, C. Park, R. Faller, J. E. Evans and N. D. Browning, ACS Nano, 2016, 10, 181–187.
25. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
26. P. Vashishta and A. Rahman, United States, 1979.
27. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
28. H. Heinz, R. A. Vaia, B. L. Farmer and R. R. Naik, J. Phys. Chem. C, 2008, 112, 17281–17290.
29. I. Y. Gotlib, A. K. Ivanov-Schitz, I. V. Murin, A. V. Petrov and R. M. Zakalyukin, Solid State Ionics, 2011, 188, 6–14.
30. S. Toxvaerd and J. C. Dyre, J. Chem. Phys., 2011, 134, 081102.
31. C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104.
32. P. Kumar, F. W. Starr, S. V. Buldyrev and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 011202.
33. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graph., 1996, 14, 33–38.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Mont-gomery, J. E. Peralta Jr., F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
35. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
36. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
37. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
38. W. J. Stevens, H. Basch and M. Krauss, J. Chem. Phys., 1984, 81, 6026–6033.
39. W. J. Stevens, M. Krauss, H. Basch and P. G. Jasien, Can. J. Chem., 1992, 70, 612–630.
40. T. R. Cundari and W. J. Stevens, J. Chem. Phys., 1993, 98, 5555–5565.
41. S. Huzinaga, J. Andzelm, E. Radzio-Andzelm, Y. Sakai, H. Tatewaki and M. Klobukowski, Gaussian Basis Sets for Molecular Calculations, Volume 16, 1st Edition, Elsevier Science, 1984.
42. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
43. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
44. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
45. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
46. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
47. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
48. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
49. K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883.
50. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
51. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
52. A. W. Kelly, J. V. Handy, A. D. Nicholas, F. H. Barnes, H. H. Patterson, L. Wojtas and R. D. Pike, J. Inorg. Organomet. Polym. Mater., 2017, 27, 90–100.
53. K. Duanmu and D. G. Truhlar, J. Chem. Theory Comput., 2017, 13, 835–842.
54. R. G. Surbella, L. C. Ducati, K. L. Pellegrini, B. K. McNamara, J. Autschbach, J. M. Schwantes and C. L. Cahill, J. Am. Chem. Soc., 2017, 139, 10843–10855.
55. A. D. Nicholas, B. W. Walusiak, L. C. Garman, M. N. Huda and C. L. Cahill, J. Mater. Chem. C 10.1039/D0TC06000C.
56. M. Borovina, I. Kodrin and M. Đaković, Cryst. Growth Des., 2019, 19, 1985–1995.
57. M. Borovina, I. Kodrin and M. Đaković, CrystEngComm, 2018, 20, 539–549.
58. A. Herráez, Biochem. Mol. Biol. Educ., 2006, 34, 255–261.
59. Jmol: an open-source Java viewer for chemical structures in 3D, http://www.jmol.org/, (accessed 12 April 2021).
60. J. H. Stenlid and T. Brinck, J. Am. Chem. Soc., 2017, 139, 11012–11015.
61. F. Zhou, Y. Liu, Z. Wang, Q. Yang and B. Zheng, Comput. Theor. Chem., 2020, 1179, 112800.
62. A. Frontera and A. Bauzá, Chem. – Eur. J., 2018, 24, 7228–7234.
63. I. Alkorta, J. Elguero and A. Frontera, Crystals, 2020, 10, 180.
64. A. Bauzá and A. Frontera, Inorganics, 2018, 6, 64.
65. J. Halldin Stenlid, A. J. Johansson and T. Brinck, Phys. Chem. Chem. Phys., 2019, 21, 17001–17009.
66. C.-Y. Chiu, H. Wu, Z. Yao, F. Zhou, H. Zhang, V. Ozolins and Y. Huang, J. Am. Chem. Soc., 2013, 135, 15489–15500.
67. R. Thakuria, N. K. Nath and B. K. Saha, Cryst. Growth Des., 2019, 19, 523–528.
68. Z.-F. Yao, J.-Y. Wang and J. Pei, Cryst. Growth Des., 2018, 18, 7–15.
69. C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896.
70. E. M. Cabaleiro-Lago and J. Rodríguez-Otero, ACS Omega, 2018, 3, 9348–9359.

---

Footnote

† Electronic supplementary information (ESI) available: Description of DFT derived models, orbital interaction renderings, and additional NBO/NLMO calculations (PDF). See DOI: 10.1039/d1cp05888f

---