Core-electron contributions to the molecular magnetic response

Abstract

Orbital contributions to the magnetic response depend on the method used to compute them. Here, we show that dissecting nuclear magnetic shielding tensors using natural localized molecular orbitals (NLMOs) leads to anomalous core contributions. The arbitrariness of the assignment might significantly affect the interpretation of the magnetic response of nonplanar molecules such as C₆₀ or [14]helicene and the assessment of their aromatic character. We solve this problem by computing the core- and σ-components of the induced magnetic field (and NICS) and the magnetically induced current density by removing the valence electrons (RVE). We estimate the core contributions to the magnetic response by performing calculations on the corresponding highly charged molecules, such as C₆H₆³⁰⁺ for benzene, using gauge-including atomic orbitals and canonical molecular orbitals (CMOs). The orbital contributions to nuclear magnetic shielding tensors are usually estimated by employing a natural chemical shielding (NCS) analysis in NLMO or CMO bases. The RVE approach shows that the core contribution to the magnetic response is small and localized at the nuclei, contrary to what NCS calculations suggest. This may lead to a completely incorrect interpretation of the magnetic σ-orbital response of nonplanar structures, which may play a major role in the overall magnetic shielding of the system. The RVE approach is thus a simple and inexpensive way to determine the magnetic response of the core- and σ-electrons.

---

Introduction

One of the many ways to diagnose whether a molecule is aromatic or not is by analyzing its response to an external magnetic field.^1,2 In the presence of this field, some cyclic molecules induce a current density forming two- or three-dimensional circuits.^3,4 In planar aromatic molecules, the external magnetic field (B^ext) is usually applied perpendicularly to the molecular plane sustaining a diatropic current density that concomitantly creates an induced magnetic field, B^ind, in the opposite direction to the external field.^5–7 However, in nonplanar systems, B^ext cannot be applied perpendicularly to the rings, which implies that the x- and y-components of B^ind also become relevant.^8,9

Recently, we found that the response of the core electrons to the external magnetic field (B^ind_core) in helicenes produces a cumulative and curvature-sensitive shielding cone due to the overlapping of the magnetic responses of the rings.⁹ In C₆₀, this response is even more pronounced, resulting in strong shielding within the cage.^10,11 These facts motivated us to study in detail the characteristics of B^ind_core in nonplanar structures.

Typically, nuclear magnetic shielding tensors are calculated with the popular gauge-including atomic orbital (GIAO) scheme,^12,13 using a methodology based on analytical gradient theory that employs explicit field-dependent basis functions, which is implemented in most electronic structure programs. Furthermore, a dissection of the shielding tensor into individual orbital contributions can be obtained by transforming canonical molecular orbitals (CMOs) into the natural localized molecular orbitals (NLMOs) by a unitary transformation using the natural chemical shielding (NCS) analysis.¹⁴ Alternatively, a direct dissection of the shielding tensor to CMO contributions, within the GIAO scheme, can be provided by numerical integration.¹⁵ The shielding tensor can then be constructed and interpreted in terms of CMO contributions. However, Steiner and Fowler proved that dissections such as the NCS scheme provide unphysical core- and σ-contributions to current densities and magnetic shieldings due to the occupied-occupied mixing of the orbitals.¹⁶ For nonplanar molecules, this type of dissection can also lead to a mixing of the σ- and π-contributions to the shielding tensor. The ipsocentric method,^17,18 which works on a continuous set of gauge-origin transformations,^19,20 removes these unphysical occupied–occupied transitions in the orbital contributions of the current density because it locates the origin at the individual evaluation points when calculating the current density. Consequently, the corresponding ipsocentric orbital contributions to the shielding tensor can be realized from the Biot–Savart integral expression.^16,21 A comprehensive analysis of the core-electron contributions to the magnetic response has not been explored, except in benzene.^16,19 These calculations performed with the ipsocentric approach suggest that the core-electron contribution is minimal, contrary to what is predicted by the NCS analysis.

Unlike GIAO-based magnetic property calculations, the ipsocentric approach has not been widely adopted by the chemical community, so addressing a possible solution to the problem of orbital contributions in GIAOs is quite attractive and convincing. Moreover, modern analyses of the magnetic response consist of calculating these properties in the molecular environment leading to a detailed quantitative and qualitative description of the magnetic behavior and not only at one point in space. Since the core-electron orbitals are much lower in energy than the valence orbitals (at least in organic molecules), the core contribution can also be estimated by computing the magnetic response, whose valence electrons have been removed, using GIAO and the analytical gradient approach. This strategy can also provide a corrected σ-electron contribution.

Here, we first analyze benzene to estimate the core- and σ-contributions in the prototypical planar aromatic ring. Next, we investigate the role of curvature in the magnetic response of the core electrons in corannulene, C₆₀, and [14]helicene. The discussion of the magnetic response is focused on the induced magnetic field^5–7 (B^ind) and the magnetically induced current densities (J^ind),^22–24 computed in the molecular surroundings. Removal of valence electrons (RVE) provides different aspects of the core- and σ-electron effects of the magnetic response compared to previous studies,^9–11 whereas the core-electron contributions do not affect the topology of the current density and ring-current strengths because the core contributions of the induced current density are localized close to the nuclei.

Computational details

The geometries were fully optimized at the PBE0-D3/def2-TZVP level.^25–27 Magnetic shielding tensors were determined at the PBE0/def2-SVP level^25,26 using the GIAO method.^12,13 These computations were performed with Gaussian 09.²⁸ While the Aromagnetic code²⁹ was used in the B^ind calculations, the J^ind analysis was performed using the gauge-including magnetically induced current (GIMIC)^22–24 program. The Aromagnetic and GIMIC programs are interfaced to Gaussian. We assumed a B^ext direction oriented parallel to the highest symmetry axis (z-axis) of the molecule; the z-component of B^ind (B^ind_z) is then the largest one. B^ind_z is a scalar field equal to the zz-component of the nucleus-independent chemical shift³⁰ (NICS_zz) for planar molecules. GIMIC integrates the J^ind flux through planes that intersect bonds or atoms yielding ring-current strengths (J^ind).^22–24 The current-density flux in different parts of the plane can be determined by calculating the derivative of J^ind (dJ^ind/dr) with respect to one of the plane coordinates (r). The r coordinate can be chosen to begin with r = 0 at the horizontal axis in, for example, the center of a molecular ring.^22–24 The integration planes usually extend 5 Å in three directions and end outside the molecule, where the current density practically vanishes.

The magnetic shielding tensor was dissected into orbital contributions using the NCS analysis¹⁴ as implemented in the NBO6³¹ code. B^ind_core and J^ind_corewere also computed using the RVE method, that is, for highly charged molecules whose valence electrons have been removed, but without relaxing the molecular structure. The RVE approach takes advantage of the fact that a weak perturbation due to a weak homogeneous external magnetic field does not modify the electronic structure of the core electrons. Therefore, calculating the induced current density or magnetic shielding of a system without its valence electrons is equivalent to calculating the magnetic response of the core electrons. The RVE approach is valid as long as the energy gap between the lowest occupied σ orbital and the highest occupied core-electron orbital (Δ_Lσ-Hcore) is large (> 250 eV). The Δ_Lσ-Hcore values are included in Table S1 of the ESI.† The B^ind_core and J^ind_core contributions of benzene, corannulene, C₆₀, and [14]helicene have been estimated by calculating the magnetic responses of C₆H₆³⁰⁺, C₂₀H₁₀⁹⁰⁺, C₆₀²⁴⁰⁺, and C₅₈H₃₂²⁶⁴⁺, respectively, at the fixed structures from the neutral counterparts. We also calculated the NICS(0) values to compare and validate the RVE approach with the isotropic values reported by Fowler and Steiner. This also proves the applicability of the RVE approach to NICS, which is one of the most widely used aromaticity indices.

Steiner and Fowler noted that the total shielding is the same for any dissection scheme.¹⁶ For planar molecules, the same is true for the π-contribution and, consequently, for the contribution resulting from the sum of the core-electron and the σ-electron components (core + σ). The challenge is to separate the (core + σ)-contribution into its core- and σ-parts. Here, the σ-contribution is obtained by subtracting the core-electron component provided by RVE from the (core + σ)-contribution of the original system. Furthermore, to confirm the magnitude of the contributions coming from occupied–occupied transitions in the core-electron component, a detailed analysis of the shielding tensor was performed with the nuclear magnetic resonance (NMR) module^15,32,33 of ADF,³⁴ employing the PBE0 functional and the Slater type triple-ζ with two polarization function (TZ2P) basis set.

Results and discussion

Benzene

Aromaticity in organic molecules, such as benzene, is explained in terms of the delocalization of the π-electrons because they are primarily responsible for the ring current and the corresponding magnetic shielding contribution.^6,18,35 In contrast, while σ-electrons induce a local magnetic response near the molecular plane, the core electrons should be located at the nuclei. Calculations of orbital contributions of NICS(0) and B^ind_z(0) in benzene, using the Biot–Savart expression, show that the core contribution is tiny in both cases.^16,21 This contrasts with the NCS results, whose core contribution to B^ind_z(0), B^ind_z,core(0), of −10.52 ppm is almost 30% of the π-one to the overall B^ind_z(0) (see Table 1). These results could be interpreted to mean that core electrons also contribute to the benzene ring current, which is at odds with the accepted notion of aromaticity where π-electrons are the ones inducing that response (or σ-electrons in the case of all-metallic systems).

Table 1 The NICS(0) and B^ind_z(0) values (in ppm) calculated at the ring center of benzene at the PBE0/def2-SVP level

	NICS(0)	B ^indz (0)
core (NCS)	−3.69	−10.52
core (RVE)	−0.14	0.36
σ (NCS)	19.60	33.68
σ (RVE)	16.03	22.81
core + σ	15.90	23.17
π	−25.0	−36.41
Total	−9.10	−13.24

---

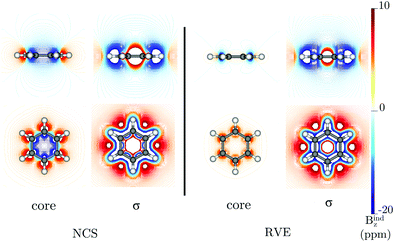
RVE yields a core contribution (core_RVE) to NICS_core(0) and B^ind_z,core(0) of −0.14 and 0.36 ppm, respectively, (see Table 1) in C₆H₆³⁰⁺, which are similar to the values of −0.13 and 0.46 ppm reported by Steiner and Fowler and much smaller than those obtained by the NCS (core_NCS) approach. The authors also showed that the contributions from the core orbitals are small in the center of the ring, but no visualization of the magnetic response of the core electrons was reported. However, since single-point shielding calculations (such as NICS(0) or B^ind_z(0)) do not provide a complete image of the overall magnetic behavior, we compute B^ind_z,core on a grid. Fig. 1 shows that while core_NCS yields a shielding cone with magnetic shieldings between −10 and −20 ppm around the ring, RVE provides a negligible core contribution at the ring center. Consequently, the σ-contributions obtained via NCS (σ_NCS) and RVE (σ_RVE) show differences mainly in the molecular plane. The size of the deshielding cone inside the ring also differs.

Fig. 1 Isolines of the core- and σ-contributions to B^ind_z computed in a plane perpendicular (top) and parallel (bottom) to the molecular plane of benzene using the NCS scheme (left) and the RVE approach (right).

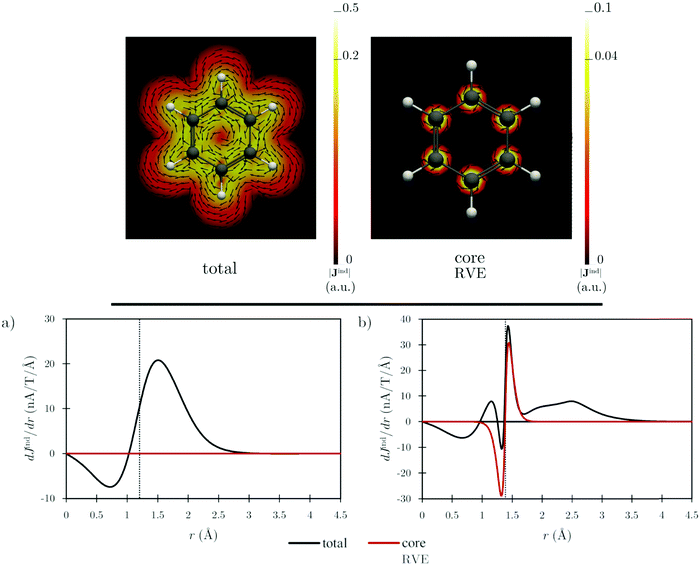
The diatropic current density induced by the core orbitals, using RVE, is localized at the carbon atoms, implying that the core contribution to the ring-current strength in a plane intersecting the C–C bond is negligible, as shown by the dJ^ind/dr profile in Fig. 2a. Integration of the total J^ind flowing through that plane yields a ring-current strength of 12 nA T⁻¹.^22–24 The dJ^ind/dr profile of the current density flowing through a plane intersecting the carbon and hydrogen atoms yields positive and negative peaks in the vicinity of the carbon atoms for both the total response and the core contribution, respectively. Integrating one of the peaks of the red curve in Fig. 2b yields a value of 4.38 nA T⁻¹, which is the strength of the current of the carbon core. The negative peak at the carbon core is much smaller when current-density contributions from all-orbitals are considered, resulting in a current with a magnitude of about 45% (2 nA T⁻¹) of the core_RVE contribution.³⁶

Fig. 2 The top panel shows J^ind plots of the total (left) and J^ind_core obtained from the RVE approach (right) computed in the molecular plane of benzene. |J^ind| values are given in atomic units (1 a.u. = 100.63 nA T⁻¹ Å⁻²). The bottom panel shows the dJ^ind/dr profiles computed along a plane intersecting: (a) a C–C bond and (b) a carbon and a hydrogen atom of benzene. The vertical dotted lines show the r values corresponding to (a) the C–C bond and to (b) the carbon nucleus, respectively.

Corannulene

The orientation of the rings with respect to the external magnetic field influences the strength of the magnetic response of the π-electrons, especially in nonplanar organic molecules.^8,9,37 This could lead to a scenario in which the separation of σ and π contributions is complicated. In the case of nonplanar organic molecules, such as the systems discussed here, whose hybridization does not deviate considerably from sp², it is possible to separate the different orbital contributions.^38,39 This is also the principle of approximations such as the pseudo-π model,⁴⁰ which provide results quite similar to those of the π-electron response computed within the ipsocentric approach, allowing its applicability in both planar and nonplanar molecules.^{35,38,40–45} Thus, since the π-block is “easy” to identify, the (core + σ)-contribution, which is the result of subtracting the π-block contribution from the total magnetic response, is therefore also feasible to determine. Under these considerations, the π-type contributions of spherical, cylindrical, or quasi-planar molecules are ascertainable. Moreover, subtracting the core_RVE response from the (core + σ)-contribution yields the σ-corrected component as well.

In the case of corannulene, there is a bowl-to-bowl inversion process through a planar transition state. Given the shallow curvature, both sides (convex and concave) of corannulene generate a similar magnetic response.⁴⁶ Interestingly, the ring current of the molecular structure of the planar transition state and the bowl minimum has the same tropicity, while its strength is slightly affected by the deformation from planarity.⁴⁷ Previous analyses identified a diatropic current in the peripheral carbon π-circuit and a paratropic ring current in the central five-membered ring (5-MR).^47,48Table 2 summarizes the B^ind_z(0) and NICS(0) values in the center of the 5-MR and 6-MRs. For the 6-MRs, B^ind_z(0) is close to zero, which has been interpreted as a nonaromatic character of these rings, whereas for the 5-MRs, B^ind_z (0) is positive due to the paratropic ring current of the hub. The core_RVE and σ_RVE values differ significantly from the core_NCS and σ_NCS ones. The RVE values of the B^ind_z,core(0) are smaller than 0.42 ppm, whereas the core_NCS values are about 30 times larger with the opposite sign. The difference is even more striking when comparing the B^ind_z isolines (see Fig. 3). In NCS formulation, the core electrons seem to induce a long-range shielding zone in both planar and nonplanar forms, whereas in the RVE approach, a weak magnetic response of the core is obtained, localized in the vicinity of the carbon nuclei. Concomitantly, the σ-shielding appears more pronounced in the bowl-shaped configuration considering the RVE approach.

Table 2 The B^ind_z(0) and NICS(0) values (in parentheses) in ppm, calculated at the PBE0/def2-SVP level in the center of the 5-MR and 6-MRs of the corannulene structures.

Point group		core (NCS)	core (RVE)	σ (NCS)	σ (RVE)	core + σ	π	Total
D 5h	5-MR	−11.06 (−2.74)	0.29 (−0.41)	45.42 (21.80)	34.07 (19.44)	34.36 (19.03)	30.46 (−6.00)	64.82 (13.03)
	6-MR	−12.20 (−3.97)	0.42 (−0.19)	38.31 (20.09)	25.70 (16.32)	26.11 (16.13)	−23.77 (−21.21)	2.34 (−5.08)
C 5v	5-MR	−15.14 (−5.18)	0.38 (−0.28)	28.94 (10.78)	13.42 (5.88)	13.80 (5.60)	43.45 (4.45)	57.25 (10.05)
	6-MR	−12.05 (−5.16)	0.29 (−0.17)	29.12 (14.98)	16.77 (10.02)	17.07 (9.85)	−18.30 (−17.21)	−1.23 (−7.36)

---

Fig. 3 The isolines of the core- and σ-contributions to B^ind_z calculated for the corannulene structures using the NCS scheme (left) and with the RVE approach (right).

The RVE calculations reveal that J^ind_core is highly localized at the nuclei implying that the atomic currents of the carbon atoms do not contribute to the total ring current. Bending the corannulene structure does not significantly affect the core-electron contribution to the ring current, which also remains localized at each carbon atom given by their 1s² core orbitals (see Fig. 4). The dJ^ind/dr profiles, in the plane intersecting the C–C bonds of the 5-MR and a 6-MR (Fig. S1 in the ESI†), show that the transitions between maxima and minima are smooth and somewhat smaller for the bowl-shaped structure because the diatropic and paratropic contributions to the current density are weaker than those of the planar transition state. Like benzene, the core-electron contribution to dJ^ind/dr vanishes when the current strength is computed in a plane intersecting the C–C bond (Fig. S1a in ESI†). The strength of the atomic current of the bowl-shaped structure is 4.35 nA T⁻¹, which is almost the same strength as for the planar form of 4.32 nA T⁻¹ (Table 3).

Fig. 4 The J^ind plots of the total current density calculated in the molecular plane of the corannulene structures (left). The J^ind_core plots calculated using the RVE approach (right). The |J^ind| values are given in atomic units (1 a.u. = 100.63 nA T⁻¹ Å⁻²).

Table 3 The net ring-current strengths (J^ind in nA T⁻¹) of the 5-MR hub and of the rim of the bowl-shaped (C_5v) and planar (D_5h) corannulene structures.

Structure	Hub	Rim
Planar	−17.94	15.38
Bowl-shaped	−12.97	14.74

---

C₆₀ fullerene

C₆₀ exhibits a π-type current inside and outside the cage flowing in the paratropic and diatropic directions, respectively.^35,49 When the core- and σ-contributions are calculated using NCS, large alternating core shielding and σ-deshielding contributions are obtained.^10,11 NCS provides core- and σ-contributions to B^ind_z(0) of −29.76 and 6.40 ppm, respectively, whereas the core_RVE values are −0.25 and −23.11 ppm. Comparison of core_NCS and core_RVE values reveal diametral differences inside and outside the cage (Fig. 5). The core_RVE contribution is negligible inside the carbon cage. Therefore, the orbital contributions to B^ind_z obtained with the NCS scheme are incorrect, leading to an incorrect interpretation of the σ-component. Therefore, instead of what had been pointed out before,^10,11 the inside of the fullerene is fully shielded because of the σ-electrons.

Fig. 5 The isolines of the core and σ-contributions to B^ind_z calculated in a plane parallel (top) and perpendicular (bottom) to the C₃ axis of C₆₀ with the NCS (left) and RVE (right) approaches.

Likewise, the J^ind calculations also show that the currents in Fig. 6 are localized to the vicinity of the nuclei. From the B^ind_z calculations, it can be concluded that the truly σ-contribution to J^ind has some diatropic circulation inside the cage.

Fig. 6 The J^ind plots of the total current density (left) and the J^ind_core obtained from the RVE approach (right) calculated on the molecular surface of C₆₀. |J^ind| values are given in atomic units (1 a.u. = 100.63 nA T⁻¹ Å⁻²).

[14]helicene

The shielding of [14]helicene is strongly affected by its curved structure due to the overlapping and superposition of the shielding cones.⁹ The π-component induces a strong deshielding region along the helical axis that covers some rings, which significantly affects the interpretation of the local aromaticity when NICS(0) or any of its variants are used. The deshielding region is mainly caused by the π-current density flowing along the periphery of the helical structure.^35,50 NCS yields large core contributions to B^ind_z covering the entire structure,⁹ whereas RVE leads to a completely different interpretation with a core contribution located at the carbon atoms (see Fig. 7). Therefore, in large nonplanar molecules, such as helicenes, the σ-electrons contribute significantly to the shielding cone. This does not mean that the σ-electrons sustain the ring currents in helicenes. In contrast, σ-electrons respond with local shieldings at the C–C bonds, which accumulate and produce the pronounced global shielding cone in these curved structures. It has been shown that π-electrons promote the ring currents in helicenes but form a helical circulation along the edge of the molecular frame that produces a deshielding cone along the helical axis.^9,35

Fig. 7 Comparison of the core- and σ-contributions to the B^ind_z isosurface of [14]helicene calculated with the NCS (left) and the RVE (right) schemes. The isosurfaces at −15 ppm and 15 ppm of the σ-shielding cone are indicated in blue and red, respectively. The corresponding isosurfaces of the core contributions are at −3 ppm and 3 ppm, respectively.

The role of occupied-to-occupied contributions

The orbital contributions to the magnetic response depend on the gauge-origin. The paramagnetic component of the orbital current density, which formally can be written as a sum over the states in the first-order orbitals, gives rise to unphysical occupied-to-occupied transitions when the gauge-origin does not coincide with the point at which the current density is calculated.^17,18

Finally, to investigate the origin of the substantial diamagnetic response of core orbitals predicted by a scheme working with GIAOs, we have also used the NMR module of ADF.^15,32,33 In this case, orbital contributions to the shielding tensor can be divided into diamagnetic and paramagnetic terms. The paramagnetic term of the core-electron orbitals can be further analyzed for contributions from occupied-to-occupied and occupied-to-virtual orbitals excitations, and contributions from gauge transformations, according to the GIAO formulation:

This orbital analysis (Table S2 in the ESI†) is in good agreement with the NCS procedure. The different terms of Eqn 1 for B^ind_z,core(0) and NICS_core(0) of benzene, corannulene and C₆₀ are summarized in Table 4. They show that the strongly shielded response of core orbitals originate exclusively from the occupied-to-occupied term involving core-to-valence excitations, whereas the other components of the shielding tensor have minimal paramagnetic contributions of ∼1 ppm (∼0.2 ppm) to B^ind_z (NICS), in full agreement with Fowler and Steiner's affirmations.¹⁶

Table 4 The analysis of the core contributions dissected into its diamagnetic and paramagnetic components to B^ind_z(0) and NICS(0) (in parenthesis) values calculated at the PBE0/TZ2P level at the center of benzene, the centers of 5-MR and 6-MR rings of corannulene structures (D_5h and C_5v), the center of the C₆₀ cage, and the centers of each 6-MR of [14]helicene labeled from A to G from the outermost to the middle ring

Molecule		Core
		Total	occ–occ	dia + gauge + occ–vir
Benzene		−12.37 (−4.28)	−13.29 (−4.53)	0.92 (0.24)
Corannulene D5h	5-MR	−22.91 (−7.95)	−24.03 (−8.02)	1.12 (0.07)
	6-MR	−15.90 (−5.50)	−16.97 (−5.71)	1.07 (0.21)
Corannulene C5v	5-MR	−22.16 (−8.65)	−23.37 (−8.79)	1.21 (0.14)
	6-MR	−16.27 (−6.56)	−17.17 (−6.78)	0.90 (0.22)
C60		−28.62 (−28.64)	−29.16 (−29.17)	0.55 (0.53)
[14]helicene	A	−19.03 (−7.24)	−19.95 (−7.53)	0.92 (0.29)
	B	−21.95 (−8.91)	−22.85 (−9.14)	0.90 (0.22)
	C	−22.63 (−9.87)	−23.56 (−10.12)	0.93 (0.25)
	D	−22.06 (−10.55)	−22.97 (−10.78)	0.91 (0.24)
	E	−22.13 (−11.79)	−23.05 (−12.04)	0.92 (0.25)
	F	−23.13 (−14.08)	−24.07 (−14.34)	0.94 (0.27)
	G	−24.52 (−15.98)	−25.48 (−16.28)	0.97 (0.30)

---

Conclusions

Orbital dissection schemes involving CMO (or NLMO), which works on GIAOs such as the NCS analysis, result in spurious unphysical core-electron contributions due to occupied-to-occupied orbital transitions that lead to a mixing of nuclear magnetic shielding contributions from the core and σ orbitals,¹⁶ especially in nonplanar molecules. We have tackled this problem by estimating the core contribution from magnetic shielding calculations using GIAOs on highly charged molecules by removing the valence electrons (RVE). The RVE approach offers a clear representation of their contribution to the overall magnetic behavior, which can be extended to structures involving different elements from the periodic table. RVE yield the magnetic response of the core orbitals, whereas the σ-contribution was estimated by subtracting the core-electron component from the (core + σ)-contribution. RVE shows that the core-electron contributions are localized to the vicinity of the nuclei, which agrees with previous calculations using orbital contributions to the current density and the Biot–Savart integral expression but in disagreement with conclusions drawn from calculations using the NCS approach. The RVE approach can be applied in the cases where the energy gap between the lowest occupied σ orbital and the highest occupied core-electron orbital is large (>250 eV). In organic systems, this condition is usually satisfied, but in inorganic systems, especially in molecules with heavy atoms, it may not be satisfied, and there may be a significant contribution of core electrons to the total response.^51–53 In nonplanar molecules the determination of the orbital contributions is not always reliable because the molecular curvature can lead to combined σ and π characters in their orbitals. However, those highly symmetrical systems have π-type orbitals that can be easily identified, so the RVE approach can be employed to obtain the core-electron and σ-corrected contributions as well.

RVE calculations on the planar (benzene) and nonplanar molecules (corannulene, C₆₀, and [14]helicene) indicate that the core electrons do not significantly contribute to the magnetic response, despite the curvature of the π-surface. The core-electron contribution to the magnetic shielding cone and the ring-current strength is very small for the case of 1s² core orbitals. RVE on C₆₀ and [14]helicene reveals that the σ orbitals play an important role in their magnetic shielding, whereas the contribution from the core orbitals is negligible. These conclusions do not agree with those drawn from the NCS calculations. So, the RVE approach will be helpful when determining the correct orbital contributions to the magnetic response of molecules with multiple aromatic characters or of molecules containing heavier elements where the core- and σ-electron contributions are also relevant.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The work in Mexico was supported by Conacyt (Proyecto Sinergia 1561802) and in Finland by the Academy of Finland (Project 314821). We also thank Magnus Ehrnrooth foundation and the Swedish Cultural Foundation in Finland for financial support.

References

1. P. v. R. Schleyer, Introduction: Aromaticity, Chem. Rev., 2001, 101, 1115–1118.
2. G. Merino and M. Solà, Celebrating the 150th Anniversary of the Kekulé Benzene Structure, Phys. Chem. Chem. Phys., 2016, 18, 11587–11588.
3. P. Lazzeretti, Ring Currents, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88.
4. J. A. N. F. Gomes and R. B. Mallion, Aromaticity and Ring Currents, Chem. Rev., 2001, 101, 1349–1384.
5. G. Merino, T. Heine and G. Seifert, The Induced Magnetic Field in Cyclic Molecules, Chem. – Eur. J., 2004, 10, 4367–4371.
6. T. Heine, R. Islas and G. Merino, σ and π Contributions to the Induced Magnetic Field: Indicators for the Mobility of Electrons in Molecules, J. Comput. Chem., 2007, 28, 302–309.
7. R. Islas, T. Heine and G. Merino, The Induced Magnetic Field, Acc. Chem. Res., 2012, 45, 215–228.
8. F. A. L. Anet and D. J. O’Leary, The Shielding Tensor. Part I: Understanding Its Symmetry Properties, Concepts Magn. Reson., Part A, 1991, 3, 193–214.
9. M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Consequences of the Curvature on the Induced Magnetic Field: Case of Helicenes, Chem. – Eur. J., 2020, 26, 326–330.
10. N. D. Charistos and A. Muñoz-Castro, Induced Magnetic Field of Fullerenes: Role of σ- and π- Contributions to Spherical Aromatic, Nonaromatic, and Antiaromatic Character in C₆₀^q (q = 10, 0, −6, −12), and Related Alkali-Metal Decorated Building Blocks, Li₁₂C₆₀ and Na₆C₆₀, J. Phys. Chem. C, 2018, 122, 9688–9698.
11. Z. Chen, J. I. Wu, C. Corminboeuf, J. Bohmann, X. Lu, A. Hirsch and P. v. R. Schleyer, Is C₆₀ Buckminsterfullerene Aromatic?, Phys. Chem. Chem. Phys., 2012, 14, 14886–14891.
12. R. Ditchfield, Self-Consistent Perturbation Theory of Diamagnetism, Mol. Phys., 1974, 27, 789–807.
13. K. Wolinski, J. F. Hinton and P. Pulay, Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations, J. Am. Chem. Soc., 1990, 112, 8251–8260.
14. J. A. Bohmann, F. Weinhold and T. C. Farrar, Natural Chemical Shielding Analysis of Nuclear Magnetic Resonance Shielding Tensors from Gauge-Including Atomic Orbital Calculations, J. Chem. Phys., 1997, 107, 1173–1184.
15. G. Schreckenbach and T. Ziegler, Calculation of NMR Shielding Tensors Using Gauge-Including Atomic Orbitals and Modern Density Functional Theory, J. Phys. Chem., 1995, 99, 606–611.
16. E. Steiner and P. W. Fowler, On the Orbital Analysis of Magnetic Properties, Phys. Chem. Chem. Phys., 2004, 6, 261–272.
17. E. Steiner and P. W. Fowler, Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions, J. Phys. Chem. A, 2001, 105, 9553–9562.
18. E. Steiner, P. W. Fowler and R. W. A. Havenith, Current Densities of Localized and Delocalized Electrons in Molecules, J. Phys. Chem. A, 2002, 106, 7048–7056.
19. T. A. Keith and R. F. W. Bader, Calculation of Magnetic Response Properties using a Continuous Set of Gauge Transformations, Chem. Phys. Lett., 1993, 210, 223–231.
20. T. A. Keith and R. F. W. Bader, Topological Analysis of Magnetically Induced Molecular Current Distributions, J. Chem. Phys., 1993, 99, 3669–3682.
21. G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Interpreting the Behavior of the NICSzz by Resolving in Orbitals, Sign, and Positions, J. Comput. Chem., 2018, 39, 511–519.
22. J. Jusélius, D. Sundholm and J. Gauss, Calculation of Current Densities Using Gauge-Including Atomic Orbitals, J. Chem. Phys., 2004, 121, 3952–3963.
23. H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, The Gauge Including Magnetically Induced Current Method, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518.
24. D. Sundholm, H. Fliegl and R. J. F. Berger, Calculations of Magnetically Induced Current Densities: Theory and Applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 639–678.
25. C. Adamo, M. Cossi and V. Barone, An Accurate Density Functional Method for the Study of Magnetic Properties: The PBE0 Model, J. Mol. Struct. THEOCHEM, 1999, 493, 145–157.
26. F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
27. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, D. J. Fox, Gaussian 16, revision D.01, Gaussian Inc., 2016.
29. M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, 2016, Cinvestav-Merida, Mexico.
30. Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888.
31. F. Weinhold, C. R. Landis and E. D. Glendening, What Is NBO Analysis and How Is It Useful?, Int. Rev. Phys. Chem., 2016, 35, 399–440.
32. G. Schreckenbach, On the Relation between a Common Gauge Origin Formulation and the GIAO Formulation of the NMR Shielding Tensor, Theor. Chem. Acc., 2002, 108, 246–253.
33. C. M. Widdifield and R. W. Schurko, Understanding Chemical Shielding Tensors Using Group Theory, MO Analysis, and Modern Density-Functional Theory, Concepts Magn. Reson., Part A, 2009, 34A(2), 91–123.
34. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
35. M. Orozco-Ic, M. Dimitrova, J. Barroso, D. Sundholm and G. Merino, Magnetically Induced Ring-Current Strengths of Planar and Nonplanar Molecules: New Insights from the Pseudo-π Model, J. Phys. Chem. A, 2021, 125, 5753–5764.
36. M. Dimitrova and D. Sundholm, Current density, current-density pathways, and molecular aromaticity, in Aromaticity: Modern Computational Methods and Applications, Elsevier, 2021, pp. 155–194.
37. A. G. Papadopoulos, N. D. Charistos and A. Muñoz-Castro, Magnetic Response of Aromatic Rings Under Rotation: Aromatic Shielding Cone of Benzene Upon Different Orientations of the Magnetic Field, ChemPhysChem, 2017, 18, 1499–1502.
38. A. Soncini, R. G. Viglione, R. Zanasi, P. W. Fowler and L. W. Jenneskens, Efficient mapping of ring currents in fullerenes and other curved carbon networks, C. R. Chim., 2006, 9, 1085–1093.
39. G. Monaco, F. F. Summa and R. Zanasi, Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems, J. Chem. Inf. Model., 2021, 61, 270–283.
40. P. W. Fowler and E. Steiner, Pseudo-π Currents: Rapid and Accurate Visualisation of Ring Currents in Conjugated Hydrocarbons, Chem. Phys. Lett., 2002, 364, 259–266.
41. N. D. Charistos, A. Muñoz-Castro and M. P. Sigalas, The Pseudo-π Model of the Induced Magnetic Field: Fast and Accurate Visualization of Shielding and Deshielding Cones in Planar Conjugated Hydrocarbons and Spherical Fullerenes, Phys. Chem. Chem. Phys., 2019, 21, 6150–6159.
42. M. Antić, S. Đorđević, B. Furtula and S. Radenković, Magnetically Induced Current Density in Nonplanar Fully Benzenoid Hydrocarbons, J. Phys. Chem. A, 2020, 124, 371–378.
43. P. W. Fowler, W. Myrvold, C. Gibson, J. Clarke and W. H. Bird, Ring-Current Maps for Benzenoids: Comparisons, Contradictions, and a Versatile Combinatorial Model, J. Phys. Chem. A, 2020, 124, 4517–4533.
44. M. Orozco-Ic and G. Merino, The Magnetic Response of Starphenes, Chemistry, 2021, 3, 1381–1391.
45. M. Orozco-Ic, R. R. Valiev and D. Sundholm, Non-intersecting ring currents in [12]infinitene, Phys. Chem. Chem. Phys., 2022, 24, 6404–6409.
46. A. Reisi-Vanani and A. A. Rezaei, Evaluation of the Aromaticity of Non-Planar and Bowl-Shaped Molecules by NICS Criterion, J. Mol. Graphics Modell., 2015, 61, 85–88.
47. E. Steiner, P. W. Fowler and L. W. Jenneskens, Counter-Rotating Ring Currents in Coronene and Corannulene, Angew. Chem., Int. Ed., 2001, 40, 362–366.
48. A. Acocella, R. W. A. Havenith, E. Steiner, P. W. Fowler and L. W. Jenneskens, A Simple Model for Counter-Rotating Ring Currents in [n]circulenes, Chem. Phys. Lett., 2002, 363, 64–72.
49. M. P. Johansson, J. Jusélius and D. Sundholm, Sphere Currents of Buckminsterfullerene, Angew. Chem., Int. Ed., 2005, 44, 1843–1846.
50. E. Cherni, B. Champagne, S. Ayadi and V. Liégeois, Magnetically-Induced Current Density Investigation in Carbohelicenes and Azahelicenes, Phys. Chem. Chem. Phys., 2019, 21, 14678–14691.
51. Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, All-Metal Aromaticity: Revisiting the Ring Current Model among Transition Metal Clusters, J. Chem. Theory Comput., 2013, 9, 4789–4796.
52. C. Foroutan-Nejad, J. Vícha and A. Ghosh, Relativity or Aromaticity? A First-Principles Perspective of Chemical Shifts in Osmabenzene and Osmapentalene Derivatives, Phys. Chem. Chem. Phys., 2020, 22, 10863–10869.
53. G. Periyasamy, N. A. Burton, I. H. Hillier and J. M. H. Thomas, Electron Delocalization in the Metallabenzenes: A Computational Analysis of Ring Currents, J. Phys. Chem. A, 2008, 112(26), 5960–5972.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 with dJ^ind/dr plots of corannulene is reported. Table S1 shows the Δ_Lσ-Hcore values for all systems and Table S2 shows the orbital components of the B^ind_z(0) and NICS(0) values computed with ADF's NMR module. See DOI: https://doi.org/10.1039/d1cp05713h

---