 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Interactions of Si+(2PJ) and Ge+ (2PJ) with rare gas atoms (He–Rn): interaction potentials, spectroscopy, and ion transport coefficients†
Alexander R.
Davies
a,
Aiden
Cranney
a,
Larry A.
Viehland
 *b and
Timothy G.
Wright
*b and
Timothy G.
Wright
 *a
*a
aSchool of Chemistry, University Park, University of Nottingham, Nottingham NG7 2RD, UK. E-mail: tim.wright@nottingham.ac.uk
bScience Department, Chatham University, Pittsburgh, Pennsylvania 15232, USA. E-mail: viehland@Chatham.edu
First published on 28th February 2022
Abstract
Accurate interatomic potentials were calculated for the interaction of a singly-charged silicon cation, Si+, with a single rare gas atom, RG (RG = Kr–Rn), as well as a singly-charged germanium cation, Ge+, with a single rare gas atom, RG (RG = He–Rn). The RCCSD(T) method and basis sets of quadruple-ζ and quintuple-ζ quality were employed; each interaction energy is counterpoise corrected and extrapolated to the basis set limit. The lowest electronic term (2P) of each cation was considered, and the interatomic potentials calculated for the diatomic terms that arise from these: 2Π and 2Σ+. Additionally, the interatomic potentials for the respective spin–orbit levels were calculated, and the effect on the spectroscopic parameters was examined. Variations in several spectroscopic parameters with the increasing atomic number of RG were examined. The presence of incipient chemical interaction was also examined via Birge–Sponer-like plots and various population analyses across the series. In the cases of heavier RG, these were consistent with a small amount of electron transfer from the heavier RG atom to the cation, rationalizing the spin–orbit splittings. This was also supported by the observed larger-than-expected spin–orbit splittings for the Si+–RG complexes. Finally, each set of RCCSD(T) potentials including spin–orbit coupling was employed to calculate transport coefficients for the cation moving through a bath of the RG. The calculated ion mobilities showed significant differences for the two atomic spin–orbit states, arising from subtle changes in the interaction potentials.
1. Introduction
Silicon and germanium have wide-ranging applications in electronic components, and the fabrication of these often involves the need to produce thin layers, such as by laser ablation or plasma-enhanced chemical vapour deposition (CVD).1–4 In such systems, Si+ or Ge+ (as well as many other) ions may be expected to be present, although these are not always explicitly considered. Attempts to model and refine the chemical processes depend on being able to determine reaction kinetics and model the chemistry comprehensively and reliably – such modelling and kinetic studies with atmospheric ligands has been carried out by Plane and co-workers for silicon5 and also several metal ions.6–12Silicon atoms are present in the Earth's upper atmosphere as a result of the ablation of meteoroids.13 Rapid reaction of Si with O2 or O3 leads to the formation of SiO, and then SiO+ by subsequent charge transfer; the reaction between SiO+ and O then leads to the production of Si+ ions in the upper atmosphere.5 This leads to Si+ having an abundance similar to those of Fe+ and Mg+ above 100 km, although very little is found below 95 km,5 which has attracted significant interest.1,5,14 Silicon ions are also present in both the solar wind15 and dense interstellar clouds, where ion–molecule reactions between Si+ and H2O are thought to be key in forming SiO16 a key silicon-containing species.17 Silicon ion chemistry is also important in other applications,18 such as flames19 and in state-of-the-art electronics fabrication.20
Germanium is known to be present in meteorites,21 and Ge+ has also been detected in the interstellar medium (ISM).22 Rationalizing concentrations observed in the latter depends on understanding the process of depletion, whereby gas phase ions are trapped within dust particles.23 Efforts to study this phenomenon are ongoing, but understanding is hampered by the uncertainty of the requisite data.24 Additionally, although apparently not considered in the literature, cooling of both Si+ and Ge+ ions in astrochemistry, via interaction/complexation with prevalent He, may be possible – in the same way as has been discussed with C+ ions.25,26 Also, for RG = rare gas, both Ge+–RG and Ge2+–RG (RG = Ne–Xe) have been detected in mass spectrometric experiments,27 indicating that these are relatively stable species; however, no spectroscopic studies of these species exists, to the authors’ knowledge.
Obtaining detailed kinetic information for modelling atmospheric or interstellar chemistry often involves flow tube experiments, with such having been carried out for Si+.28–30 In these experiments, obtaining accurate ion mobility data for Si+ in RG is important for determining non-chemical loss mechanisms, as the flow gases are usually rare gases, and the Ge+ results herein will be of use in corresponding kinetics studies. Mobilities also determine the relative energy of ions in flow and drift tubes,31 and so there are wider incentives for obtaining such data.32
Molecular complexes are often described as being “pre-reactive” species and can be used to interrogate nascent interactions that occur prior to full chemical reaction. The interactions of atomic cations with rare gas atoms are amongst the simplest interactions that can be investigated, and although even the lightest RG atoms have been hypothesised to exhibit chemical interactions (see, for example ref. 33 and 34), in the present work these evolve from physical interactions, with the weakly-polarizable He atom, with possibility of chemical interactions only occurring for the more-polarizable Kr, Xe and Rn atoms.
The initial stage in investigating such interactions is through the determination of the interatomic potentials. These can then be used to determine values of various spectroscopic parameters, and the trends in these can reveal the changing nature of the interaction, for example as the atomic number of the RG atom increases. Additionally, the electronic wavefunctions can be analysed to obtain populations, and to determine whether electrons remain localized on a moiety or are shared between the interacting species. Although delocalization of electron density from one nuclear centre is an obvious indicator of chemical interaction, hybridization can also be considered as a chemical effect.35 Reliable interaction potentials can also be employed in the calculation of a range of quantities including collision cross sections – important in the calculation of ion transport data and atomic collisional energy transfer.
In the present paper, we extend our earlier work on the C+–RG (RG = He–Xe)36,37 and Si+–RG (RG = He–Ar)38 complexes. We consider Si+ interacting with the heavier RG atoms (RG = Kr–Rn) and Ge+ interacting with RG = He–Rn. In each case, we shall investigate the interatomic potentials that arise from the lowest atomic asymptotes of the open-shell M+–RG complex, M+(2PJ) + RG(1S0), J = ½ and ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) , M = Si or Ge. The asymptotes arise from the closed-shell ground state configuration of the RG atom, and the lowest energy electronic configuration for the M+: [Ne]3s23p1 and [Ar]3d104s24p1, for M = Si and Ge, respectively, once the spin–orbit interaction is included. From these interatomic potentials, we shall obtain accurate spectroscopic constants and investigate whether the spin–orbit interaction affects these significantly. For each of the two spin–orbit states arising from the ground electronic states of the atomic cations, the spin–orbit potentials are also used to obtain transport coefficients for the cation moving through a bath of RG.
, M = Si or Ge. The asymptotes arise from the closed-shell ground state configuration of the RG atom, and the lowest energy electronic configuration for the M+: [Ne]3s23p1 and [Ar]3d104s24p1, for M = Si and Ge, respectively, once the spin–orbit interaction is included. From these interatomic potentials, we shall obtain accurate spectroscopic constants and investigate whether the spin–orbit interaction affects these significantly. For each of the two spin–orbit states arising from the ground electronic states of the atomic cations, the spin–orbit potentials are also used to obtain transport coefficients for the cation moving through a bath of RG.
When a closed-shell RG atom interacts with a cation, degenerate atomic states may become split. In the present cases, initially in the absence of the spin–orbit interaction, the 2P ground electronic term of M+ gives rise to a lower-energy 2Π and a higher-energy 2Σ+ diatomic term. However, it is, of course, the spin–orbit levels that are present experimentally. Upon the inclusion of the spin–orbit interaction, the M+(2P) term splits into a lower 2P1/2 and a higher 2P3/2 level, with separations of 287.24 cm−1 and 1767.36 cm−1, for M = Si and Ge, respectively.39 The spin–orbit interaction causes the 2Π diatomic term to split into 2Π1/2 and 2Π3/2 levels, and the 2Σ+ term becomes 2Σ1/2+; the lowest 2Π1/2 level correlates to the M+(2P1/2) + RG(1S0) asymptote, while the 2Π3/2 and 2Σ1/2+ levels both correlate to M+(2P3/2) + RG(1S0).
Since Ω levels of the same value can mix, an interaction between the 2Π1/2 and 2Σ1/2+ levels is expected. At most internuclear separations, the mixing of these is expected to be small, and so we consider the resulting Ω = 1/2 levels as perturbed versions of the original 2Π1/2 and 2Σ1/2+ levels, and maintain these Russell–Saunders labels. In principle, additional, smaller mixings occur, involving higher energy atomic states, but these are not considered here.
To our knowledge there has been no published work, experimental or theoretical, on Si+–RG (RG = Kr–Rn), or Ge+–RG (RG = He–Rn), but we shall comment on some published spectroscopic results for Si–Ar and Ge–Ar.
2. Computational methodology
2.1 Quantum chemistry
Interaction potentials with and without the spin–orbit interaction have been computed for the diatomic states arising from the lowest atomic asymptotes of M+–RG in the following manner. Energies over a wide range of internuclear separations within the range 0.8–100 Å were evaluated at the RCCSD(T) level of theory as implemented in MOLPRO.40,41 Standard basis sets were employed: aug-cc-pVXZ for He;42 aug-cc-pwCVXZ43 basis sets (X = Q, 5) for Ne, Si and Ar; while for Ge, Kr, Xe, and Rn, small-core relativistic effective core potentials (ECPs) were employed to describe the innermost electrons (ECP10MDF for Ge and Kr, ECP28MDF for Xe and ECP60MDF for Rn) together with the standard aug-cc-pwCVXZ-PP valence basis sets44,45 to describe the non-ECP electrons. In the RCCSD(T) treatment, the following orbitals were frozen for Si+–RG: Si (1s2s2p); Kr (3s3p3d); Xe(4s4p4d); and Rn (5s5p5d). For the RCCSD(T) calculations on Ge+–RG, the following orbitals were frozen: Ge (3s3p); Ne (1s); Ar (1s2s2p); Kr (3s3p); Xe(4s4p); and Rn (5s5p). Interaction energies at each separation were counterpoise (CP) corrected to account for basis set superposition error. To include the spin–orbit interaction, the CP-corrected RCCSD(T) interaction energies were used as the unperturbed eigenvalues of the Breit-Pauli spin–orbit matrix as implemented46 in MOLPRO at each separation, using the quadruple-ζ and quintuple-ζ basis sets as described. The spin–orbit calculation employed state-averaged complete-active space self-consistent field (SA-CASSCF) wavefunctions of the lowest 2Π and 2Σ+ states. In the latter calculations, for Si+–RG, the following orbitals were frozen (i.e. doubly occupied and not optimized): Si+(1s2s2p); Kr (3s3p3d); Xe (4s4p4d); Rn (5s5p5d). For Ge+–RG (RG = Ar–Rn), the following orbitals were frozen: Ge (3s3p); Ar(1s2s2p); Kr (3s3p); Xe (4s4p); Rn (5s5p), while for Ge+–RG (RG = He and Ne), all orbitals outside of the ECP were included in the correlation treatment. Finally, both the spin–orbit and non-spin–orbit CP-corrected interaction potentials were point-by-point extrapolated to the basis set limit utilizing the two-point (cubic) formula of Halkier et al.47,48 at each separation; these final potentials are denoted RCCSD(T)/aV∞Z.We note that the ECP and basis sets for Ge and RG atoms have been tested thoroughly in the original studies.44,45 In addition, we experimented with the frozen orbitals, with the active spaces indicated above being those that ensured all orbitals remained as either correlated or not in the calculations; in particular, we observed that there was sometimes energetic overlap between the M+ and RG atomic orbitals, and in such cases, the active space had to be expanded to include all such orbitals; failure to do so led to discontinuities in the potential energy curves at certain internuclear separations. The core electrons are not expected to contribute to the relatively weak interactions covered in the present work.
Potentials were calculated with default convergence thresholds in MOLPRO, except for the Ge+–He and Ge+–Ne potentials, where the convergence was tightened to ensure smooth curves over a wide-enough range, with convergence of the energy to 10−12Eh, orbitals in the SCF program to 10−8 and the CCSD coefficients to 10−7. For all systems, at the longest R values, the curves lost their smoothness; as a consequence, we omit the data for these regions in the reported potentials – see ESI.†
It is generally accepted that T1 diagnostic values <0.02 indicate that there is little multireference character in the CCSD electronic wavefunction.49 In the present case, they are <0.02 for all except a small number of cases, which were localized to the 2Σ+ state, where values crept above this value high on the repulsive wall (generally <0.04). This is not expected to affect the calculated spectroscopic parameters, and will only affect the ion transport properties at temperatures much higher than those that are used experimentally. We do note, however, that the spin–orbit splittings of the 2ΠΩ states (see Section 3.2) are supportive of some charge transfer in these complexes.
Population analyses were carried out for the X2Π state at the Re value determined from the RCCSD(T)/aV∞Z potential, using standard Mulliken population analysis. Additionally, we used the NBO program50 embedded in Gaussian 1651 to undertake a natural population analysis (NPA) for each of the complexes. Charge analyses were also undertaken with Bader's atoms-in-molecules (AIM) method, employing the program AIMAll.52 In all cases, triple-ζ quality versions of the basis sets employed for the potential energy curves above were used, and the QCISD density (from Gaussian 16) was employed for the NPA and AIM analyses.
Rovibrational energy levels were obtained from the calculated RCCSD(T)/aV∞Z interaction potentials using the LEVEL program.53 The lowest two relevant levels were used in each case to obtain the spectroscopic constants from standard formulae. We calculated these for 28Si+ and 74Ge+ with the most abundant, naturally-occurring RG isotope in each case.
2.2 Transport coefficients
We calculated the transport cross sections for Si+ and Ge+ travelling through a bath of each RG from the respective RCCSD(T)/aV∞Z ab initio interaction potential energy curves as functions of the ion-neutral collision energy using the classical-mechanical program PC54 that is an improved version of the earlier program QVALUES.55,56 The cross sections converged within 0.05% in all cases. The range of collision energies covered was from 1 × 10−9Eh to the energy calculated at the smallest internuclear separation, always above 1 Eh, depending on the system. Only the potentials of the spin–orbit states were considered for these calculations.The cross sections as a function of collision energy were used in the Gram-Charlier program GC55,57,58 to determine the reduced mobility, K0, and the other gaseous ion transport coefficients as functions of E/n0 (the ratio of the electric field to the gas number density) at gas temperatures, T, of 100, 200, 300, 400 and 500 K for all species, and additionally 4.35 K for systems containing He. The range of E/n0 covered was 0.01–1000 Td (1 Td = 10−21 V m2). We also used program VARY59 to determine the zero-field values of the mobility and the ion diffusion coefficient as a function of T from 0.001 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Calculations were performed separately for all of the naturally-occurring isotopes for each cation, while each RG was assumed to be composed of the naturally-occurring mixture of isotopes. The calculated mobilities are generally precise to within the precision of the cross sections at E/n0 values below 20 Td. The results are progressively less precise as E/n0 increases to 1000 Td. These details, as well as the mobilities and other transport properties, can be obtained from the tables placed in an online database.60 The accuracy of the calculated mobilities is the same as the reported precision if the interaction potentials are correct; owing to the possible errors in these (see below), we expect the transport properties to be accurate only within 5%.
000 K. Calculations were performed separately for all of the naturally-occurring isotopes for each cation, while each RG was assumed to be composed of the naturally-occurring mixture of isotopes. The calculated mobilities are generally precise to within the precision of the cross sections at E/n0 values below 20 Td. The results are progressively less precise as E/n0 increases to 1000 Td. These details, as well as the mobilities and other transport properties, can be obtained from the tables placed in an online database.60 The accuracy of the calculated mobilities is the same as the reported precision if the interaction potentials are correct; owing to the possible errors in these (see below), we expect the transport properties to be accurate only within 5%.
For cations in the 2P1/2 state, the cross-sections were calculated from the 2Π1/2 potential, while for the 2P3/2 state, cross-sections were obtained as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weighting of those arising from the 2Π3/2 and 2Σ1/2+ potentials. In addition, we also undertook calculations for the case where both spin–orbit states were present with equal concentrations, these “averaged spin–orbit” values are denoted ASO and arise from a 1
1 weighting of those arising from the 2Π3/2 and 2Σ1/2+ potentials. In addition, we also undertook calculations for the case where both spin–orbit states were present with equal concentrations, these “averaged spin–orbit” values are denoted ASO and arise from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weighting of the cross-sections arising from the three spin–orbit states.
1 weighting of the cross-sections arising from the three spin–orbit states.
Additionally, for the transport calculations, each spin–orbit interaction potential was shifted such that the interaction energies merged smoothly with the appropriate 1/R4 ion-induced dipole interaction energy at 30 Å. This was done to avoid round-off errors that could prevent the transport cross sections from smoothly approaching the ion/induced-dipole values that are correct at zero energy for the transport cross sections.
3. Results and discussion
3.1 Spectroscopic constants for Si+–RG and Ge+–RG
All of the calculated spin–orbit and non-spin–orbit RCCSD(T)/aV∞Z potentials are presented in the ESI.†Portions of these potentials, showing the regions around the potential energy minima, are shown in Fig. 1 for Si+(2P)–RG (RG = He–Rn). The potentials for Si+–RG (RG = He–Ar) were shown and discussed in ref. 38, and an analysis of the spectroscopic constants was given therein. (The Si+–RG potential data were not given in ref. 38 for RG = He–Ar, and so they are included in the ESI† herein, for completeness.) Similarly, portions of the calculated non-spin–orbit and spin–orbit RCCSD(T)/aV∞Z potentials are shown in Fig. 2 for Ge+(2P)–RG (RG = He–Rn). The calculated values for the atomic cation spin–orbit separation of the 2P3/2 and 2P1/2 states were 256.5 cm−1 for Si+, which compares well to the experimental value39 of 287.24 cm−1. For Ge+, we calculate values of 1724 cm−1 (RG = Ar–Rn), while a value of 1734 cm−1 was obtained for RG = He and Ne, where tighter convergence criteria were employed. For those latter calculations, all non-ECP orbitals of Ge+ were included in the SA-CASSCF procedure used to generate the wavefunctions for the spin–orbit calculations – these compare well to the experimental value of 1767.36 cm−1.39 The agreement is good enough for our purposes, with the differences likely arising from higher-order interactions than those treated here, basis set incompleteness, and also the neglect of inclusion of higher-energy spin–orbit states.
From the plots in Fig. 1 and 2, it can be seen that the X2Π states are always much more strongly bound than are the A2Σ+ ones. For the 2Π state, the unpaired electron is positioned perpendicular to the internuclear axis, so allowing the RG atom to get closer to, and hence to interact more strongly with, the positive charge located on Si+ or Ge+. Similar observations were made for the C+–RG complexes (see ref. 26 and 37). The resultant equilibrium position arises from a balance of electrostatic attractive and repulsive interactions, as well as Pauli repulsion and has been discussed by Bellert and Breckenridge in ref. 61. The spectroscopic constants obtained from the non-spin–orbit interaction potentials are presented in Table 1 for Si+–RG and in Table 2 for Ge+–RG; for the former, we have included the values from ref. 38 for Si+–RG (RG = He–Ar), for comparison.
| State | R e/Å | D e/cm−1 | D 0/cm−1 | ω e/cm−1 | ω e x e/cm−1 | k/N m−1 | B e/cm−1 | α/cm−1 | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| a Symbols in the headers have their usual spectroscopic meaning. See text for further details, as well as a discussion of the trends in these values – see also Fig. 3. Spin–orbit states are labelled with their Ω quantum number, while non-spin–orbit states have no Ω quantum number given. | |||||||||
| Si+–He | |||||||||
| 2Π1/2 | 2.803 | 175 | 131 | 97.3 | 17.36 | 1.95 | 0.6128 | 1.084 × 10−1 | 38 |
| 2Π3/2 | 2.769 | 246 | 193 | 112.5 | 13.93 | 2.61 | 0.6279 | 7.887 × 10−2 | 38 |
| 2Π | 2.769 | 246 | 193 | 112.5 | 13.93 | 2.61 | 0.6279 | 7.920 × 10−2 | 38 |
| 2Σ1/2+ | 3.703 | 60 | 38 | 49.5 | 11.93 | 0.51 | 0.3511 | 8.477 × 10−2 | 38 |
| 2Σ+ | 3.861 | 46 | 29 | 40.4 | 10.19 | 0.34 | 0.3229 | 8.374 × 10−2 | 38 |
| Si+–Ne | |||||||||
| 2Π1/2 | 2.732 | 459 | 415 | 90.3 | 4.947 | 5.60 | 0.1937 | 9.743 × 10−3 | 38 |
| 2Π3/2 | 2.724 | 538 | 492 | 93.1 | 4.333 | 5.96 | 0.1948 | 9.006 × 10−3 | 38 |
| 2Π | 2.724 | 538 | 492 | 93.1 | 4.332 | 5.96 | 0.1948 | 9.002 × 10−3 | 38 |
| 2Σ1/2+ | 3.648 | 129 | 110 | 40.7 | 4.104 | 1.14 | 0.1086 | 9.248 × 10−3 | 38 |
| 2Σ+ | 3.763 | 103 | 87 | 33.6 | 3.444 | 0.78 | 0.1021 | 9.387 × 10−3 | 38 |
| Si+–Ar | |||||||||
| 2Π1/2 | 2.611 | 2686 | 2603 | 167.9 | 2.585 | 27.3 | 0.1503 | 2.492 × 10−3 | 38 |
| 2Π3/2 | 2.611 | 2770 | 2686 | 168.1 | 2.572 | 27.4 | 0.1503 | 2.574 × 10−3 | 38 |
| 2Π | 2.611 | 2771 | 2687 | 168.1 | 2.573 | 27.4 | 0.1503 | 2.492 × 10−3 | 38 |
| 2Σ1/2+ | 3.767 | 455 | 427 | 55.2 | 1.784 | 2.95 | 0.07219 | 2.207 × 10−3 | 38 |
| 2Σ+ | 3.803 | 394 | 369 | 50.5 | 1.872 | 2.48 | 0.07083 | 2.453 × 10−3 | 38 |
| Si+–Kr | |||||||||
| 2Π1/2 | 2.651 | 4237 | 4146 | 183.4 | 1.880 | 41.6 | 0.1143 | 1.289 × 10−3 | Present work |
| 2Π3/2 | 2.656 | 4290 | 4200 | 182.6 | 1.874 | 41.2 | 0.1139 | 1.293 × 10−3 | Present work |
| 2Π | 2.654 | 4307 | 4216 | 183.0 | 1.871 | 41.4 | 0.1141 | 1.199 × 10−3 | Present work |
| 2Σ1/2+ | 3.792 | 652 | 625 | 54.7 | 1.188 | 3.70 | 0.05588 | 1.268 × 10−3 | Present work |
| 2Σ+ | 3.812 | 582 | 556 | 51.9 | 1.306 | 3.33 | 0.05529 | 1.370 × 10−3 | Present work |
| Si+–Xe | |||||||||
| 2Π1/2 | 2.756 | 6541 | 6439 | 202.9 | 1.408 | 56.0 | 0.09616 | 7.313 × 10−4 | Present work |
| 2Π3/2 | 2.768 | 6502 | 6402 | 200.6 | 1.395 | 54.7 | 0.09532 | 7.557 × 10−4 | Present work |
| 2Π | 2.762 | 6563 | 6462 | 201.7 | 1.402 | 55.3 | 0.09574 | 7.717 × 10−4 | Present work |
| 2Σ1/2+ | 3.809 | 1002 | 972 | 61.2 | 1.077 | 5.09 | 0.05034 | 8.569 × 10−4 | Present work |
| 2Σ+ | 3.816 | 913 | 892 | 59.9 | 1.156 | 4.88 | 0.05016 | 9.341 × 10−4 | Present work |
| Si+–Rn | |||||||||
| 2Π1/2 | 2.795 | 8026 | 7921 | 210.3 | 1.214 | 64.8 | 0.08685 | 6.210 × 10−4 | Present work |
| 2Π3/2 | 2.835 | 7607 | 7506 | 201.7 | 1.173 | 59.6 | 0.08442 | 5.874 × 10−4 | Present work |
| 2Π | 2.817 | 7823 | 7721 | 205.0 | 1.178 | 61.5 | 0.08550 | 6.201 × 10−4 | Present work |
| 2Σ1/2+ | 3.737 | 1306 | 1272 | 67.4 | 1.117 | 6.44 | 0.04858 | 8.137 × 10−4 | Present work |
| 2Σ+ | 3.737 | 1219 | 1186 | 66.6 | 1.164 | 6.50 | 0.04858 | 8.113 × 10−4 | Present work |
| State | R e/Å | D e/cm−1 | D 0/cm−1 | ω e/cm−1 | ω e x e/cm−1 | k/N m−1 | B e/cm−1 | α/cm−1 |
|---|---|---|---|---|---|---|---|---|
| a Values all obtained in the present work. Symbols in the headers have their usual spectroscopic meaning. See text for further details, as well as a discussion of the trends in these values – see also Fig. 3. Spin–orbit states are labelled with their Ω quantum number, while non-spin–orbit states have no Ω quantum number given. | ||||||||
| Ge+–He | ||||||||
| 2Π1/2 | 3.183 | 113 | 86 | 59.6 | 8.273 | 0.79 | 0.4382 | 6.170 × 10−2 |
| 2Π3/2 | 2.706 | 289 | 232 | 122.4 | 14.07 | 3.35 | 0.6063 | 6.937 × 10−2 |
| 2Π | 2.708 | 288 | 231 | 122.1 | 14.07 | 3.33 | 0.6054 | 6.937 × 10−2 |
| 2Σ1/2+ | 3.695 | 60 | 40 | 45.5 | 10.04 | 0.46 | 0.3252 | 7.266 × 10−2 |
| 2Σ+ | 3.916 | 44 | 28 | 37.2 | 9.107 | 0.31 | 0.2895 | 7.218 × 10−2 |
| Ge+–Ne | ||||||||
| 2Π1/2 | 2.933 | 297 | 273 | 49.3 | 2.261 | 2.26 | 0.1245 | 7.221 × 10−3 |
| 2Π3/2 | 2.718 | 586 | 544 | 87.5 | 3.523 | 7.10 | 0.1450 | 5.661 × 10−3 |
| 2Π | 2.719 | 585 | 543 | 87.4 | 3.518 | 7.09 | 0.1449 | 5.552 × 10−3 |
| 2Σ1/2+ | 3.590 | 136 | 119 | 34.8 | 2.817 | 1.12 | 0.08312 | 5.999 × 10−3 |
| 2Σ+ | 3.802 | 100 | 86 | 28.1 | 2.476 | 0.73 | 0.07411 | 5.797 × 10−3 |
| Ge+–Ar | ||||||||
| 2Π1/2 | 2.714 | 2091 | 2029 | 125.2 | 1.954 | 24.0 | 0.08823 | 1.359 × 10−3 |
| 2Π3/2 | 2.697 | 2581 | 2515 | 132.6 | 1.743 | 26.9 | 0.08935 | 1.212 × 10−3 |
| 2Π | 2.698 | 2580 | 2514 | 132.3 | 1.742 | 26.8 | 0.08928 | 1.197 × 10−3 |
| 2Σ1/2+ | 3.660 | 531 | 506 | 50.7 | 1.474 | 3.92 | 0.04852 | 1.243 × 10−3 |
| 2Σ+ | 3.843 | 380 | 361 | 39.3 | 1.187 | 2.37 | 0.04400 | 1.225 × 10−3 |
| Ge+–Kr | ||||||||
| 2Π1/2 | 2.746 | 3352 | 3290 | 125.4 | 1.150 | 36.4 | 0.05689 | 5.148 × 10−4 |
| 2Π3/2 | 2.740 | 3861 | 3797 | 128.8 | 1.066 | 38.4 | 0.05714 | 4.920 × 10−4 |
| 2Π | 2.739 | 3867 | 3803 | 128.7 | 1.066 | 38.4 | 0.05718 | 4.979 × 10−4 |
| 2Σ1/2+ | 3.692 | 772 | 748 | 47.9 | 0.8615 | 5.32 | 0.03147 | 5.096 × 10−4 |
| 2Σ+ | 3.856 | 554 | 535 | 37.0 | 0.7123 | 3.17 | 0.02885 | 5.216 × 10−4 |
| Ge+–Xe | ||||||||
| 2Π1/2 | 2.838 | 5338 | 5271 | 133.8 | 0.7588 | 50.0 | 0.04418 | 2.418 × 10−4 |
| 2Π3/2 | 2.842 | 5824 | 5757 | 134.9 | 0.7273 | 50.8 | 0.04406 | 2.571 × 10−4 |
| 2Π | 2.838 | 5859 | 5791 | 135.2 | 0.7289 | 51.0 | 0.04418 | 2.544 × 10−4 |
| 2Σ1/2+ | 3.752 | 1186 | 1161 | 51.0 | 0.5633 | 7.25 | 0.02528 | 2.564 × 10−4 |
| 2Σ+ | 3.874 | 863 | 843 | 40.4 | 0.5421 | 4.55 | 0.02371 | 3.253 × 10−4 |
| Ge+–Rn | ||||||||
| 2Π1/2 | 2.865 | 6605 | 6539 | 133.5 | 0.5997 | 58.2 | 0.03703 | 2.088 × 10−4 |
| 2Π3/2 | 2.899 | 6831 | 6766 | 130.3 | 0.5632 | 55.5 | 0.03617 | 1.864 × 10−4 |
| 2Π | 2.883 | 7003 | 6937 | 132.1 | 0.5675 | 57.0 | 0.03657 | 1.904 × 10−4 |
| 2Σ1/2+ | 3.714 | 1546 | 1520 | 52.5 | 0.4271 | 8.99 | 0.02204 | 1.738 × 10−4 |
| 2Σ+ | 3.810 | 1120 | 1099 | 42.5 | 0.4731 | 5.89 | 0.02094 | 2.393 × 10−4 |
Below, we shall comment on the trends in four of the key parameters. Once spin–orbit interaction is included, then we see significant changes in the parameters for the 2Σ1/2+ and 2Π1/2 states, when compared to the corresponding non-spin–orbit states, with the 2Σ1/2+ state generally becoming more-strongly bound, and the 2Π1/2 state generally becoming more-weakly bound, owing to the mixing between these same-Ω states. Here, we expect the parameters for the 2Π3/2 state to be the same as for the 2Π state, since there are no other Ω = 3/2 states with which to interact, and this is largely the case for RG = He–Ar, but with small deviations occurring for the cases with the heavier RG, particularly for Si+–RG. Such deviations were also seen for C+–RG,37 and are commented on later.
For the non-spin–orbit potentials, we first consider the trends in Re, which are presented graphically in Fig. 3. For each of Si+–RG and Ge+–RG, the trends are not monotonically increasing with the atomic number of RG, as might have been expected from their increasing radius. This is due to a balance of that trend with the increasing strength of interaction, arising from the concomitant increase of the polarizability of the RG atom. As a consequence of this balance, the Re values for the 2Π states of Si+–RG slightly decrease before increasing, while for Ge+–RG the values are almost constant initially, before rising. Thus, for the 2Π states, we conclude that the size of the RG atom eventually dominates Re for the gases with higher atomic numbers, outweighing the effect of the increasing polarizability. The trends are similar, but not identical, for the 2Σ+ states, with notably a small dip in the value of Re between RG = Xe and Rn for both Si+–RG and Ge+–RG, emphasising the subtle balance between the aforementioned factors. In contrast, for both the 2Π and 2Σ+ states, the De values are dominated by the increasing RG polarizability throughout. Similar, but not identical, trends are seen for the 2Π and 2Σ+ states, with the 2Σ+ state being more-weakly bound and with a significantly longer Re values in all cases, in line with the orientation of the unpaired valence p electron, as mentioned previously.
The trends in ωe are also non-monotonic, but this time it is the increasing mass of the RG atom that counteracts the increasing strength of interaction: once the mass effect is removed by calculating the force constants, the trends in k are very similar to those of De, as expected – see Fig. 3. Again, there are similar, but slightly different trends observed for the 2Π and 2Σ+ states, with the 2Σ+ state having a significantly smaller ωe value in all cases, and a lower k value, in line with the weaker interaction.
We have also used the LEVEL program53 to calculate the bound vibrational levels for both the spin–orbit and non-spin–orbit potentials, and these are presented in the ESI.† In Fig. 4 and 5, for both the 2Σ+ and 2Π states, we plot the vibrational energy level spacings against v + 1 (Birge–Sponer-like plots), for all Si+–RG and Ge+–RG complexes, except for RG = He, where there were very few bound levels (see ESI†). On these diagrams, the solid straight line represents the expected trend for levels obeying the vibrational energy expression arising from the Morse potential, truncated at the quadratic term, with values of ωe and ωexe obtained from the lowest two vibrational energy levels (these values are given in Tables 1 and 2). It can be seen in all cases that the lower v values follow this line closely, but that there are significant deviations later on. Further, at the highest v levels, which correspond to the long-R regions of the potential, where charge/induced-dipole interactions are dominant, the trend is expected to follow LeRoy–Bernstein behaviour.62–64 This long-range behaviour is expected to follow a (ΔGv+1/2)2n/(n+2) dependence, where n is that of the R−n dependence of the potential at long range, i.e. the leading term in the interaction potential. For an atomic cation/rare gas interaction, an R−4 dependence is expected, and so we expect a (ΔGv+1/2)4/3 dependence in the Birge–Sponer plots close to the dissociation limit. These overall expectations are largely met by the 2Σ+ plots for both Si+–RG and Ge+–RG. For the 2Π states, in the intermediate regions the calculated energies of the vibrational levels dip below this line, most noticeably for the heavier RG atoms. Approaching from larger R, corresponding to the high-v levels, the implication is that the interaction potential in the intermediate region initially softens compared to that close to the minimum, as a result of electron density movement away from the internuclear region, for example partial hybridization;35 however, gradually the increasing cost of this cannot be met from the decrease in repulsion, and the curvature of the potential changes. Close to Re, there is also the possibility of partial charge transfer, and some further insight into the latter is obtained from the calculated charges and H(R) parameter, discussed in the following subsection.
 | ||
| Fig. 4 Birge–Sponer-like plots for the (a) 2Σ+ and (b) 2Π states of Si+–RG constructed from the calculated vibrational energy spacings obtained from the RCCSD(T)/aV∞Z potentials. The solid lines are obtained from the ωe and ωexe values reported in Table 1 and are obtained from the lowest two vibrational energy levels and De. Note that the ordinate and abscissa scales are not the same for all plots. (Values for RG = He are not plotted since there are only very few calculated values – see text and ESI.†) | ||
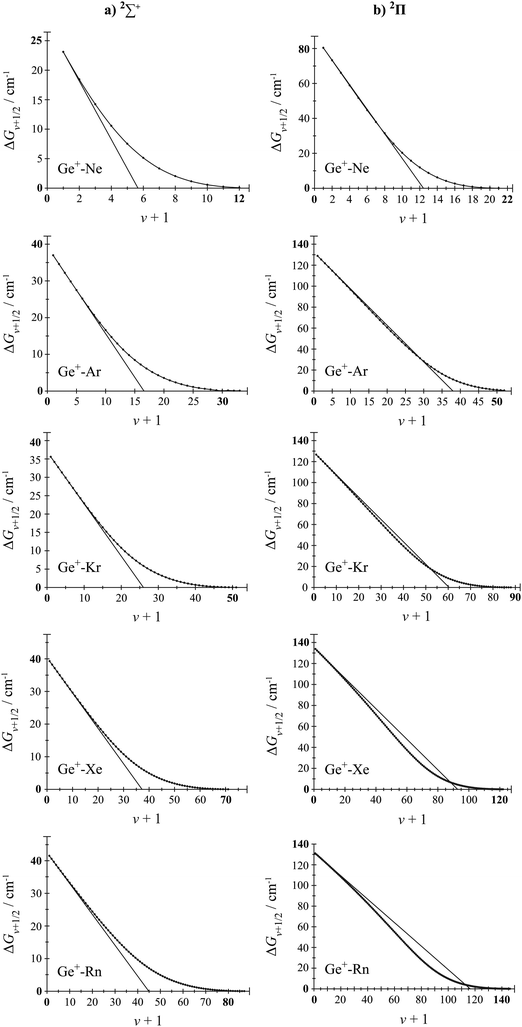 | ||
| Fig. 5 Birge–Sponer-like plots for the (a) 2Σ+ and (b) 2Π states of Ge+–RG constructed from the calculated vibrational energy spacings obtained from the RCCSD(T)/aV∞Z potentials. The solid lines are obtained from the ωe and ωexe values reported in Table 2 and are obtained from the lowest two vibrational energy levels and De. Note that the ordinate and abscissa scales are not the same for all plots. (Values for RG = He are not plotted since there are only very few calculated values – see text and ESI.†) | ||
3.2 Charges and chemical bonding
The calculated values for the local energy parameter, H(R),65 evaluated at the bond critical point, are presented in Table 3, with negative H(R) values suggested as indicating that there is a chemical bonding contribution, based upon observations for known covalent molecules. (It has been argued in ref. 65 that this parameter is more reliable than the deformation electron density, owing to the difficulty of defining a reference density; however, definitive methods of establishing criteria for chemical interactions are still not available, and as such, H(R) must be viewed as a qualitative parameter, rather than a quantitative one.) The values suggest that the cases involving He and Ne show essentially no chemical bonding, while some contribution from such may be present for RG = Ar–Rn. Similarly, the NPA and AIM calculated charges are in line with this interpretation, suggesting some charge transfer from M+ → RG. Thus, we infer that, at R values approaching Re, some charge transfer may be occurring, which would increase the interaction above that expected from a neutral atom interacting with an atomic cation. As is well-known, Mulliken charges are often unreliable, and the close agreement between the NPA and AIM charges here, and the fact that they are discrepant with the Mulliken charges confirms this in the present case. We hypothesise that the Mulliken analyses are misattributing the electron density, owing to the large size of the RG atom, and also the “embedding” of the cation into the region where the RG density would be expected – see ref. 37 for orbital contour plots that show this effect for C+–RG.| M | RG | q(M) | q(RG) | H(R)b | ||||
|---|---|---|---|---|---|---|---|---|
| Mulliken | NPA | AIM | Mulliken | NPA | AIM | |||
| a Values are from Mulliken population analysis, natural population analysis (NPA) and Bader's atoms-in-molecules (AIM) approach – see text for further details and comments. Calculations were performed at the Re values reported in ref. 36 and 37 for C+–RG, and in Tables 1 and 2 for Si+–RG (RG = Kr–Rn) and Ge+–RG, respectively. b The H(R) parameter is described in ref. 65 and is evaluated at the bond critical point: a negative value indicates an element of chemical bonding. c Values for Si+–RG (RG = He–Ar) are undertaken as part of the work reported in ref. 38, but were not reported therein. | ||||||||
| C | He | 1.00 | 0.99 | 0.99 | 0.00 | 0.01 | 0.01 | 2.5 × 10−3 |
| Ne | 0.96 | 0.97 | 0.97 | 0.04 | 0.03 | 0.03 | 2.5 × 10−3 | |
| Ar | 0.57 | 0.67 | 0.71 | 0.43 | 0.33 | 0.29 | −4.5 × 10−2 | |
| Kr | 0.53 | 0.53 | 0.57 | 0.47 | 0.47 | 0.43 | −4.6 × 10−2 | |
| Xe | 0.10 | 0.34 | 0.38 | 0.90 | 0.66 | 0.62 | −4.7 × 10−2 | |
| Si | Hec | 1.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 1.4 × 10−3 |
| Nec | 0.98 | 0.99 | 1.00 | 0.02 | 0.01 | 0.00 | 3.1 × 10−4 | |
| Arc | 0.93 | 0.91 | 0.95 | 0.07 | 0.09 | 0.05 | −6.7 × 10−3 | |
| Kr | 0.84 | 0.85 | 0.91 | 0.16 | 0.15 | 0.09 | −1.1 × 10−2 | |
| Xe | 0.67 | 0.75 | 0.83 | 0.33 | 0.25 | 0.17 | −1.4 × 10−2 | |
| Rn | 0.57 | 0.71 | 0.78 | 0.43 | 0.29 | 0.22 | −1.5 × 10−2 | |
| Ge | He | 1.01 | 1.00 | 1.00 | −0.01 | 0.00 | 0.00 | 1.7 × 10−3 |
| Ne | 0.98 | 0.99 | 1.00 | 0.02 | 0.01 | 0.00 | 9.3 × 10−4 | |
| Ar | 0.96 | 0.93 | 0.95 | 0.04 | 0.07 | 0.05 | −2.2 × 10−3 | |
| Kr | 0.89 | 0.88 | 0.91 | 0.11 | 0.12 | 0.09 | −5.5 × 10−3 | |
| Xe | 0.74 | 0.79 | 0.83 | 0.26 | 0.21 | 0.17 | −8.1 × 10−3 | |
| Rn | 0.66 | 0.74 | 0.78 | 0.34 | 0.26 | 0.22 | −8.9 × 10−3 | |
This charge transfer was discussed in depth in ref. 37 for C+–RG, where multireference configuration interaction (MRCI) calculations were also undertaken. These confirmed the role of charge transfer in these systems. The RCCSD(T) method, employed in the present calculations, is a single-reference method but the T1 diagnostic values (see above) suggest that this is mostly adequate for the present cases. We do not report any MRCI calculations in the present work, although we would expect the results to be similar to those for C+–RG.37
Further insight into the interaction can be obtained by examining the spin–orbit splitting between the minima of the 2Π1/2 and 2Π3/2 states (see Tables 4 and 5) and comparing that to the splitting at the dissociation asymptotes. In the latter case, we expect the splitting to be that of the atomic cation states, 2P1/2 and 2P3/2 that, as we noted earlier, have experimental values39 of 287.24 cm−1 for Si+, and 1767.36 cm−1 for Ge+, with the calculated asymptotic spin–orbit splittings being 256.5 cm−1, and 1724 cm−1 or 1734 cm−1, respectively. (The calculated splittings between the 2Π1/2 and 2Π3/2 states are given in Tables 4 and 5.)
| Si+–He | Si+–Ne | Si+–Ar | Si+–Kr | Si+–Xe | Si+–Rn | |
|---|---|---|---|---|---|---|
| a ζ is the atomic spin–orbit splitting constant. b These are calculated at the Re values of the 2Π3/2 state reported in Table 1. c Accessing the lowest spin–orbit cationic state. d This is the experimental spin–orbit splitting for the …np5 ground electronic state configuration.39 | ||||||
| Calculated asymptotic splitting (= 3/2ζ)a/cm−1 | 256.5 | 256.5 | 256.5 | 256.5 | 256.5 | 256.5 |
| Predicted calculated Hund's case (a) splitting at Re/cm−1 | 171.0 | 171.0 | 171.0 | 171.0 | 171.0 | 171.0 |
| Calculated 2Π1/2 − 2Π3/2 splitting at Reb/cm−1 | 187.9 | 180.9 | 177.9 | 179.4 | 266.6 | 650.6 |
| Actual/predicted splitting | 1.10 | 1.06 | 1.04 | 1.05 | 1.56 | 3.81 |
| IE (RG)c/eV | 24.59 | 21.57 | 15.76 | 14.00 | 12.13 | 10.75 |
| 2 P 3/2 − 2P1/2 splitting (RG+)d/cm−1 | n/a | 780.4 | 1432 | 5370 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537 537 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 895 |
| Ge+–He | Ge+–Ne | Ge+–Ar | Ge+–Kr | Ge+–Xe | Ge+–Rn | |
|---|---|---|---|---|---|---|
| a ζ is the atomic spin–orbit splitting constant. The values differ for RG = He, Ne from those of RG = Ar–Rn, owing to the correlation of different Ge+ electrons – see text for details. b These are calculated at the Re values of the 2Π3/2 state reported in Table 2. c Accessing the lowest spin–orbit cationic state. d This is the experimental spin–orbit splitting for the …np5 ground electronic state configuration.39 | ||||||
| Calculated asymptotic splitting (= 3/2ζ)a/cm−1 | 1734 | 1734 | 1724 | 1724 | 1724 | 1724 |
| Predicted calculated Hund's case (a) splitting at Re/cm−1 | 1156 | 1156 | 1149 | 1149 | 1149 | 1149 |
| Calculated 2Π1/2 − 2Π3/2 splitting at Reb/cm−1 | 1476 | 1406 | 1230 | 1194 | 1218 | 1465 |
| Actual/predicted splitting | 1.28 | 1.22 | 1.07 | 1.04 | 1.06 | 1.28 |
| IE (RG)c/eV | 24.59 | 21.57 | 15.76 | 14.00 | 12.13 | 10.75 |
| 2 P 3/2 − 2P1/2 splitting (RG+)d/cm−1 | n/a | 780.4 | 1432 | 5370 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 537 537 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 895 895 |
If the interaction is significant, we expect the spin and orbital angular momenta to couple to the internuclear axis, and for Hund's case (a) behaviour to be seen. The evolution from Hund's case (a) to Hund's case (c) has been discussed in ref. 66 for …p1 excited states of Au–RG complexes. In such cases, the splitting at the minima would be expected to be 2/3 that at the asymptote, in the absence of other interactions. In ref. 36 we discussed this for C+–RG (RG = He–Xe), noting that the expectation was well exhibited for C+–He and C+–Ne, but that the splitting swiftly rose as the atomic number of the RG atom increased, becoming over ten times the expected splitting for C+–Xe, consistent with involvement of RG+ in determining the value.
For Si+–RG, it can be seen that a similar scenario unfolds (Table 4), but now the differences to the expected splitting are much less, becoming “only” just less than four times as large for Si+–Rn. This indicates that the role of charge transfer is significantly less for the Si+–RG complexes, in line with the calculated AIM and NPA charges (Table 3). This trend continues for Ge+–RG, where now the calculated splittings in the Ge+–RG complexes are almost precisely as expected for RG = Ar–Xe (Table 5), but slightly more for RG = Rn. It is interesting that for the lightest two RG atoms, He and Ne, where the interaction with the cation is weakest, the splitting is always slightly more than that expected. We interpret the latter as indicating that Hund's case (a) coupling is not quite complete. For RG = Ar, the splitting is close to that expected for Hund's case (a) coupling – whether this is wholly due to the presence of Hund's case (a) coupling, or a coincidence as the charge-transfer starts to turn on, is unclear.
The influence of the configuration mixing can also be seen in the spectroscopic constants. If we consider solely the spin–orbit states that arise from the M+ (…ns2np1) + RG configuration, then, since there is only the one Ω = 3/2 state, the 2Π3/2 state should have precisely the same shape as the non-spin–orbit 2Π state – it is merely shifted up in energy; hence, the spectroscopic constants in Tables 1 and 2 should be the same for these two states. Indeed, they are essentially identical for RG = He–Ar for Si+–RG, and for RG = He and Ne for Ge+–RG, but significant, increasing deviations, occur as the atomic number of RG increases. We attribute this to “contamination” of the SA-CASSCF wavefunction employed for the spin–orbit calculations by contributions that affect the values from the diagonalized spin–orbit matrix, and consequently the spin–orbit curves. This behaviour was also observed for the C+–RG complexes.37
3.3 Comparison to …np1(n + 1)s1 neutral excited states
For C, Si or Ge, if one of the np electrons of the ground electronic state is excited to a high-lying, Rydberg s orbital, this will lead to a …p1 ionic core. For the complex, one might expect to produce a state whose spectroscopic parameters would be close to those of the ion itself, i.e. to those of C+–Ar, for example. However, for low values of n, as is the case for the 3s Rydberg states of NO interacting with RG,67–69 there is expected to be a competition between the Rydberg electron and the RG atom, for the region close to the cationic core. This is expected to lead to a weakening of the cation–RG interaction in a Rydberg state of a complex over that of the cation itself. Such a picture was also seen for the related 6p ← 6s excitation in Au–RG complexes, where the binding energy of the excited 2Π3/2 state was calculated to be less strongly bound than was the corresponding cation.66Although the electronic spectroscopy of C–Ar has been studied experimentally, spectra arose there from states arising from the 2s12p3 ← 2s22p2 atomic transition.70 States arising from the 2s22p13s1 ← 2s22p2 transition were deduced to be predissociated, and these states have been studied theoretically, including spin–orbit interactions.71 From that work, the vibrational wavenumber of the upper state, designated B3Π therein, can be derived from the given vibrational energy levels as 413 cm−1, which is slightly less than the value for C+–Ar that we calculated previously37 – and is in line with the expectations outlined in the previous paragraph. (In a similar way, a calculated value for the B3Π state of ωexe = 5.4 cm−1 can be obtained, close to the value of 4.2 cm−1 reported for the 2Π state of C+–Ar in our previous work.37) Also, the D0 value was derived as 4895 cm−1, which is significantly less than the calculated values for C+–Ar (2Π) of very close to 8000 cm−1,37 consistent with shielding of the C+ core by the 3s electron. In ref. 71, the “heavy atom” effect was invoked, whereby the carbon “borrows” spin–orbit coupling from the Ar atom, analogous to the discussion given earlier herein for the present cases, and in previous work for C+–RG.37
Looking now at the …3s23p14s1 ← …3s23p2 transition in Si–Ar, this has been studied experimentally by Dedonder-Lardeux et al.,72 who derive a value for ωe of 200.5 cm−1 for the 3Π1 state. This can be compared to the interaction of Ar with Si+…3s23p1 2P, with the value for the 3Π1 state being higher than the calculated value here for the 2Π3/2 state of the cation (Table 1), of 168.1 cm−1. The dissociation energy of ∼2010 cm−1 in ref. 72 was refined to a value of ∼1890 cm−1 by Tao et al.73 and this latter value is significantly below that of the corresponding value in Si+–Ar (see Table 1 and ref. 38), which would be consistent with the Ar atom being shielded from the Si+ by the 4s electron in the 3Π state. The authors of ref. 72 discussed the nature of the observed 3Π excited state, and concluded that it was not wholly Rydberg-like in character, and hypothesised interactions with higher electronic states. Given the differing behaviour of the dissociation energy and the vibrational wavenumber, this would be consistent with a potential energy curve that was changing its character with internuclear separation; the role of interactions of the penetrating 4s electron with the ionic core could also then be dependent on this separation.
Also, spin–orbit transitions of the corresponding state in Ge–Ar have been studied by Tao and Dagdigian.74 From detailed analyses of the spectra of different isotopologues, they were able to deduce absolute vibrational numbering, and hence values for ωe and ωexe, which differed for different spin–orbit states. Vibrational constants were derived for three spin–orbit levels, with two ωe values (for the Ω = 0− and 0+ states) being in the range 164–168 cm−1, while one (for the Ω = 2 state) was ∼194 cm−1. These are all significantly higher than the calculated values for the 2Π state of Ge+–Ar, calculated here, and also the ωexe values were also quite different to the present ones – see Table 2. Also, dissociation energies were estimated, with upper bounds for D0 values for three spin–orbit levels, Ω = 0−, 0+ and 2 being 1012 cm−1, 1322 cm−1 and 1714 cm−1, respectively; these are all significantly less than the values calculated here for Ge+–Ar, and this is also true for the corresponding “Morse” values of De (=ωe2/4ωexe) of 1130 cm−1, 1404 cm−1 and 1855 cm−1, that can be obtained from the ωe and ωexe values reported therein. Thus, as with Si–Ar in the previous paragraph, the experimental dissociation energies being lower than that of the cation is consistent with that expected for a Rydberg state, while the higher ωe values are not. Again, it is plausible that interactions with other higher-lying states are perturbing the potentials of the 3ΠΩ states, and this is supported by the suggestion74 that barriers in the potential energy curves are present in the 3ΠΩ potentials. In addition, the penetrating 5s electron can interact with the ion core electrons and Ar atom, so that the Ge–Ar states are far from Rydberg-like in character.
In summary, although the calculated values for the …2s12p13s1 3Π state of C–Ar are in line with expectations if it were a Rydberg state, this is not wholly the case for the corresponding states of Si–Ar and Ge–Ar, where the dissociation energies and the ωe values show discrepant behaviour with expectations. It can be seen from the Birge–Sponer plots in Fig. 4 and 5 that the vibrational spacings of the cation do not follow that expected for a simple Morse potential, but also it is possible that spin–orbit interactions, together with involvement of higher electronic states, are also the source of these anomalies. Spin–orbit interactions between states that arose from the 6p ← 6s excitation in Au–RG complexes, led to complications to the derived curves, such as a “shelf” in the 2Π1/2 state of Au–Ar,75 and the lack of a minimum in the 2Π1/2 state of Au–Ne.66
It is also interesting to see that the spectroscopy of the states that arise from the …np1(n + 1)s1 configuration is so different, with those of C–Ar being predissociative, only the 3Π1 state being seen for Si–Ar, while three 3ΠΩ levels were observed for Ge–Ar. These differences likely arise from a combination of the differing spin–orbit interactions, and also the different jet expansion conditions that led to different lower Ω-state populations in the experiments, as suggested in that work.
3.4 Ion transport
In Fig. 6 and 7 we show the zero-field mobilities for each of 28Si+ and 74Ge+ moving through a bath of each RG, as a function of the bath temperature. In Fig. 8 and 9, we show the calculated ion mobilities of each of 28Si+ and 74Ge+ moving through a bath of each RG at 300 K, as a function of E/n0. (Other ion transport data, at a range of different temperatures have been deposited in an online database.60) | ||
| Fig. 6 Calculated zero-field mobilities versus T for the 2P1/2 and 2P3/2 states of 28Si+–RG presented as a log–log plot. The polarization limit is given in each case at the left-hand side of the plot. The RG bath was taken as a mixture of isotopes with their natural abundances; although a single isotope of Si+ was employed here, in fact the mobilities will be quite similar for all naturally-occurring isotopes, with the full set of data included in an online database.60 (Note that each RG will condense at the lowest T values reported herein.) | ||
 | ||
| Fig. 7 Calculated zero-field mobilities versus T for the 2P1/2 and 2P3/2 states of 74Ge+–RG presented as a log–log plot. The polarization limit is given in each case at the left-hand side of the plot. The RG bath was taken as a mixture of isotopes with their natural abundances; although a single isotope of Ge+ was employed here, in fact the mobilities will be quite similar for all naturally-occurring isotopes, with the full set of data included in an online database.60 (Note that each RG will condense at the lowest T values reported herein.) | ||
 | ||
| Fig. 8 Calculated reduced ion mobilities, K0, versus E/n0 for 28Si+ in a bath of RG at 300 K, presented as semi-logarithmic plots. Note that the ordinate scales are not the same for all plots. In all plots, the values for solely 2P1/2 and solely 2P3/2 states are given, as well as a statistical mix of the two, denoted ASO. The legend at the top of the figure applies to all plots. The RG bath was taken as a mixture of isotopes with their natural abundances; although a single isotope of Si+ was employed here, in fact the mobilities will be quite similar for all naturally-occurring isotopes, with the full set of data included in an online database.60 Calculated data points are shown, with the lines merely being a guide to the eye; the dashed line indicated regions where the ion transport coefficients did not converge satisfactorily. [Units on the abscissa are townsend (1 Td = 10−17 V cm2).]. | ||
 | ||
| Fig. 9 Calculated reduced ion mobilities, K0, versus E/n0 for 74Ge+ in a bath of RG at 300 K, presented as semi-logarithmic plots. Note that the ordinate scales are not the same for all plots. In all plots, the values for solely 2P1/2 and solely 2P3/2 states are given, as well as a statistical mix of the two, denoted ASO. The legend at the top of the figure applies to all plots. The RG bath was taken as a mixture of isotopes with their natural abundances; although a single isotope of Ge+ was employed here, in fact the mobilities will be quite similar for all naturally-occurring isotopes, with the full set of data included in an online database.60 Calculated data points are shown, with the lines merely being a guide to the eye; the dashed line indicated regions where the ion transport coefficients did not converge satisfactorily. [Units on the abscissa are townsend (1 Td = 10−17 V cm2).] | ||
We first make some general comments regarding mobility. Not only does the gas temperature affect the average energy of a collision between an ion and a neutral, so does E/n0. The primary difference is that the average collision energy is directly proportional to T but its dependence upon E/n0 is not analytic. Increasing E causes the ion to continually accelerate between collisions, while increasing n0 decreases the time between collisions; the two effects are exactly balanced within the E/n0 ratio.
Consider a special case first, where the electric field is negligible: then both the ions and neutrals are moving with thermal energy. To a good approximation, the temperature dependence of the mobility then varies as  , where
, where 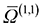 is a collision integral, which contains the effect of the ion–RG potential.76 At very low temperatures, the interactions between the collision partners are dominated by the long-range potential, which approaches the ion/induced-dipole limit for long R, and hence varies as R−4; then
is a collision integral, which contains the effect of the ion–RG potential.76 At very low temperatures, the interactions between the collision partners are dominated by the long-range potential, which approaches the ion/induced-dipole limit for long R, and hence varies as R−4; then  varies as T−1/2, so that overall, the mobility is expected to be largely independent of T, as is seen in Fig. 6 and 7 for the lower values of T. The zero-field mobility, K0(0), at 0 K, is called the polarization limit, Kp, and its value is given76 by the expression
varies as T−1/2, so that overall, the mobility is expected to be largely independent of T, as is seen in Fig. 6 and 7 for the lower values of T. The zero-field mobility, K0(0), at 0 K, is called the polarization limit, Kp, and its value is given76 by the expression 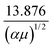 in units of cm2 V−1 s−1, where α is the polarizability of RG in Å3, and μ is the reduced mass of the ion/RG system in g mol−1; its value is indicated in Fig. 6 and 7 for each system. (We highlight that it takes incredibly low gas temperatures for the mobility to be almost identical with the polarization limit.) As T starts to increase, more collisions sample the interaction potential to smaller separations. If, at these smaller separations, the potential is still close to the ion–dipole potential, the mobility is little changed. As T continues to increase, an increasing number of collisions probe smaller internuclear separations, where attractive terms of higher orders than ion/induced dipole become important, and the mobility usually increases. This continues until eventually the role of the repulsive part of the potential will become the most important, eventually causing a reduction in the mobility along the drift tube axis. The observed mobility is thus the overall result of the combined effects of the attractive and repulsive parts of the potential that are experienced by the collisions. Interestingly, the higher-order attractive terms can often cause a mobility minimum to appear, whereby the mobility is lower than the polarization limit – see Fig. 6 and 7. These occur at lower temperatures, and are then followed by a rise in mobility towards a maximum; the mobility minima are not well understood, but are thought to arise when the collision complex is particularly stable.76 (When it occurs, it is generally accepted that the maximum in the zero-field mobility occurs when the majority of collisions experience the interaction potential close to its minimum.) It is important to acknowledge that the repulsive part of the potential increases rapidly for smaller separations – much faster than the corresponding changes for the attractive parts of the potential. As a consequence, at even higher T, where many of the separations experienced during the collisions are even shorter, the repulsive parts of the potential dominate the collisions, leading to the mobility decreasing monotonically as T continues to increase.
in units of cm2 V−1 s−1, where α is the polarizability of RG in Å3, and μ is the reduced mass of the ion/RG system in g mol−1; its value is indicated in Fig. 6 and 7 for each system. (We highlight that it takes incredibly low gas temperatures for the mobility to be almost identical with the polarization limit.) As T starts to increase, more collisions sample the interaction potential to smaller separations. If, at these smaller separations, the potential is still close to the ion–dipole potential, the mobility is little changed. As T continues to increase, an increasing number of collisions probe smaller internuclear separations, where attractive terms of higher orders than ion/induced dipole become important, and the mobility usually increases. This continues until eventually the role of the repulsive part of the potential will become the most important, eventually causing a reduction in the mobility along the drift tube axis. The observed mobility is thus the overall result of the combined effects of the attractive and repulsive parts of the potential that are experienced by the collisions. Interestingly, the higher-order attractive terms can often cause a mobility minimum to appear, whereby the mobility is lower than the polarization limit – see Fig. 6 and 7. These occur at lower temperatures, and are then followed by a rise in mobility towards a maximum; the mobility minima are not well understood, but are thought to arise when the collision complex is particularly stable.76 (When it occurs, it is generally accepted that the maximum in the zero-field mobility occurs when the majority of collisions experience the interaction potential close to its minimum.) It is important to acknowledge that the repulsive part of the potential increases rapidly for smaller separations – much faster than the corresponding changes for the attractive parts of the potential. As a consequence, at even higher T, where many of the separations experienced during the collisions are even shorter, the repulsive parts of the potential dominate the collisions, leading to the mobility decreasing monotonically as T continues to increase.
At a fixed temperature, such as 300 K, the mobility value as E/n0 → 0 (see Fig. 8 and 9) is the same as the zero-field mobility (see Fig. 6 and 7) at that temperature – we have marked the position of 300 K in Fig. 6 and 7. The behaviour of K0 as E/n0 increases is qualitatively the same as just described for K0(0) and temperature; the quantitative difference is that the collision energy (sometime described in terms of an effective temperature) is not directly proportional to E/n0.
In the present situations, if a mobility experiment were to be undertaken for either Si+ or Ge+ moving through a bath of RG, then we would expect the ground state cation, 2P1/2, to be the predominant ion under thermal conditions. However, it is possible that the excited spin–orbit level, 2P3/2, may also be present, depending on how the ions were produced. Indeed, there was evidence36 that both spin–orbit states were present in ion mobility experiments77–82 involving C+ in He, while calculations37 indicated that those for C+ in Ar83seemed to have a predominance of 2P1/2. In addition, electronically excited C+ has also been observed in ion mobility experiments.36,80 To investigate the possible differences between the mobility behaviour of these two spin–orbit states as a function of RG, we show the calculated mobilities for both spin–orbit states of Si+ in all RG (Fig. 8) and Ge+ in all RG (Fig. 9); in addition, we show the mobility for what would be an equal mixture of the two spin–orbit states, denoted ASO. In Fig. 8, we have included the results for Si+ in He, Ne and Ar, reported in ref. 38 for comparison; in that work we also reported comparison of calculated mobilities with previous calculated and experimental values,84,85 concluding that there was not enough experimental detail to be sure of a fair comparison, although the comparison was suggestive of a mixture of spin–orbit states in the experiments. The mobility curves in Fig. 8 and 9 each show mobility maxima and that a mobility minimum develops for the heavier RG, where the potentials are much deeper, owing to the stronger attractive terms in the interaction. Another interesting observation is that at low E/n0, the mobilities of the two spin–orbit states are not in the same order for all RG, although the ASO curve is always closer to that of the 2P3/2 state. This differing mobility would mean that for a particular system, ions in one or the other spin–orbit states would arrive first at the detector, and so provide a means for state selection.
To understand the latter point, we comment that for the cations under consideration here, if we initially ignore spin–orbit effects, then collisions can occur that sample the 2Σ+ curve or the 2Π curve, with the latter having the larger interaction energy. Thus, mobilities of ions in the 2Π state would be expected to be different to those in the 2Σ+ state. Things are more complicated here as spin–orbit coupling mixes these states: the 2Π1/2 state contains mostly 2Π character, but with some 2Σ+, while the 2Σ1/2+ state is largely of 2Σ+ character, with some 2Π; the 2Π3/2 state is expected to be purely 2Π in character, with some caveats, as discussed above. When we then consider the atomic cations, we recall that the 2P3/2 state evolves along two potential energy curves, 2Π3/2 and 2Σ1/2+, while the 2P1/2 state evolves along the single 2Π1/2 curve – see Fig. 1 and 2. For the 2P3/2 state, therefore, it is the combined effects of the 2Σ1/2+ and 2Π3/2 states on the collision cross-sections that will determine its mobility, while it is solely that of the 2Π1/2 state for 2P1/2; thus for both atomic spin–orbit states, there are (different) contributions from both non-spin–orbit diatomic states. As the atomic number of the rare gas gets larger, the 2Π potential gets deeper (Fig. 1 and 2), and the repulsive part of the 2Σ+ potential is expected to start to rise more steeply at progressively larger values of internuclear separation (thus, the degree of mixing of the 2Σ+ and 2Π states in the spin–orbit states will vary with R); these two effects will affect the mobility in opposite directions, making it difficult to predict the final ordering of the 2P3/2 and 2P1/2 mobilities. The overall balance of these effects on the two spin–orbit states can be seen to be quite subtle, since at low E/n0: for C+/RG, the 2P3/2 mobility is the higher for He–Kr, then switches for Xe;36,37 for Si+/RG, the 2P3/2 mobility is the lower for He, then switches for Ne–Rn; while, for Ge+/RG, the 2P3/2 mobility is the lower for He and Ne, then switches for Ar–Rn. For the zero-field mobilities as a function of temperature (Fig. 6 and 7), again it is evident that the ordering of the K0(0) values for the two spin–orbit levels is not consistent across the RG series, and is also rationalized by the subtle effects mentioned above.
Finally, we did not consider C+ interacting with Rn in our earlier work.36,37 We have now undertaken some calculations, but this system is more complicated, since the ionization energy of Rn is lower than that of C+; as such the lowest electronic state will arise from the C(3P0) + Rn+(2P3/2) asymptote. If, however, a mobility experiment for C+ passing through Rn were undertaken, then the interactions would be dictated by C+–Rn curves. Hence, we would expect some charge transfer to occur during such an experiment, and so the C+ signal to deplete, and some Rn+ ions formed. Given the esoteric nature of the [C/Rn]+ system, we refrain from reporting and discussing our calculations in full, but note that the mobility data for C+ in Rn have been calculated using the same methods reported herein and in ref. 37, and these are available in an online database.60
4. Concluding remarks
Here, we have presented high-level calculated potentials for Si+–RG (RG = Kr–Rn) and Ge+–RG (RG = He–Rn). These have been used to obtain spectroscopic constants, which, based on experience with a number of other systems, are expected to be very reliable. We have discussed the trends in the main constants as RG varies, finding that there is a balance between the increasing size and polarizability of the RG atom, as far as Re is concerned, while the dissociation energy and force constants increase monotonically with the atomic number of RG; as usual, the harmonic vibrational wavenumber has both mass and force constant variations, which, again, act in opposite directions. We also suggested that the Si+–He and Ge+–He potentials may be useful in investigations of ion cooling in interstellar chemistry.We have commented on the nature of the interactions in terms of the calculated charges on the different atoms, and the calculated spin–orbit splitting in the complex compared to that in the isolated atoms. We conclude that for the RG atoms with a higher atomic number, the role of charge-transfer with the RG atom is likely to be becoming increasingly important – this has the most notable effect for C+–RG, less so for Si+–RG, much smaller in the case of Ge+–RG. This trend is likely due to the decreasing ionization energy from C → Ge.
Interestingly, if one calculates the ionic radius of the ions C+, Si+ and Ge+ using the ideas presented in ref. 86, whereby 1.49 Å is subtracted from the M+–He Re value, then different values are obtained for the 2Π and 2Σ+ states. For the former, values of 0.71 Å, 1.28 Å and 1.22 Å are obtained, while for the latter 1.48 Å, 2.37 Å and 2.43 Å, respectively. These values are different, owing to the different orientation of the unpaired p electron; furthermore, the trend for 2Π states is not monotonically increasing, probably related to a balance of factors discussed above when focusing on the RG atom, in relation to the trends shown in Fig. 3. These facts illustrate that it is difficult to arrive at a unique value for an ionic radius – see further commentary in ref. 86 – particularly in non-spherically-symmetric environments.
We have discussed the comparison of the spectroscopic constants of …np1(n + 1)s1 states of C–Ar, Si–Ar and Ge–Ar with those of the corresponding cation, finding unexpected results. In line with previous suggestions, we attribute this to the penetrating nature of the (n + 1)s electron, which will lead to an increase in their interaction with the cationic core. This, and the differing magnitudes of the atomic spin–orbit coupling, will affect the effect of spin–orbit coupling in the complex. It would be of great interest to study related species with different RG atoms, and for ns states for larger principal quantum number.
We have also used the potentials to calculate ion transport properties, with the mobilities of the atomic cation in a bath of each RG discussed herein. We have highlighted that the behaviour of the two atomic spin–orbit states is complicated owing to the differing roles of the repulsive and attractive aspects of the underlying potentials; particularly, as these are each admixtures of the underlying 2Σ+ and 2Π states, which become mixed by spin–orbit coupling. Nonetheless, earlier work on C+/RG has shown that the calculated mobility curves can be used to gain insight into the ionic state populations that may be present in an experiment. Further, this differing behaviour may then be used to separate different states. We highlight that the bulk properties of ion mobilities and other transport coefficients are exquisitely sensitive to the potential energy surfaces, and so provide a robust test of such potentials, if precise and accurate experimental data are available to which to compare.
Author contributions
TGW conceived and supervised the research and wrote the manuscript. AC performed quantum chemistry calculations and approved the final version of the manuscript. ARD performed quantum chemistry calculations, undertook analyses, commented on drafts of the manuscript and approved the final version. LAV performed the transport coefficient calculations, commented on drafts of the manuscript and approved the final version.Conflicts of interest
The authors declare that they have no competing interests.Acknowledgements
We are grateful for access to the University of Nottingham High Performance Computing Facility. The EPSRC and the University of Nottingham are thanked for the provision of a studentship to A. R. D.References
- T. I. Kamins and D. J. Meyer, Appl. Phys. Lett., 1991, 59, 178 CrossRef CAS.
- S. Nunomura and M. Kondow, Appl. Phys. Lett., 2008, 93, 231502 CrossRef.
- S. Yamada, S. Oguri, A. Morimoto, T. Shimizu, T. Minamikawa and Y. Yonezawa, Jpn. J. Appl. Phys., 2000, 39, 278 CrossRef.
- G. Dushaq, M. Rasras and A. Nayfeh, Thin Solid Films, 2017, 636, 585 CrossRef CAS.
- J. M. C. Plane, J. C. Gómez-Martin, W. Feng and D. Janches, J. Geophys. Res.: Atmos., 2016, 121, 3718 CrossRef CAS PubMed.
- R. J. Plowright, T. J. McDonnell, T. G. Wright and J. M. C. Plane, J. Phys. Chem. A, 2009, 113, 9354 CrossRef CAS PubMed.
- C. L. Whalley, J. C. Gomez Martin, T. G. Wright and J. M. C. Plane, Phys. Chem. Chem. Phys., 2011, 13, 6352 RSC.
- R. J. Plowright, T. G. Wright and J. M. C. Plane, J. Phys. Chem. A, 2008, 112, 6550 CrossRef CAS PubMed.
- S. Broadley, T. Vondrak, T. G. Wright and J. M. C. Plane, Phys. Chem. Chem. Phys., 2008, 10, 5287 RSC.
- S. E. Daire, J. M. C. Plane, S. D. Gamblin, P. Soldán, E. P. F. Lee and T. G. Wright, J. Atmosph. Solar-Terrestial Phys, 2002, 64, 863 CrossRef.
- J. M. C. Plane, R. J. Plowright and T. G. Wright, J. Phys. Chem. A, 2006, 110, 3093 CrossRef CAS PubMed.
- T. Vondrák, K. R. I. Woodcock and J. M. C. Plane, Phys. Chem. Chem. Phys., 2006, 8, 1812 RSC.
- E. Kopp, F. Balsiger and E. Murad, Geophys. Res. Lett., 1995, 22, 3473 CrossRef CAS.
- E. E. Ferguson, D. W. Fahey, F. C. Fehsenfeld and D. L. Albritton, Planet. Space Sci., 1981, 29, 307 CrossRef CAS.
- P. Boschler, J. Geophys. Res. Space Phys., 1989, 94, 2365 CrossRef.
- S. Wlodek, D. K. Bohme and E. Herbst, Mon. Not. R. Astron. Soc., 1990, 242, 674 CrossRef CAS.
- E. Herbst, T. J. Millar, S. Wlodek and D. K. Bohme, Astron. Astrophys., 1989, 222, 205 Search PubMed.
- S. Fornarini, Ion–Molecule Reactions of Silicon Cations. Patai's Chemistry of Functional Groups, Wiley Online, 1992, DOI:10.1002/9780470682531.pat0252.
- J. H. Horton and J. M. Goodings, Can. J. Chem., 1992, 70, 1069 CrossRef CAS.
- S. Morozova, M. Alikina, A. Vinogradov and M. Pagliaro, Front. Chem., 2020, 8, 191 CrossRef CAS PubMed.
- J. T. Wasson, Science, 1966, 153, 976 CrossRef CAS PubMed.
- L. M. Hobbs, D. E. Welty, D. C. Morton, L. Spitzer and D. G. Tork, Astrophys. J., 1993, 411, 750 CrossRef CAS.
- S. I. B. Cartledge, J. T. Lauroesch, D. M. Meyer and U. J. Sofia, Astrophys. J., 2006, 641, 327 CrossRef CAS.
- E. B. Jenkins, Astrophys. J., 2009, 700, 1299 CrossRef CAS.
- S. W. Harrison, G. A. Henderson, L. J. Massa and P. Solomon, Astrophys. J., 1974, 189, 605 CrossRef CAS.
- N. Toshima, J. Phys. Soc. Jpn., 1975, 38, 1464 CrossRef CAS.
- J. M. Curtis and L.-S. Rong, Rap. Comm. Mass Spectrom., 1991, 5, 62 CrossRef CAS PubMed.
- J. C. Goméz-Martín, M. A. Blitz and J. M. C. Plane, Phys. Chem. Chem. Phys., 2009, 11, 671 RSC.
- J. C. Goméz-Martín, M. A. Blitz and J. M. C. Plane, Phys. Chem. Chem. Phys., 2009, 11, 10945 RSC.
- J. C. Goméz-Martín and J. M. C. Plane, Phys. Chem. Chem. Phys., 2011, 13, 3764 RSC.
- L. A. Viehland, A. Lutfullaeva, J. Dashdorj and R. Johnsen, Int. J. Ion Mob. Spectrom., 2017, 20, 95 CrossRef CAS.
- E. Carbone, W. Graef, G. Hagelaar, D. Boer, M. M. Hopkins, J. C. Stephens, B. T. Yee, S. Pancheshnyi, J. van Dijk and L. Pitchford, Atoms, 2021, 9, 16 CrossRef CAS.
- S. Pan, G. Jana, G. Merino and P. K. Chattaraj, ChemistryOpen, 2019, 8, 173 CrossRef CAS PubMed.
- C. J. Evans, T. G. Wright and A. M. Gardner, J. Phys. Chem. A, 2010, 114, 4446–4454 CrossRef CAS PubMed.
- W. D. Tuttle, J. P. Harris, Y. Zheng, W. H. Breckenridge and T. G. Wright, J. Phys. Chem. A, 2018, 122, 7679 CrossRef CAS PubMed.
- W. D. Tuttle, R. L. Thorington, L. A. Viehland and T. G. Wright, Molec. Phys., 2015, 113, 3767 CrossRef CAS.
- W. D. Tuttle, R. L. Thorington, L. A. Viehland, W. H. Breckenridge and T. G. Wright, Phil. Trans. Roy. Soc. Lond, 2018, 376, 20170156 Search PubMed.
- W. D. Tuttle, R. L. Thorington, L. A. Viehland and T. G. Wright, Mol. Phys., 2017, 115, 437 CrossRef CAS.
- Spectra Database (ver. 5.9), https://physics.nist.gov/asd [accessed: 2021, November 29]. National Institute of Standards and Technology, Gaithersburg, MD DOI:10.18434/T4W30F.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklaß, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO is a package of ab initio programs Search PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242, DOI:10.1002/wcms.82.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975 CrossRef CAS.
- K. A. Peterson and T. H. Dunning, Jr, J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- A. Berning, M. Schweizer, H. J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch and J. Olsen, Chem. Phys. Lett., 1999, 302, 437 CrossRef CAS.
- T. J. Lee and P. R. Taylor, Int. J. Quant. Chem., 1989, S23, 199 Search PubMed.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- T. A. Keith, AIMAll, T. K. Gristmill Software, Overland Park, KS, 2011, see http://aim.tkgristmill.com Search PubMed.
- R. J. Le Roy, Level 8.0: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels, University of Waterloo Chemical Physics Research Report CP-663, 2007 Search PubMed.
- L. A. Viehland and Y. Chang, Comput. Phys. Commun., 2010, 181, 1687 CrossRef CAS.
- L. A. Viehland, Chem. Phys., 1982, 70, 149 CrossRef CAS.
- L. A. Viehland, Chem. Phys., 1984, 85, 291 CrossRef CAS.
- L. A. Viehland, Comput. Phys. Commun., 2001, 142, 7 CrossRef CAS.
- D. M. Danailov, L. A. Viehland, R. Johnsen, T. G. Wright and A. S. Dickinson, J. Chem. Phys., 2008, 128, 134302 CrossRef PubMed.
- L. A. Viehland, Int. J. Ion Mobil. Spec., 2012, 15, 21 CrossRef CAS.
- https://fr.lxcat.net/data/set_type.php .
- D. Bellert and W. H. Breckenridge, Chem. Rev., 2002, 5, 1595 CrossRef PubMed.
- R. J. LeRoy and R. B. Bernstein, Chem. Phys. Lett., 1970, 5, 42 CrossRef CAS.
- R. J. LeRoy and R. B. Bernstein, J. Molec. Spectrosc., 1971, 37, 109 CrossRef CAS.
- R. J. LeRoy and R. B. Bernstein, J. Chem. Phys., 1970, 52, 3869 CrossRef CAS.
- See, for example, D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627 CrossRef.
- R. J. Plowright, A. M. Gardner, C. D. Withers, T. G. Wright, M. D. Morse and W. H. Breckenridge, J. Phys. Chem. A, 2010, 114, 3103 CrossRef CAS PubMed.
- S. D. Gamblin, S. E. Daire, J. Lozeille and T. G. Wright, Chem. Phys. Lett., 2000, 325, 232 CrossRef CAS.
- J. Lozeille, S. E. Daire, S. D. Gamblin, T. G. Wright and D. M. Smith, J. Chem. Phys., 2000, 113, 7224 CrossRef CAS.
- V. L. Ayles, R. J. Plowright, M. J. Watkins, T. G. Wright, J. Klos, M. H. Alexander, P. Pajón-Suarez, J. Rubayo-Soneira and R. Hernández-Lamoneda, Chem. Phys. Lett., 2007, 441, 181 CrossRef CAS.
- J. Lei and P. J. Dagdigian, J. Chem. Phys., 2000, 113, 602 CrossRef CAS.
- K. Sohlberg and D. R. Yarkony, J. Chem. Phys., 1999, 111, 3070 CrossRef CAS.
- C. Dedonder-Lardeux, C. Jouvet, M. Richard-Viard and D. Solgadi, J. Chem. Phys., 1990, 92, 2828 CrossRef CAS.
- C. Tao, A. Teslja, P. J. Dagdigian, S. Atahan and M. H. Alexander, J. Chem. Phys., 2002, 116, 9239 CrossRef CAS.
- C. Tao and P. J. Dagdigian, J. Chem. Phys., 2002, 118, 1242 CrossRef.
- T. G. Wright, M. J. Watkins, R. J. Plowright and W. H. Breckenridge, Chem. Phys. Lett., 2008, 459, 70 CrossRef CAS.
- E. W. McDaniel and E. A. Mason, The Mobility and Diffusion of Ions in Gases, Wiley, New York, 1973 Search PubMed.
- I. Dotan, F. C. Fehsenfeld and D. L. Albritton, J. Chem. Phys., 1979, 71, 4762 CrossRef CAS.
- R. Thomas, J. Barassin and A. Barassin, Int. J. Mass Spectrom. Ion Phys., 1979, 31, 227 CrossRef CAS.
- N. Peska, Dissertation, Leopold-Franzens-Universität, 1981.
- N. D. Twiddy, A. Mohebati and M. Tichy, Int. J. Mass Spectrom. Ion Proc., 1986, 74, 251 CrossRef CAS.
- S. T. Grice, P. W. Harland, R. G. A. R. Maclagan and R. W. Simpson, Int. J. Mass Spectrom. Ion Proc., 1989, 87, 181 CrossRef CAS.
- S. Matoba, H. Tanuma and K. Ohtsuki, J. Phys. B: At., Mol. Opt. Phys., 2008, 41, 145205 CrossRef.
- E. Basurto and J. de Urquijo, J. Appl. Phys., 2002, 91, 36 CrossRef CAS.
- D. W. Fahey, F. C. Fehsenfeld, E. E. Ferguson and L. A. Viehland, J. Chem. Phys., 1981, 75, 669 CrossRef CAS.
- S. T. Grice, P. W. Harland, R. G. A. R. Maclagan and A. E. Thompson, J. Chem. Soc., Faraday Trans., 1995, 91, 4355 RSC.
- T. G. Wright and W. H. Breckenridge, J. Phys. Chem. A, 2010, 114, 3182 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp05710c |
| This journal is © the Owner Societies 2022 |



