Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structure, energetics, and spectroscopy of the chromophores of HHe+n, H2He+n, and He+n clusters and their deuterated isotopologues
Dariusz
Kędziera
 *a,
Guntram
Rauhut
*a,
Guntram
Rauhut
 *b and
Attila G.
Császár
*b and
Attila G.
Császár
 *c
*c
aFaculty of Chemistry, Nicolaus Copernicus University in Torun, 87-100 Torun, Poland. E-mail: teodar@chem.umk.pl
bInstitute for Theoretical Chemistry, University of Stuttgart, Pfaffenwaldring 55, 70569 Stuttgart, Germany. E-mail: rauhut@theochem.uni-stuttgart.de
cLaboratory of Molecular Structure and Dynamics, Institute of Chemistry, ELTE Eötvös Loránd University and MTA-ELTE Complex Chemical Systems Research Group, Pázmány Péter sétány 1/A, H-1117 Budapest, Hungary. E-mail: attila.csaszar@ttk.elte.hu
First published on 11th May 2022
Abstract
The linear molecular ions H2He+, HHe+2, and He+3 are the central units (chromophores) of certain He-solvated complexes of the H2He+n, HHe+n, and He+n families, respectively. These are complexes which do exist, according to mass-spectrometry studies, up to very high n values. Apparently, for some of the H2He+n and He+n complexes, the linear symmetric tetratomic H2He+2 and the diatomic He+2 cations, respectively, may also be the central units. In this study, definitive structures, relative energies, zero-point vibrational energies, and (an)harmonic vibrational fundamentals, and, in some cases, overtones and combination bands, are established mostly for the triatomic chromophores. The study is also extended to the deuterated isotopologues D2He+, DHe+2, and D2He+2. To facilitate and improve the electronic-structure computations performed, new atom-centered, fixed-exponent, Gaussian-type basis sets called MAX, with X = T(3), Q(4), P(5), and H(6), are designed for the H and He atoms. The focal-point-analysis (FPA) technique is employed to determine definitive relative energies with tight uncertainties for reactions involving the molecular ions. The FPA results determined include the 0 K proton and deuteron affinities of the 4He atom, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875(9) cm−1 [177.95(11) kJ mol−1] and 15
875(9) cm−1 [177.95(11) kJ mol−1] and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229(8) cm−1 [182.18(10) kJ mol−1], respectively, the dissociation energies of the He+2 → He+ + He, HHe+2 → HHe+ + He, and He+3 → He+2 + He reactions, 19
229(8) cm−1 [182.18(10) kJ mol−1], respectively, the dissociation energies of the He+2 → He+ + He, HHe+2 → HHe+ + He, and He+3 → He+2 + He reactions, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 099(13) cm−1 [228.48(16) kJ mol−1], 3948(7) cm−1 [47.23(8) kJ mol−1], and 1401(12) cm−1 [16.76(14) kJ mol−1], respectively, the dissociation energy of the DHe+2 → DHe+ + He reaction, 4033(6) cm−1 [48.25(7) kJ mol−1], the isomerization energy between the two linear isomers of the [H, He, He]+ system, 3828(40) cm−1 [45.79(48) kJ mol−1], and the dissociation energies of the H2He+ → H+2 + He and the H2He+2 → H2He+ + He reactions, 1789(4) cm−1 [21.40(5) kJ mol−1] and 435(6) cm−1 [5.20(7) kJ mol−1], respectively. The FPA estimates of the first dissociation energy of D2He+ and D2He+2 are 1986(4) cm−1 [23.76(5) kJ mol−1] and 474(5) cm−1 [5.67(6) kJ mol−1], respectively. Determining the vibrational fundamentals of the triatomic chromophores with second-order vibrational perturbation theory (VPT2) and vibrational configuration interaction (VCI) techniques, both built around the Eckart–Watson Hamiltonian, proved unusually challenging. For the species studied, VPT2 has difficulties yielding dependable results, in some cases even for the fundamentals of the H-containing molecular cations, while carefully executed VCI computations yield considerably improved spectroscopic results. In a few cases unusually large anharmonic corrections to the fundamentals, on the order of 15% of the harmonic value, have been observed.
099(13) cm−1 [228.48(16) kJ mol−1], 3948(7) cm−1 [47.23(8) kJ mol−1], and 1401(12) cm−1 [16.76(14) kJ mol−1], respectively, the dissociation energy of the DHe+2 → DHe+ + He reaction, 4033(6) cm−1 [48.25(7) kJ mol−1], the isomerization energy between the two linear isomers of the [H, He, He]+ system, 3828(40) cm−1 [45.79(48) kJ mol−1], and the dissociation energies of the H2He+ → H+2 + He and the H2He+2 → H2He+ + He reactions, 1789(4) cm−1 [21.40(5) kJ mol−1] and 435(6) cm−1 [5.20(7) kJ mol−1], respectively. The FPA estimates of the first dissociation energy of D2He+ and D2He+2 are 1986(4) cm−1 [23.76(5) kJ mol−1] and 474(5) cm−1 [5.67(6) kJ mol−1], respectively. Determining the vibrational fundamentals of the triatomic chromophores with second-order vibrational perturbation theory (VPT2) and vibrational configuration interaction (VCI) techniques, both built around the Eckart–Watson Hamiltonian, proved unusually challenging. For the species studied, VPT2 has difficulties yielding dependable results, in some cases even for the fundamentals of the H-containing molecular cations, while carefully executed VCI computations yield considerably improved spectroscopic results. In a few cases unusually large anharmonic corrections to the fundamentals, on the order of 15% of the harmonic value, have been observed.
1 Introduction
Molecular cations formed by hydrogen and helium, HmHe+n, the two most abundant elements of the universe, have special relevance to astronomy.1–6 This holds especially true for the H+3 cation,1,7–14 with m = 3 and n = 0, as it is one of the most important drivers of astrochemistry in the gas phase.4,9 It also holds for HHe+, the first molecule formed, through radiative association,4 in our universe; it has recently been detected in the hot gas of the planetary nebula NGC 7027.6 Further simple molecular ions, like He+2, also had special relevance during the early formation of our molecular universe.2 Members of the HHe+n and possibly the H2He+n and He+n series, in particular with low n values, are also important for several fields of chemistry. For example, solvation of the positive charge, not just that of the proton and H+2, in helium, yielding the He+n species, has attracted the attention of a number of physicists and chemists,15–36 especially since liquid helium provides an ideal matrix for a large number of physicochemical studies. To improve the chances of the detection of further HmHe+n species, as well as their deuterated isotopologues, in the laboratory as well as outside of Earth, further spectroscopic studies of at least some of the most important species are needed. These technically difficult laboratory studies must be supplemented with and guided by advanced first-principles computations, both with regard to the electronic structure and the nuclear motion. It is only the interplay of experiment and theory37,38 which can ensure that our understanding29,36,39,40 is advanced for these unusual, interesting, and important systems. As the smaller molecular cations contain only a few electrons, electronic-structure computations can be pushed to the full configuration interaction (FCI) limit, but studying the dynamics and the spectroscopy of the ions remains quite challenging due to the unusual bonding involved. Note also that some of these ions may be important as subjects of microscopic superfluidity studies41 and some are expected to behave as quasistructural molecules.42 The smallest systems, like HHe+, can also be subjected to extensive non-Born–Oppenheimer calculations (see, e.g., ref. 43).Despite their overall relevance, surprisingly little is known about the structure, energetics, and especially the spectroscopy and nuclear dynamics of the HmHe+n species, with m = 0, 1, 2, and 3 and n larger than 1. Definitive high-resolution spectroscopic31,37,38,44–55 and accurate first-principles quantum chemical27,43,56–65 information is available for the different isotopologues of HHe+. However, most of the experimental investigations for the larger systems are still limited to mass spectrometry (MS).29,39,66–70 This is unfortunate as detailed structural and dynamic information, especially relevant for astronomy, cannot be obtained from MS measurements. There are only a handful of optical spectroscopic and variational quantum dynamics investigations on the smallest members of the HmHe+n family,27,29,37,38,41,43–59,61–65,71–79 and even the experimental spectroscopic studies contain data not fully understood (vide infra), due to the limited spectral range and the low resolution of some of the measurements.
Most modern electronic-structure computations agree that HHe+2 is a highly stable, linear, symmetric molecular ion and it forms the central unit, the “dopant”, the “chromophore”, of all the HHe+n clusters studied. The situation about the chromophore of the H2He+n and He+n systems is somewhat more complex. For the H2He+n family, the tetratomic ion H2He+2 is the chromophore for n = 3–5, while for n ≥ 8, the triatomic H2He+ ion becomes the chromophore. In between these n values two isomers seem to coexist. As to the He+n family, for the smaller clusters He+3 is the chromophore, but for larger clusters the chromophore is the diatomic He+2 cation. Obviously, it is the stability of the H2He+2 and He+3 ions toward loosing a He which determines which ion is the chromophore. Due to the change in the chromophore, it is just to call the H2He+n and He+n systems chameleonic.
In recent studies37,38,41,55,79 performed on some of the HmHe+n systems it was observed that computing relative energies and especially anharmonic vibrational fundamentals, especially with n ≥ 3, provides challenges for electronic-structure theory. Thus, we decided to redesign the Gaussian basis sets applied for the electronic-structure computations. We report new atom-centered, fixed-exponent, Gaussian-type basis sets for hydrogen and helium, from triple-ζ (TZ) to hextuple-ζ (6Z) quality. With the help of these basis sets, we determine definitive energies for a number of chemical reactions involving the title ions. Following well-established recommendations,80 all the final relative energies reported in this paper carry a conservative uncertainty estimate. Determination of the final, accurate relative energies and their uncertainties is based on the focal-point-analysis (FPA) technique,81,82 which has been employed successfully during a large number of studies of small and medium-sized species for three decades.83–93
In this study, the zero-point vibrational energies (ZPVE) and the vibrational fundamentals of the triatomic and tetratomic chromophores are determined with the help of second-order vibrational perturbation theory (VPT2)94–96 and the vibrational configuration interaction (VCI)97–100 technique, both built around the Eckart–Watson Hamiltonian.101 It must be noted that determining even the vibrational fundamentals of these molecular cations beyond the harmonic-oscillator model proved to be quite challenging. In the cases when the computed results were deemed to be converged and reasonable, vibrational overtones and combination bands are also reported. Since D-substituted molecular ions of the title compounds of this study are also of interest, both experimentally37,55 and theoretically, spectroscopic results are also reported for the global minima of DHe+, DHe+2, D2He+, and D2He+2, as well.
The rest of the paper is structured as follows. Section 2 provides details about the derivation of the MAX family of Gaussian basis sets for H and He, with the cardinal number of the basis X = T(3), Q(4), P(5), and H(6). The most relevant computational details concerning this study are found in Section 3. Sections 4, 5, and 6 deal with the HHe+n, H2He+n, and He+n species, respectively, as well as with their deuterated isotopologues. To facilitate reading of these sections, the FPA tables are placed into an Appendix. Section 7 summarizes the most important conclusions of this study.
2 Development of improved H and He bases
In our previous studies on the structure, energetics, spectroscopy, and dynamics of some of the HHe+n and H2He+n systems,37,38,41,55 the correlation-consistent (cc) family102 of atom-centered, fixed-exponent, Gaussian basis functions, developed by Dunning and co-workers, has been employed. Taking into account that He is a noble gas and that members of these systems with n larger than 3 are all characterized by long He⋯He distances, diffuse (“aug”) functions must be part of the basis sets used. The computations of ref. 37, 38 and 41 revealed the need to improve at least the smaller members of the cc basis set family when studying such He-solvated molecular ions. Therefore, in this study an attempt was made to improve these basis sets, following the basic design principles102 of the aug-cc-pVXZ basis sets, where X is the so-called cardinal number.As a result, a new family of basis sets, called MA X, with cardinal numbers X = T(3), Q(4), P(5), and H(6), designed similar to the aug-cc-pVXZ family of Gaussian basis sets,103 was constructed employing neutral and positively charged systems consisting only of H and He atoms (see Table 1 for the structure of the primitive and contracted sets). We did not develop a MAD (X = 2) basis as that would appear to be too small to lead to meaningful results for the systems we are interested in.
| Atom | Name | Primitive set | Contracted set | No. of basis functions | |
|---|---|---|---|---|---|
| H and He | MAT | (10s3p2d) | → | [7s3p2d] | 26 |
| MAQ | (11s4p3d2f) | → | [8s4p3d2f] | 49 | |
| MAP | (12s5p4d3f2g) | → | [9s5p4d3f2g] | 83 | |
| MAH | (13s6p5d4f3g2h) | → | [10s6p5d4f3g2h] | 130 | |
| H | aug-cc-pVTZ | (6s3p2d) | → | [4s3p2d] | 23 |
| aug-cc-pVQZ | (7s4p3d2f) | → | [5s4p3d2f] | 46 | |
| aug-cc-pV5Z | (9s5p4d3f2g) | → | [6s5p4d3f2g] | 80 | |
| aug-cc-pV6Z | (11s6p5d4f3g2h) | → | [7s6p5d4f3g2f] | 127 | |
| He | aug-cc-pVTZ | (7s3p2d) | → | [4s3p2d] | 23 |
| aug-cc-pVQZ | (8s4p3d2f) | → | [5s4p3d2f] | 46 | |
| aug-cc-pV5Z | (9s5p4d3f2g) | → | [6s5p4d3f2g] | 80 | |
| aug-cc-pV6Z | (11s6p5d4f3g2h) | → | [7s6p5d4f3g2f] | 127 |
To ensure the general applicability of the MAX basis sets without biasing them to particular molecular systems, the basis sets were optimized based on the sum of CCSD energies of the He atom, the He2 and H2 molecules, and the He+2 and HHe+ molecular cations. The reference interatomic distances of the diatomic systems, resulting from geometry optimization at the aug-cc-pV5Z CCSD or CCSD(T) levels, were set to 0.7416 Å, 1.0809 Å, and 0.7746 Å for H2, He+2, and HHe+, respectively. In the case of He2, a strange behavior of the aug-cc-pV5Z basis was observed, which we now address. An irregularity in the geometry convergence pattern was observed: the aug-cc-pV5Z CCSD(T) bond length, at 2.98821 Å, is longer than those coming from aug-cc-pVQZ and aug-cc-pV6Z CCSD(T) computations at 2.98612 Å and 2.97975 Å, respectively. One would expect smooth convergence for geometry parameters, just as observed for the other systems investigated. The end result of our related investigation is that the problem lies in the augmentation exponent for the p shell. The original value of the exponent is 0.14. Increasing this single exponent within the extended aug-cc-pV5Z basis visibly shortens the bond length and slightly modifies the interaction energy (see Table 2). It is also important to point out that the reference geometry of the He2 molecule has a negligible impact on the basis-set optimization as the interaction is extremely weak and thus the optimization minimum is “broad”. Finally, we decided to set the reference HeHe distance to 2.9818 Å, which corresponds to the augmentation p exponent of 0.20 (see Table 2). The optimized MAP basis leads to a very similar bond length, 2.9812 Å, with a p augmentation exponent equal to 0.2074, which perfectly fits the aug-cc-pV5Z_p = 0.21 result (see Table 2). It should also be emphasized that this perfect agreement does not hold for basis sets without diffuse functions, with values of 3.1620 Å for cc-pV5Z and 3.1702 Å for the MP basis, which is the MAP basis with deleted augmentation functions. This points toward the importance of the augmentation exponent for the p shell and is a reason why we suggest using its slightly increased value, 0.16, or, in the case of a structure-oriented investigation, even 0.21.
| Basis | r e(HeHe) | Interaction energy | ||
|---|---|---|---|---|
| No-CBS | CBS(4–5) | CBS(5–6) | ||
| aug-cc-pVTZ | 3.0154 | −5.93 | ||
| aug-cc-pVQZ | 2.9861 | −6.49 | ||
| aug-cc-pV5Z | 2.9882 | −6.86 | −7.20 | −7.79 |
| aug-cc-pV5Z_p = 0.15 | 2.9868 | −6.90 | −7.33 | −7.69 |
| aug-cc-pV5Z_p = 0.16 | 2.9855 | −6.94 | −7.44 | −7.60 |
| aug-cc-pV5Z_p = 0.17 | 2.9844 | −6.97 | −7.52 | −7.52 |
| aug-cc-pV5Z_p = 0.18 | 2.9834 | −6.99 | −7.58 | −7.47 |
| aug-cc-pV5Z_p = 0.19 | 2.9826 | −7.00 | −7.63 | −7.42 |
| aug-cc-pV5Z_p = 0.20 | 2.9818 | −7.01 | −7.67 | −7.38 |
| aug-cc-pV5Z_p = 0.21 | 2.9812 | −7.01 | −7.69 | −7.36 |
| aug-cc-pV5Z_p = 0.22 | 2.9806 | −7.01 | −7.70 | −7.34 |
| aug-cc-aug-pV6Z | 2.9798 | −7.14 | ||
| MAT | 3.0218 | −5.98 | ||
| MAQ | 2.9872 | −6.78 | ||
| MAP | 2.9812 | −7.05 | −7.46 | −7.62 |
| MAH | 2.9771 | −7.24 | ||
Table 3 contains the bond lengths of the species of this study optimized at the MAQ FCI level. The only difference which can be considered significant between the aug-cc-pV5Z CCSD(T) and the MAQ FCI structural parameters is for He2, exhibiting one of the weakest bonds, where the bond length at the MAQ FCI level is 0.0018 Å shorter than the aug-cc-pV5Z CCSD(T) value (vide supra).
| Molecular species | EC | ES | Symmetry | r e(HHe) | r e(HeHe) | r e(He⋯He) | r e(HH) |
|---|---|---|---|---|---|---|---|
| H+2 | 1 | X2Σ+g | D ∞h | 1.05681 | |||
| H2 | 2 | X1Σ+g | D ∞h | 0.74163 | |||
| HHe+ | 2 | X1Σ+ | C ∞v | 0.77457 | |||
| He+2 | 3 | X2Σ+u | D ∞h | 1.08117 | |||
| H2He+ | 3 | ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+ 2Σ+ |
C ∞v | 1.02324 | 1.09798 | ||
| He2 | 4 | ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1Σ+g 1Σ+g |
D ∞h | 2.98005 | |||
| HHe+2 | 4 | ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1Σ+g 1Σ+g |
D ∞h | 0.92475 | |||
| C ∞v | 0.77272 | 2.10340 | |||||
| H2He+2 | 5 | ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+g 2Σ+g |
D ∞h | 1.23731 | 1.06172 | ||
| He+3 | 5 | ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+g 2Σ+g |
D ∞h | 1.23608 |
It is worth discussing some of the bond lengths of Table 3. The shortest re(HHe) bond lengths, about 0.77 Å for HHe+ and the complex HHe+⋯He, clearly reflect dative, less strong than the usually covalent, two-electron–two-center (2e–2c) bonds, perturbed slightly in the latter case. Significantly longer re(HHe) bond lengths characterize the global minima of HHe+2 and H2He+. These elongated bonds reflect the change in bond length between a (2e–2c) and a one-electron–two-center (1e–2c) bond, as also seen for the case of H2 and H+2.
The possible problem of linear dependency, that may occur during the optimization of basis-set parameters, was eliminated, following the work of Petersson et al.,104 by an expansion, up to six terms, of the Gaussian exponents' logarithms into orthonormal Legendre polynomials. Exponents of the diffuse functions, one for each shell, were optimized based on the E(20)disp dispersion energy correction105 for two interacting dimers of helium (the He4 system) or two hydrogen molecules (the H4 system), the geometries of which were previously optimized at the aug-cc-pV5Z CCSD(T) level of theory. All basis set optimization calculations were supported by the codes ChemTools106 and MOLPRO.107
During the design of the MAX basis sets the correlation-consistent nature of the Dunning-type basis sets103 was preserved. Nevertheless, the number of s-type exponents has been increased both in the primitive and the contracted sets for all the MAX bases of hydrogen and helium. For the MAT basis adding the s exponents leads to better convergence of the anharmonic vibrational contributions. This is a much cheaper alternative than going to a basis set with an increased cardinal number. This behavior is likely connected to a better description of σ bonds. Note that increasing the number of p exponents fails for the challenging case of He+3 and thus has not been pursued.
The composition of the MAX basis sets, along with that of the correlation-consistent basis sets, of H and He is summarized in Table 1 (vide supra). During this study even the MAH basis, definitely close to the CBS limit, could be employed at the FCI level for most of the species (vide infra).
3 Computational details
3.1 Focal-point analysis (FPA)
Our investigation of the energetics of the molecular ions of this study is based on the FPA technique.81,82 FPA requires the execution of a predetermined set of single-point electronic-structure computations at fixed, in fact the best possible,108 reference structures (see Table 3 for the actual structural parameters employed), using a systematically improved set of electron-correlation treatments, approaching FCI, and the MAX basis sets, approaching the complete basis set (CBS) limit,87,109,110 together yielding an approximation of the CBS FCI limit.87As part of the FPA scheme, extrapolations to the CBS limit need to be performed. These extrapolations are done separately for the Hartree–Fock (HF) level and for the electron-correlation increments. The usual111–113 two-points formulas were employed for this task.
The CBS FCI energies are augmented with so-called “small (auxiliary) corrections”,81,82 in the present case the diagonal Born–Oppenheimer (DBOC)114 and the relativistic115 corrections. Finally, the electronic energies of the molecular species are corrected for the effect of vibrations through the inclusion of ZPVEs. The most significant advantage of the original FPA method, compared to derivative composite approaches (e.g., HEAT116,117), is that FPA is designed to yield appropriate uncertainties for the computed relative energies.80–82
The tables corresponding to the FPA analyses of this study, Tables 8–14, are put into the Appendix. All of them are quoted in the appropriate sections of the main body of the paper; in particular, in Sections 4–6.
3.2 Reference structures
The reference equilibrium structures of the chromophores of HHe+n, H2He+n, and He+n have been determined at the MAQ CCSDTQ level of electronic-structure theory (see Table 3). Due to the fact that most of these chromophores contain only a few electrons, CCSDTQ often corresponds to FCI.Geometry optimizations were performed not only for primary but also for secondary minima, corresponding to He-solvated ions. For example, in the case of HHe+2 the global minimum is linear He–H+–He, with an equilibrium structure of D∞h point-group symmetry, while the secondary minimum is linear He⋯He–H+, with an equilibrium structure of C∞v point-group symmetry (Table 3). The effect of basis set superposition error on the computed distances118 was not investigated.
3.3 Auxiliary corrections
The relativistic corrections determined in this study for each species were obtained within the mass-velocity and one-electron Darwin (MVD1) approximation,82,115,119,120 employing the MAQ basis and up to the CCSD(T) level of electronic-structure theory. Relativistic corrections are known to exhibit protracted basis-set dependence.115 Since their absolute magnitude is small for systems composed of H and He atoms only and their change among the different systems on the left- and right-hand sides of the chemical reaction equations investigated should be especially small, it was deemed to be sufficient to stay within the simple MVD1 formalism.The diagonal Born–Oppenheimer corrections114 to the electronic energies were estimated at the MAQ CCSD level. These “small corrections”81,82 are expected to be larger than the relativistic ones for the light H- and He-containing systems studied here. Nevertheless, if sufficiently large uncertainties are attached to these computed values than there is little doubt that their effect is taken correctly into account during the FPA study of relative energies of the title molecular cations. As the systems studied are light, the choice of masses used during the DBOC computations does matter for them.60 In this study, the following masses have been used: m(H) = 1.007 825 u, m(D) = 2.014 102 u, and m(4He) = 4.002 603 u.
3.4 Harmonic and anharmonic vibrational frequencies
To determine accurate relative and reaction energies through the FPA approach, it is preferred to use anharmonic ZPVEs, as usually the vibrational corrections have the largest uncertainties, especially when only harmonic estimates are available. Harmonic frequencies, and thus harmonic ZPVEs, have been determined during this study, as well, but mostly just to check whether an optimized stationary point corresponds to a minimum or not.During the execution of the project, issues have been found with some of the VPT294–96 results, which are usually quite accurate for the fundamentals of semirigid molecules when resonances are absent or not overly strong. Due to these problems, we decided to obtain the ZPVE values and the vibrational fundamentals with the VCI technique, which should be devoid of vibrational resonances. When the difficulties encountered could not be solved either at the VPT2 or VCI levels, the corresponding entries in Tables 4–7 are not provided. In such cases variational nuclear-motion computations utilizing a nuclear Hamiltonian written in internal coordinates121 and a carefully fitted purpose-built PES are required to obtain meaningful results.
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1–
1–![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3), their overtones, and the combination band
3), their overtones, and the combination band ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 +
1 + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 of HHe+2 and DHe+2, all in cm−1, determined with different theoretical modelsa
3 of HHe+2 and DHe+2, all in cm−1, determined with different theoretical modelsa
| Species | Technique | ZPVE |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g)
1(σ+g) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2(πu)
2(πu) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ−g)
3(σ−g) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g) 1(σ+g) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 02(σ+g) 02(σ+g) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 22(δg) 22(δg) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+g) 3(σ+g) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 +
1 + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ−u) 3(σ−u) |
|---|---|---|---|---|---|---|---|---|---|---|
| a All the values reported correspond to different representations of the PES around the global minimum of HHe+2 obtained at the MAQ CCSD(T) level of electronic-structure theory. | ||||||||||
| HHe+2 | Harmonic | 2298.0 | 1139.3 | 953.4 | 1550.1 | |||||
| VPT2 | 2267.0 | 896.5 | 883.7 | 1352.0 | — | — | — | — | — | |
| VCI | 2254.8 | 957.5 | 882.7 | 1318.6 | 1889.3 | 1739.4 | 1778.2 | 2972.4 | 2086.7 | |
| Experiment38 | — | 1315.8 | ||||||||
| DHe+2 | Harmonic | 1858.7 | 1139.3 | 711.1 | 1156.0 | |||||
| VPT2 | 1829.9 | 930.9 | 670.3 | 1034.6 | — | — | — | — | — | |
| VCI | 1825.7 | 975.4 | 670.3 | 1023.3 | 1854.9 | 1356.4 | 1349.8 | 2153.8 | 1848.3 | |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1–
1–![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3, with symmetries in parentheses), overtones, and a combination band of H2He+ and D2He+, all in cm−1, determined with different techniquesa
3, with symmetries in parentheses), overtones, and a combination band of H2He+ and D2He+, all in cm−1, determined with different techniquesa
| Species | Technique | ZPVE |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+)
1(σ+) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2(π)
2(π) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+)
3(σ+) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+) 1(σ+) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 02(σ+) 02(σ+) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 22(δ) 22(δ) |
2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+) 3(σ+) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 +
2 + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 (π) 3 (π) |
|---|---|---|---|---|---|---|---|---|---|---|
| a See footnote a to Table 4. b Broad estimates from low-resolution experiments. The experimental uncertainties of the FELIX data of ref. 55 are typically 0.5%. c Due to the multi-photon process of detection, the experimental signal is very broad, shifted and unspecific. Thus, the assignment of the experimental signal was deemed to be tentative in ref. 55. Therefore, no uncertainty is quoted for these data in this table. d Numerical convergence issues, see text. | ||||||||||
| H2He+ | Harmonic | 2181.0 | 1935.5 | 719.2 | 988.2 | |||||
| VPT2 | 2096.5 | 1860.5 | 655.3 | 741.9 | — | — | — | 1297.2 | 1291.4 | |
| VCI | 2092.3 | 1830.1 | 640.0 | 735.4 | —d | —d | —d | 1302.9 | 1243.1 | |
| Variational78 | 1832 | 648 | 734 | |||||||
| Variational55 | 2090.8 | 1833 | 640.0 | 732 | 1136.1 | 1256.4 | ||||
| Experiment55b | — | 1840(9) | 695 | 840 | 1159 | |||||
| D2He+ | Harmonic | 1610.1 | 1369.4 | 521.8 | 807.3 | |||||
| VPT2 | 1560.9 | 1350.3 | 484.2 | 641.9 | 2455.4 | 929.2 | 970.1 | 1120.8 | 1061.6 | |
| VCI | 1559.1 | 1323.8 | 478.3 | 642.6 | 2533.9 | 902.3 | 950.8 | 1158.5 | 1052.2 | |
| Variational55 | 1317.5 | 478.4 | 640.9 | 891.1 | 1139.6 | |||||
| Experiment55b | — | 1309 | 459 | 670 | 860 | 1145 | ||||
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1–
1–![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3), three overtones, and a combination band of He+3, all in cm−1, determined with different techniquesa
3), three overtones, and a combination band of He+3, all in cm−1, determined with different techniquesa
The VPT2 calculations of this study were executed with the help of the MOLPRO99,100,107 package. The vibrational configuration interaction (VCI) facility of MOLPRO has been used extensively to determine ZPVEs and vibrational fundamentals, overtones, and combination bands. While the VPT2 calculations rely on a quartic force field (QFF) approximation122,123 of the potential energy surface (PES) around the reference structure, the VCI treatment employs a multidimensional PES represented by an n-mode expansion, truncated after the 4-mode coupling terms.124 Symmetry has been fully exploited within the electronic structure calculations and within the individual terms of the n-mode expansions.100 The resulting grid representation of the PES has been transformed to polynomials using efficient Kronecker product fitting, with up to 12 monomials per mode.125 Optimized one-mode wave functions (modals) have been determined from vibrational self-consistent field (VSCF) theory based on a primitive basis of 16 distributed Gaussians.126 Subsequent state-specific configuration-selective VCI calculations made use of a basis of single Hartree products, including up to quadruple excitations. A constant μ-tensor has been used throughout. In order to ensure that the VCI results are converged, a large number of consistency checks have been performed with respect to the polynomial fit and the correlation space.
3.5 Bonds and atomic charges
Since all the complexes studied have a unit positive charge, it is of interest to understand where the nominal, partial charges are within these molecular cations. Mulliken charges are to some extent unreliable and they definitely cannot be considered to be dependable for the larger He-solvated ions. Thus, QTAIM127 charges have been determined for the molecular cations of this study.The QTAIM approach127 relies on the fact that critical points of the electron density, ρ, defined by the equation ∇ρ = 0, arise when there is interaction between atoms of the molecule. In other words, presence of a bond path linking the interacting atoms via a bond critical point (BCP) is evidence of an interaction. In all cases studied, BCPs and bond paths have been found where expected, suggesting that simple chemical intuition agrees with the sophisticated analysis of the electron density.
The code AIMAll128 has been used for the QTAIM127 calculations, yielding atomic charges, bond critical points (BCP), and bond paths, supporting a qualitative understanding of some of the quantitative results of this study (for this reason, no quantitative results, apart for charges, are provided). MAQ CCSD wave functions computed with the Gaussian16 code129 have been utilized for these calculations.
3.6 Electronic-structure computations
The FPA approach requires the execution of a large number of increasingly sophisticated electronic-structure computations approaching the FCI limit in a systematic fashion. These computations facilitate the accurate estimation of correlation-energy increments and their uncertainties. The coupled-cluster (CC) techniques form such a hierarchy; thus, they have been used extensively.The electronic-structure computations utilized the packages MOLPRO,107 CFOUR,130 and MRCC.131 The CCSDTQ geometry optimizations were performed with the MRCC code, employing ultratight convergence criteria in order to avoid the nonzero-force dilemma.108 The CFOUR package was used for the auxiliary relativistic (MVD1) and the DBOC computations. All VPT2 and VCI results reported were obtained with the help of the MOLPRO package. Note that extensive modifications of the default values characterizing the VCI procedure within MOLPRO were required to obtain converged results for almost all of the molecular cations studied.
4 (H/D)He+n species
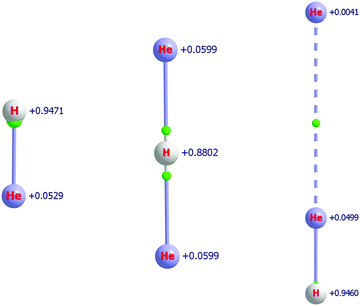
The attachment of one and two He atoms to the proton, H+, or the deuteron, D+, results in stable molecular cations with linear equilibrium structures, see Fig. 1. As established in previous studies,37,38,41 the symmetric He–(H/D)+–He molecular cation appears to form the chromophore of all the He-solvated (H/D)He+n, n ≥ 3, complexes. In this section the relatively strongly bound (H/D)He+ and (H/D)He+2 molecular ions, as well as the He-solvated isomer He⋯He–(H/D)+ (a secondary minimum, SM, on the PES of the [(H/D), He, He]+ system) are investigated, and we provide definitive structural, energetic, and spectroscopic quantities with statistically significant uncertainties.4.1 HHe+ and DHe+
HHe+ is the first molecule formed in space4,132 and it is the founding member of the HHe+n series, though it is not the chromophore of it.41 The short internuclear distance characterizing HHe+, the hydrohelium cation, 0.775 Å (see Table 3), suggests the presence of a relatively strong, “true” chemical bond in this diatomic species. As shown in Fig. 1, the BCP is extremely close to the proton and there is very little charge transfer from the proton to the helium atom, only 0.05. Nevertheless, the He atom of HHe+ does acquire a small positive charge.As detailed in Table 8, the electronic proton affinity (PA) of He, defined by the reaction He + H+ → HHe+, obtained with the FPA approach and the MAX basis-set family, is 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459(7) cm−1, very similar to a previous theoretical estimate, 16 457(8) cm−1,41 and an empirical estimate of 16
459(7) cm−1, very similar to a previous theoretical estimate, 16 457(8) cm−1,41 and an empirical estimate of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456.2(1) cm−1.60 The electron-correlation contribution to this value is unusually small: the CBS HF estimate is 15 673(1) cm−1. It is noteworthy that the reaction energy obtained at the MAT HF level is substantially closer, by more than 50%, to the CBS HF value than the one obtained with the aug-cc-pVTZ basis set, proving the good performance of the MAT basis, at least for cationic He-containing species.
456.2(1) cm−1.60 The electron-correlation contribution to this value is unusually small: the CBS HF estimate is 15 673(1) cm−1. It is noteworthy that the reaction energy obtained at the MAT HF level is substantially closer, by more than 50%, to the CBS HF value than the one obtained with the aug-cc-pVTZ basis set, proving the good performance of the MAT basis, at least for cationic He-containing species.
The mass-dependent DBOC corrections to the reaction partners are relatively substantial, at the MAQ FCI level they are +92.1, +100.2, and +92.4 cm−1 for He, HHe+, and DHe+, respectively. The reaction-energy DBOC corrections are, of course, much smaller, −8.1(25) and −0.3(10) cm−1 for HHe+ and DHe+, respectively. The relativistic corrections are −24.7 and −23.9 cm−1 for He and HHe+, respectively, yielding a relativistic correction of −0.8(10) cm−1, which is negligible even at the level of accuracy sought in this study. Overall, the auxiliary corrections to the proton and deuteron affinities of 4He amount to −9(3) and −1(1) cm−1, respectively.
The harmonic ZPVE estimates for HHe+ and DHe+ are 1610(2) and 1248(2) cm−1, obtained at the MAQ FCI level, where the attached uncertainties reflect other harmonic ZPVE values computed with different basis sets (not reported). The VPT2 corrections to these values are −35.2(30) and −21.1(25) cm−1, obtained at the same level, yielding anharmonic ZPVE estimates of 1575(4) and 1227(3) cm−1 for HHe+ and DHe+, respectively. The electronic proton and deuteron affinities must be corrected with these anharmonic ZPVE estimates as the other reaction partners are atoms. Note that (a) the ZPVE values obtained are significantly higher than half of the calculated fundamentals of these diatomic molecular ions, 2911 and 2310 cm−1 for HHe+ and DHe+, respectively; and (b) the anharmonic corrections to the fundamentals are unusually large, approaching 10%.
Overall, our FPA estimate of the 0 K proton affinity of the ground-state 4He atom is 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875(9) cm−1. This computed value compares extremely well with the best available literature results, namely 14
875(9) cm−1. This computed value compares extremely well with the best available literature results, namely 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876(12),41 14
876(12),41 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873,57 and 14
873,57 and 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863(8)133 cm−1. Based on the present FPA analysis, the deuteron affinity of 4He is 15
863(8)133 cm−1. Based on the present FPA analysis, the deuteron affinity of 4He is 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229(8) cm−1. To the best of our knowledge, there are no experimental values to compare this predicted estimate with.
229(8) cm−1. To the best of our knowledge, there are no experimental values to compare this predicted estimate with.
4.2 HHe+2 and DHe+2
The ground electronic state,![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1Σ+g, PES of the HHe+2 molecular ion is characterized by the presence of two linear minima. The global minimum (GM) corresponds to the symmetric He–H+–He arrangement with an equilibrium structure of D∞h point-group symmetry. As expected, the HHe bond length is significantly longer than that in HeH+ (see Table 3). The secondary minimum (SM) is of C∞v point-group symmetry, the He atom attaches to the He end, so it corresponds to the He-solvated HHe+ molecule. The two relative energies investigated via the FPA technique are the HHe+2 → HeH+ + He dissociation reaction (Table 9) and the isomerization reaction involving GM and SM (Table 10).
1Σ+g, PES of the HHe+2 molecular ion is characterized by the presence of two linear minima. The global minimum (GM) corresponds to the symmetric He–H+–He arrangement with an equilibrium structure of D∞h point-group symmetry. As expected, the HHe bond length is significantly longer than that in HeH+ (see Table 3). The secondary minimum (SM) is of C∞v point-group symmetry, the He atom attaches to the He end, so it corresponds to the He-solvated HHe+ molecule. The two relative energies investigated via the FPA technique are the HHe+2 → HeH+ + He dissociation reaction (Table 9) and the isomerization reaction involving GM and SM (Table 10).
The QTAIM analysis, see Fig. 1, indicates that the bond critical points are close to the proton for both isomers of HHe+2. Clearly, the larger the charge on the H atom the closer the BCP is to it. Furthermore, in the case of the SM, there is a BCP in between the two He atoms, indicating the presence of a weak interaction. The QTAIM charges have very different numerical values compared to the Mulliken charges reported in ref. 41; nevertheless, the qualitative picture does not change in a significant way. According to QTAIM, the positive charge remains much more localized on the proton and delocalizes much less to the He atom(s). The solvating He acquires only a very small positive charge, it is only +0.004, as shown in the example of the secondary minimum. It is also important to point out that upon solvation by a He atom the charge on the proton remains basically the same, the charge on the proton in HHe+ and the SM of HHe+2 are +0.947 and +0.946, respectively (see Fig. 1).
The T1 diagnostic values of CCSD theory134 are 0.0015, 0.0053, 0.0051, and 0.0040 for He, HHe+, HHe+2(GM), and HHe+2(SM), respectively, obtained with the MAQ basis, suggesting that the electronic structure of all these chemical entities can be described very well with single-reference CC techniques. Furthermore, very fast convergence of the correlation-energy increments in the He + H+ → HHe+ and HHe+ + He → HHe+2 reaction energies is expected, which is indeed the case (see the relevant entries of Tables 8 and 9). The energies of the reactions HHe+2 → HHe+ + He (Table 9) and HHe+2 → H+ + 2He (total atomization energy (TAE), which can be deduced from Tables 8 and 9 by adding the appropriate entries) suggest that the binding of one and two He atoms to a proton is strongly exothermic. The CBS FCI-based FPA value for the TAE of HHe+2 is 21 091(12) cm−1, which should be compared to the electronic TAE of HHe+, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459(7) cm−1.
459(7) cm−1.
The pure electronic dissociation energy of the HHe+2 → HHe+ + He process is 4632(4) cm−1 (Table 9), very similar to its previous estimate, 4631(10) cm−1.41 As expected, convergence of the CC series is very pronounced. The small auxiliary DBOC corrections to the electronic energy of the GM of HHe+2 and DHe+2 are +194.4 and +185.8 cm−1, respectively. Thus, the DBOC corrections to the dissociation reactions are 2.1 and 1.3 cm−1 for HHe+2 and DHe+2, respectively, minuscule values to which a reasonable uncertainty of ±2 cm−1 can be attached. The relativistic correction to the energy of the GM is −48.7 cm−1. Thus, using the relativistic corrections of −23.9 and −24.7 cm−1 for HHe+ and He, respectively, the relativistic correction to the reaction is 0.1(10) cm−1, a completely negligible value. Overall, the auxiliary correction to the first dissociation energy is 2(2) cm−1 for both HHe+2 and DHe+2.
The harmonic ZPVE of HHe+2 is estimated to be 2298 and 2299 cm−1 at the MAQ CCSD(T) and CCSDTQ ≡ FCI levels, respectively (Table 4 contains the MAQ CCSD(T) value). The VCI treatment yields an anharmonic ZPVE estimate of 2254.8 cm−1, and, based also on further, unreported results, we accept 2255(3) cm−1 as the best estimate of the ZPVE of the GM of HHe+2. The value of 2255(3) cm−1 for the ZPVE of GM-HHe+2 is unusual in the sense that it is more than 200 cm−1 higher than half of the sum of the calculated fundamentals. The ZPVE of DHe+2 is 1826(3) cm−1, with characteristics similar to those of HHe+2.
Based on the ZPVE estimates of 1575(4) and 2255(3) cm−1 for HHe+ and HHe+2, respectively, the estimated ZPVE-corrected first dissociation energy of HHe+2 becomes 3948(7) cm−1, comparing favorably with a previous estimate, 3931(20) cm−1.41 As to the first dissociation energy of DHe+2, it can be estimated by using the ZPVE values of 1227(3) and 1826(3) cm−1 for DHe+ and DHe+2, respectively. The final FPA estimate is thus 4033(6) cm−1.
The FPA energy difference between the GM and SM isomers of HHe+2 is substantial on the energy scale of cations containing He-solvated proton, it is 4368(6) cm−1 (see Table 10), without taking into account the ZPVEs. Comparison of this value with the estimate of the first dissociation energy, 4632(4) cm−1, suggests a very shallow minimum and a small He-solvation energy, 264(7) cm−1. It is also of interest to note that while the HF contribution is very substantial for the global minimum, a direct consequence of the two strong bonds within this ion, for the secondary minimum of HHe+2 the solvation energy comes to a much larger extent from electron correlation. The mass-dependent DBOC corrections to the electronic energy of the SM of HHe+2 and DHe+2 are +192.3 and +185.8 cm−1, respectively. Not too surprisingly, these values are almost exactly the same as the sum of the DBOC corrections of the He and (H/D)He+ systems, (+192.3/+184.5) cm−1. This means that the DBOC corrections to the isomerization reaction are 0.0(10) and 1.3(10) cm−1 for HHe+2 and DHe+2, respectively. The relativistic correction to the electronic energy of the SM is −48.6 cm−1. This means that the relativistic correction to the isomerization reaction is 0.1 cm−1, once again a completely negligible quantity. Given the uncertainties of all the other contributions to the izomerization energy, especially that coming from the vibrations (vide infra), the auxiliary corrections can be safely neglected.
Due to the extremely weakly-bound nature of the SM, we did not make an attempt to determine the anharmonic estimate of its ZPVE. The energy difference of the two linear isomers of HHe+2 becomes 3828(40) cm−1 when the harmonic ZPVE correction of 540(40) cm−1 is taken into account.
The dissociation energy of the SM of HHe+2 can be associated with the He-solvation energy of the HHe+ molecular ion. The He-solvation energy thus determined is 124(42) cm−1. Note that the smallness of the He-solvation energies is what allowed the characterization of the dynamics of these molecular ions via action spectroscopy in the infrared region.37,38
Table 4 contains a considerable amount of accurate information about the vibrational fundamentals, overtones, and a combination band, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 +
1 + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ−u), of HHe+2 and DHe+2, obtained with the help of different theoretical models. Note that the potential for HHe+2 along the normal coordinate of ω3 is strongly quartic in nature, with a huge quartic normal-coordinate force constant of F3333 = 6611.3 cm−1. This, associated with the need for high-order monomials within the fitting of the n-mode representation of the PES, leaves some doubt whether a representation of the PES by a QFF, as used within the VPT2 calculations, is appropriate. The strong quartic character of the
3(σ−u), of HHe+2 and DHe+2, obtained with the help of different theoretical models. Note that the potential for HHe+2 along the normal coordinate of ω3 is strongly quartic in nature, with a huge quartic normal-coordinate force constant of F3333 = 6611.3 cm−1. This, associated with the need for high-order monomials within the fitting of the n-mode representation of the PES, leaves some doubt whether a representation of the PES by a QFF, as used within the VPT2 calculations, is appropriate. The strong quartic character of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 vibration is also revealed by the fact that the computed values for 2
3 vibration is also revealed by the fact that the computed values for 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 are significantly larger than twice the value of the corresponding fundamental. As a consequence, the results are very sensitive to the potential and the only calculation in good agreement with the experimental value38 for
3 are significantly larger than twice the value of the corresponding fundamental. As a consequence, the results are very sensitive to the potential and the only calculation in good agreement with the experimental value38 for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 is provided by the VCI calculation, based on the n-mode representation of the PES, which accounts for high-order terms. The sensitivity of the computed fundamentals on the level of theory can be further demonstrated by a comparison of the harmonic frequency for ω1 at 1139.3 cm−1 (MAQ CCSD(T)) and the respective anharmonic values for
3 is provided by the VCI calculation, based on the n-mode representation of the PES, which accounts for high-order terms. The sensitivity of the computed fundamentals on the level of theory can be further demonstrated by a comparison of the harmonic frequency for ω1 at 1139.3 cm−1 (MAQ CCSD(T)) and the respective anharmonic values for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 listed in Table 4. An anharmonicity correction of about 21% (VPT2) would be exceptionally large, while a value of about 15% (VCI) is still very large, but it is closer to the usual range. The expected uncertainty of the fundamentals of HHe+2 obtained by VCI should be about ±5 cm−1. This means that the VPT2 value for the
1 listed in Table 4. An anharmonicity correction of about 21% (VPT2) would be exceptionally large, while a value of about 15% (VCI) is still very large, but it is closer to the usual range. The expected uncertainty of the fundamentals of HHe+2 obtained by VCI should be about ±5 cm−1. This means that the VPT2 value for the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g) fundamental is seriously in error. As to the overtones of HHe+2, 2
1(σ+g) fundamental is seriously in error. As to the overtones of HHe+2, 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 02(σ+g) and 2
02(σ+g) and 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g) are coupled by a strong Darling–Dennison resonance. This is an unexpected observation as the corresponding harmonic energy difference is larger than 370 cm−1. However, the strong anharmonic corrections bring these states close together. Therefore, we do not report VPT2 results for the overtones and the combination band of this system as resonance corrections were found to be large and tend to deteriorate the results in comparison to the VCI values. Differences between these two sets of data were found to be huge and thus we conclude that VPT2 is not capable of predicting the overtones of HHe+2 correctly. It is also expected that the accuracy of the overtones and the combination band computed with VCI is worse than that of the fundamentals, i.e., it would not be surprising if some of the VCI values were in error by as much as 30 cm−1.
1(σ+g) are coupled by a strong Darling–Dennison resonance. This is an unexpected observation as the corresponding harmonic energy difference is larger than 370 cm−1. However, the strong anharmonic corrections bring these states close together. Therefore, we do not report VPT2 results for the overtones and the combination band of this system as resonance corrections were found to be large and tend to deteriorate the results in comparison to the VCI values. Differences between these two sets of data were found to be huge and thus we conclude that VPT2 is not capable of predicting the overtones of HHe+2 correctly. It is also expected that the accuracy of the overtones and the combination band computed with VCI is worse than that of the fundamentals, i.e., it would not be surprising if some of the VCI values were in error by as much as 30 cm−1.
In Table 4 spectrocopic results are presented for DHe+2, as well. It is considerably easier, compared to HHe+2, to obtain converged results for DHe+2. As to the fundamentals, the VPT2 and VCI results agree with each other rather well, except for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g). In fact, the situation is similar to the case of HHe+2, where the VCI result is some 60 cm−1 higher than the VPT2 result. For DHe+2, the difference is less, about 45 cm−1, but clearly the VPT2 value for
1(σ+g). In fact, the situation is similar to the case of HHe+2, where the VCI result is some 60 cm−1 higher than the VPT2 result. For DHe+2, the difference is less, about 45 cm−1, but clearly the VPT2 value for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g) must be the incorrect one. An inspection of the polynomial coefficients for the one-dimensional cut along this mode reveals that there are fairly strong contributions from the fifth- and seventh-order terms; these terms, of course, are not included in the QFF of the VPT2 calculations. The uncertainties of the VCI fundamentals of DHe+2 are estimated to be ±4 cm−1. While VCI values are presented for the overtones and the
1(σ+g) must be the incorrect one. An inspection of the polynomial coefficients for the one-dimensional cut along this mode reveals that there are fairly strong contributions from the fifth- and seventh-order terms; these terms, of course, are not included in the QFF of the VPT2 calculations. The uncertainties of the VCI fundamentals of DHe+2 are estimated to be ±4 cm−1. While VCI values are presented for the overtones and the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 +
1 + ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ−u) combination band, the reported values might have a sizeable uncertainty, up to about 25 cm−1.
3(σ−u) combination band, the reported values might have a sizeable uncertainty, up to about 25 cm−1.
5 (H2/D2)He+n species
Unlike the case of the (H/D)He+n systems, where all the molecular ions are necessarily closed shell, the (H2/D2)He+n ions are all open-shell systems, making the electronic-structure computations for them slightly more expensive and problematic. The ground electronic states of (H2/D2)He+ and (H2/D2)He+2 are![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+ and
2Σ+ and ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+g, respectively. The T1 diagnostic values of CCSD theory, obtained with the help of the MAQ basis, are only 0.0057, 0.0088, and 0.0092 for H+2, H2He+, and H2He+2, respectively. Thus, the single-reference CC techniques are perfectly adequate for studying the structure, energetics, and the dynamics of these systems.
2Σ+g, respectively. The T1 diagnostic values of CCSD theory, obtained with the help of the MAQ basis, are only 0.0057, 0.0088, and 0.0092 for H+2, H2He+, and H2He+2, respectively. Thus, the single-reference CC techniques are perfectly adequate for studying the structure, energetics, and the dynamics of these systems.
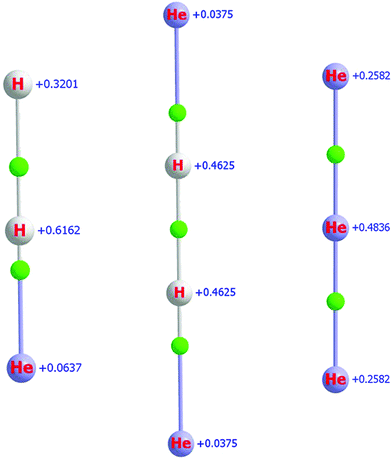
Fig. 2 presents the equilibrium structures of the H2He+, H2He+2, and He+3 molecular ions, together with QTAIM atomic charges and BCPs. As observed for HHe+ and HHe+2 (vide supra), the partial charges on the He atoms are relatively small for both H2He+ and H2He+2, only 0.06 and 0.04, respectively. The position of the BCPs clearly confirm that all these systems are molecular ions.
5.1 H2He+ and D2He+
The![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+ PES135 of H2He+ is characterized by a single, linear minimum, corresponding to the point group C∞v. Seemingly, there is no secondary minimum on this PES. Nevertheless, the complete nuclear dynamics of the ion, when all the bound and some of the resonance vibrational states are considered, is more complex than one would first expect.55,135 On the one hand, based on the significant first dissociation energy (see Table 11), in their
2Σ+ PES135 of H2He+ is characterized by a single, linear minimum, corresponding to the point group C∞v. Seemingly, there is no secondary minimum on this PES. Nevertheless, the complete nuclear dynamics of the ion, when all the bound and some of the resonance vibrational states are considered, is more complex than one would first expect.55,135 On the one hand, based on the significant first dissociation energy (see Table 11), in their ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+ electronic state and with respect to their fundamentals, H2He+ and D2He+ may be considered as semi-rigid molecules (obviously, D2He+ more so than H2He+). On the other hand, especially in the higher rovibrational states, less of interest here but more in ref. 55, where all the bound vibrational states of H2He+ and D2He+ were considered, one may consider H2He+ and D2He+ as van der Waals complexes “tunneling” between two equivalent linear structures, those with He on either side of the H+2 and D+2 central units, respectively. In the latter case one must treat the dynamics according to the molecular-symmetry (MS) group C2v(M).136
2Σ+ electronic state and with respect to their fundamentals, H2He+ and D2He+ may be considered as semi-rigid molecules (obviously, D2He+ more so than H2He+). On the other hand, especially in the higher rovibrational states, less of interest here but more in ref. 55, where all the bound vibrational states of H2He+ and D2He+ were considered, one may consider H2He+ and D2He+ as van der Waals complexes “tunneling” between two equivalent linear structures, those with He on either side of the H+2 and D+2 central units, respectively. In the latter case one must treat the dynamics according to the molecular-symmetry (MS) group C2v(M).136
The first dissociation energy of H2He+, toward loosing the He atom, is not large. As Table 11 attests, the pure electronic part is just 2730(3) cm−1. The HF contribution, at the CBS limit, is only about half of this value, 1422(1) cm−1. All energy increments in the FPA hierarchy of HF → MP2 → CCSD → CCSD(T) → CCSDT ≡ FCI are positive and decrease drastically with each consecutive improvement of the level of electron-correlation treatment. In fact, the increment from CCSD(T) to CCSDT (≡FCI) is only 7(1) cm−1, making, not too surprisingly, the gold-standard CCSD(T) level very accurate for this three-electron system.
The availability of high-quality PESs135,137 and related variational estimates55,135 of the rovibrational states of H2He+ allows the tight determination of the ZPVE of this molecular ion (Table 5). According to ref. 55, the ZPVE of H2He+ is 2090.8(20) cm−1. This, in turn, allows the estimation of the accuracy of the VPT2 and VCI ZPVE results for this species, which are 2096 and 2092 cm−1, respectively, both at the MAQ CCSD(T) level. Clearly, for this basically semirigid system both VPT2 and VCI perform very well, as expected123 for a system where the stretching motions dominate for the ZPVE. The suggested ZPVE of H2He+ is 2091(2) cm−1. The tight agreement of the various first-principles results for H2He+ suggest a similarly high accuracy, ±2 cm−1, for the VCI estimate of the ZPVE of D2He+, which is thus 1559(2) cm−1.
The ZPVE corrections to the dissociation reactions H2He+ → H+2 + He and D2He+ → D+2 + He can be calculated utilizing the ZPVEs of H+2 and D+2, 1149.5(1)138 and 815(1) cm−1, respectively (the latter value was obtained with the MAQ basis and a VPT2 treatment). Thus, the ZPVE-corrected dissociation energies are 1789(4) and 1986(4) cm−1 for H2He+ and D2He+, respectively. The so-called FCI PES of ref. 135 exhibits a dissociation energy of D0 = 1794 cm−1 for para-H2He+ and D0 = 1852 cm−1 for ortho-H2He+.55,135 The latter value is higher due to the allowed dissociation to a j = 1 state, where j is the quantum number associated with the rotation of the H+2 product. The nearly perfect agreement of the FPA estimate of the dissociation energy of para-H2He+, 1789(4) cm−1, with the one characterizing the FCI PES of ref. 135, 1794 cm−1, points toward the accuracy of the rovibrational results obtained with the FCI PES reported in ref. 55. Note that the ν1 fundamental of H2He+, 1840(9) cm−1,55 see also Table 5, is right in between the two D0 dissociation energies. This ensured the straightforward spectroscopic observation of this fundamental.55
The fundamentals of H2He+ are 1861(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+)), 655(
1(σ+)), 655(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2(π)), and 742(
2(π)), and 742(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+)) cm−1 within the VPT2 approximation at the MAQ CCSD(T) level and 1833, 640, and 732 cm−1, respectively, obtained variationally.55 Previous variational results,78 employing a different PES, resulted in fundamentals at 1832, 648, and 734 cm−1, respectively. This is a quite reasonable agreement among the different modeling results and supports the relative rigidity of the structure against single-quantum excitation. The present VCI and the previous variational results also agree very well. The uncertainty of the variational values55,78 is probably a maximum of ±5 cm−1, judged by the accuracy of the D0 value of the PES.
3(σ+)) cm−1 within the VPT2 approximation at the MAQ CCSD(T) level and 1833, 640, and 732 cm−1, respectively, obtained variationally.55 Previous variational results,78 employing a different PES, resulted in fundamentals at 1832, 648, and 734 cm−1, respectively. This is a quite reasonable agreement among the different modeling results and supports the relative rigidity of the structure against single-quantum excitation. The present VCI and the previous variational results also agree very well. The uncertainty of the variational values55,78 is probably a maximum of ±5 cm−1, judged by the accuracy of the D0 value of the PES.
One must note that near resonances have been detected in the VPT2 calculations, e.g., 2ω3 ≈ ω1 (see Table 5), for H2He+. These resonances lead to shifts for several of the calculated vibrational modes, even up to hundreds of cm−1, i.e., huge discrepancies can be observed between the perturbed and the diagonalization-corrected VPT2 results. For the overtones of H2He+, with the exception of 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+), the VCI calculations did not converge with respect to a systematically increased correlation space. For this reason these values are not provided in Table 5.
3(σ+), the VCI calculations did not converge with respect to a systematically increased correlation space. For this reason these values are not provided in Table 5.
Convergence problems proved to be much less severe for the deuterated compound. It is expected that the fundamentals and overtones obtained for D2He+via the present VCI and the previous variational treatments are accurate, to better than ±5 cm−1 for the fundamentals and better than ±20 cm−1 for the overtones. Note, the 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+) overtone for D2He+ computed at the VPT2 level deviates by almost 40 cm−1 from the VCI value. However, this arises mainly from a significant resonance correction, while the original perturbed value of 1166.2 cm−1 is in much better agreement with the VCI number, 1159 cm−1. The VCI result of this study and a dependable variational estimate,55 1140 cm−1, are in good agreement with the experimentally measured value, 1145 cm−1.55
3(σ+) overtone for D2He+ computed at the VPT2 level deviates by almost 40 cm−1 from the VCI value. However, this arises mainly from a significant resonance correction, while the original perturbed value of 1166.2 cm−1 is in much better agreement with the VCI number, 1159 cm−1. The VCI result of this study and a dependable variational estimate,55 1140 cm−1, are in good agreement with the experimentally measured value, 1145 cm−1.55
Finally, a few words about the experimental estimates of the fundamentals of H2He+ and D2He+.55 The spectroscopic measurements are supported by the quoted first-principles results for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 (1840(9)55vs. 1833(5) cm−1). Due to substantial technical difficulties related to the measurements, dependable experimental results are still not available for the other two fundamentals, as the “tentative experimental results” published for
1 (1840(9)55vs. 1833(5) cm−1). Due to substantial technical difficulties related to the measurements, dependable experimental results are still not available for the other two fundamentals, as the “tentative experimental results” published for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 and
2 and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 in ref. 55 for H2He+ are supported neither by the VPT2 nor by the variational computations. As to D2He+, while the
3 in ref. 55 for H2He+ are supported neither by the VPT2 nor by the variational computations. As to D2He+, while the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 2 fundamental's position might be approximately correct, it seems very likely that the position of the
2 fundamental's position might be approximately correct, it seems very likely that the position of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 fundamental is incorrect. Thus, high-resolution spectroscopic studies are needed to settle the position of these two fundamentals both for H2He+ and D2He+.
3 fundamental is incorrect. Thus, high-resolution spectroscopic studies are needed to settle the position of these two fundamentals both for H2He+ and D2He+.
5.2 H2He+2
For the smaller members of the (H2/D2)He+n He-solvated family of ions, up to n = 7, the four-atomic H2He+2 molecular ion serves as the chromophore. This means that the first solvation shell develops around the middle point of the H+2 and D+2 units (see the related BCP of Fig. 2), forming a “planar” belt with up to a few He atoms. The placement of the solvating heliums becomes asymmetric with respect to the symmetry axis of the chromophore when it changes from H2He+2 to H2He+ (see the left two panels of Fig. 2).At the levels of electronic-structure theory employed, CCSD(T) and CCSDT, and with basis sets MAT and MAQ, the solvated linear complex of H2He+2, an assumed secondary minimum on the PES of the [H, H, He, He]+ system, is not a minimum but a second-order saddle point. Thus, this possible isomer was not considered further during this study. Nevertheless, this configuration may become important, even if it is not a minimum, once the true dynamics of H2He+2 will be studied, either experimentally under high resolution or computationally via suitable variational nuclear-motion techniques, close to the first dissociation limit.
The reaction studied for the title species is H2He+2 → H2He+ + He (see Table 12 for the FPA results). As the data of Table 12 show, the dissociation energy is not large, the CBS FCI electronic energy is only 652(3) cm−1. HF theory does not provide a good estimate of this value, as the CBS HF estimate is only 91.3(2) cm−1. Nevertheless, MP2 theory is able to provide most (almost 80%) of the correlation energy and then the convergence of the correlation-energy increments is fast. In fact, the increments beyond CCSDT are negligible, considerably smaller than the assumed uncertainty of the CBS FCI estimate.
While harmonic fundamentals could be determined for H2He+2, see Table 6, attempts to use VPT2 and VCI to treat the unusual spectroscopic characteristics of this relatively weakly bound molecular ion did not result in reasonable and converged fundamentals. Part of the problem is that, for H2He+2, during the calculation of the outer regions of the PES convergence problems within the underlying RHF calculations were observed. Such behavior usually indicates close-lying, intruder electronically excited states. It seems that a variational treatment utilizing an internal-coordinate Hamiltonian and a carefully derived high-level PES, obtained after taking care of the intruder state problem, is needed to estimate accurate anharmonic fundamentals for H2He+2.
For He–H+2–He, the VCI and the VPT2 treatments yield 2311 and 2305 cm−1 for the ZPVE. For He–D+2–He, the VCI and VPT2 ZPVE values are 1738 and 1735 cm−1, respectively. Thus, unlike the fundamentals, the ZPVE results look fairly reliable and consistent and the anharmonic values of 2308(5) and 1737(4) cm−1 are accepted for He–H+2–He and He–D+2–He, respectively.
It is clear that the pure electronic contribution to the binding energy of the second helium to the H+2 core is much smaller, 652(3) cm−1, than that of the first helium, 2730(3) cm−1. Based on the computed values for the triatomic species, the “auxiliary” corrections are neglected for (H2/D2)He+2, they are considered only as contributions of 0(3) cm−1. The ZPVE corrections decrease these values significantly. Our final estimates are 1789(4) cm−1 and 435(6) cm−1 for the attachment of one or two He atoms to the H+2 core. The disparity in these values helps to explain why the chromophore of the H2He+n complexes changes with the increase in n from H2He+2 to H2He+. The first dissociation energy of D2He+2 is 474(5) cm−1.
6 He+n species
The unusually low ion mobility values detected17,31,33–35 for charged species in liquid helium have been explained by the formation of charged helium clusters. As it turned out, the situation is similar even in the absence of atomic “contaminants”: computational studies31,33 indicated the considerable stability of the He+2 and He+3 ions, though formation of the former in liquid helium is hindered significantly by the fact that the internuclear distances of He2 and He+2 are drastically different.According to ref. 25 and 31, in ionized helium clusters the core (chromophore) contains either two or three He atoms. The smaller clusters are characterized by the triatomic chromophore, He+3, while the larger ones by the diatomic chromophore, He+2.
All He+n clusters are open-shell species, the ground electronic states of He+2 and He+3 are X2Σ+u and X2Σ+g, respectively. The T1 diagnostic values of CCSD theory, obtained with the help of the MAQ basis, are 0.0039 and 0.0233 for the He+2 and He+3 cations. Thus, the single-reference CC techniques should perform reasonably well even for He+3, though this is by far the largest T1 diagnostic value found during this study.
As seen in Fig. 2, in the case of He+3, the charge on the middle He atom is about twice as large as that on the terminal ones. Thus, the solvating He atoms of the larger He+n complexes will be placed around the middle atom, as expected.
6.1 He+2
The dissociation energy of X2Σ+u He+2 is simply defined by the reaction He+2 → He+ + He, involving ground-state species. As shown in Table 13, the FPA estimate of the dissociation energy is substantial, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957(8) cm−1. Thus, once it is formed, He+2 is a strongly bound molecular ion; in fact, the bonding energy is considerably larger than in HHe+, whereby it is 14
957(8) cm−1. Thus, once it is formed, He+2 is a strongly bound molecular ion; in fact, the bonding energy is considerably larger than in HHe+, whereby it is 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875(9) cm−1. The Hartree–Fock contribution to the dissociation energy is substantial, about 80% of the total. Convergence to the FCI and CBS limits is fast, of course, making the final CBS FCI estimate, 19
875(9) cm−1. The Hartree–Fock contribution to the dissociation energy is substantial, about 80% of the total. Convergence to the FCI and CBS limits is fast, of course, making the final CBS FCI estimate, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957(8) cm−1, a dependable value with a minuscule uncertainty (only 0.1 kJ mol−1). As usually observed, the largest uncertainty in the CBS value comes from the MP2 increment, which itself is by far the largest electron-correlation increment.
957(8) cm−1, a dependable value with a minuscule uncertainty (only 0.1 kJ mol−1). As usually observed, the largest uncertainty in the CBS value comes from the MP2 increment, which itself is by far the largest electron-correlation increment.
The auxiliary relativistic and DBOC corrections to the dissociation energy are minuscule, only 2.2 and 0.2 cm−1, respectively. Their overall effect can be estimated as 2(2) cm−1, a basically negligible correction.
The ZPVE correction to the dissociation reaction, coming simply from He+2, is −860 cm−1, obtained from VPT2 theory, and it can be considered well determined at the MAQ CCSD level, perhaps with an uncertainty of ±4 cm−1. Thus, the final FPA estimate of the dissociation energy of He+2 is 19 099(13) cm−1. This value is in excellent agreement with the literature value of 19 075(50) cm−1 (2.365 ± 0.006 eV),139 but it has a considerably smaller uncertainty.
6.2 He+3
He+3 was first observed in 196818 and its first dissociation energy was measured to be 1371(242) cm−1,18 which is probably still the only available experimental result for D0 of He+3(![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2Σ+g) with respect to He+2(X2Σ+u) and He(1S). Later electronic-structure computations, among them those reported in ref. 20 and 28, established that electron correlation is important for the proper description of the ground electronic state of He+3 and that the centrosymmetric linear arrangement of the three He atoms is the only minimum, making He+3 distinctively different from other homonuclear triatomic molecules, like Ar3, Na3, and H+3, for which an equilateral triangle (of D3h point-group symmetry) is the single minimum.
2Σ+g) with respect to He+2(X2Σ+u) and He(1S). Later electronic-structure computations, among them those reported in ref. 20 and 28, established that electron correlation is important for the proper description of the ground electronic state of He+3 and that the centrosymmetric linear arrangement of the three He atoms is the only minimum, making He+3 distinctively different from other homonuclear triatomic molecules, like Ar3, Na3, and H+3, for which an equilateral triangle (of D3h point-group symmetry) is the single minimum.
At all the high levels of electronic-structure theory employed, CCSD(T), CCSDT, and CCSDTQ, and with basis sets MAT and MAQ, the solvated linear complex He⋯He+2, an assumed second stationary point on the PES of the [He, He, He]+ system, could not be located. We also attempted to locate another possible He-solvated complex, a T-shaped stationary point of C2v point-group symmetry. This stationary point turned out to be, in accordance with previous electronic-structure studies,20,28 a first-order saddle point. Since it is not a secondary minimum on the PES of the [He, He, He]+ system, this stationary point was not considered further.
The dissociation energy of He+3 is simply defined by the reaction He+3 → He+2 + He. As shown in Table 14, the electronic dissociation energy is relatively small, 1490(10) cm−1. The HF limit value is basically achieved with the MAQ basis. The most interesting aspect of the FPA table is that at the HF level He+3 is simply unbound, as shown by the negative HF entries of Table 14. This points toward the uniqueness of He+3 in the set of chromophores investigated. In other words, He+3 is bound by correlation forces. With a ZPVE of 949(4) cm−1 (Table 7), the final FPA estimate of the dissociation energy becomes 1401(12) cm−1. The present FPA estimate compares fairly well with a much less accurate experimental value, 1371(242) cm−1.18
The vibrational wavenumbers obtained for He+3 during this study are listed in Table 7. Except for ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1, the agreement of the VPT2 fundamentals with the VCI values is good.
1, the agreement of the VPT2 fundamentals with the VCI values is good. ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 shows a strong Fermi resonance with the overtone of
1 shows a strong Fermi resonance with the overtone of ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3, i.e., 2
3, i.e., 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3, which leads to huge corrections within the VPT2 formalism. Furthermore, the leading VCI coefficient for the
3, which leads to huge corrections within the VPT2 formalism. Furthermore, the leading VCI coefficient for the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 state is as low as 0.57 and the underlying leading configuration contributes significantly to five different states. This makes it rather difficult to name the transition at 617.1 cm−1 a fundamental transition as it carries no distinct state identity. Formally this mode shows an anharmonicity effect of more than 30%, but such a consideration is at its limit when the state identity has been lost. Note, the one-dimensional potential along the normal coordinate shows extremely strong anharmonic contributions up to high order monomials, which readily explains the difference between the VPT2 and VCI results. The VCI calculations rely on ground-state-based modals as the underlying VSCF calculations did not converge for the vibrational state corresponding to
1 state is as low as 0.57 and the underlying leading configuration contributes significantly to five different states. This makes it rather difficult to name the transition at 617.1 cm−1 a fundamental transition as it carries no distinct state identity. Formally this mode shows an anharmonicity effect of more than 30%, but such a consideration is at its limit when the state identity has been lost. Note, the one-dimensional potential along the normal coordinate shows extremely strong anharmonic contributions up to high order monomials, which readily explains the difference between the VPT2 and VCI results. The VCI calculations rely on ground-state-based modals as the underlying VSCF calculations did not converge for the vibrational state corresponding to ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3. (Note that Rosi and Bauschlicher20 identified the extreme anharmonicity in the one-dimensional potential of the
3. (Note that Rosi and Bauschlicher20 identified the extreme anharmonicity in the one-dimensional potential of the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 mode.) The VPT2 and VCI results for the 2
3 mode.) The VPT2 and VCI results for the 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 02(σ+g) overtone deviate significantly, but this arises mainly from the resonance correction within the VPT2 formalism, while the uncorrected VPT2 value of 447.8 cm−1 is in reasonable agreement with the VCI result. The VCI results for 2
02(σ+g) overtone deviate significantly, but this arises mainly from the resonance correction within the VPT2 formalism, while the uncorrected VPT2 value of 447.8 cm−1 is in reasonable agreement with the VCI result. The VCI results for 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1(σ+g) and 2
1(σ+g) and 2![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3(σ+g) were found to be strongly dependent on the correlation space and are thus numerically not stable. Therefore, they are not reported in Table 7. It'd be interesting to investigate experimentally, under high resolution, the challenging internal dynamics of the He+3 molecular ion, in order to confirm the curious quantum-chemical results of the present study. The uncertainty of the VCI estimates of the fundamentals of He+3 is about ±8 cm−1. The best candidate for a dipole-allowed spectroscopic observation is the
3(σ+g) were found to be strongly dependent on the correlation space and are thus numerically not stable. Therefore, they are not reported in Table 7. It'd be interesting to investigate experimentally, under high resolution, the challenging internal dynamics of the He+3 molecular ion, in order to confirm the curious quantum-chemical results of the present study. The uncertainty of the VCI estimates of the fundamentals of He+3 is about ±8 cm−1. The best candidate for a dipole-allowed spectroscopic observation is the ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 3 fundamental at 443(8) cm−1.
3 fundamental at 443(8) cm−1.
7 Summary and conclusions
As part of this project, four new atom-centered, fixed-exponent, Gaussian-type basis sets, called MAX, with cardinal numbers X = 3(T), 4(Q), 5(P), and 6(H), have been developed for the hydrogen and helium atoms, applicable especially for correlated-level electronic-structure computations. The MAX basis sets are designed to improve electronic-structure computations for species where the He atoms are involved in stronger, “chemical-type” bonds as well as in van der Waals contacts. It is especially notable that the MAT basis performs significantly better than the original aug-cc-pVTZ basis, upon which its design is based. This means that this basis can be used in future computations on much larger members of the HmHe+n family.The MAX basis sets have been employed to obtain definitive results for the structure, energetics, and vibrational characteristics of the chromophores of He-solvated HmHe+n complexes with m = 0, 1, and 2, as well as for their deuterated analogues. In order to obtain well-defined uncertainties for the computed relative energies, the focal-point analysis (FPA) approach was employed. For the FPA analysis extensive coupled-cluster electronic-structure computations up to full configuration interaction (FCI) were performed, which usually could be afforded even with the MAH basis. The large set of computations performed allow to estimate the CBS FCI limit for the relative energies. It holds for all the reactions studied that special relativity has no significant effect on the energetics (less than 1 cm−1). The DBOC corrections to the dissociation energies are basically zero for the weakly-bound cases but somewhat more significant, with values of a few cm−1, for the more strongly bound molecular ions. The complete neglect of the “auxiliary” corrections seems to be justifiable for the set of HmHe+n molecular cations studied. Nevertheless, in a number of cases the “auxiliary” corrections have been considered explicitly and added to the CBS FCI values.
HHe+ and HHe+2 are relatively strongly bound, linear molecular ions, with equilibrium bond lengths of 0.775 and 0.925 Å, respectively (obtained at the MAQ FCI level). HHe+2 is the chromophore of the He-solvated HHe+n complexes. The FPA estimates of the proton and deuteron affinities of He are 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875(9) and 15
875(9) and 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 229(8) cm−1, respectively. The former value agrees with the best experimental value, 14
229(8) cm−1, respectively. The former value agrees with the best experimental value, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863(8) cm−1.133 The first dissociation energy of HHe+2 (the reaction energy of the HHe+2 → HHe+ + He process) is 3948(7) cm−1. The isomerization energy between the two linear isomers of HHe+2, the global minimum, He–H+–He, and the secondary minimum, He⋯He–H+, is 3828(40) cm−1, clearly reflecting the instability of the He-solvated He⋯He–H+ complex.
863(8) cm−1.133 The first dissociation energy of HHe+2 (the reaction energy of the HHe+2 → HHe+ + He process) is 3948(7) cm−1. The isomerization energy between the two linear isomers of HHe+2, the global minimum, He–H+–He, and the secondary minimum, He⋯He–H+, is 3828(40) cm−1, clearly reflecting the instability of the He-solvated He⋯He–H+ complex.
The molecule-like species H2He+, the chromophore of the H2He+n species with smaller n values, also has a linear equilibrium structure. The FPA dissociation energy of the H2He+ → H+2 + He reaction is 1789(4) cm−1. The FPA estimate of the similar dissociation energy of D2He+ 1986(4) cm−1.
The species He+n allow the investigation of the solvation of a positive charge by an increasing number of He atoms. He+3 has a linear equilibrium structure and this is the chromophore of a number of He+n species with smaller n values. An interesting property of the He+3 molecular cation is that it is not bound at the HF level, it is hold together by correlation forces. The FPA estimate of the first dissociation energy of He+3 is 1401(12) cm−1.
The triatomic chromophores investigated are neither particularly strongly bound (they have a low first dissociation energy toward loosing a helium atom) nor they contain heavy elements. Consequently, both the perturbational second-order vibrational perturbation theory (VPT2) and the variational vibrational configuration interaction (VCI) treatments are prone to difficulties, though of different nature. The level of difficulty increases as the dissociation energy decreases, the most problematic molecular ion is clearly He+3. For the class of species investigated, VPT2 turns out to be unreliable to predict the ions' spectroscopic signatures. VPT2 does work in some cases but the importance of high-order potential terms and exceptionally strong resonances lead to clear failures of VPT2 even for the fundamentals of the molecular cations. The occurrence of strong mode couplings and a multitude of resonances within the vibrational structure calculations require highly accurate potential energy surfaces and carefully converged vibrational wavefunctions. VCI seems to perform well for the fundamentals, but larger correlation spaces are needed than in standard calculations. In some cases very low leading VCI coefficients render a clear state assignment problematic and result in a loss of state identities. The most clearcut failure of the VPT2 and VCI treatments is for H2He+2, for which we were not able to report even the anharmonic fundamentals. Sizeable anharmonic corrections, up to 30%, for the vibrational fundamentals is another unique feature of these species.
Zero-point vibrational energy (ZPVE) values of the triatomic and tetratomic molecular cations could be determined in all cases at the variational VCI level, employing PES representations determined at the MAQ CCSD(T) level. With conservative uncertainty estimates, the best ZPVE estimates for the triatomic ions HHe+2, H2He+, and He+3 are 2255(1), 2092(2), and 949(4) cm−1, respectively. The corresponding values for the deuterated isotopologues DHe+2 and D2He+ are 1826(1) and 1559(2) cm−1, respectively. The ZPVE values of the H2He+2 and the D2He+2 ions are 2308(5) and 1737(4) cm−1, respectively.
Conflicts of interest
There are no conflicts to declare.Appendix
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | ΔEe[FCI] |
|---|---|---|---|---|
| a The symbol δ denotes the increment in the relative energy (ΔEe) with respect to the preceding level of theory in the hierarchy HF → MP2 → CCSD ≡ FCI. CBS = complete basis set. The basis set extrapolations are described in the text, they are based on the cardinal number X of the bases. Uncertainties are given in parentheses. All energy values are given in cm−1. | ||||
| aug-cc-pVTZ | 15601.8 | +587.3 | +226.3 | 16415.4 |
| aug-cc-pVQZ | 15660.6 | +569.5 | +231.6 | 16461.7 |
| aug-cc-pV5Z | 15670.7 | +561.6 | +232.7 | 16465.0 |
| aug-cc-pV6Z | 15672.7 | +554.8 | +235.3 | 16462.8 |
| CBS(3–4) | 15668.6 | +556.6 | +235.5 | 16460.7 |
| CBS(4–5) | 15672.5 | +553.3 | +233.9 | 16459.6 |
| CBS(5–6) | 15673.2(10) | +545.4(60) | +238.8(30) | 16457.4(80) |
| MAT | 15643.3 | +577.6 | +222.2 | 16443.1 |
| MAQ | 15668.6 | +569.2 | +227.8 | 16465.5 |
| MAP | 15671.9 | +560.0 | +232.7 | 16464.5 |
| MAH | 15673.1 | +554.8 | +234.9 | 16462.8 |
| CBS(3–4) | 15672.0 | +563.0 | +231.9 | 16466.9 |
| CBS(4–5) | 15672.5 | +550.3 | +237.8 | 16460.6 |
| CBS(5–6) | 15673.4(10) | +547.8(50) | +237.9(30) | 16459.1(70) |
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | δ[CCSD(T)] | δ[CCSDT] | δ[CCSDTQ] | ΔEe[FCI] |
|---|---|---|---|---|---|---|---|
| a See footnote a to Table 8, with the exception that the hierarchy of electronic-structure techniques utilized is HF → MP2 → CCSD → CCSD(T) → CCSDT → CCSDTQ ≡ FCI. | |||||||
| aug-cc-pVTZ | 3983.1 | +604.2 | +26.8 | +54.3 | +9.5 | +0.9 | 4678.8 |
| aug-cc-pVQZ | 3963.3 | +595.1 | +21.2 | +56.9 | +9.1 | +0.9 | 4646.5 |
| aug-cc-pV5Z | 3962.1 | +589.6 | +21.8 | +57.6 | +8.8 | +0.9 | 4640.7 |
| aug-cc-pV6Z | 3959.9 | +585.4 | +23.3 | +57.8 | +8.7 | +0.9 | 4636.0 |
| CBS(3–4) | 3960.6 | +588.5 | +17.1 | +58.8 | +8.8 | +0.9 | 4634.7 |
| CBS(4–5) | 3961.9 | +583.8 | +22.4 | +58.3 | +8.6 | +0.9 | 4635.8 |
| CBS(5–6) | 3959.5(20) | +579.6(40) | +25.3(20) | +58.2(10) | +8.5(10) | +0.9(10) | 4632.0(60) |
| MAT | 3965.7 | +579.7 | +22.5 | +55.2 | +9.6 | +0.9 | 4633.5 |
| MAQ | 3958.5 | +585.8 | +22.1 | +57.1 | +9.1 | +0.9 | 4633.5 |
| MAP | 3959.6 | +587.0 | +22.6 | +57.6 | +8.8 | +0.9 | 4636.6 |
| MAH | 3959.6 | +584.2 | +23.6 | +57.9 | +8.7 | +0.9 | 4634.8 |
| CBS(3–4) | 3957.6 | +590.3 | +21.9 | +58.4 | +8.7 | +0.9 | 4637.7 |
| CBS(4–5) | 3959.8 | +588.3 | +23.2 | +58.3 | +8.6 | +0.9 | 4639.0 |
| CBS(5–6) | 3959.5(10) | +580.2(30) | +25.0(10) | +58.1(10) | +8.5(10) | +0.9(10) | 4632.3(40) |
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | δ[CCSD(T)] | δ[CCSDT] | δ[CCSDTQ] | ΔEe[FCI] |
|---|---|---|---|---|---|---|---|
| a See footnote a to Table 8, with the exception that the hierarchy of electronic-structure techniques utilized is HF → MP2 → CCSD → CCSD(T) → CCSDT → CCSDTQ ≡ FCI. | |||||||
| aug-cc-pVTZ | 3821.7 | +522.0 | +13.8 | +49.1 | +8.4 | +0.8 | 4415.9 |
| aug-cc-pVQZ | 3801.1 | +512.2 | +9.6 | +51.3 | +8.1 | +0.8 | 4383.1 |
| aug-cc-pV5Z | 3799.3 | +506.2 | +10.4 | +51.8 | +7.8 | +0.8 | 4376.4 |
| aug-cc-pV6Z | 3797.1 | +502.0 | +11.9 | +52.0 | +7.7 | +0.8 | 4371.6 |
| CBS(3–4) | 3798.3 | +505.1 | +6.6 | +52.8 | +7.8 | +0.8 | 4371.5 |
| CBS(4–5) | 3799.0 | +499.9 | +11.3 | +52.4 | +7.6 | +0.8 | 4370.9 |
| CBS(5–6) | 3796.6(10) | +496.3(60) | +14.0(20) | +52.3(10) | +7.5(10) | +0.8(10) | 4367.6(80) |
| MAT | 3804.0 | +499.5 | +10.3 | +49.9 | +8.5 | +0.8 | 4373.1 |
| MAQ | 3796.0 | +503.6 | +10.5 | +51.4 | +8.0 | +0.8 | 4370.4 |
| MAP | 3796.8 | +503.8 | +11.2 | +51.9 | +7.8 | +0.8 | 4372.4 |
| MAH | 3796.7 | +500.9 | +12.3 | +52.0 | +7.7 | +0.8 | 4370.4 |
| CBS(3–4) | 3794.9 | +506.6 | +10.7 | +52.5 | +7.7 | +0.8 | 4373.2 |
| CBS(4–5) | 3797.0 | +504.1 | +12.0 | +52.3 | +7.6 | +0.8 | 4373.7 |
| CBS(5–6) | 3796.7(10) | +496.8(40) | +13.8(15) | +52.3(10) | +7.6(10) | +0.8(10) | 4367.8(60) |
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | δ[CCSD(T)] | δ[CCSDT] | ΔEe[FCI] |
|---|---|---|---|---|---|---|
| a See footnote a to Table 8, with the exception that the hierarchy of electronic-structure techniques utilized is HF → MP2 → CCSD → CCSD(T) → CCSDT ≡ FCI. | ||||||
| aug-cc-pVTZ | 1418.0 | +991.8 | +279.9 | +37.6 | +7.8 | 2735.1 |
| aug-cc-pVQZ | 1424.3 | +991.6 | +275.5 | +39.5 | +7.5 | 2738.3 |
| aug-cc-pV5Z | 1422.6 | +992.1 | +273.1 | +39.9 | +7.3 | 2735.1 |
| aug-cc-pV6Z | 1421.6 | +989.8 | +273.3 | +40.1 | +7.2 | 2732.1 |
| CBS(3–4) | 1425.1 | +991.4 | +272.2 | +40.8 | +7.4 | 2737.0 |
| CBS(4–5) | 1422.3 | +992.6 | +270.7 | +40.4 | +7.1 | 2733.1 |
| CBS(5–6) | 1421.4(10) | +986.7(40) | +273.6(15) | +40.3(5) | +7.1(3) | 2729.1(50) |
| MAT | 1419.3 | +972.6 | +277.8 | +38.0 | +7.9 | 2715.6 |
| MAQ | 1421.6 | +986.8 | +274.0 | +39.4 | +7.5 | 2729.4 |
| MAP | 1421.4 | +990.5 | +273.2 | +39.9 | +7.3 | 2732.5 |
| MAH | 1421.6 | +989.4 | +273.2 | +40.1 | +7.2 | 2731.5 |
| CBS(3–4) | 1421.9 | +997.2 | +271.3 | +40.5 | +7.3 | 2738.2 |
| CBS(4–5) | 1421.4 | +994.4 | +272.4 | +40.5 | +7.1 | 2735.8 |
| CBS(5–6) | 1421.6(10) | +987.9(25) | +273.1(10) | +40.3(3) | +7.1(2) | 2730.1(30) |
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | δ[CCSD(T)] | δ[CCSDT] | δ[CCSDTQ] | δ[CCSDTQP] | ΔEe[FCI] |
|---|---|---|---|---|---|---|---|---|
| a See footnote a to Table 8, except that hierarchy is HF → MP2 → CCSD → CCSD(T) → CCSDT → CCSDTQ → CCSDTQP ≡ FCI. Fixed increments taken from a smaller basis set are given in brackets. | ||||||||
| aug-cc-pVTZ | 97.7 | +387.1 | +123.4 | +29.4 | +7.2 | +0.3 | +0.004 | 645.1 |
| aug-cc-pVQZ | 92.8 | +407.5 | +116.4 | +31.2 | +7.0 | +0.3 | +0.004 | 655.3 |
| aug-cc-pV5Z | 92.5 | +405.1 | +115.4 | +31.5 | +6.9 | +0.3 | [+0.004] | 651.7 |
| aug-cc-pV6Z | 91.4 | +407.1 | +114.1 | +31.7 | +6.8 | [+0.3] | [+0.004] | 651.3 |
| CBS(3–4) | 92.2 | +422.5 | +111.2 | +32.4 | +6.9 | +0.3 | [+0.004] | 665.6 |
| CBS(4–5) | 92.4 | +402.5 | +114.3 | +31.9 | +6.7 | +0.3 | [+0.004] | 648.2 |
| CBS(5–6) | 91.2(10) | +409.8(15) | +112.2(15) | +31.9(5) | +6.7(3) | [+0.3](10) | [+0.004](4) | 652.1(20) |
| MAT | 88.7 | +378.4 | +123.7 | +29.7 | +7.3 | +0.3 | +0.004 | 628.2 |
| MAQ | 90.8 | +397.0 | +117.7 | +31.0 | +7.0 | +0.3 | +0.004 | 643.9 |
| MAP | 91.3 | +404.7 | +115.3 | +31.5 | +6.9 | +0.3 | [+0.004] | 650.0 |
| MAH | 91.3 | +406.7 | +114.0 | +31.7 | +6.8 | [+0.3] | [+0.004] | 650.9 |
| CBS(3–4) | 91.1 | +410.6 | +113.2 | +31.9 | +6.8 | +0.3 | +0.004 | 654.1 |
| CBS(4–5) | 91.4 | +412.8 | +112.8 | +32.1 | +6.7 | +0.3 | [+0.004] | 656.1 |
| CBS(5–6) | 91.3(3) | +409.4(10) | +112.3(10) | +31.9(4) | +6.7(3) | [+0.3](10) | [+0.004](4) | 652.0(10) |
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | δ[CCSD(T)] | δ[CCSDT] | ΔEe[FCI] |
|---|---|---|---|---|---|---|
| a See footnote a to Table 8, with the exception that the hierarchy is HF → MP2 → CCSD → CCSD(T) → CCSDT ≡ FCI. | ||||||
| aug-cc-pVTZ | 15966.5 | +2590.5 | +1173.3 | +46.9 | +9.1 | 19786.3 |
| aug-cc-pVQZ | 15938.5 | +2717.1 | +1184.7 | +51.5 | +8.9 | 19900.6 |
| aug-cc-pV5Z | 15940.8 | +2757.5 | +1174.4 | +52.8 | +8.6 | 19934.0 |
| aug-cc-pV6Z | 15940.4 | +2771.6 | +1170.3 | +53.3 | +8.4 | 19944.0 |
| CBS(3–4) | 15934.7 | +2809.5 | +1193.1 | +54.8 | +8.7 | 20000.7 |
| CBS(4–5) | 15941.2 | +2799.9 | +1163.6 | +54.1 | +8.3 | 19967.1 |
| CBS(5–6) | 15940.3(10) | +2790.9(100) | +1164.7(70) | +54.0(10) | +8.2(3) | 19958.2(120) |
| MAT | 15922.4 | +2626.4 | +1201.1 | +48.4 | +9.3 | 19807.7 |
| MAQ | 15934.3 | +2726.3 | +1181.3 | +51.6 | +8.8 | 19902.3 |
| MAP | 15938.7 | +2759.0 | +1173.7 | +52.8 | +8.6 | 19932.8 |
| MAH | 15940.1 | +2772.3 | +1169.6 | +53.3 | +8.4 | 19943.8 |
| CBS(3–4) | 15935.9 | +2799.2 | +1166.7 | +54.0 | +8.5 | 19964.3 |
| CBS(4–5) | 15939.5 | +2793.3 | +1165.7 | +54.1 | +8.3 | 19960.9 |
| CBS(5–6) | 15940.4(10) | +2790.5(60) | +1164.1(40) | +53.9(10) | +8.2(3) | 19957.2(65) |
| Basis | ΔEe(HF) | δ[MP2] | δ[CCSD] | δ[CCSD(T)] | δ[CCSDT] | δ[CCSDTQ] | δ[CCSDTQP] | ΔEe[FCI] |
|---|---|---|---|---|---|---|---|---|
| a See footnote to Table 8, with the exception that the hierarchy is HF → MP2 → CCSD → CCSD(T) → CCSDT → CCSDTQ → CCSDTQP ≡ FCI. Fixed increments taken from a smaller basis set are given in brackets. | ||||||||
| aug-cc-pVTZ | −783.4 | +1578.0 | +506.3 | +113.6 | +27.2 | +1.4 | +0.004 | 1443.1 |
| aug-cc-pVQZ | −789.1 | +1613.7 | +501.7 | +121.1 | +26.8 | +1.5 | +0.005 | 1475.6 |
| aug-cc-pV5Z | −786.5 | +1621.6 | +498.3 | +123.0 | +26.2 | +1.5 | [+0.005] | 1484.1 |
| aug-cc-pV6Z | −786.8 | +1625.5 | +496.5 | +123.8 | +25.9 | [+1.6] | [+0.005] | 1486.5 |
| CBS(3-4) | −789.8 | +1639.7 | +498.3 | +126.5 | +26.5 | +1.6 | +0.005 | 1502.7 |
| CBS(4-5) | −786.1 | +1629.9 | +494.7 | +125.1 | +25.6 | +1.6 | [+0.005] | 1490.8 |
| CBS(5-6) | −786.8(10) | +1630.9(60) | +494.1(30) | +124.9(10) | +25.5(10) | [+1.6](2) | [+0.005](5) | 1490.1(70) |
| MAT | −789.5 | +1574.6 | +510.4 | +116.1 | +27.8 | +1.5 | +0.004 | 1440.8 |
| MAQ | −785.8 | +1610.6 | +500.5 | +121.3 | +26.8 | +1.5 | +0.005 | 1475.0 |
| MAP | −785.7 | +1621.3 | +498.0 | +123.1 | +26.2 | +1.6 | [+0.005] | 1484.5 |
| MAH | −786.5 | +1625.4 | +496.4 | +123.8 | +25.9 | +1.6 | [+0.005] | 1486.6 |
| CBS(3-4) | −785.3 | +1636.9 | +493.3 | +125.1 | +26.0 | +1.6 | +0.005 | 1497.7 |
| CBS(4-5) | −785.7 | +1632.5 | +495.4 | +125.0 | +25.6 | +1.6 | [+0.005] | 1494.4 |
| CBS(5-6) | −786.6(10) | +1630.9(60) | +494.2(30) | +124.8(10) | +25.5(10) | +1.6(1) | [+0.005](5) | 1490.4(70) |
Acknowledgements
The work performed in Budapest received support from NKFIH (grant no. K138233). DK acknowledges financial support from a SONATA BIS 9 grant of the National Science Centre, Poland (no. 2019/34/E/ST4/00451). Collaborative work between DK and AGC started during the lifetime of the COST action CM1405, MOLIM: Molecules in Motion. The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster).References
- J. Tennyson, Spectroscopy of H+3: Planets, chaos and the Universe, Rep. Prog. Phys., 1995, 58, 421–476 CrossRef CAS.
- S. Lepp, P. C. Stancil and A. Dalgarno, Atomic and molecular processes in the early Universe, J. Phys. B: At. Mol. Opt. Phys., 2002, 35, R57–R80 CrossRef CAS.
- E. A. Engel, N. Doss, G. J. Harris and J. Tennyson, Calculated spectra for HeH+ and its effect on the opacity of cool metal-poor stars, Mon. Not. R. Astron. Soc., 2005, 357, 471–477 CrossRef CAS.
- D. Galli and F. Palla, The dawn of chemistry, Ann. Rev. Astron. Astrophys., 2013, 51, 163–206 CrossRef CAS.
- E. Zicler, O. Parisel, F. Pauzat, Y. Ellinger, M.-C. Bacchus-Montabonel and J.-P. Maillard, Search for hydrogen–helium molecular species in space, Astron. Astrophys., 2017, 607, A61 CrossRef.
- R. Güsten, H. Wiesemeyer, D. Neufeld, K. M. Menten, U. U. Graf, K. Jacobs, B. Klein, O. Ricken, C. Risacher and J. Stutzki, Astrophysical detection of the helium hydride ion HeH+, Nature, 2019, 568, 357–359 CrossRef PubMed.
- I. R. McNab, The spectroscopy of H+3, Adv. Chem. Phys., 1994, 89, 1–87 Search PubMed.
- B. J. McCall, T. R. Geballe, K. H. Hinkle and T. Oka, Detection of H+3 in the diffuse interstellar medium toward Cygnus OB2 No. 12, Science, 1998, 279, 1910–1913 CrossRef CAS PubMed.
- E. Herbst, The astrochemistry of H+3, Philos. Trans. R. Soc., A, 2000, 358, 2523–2534 CrossRef CAS.
- B. J. McCall and T. Oka, H+3 – An ion with many talents, Science, 2000, 287, 1941–1942 CrossRef CAS.
- T. Oka, Physics, chemistry and astronomy of H+3. Introductory remarks, Philos. Trans. R. Soc., A, 2006, 364, 2847–3151 CrossRef CAS PubMed.
- H. Krogh, To be or not to be: the early history of H3 and H+3, Philos. Trans. R. Soc., A, 2012, 370, 5225–5235 CrossRef PubMed.
- M. Pavanello, L. Adamowicz, A. Alijah, N. F. Zobov, I. I. Mizus, O. L. Polyansky, J. Tennyson, T. Szidarovszky, A. G. Császár, M. Berg, A. Petrignani and A. Wolf, Precision measurements and computations of transition energies in rotationally cold triatomic hydrogen ions up to the mid-visible spectral range, Phys. Rev. Lett., 2012, 108, 023002 CrossRef PubMed.
- T. Furtenbacher, T. Szidarovszky, E. Mátyus, C. Fábri and A. G. Császár, Analysis of the rotational-vibrational states of the molecular ion H+3, J. Chem. Theor. Comput., 2013, 9, 5471–5478 CrossRef CAS PubMed.
- L. Pauling, The normal state of the helium molecule-ions He+2 and He++2, J. Chem. Phys., 1933, 1, 56–59 CrossRef CAS.
- O. Tüxen, Massenspektrographische Untersuchungen negativer Ionen in Gasentladungen bei höheren Drucken, Z. Physik, 1936, 103, 463–484 CrossRef.
- K. R. Atkins, Ions in liquid helium, Phys. Rev., 1959, 116, 1339–1343 CrossRef CAS.
- P. L. Patterson, Evidence of the existence of an He+3 ion, J. Chem. Phys., 1968, 48, 3625–3631 CrossRef CAS.
- N. Yu and W. H. Wing, Observation of the infrared spectrum of the helium molecular ion(3He4He)+, Phys. Rev. Lett., 1987, 59, 2055–2058 CrossRef CAS PubMed.
- M. Rosi and C. W. Bauschlicher, On the binding energy of He+n, for n = 2–7, Chem. Phys. Lett., 1989, 159, 479–484 CrossRef CAS.
- A. Carrington, C. H. Pyne and P. J. Knowles, Microwave electronic spectrum of the He+2 ion, J. Chem. Phys., 1995, 102, 5979–5988 CrossRef CAS.
- P. J. Knowles and J. N. Murrell, The metastable quartet state of He+4, J. Chem. Phys., 1995, 102, 9442–9443 CrossRef CAS.
- F. Gianturco and M. P. de Lara-Castells, Stability and structure of rare-gas ionic clusters using density functional methods: A study of helium clusters, Int. J. Quant. Chem., 1996, 60, 593–608 CrossRef CAS.
- P. J. Knowles and J. N. Murrell, The structures and stabilities of helium cluster ions, Mol. Phys., 1996, 87, 827–833 CrossRef CAS.
- B. E. Callicoatt, K. Förde, L. F. Jung, T. Ruchti and K. C. Janda, Fragmentation of ionized liquid helium droplets: A new interpretation, J. Chem. Phys., 1998, 109, 10195–10200 CrossRef CAS.
- L. Coman, M. Guna, L. Simons and K. A. Hardy, First measurement of the rotationalconstants for the homonuclear molecular ion He+2, Phys. Rev. Lett., 1999, 83, 2715–2717 CrossRef CAS.
- B. Balta and F. A. Gianturco, Structural properties and quantum effects in protonated helium clusters. I. The ab initio interaction potential, Chem. Phys., 2000, 254, 203–213 CrossRef CAS.
- D. T. Chang and G. I. Gellene, An ab initio, analytically fitted, global potential energy surface for the ground electronic state of He+3, J. Chem. Phys., 2003, 119, 4694–4699 CrossRef CAS.
- F. Grandinetti, Helium chemistry: A survey of the role of the ionic species, Int. J. Mass Spectrom., 2004, 237, 243–267 CrossRef CAS.
- E. Scifoni, E. Bodo, G. Dellepiane and F. A. Gianturco, Charged cores in ionized 4He clusters III: A quantum modeling for the collisional relaxation dynamics, Eur. Phys. J. D, 2004, 30, 363–368 CrossRef CAS.
- K. Oleksy, F. Karlický and R. Kalus, Structures and energetics of helium cluster cations: Equilibrium geometries revisited through the genetic algorithm approach, J. Chem. Phys., 2010, 133, 164314 CrossRef PubMed.
- B. Shepperson, J. Liu, A. M. Ellis and S. Yang, Communication: The formation of helium cluster cations following the ionization of helium nanodroplets: Influence of droplet size and dopant, J. Chem. Phys., 2011, 135, 041101 CrossRef PubMed.
- D. Mateo and J. Eloranta, Solvation of intrinsic positive charge in superfluid helium, J. Phys. Chem. A, 2014, 118, 6407–6415 CrossRef CAS PubMed.
- F. Aitken, N. Bonifaci, L. G. Mendoza-Luna and K. von Haeften, Modelling the mobility of positive ion clusters in normal liquid helium over large pressure ranges, Phys. Chem. Chem. Phys., 2015, 17, 18535–18540 RSC.
- A. Mauracher, O. Echt, A. Ellis, S. Yang, D. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Cold physics and chemistry: Collisions, ionization and reactions inside helium nanodroplets close to zero K, Phys. Rep., 2018, 751, 1–90 CrossRef CAS.
- L. Lundberg, P. Bartl, C. Leidlmair, P. Scheier and M. Gatchell, Protonated and cationic helium clusters, Molecules, 2020, 25, 1066 CrossRef CAS PubMed.
- O. Asvany, S. Schlemmer, T. Szidarovszky and A. G. Császár, Infrared signatures of the HHe+n and DHe+n (n = 3–6) complexes, J. Phys. Chem. Lett., 2019, 10, 5325–5330 CrossRef CAS PubMed.
- M. Töpfer, A. Jensen, K. Nagamori, H. Kohguchi, T. Szidarovszky, A. G. Császár, S. Schlemmer and O. Asvany, Spectroscopic signatures of HHe+2 and HHe+3, Phys. Chem. Chem. Phys., 2020, 22, 22885–22888 RSC.
- P. Bartl, C. Leidlmair, S. Denifl, P. Scheier and O. Echt, Cationic complexes of hydrogen with helium, ChemPhysChem, 2013, 14, 227–232 CrossRef CAS PubMed.
- F. Grandinetti, Noble Gas Chemistry: Structure, Bonding, and Gas-Phase Chemistry, Wiley, 2018 Search PubMed.
- A. G. Császár, T. Szidarovszky, O. Asvany and S. Schlemmer, Fingerprints of microscopic superfluidity in HHe+n clusters, Mol. Phys., 2019, 117, 1559–1583 CrossRef.
- A. G. Császár, C. Fábri and J. Sarka, Quasistructural molecules, WIREs Comp. Mol. Sci., 2020, 10, e1432 Search PubMed.
- M. Pavanello, S. Bubin, M. Molski and L. Adamowicz, Non-Born–Oppenheimer calculations of the pure vibrational spectrum of HeH+, J. Chem. Phys., 2005, 123, 104306 CrossRef PubMed.
- D. E. Tolliver, G. A. Kyrala and W. H. Wing, Observation of the infrared spectrum of the helium hydride molecular ion 4HeH+, Phys. Rev. Lett., 1979, 43, 1719–1722 CrossRef CAS.
- A. Carrington, J. Buttenshaw, R. A. Kennedy and T. P. Softley, Observation of bound to quasibound vibration-rotation transitions in the HeH+ ion, Mol. Phys., 1981, 44, 1233–1237 CrossRef CAS.
- P. Bernath and T. Amano, Detection of the infrared fundamental band of HeH, Phys. Rev. Lett., 1982, 48, 20–22 CrossRef CAS.
- A. Carrington, R. A. Kennedy, T. P. Softley, P. G. Fournier and E. G. Richard, Infrared bound to quasibound vibration–rotation spectrum of HeH+ and its isotopes, Chem. Phys., 1983, 81, 251–261 CrossRef CAS.
- D.-J. Liu, W.-C. Ho and T. Oka, Rotational spectroscopy of molecular ions using diode lasers, J. Chem. Phys., 1987, 87, 2442–2446 CrossRef CAS.
- M. W. Crofton, R. S. Altman, N. N. Haese and T. Oka, Infrared spectra of 4HeH+, 4HeD+, 3HeH+, and 3HeD+, J. Chem. Phys., 1989, 91, 5882–5886 CrossRef CAS.
- J. Purder, S. Civiš, C. E. Blom and M. C. van Hemert, Diode laser spectra and potential energy curve for the molecular ion HeH+, J. Mol. Spectrosc., 1992, 153, 701–709 CrossRef CAS.
- Z. Liu and P. B. Davies, Infrared laser absorption spectroscopy of rotational and vibration rotational transitions of HeH+ up to the dissociation threshold, J. Chem. Phys., 1997, 107, 337–341 CrossRef CAS.
- F. Matsushima, T. Oka and K. Takagi, Observation of the rotational spectra of 4HeH+, 3HeH+, and 3HeD+, Phys. Rev. Lett., 1997, 78, 1664–1666 CrossRef CAS.
- M. Stanke, D. Kedziera, M. Molski, S. Bubin, M. Barysz and L. Adamowicz, Convergence of experiment and theory on the pure vibrational spectrum of HeH+, Phys. Rev. Lett., 2006, 96, 233002 CrossRef PubMed.
- A. J. Perry, J. N. Hodges, C. R. Markus, G. S. Kocheril and B. J. McCall, Communication: High precision sub-Doppler infrared spectroscopy of the HeH+ ion, J. Chem. Phys., 2014, 141, 101101 CrossRef PubMed.
- O. Asvany, S. Schlemmer, A. van der Avoird, T. Szidarovszky and A. G. Császár, Vibrational spectroscopy of H2He+ and D2He+, J. Mol. Spectrosc., 2021, 377, 111423 CrossRef CAS.
- H. H. Michels, Molecular orbital studies of the ground and low-lying excited states of the HeH+ molecular ion, J. Chem. Phys., 1966, 44, 3834–3850 CrossRef.
- D. M. Bishop and L. M. Cheung, A theoretical investigation of HeH+, J. Mol. Spectrosc., 1979, 75, 462–473 CrossRef CAS.
- J. Tennyson and S. Miller, Predicted vibration-rotation levels of H2He+ and its isotopomers, J. Chem. Phys., 1987, 87, 6648–6652 CrossRef CAS.
- M. Juřek, V. Špirko and W. P. Kraemer, Ab initio calculated rotation-vibration linestrengths for HeH+2, J. Mol. Spectrosc., 1997, 182, 364–370 CrossRef PubMed.
- J. A. Coxon and P. G. Hajigeorgiou, Experimental Born–Oppenheimer potential for the X1Σ+ ground state of HeH+: Comparison with the ab initio potential, J. Mol. Spectrosc., 1999, 193, 306–318 CrossRef CAS PubMed.
- B. Balta, F. A. Gianturco and F. Paesani, Structural properties and quantum effects in protonated helium clusters. II. Quantum Monte Carlo calculations for the smaller aggregates, Chem. Phys., 2000, 254, 215–229 CrossRef CAS.
- M. Šindelka, V. Špirko and W. P. Kraemer, Vibrational linestrengths for the ground and first excited electronic states of HeH+2, Theor. Chem. Acc., 2003, 110, 170–175 Search PubMed.
- A. Chakraborty, S. Giri and P. K. Chattaraj, Trapping of noble gases (He–Kr) by the aromatic H+3 and Li+3 species: a conceptual DFT approach, New J. Chem., 2010, 34, 1936–1945 RSC.
- W.-C. Tung, M. Pavanello and L. Adamowicz, Accurate potential energy curves for HeH+ isotopologues, J. Chem. Phys., 2012, 137, 164305 CrossRef PubMed.
- D. de Fazio, M. de Castro-Vitores, A. Aguado, V. Aquilanti and S. Cavalli, The He + H+2 →HeH+ + H reaction: ab initio studies of the potential energy surface, benchmark time-independent quantum dynamics in an extended energy range and comparison with experiments, J. Chem. Phys., 2012, 137, 244306 CrossRef PubMed.
- T. R. Hogness and E. G. Lunn, The ionization of hydrogen by electron impact as interpreted by positive ray analysis, Phys. Rev., 1925, 26, 44–55 CrossRef CAS.
- G. E. Veatch and H. J. Oskam, Mass spectrometric evidence for the existence of the He2H+ ion, Phys. Lett. A, 1969, 28, 740–741 CrossRef CAS.
- T. M. Kojima, N. Kobayashi and Y. Kaneko, Formation of helium cluster ions HHe+x (x ≤ 14) and H3He+x (x ≤ 13) in a very low temperature drift tube, Z. Phys. D Atom. Mol. Cl, 1992, 23, 181–185 CrossRef CAS.
- S. Jaksch, A. Mauracher, A. Bacher, S. Denifl, F. Ferreira da Silva, H. Schöbel, O. Echt, T. D. Märk, M. Probst, D. K. Bohme and P. Scheier, Formation of evennumbered hydrogen cluster cations in ultracold helium droplets, J. Chem. Phys., 2008, 129, 224306 CrossRef CAS PubMed.
- S. Jaksch, F. F. da Silva, S. Denifl, O. Echt, T. D. Märk and P. Scheier, Experimental evidence for the existence of an electronically excited state of the proposed dihydrogen radical cation He–H–H–He+, Chem. – Eur. J., 2009, 15, 4190–4194 CrossRef CAS PubMed.
- A. Carrington, D. I. Gammie, A. M. Shaw, S. M. Taylor and J. M. Hutson, Observation of a microwave spectrum of the long-range He⋯H+2 complex, Chem. Phys. Lett., 1996, 260, 395–405 CrossRef CAS.
- F. Filippone and F. A. Gianturco, Charged chromophoric units in protonated rare-gas clusters: A dynamical simulation, Europhys. Lett., 1998, 44, 585–591 CrossRef CAS.
- F. A. Gianturco and F. Filippone, Competitive shell-filling in protonated helium clusters, Chem. Phys., 1999, 241, 203–212 CrossRef CAS.
- I. Baccarelli, F. A. Gianturco and F. Schneider, Spatial structures and electronic excited states of small protonated helium clusters, Int. J. Quantum Chem., 1999, 74, 193–212 CrossRef CAS.
- W. P. Kraemer, V. Špirko and O. Bludský, Bound and low-lying quasi-bound rotationvibration energy levels of the ground and first excited electronic states of HeH+2, Chem. Phys., 2002, 276, 225–242 CrossRef CAS.
- I. Savic, D. Gerlich, O. Asvany, P. Jusko and S. Schlemmer, Controlled synthesis and analysis of He–H+3 in a 3.7 K ion trap, Mol. Phys., 2015, 113, 2320–2332 CrossRef CAS.
- T. Szidarovszky and K. Yamanouchi, Full-dimensional simulation of the laser-induced alignment dynamics of H2He+, Mol. Phys., 2017, 115, 1916–1926 CrossRef CAS.
- D. Papp, T. Szidarovszky and A. G. Császár, A general variational approach for computing rovibrational resonances of polyatomic molecules. Application to the weakly bound H2He+ and H2·CO systems, J. Chem. Phys., 2017, 147, 094106 CrossRef PubMed.
- D. Papp, A. G. Császár, K. Yamanouchi and T. Szidarovszky, Rovibrational resonances in H2He+, J. Chem. Theor. Comput., 2018, 14, 1523–1533 CrossRef CAS PubMed.
- H.-K. Chung, B. J. Braams, K. Bartschat, A. G. Császár, G. W. F. Drake, T. Kirchner, V. Kokoouline and J. Tennyson, Uncertainty estimates for theoretical atomic and molecular data, J. Phys. D: Appl. Phys., 2016, 49, 363002 CrossRef.
- W. D. Allen; A. L. L. East and A. G. Császár, in Structures and conformations of nonrigid molecules, ed. Laane, J., Dakkouri, M., van der Veken, B. and Oberhammer, H., Kluwer, Dordrecht, 1993, pp. 343–373 Search PubMed.
- A. G. Császár, W. D. Allen and H. F. Schaefer III, In pursuit of the ab initio limit for conformational energy prototypes, J. Chem. Phys., 1998, 108, 9751–9764 CrossRef.
- A. L. L. East, C. S. Johnson and W. D. Allen, Characterization of the
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A′ state of isocyanic acid, J. Chem. Phys., 1993, 98, 1299–31328 CrossRef CAS.
1A′ state of isocyanic acid, J. Chem. Phys., 1993, 98, 1299–31328 CrossRef CAS. - I. M. B. Nielsen, W. D. Allen, A. G. Császár and H. F. Schaefer, Toward resolution of the silicon dicarbide (SiC2) saga: Ab initio excursions in the web of polytopism, J. Chem. Phys., 1997, 107, 1195–1211 CrossRef CAS.
- G. Tarczay, A. G. Császár, W. Klopper, V. Szalay, W. D. Allen and H. F. Schaefer III, The barrier to linearity of water, J. Chem. Phys., 1999, 110, 11971–11981 CrossRef CAS.
- K. Aarset, A. G. Császár, E. Sibert, W. D. Allen, H. F. Schaefer III, W. Klopper and J. Noga, Anharmonic force field, vibrational energy levels, and barrier to inversion of SiH−3, J. Chem. Phys., 2000, 112, 4053–4063 CrossRef CAS.
- A. G. Császár; G. Tarczay; M. L. Leininger; O. L. Polyansky; J. Tennyson and W. D. Allen, in Spectroscopy from space, ed. Demaison, J., Sarka, K. and Cohen, E. A., Kluwer, Dordrecht, 2001, pp. 317–339 Search PubMed.
- W. Klopper, C. C. M. Samson, G. Tarczay and A. G. Császár, Equilibrium inversion barrier of NH3 from extrapolated coupled-cluster pair energies, J. Comput. Chem., 2001, 22, 1306–1314 CrossRef CAS.
- F. Pollreisz, A. Gömöry, G. Schlosser, K. Vékey, I. Solt and A. G. Császár, Mass spectrometric and quantum-chemical study on the structure, stability, and chirality of protonated serine dimers, Chem. – Eur. J., 2005, 11, 5908–5916 CrossRef CAS PubMed.
- G. Czakó, E. Mátyus, A. C. Simmonett, A. G. Császár, H. F. Schaefer and W. D. Allen, Anchoring the absolute proton affinity scale, J. Chem. Theor. Comput., 2008, 4, 1220–1229 CrossRef PubMed.
- P. R. Schreiner, H. P. Reisenauer, F. C. Pickard, A. C. Simmonett, W. D. Allen, E. Mátyus and A. G. Császár, Capture of hydroxymethylene and its fast disappearance through tunnelling, Nature, 2008, 453, 906–909 CrossRef CAS PubMed.
- H. M. Jaeger, H. F. Schaefer, J. Demaison, A. G. Császár and W. D. Allen, Lowest-lying conformers of alanine: Pushing theory to ascertain precise energetics and semiexperimental Re structures, J. Chem. Theor. Comput., 2010, 6, 3066–3078 CrossRef CAS PubMed.
- D. Barna, B. Nagy, J. Csontos, A. G. Császár and G. Tasi, Benchmarking experimental and computational thermochemical data: A case study of the butane conformers, J. Chem. Theor. Comput., 2012, 8, 479–486 CrossRef CAS PubMed.
- H. H. Nielsen, The vibration–rotation energies of molecules, Rev. Mod. Phys., 1951, 23, 90–136 CrossRef CAS.
- D. A. Clabo, W. D. Allen, R. B. Remington, Y. Yamaguchi and H. F. Schaefer III, A systematic study of molecular vibrational anharmonicity and vibration–rotation interaction by self-consistent-field higher derivative methods. Asymmetric top molecules, Chem. Phys., 1988, 123, 187–239 CrossRef CAS.
- W. D. Allen, Y. Yamaguchi, A. G. Császár, D. A. Clabo Jr., R. B. Remington and H. F. Schaefer III, A systematic study of molecular vibrational anharmonicity and vibration-rotation interaction by self-consistent-field higher derivative methods. Linear polyatomic molecules, Chem. Phys., 1990, 145, 427–466 CrossRef CAS.
- J. M. Bowman, K. M. Christoffel and F. Tobin, Application of SCF-SI theory to vibrational motion in polyatomic molecules, J. Phys. Chem., 1979, 83, 905–912 CrossRef CAS.
- S. Carter, J. M. Bowman and N. C. Handy, Extensions and tests of MULTIMODE: A code to obtain accurate vibration/rotation energies of many-mode molecules, Theor. Chem. Acc., 1998, 100, 191–198 Search PubMed.
- R. Ramakrishnan and G. Rauhut, Semi-quartic force fields retrieved from multi-mode expansions: Accuracy, scaling behavior, and approximations, J. Chem. Phys., 2015, 142, 154118 CrossRef PubMed.
- B. Ziegler and G. Rauhut, Rigorous use of symmetry within the construction of multidimensional potential energy surfaces, J. Chem. Phys., 2018, 149, 164110 CrossRef PubMed.
- J. K. G. Watson, The vibration-rotation Hamiltonian of linear molecules, Mol. Phys., 1970, 19, 465–487 CrossRef CAS.
- T. H. Dunning Jr., Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- T. van Mourik, A. K. Wilson and T. H. Dunning Jr., Benchmark calculations with correlated molecular wavefunctions. XIII. Potential energy curves for He2, Ne2 and Ar2 using correlation consistent basis sets through augmented sextuple zeta, Mol. Phys., 1999, 99, 529–547 CrossRef.
- G. A. Petersson, S. Zhong, J. A. Montgomery and M. J. Frisch, On the optimization of Gaussian basis sets, J. Chem. Phys., 2003, 118, 1101–1109 CrossRef CAS.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation theory approach to intermolecular potential energy surfaces of van der Waals complexes, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- L. Mentel, ChemTools – A Python toolbox for computational chemistry, https://github.com/lmmentel/chemtools.
- H.-J. Werner, P. Knowles, F. Manby, J. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. Kreplin, Q. Ma, T. Miller, A. Mitrushchenkov, K. Peterson, I. Polyak, G. Rauhut and M. Sibaev, The MOLPRO quantum chemistry package, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- W. D. Allen and A. G. Császár, On the ab initio determination of higher-order force constants at nonstationary reference geometries, J. Chem. Phys., 1993, 98, 2983–3015 CrossRef CAS.
- D. Feller, The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water, J. Chem. Phys., 1993, 98, 7059–7071 CrossRef CAS.
- A. G. Császár, W. D. Allen, Y. Yamaguchi and H. F. Schaefer, Ab initio determination of accurate ground electronic state potential energy hypersurfaces for small molecules, in Computational Molecular Spectroscopy, ed. P. Jensen and P. R. Bunker, Wiley, Chichester, 2000, pp. 15–68 Search PubMed.
- W. Klopper and W. Kutzelnigg, Gaussian basis sets and the nuclear cusp problem, THEOCHEM, 1986, 135, 339–356 CrossRef.
- T. Helgaker, W. Klopper, H. Koch and J. Noga, Basis-set convergence of correlated calculations on water, J. Chem. Phys., 1997, 106, 9639–9646 CrossRef CAS.
- G. Tasi and A. G. Császár, Hartree–Fock-limit energies and structures with a few dozen distributed Gaussians, Chem. Phys. Lett., 2007, 438, 139–143 CrossRef CAS.
- N. C. Handy, Y. Yamaguchi and H. F. Schaefer III, The diagonal correction to the Born–Oppenheimer approximation: Its effect on the singlet-triplet splitting of CH2 and other molecular effects, J. Chem. Phys., 1986, 84, 4481–4484 CrossRef CAS.
- G. Tarczay, A. G. Császár, W. Klopper and H. M. Quiney, Anatomy of relativistic energy corrections in light molecular systems, Mol. Phys., 2001, 99, 1769–1794 CrossRef CAS.
- A. Tajti, P. G. Szalay, A. G. Császár, M. Kállay, J. Gauss, E. F. Valeev, B. A. Flowers, J. Vázquez and J. F. Stanton, HEAT: High accuracy extrapolatedab initiothermochemistry, J. Chem. Phys., 2004, 121, 11599–11613 CrossRef CAS PubMed.
- Y. J. Bomble, J. Vázquez, M. Kállay, C. Michauk, P. G. Szalay, A. G. Császár, J. Gauss and J. F. Stanton, High-accuracy extrapolated ab initio thermochemistry. II. Minor improvements to the protocol and a vital simplification, J. Chem. Phys, 2006, 125, 064108 CrossRef PubMed.
- B. Paizs, P. Salvador, A. G. Császár, M. Duran and S. Suhai, Intermolecular bond lengths: Extrapolation to the basis set limit on uncorrected and BSSE-corrected potential energy hypersurfaces, J. Comput. Chem., 2001, 22, 196–207 CrossRef CAS.
- R. D. Cowan and D. C. Griffin, Approximate relativistic corrections to atomic radial wave functions, J. Opt. Soc. Am., 1976, 66, 1010–1014 CrossRef CAS.
- D. Kedziera, M. Stanke, S. Bubin, M. Barysz and L. Adamowicz, Darwin and massvelocity relativistic corrections in non-Born–Oppenheimer variational calculations, J. Chem. Phys., 2006, 125, 084303 CrossRef PubMed.
- A. G. Császár, C. Fábri, T. Szidarovszky, E. Mátyus, T. Furtenbacher and G. Czakó, The fourth age of quantum chemistry: Molecules in motion, Phys. Chem. Chem. Phys., 2012, 14, 1085–1106 RSC.
- A. R. Hoy, I. M. Mills and G. Strey, Anharmonic force constant calculations, Mol. Phys., 1972, 24, 1265–1290 CrossRef CAS.
- A. G. Császár, Anharmonic molecular force fields, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 273–289 Search PubMed.
- J. M. Bowman, T. Carrington and H.-D. Meyer, Variational quantum approaches for computing vibrational energies of polyatomic molecules, Mol. Phys., 2008, 106, 2145–2182 CrossRef CAS.
- B. Ziegler and G. Rauhut, Efficient generation of sum-of-products representations of high-dimensional potential energy surfaces based on multimode expansions, J. Chem. Phys., 2016, 144, 114114 CrossRef PubMed.
- J. Meisner, P. P. Hallmen, J. Kästner and G. Rauhut, Vibrational analysis of methyl cation – rare gas atom complexes: CH+3–Rg (Rg = He, Ne, Ar, Kr), J. Chem. Phys., 2019, 150, 084306 CrossRef PubMed.
- R. Bader, Atoms in Molecules – A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- AIMAll (Version 19.10.12), Todd A. Keith, TK Gristmill Software, Overland Park KS, USA, 2019 (http://aim.tkgristmill.com).
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, Coupled-cluster techniques for computational chemistry: The CFOUR program package, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and A. Ganyecz, The MRCC program system: Accurate quantum chemistry from water to proteins, J. Chem. Phys., 2020, 152, 074107 CrossRef PubMed.
- D. R. G. Schleicher, D. Galli, F. Palla, M. Camenzind, R. S. Klessen, M. Bartelmann and S. C. O. Glover, Effects of primordial chemistry on the cosmic microwave background, Astron. Astrophys., 2008, 490, 521–535 CrossRef CAS.
- E. P. Hunter and S. G. Lias, Evaluated gas phase basicities and proton affinities of molecules: an update, J. Phys. Chem. Ref. Data, 1998, 27, 413–656 CrossRef CAS.
- T. J. Lee and P. R. Taylor, A diagnostic for determining the quality of single-reference electron correlation methods, Int. J. Quantum Chem., 1989, 23, 199–207 CAS.
- D. Koner, J. C. S. V. Veliz, A. van der Avoird and M. Meuwly, Near dissociation states for H+2 He on MRCI and FCI potential energy surfaces, Phys. Chem. Chem. Phys., 2019, 21, 24976–24983 RSC.
- P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC, Ottawa, 1998 Search PubMed.
- D. G. Hopper, The electronic structure of HeH+2, Int. J. Quantum Chem., 1978, 12, 305–322 CAS.
- C. Fábri, G. Czakó, G. Tasi and A. G. Császár, Adiabatic Jacobi corrections on the vibrational energy levels of H+2 isotopologues, J. Chem. Phys., 2009, 130, 134314 CrossRef PubMed.
- K. P. Huber and G. Herzberg, Molecular spectra and molecular structure: constants of diatomic molecules, D. van Nostrand, New York, 1979 Search PubMed.
| This journal is © the Owner Societies 2022 |