Surface plasmon resonance sensing with thin films of palladium and platinum – quantitative and real-time analysis

Abstract

Surface plasmon resonance (SPR) is a highly useful technique in biology and is gradually becoming useful also for materials science. However, measurements to date have been performed almost exclusively on gold, which limits the possibility to probe chemical modifications of other metals. In this work we show that 20 nm Pd and Pt films work “fairly well” for quantitative SPR sensing of organic films despite the high light absorption. In the interval between total reflection and the SPR angle, high intensity changes occur when a film is formed on the surface. Fresnel models accurately describe the full angular spectra and our data analysis provides good resolution of surface coverage in air (a few ng cm⁻²). Overall, the Pd sensors behave quite similarly to 50 nm gold in terms of sensitivity and field extension, although the noise level in real-time measurements is ∼5 times higher. The Pt sensors exhibit a longer extension of the evanescent field and ∼10 times higher noise compared to gold. Yet, formation of organic layers a few nm in thickness can still be monitored in real-time. As a model system, we use thiolated poly(ethylene glycol) to make Pd and Pt protein repelling. Our findings show how SPR can be used for studying chemical modifications of two metals that are important in several contexts, for instance within heterogeneous catalysis. We emphasize the advantages of simple sample preparation and accurate quantitative analysis in the planar geometry by Fresnel models.

---

Introduction

Surface plasmon resonance (SPR) is the “golden” standard for biomolecular interaction analysis.¹ Besides providing high resolution, SPR operates label-free and provides real-time analysis of binding events so that rate constants for interactions of interest can be determined.² SPR sensors are also being evaluated for detection of analytes from complex samples by improving the surface functionalization³ or by introducing filtering steps.⁴ Lately, the range of applications of SPR has been extended and the method has started to become a useful tool also in materials science. For instance, several suppliers now provide instruments with goniometric scanning to capture a wider range in the angular spectrum, thereby enabling measurements in environments other than water. Chemical modifications of dielectric materials can also be studied by depositing sufficiently thin films,⁵ so that the new material interface remains inside the evanescent field extension (hundreds of nm on standard gold sensors). Notably, plasmonic signals can also be used to monitor processes inside a material, such as corrosion⁶ or gas adsorption.^7,8

However, despite early discussions when SPR emerged,⁹ there have been relatively few developments of SPR (utilizing planar metal films) in terms of other metals, although nanoparticle plasmons have been studied using many metals.¹⁰ Silver films were evaluated already in pioneering work with SPR sensors¹¹ and in several later studies.^12–14 In principle, silver has better optical properties (lower absorption) than gold, but spontaneous oxidation makes it very difficult to work with. The same is true for copper,⁵ which has also been tested in the Kretschmann configuration.¹⁵ Attempts have been made to use alloys to maintain a sufficient level of chemical stability for the thin film,¹⁵ but this makes the optical properties harder to model and excludes studies of chemical modifications of a single metal type. Palladium (Pd) and platinum (Pt) are both important metals for many applications whereof the most known are related to heterogeneous catalysis. Furthermore, Pd is highly useful for zero mode waveguides¹⁶ and Pt surfaces are precious because of their suitability for electrochemical cells.¹⁷ In addition, the chemical stability is good for Pd and excellent for Pt. Yet, there are very few reports on SPR sensing in the Kretschmann configuration using these metals. In particular, to date no study has evaluated the applicability of unstructured Pd and Pt films for quantitative analysis of adsorbed organic films or the monitoring of surface binding events in real-time. Sadowski et al. measured reflectivity spectra from Pd films and pointed out that this metal can be useful despite the high optical absorption.¹⁸ Since then, hydrogen adsorption (gas phase measurements) into thin Pd films has been measured in a few studies.^8,19 Also, some studies have investigated plasmonic nanoparticles consisting of Pd or Pt,^20–22 but not utilized them for sensing applications. Making such structures on solid supports requires nanofabrication techniques and quantitative analysis is much more difficult when the geometry is no longer planar. Plasmonics (whether SPR or nanostructure-based) with Pd and Pt is often perceived as a dead end because of the high light absorption of these metals, which goes against the trend to work towards spectrally narrow resonances²³ and high sensitivity in terms of resonance shifts. Yet many of the typical benchmark parameters (e.g. the “figure of merit”) do not, in fact, need to be particularly high for reaching sufficient signal to noise: it is enough that the spectrum (angular or wavelength) has at least one region with reasonably large intensity changes when the refractive index is altered at the metal surface.²⁴

Here we present the use of simple SPR sensors based on pure planar Pd or Pt films for analyzing surface binding. We show for the first time that these sensors work quite well to quantify binding of organic molecules, given that the full angular spectrum is obtained and data analysis performed properly. Quantification of surface coverage is performed by Fresnel modelling of spectra obtained in air. Although the Pd and Pt plasmon resonances are extremely broad, the inflection point close to the total internal reflection (TIR) angle is shown to exhibit sufficient intensity changes for quantitative analysis. In water, reflectivity minima can be identified and binding kinetics of thiol-terminated polymers monitored with reasonable resolution, albeit not as high as for gold. Our results show how SPR can be used as a label-free quantitative analysis tool for evaluating surface modifications or other interfacial processes associated with two important metals.

Experimental

Chemicals

PEG was purchased from Laysan Bio Inc. BSA was from Sigma Aldrich. Phosphate buffered saline (PBS) tablets were from Thermo Fischer. ASTM research grade type 1 ultrafiltered water was used for all aqueous solutions.

Sample preparation

Samples were prepared by electron beam heated physical vapor deposition (Lesker PVD 225) of metals on SPR glass substrates (Bionavis) cleaned using RCA2 (1 : 1 : 5 volume of conc. HCl : H₂O₂ (30%) : H₂O, at 80 °C) and 50 W O₂ plasma at 250 mTorr. Prior to experiments, Pd surfaces were cleaned with H₂O₂ at 45 °C for 15 min followed by rinsing in water, immersion in 99.5% EtOH for 20 min and drying with N₂. Pt was instead cleaned with piranha wash (3 : 1 volume of conc. H₂SO₄ : H₂O₂) for 20 min followed by rinsing in water and drying with N₂.

Measurements

Angular spectra were obtained using a Bionavis SPR Navi instrument. The instrument has two channels, one with wavelengths of 670 nm and 785 nm, the other with 670 nm and 985 nm. Throughout this paper we show data obtained at 670 nm.

Data analysis

The resonance dip position for Pd and Pt in liquid could be monitored using the software that comes with the instrument, but a second-degree polynomial including 200–400 points around the resonance dip was fitted to improve signal-to-noise. The built-in TIR angle tracking did not function with Pd and Pt samples. To track TIR angle, the spectrum was smoothened with a moving average filter and the TIR angle was defined as the maximum of a third order polynomial fit around the peak in the first derivative of the spectrum. For Fresnel modelling to quantify bound amounts, the metal permittivity was kept to the fitted values and an additional film was introduced.²⁵ Only the thickness of this layer was allowed to vary and the RI was fixed to 1.46 for PEG.²⁶

Simulations

Fitted values of metal permittivity for clean sensors were used in the simulations results. (Qualitatively similar results were achieved when using common literature values^27,28 and the calculated field extension and sensitivity differed by up to ∼20%). Transfer matrix calculations were performed in Matlab to model reflectivity as described previously.²⁴ Fields were obtained by calculating the dispersion relation in the thin film system, using a previously described method.²⁹ Initial values were chosen in order to solve for the mode with longer propagation (lower imaginary part of in-plane wavevector) in the finite film.

Results and discussion

We started by estimating the optimal thickness of the metals for coupling to surface plasmons. The reflectivity spectra of thin Pd and Pt films were simulated by Fresnel calculations, using the transfer matrix method.²⁴Fig. 1A shows calculated reflectivity spectra for different thicknesses, including a Cr adhesion layer with a thickness of ∼1 nm,²⁵ which is necessary to promote adhesion to glass.²⁵ Notably, the spectra for the thinnest films show reflectivity minima, although extremely broadened due to the high absorption. Furthermore, a region with steep reflectivity changes with incident angle can be identified in between the SPR angle (θ_SPR) and the total internal reflection (TIR) angle (θ_TIR = arcsin(1/1.52) by Snell's law). It is clearly the higher angle spectral regions (θ > θ_SPR) that strongly deviate from the spectrum of ordinary gold sensors,²⁵ for which the reflectivity rises steeply again and forms a narrow dip.¹⁸ The optimal film thickness for distinguishing a reflectivity minimum is as low as 10 nm according to the simulations, for both Pd and Pt. This is because the dissipation of the leaky mode (which exchanges energy with the plane wave in the prism) in a finite metal film decreases with film thickness,²⁹ which leads to a less broad reflectivity dip. However, it may be difficult to make a continuous metal film so thin when using vacuum deposition techniques, which is why we settled for 20 nm thickness on the experimental samples. The experimental spectra in air (Fig. 1B) were in fair agreement with the simulations, although no clear reflectivity minima could be identified. For Pd, agreement with previous studies is also clear,¹⁸ while we have not found any previous experimental spectra of Pt to compare with. When the samples were immersed in water, both Pd and Pt samples did exhibit a reflectivity minimum (Fig. 1C).

Fig. 1 Angular spectra in reflection mode. (A) Simulated angular reflectivity spectra for different thickness of Pd and Pt films with 670 nm incident light in the Kretschmann configuration. The RI is set to n = 1.52 for the prism (and n = 1 for air). (B) Experimental spectra for 20 nm Pd and Pt in air, showing no clear minima. (C) Experimental spectra in water. The arrows indicate the reflectivity minima (θ_SPR) that become identifiable.

We determined the permittivity of the metal films by allowing the complex RI to vary when fitting the initial “background” model describing the clean sensors, while the thickness was fixed to 20 nm as measured from the deposition tool. We then obtained n = 2.25 + 4.60i for Pd and n = 2.47 + 5.28i for Pt at 670 nm. These values deviate somewhat from the most commonly used data sets: Johnson and Christy reported n = 1.81 + 4.48i for Pd²⁸ and Rakic et al. reported n = 2.43 + 4.36i for Pt.²⁷ However, our values are in good agreement with other studies. For instance, Palm et al. reported n = 2.12 + 4.77i for Pd films prepared by electron beam evaporation³⁰ and Werner et al. reported n = 2.45 + 5.51i for Pt based on DFT calculations.³¹ Thus, we consider our values reasonable (and they were implemented in all simulations). In general, differences in permittivity values are not necessarily due to limited accuracy in the measurements, but may reflect true changes in optical properties due to factors such as variable grain size, oxide formation, etc. These factors, in turn, are strongly dependent on how the films are prepared and treated. In this work, standard physical vapor deposition by electron beam heating was used and the films were not annealed.

To show the feasibility of quantifying adsorbed materials on the surfaces, we performed measurements in air after binding events and extended the Fresnel models to include another layer.³² The main advantage with this approach is that the RI of an adsorbed film is better known when it is not hydrated, with values around 1.5 for most organic molecules such as polymers and proteins.²⁶ Thus, the film thickness becomes the only unknown parameter and the density of the adsorbed material (also normally known) can subsequently be used to obtain a mass coverage.²⁶Fig. 2A shows an example of Fresnel models fitted to a Pd sample before and after coating with an organic layer, in this case two different poly(ethylene glycol) (PEG) brushes.³³ Similarly, Fig. 2B shows a Pt sample before and after binding of thiolated PEG. (Other polymer coatings were analyzed in the same manner, but only PEG data is shown here.) Note that spontaneous water uptake (hygroscopy) by PEG is expected to be negligible at normal ambient air humidity,³⁴ which means that the bulk properties of PEG should describe the organic film quite accurately.

Fig. 2 Quantitative analysis of thin films in air. (A) Spectra in air before and after binding of PEG-SH to Pd sensors. Two different molecular weights were used. A Fresnel model fit is shown for each case (practically indistinguishable from the data). (B) Same data for Pt, showing only one molecular weight of PEG but 10 repeated measurements to illustrate measurement variation. A fit is shown for the clean 20 nm Pt sensor.

Notably, in the region with a steep reflectivity decrease between θ_TIR and θ_SPR, clear intensity changes are detected after coating the surfaces. Also, the residual (difference between Fresnel model and data) was lowest in this region. For Pd, the fit is practically indistinguishable from the data points with R² > 0.9999 in a 1° interval (inset in Fig. 2A). For Pt the fit is somewhat poorer, but not in the region θ_TIR < θ < θ_SPR (inset in Fig. 2B). We found that spectral analysis should be performed here for best accuracy and resolution, as initially proposed by Sadowski et al.¹⁸ Furthermore, we performed multiple measurements and Fresnel fits to each spectrum to estimate the uncertainty when determining the organic film thickness. An example of ten spectra is shown in Fig. 2B for PEG on Pt, yielding an average thickness of 2.23 nm with standard deviation of 0.02 nm. This translates to a detection limit for a typical organic coating (density 1.1 g cm⁻³) of a few ng cm⁻². The analysis could be performed in the same manner at the other wavelengths (785 or 980 nm) with small changes in the results. For instance, when determining the surface coverage of PEG on Pd, using another wavelength altered the result by 11.8% on average (6 experiments). The sample-to-sample variation was similar in magnitude (11.4%) when using the same wavelength for the measurements.

Fig. 3A shows example data when tracking the SPR minimum in real-time with Pd surfaces in a water environment (PBS buffer). Despite the very broad minimum (Fig. 1C), the short-term noise level for θ_SPR is <0.01° for a temporal resolution of ∼10 s. We monitored binding of thiolated PEG (2 kg mol⁻¹) and subsequent injections of the protein bovine serum albumin (BSA) to verify that the surface is inert. For BSA, the baseline is recovered. (This was not the case if the metal was not modified with a PEG coating due to irreversible protein adsorption to the metal, not shown.) The signals from the BSA injections are due to the RI change in the bulk, as can be verified by the complementary θ_TIR signals (Fig. 3A) which perfectly followed θ_SPR.²⁵ The same experiment is shown for a Pt sensor in Fig. 3B. The most notable differences compared to Pd are a lower signal from PEG and higher noise. Typical baselines for Pd, Pt and standard 50 nm gold sensors are shown in Fig. 3C, measured with the same instrument and settings.

Fig. 3 Examples of real-time measurements in liquid. (A) Pd sensor, showing binding of 2 kg mol⁻¹ PEG-SH (1 g L⁻¹) and injections of BSA (10 g L⁻¹). Arrows indicate injections and buffer rinsing. (B) Same experiment as in (A) but for Pt. (C) Characteristic baselines showing noise levels in PBS buffer for Pd, Pt and Au surfaces.

To further describe the surface plasmons in the thin Pd and Pt films, we performed various calculations on the surface plasmon dispersion relation and the near field distribution.²⁹Fig. 4A shows the calculated shifts in θ_SPR with changes in the bulk RI using Fresnel models. The curves are almost fully linear with sensitivities of 72 and 60 degrees per RI unit in water for Pd and Pt respectively (to be compared with 121° per RI unit for 50 nm gold). The absolute values of θ_SPR are in fair agreement with the experimental spectra (Fig. 1C) and correctly predict that the resonance angle is slightly lower on Pt. Furthermore, the calculated signals are in agreement with the bulk signals from BSA injections (Fig. 3A). Specifically, Δθ_SPR = 0.12° is predicted on Pd based on the observed value of Δθ_TIR = 0.13° from BSA (θ_TIR has a bulk sensitivity of 77° per RI unit). The measured value is indeed Δθ_SPR = 0.12 ± 0.005°, showing excellent agreement given that the ∼5 nm PEG coating³³ (in water) occupies a negligible part of the total probing volume. To confirm this and to quantify bound amounts from signals in liquid, information about the evanescent field extension is needed.³³

Fig. 4 Simulation results of sensitivity and field extension for 20 nm Pd and Pt films. (A) Calculated sensitivities in terms of θ_SPR for bulk refractive index changes. Fresnel models were used. Note that for these small changes in bulk RI, the curves are almost fully linear. The values are the initial slopes at n = 1.33. (B) Calculated field in a water environment with the decay lengths indicated. Dispersion relation calculations were used.

Fig. 4B shows the calculated field magnitude as a function of distance from the metal surface. The exponential field decay has a characteristic extension (factor 1/e) of δ = 192 nm for Pd, which is very similar to standard 50 nm gold sensors,³⁵ while a considerably larger value of δ = 234 nm was obtained for Pt. The lower sensitivity (Fig. 4A) and the longer field extension on Pt together explain why the signal from PEG binding on Pt (Fig. 3B) is lower than for Pd. In other words, for Pt sensors, the layer of bound molecules influences the plasmons less but it also causes a smaller effective RI change as it represents a smaller part of the total probing volume. (Measurements in the dry state did not suggest that more PEG binds to Pd than Pt.)

Finally, Fig. 5 shows the electric near fields as vector plots. For Pd, they show a quite ordinary surface plasmon wave (similar to 50 nm Au) which exchanges energy with a planar wave propagating in the prism at the resonance angle. For Pt the near field on the water side looks slightly “inclined” along the propagation direction because of the longer decay of the field, including a stronger oscillating component.

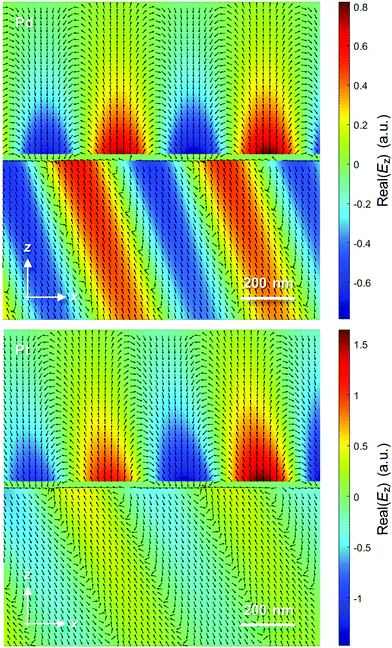Fig. 5 Visualization of the near-field by vector plots of calculated electric fields. The top medium has RI 1.33 and the bottom prism has RI 1.52. The vacuum wavelength is 670 nm in both cases.

Conclusion

In summary, we have shown how to perform SPR experiments and data analysis using Pd and Pt thin films. The main motivation for this work is that these metals are important for many applications such as zero-mode waveguides (Pd), electrochemistry (Pt) and catalysis (both Pd and Pt). Our results enable the use of SPR for evaluating chemical modifications of the surface of these metals (or the metal interior). In brief, the key is to obtain the full angular spectrum and perform proper spectral analysis. For quantitative measurements in air, Fresnel models should be used for fitting the spectral region between the TIR and SPR angles, where the intensity changes are highest. Real-time measurements in water are also possible given that a sufficiently broad angular range is measured to capture the reflectivity minimum. The resolution in the real-time measurements in liquid is poorer than for ordinary gold-based SPR, but sufficient to monitor typical binding reactions, especially for Pd. Calculations show that the 20 nm Pd and Pt sensors are both quite similar to standard 50 nm gold sensors in terms of resonance angle shifts and near field distribution. For Pt, the sensitivity to bulk RI changes is slightly lower, the field extension considerably longer and the noise level quite high in real-time measurements. Nevertheless, it is possible to monitor formation of an organic film in liquid also on Pt. Finally, the model system analyzed shows that thiol-PEG can be used to make the metals protein repelling. Our results widen the applicability of plasmonics as a generic physical tool to probe various processes in materials science,³⁶ with particular focus on accurate quantitative measurements enabled with planar surface SPR.

Author contributions

J. A. investigation, data curation, software. J. S. investigation, data curation. G. F. D. investigation. T. S. methodology, visualization. A. D. conceptualization, methodology, supervision, visualization, writing.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was funded by the Knut & Alice Wallenberg Foundation (2015.0161) and the Erling-Persson Foundation (Swedish Foundations Starting Grant 2017). This work was performed in part at the Chalmers Material Analysis Laboratory (CMAL).

References

1. J. Homola, Chem. Rev., 2008, 108, 462–493.
2. E. Helmerhorst, D. J. Chandler, M. Nussio and C. D. Mamotte, Clin. Biochem. Rev., 2012, 33, 161–173.
3. H. Vaisocherova-Lisalova, F. Surman, I. Visova, M. Vala, T. Springer, M. L. Ermini, H. Sipova, P. Sedivak, M. Houska, T. Riedel, O. Pop-Georgievski, E. Brynda and J. Homola, Anal. Chem., 2016, 88, 10533–10539.
4. J. Breault-Turcot and J.-F. Masson, Chem. Sci., 2015, 6, 4247–4254.
5. S. S. Hinman, K. S. McKeating and Q. Cheng, Anal. Chem., 2018, 90, 19–39.
6. Z. Yang, J. Wang, Y. Shao, Y. Jin and M. Yi, Opt. Quantum Electron., 2019, 52, 31.
7. P. Tobiska, O. Hugon, A. Trouillet and H. Gagnaire, Sens. Actuators, B, 2001, 74, 168–172.
8. B. Chadwick and M. Gal, Appl. Surf. Sci., 1993, 68, 135–138.
9. H. E. de Bruijn, R. P. H. Kooyman and J. Greve, Appl. Opt., 1992, 31, 441–442.
10. A. Lalisse, G. Tessier, J. Plain and G. Baffou, J. Phys. Chem. C, 2015, 119, 25518–25528.
11. B. Liedberg, C. Nylander and I. Lundstrom, Sens. Actuators, 1983, 4, 299–304.
12. H. Liu, B. Wang, E. S. P. Leong, P. Yang, Y. Zong, G. Si, J. Teng and S. A. Maier, ACS Nano, 2010, 4, 3139–3146.
13. S. Szunerits, X. Castel and R. Boukherroub, J. Phys. Chem. C, 2008, 112, 10883–10888.
14. M. Manesse, R. Sanjines, V. Stambouli, C. Jorel, B. Pelissier, M. Pisarek, R. Boukherroub and S. Szunerits, Langmuir, 2009, 25, 8036–8041.
15. C. Gong and M. S. Leite, ACS Photonics, 2016, 3, 507–513.
16. N. Klughammer and C. Dekker, Nanotechnology, 2021, 32, 18LT01.
17. M. K. Debe, Nature, 2012, 486, 43–51.
18. J. W. Sadowski, J. Lekkala and I. Vikholm, Biosens. Bioelectron., 1991, 6, 439–444.
19. K. Lin, Y. Lu, J. Chen, R. Zheng, P. Wang and H. Ming, Opt. Express, 2008, 16, 18599–18604.
20. Y. Xiong, J. Chen, B. Wiley, Y. Xia, Y. Yin and Z.-Y. Li, Nano Lett., 2005, 5, 1237–1242.
21. J. Chen, B. Wiley, J. McLellan, Y. Xiong, Z.-Y. Li and Y. Xia, Nano Lett., 2005, 5, 2058–2062.
22. C. Langhammer, Z. Yuan, I. Zoric and B. Kasemo, Nano Lett., 2006, 6, 833–838.
23. G. V. Naik, V. M. Shalaev and A. Boltasseva, Adv. Mater., 2013, 25, 3264–3294.
24. J. Junesch, T. Sannomiya and A. B. Dahlin, ACS Nano, 2012, 6, 10405–10415.
25. G. Ferrand-Drake del Castillo, G. Emilsson and A. Dahlin, J. Phys. Chem. C, 2018, 122, 27516–27527.
26. J. Andersson, G. Ferrand-Drake del Castillo, P. Bilotto, F. Hook, M. Valtiner and A. Dahlin, Langmuir, 2021, 37, 4943–4952.
27. A. D. Rakic, A. B. Djurisic, J. M. Elazar and M. L. Majewski, Appl. Opt., 1998, 37, 5271–5283.
28. P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1974, 9, 5056–5070.
29. A. B. Dahlin, M. Mapar, K. L. Xiong, F. Mazzotta, F. Hook and T. Sannomiya, Adv. Opt. Mater., 2014, 2, 556–564.
30. K. J. Palm, J. B. Murray, T. C. Narayan and J. N. Munday, ACS Photonics, 2018, 5, 4677–4686.
31. W. S. M. Werner, K. Glantschnig and C. Ambrosch-Draxl, J. Phys. Chem. Ref. Data, 2009, 38, 1013–1092.
32. G. Ferrand-Drake del Castillo, M. Koenig, M. Muller, K.-J. Eichhorn, M. Stamm, P. Uhlmann and A. Dahlin, Langmuir, 2019, 35, 3479–3489.
33. G. Emilsson, R. L. Schoch, L. Feuz, F. Hook, R. Y. H. Lim and A. B. Dahlin, ACS Appl. Mater. Interfaces, 2015, 7, 7505–7515.
34. J. A. Baird, R. Olayo-Valles, C. Rinaldi and L. S. Taylor, J. Pharm. Sci., 2010, 99, 154–168.
35. D. L. M. Rupert, G. V. Shelke, G. Emilsson, V. Claudio, S. Block, C. Lasser, A. B. Dahlin, J. O. Lotvall, M. Bally, V. P. Zhdanov and F. Hook, Anal. Chem., 2016, 88, 9980–9988.
36. E. M. Larsson, S. Syrenova and C. Langhammer, Nanophotonics, 2012, 1, 249.

---