Understanding excited state properties of host materials in OLEDs: simulation of absorption spectrum of amorphous 4,4-bis(carbazol-9-yl)-2,2-biphenyl (CBP)

Abstract

4,4-Bis(carbazol-9-yl)-2,2-biphenyl (CBP) is widely used as a host material in phosphorescent organic light-emitting diodes (PhOLEDs). In the present study, we simulate the absorption spectra of CBP in gas and condensed phases, respectively, using the efficient time-dependent long-range corrected tight-binding density functional theory (TD-LC-DFTB). The accuracy of the condensed-phase absorption spectra computed using the structures obtained from classical molecular dynamics (MD) and quantum mechanical/molecular mechanical (QM/MM) simulations is examined by comparison with the experimental absorption spectrum. It is found that the TD-LC-DFTB gas-phase spectrum is in good agreement with the GW-BSE spectrum, indicating TD-LC-DFTB is an accurate and robust method in calculating the excitation energies of CBP. For the condensed-phase spectrum, we find that the electrostatic embedding has a minor influence on the excitation energy. Computing accurate absorption spectra is a particular challenge since static and dynamic disorders have to be taken into account. The static disorder results from the molecular packing in the material, which leads to molecule deformations. Since these structural changes sensitively impact the excitation energies of the individual molecules, a proper representation of this static disorder indicates that a reasonable structural model of the material has been generated. The good agreement between computed and experimental absorption spectra is therefore an indicator for the structural model developed. Concerning dynamic disorder, we find that molecular changes occur on long timescales in the ns-regime, which requires the use of fast computation approaches to reach convergence. The structural models derived in this work are the basis for future studies of charge and exciton transfer in CBP and related materials, also concerning the degradation mechanisms of CBP-based PhOLEDs.

---

1 Introduction

Nowadays, organic light-emitting diodes (OLEDs) have been considered as a new generation of technologies due to their high brightness, low-cost, low energy consumption, light weight and mechanical flexibility.^1–4 They can be used in many devices such as televisions, mobile phones, and other lighting resources.^5,6 Among different types of OLEDs, the phosphorescent OLEDs (PhOLEDs), serving as the second-generation OLEDs, have recently attracted much attention because they can generate light from both singlet and triplet states and thus allow the internal quantum efficiency to reach nearly 100%.^7,8 In PhOLEDs, the heavy metal-based phosphorescent emitter is doped in an appropriate host material, which is used to transfer excitation energy to the emitter and confine the exciton in the emissive layer. Amorphous materials have been widely used as host materials in PhOLEDs, because the emitter is uniformly distributed in the amorphous matrix to minimize the concentration quenching effect.⁹ In addition, the absence of grain boundaries in amorphous materials further minimizes the exciton recombination.¹⁰ The excited-state properties of the host material play an important role in photoluminescence characteristics of OLEDs. For instance, it has been found that the excited-state molecular aggregation in the vicinity of host material/emitter layer interfaces limits the operation lifetimes of PhOLEDs.¹¹ Therefore, the fundamental understanding of the excited-state properties of host materials is the key for the design of highly efficient PhOLEDs. In the present work, we explore the excited-state properties of a representative host material using reliable and efficient quantum chemistry methods. Hence, we obtain an accurate description of excited states energies and exciton couplings, where the phase space has been sufficiently sampled. To achieve this, we first benchmark semi-empirical quantum chemical methods, the so-called density functional based tight-binding method (DFTB), as well as its long-range corrected version called LC-DFTB, which allows us to describe excited state properties with reasonable accuracy.

In the past decades, DFTB has been used as an alternative to the widely used density functional theory (DFT) to compute molecular properties. DFTB is 2–3 orders of magnitude faster than DFT and can reach the accuracy of DFT methods by using careful parameterization approaches.^12,13 However, DFTB uses semilocal PBE functionals^14,15 for calculations of the Hamiltonian matrix and thus inherits the errors of typical DFT functionals using generalized gradient approximations (GGA).^16,17 Recently, the LC-DFTB approach was developed by the incorporation of arbitrary LC functionals in the DFTB to partly cure the DFT-GGA errors.¹⁸ The time-dependent scheme of LC-DFTB (TD-LC-DFTB) has been successfully parameterized and benchmarked for a test set of small organic molecules involving charge-transfer excitations,¹⁹ rhodopsins and light-harvesting complexes²⁰ and biological molecules.¹⁸ In the present study, we will examine the quantitative accuracy of TD-LC-DFTB in calculating the absorption spectra of a most widely used host material in PhOLEDs,^21,22 4,4′-bis(9-carbazolyl)-biphenyl or CBP.

By combining classical MD simulations with quantum mechanical/molecular mechanical methods (QM/MM), where the DFTB methods are used in the QM part, we will be able to address the effects of static and dynamic disorders on the absorption spectra of CBP. The paper will proceed as follows: first, the benchmark calculations of TD-LC-DFTB approach are performed by comparing the excitation energies of CBP molecules using various quantum chemistry methods. Second, the absorption spectra of CBP in the gas and condensed phase are computed using TD-LC-DFTB and different structure sampling methods are discussed. Finally, the aggregation effect on the optical properties of amorphous CBP has been addressed.

2. Simulation details

2.1 Benchmark of TD-LC-DFTB

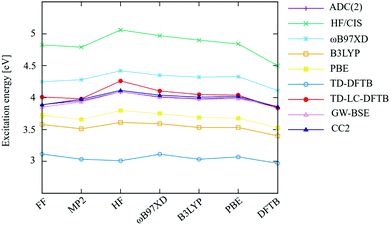
The bond length alternation (BLA) is defined as the difference in average single and double bond lengths along extended π systems. In the present study, the π-conjugated chain marked with red color in Fig. 1(b) is used to evaluate BLA of CBP. To compare the accuracy of different quantum chemistry methods, geometry optimizations of CBP molecule at the ground state are performed using HF, DFT functionals (B3LYP, PBE, ωB97XD) and MP2 with 6-31+g* basis set, respectively. The geometry optimization using DFTB is performed using the third-order DFTB (DFTB3) with 3OB parameter set.²³ In the constrained optimizations, the central, side and improper dihedral angles are fixed at 45°, 60° and 0°, respectively, which are obtained by fully optimization by ωB97XD/6-31+g*, while the other degrees of freedom are relaxed. The excitation energies are computed using CIS, TD-DFT, ADC(2), CC2 and the Bethe–Salpeter equation (BSE) from the GW approximation (GW-BSE) method with 6-31+g* basis set and TD-LC-DFTB with mio-0.8 parameter set,²⁴ respectively. All DFTB and TD-LC-DFTB calculations in the present study are performed using the DFTB+ program suite,²⁵ if not specified otherwise. The GW-BSE and ADC(2) calculations are performed using the TURBOMOLE v7.4 computational chemistry package.²⁶ All other calculations are carried out with the GAUSSIAN 09 package.²⁷

Fig. 1 (a) Schematic representation of the 4,4′-bis(N-carbazolyl)-1,1′-biphenyl (CBP). α, β and γ are the side dihedral angle, central dihedral angle, and improper dihedral angle. (b) Marked bonds in red are considered in calculation of BLA.

Recently, the gas phase single-point absorption spectrum of CBP has been studied using GW-BSE method.²⁸ The GW-BSE method is an accurate and reliable approach for calculating the excited-state properties of extended systems^29,30 and thus it is used to assess the performance of TD-LC-DFTB in this work. Therefore, the geometry is adopted from ref. 28 which is optimized at the ground state using PBE0 functional³¹ with the def2-TZVP basis set^32,33. Afterward, vertical excitation energies and oscillator strengths of the lowest 25 excited singlet states are computed using TD-LC-DFTB with mio-0.8 parameter set. The energy lines are broadened by a Lorentzian function with a width of 0.05 eV and summed up to provide the absorption spectra normalized to the highest peak. Note that the inclusion of the dielectric screening into LC corrected functional can lead to significant shifts in the condensed-phase adsorption spectra. However, we would expect that the inclusion of the dielectric screening makes negligible differences in the adsorption spectra for the systems with strongly localized excitations. The small exitonic couplings between the CBP monomers (shown below) indicates that the localized electronic structure of CBP, which justifies the use of LC corrected functional with bare (i.e., unscreened 1/r) electron–hole interaction.

The self-consistent eigenvalue-only GW method with def2-TZVP basis set is performed to benchmark the accuracy of TD-LC-DFTB for the calculation of the adsorption spectrum of CBP. We use the spectral representations for the response and Green's function,^30,55 which enables an analytic evaluation of energy integrals and derivatives. The advantage of this approach is that it avoids the uncertainties that may arise from the widely used plasmon-pole models and prevents additional computational parameters needed in numerical frequency integration methods.

2.2 Molecular dynamics simulations

The force field parameters are taken from the general AMBER force field (GAFF),^34,35 where the atomic charges are generated by the restrained electrostatic potential^36,37 fitting procedure (RESP) calculated at the HF/6-31g*^38,39 level using the Gaussian 09 package.²⁷ The force field parameterizations are imposed on two types of dihedral angles (see Fig. 1). The first are the proper dihedral angles between two central phenyl groups and the dihedral angle between carbazole moiety and phenyl group (henceforth, referred to as “central angle” and “side angle” or α and β) and the second type is improper dihedral angles (referred to as γ). The dihedral constants for α, β and γ are parametrized by fitting to the relaxed potential energy scan along each angle using ωB97XD/6-31+g* method. The force-field parameterization procedures as well as the fitting parameters can be found in the ESI† (S-1). The van der Waals (vdW) interactions are represented by a 6–12 Lennard-Jones potential,
where the parameters ε and R_min,ij are derived from the GAFF force field. Since we take the structures from the MD-trajectories, vdW effects are included. This also holds for the QM/MM simulations, where the vdW interactions are included in the QM/MM Hamiltonian.

In gas-phase classical MD simulation, a CBP molecule is first minimized using the steepest descent algorithm and then equilibrated at 300 K for 5 ns with a time step of 1 fs. The Nose–Hoover thermostat⁴⁰ is employed to control the temperature. 5000 structures are saved during the equilibrium simulation. For each CBP structure, 25 excitation energies are computed using TD-LC-DFTB and the absorption spectrum is given by the sum of all energy lines broadened by a Lorentzian function with a broadening width of 0.05 eV. In the present study, all classical MD simulations are carried out using the GROMACS (version 2016.3) program package⁴¹ unless stated otherwise.

A disordered thin-film morphology of 5000 CBP-molecules is generated by simulating physical vapor deposition, based on a Monte-Carlo (MC) protocol. During the deposition process, molecules are added to the simulation box (L_x = L_y = L_z = 90 Å) one after another where the flux of molecules is parallel to the z-axis and the xy-plane represents the surface of the substrate. The deposition simulation starts with a molecule at a random initial position, followed by 32 simulated annealing (SA) cycles. Within each SA-cycle, the molecules' conformation space is sampled by 130 000 MC-steps, where only molecule translations or rotations of a dihedral (alpha or beta) are considered. Based on a Metropolis criterion, MC moves are accepted and stored or rejected, where the temperature at MC-step n is given by T_n = T_scⁿ. The c = (T_e/T_s)^1/N determines the cooling rate as per MC step, T_s = 4000 K and T_e = 300 K denote the start- and end-temperature, respectively. After the SA-cycles are performed, the conformation with the lowest energy is accepted as the final conformation. Subsequently, the electrostatic and Lennard-Jones potential are updated. This procedure is repeated 5000 times until all molecules are deposited.⁴². After deposition, an equilibrium simulation of 2 ns at 300 K and 1 bar is performed to equilibrate the temperature and pressure. The Nose–Hoover thermostat⁴⁰ and Parrinello–Rahman barostat⁴³ are employed to obtain a reasonable canonical ensemble.

The absorption spectra of CBP in the condensed phase are simulated using two initial sampling methods, ensemble sampling and time-series sampling. In the former approach, the vertical excitation energies of 25 excited states are computed using TD-LC-DFTB for each monomer (5000 in total) in the equilibrated CBP supercell and summed up to generate the absorption spectra. In the time-series sampling, the absorption spectra are simulated using the structures of a specific CBP molecule in 5000 snapshots uniformly selected along 5 ns MD simulation. In both cases, the electrostatic effects from the environment on the excitation energies are considered by including the MM point charges in the DFTB calculation.

In the quantum mechanics/molecular mechanical molecular dynamics (QM/MM MD) simulations, the whole system is divided into a quantum mechanical (QM) region, containing only one CBP molecule treated by DFTB3 with 3OB parameter set, and molecular mechanical (MM) region, where the remaining CBP molecules are treated on a molecular mechanics (MM) level using the modified GAFF. The equilibrated supercell obtained from the classical MD simulation is used as a starting point for a 1 ns QM/MM simulation with a time step of 1 fs, where 5000 snapshots are taken as reference structures for the excited-state calculations of the CBP molecule in the QM region. The QM/MM MD simulations are performed with the GROMACS program package.⁴⁴ The excitation energy calculations including the effects of the electrostatic interactions from the environment are carried out with the DFTB+ program suite.²⁵ The experimental data⁴⁵ are digitized using the open-source tool WebPlotDigitizer.⁴⁶

The static and dynamic properties of molecular aggregations are described by the excitonic coupling between the excited states of monomers. Excitonic couplings are conventionally composed of the long-range Coulomb contributions and the short-range (exchange and overlap) contributions. In the present work, only the Coulomb contributions are considered and the complete evaluation of excitonic coupling is planned for the future. The Coulomb coupling can be determined as the interactions between the atomic transition charges of monomers.⁴⁷ The Coulomb coupling with the nearest neighbour is considered in the present study. The atomic transition charges are computed using the TD-LC-DFTB method implemented in the DFTB+ program suite.²⁵ Recently, TD-LC-DFTB excitonic couplings have been successfully benchmarked for rhodopsins and light-harvesting complexes.²⁰

3. Results and discussion

Optical properties of CBP have been studied in detail in a recent work,²⁸ where the performance of DFT approaches has been compared with GW-BSE estimates. As described for many other molecules, standard DFT-GGA and even several hybrid DFT functionals such as B3LYP or PBE0 suffer from the delocalization error, which renders their prediction for many molecules of interest unreliable. Especially for charge-transfer excited states, excitation energies are severely underestimated, which is also the case for CBP. Range-separated DFT functionals, however, can systematically improve the description of these states. In the following, TD-LC-DFTB will be tested and applied for the description of CBP excited states.

3.1 Bond length alternation and excitation energies

Excitation energies of conjugated organic molecules are very sensitive to the molecular structure. Dihedral angles and the BLA are two parameters which have a sizable impact on excitation energies. Recently, the importance of these structural details for excitation energies has been discussed in detail.²⁰ For CBP, different quantum chemical methods predict slight differences in the central geometrical parameters, as can be seen from Table 1. Further information regarding the bond lengths is provided in the Table. S1 (ESI†).

Table 1 Bond length alternation and dihedral angles for the CBP molecule optimized by various quantum chemistry methods. The bond length alternation is defined in Fig. 1(b)

	DFTB	MP2	PBE	B3LYP	ωB97XD	HF	FF
BLA	0.014	0.017	0.020	0.021	0.025	0.031	0.036
α	43.3	53.0	53.3	56.9	55.8	94.2	54.4
β	28.0	39.4	37.4	39.0	42.0	43.4	41.9
γ	0.0	0.0	0.0	0.0	0.0	0.3	0.0

---

DFTB gives the lowest value of BLA while HF leads to the highest BLA. The values for BLA obtained by hybrid methods lie in between due to the varying moderate amount of exact exchange.^20,48 This finding is in line with an earlier work on other conjugated molecules.²⁰ The method for optimization of the ground state structure has a notable impact on excitation energies, as can be seen in Fig. 2. The vertical excitation energies computed with various quantum chemistry methods for ground state geometries are provided in the Table S2 (ESI†).

Fig. 2 Influence of the applied methods on the computed vertical excitation energies. The x-axis shows the methods used to compute the ground state geometries; vertical excitation energies are then computed with various methods for these respective geometries. Note that, ADC(2) and GW-BSE are superimposed.

All methods show a slight variation with optimized structures, but differ significantly in absolute excitation energy values. As expected, HF/CIS overestimates the excitation energies for all optimized geometries, while the local and semi-local methods underestimate them due to the (semi-) local nature of the functionals. CC2, ADC(2) and GW-BSE are in excellent agreement with each other. The excitation energies computed by the range-separated ωB97XD method are slightly higher, as reported before, probably due to the amount of exact exchange used in this functional. LC-DFTB, similar to the LC-DFT methods, tends to overestimate excitation energies systematically, as has been shown for both ground state¹⁹ as well as excited-state⁴⁸ optimized geometries, representing absorption and fluorescence energies. Different range-separated functionals have been shown to differ slightly in their predictions, and the excellent absolute agreement of LC-DFTB in this matter can be regarded as fortuitous. For the calculation of absorption spectra, this will simplify the comparison with experimental data. However, more important is the fact that the effect of structural changes on excitation energies is represented accurately, which will be investigated in the following.

As can be seen from Table 1, the different methods predict variations in both, BLA and dihedral angles. As it will be discussed later, the values of the dihedral angles in the bulk are determined by the intermolecular interactions. For the isolated molecule, the rotational barriers (6.5 kcal mol⁻¹ and 3 kcal mol⁻¹ for central and side angles, respectively, see Fig. S1, ESI†) are low and can be overcome at room temperature; however, rotations may be constrained by the surrounding molecules in the bulk which stabilizes the rotamers. On the other hand, the BLA is found to impact excitation energies in conjugated molecules.²⁰ To estimate the effect of BLA on excitation energies, the CBP molecule in the gas phase is optimized with the side-, central- (α, β) and improper dihedral (γ) angles constrained to 45°, 60° and 0°, respectively. The optimizations are performed by ωB97XD/6-31+g*. As shown in Table 2, a clear pattern of increasing BLA with increasing amount of exact exchange is observed in the DFT methods, while the BLA tends to be more precisely predicted with MP2, since HF tends to overestimate this value.²⁸

Table 2 Bond lengths and bond-length alternation (BLA) for the constrained optimizations with the different methods. Bond length and BLA are given in Å

	Bond length [Å]							BLA
	C1=C2	C2–C3	C3=C4	C4–C5	C5=C6	C6–C7	C7=C8
FF	1.397	1.400	1.418	1.510	1.410	1.400	1.393	0.032
HF	1.376	1.383	1.391	1.490	1.391	1.383	1.386	0.030
ωB97XD	1.392	1.386	1.396	1.483	1.396	1.386	1.392	0.024
B3LYP	1.398	1.390	1.402	1.484	1.402	1.390	1.397	0.021
PBE	1.394	1.386	1.398	1.477	1.398	1.386	1.393	0.021
DFTB	1.406	1.392	1.407	1.487	1.407	1.393	1.406	0.018
MP2	1.403	1.395	1.407	1.476	1.407	1.395	1.403	0.017

---

The excitation energies follow the BLA trends, i.e. a blue shift with increasing BLA is observed, because the dihedral angles are the same for all methods and the vertical excitation energies only depend on the BLA. The vertical excitation energies can be found in the Fig. S2 and Table S3 (ESI†). A closer inspection of the bond lengths shows that the force field gives the least reliable estimates. In particular, the C–N bond-lengths deviate from the values computed by the other methods, which leads to a smaller excitation energy, as would be expected from the value of the BLA. Therefore, for the final estimation of absorption spectra, the QM/MM geometries using DFTB for the QM region are used. DFTB uses the PBE functional, and its geometrical prediction is therefore quite close to that of the other DFT methods, as discussed in detail in recent works.^20,49

3.2 Absorption spectra in gas phase

Recently, a detailed study on CPB electronic structure has been published based on the GW-BSE method, which is taken as a reference here.²⁸ The lower panel of Fig. 3 shows a comparison of the gas-phase absorption spectra of CBP using TD-DFTB, TD-LC-DFTB and the GW-BSE reference (using the global minimum geometry taken from ref. 28), respectively. As expected, TD-DFTB largely underestimates the excitation energies by about 1 eV, compared to GW-BSE, while TD-LC-DFTB reproduces the GW-BSE absorption spectrum well. The strong red-shift of TD-DFTB spectrum can be related to the well-known notorious self-interaction error of GGA functionals. It is not surprising that the introduction of long-range (LC) functionals in DFTB can reduce the errors of GGA, which leads to a good agreement between TD-LC-DFTB and GW-BSE spectra.

Fig. 3 Absorption spectra of CBP in the gas phase and Kohn–Sham orbitals involved in the main orbital transitions of CBP. TD-DFTB, TD-LC-DFTB and GW-BSE calculations are shown in purple, blue and green lines, respectively. The excited states calculations are based on the global minimum geometry taken from ref. 28.

The upper panel of Fig. 3 shows the main orbital transitions in the gas-phase absorption spectrum of CBP. Some other electron transitions are shown in Table S4 in the ESI.† The electron density of HOMO is delocalized over the whole molecule, while the lower occupied orbitals (HOMO−n, n = 2, 3, 5) exhibit a strong electron localization on the carbazole groups. The electron density of LUMO is localized on biphenyl rings, while the electron density of higher unoccupied orbitals (LUMO–n, n = 1, 2, 6) is localized on two carbazole groups. The peak at 308 nm corresponds to the charge transfer (CT) from the carbazole groups to biphenyl rings, which may be sensitive to the rotation of the central dihedral angle. Two higher energy excitations (<250 nm) are related to the locally excited states in the carbazole groups. Therefore, the rotation of central and side dihedral angles may have little impact on high energy excitations, while it affects the lowest excitation energy significantly.²⁸

To estimate the effect of dihedral angles on excitation energies, we compute the 25 lowest vertical excitation energies and consequently the absorption spectra for different central and side angles, respectively. The dihedral angles are incremented in 10° from 0 to 90° using the ground-state optimized structure at the PBE0/def2-TZVP as the starting structure, taken from ref. 28. For these structures, single-point energy calculations are carried out with TD-LC-DFTB and GW-BSE, respectively. Fig. 4(a) shows that for the central dihedral angles, the lowest-energy peak shifts from 3.91 eV to the higher energy at 4.15 eV and the intensity becomes lower with the increasing central angles, while the location and intensity of the high-energy peak at about 5.2 eV change slightly. Further information regarding the comparison between TD-LC-DFTB and GW-BSE excitation energies of the lowest-energy peaks, as well as the corresponding Kohn–Sham orbitals, is provided in the Tables S5 and S6 in ESI.† It is noted that for the central angle from 0 to 90°, the lowest-peak exhibits the excitation transition from charge-transfer excitation to local excitation.

Fig. 4 Absorption spectra computed by TD-LC-DFTB for different central (a) and side (b) dihedral angles.

Furthermore, Fig. 4(b) shows a weak, blue-shifted absorption band at the lowest-energy peak in comparison to the central dihedral angle. To quantify the variation found for the different dihedral angles, the standard deviation of the lowest-energy peak has been calculated for central dihedral angle (4.04 ± 0.09 eV), which is about 2 times larger than that for side dihedral angle (4.02 ± 0.05 eV). This finding is consistent with the recent study on the excited-state properties of CBP that the rotational conformation has significant impacts on the low-energy absorption band, while it has minor effects on high-energy bands.²⁸ Therefore, the CT-type excitation is more sensitive to the central dihedral angle than the side dihedral angle.

3.3 Absorption spectra in condensed phase using force field geometries

The absorption in the bulk phase critically depends on the distribution of dihedral angles of the individual molecules, which results from the intermolecular interactions. Different values of the dihedral angles can be stabilized by steric interactions, leading to static disorder in the system. Furthermore, it is expected that dynamic disorder will lead to an additional broadening of the absorption spectrum. In principle, both effects could be included by computing excitation energies along the trajectories of all molecules in the simulation box. Since this is computationally demanding, a stepwise procedure is followed, as described below. In order to get a sufficiently large sample of molecules, force field trajectories are used, and absorption energies along each trajectory are computed with TD-LC-DFTB. Then, the trajectories using DFTB/MM are computed in order to obtain spectra based on more accurate geometries.

For one MD-snapshot containing all 5000 molecules in the supercell, the absorption energy of the bulk is then computed by successively evaluating the excitation energy of every molecule in the sample using TD-LC-DFTB, surrounded by the others using electrostatic embedding. The total spectrum is then the overlay of all 5000 single molecule spectra, as shown in Fig. 5(a). It is noted that the absorption spectrum is identical with the spectrum computed without considering the electrostatic interactions from surrounding molecules, which indicates that the electrostatic effects have a negligible influence on the absorption spectrum (see Fig. S4 in the ESI†). As shown in Fig. 5(b), the static disorder is characterized by a significant spread in the distribution of the dihedral angles. The maxima of the α- and β-dihedral angles are around 60 and 40 degrees, respectively, consistent with the values of α and β for the structure optimized by ωB97XD method in the gas phase. As expected from Fig. 4, planarization of the molecule will lead to a red shift in the lowest absorption band, which is reflected in the absorption spectrum of the ensemble snapshot (red dashed line in Fig. 5(a)). It is red-shifted by 0.09 eV compared to the gas-phase spectrum of the optimized molecule in Fig. 3.

Fig. 5 (a) Absorption spectra for the ensemble-snapshot of 5000 molecules (ensemble, displayed top at the left) and for the 5 ns trajectories of the three molecules picked from the ensemble. (b) Distribution of dihedral angles obtained for the ensemble and along the time-series of the three individual molecules. Note that the molecule is not symmetric and therefore a presentation 0°–90° is not appropriate.

3.3.1 Absorption spectra along trajectories of individual molecules. To investigate the impact of dynamic disorder, three molecules (referred to as M1, M2 and M3) are selected at random positions of the supercell. Afterwards, absorption spectra are computed on a 5 ns classical MD trajectories and excitation energies are evaluated for snapshots every 1 ps, resulting in 5000 conformations in total. As shown in Fig. 5(a), the absorption spectra of M1, M2 and M3 are quite close to the absorption spectrum computed based on the ensemble sampling. Fig. 5(b) shows the comparison of the angle distributions of side and central dihedrals for M1 to M3 with the angle distributions of the ensemble. For the canonical ensemble, it is seen that the mean values of the central angle distribution are at 40° and 140°, and the mean values of the side angle distribution are at 60° and 120°. The angle distributions for M1 to M3 only exhibit one peak, showing that free rotation of the dihedral angles is impossible and the fluctuations are constrained to a limited range. It is interesting to see that individual monomers sample only a restricted part of phase space. The results on the ns time scale indicate that the computation of absorption spectra needs to be performed using longer-simulation-time trajectories until convergence. Therefore, using the same starting configurations, the classical MD trajectory is extended to 10 ns and excitation energies are evaluated for snapshots every 2 ps, leading to 5000 conformations in total. The convergence behavior is observed for M2 and M3 using the 10 ns-trajectory, whereas M1 is not converged and its respective angle distribution (mean value = 30°) is different from those obtained for M1 in the 5 ns trajectory (mean value = 40°) (see Fig. 6) which will lead to a stronger red shift and increased intensities of spectrum. In order to get further insight into the sampling methods, the absorption spectra as well as central angle distribution are examined for snapshots of molecule M1 at each nanosecond (Fig. 7). The importance of the central dihedral angle compared to the side dihedral angle on the CT-type excitation is demonstrated in Section 3.2. As shown in Fig. 7(b), the mean value of the central dihedral angle between 1–5 ns of the trajectory is around 35° whereas between 5–10 ns is around 20°.

Fig. 6 (a) Absorption spectra and (b) distribution of dihedral angles for the ensemble-snapshot of 5000 molecules and molecules M1, M2 and M3 obtained by a 10 ns trajectory.

Fig. 7 Absorption spectra (a) and central dihedral angle distributions (b) for each ns MD simulation in a 10 ns trajectory of molecule M1.

As shown in Fig. 3, the lowest absorbance peak is located at 4 eV for the optimized structure in the gas phase, while in the condensed phase it is red-shifted by about 0.3 eV (Fig. 5a). In principle, there are several factors determining the absorption maximum, which are (i) the dihedral angles, (ii) the electrostatic environment, (iii) and the exciton couplings. It is shown in ESI† (see Fig. S4) that the electrostatic environment has a minor effect on the absorption spectrum. In the following, the effect of the other two factors will be assessed individually.

3.3.2 Comparison to gas-phase MD spectrum. To estimate the effect of the molecular interactions within the bulk, a MD simulation of CBP in the gas phase is performed, and the excitation energies along this trajectory are computed. Fig. 8(a) shows a comparison of absorption spectra of CBP for 5000 conformations from gas-phase MD and 5000 structures from one condensed-phase MD-snapshot. The lowest-absorbance peak in the condensed-phase spectrum exhibits a red shift of 0.05 eV in comparison with the gas-phase MD spectrum. This is consistent with the central/side dihedral angle distribution shown in Fig. 4, i.e., more conformations with smaller angles occur in the condensed phase than in the gas phase. This indicates that intermolecular interactions in the bulk have a moderate influence on the absorption spectrum of CBP. The difference is not due to the electrostatic effect, but due to the accessible phase space. In the gas-phase MD, the molecule can sample the full angular degrees of freedom, since rotational barriers can be overcome at room temperature. However, in condensed phase molecules may be more restrained, leading to a narrower angular distribution. Since in the bulk, the molecules sample more planar structures, a red-shift of the spectrum is observed (see Fig. 4).

Fig. 8 (a) Absorption spectra of CBP obtained using the conformations from gas-phase MD (blue line) and one condensed-phase MD-snapshot (red line) and (b) the corresponding central and side dihedral angle distributions.

3.3.3. Effects of rotational conformation. The distribution of dihedral angles for the amorphous ensemble containing 5000 molecules (Fig. 5(b)) is split into 6 categories, where each category represents molecules with dihedral angles in increment of 30°. To obtain good statistics, the absorption spectra of each category from 0° to 90° and their complementary categories from 90 to 180 degrees are merged, e.g., structures with dihedral angles of 0°–30° and 150°–180° are pooled together. Fig. 9 shows the partial absorption spectra of dihedral angles for all 3 pooled categories: Category 1: 0°–30° and 150°–180°, Category 2: 30°–60° and 120°–150° and Category 3: 60°–90° and 90°–120°. For the central dihedral angle at the peak with the lowest energy, as the angle gets closer to 0° (i.e., the planarity of biphenyl increases), the spectrum becomes more red-shifted and the intensity increases. Furthermore, it seems there are additional peaks around 4.4 and 5.4 eV for Category 3. For the side dihedral angle, it seems there is no dependency between intensity and dihedral angles. It is also noted that the curve for the side dihedral angle in Category 1 is not smooth due to the low sample size.

Fig. 9 Partial absorption spectra of (a) central and (b) side dihedral angles are shown for three categories, 0°–30° and 150°–180° (blue), 30°–60° and 120°–150° (green) and 60°–90° and 90°–120° (red).

3.4 Absorption spectra for QM/MM sampling

As discussed above, the structures of a single molecule over a long simulation time are unable to represent all structures in the phase space. The snapshot of the ensemble, on the other hand, includes static disorder but misses the explicit treatment of dynamic disorder, which can be obtained by analysing MD trajectories. To investigate how many molecules are sufficient to represent the ensemble, 3 sets of molecules containing 10, 20 and 50 molecules are randomly selected from different locations of the supercell. A 5 ns long NPT MD simulation is performed. From this trajectory 500, 250 and 100 snapshots are taken for these 3 sets of molecules, respectively, to maintain the same number of structures in every test set. The convergence test with respect to the number of molecules (Fig. S5, ESI†) shows that 50 molecules is sufficient to obtain converged angle distributions as well as a converged absorption spectrum.

As discussed in Section 3.1, DFTB gives a reasonably accurate estimation for the bond lengths in CBP molecules. Here, the QM/MM simulations are performed for amorphous CBP, where 50 molecules randomly distributed in the CBP supercell are treated by DFTB/3OB while the remaining molecules of the system are treated by the modified force field. Fig. 10(a) shows the comparison of the experimental absorption spectrum of CBP⁴⁵ with the absorption spectrum using the structures from QM/MM simulations and 5000 conformations from one MD-snapshot, respectively. The QM/MM simulation reproduces the peaks of the experimental absorption spectrum of CBP quite well. The experimental spectrum is much broader than the computed spectrum., which may be due to the defect absorption in the CBP film. A key ingredient of this good agreement for the absorption peaks is the (fortuitous) accuracy of LC-DFTB for the CBP excited states, as discussed above, which allows us to compute absolute excitation energies in this case. In particular, the BLA is sufficiently well represented by the ground state DFTB/MM calculations. In comparison to the spectrum based on the FF geometries, the lowest-energy peak of the QM/MM absorption spectrum exhibits a red shift of 0.2 eV. The red-shift of excitation energy can be attributed to the smaller BLA using GGA-type DFT method,⁵⁰ in comparison to the BLA obtained by the parameterized force field. (see Table 2). In addition, there is a slight deviation in the description of the angular distribution. Fig. 10(b) shows the angle distributions of CBP monomers obtained by MD and QM/MM simulations, respectively. MD simulation with modified force field generates fewer molecules with angles smaller than 30° (larger than 150°) than DFTB/MM simulation, which indicates a more planarity of CBP conformations obtained by DFTB than force field.

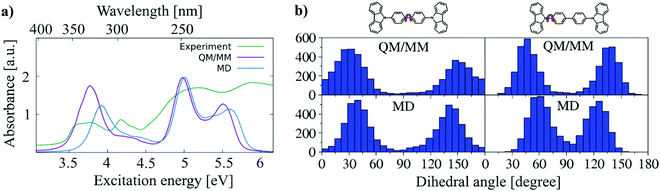Fig. 10 (a) A comparison of the experimental absorption spectrum of CBP taken from ref. 45 with the absorption spectra obtained using the structures from QM/MM simulations and one condensed-phase MD-snapshot. (b) Central and side dihedral angle distributions obtained by QM/MM (upper panel) and MD (lower panel) simulations.

3.3.5 Effects of aggregation. It is well known that the aggregation of chromophores has a significant influence on the absorption spectrum.^51–54 Delocalization of excited states over two or more molecules could lead to a further red-shift of adsorption spectrum. To examine the aggregation effect on the absorption spectrum of CBP, we compute the nearest-neighbor excitonic coupling, which is an important quantity to describe the extent of molecular aggregation. For all 5000 nearest neighbours, those dimers which are doubly counted (28 dimers), are removed. As shown in Fig. 11(a), the excitonic couplings exhibit a broad distribution with the average value of 30 meV, which indicates a weak aggregation effect in amorphous CBP. Moreover, all 4972 dimers are split into three categories with the excitonic couplings J < 30, 30 < J < 60 and J > 60 meV, where each contains 4226, 682 and 64 dimers, respectively. Afterwards, 25 excitation energies for each CBP monomer and 70 excitation energies for each CBP dimer are computed, in each respective category.

Fig. 11 (a) Nearest-neighbor excitonic coupling distributions. (b) Excitonic coupling dependent absorption spectra of monomers (solid lines) and dimers (dashed lines). (c) Central and side dihedral angle distributions.

The absorption spectra are shown in Fig. 11(b). The low energy part of the monomer absorption spectra is very close to that of the dimer absorption spectra, for all coupling strengths, i.e., there is no indication for a substantial delocalization of excited states. The small couplings of J < 100 meV is in the same range with the dynamical disorder, i.e., the dynamical disorder enforces localization. This is indicated by the fact that the excitation energies computed for monomers and dimers in every class are very similar. If a coupling of the low energy states occurred, an additional red-shift would be expected. Nevertheless, it is very interesting to see that a red-shift occurs which correlates with the coupling strength, although this cannot be induced by electronic delocalization. The results can be interpreted as follows: High excitonic couplings may indicate that dimers are stacked very well. This stacking induces conformations more shifted towards planar conformations, as shown in Fig. 11(c), and more planar conformations lead to a red-shift in the absorption spectrum.

4 Conclusions

The absorption spectrum of CBP molecules is significantly altered in the amorphous phase due to interactions among the monomers. While electrostatic interactions as well as excitonic couplings turn out to be of minor importance, structural effects, in particular torsion around the main dihedral angles play a major role. Steric interactions induce a planarization of the molecules in the ensemble, which leads to an absorption red-shift of about 0.3 eV w.r.t. a gas phase absorption spectrum.

Conformational sampling is a key to capture the static and dynamic disorder in the system. Due to the packing in the amorphous phase, the individual monomers show only restricted motions, however, relevant conformational changes appear also on the nanosecond timescale, which requires efficient sampling techniques.

Standard force field parameters have to be taken with some care; we found that a major reparametrization of dihedral potentials is required for a realistic model of the amorphous structure. If these important degrees of freedom are modelled too soft or too stiff, the molecular ensembles may be largely misrepresented, since certain parts of the conformational space may be under- or oversampled. This, however, would show up in the absorption spectrum, since excitation energies are very sensitive to these degrees of freedom.

Our simulations could successfully reproduce the experimental absorption spectrum which may indicate that our structural model is quite accurate. We can deduce this from the computed spectrum, since the applied LC-DFTB method very accurately reproduces the excitation energies of high-level quantum chemical methods as GW-BSE, CC2 or ADC(2). Further, the ground state structures have been sampled with DFTB, which shows a very good agreement for the molecular structures, particularly, for the BLA.

The structural model derived here will be used in future work to investigate charge and exciton transfer processes in CBP, which will allow study of the processes behind the degradation of this material.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the support by the German Research Foundation (DFG) through the Research Training Group 2450 “Tailored Scale-Bridging Approaches to Computational Nanoscience”. Additional support from the state of Baden Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/467-1 FUGG (JUSTUS cluster) is appreciated.

References

1. Q. Wang, B. Sun and H. Aziz, Exciton–Polaron-Induced Aggregation of Wide-Bandgap Materials and Its Implication on the Electroluminescence Stability of Phosphorescent Organic Light Emitting Devices, Adv. Funct. Mater., 2014, 24, 2975–2985.
2. R. Braveenth, H. Jung, K. Kim, B. M. Kim, J. Bae, M. Kim and K. Y. Chai, Fluorene Triphenylamine-Based Bipolar Materials: Fluorescent Emitter and Host for Yellow Phosphorescent OLEDs, Appl. Sci., 2020, 10(2), 519.
3. T. Ito, H. Sasabe, Y. Nagai, Y. Watanabe, N. Onuma and J. A. Kido, Series of Dibenzofuran-Based n-Type Exciplex Host Partners Realizing High-Efficiency and Stable Deep-red Phosphorescent OLEDs, Chem. – Eur. J., 2019, 25, 7308–7314.
4. J. Kido, M. Kimura and K. Nagai, Multilayer White Light-Emitting Organic Electroluminescent Device, Science, 1995, 267, 1332–1334.
5. R. Braveenth, H. W. Bae, I. J. Ko, W. Qiong, Q. P. B. Nguyen, P. G. S. Jayashantha, J. H. Kwon and K. Y. Chai, Thermally Stable Efficient Hole Transporting Materials Based on Carbazole and Triphenylamine Core for Red Phosphorescent OLEDs, Org. Electron., 2017, 51, 463–470.
6. B. M. Kim, Q. P. B. Nguyen, J. G. Fan, M. J. Kim, R. Braveenth, G. W. Kim, G. J. H. Kwon and K. Y. Chai, Novel Star-Shaped Hole-Transporting Materials Based on Triphenylamine Cores End-Capped with Carbazole and Triarylamine Derivatives for Use in Oleds, Bull. Korean Chem. Soc., 2015, 36, 1303–1306.
7. Y. Tao, C. Yang and J. Qin, Organic Host Materials for Phosphorescent Organic Light-Emitting Diodes, Chem. Soc. Rev., 2011, 40, 2943–2970.
8. J.-X. Chen, W.-W. Tao, Y.-F. Xiao, S. Tian, W.-C. Chen, K. Wang, J. Yu, F.-X. Geng, X.-H. Zhang and C.-S. Lee, Isomeric Thermally Activated Delayed Fluorescence Emitters Based on Indolo[2,3-b] Acridine Electron-Donor: A Compromising Optimization for Efficient Orange–Red Organic Light-Emitting Diodes, J. Mater. Chem. C, 2019, 7, 2898–2904.
9. P. Strohriegl and J. Grazulevicius, Charge-Transporting Molecular Glasses, Adv. Mater., 2002, 14, 1439–1452.
10. R. Schmechel and H. von Seggern, Electronic traps in organic transport layers, Phys. Status Solidi A, 2004, 201, 1215–1235.
11. Y. Zhang and H. Aziz, Influence of the Guest on Aggregation of the Host by Exciton–Polaron Interactions and Its Effects on the Stability of Phosphorescent Organic Light-Emitting Devices, ACS Appl. Mater. Interfaces, 2016, 8(22), 14088–14095.
12. M. Elstner and G. Seifert, Density functional tight binding, Philos. Trans. R. Soc., A, 2014, 372, 20120483.
13. T. Kubař, Z. Bodrog, M. Gaus, C. Köhler, B. Aradi, T. Frauenheim and M. Elstner, Parametrization of the SCC-DFTB Method for Halogens, J. Chem. Theory Comput., 2013, 9(7), 2939–2949.
14. T. Niehaus, Approximate time-dependent density functional theory, THEOCHEM, 2009, 914, 38–49.
15. J. P. Perdew, M. Ernzerhof and K. Burke, Rationale for mixing exact exchange with density functional approximations, J. Chem. Phys., 1996, 105, 9982–9985.
16. T. Kubař, P. B. Woiczikowski, G. Cuniberti and M. Elstner, Efficient Calculation of Charge-Transfer Matrix Elements for Hole Transfer in DNA, J. Phys. Chem. B, 2008, 112(26), 7937–7947.
17. Q. Cui, M. Elstner, E. Kaxiras, T. Frauenheim and M. Karplus, A QM/MM Implementation of the Self-Consistent Charge Density Functional Tight Binding (SCC-DFTB) Method, J. Phys. Chem. B, 2001, 105, 569–585.
18. V. Q. Vuong, J. A. Kuriappan, M. Kubillus, J. J. Kranz, T. Mast, T. A. Niehaus, S. Irle and M. Elstner, Parametrization and Benchmark of Long-Range Corrected DFTB2 for Organic Molecules, J. Chem. Theory Comput., 2018, 14(1), 115–125.
19. J. J. Kranz, M. Elstner, B. Aradi, T. Frauenheim, V. Lutsker, A. D. Garcia and T. A. Niehaus, Time-Dependent Extension of the Long-Range Corrected Density Functional Based Tight-Binding Method, J. Chem. Theory Comput., 2017, 13, 1737–1747.
20. B. M. Bold, M. Sokolov, S. Maity, M. Wanko, P. M. Dohmen, J. J. Kranz, U. Kleinekathofer, S. Hofener and M. Elstner, Benchmark and Performance of Long-Range Corrected Time-Dependent Density Functional Tight Binding (LC-TD-DFTB) on Rhodopsins and Light-Harvesting Complexes, Phys. Chem. Chem. Phys., 2020, 22, 10500.
21. Y. Tao, C. Yang and J. Qin, Organic host materials for phosphorescent organic light-emitting diodes, Chem. Soc. Rev., 2011, 40, 2943–2970.
22. Y. Shirota and H. Kageyama, Charge Carrier Transporting Molecular Materials and Their Applications in Devices, Chem. Rev., 2007, 107, 953–1010.
23. M. Gaus, A. Goez and M. Elstner, Parametrization and Benchmark of DFTB3 for Organic Molecules, J. Chem. Theory Comput., 2013, 9(1), 338–354.
24. N. Schieschke, B. M. Bold, P. M. Dohmen, D. Wehl, M. Hoffmann, A. Dreuw, M. Elstner and S. Höfener, Geometry dependence of excitonic couplings and the consequences for configuration-space sampling, J. Comput. Chem., 2021, 42, 1402.
25. B. Hourahine, B. Aradi, V. Blum, F. Bonafe, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Kohler, T. Kowalczyk, T. Kubar, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Rezac, C. G. Sanchez, M. Sternberg, M. Stohr, F. Stuckenberg, A. Tkatchenko, V. W.-z. Yu and T. Frauenheim, DFTB +, a software package for efficient approximate density functional theory based atomistic simulations, J. Chem. Phys., 2020, 152, 124101.
26. TURBOMOLE V7.4 2019, A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, (1989–2007), TURBOMOLE GmbH, since 2007. http://www.turbomole.com.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, A. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
28. R. Cortés-Mejía, S. Höfener and W. Klopper, Effects of rotational conformation on electronic properties of 4,4′-bis(carbazol-9-yl)biphenyl (CBP): the single molecule picture and beyond, Mol. Phys., 2021, 119, 8.
29. K. Krause and W. Klopper, Implementation of the Bethe−Salpeter equation in the TURBOMOLE program, J. Comput. Chem., 2017, 38, 383–388.
30. X. Gui, C. Holzer and W. Klopper, Accuracy Assessment of GW Starting Points for Calculating Molecular Excitation Energies Using the Bethe–Salpeter Formalism, J. Chem. Theory Comput., 2018, 14(4), 2127–2136.
31. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
32. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
33. A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577.
34. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174.
35. J. Wang, W. Wang, P. A. Kollman and D. A. Case, Automatic atom type and bond type perception in molecular mechanical calculations, J. Mol. Graphics Modell., 2006, 25, 247–260.
36. U. C. Singh and P. A. Kollman, An approach to computing electrostatic charges for molecules, J. Comput. Chem., 1984, 5, 129–145.
37. B. H. Besler, K. M. Merz and P. A. Kollman, Atomic charges derived from semiempirical methods, J. Comput. Chem., 1990, 11, 431–439.
38. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements, J. Chem. Phys., 1988, 89, 2193–2218.
39. G. A. Petersson and M. A. Al-Laham, A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms, J. Chem. Phys., 1991, 94, 6081–6090.
40. D. J. Evans and B. L. Holian, The Nose-Hoover thermostat, J. Chem. Phys., 1985, 83, 4069.
41. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4:  Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4(3), 435–447.
42. T. Neumann, D. Danilov, C. Lennartz and W. Wenzel, Modeling disordered morphologies in organic semiconductors, J. Comput. Chem., 2013, 34.
43. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52, 7182–7190.
44. T. Kubař, K. Welke and G. Groenhof, New QM/MM Implementation of the DFTB3 Method in the Gromacs Package, J. Comput. Chem., 2015, 36, 1978–1989.
45. L. Zhou, H. Zhang, R. Deng, Z. Li, J. Yu and Z. Guo, Conversion process of the dominant electroluminescence mechanism in a molecularly doped organic light-emitting device with only electron trapping, J. Appl. Phys., 2007, 102, 064504.
46. A. Rohatgi, Webplotdigitizer: Version 4.2, (2019). https://automeris.io/WebPlotDigitizer.
47. P. A. Plötz, T. Niehaus and O. Kühn, A new efficient method for calculation of Frenkel exciton parameters in molecular aggregates, J. Chem. Phys., 2014, 140, 174101.
48. M. Sokolov, B. M. Bold, J. J. Kranz, S. Hofener, T. Niehaus and M. Elstner, Analytical Time-Dependent Long-Range Corrected Density Functional Tight Binding (TD-LC-DFTB) Gradients in DFTB +: Implementation and Benchmark for Excited-State Geometries and Transition Energies, J. Chem. Theory Comput., 2021, 17(4), 2266–2282.
49. M. Wanko, M. Hoffmann, P. Strodel, A. Koslowski, W. Thiel, F. Neese, T. Frauenheim and M. Elstner, Calculating Absorption Shifts for Retinal Proteins:  Computational Challenges, J. Phys. Chem. B, 2005, 109(8), 3606–3615.
50. M. E. Madjet, A. Abdurahman and T. Renger, Intermolecular Coulomb Couplings from Ab Initio Electrostatic Potentials:  Application to Optical Transitions of Strongly Coupled Pigments in Photosynthetic Antennae and Reaction Centers, J. Phys. Chem. B, 2006, 110(34), 17268–17281.
51. C. Olbrich, T. L. C. Jansen, J. Liebers, M. Aghtar, J. Strümpfer, K. Schulten, J. Knoester and U. Kleinekathöfer, From Atomistic Modeling to Excitation Transfer and Two-Dimensional Spectra of the FMO Light-Harvesting Complex, J. Phys. Chem. B, 2011, 115(26), 8609–8621.
52. Q. Wang and H. Aziz, Exciton-polaron-induced aggregation of organic electroluminescent materials: a major degradation mechanism in wide-bandgap phosphorescent and fluorescent organic light-emitting devices, Adv. Opt. Mater., 2015, 3, 967–975.
53. K.-Y. Ju, M. C. Fischer and W. S. Warren, Understanding the Role of Aggregation in the Broad Absorption Bands of Eumelanin, ACS Nano, 2018, 12(12), 12050–12061.
54. G. R. Suman, M. Pandey and A. S. J. Chakravarthy, Review on new horizons of aggregation induced emission: from design to development, Mater. Chem. Front., 2021, 5, 1541.
55. M. J. van Setten, F. Weigend and F. Evers, The GW-Method for Quantum Chemistry Applications: Theory and Implementation, J. Chem. Theory Comput., 2013, 9(1), 232–246.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04293a

---