Dual nature of high-temperature electronic transport in layered perovskite-like cobaltites: exhaustive consideration of experimental features observed†
B. V.
Politov
ab and
A. Yu.
Suntsov
 *a
*a
aInstitute of Solid State Chemistry UB RAS, Yekaterinburg, Russia. E-mail: suntsov@ihim.uran.ru
bInstitute of Solid State Chemistry and Mechanochemistry of SB RAS, Novosibirsk, Russia
First published on 9th December 2021
Abstract
Complex oxides with the general formula Pr1−xYxBaCo2−yNiyO6−δ (x = 0, 0.1, y = 0, 0.2) were successfully synthesized via combustion of organo-metallic precursors. The high-temperature dc conductivity of the obtained sintered materials was studied in a wide range of oxygen partial pressures and temperatures by means of the 4-probe method. The resulting dependencies were juxtaposed with the previously published data on oxygen non-stoichiometry for the oxides considered. The comprehensive analysis of these datasets in attempts to explain the observed trends has shown the large inadequacy of currently existing conduction models. Consequently, a new model approach was developed to account for the numerous experimental and theoretical peculiarities being characteristic for the cobaltites with a layered double perovskite structure. One of the key propositions made postulates mixed nature of the band structure for materials studied with spin states of Co ions acting as a spatial descriptor of a particular type of conductivity: semiconducting or a metallic one. The abovementioned hypothesis was validated by magnetic, thermodynamic and structural arguments obtained both theoretically and experimentally. The models suggested were shown to be adequate in describing large arrays of data collected. Additionally, the reasons behind doping and temperature/pressure influences on the respective conductivity changes in Pr1−xYxBaCo2−yNiyO6−δ were uncovered. Transport and thermodynamic parameters determined were used to evaluate transference numbers and mobilities of different charge carriers which revealed the dominating role of metallic conductivity under oxidative conditions and the superiority of semiconducting charge transport in reducing environments. The obtained conclusions were further supported by utilizing the derived model equations for successful description of conductivity/non-stoichiometry data for other layered cobaltites. Also, interesting correlations between cation composition, thermodynamic and transport properties were found. Finally, general review of the formulated approach was made and further research directions were proposed.
1. Introduction
To date, 3d-metal complex oxides are widely recognized as materials possessing a unique variety of physical properties including but not limited to specific magnetic orderings, superconductivity, sufficient non-stoichiometry, colossal magnetoresistance and enormous catalytic activity.1–5 Among these compounds, layered perovskites of the formula LnBaCo2O6−δ, where Ln denotes a lanthanide element, seem to be especially remarkable: they combine interesting magnetization properties and high catalytic efficiency towards oxygen reduction/oxidation under standard thermodynamic conditions with a significant level of mixed ionic and electronic conductivity at elevated temperatures.6–11 All of these are strongly interrelated with oxygen non-stoichiometry δ which can acquire values corresponding up to 20 at% of emptied sites per oxygen sublattice.12 To add, a specific ordering between Ba and Ln cations along the c-axis forces a perovskite-like structure to be transformed into a layered one, thus providing strong anisotropy of magnetization, charge transport and oxygen ion migration.13–16 The respective combination of structure-mediated functional properties in LnBaCo2O6−δ provides an exciting field for the design of new materials and applications. However, theoretical understanding of the mechanisms underlying each particular property remains unclear and all obtained experimental results can be explained from different points of view. Interestingly, when considering the processes of high-temperature electrical transport in LnBaCo2O6−δ oxides, theoretical inconsistencies are especially manifested. It is worth noting that the latter property (i.e. conductivity) is of extreme importance for practical application in high-temperature electrochemistry and the knowledge of actual regularities governing conductivity variations with external factors (temperature, doping, etc.) appears to be quite valuable.It should be stressed at this point that the understanding of ionic conduction appears to be the most agreed upon as compared to the electronic conduction.13,17–21 Contrary to that, the picture of high-temperature electronic transport in LnBaCo2O6−δ is definitely more complex. The only existing agreement on this question postulates that –O–Co–O– chains in LnBaCo2O6−δ crystal structure are responsible for electric current conduction as in the case of other cobaltites.22–24 However, further deepening into the problem gives rise to numerous contradictions. For instance, most studies reported that the oxides from the LnBaCo2O6−δ family are characterized by elevated values of total conductivity exceeding 500 S cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7,25 which is comparable with metallic systems. The respective magnitude is usually achieved when the particular compound is heated above the metal–insulator (MI) transition point which often lies below 300 K. However, some authors claim that there exists another transition from semiconductor-type to metallic behavior observed near 673–773 K.26 As a result, there is no general agreement on the band structure of LnBaCo2O6−δ and even on the nature of carriers transporting electrical current. Careful analysis of available literature distinguishes a set of contradictory reports concerning the band gap value of these compounds. Most studies classify LnBaCo2O6−δ oxides as p-type semiconductors with a relatively small band gap not exceeding 0.3 eV27 while there are some reports claiming that the respective value equals 1.5 eV.28 At the same time, recent measurements by ultraviolet-visible spectroscopy (UV-Vis) resulted in extra large band gap values of 3.3 eV being characteristic for the insulator.29 Simultaneously, a number of studies give evidence for the metallic nature of charge transfer which is characterized by itinerant carriers, the absence of band gap and is strongly supported by Hall effect measurements.30,31 It should be also noted that the temperature increase is considered as a key factor for partial delocalization of cobalt electronic states in double cobaltites.32 Moreover, some additional questions naturally arise after the literature analysis. For example, if p-type semiconducting transport is dominating in LnBaCo2O6−δ at temperatures above the MI transition point the experimentally observed negative values of the thermopower33 require comprehensive and consistent explanation. The localization degree of charge carriers is also unclear. Additional difficulty here is linked with variable oxygen stoichiometry in LnBaCo2O6−δ oxides which starts to change near 500 K and sufficiently depends on external conditions. Hence, the transport properties of layered cobaltites at elevated temperatures are also affected by δ variations which was directly shown in numerous works.28,30,34 Finally, a recent study of monocrystalline EuBaCo2O6−δ samples indicates the existence of strong anisotropy of electronic conduction.33 Some efforts aimed to resolve the problems mentioned are collected below.
7,25 which is comparable with metallic systems. The respective magnitude is usually achieved when the particular compound is heated above the metal–insulator (MI) transition point which often lies below 300 K. However, some authors claim that there exists another transition from semiconductor-type to metallic behavior observed near 673–773 K.26 As a result, there is no general agreement on the band structure of LnBaCo2O6−δ and even on the nature of carriers transporting electrical current. Careful analysis of available literature distinguishes a set of contradictory reports concerning the band gap value of these compounds. Most studies classify LnBaCo2O6−δ oxides as p-type semiconductors with a relatively small band gap not exceeding 0.3 eV27 while there are some reports claiming that the respective value equals 1.5 eV.28 At the same time, recent measurements by ultraviolet-visible spectroscopy (UV-Vis) resulted in extra large band gap values of 3.3 eV being characteristic for the insulator.29 Simultaneously, a number of studies give evidence for the metallic nature of charge transfer which is characterized by itinerant carriers, the absence of band gap and is strongly supported by Hall effect measurements.30,31 It should be also noted that the temperature increase is considered as a key factor for partial delocalization of cobalt electronic states in double cobaltites.32 Moreover, some additional questions naturally arise after the literature analysis. For example, if p-type semiconducting transport is dominating in LnBaCo2O6−δ at temperatures above the MI transition point the experimentally observed negative values of the thermopower33 require comprehensive and consistent explanation. The localization degree of charge carriers is also unclear. Additional difficulty here is linked with variable oxygen stoichiometry in LnBaCo2O6−δ oxides which starts to change near 500 K and sufficiently depends on external conditions. Hence, the transport properties of layered cobaltites at elevated temperatures are also affected by δ variations which was directly shown in numerous works.28,30,34 Finally, a recent study of monocrystalline EuBaCo2O6−δ samples indicates the existence of strong anisotropy of electronic conduction.33 Some efforts aimed to resolve the problems mentioned are collected below.
The most simple electronic transport model for LnBaCo2O6−δ materials implies only one type of charge carriers which are assumed to be p-type small polarons.35 Accordingly, the obtained data array on PrBaCo2O6−δ conductivity was analyzed via isoconcentrational (δ = const) temperature dependencies fitted to the Arrhenius-like equations. The resulting activation energies were shown to be 0.04–0.06 eV in reasonable agreement with the suggested mechanism of conduction. Later on, this model was partially corrected so as to account for the so-called spin-blockade phenomena when some Co3+ sites become unavailable for polaron hopping at high temperatures.36 Also, the concentration of p-type carriers was included in an explicit form in the model equations. The discussed theoretical approach was shown to successfully explain the functional dependencies of PrBaCo2O6−δ conductivity in both reducing and oxidative environments.36 However, the derived mobility values appear to be too high for polaronic conduction.37 Also, no adequate description was suggested for the respective data in a wider domain of external conditions.38,39 Vollestad and coauthors30 proposed the two-band conduction mechanism for double perovskites Gd0.8La0.2+xBa1−xCo2O6−δ comprising highly mobile p-type carriers in the broad O 2p-band and less mobile n-type carriers in a partially occupied σ*-band formed by degenerate spin states of Co 3d electrons. Here and thereon we’ll refer to this model as the “Vollestad model”. Despite reasonable fitting results achieved extremely small values of the Seebeck coefficient were observed and unexplained. Also, no reasonable elucidation of the conditions governing the actual contribution of each carrier to the overall conductivity was suggested. Contrary to the reports previously discussed, the model proposed in ref. 34 (we’ll further refer to it as the “Tsvetkov model”) explains the peculiarities of GdBaCo2O6−δ electronic conductivity changes with temperature and oxygen non-stoichiometry as a result of competition between n- and p-type small polarons with the former possessing higher mobilities as compared to the latter. Although the Tsvetkov model successfully describes the observed thermopower values in GdBaCo2O6−δ, the measured magnitude of total conductivity sufficiently deviates from that reported in other works.26 Also, no band structure was suggested, as well as no physical reasons for p-type over n-type dominance were provided. To add, all the models considered do not account for the anisotropy of electronic conduction in layered cobaltites.
In order to gain a deeper understanding of electronic transport mechanisms in LnBaCo2O6−δ compounds and to explain the contradictions raised we have conducted a comprehensive analysis based on a combination of experimental methods including d.c. electrical conductivity measurements, SEM and magnetochemistry coupled with the features of defect equilibrium and crystal structure at elevated temperatures with PrBaCo2O6−δ (PBC) chosen as a test object. To confirm the validity of the obtained results we’ve also studied the influence of doping on the respective properties. As a final remark, we’ve reexamined all conductivity data existing in the literature so as to draw some general conclusions and propose further research directions in the area.
2. Experimental
PBC, Pr0.9Y0.1BaCoO6−δ (PYBC), PrBaCo1.8Ni0.2O6−δ (PBCN) and Pr0.9Y0.1BaCo1.8Ni0.2O6−δ (PYBCN) oxides were synthesized by means of glycerol–nitrate synthesis in full accordance with the earlier reported procedures.12,40,41 The phase composition and crystal structure of the obtained powdered samples were examined via XRD method. The respective oxygen content in oxides considered was determined with the help of thermogravimetric analysis under reduction as described earlier.37 The magnetic properties of the synthesized cobaltites were studied using a VSM-5 magnetometer in the 5–300 K temperature range at an applied field of 5 T. In order to perform conductivity measurements, the specimens were uniaxially pressed into thick disks which were further sintered at 1423 K for 10 hours with subsequent slow cooling down to room temperature. The quality of the ceramics produced was controlled via scanning electron microscopy (SEM) in conjunction with energy dispersive X-ray (EDX) analysis. The relative porosity of the sintered samples was assessed using the color binarization procedure as implemented in ImageJ software.42 10 individual images were analyzed for each specimen to gain better statistics. Rectangular bars with controlled geometry were precisely cut from the ceramics obtained and placed into specially designed experimental setup43 for the conductivity measurements, which were performed in a 4-probe dc mode with temperature (T) and oxygen partial pressure (PO2) being varied above the sample. Actual intervals for T and PO2 alterations were 923–1223 K and 0.9–10−5 atm, respectively. Further experimental details can be found elsewhere.43 The final conductivity values of the bulk material σ were corrected on porosity via the known relation44 | (1) |
3. Results and discussion
3.1. Synthesis and structural attestation
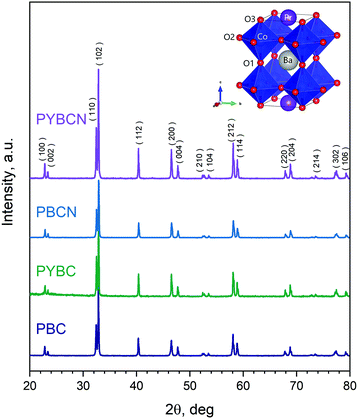
XRD patterns of the synthesized samples are presented in Fig. 1. As can be seen, all cobaltites obtained are single-phase; the observed peaks can be unambiguously attributed to the P4/mmm space group (S.G.) being characteristic for layered double perovskites13,45,46 (the respective schematic depiction of the layered perovskite crystal structure is given in the inset of Fig. 1). A small shift of reflexes with variations of chemical composition indicates little structural distortions occurring upon formation of Pr1−xYxBaCo2−yNiyO6−δ solid solutions, and hence, the magnitude of the respective unit cell changes should be negligible. This finding is in accordance with previous reports.41The results of thermogravimetric measurements of total oxygen content at 298 K for all studied compounds are presented in Table 1. It is seen that PBC and PBCN can be distinguished as more oxygen-rich materials, while Y-doped PYBC and PYBCN possess about ∼0.1 lower 6−δ values. The reason for the observed trend is linked with the lower energy of Y–O bonds compared to Pr–O as evidenced by numerous previous studies.20,47,48 Nevertheless, the overall oxygen content in cobaltites considered is of approximately the same magnitude which is reasonable due to low dopant concentrations and agrees well with earlier reports.38,40,41
| Compound | 6 − δ | μ eff, μB | ω, % | ||
|---|---|---|---|---|---|
| Experiment | Model I | Model II | |||
| PBC | 5.81 ± 0.01 | 6.59 ± 0.01 | 6.78 | 6.59 | 85 |
| PYBC | 5.7 ± 0.01 | 6.02 ± 0.008 | 6.86 | 6.02 | 39 |
| PBCN | 5.78 ± 0.01 | 5.91 ± 0.01 | 6.38 | 5.91 | 55 |
| PYBCN | 5.69 ± 0.01 | 5.35 ± 0.009 | 6.48 | 5.34 | 5 |
It is of particular interest to examine how the estimated oxygen content and cation composition interplay with the magnetic properties of the Pr1−xYxBaCo2−yNiyO6−δ system. The respective results of magnetic susceptibility (χ) measurements are presented in Fig. 2 for all studied compositions. The obtained curves are typical for layered cobaltites.37,49 Still, one can notice that doping of PBC leads to a sufficient decrease of χ values in the paramagnetic region while preserving approximately the same Curie temperature. In order to understand the uncovered features we’ve fitted χ = f(T) data according to the modified Curie–Weiss law:
 | (2) |
As can be seen, doping of PBC results in a sufficient decrease of the effective magnetic moment per cobaltite's formula unit. In our earlier studies we’ve found that similar phenomena are induced by non-magnetic additives in the B-sublattice which disrupt cobalt–oxygen chains thus producing local spin state transitions (HS → LS) of Co3+ ions resting in CoO6 octahedra.37 However, recent results36 indicate that this model is needed to be partially corrected for the case of Y/Ni doping. Indeed, in situ magnetization measurements36 suggest the predominant presence of IS/HS Co3+ pairs at high temperatures in PBC. Also, the low-temperature conductivity behavior for PBC with δ < 0.5 in a paramagnetic region50 indicates the absence of any phase transitions associated with magnetic moment increase. In its turn, LS Co3+ is known to provide insulating properties for cobaltites considered51 while there is no evidence of PBC conductivity decrease with Ni or Y doping. Nevertheless, appropriate assignment of spin states to cobalt ions is closely related to a band structure of studied compounds. Therefore, the respective linkages between cobalt spin states, effective magnetic moments and conductivity will be discussed further in more details.
3.2. Oxygen non-stoichiometry and defect equilibrium
Highly non-stoichiometric compounds possess a unique ability to preserve their crystal structure under variations of external conditions while changing other physical properties dramatically. Therefore, the knowledge of actual stoichiometry alterations in a particular material at elevated temperatures is crucial for understanding its conducting behavior. In their turn, structural and electronic defects are known to govern the transport and thermodynamic properties of cobaltites considered. Therefore, it is of special importance to have a reliable model of defect formation processes that describes equilibration of an oxide with the ambient. One should notice that there are several approaches relating δ in LnBaCo2O6−δ to specific external conditions at the moment.30,34,35 Nevertheless, the true difference between the models mentioned is hindered in highly reducing conditions (PO2 < 10−7 atm); in their turn, SOFC/SOEC applications restrict the minimal PO2 values to 10−3–10−4 atm where all proposed concepts are basically the same. Hence, the model developed in our earlier studies37,40,52 appears to be the most reasonable and will be further used as a theoretical basis for other propositions developed. The key points of the theoretical approach considered are shortly given below; more details can be found elsewhere.37,40Basically, oxygen dissolution in layered cobaltites can be described in terms of random point defect theory; excess thermodynamic terms can be reasonably neglected.37 For instance, three defect formation quasichemical reactions were shown to have an influence on defect equilibrium in LnBaCo2O6−δ including extrinsic cobalt oxidation:
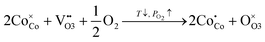 | (3) |
 | (4) |
 | (5) |
 denotes Co regular sites,
denotes Co regular sites,  and
and  denote the electron hole and electron localized on cobalt sites, and
denote the electron hole and electron localized on cobalt sites, and  and
and 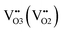 denote oxygen regular sites and vacancies located at O3 (O2) positions in the crystal lattice, respectively. Here all defects are written in the Kroeger–Vink notation53 and the respective reference crystal is chosen in accordance with the method proposed in ref. 52. It is supposed that A- and B-site doping doesn’t bring new defect formation processes, thus only modifying thermodynamic parameters of reactions (3)–(5) and changing site balance/electroneutrality requirements. Then, by assigning suitable charge neutrality and site balance conditions one can solve the system of equations so that to obtain the concentrations of all defect and regular species as a function of T and PO2.54–56 The details of defect structure modeling performed in this work are given in the supplementary file. The resulting model equation establishing linkage 6 − δ = f(T, PO2) can be shown to depend on four unknown parameters – standard enthalpies of reaction (3),
denote oxygen regular sites and vacancies located at O3 (O2) positions in the crystal lattice, respectively. Here all defects are written in the Kroeger–Vink notation53 and the respective reference crystal is chosen in accordance with the method proposed in ref. 52. It is supposed that A- and B-site doping doesn’t bring new defect formation processes, thus only modifying thermodynamic parameters of reactions (3)–(5) and changing site balance/electroneutrality requirements. Then, by assigning suitable charge neutrality and site balance conditions one can solve the system of equations so that to obtain the concentrations of all defect and regular species as a function of T and PO2.54–56 The details of defect structure modeling performed in this work are given in the supplementary file. The resulting model equation establishing linkage 6 − δ = f(T, PO2) can be shown to depend on four unknown parameters – standard enthalpies of reaction (3), 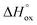 , reaction (4),
, reaction (4),  , and reaction (5),
, and reaction (5), 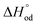 , and standard entropy change for reaction (3) –
, and standard entropy change for reaction (3) –  (entropy changes in reactions (4) and (5) are considered to be small and thus can be neglected12). Bearing this in mind the earlier obtained data on oxygen content in Pr1−xYxBaCo2−yNiyO6−δ solid solutions12,40,41 (the so-called PO2–T–δ diagrams) were refitted to the model mentioned in the 0.5–10−4 atm PO2 range; the best-fit results are shown in Fig. 3 while the obtained values of thermodynamic parameters are given in Table 2. As can be seen, theoretical estimates perfectly describe experimental points for all studied compounds. Also, the obtained values of reaction enthalpies and entropies appear to be in good agreement with the earlier reported results30,39 and reveal a weak influence of cation doping on actual high-temperature oxygen content in layered cobaltites. Still, some differences can be outlined. For instance, one can notice that Ni addition leads to some increase of oxygen deficiency for PBCN and PYBCN compared to pristine PBC which is also reflected in
(entropy changes in reactions (4) and (5) are considered to be small and thus can be neglected12). Bearing this in mind the earlier obtained data on oxygen content in Pr1−xYxBaCo2−yNiyO6−δ solid solutions12,40,41 (the so-called PO2–T–δ diagrams) were refitted to the model mentioned in the 0.5–10−4 atm PO2 range; the best-fit results are shown in Fig. 3 while the obtained values of thermodynamic parameters are given in Table 2. As can be seen, theoretical estimates perfectly describe experimental points for all studied compounds. Also, the obtained values of reaction enthalpies and entropies appear to be in good agreement with the earlier reported results30,39 and reveal a weak influence of cation doping on actual high-temperature oxygen content in layered cobaltites. Still, some differences can be outlined. For instance, one can notice that Ni addition leads to some increase of oxygen deficiency for PBCN and PYBCN compared to pristine PBC which is also reflected in  values presented in Table 2. Recently reported DFT calculations of PrBaCo2−yMyO6−δ (M = Fe, Ni, Cu) solid solutions21 suggest that this result is due to localized electron density on Ni impurity which promotes the electrostatic affinity of the positively charged oxygen vacancy appearing nearby. Quite different is the impact of Y which significantly contracts the PBC lattice,20 thus facilitating the release of oxygen from O3 positions. Accordingly, the combined Y-/Ni-codoping results in a pronounced increase of oxygen non-stoichiometry in PYBCN under oxidative conditions. One should also note that all studied materials do not reach the oxygen content value of 5.0 under reduction conditions which indicates the little influence of vacancies in O2 positions on cobaltites’ transport properties. The defects mentioned were shown to appear in large concentrations only when δ > 1 which is, evidently, out of scope for this work.
values presented in Table 2. Recently reported DFT calculations of PrBaCo2−yMyO6−δ (M = Fe, Ni, Cu) solid solutions21 suggest that this result is due to localized electron density on Ni impurity which promotes the electrostatic affinity of the positively charged oxygen vacancy appearing nearby. Quite different is the impact of Y which significantly contracts the PBC lattice,20 thus facilitating the release of oxygen from O3 positions. Accordingly, the combined Y-/Ni-codoping results in a pronounced increase of oxygen non-stoichiometry in PYBCN under oxidative conditions. One should also note that all studied materials do not reach the oxygen content value of 5.0 under reduction conditions which indicates the little influence of vacancies in O2 positions on cobaltites’ transport properties. The defects mentioned were shown to appear in large concentrations only when δ > 1 which is, evidently, out of scope for this work.
In order to analyze the dependencies of conductivity vs oxygen partial pressure and temperature it is important to know the corresponding relations for defects which can act as possible charge carriers. The respective data for PBC, PYBC, PBCN and PYBCN calculated with the help of the defect chemistry model and  parameters from Table 2 are also plotted in Fig. 3. To simplify the perception all cobalt species are given in their formal ionic charges (
parameters from Table 2 are also plotted in Fig. 3. To simplify the perception all cobalt species are given in their formal ionic charges (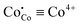 ;
;  ;
; 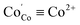 ). One can see that depending on the actual values of T and PO2 each cobaltite can be either Co2+ enriched or Co4+ enriched, thus indicating the strong influence of δ variation on electron defect concentrations. Moreover, temperature dependencies for [Co2+] are sufficiently larger as compared to [Co4+] which suggests that the influence of 2+ charged Co species on conductivity will be higher at elevated temperatures. At the same time, the total amount of Co ions in their ground state, i.e. Co3+, weakly depends on external conditions which seems to be reasonable due to the high magnitude of
). One can see that depending on the actual values of T and PO2 each cobaltite can be either Co2+ enriched or Co4+ enriched, thus indicating the strong influence of δ variation on electron defect concentrations. Moreover, temperature dependencies for [Co2+] are sufficiently larger as compared to [Co4+] which suggests that the influence of 2+ charged Co species on conductivity will be higher at elevated temperatures. At the same time, the total amount of Co ions in their ground state, i.e. Co3+, weakly depends on external conditions which seems to be reasonable due to the high magnitude of  parameters determined. On the overall, one can conclude that all studied cobaltites should possess approximately the same curvature of conductivity dependencies on oxygen partial pressure and temperature.
parameters determined. On the overall, one can conclude that all studied cobaltites should possess approximately the same curvature of conductivity dependencies on oxygen partial pressure and temperature.
3.3. Transport and sintering properties
The general overview of the obtained ceramics for Pr1−xYxBaCo2−yNiyO6−δ solid solutions is presented in Fig. 4. One can notice that the addition of impurities appears to be beneficial for obtaining more dense ceramics. The averaged porosity values calculated with the help of ImageJ software42 were shown to be 51 ± 3, 33 ± 2, 36 ± 2 and 24 ± 3% for PBC, PYBC, PBCN and PYBCN, respectively. It should be mentioned that the positive impact of doping on PBC sinterability has been already reported.37,38Still, there is no evidence of earlier attempts to use the relative porosity of PBC for describing its conductivity. This partially helps to explain the vast scattering in the respective data published by different authors.26
Porosity-corrected conductivities for Pr1−xYxBaCo2−yNiyO6−δ layered perovskites are presented in Fig. 5 as a function of temperature and oxygen partial pressure. In full accordance with earlier made propositions the data for all samples show similar behavior at reduction\heating: the conductivity of a particular cobaltite decreases. However, the magnitude of this decrease can vary significantly depending on the actual cation composition of the compound considered.
3.4. Theoretical modeling of electrical conduction in layered cobaltites
As discussed earlier in the Introduction section many factors affect the conducting properties of layered perovskite-like cobaltites. In this sense, crystal structure anisotropy should be considered as one of the most crucial parameters influencing charge transport in the studied compounds. Surprisingly, none of the previous attempts to describe the high-temperature electrical conductivity of LnBaCo2O6−δ oxides has given any attention to the problem mentioned.One should keep in mind that conductivity in general is a tensor-like quantity ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ; accordingly, systems possessing a non-cubic crystal structure impose several symmetry restrictions on the representation of this tensor. For instance, the respective
; accordingly, systems possessing a non-cubic crystal structure impose several symmetry restrictions on the representation of this tensor. For instance, the respective ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) value for a tetragonal crystalline lattice can be written as
value for a tetragonal crystalline lattice can be written as
 | (6) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) tensor component parallel to [100] and [010] directions and σ⊥ stands for a component pointed in the [001] direction. In the case of layered cobaltites this means there are two distinctive conduction pathways. Experimental studies on monocrystalline EuBaCo2O6−δ (EBC) strongly support this conclusion.33 Moreover, this research also revealed significant difference between σ‖ and σ⊥ components of the conductivity tensor: the σ‖ ≫ σ⊥ inequality was established in a vast temperature range. The result obtained in ref. 33 appears to be reasonable because of the strong tendency for oxygen vacancies to be formed in Ln–O layers as discussed previously. Consequently, –O–Co–O– chains are continuously disrupted in the [001] direction when non-stoichiometry is large while they are preserved along the a/b crystallographic axis in a wide range of δ. Assuming that the same tendency is valid for PBC and its doped derivatives, one can derive the following equation for the conductivity of a polycrystalline sample σ (the grains are supposed to be randomly distributed, surface phenomena are neglected):
tensor component parallel to [100] and [010] directions and σ⊥ stands for a component pointed in the [001] direction. In the case of layered cobaltites this means there are two distinctive conduction pathways. Experimental studies on monocrystalline EuBaCo2O6−δ (EBC) strongly support this conclusion.33 Moreover, this research also revealed significant difference between σ‖ and σ⊥ components of the conductivity tensor: the σ‖ ≫ σ⊥ inequality was established in a vast temperature range. The result obtained in ref. 33 appears to be reasonable because of the strong tendency for oxygen vacancies to be formed in Ln–O layers as discussed previously. Consequently, –O–Co–O– chains are continuously disrupted in the [001] direction when non-stoichiometry is large while they are preserved along the a/b crystallographic axis in a wide range of δ. Assuming that the same tendency is valid for PBC and its doped derivatives, one can derive the following equation for the conductivity of a polycrystalline sample σ (the grains are supposed to be randomly distributed, surface phenomena are neglected): | (7) |
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) 〉 denotes the space-averaged conductivity tensor. As seen from eqn (7) there is no need to consider the electrical conductance in the [001] direction for polycrystalline materials, and hence, LnBaCo2O6−δ cobaltites can be assumed as quasi two-dimensional (2D) conductors. However, when discussing the thermopower, one should take into account the respective term as evidenced from direct experimental observations.33 Therefore, modeling the thermopower of layered cobaltites based on the data for polycrystalline samples appears to be erroneous.34 One should also take into account that the approximate equality given by eqn (7) is fulfilled for EBC in the high-temperature region33 which additionally supports the assumptions made. Consequently, only the σ‖ component of conductivity is shown to contribute to transport properties of LnBaCo2O6−δ cobaltites. Hence, further discussions will be focused only on this particular value.
〉 denotes the space-averaged conductivity tensor. As seen from eqn (7) there is no need to consider the electrical conductance in the [001] direction for polycrystalline materials, and hence, LnBaCo2O6−δ cobaltites can be assumed as quasi two-dimensional (2D) conductors. However, when discussing the thermopower, one should take into account the respective term as evidenced from direct experimental observations.33 Therefore, modeling the thermopower of layered cobaltites based on the data for polycrystalline samples appears to be erroneous.34 One should also take into account that the approximate equality given by eqn (7) is fulfilled for EBC in the high-temperature region33 which additionally supports the assumptions made. Consequently, only the σ‖ component of conductivity is shown to contribute to transport properties of LnBaCo2O6−δ cobaltites. Hence, further discussions will be focused only on this particular value.
The next key point to develop a model of electrical transport for studied materials is assigning a suitable band structure. As discussed earlier, several approaches can be outlined in this field. One of the main challenges here is the determination of role of Co3+ in the conduction mechanism. Previous studies suggest that it can either act as an active site for localized electron excitations’ hopping35 or provide electrons in a narrow band near the valence band top30 depending on oxygen coordination and spin state. Also, there are doubts regarding the degree of localization for charge carriers considered.32,39,57 Therefore, in this work we’ve tried to examine different model assumptions and their applicability based on existing experimental and theoretical data on magnetic, electric and thermodynamic properties.
Let's remember the key points at this moment (please pay attention, we’re dealing with the so-called high temperature states which lie above the MI transition point). First of all, one should note that the process of thermal ionization represented by eqn (4) automatically invokes the semiconductor-like conductivity in cobaltites considered with Co4+ (t52ge0g) acting as p-type and Co2+ (t52ge2g) as n-type charge carriers.34 The suitable description of oxygen non-stoichiometry data without accounting for the respective reaction cannot be achieved. Also, theoretical calculations evidence58 that there can exist a band gap similar in magnitude to  enthalpy. Hence, this process is likely to be presented in materials considered. Note that the presence of Co2+ in t52ge2g configuration was confirmed for PBC by direct magnetic measurements at high temperatures.36 On the other hand, the range of conductivity values and its thermal behavior under oxidative conditions59–61 suggest metallic-like conduction. Moreover, DFT calculations can represent the metallic behavior as well.27,58 Hence, one can suppose that these two types of charge transport can exist in one material simultaneously. Thus, layered cobaltites can be considered as a separated in real space mixture of semiconducting and metallic “quasiphases” which transform into each other depending on oxygen non-stoichiometry and temperature. The key to this transformation should be the spin state of Co3+. Indeed, oxygen coordination at high temperatures was found to influence the respective parameter: CoO5 pyramids contain IS Co3+ (t52ge1g) while CoO6 octahedra are distinguished with HS Co3+ (t42ge2g).36 In its turn, the conservation of spin multiplicity suggests that Co4+ and Co2+ can move through the crystal only by means of hopping on IS Co3+. Therefore, HS Co3+ subjected to octahedral tilting by Ln/Ba ordering62 can be supposed to give two near lying eg orbitals in the vicinity of the Fermi level thus producing a quasimetallic conducting system.28 As a result, one can formulate the band structure of Pr1−xYxBaCo2−yNiyO6−δ solid solutions as a spatially separated system with localized narrow eg bands at the CoO5 site and merged (at the Fermi level) electronic states at CoO6 sites.28 Accordingly, Co3+ oxygen coordination here acts as a “spatial descriptor” pointing to the type of band structure in a particular lattice environment (pyramidal or octahedral). The model described will be labeled further as model I; the corresponding schematic band representation is given in Fig. 6.
enthalpy. Hence, this process is likely to be presented in materials considered. Note that the presence of Co2+ in t52ge2g configuration was confirmed for PBC by direct magnetic measurements at high temperatures.36 On the other hand, the range of conductivity values and its thermal behavior under oxidative conditions59–61 suggest metallic-like conduction. Moreover, DFT calculations can represent the metallic behavior as well.27,58 Hence, one can suppose that these two types of charge transport can exist in one material simultaneously. Thus, layered cobaltites can be considered as a separated in real space mixture of semiconducting and metallic “quasiphases” which transform into each other depending on oxygen non-stoichiometry and temperature. The key to this transformation should be the spin state of Co3+. Indeed, oxygen coordination at high temperatures was found to influence the respective parameter: CoO5 pyramids contain IS Co3+ (t52ge1g) while CoO6 octahedra are distinguished with HS Co3+ (t42ge2g).36 In its turn, the conservation of spin multiplicity suggests that Co4+ and Co2+ can move through the crystal only by means of hopping on IS Co3+. Therefore, HS Co3+ subjected to octahedral tilting by Ln/Ba ordering62 can be supposed to give two near lying eg orbitals in the vicinity of the Fermi level thus producing a quasimetallic conducting system.28 As a result, one can formulate the band structure of Pr1−xYxBaCo2−yNiyO6−δ solid solutions as a spatially separated system with localized narrow eg bands at the CoO5 site and merged (at the Fermi level) electronic states at CoO6 sites.28 Accordingly, Co3+ oxygen coordination here acts as a “spatial descriptor” pointing to the type of band structure in a particular lattice environment (pyramidal or octahedral). The model described will be labeled further as model I; the corresponding schematic band representation is given in Fig. 6.
Note that model I does not account for the preferential polyhedral environment of Co2+/Co4+ ionic species. Moreover, this model should be valid only when the concentration of CoO4 tetrahedra is negligible (i.e. when 0 < δ < 1). As can be seen from the data presented in Fig. 3 and 5 the latter requirement is entirely fulfilled. Doping in this case is not expected to change band positions or introduce new energy levels. Indeed, Y states will lie quite far from the Fermi level while Ni states are supposed to be placed inside O2p states above and below Fermi energy (see Fig. 6).
Now, when the general terms of the electronic structure are defined one can formulate an expression relating conductivity of a particular cobaltite to its defect concentrations. In accordance with earlier made propositions the semiconducting part of conductivity will rely on localized Co2+ and Co4+ ions (i.e. polarons) acting as n-type and p-type charge carriers, respectively (these are assumed to form on eg states in CoO5 pyramids as depicted in Fig. 6). Therefore, the amount of sites available for Co2+/Co4+ jumps will be given as concentration of IS Co3+ in CoO5 pyramids. Here and thereon these species will be denoted as Co3+IS(Δ). In its turn, the concentration of conducting electrons in a metallic subsystem is expected to be represented entirely by HS Co3+ in CoO6 octahedra (Co3+IS(⋄)). As shown in ref. 36 when δ < 1 the respective concentrations can be calculated with the help of the following relations:
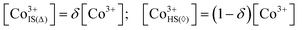 | (8) |
 | (9) |
 | (10) |
 values taken from Table 2. To add, the metallic subsystem in expression (10) is presented with the
values taken from Table 2. To add, the metallic subsystem in expression (10) is presented with the 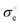 parameter which has a dimensionality of s−1 and depends on carriers’ effective mass and Fermi energy of a material (see eqn (S15) in the ESI†). The corresponding mobility term will be then expressed as
parameter which has a dimensionality of s−1 and depends on carriers’ effective mass and Fermi energy of a material (see eqn (S15) in the ESI†). The corresponding mobility term will be then expressed as  . One can immediately notice that eqn (10) can be reduced to all models discussed previously. Actually, the Tsvetkov model is obtained when
. One can immediately notice that eqn (10) can be reduced to all models discussed previously. Actually, the Tsvetkov model is obtained when  , the Vollestad model appears if ν#n → 0 and the simple p-type polaronic model can be produced under simultaneous
, the Vollestad model appears if ν#n → 0 and the simple p-type polaronic model can be produced under simultaneous  and ν#n → 0 conditions. In order to check the validity of different approaches discussed the conductivity data for PBC were fitted to the aforementioned models in a wide δ − T domain. The results obtained are presented in Fig. 7 for two extreme isotherms σ = f(δ) at 923 and 1223 K.
and ν#n → 0 conditions. In order to check the validity of different approaches discussed the conductivity data for PBC were fitted to the aforementioned models in a wide δ − T domain. The results obtained are presented in Fig. 7 for two extreme isotherms σ = f(δ) at 923 and 1223 K.
As can be seen, there is excellent agreement between theory and experiment in the case of model I. In contrast, other models are significantly deviating from experimental points. This result can be partly improved assuming the possibility of conductivity parameters’ variations with δ as supposed in ref. 34. However, keeping in mind that the main contribution to σ in LnBaCo2O6−δ is made by the σ‖ term, one can conclude that these arguments are likely to be unreasonable. Indeed, as discussed earlier –O–Co–O– conducting channels in layered cobaltites are not broken by oxygen vacancies in a wide range of δ variations. Hence, the alterations of hopping barriers/frequencies for polarons moving along the a/b axis should be quite small and can be even considered negligible. Therefore, the results obtained in the framework of the Tsvetkov model are indicative of the metallic subsystem sufficient influence on the conducting properties of materials studied. Similarly, fitting experimental points to the Vollestad model revealed the importance of accounting for n-type carriers’ contribution to the overall σ values at high temperatures. Still, model I itself possesses some flaws. In particular, it predicts a fully metallic conductivity at δ = 0 when every second Co ion in the crystalline lattice will be 4+ charged. It is unlikely that this result will be consistent with experimental observations. Moreover, the localized nature of electron holes in cobaltites considered is seriously doubted in numerous studies.32,57 Finally, Co4+ ions are supposed to be predominantly located in CoO6 octahedra due to significant electrostatic repulsion between the lattice and the respective defects.63
Consequently, it is reasonable to formulate another model (model II) of electrical conduction for LnBaCo2O6−δ compounds. The main assumption here is linked with spatial distribution of electronic defects: Co2+ can now occupy only CoO5 pyramids, Co4+ - only CoO6 octahedra while Co3+ can exist in both environments. It is important to stress at this moment that 3+ charged cobalt species can exist in both IS and HS states in octahedral oxygen coordination.64 The respective proposition is reasonable as it provides the channels for p-type electronic transport (otherwise, at δ → 0 there would be no sites for holes to move through). In order to quantitatively assess the number of IS Co3+ in octahedra (Co3+IS(⋄)) one can apply the mass action law for a hypothetical equilibrium between the spin states mentioned:
 | (11) |
 | (12) |
 | (13) |
 temperature-independent parameter appearing in expression (13) is related to the effective mass of p-type carriers (see eqn (S18) in the ESI†); all other values entering eqn (13) have the same meaning as those depicted in eqn (10). One should consider that the overall structure of formula (13) is quite similar to that of (10) which implies that the description of conductivity data would be close for both models suggested. Indeed, fitting procedures performed for PBC as a convenient example strongly support this conclusion (the respective results are given in Fig. 7). Therefore, one cannot distinguish among these models based only on their behavior at description of transport properties of studied materials. Still, the validation of the proposed theoretical concepts heavily relies on proper depiction of huge conductivity datasets attained in this work. The corresponding results are given in the next sections of this paper.
temperature-independent parameter appearing in expression (13) is related to the effective mass of p-type carriers (see eqn (S18) in the ESI†); all other values entering eqn (13) have the same meaning as those depicted in eqn (10). One should consider that the overall structure of formula (13) is quite similar to that of (10) which implies that the description of conductivity data would be close for both models suggested. Indeed, fitting procedures performed for PBC as a convenient example strongly support this conclusion (the respective results are given in Fig. 7). Therefore, one cannot distinguish among these models based only on their behavior at description of transport properties of studied materials. Still, the validation of the proposed theoretical concepts heavily relies on proper depiction of huge conductivity datasets attained in this work. The corresponding results are given in the next sections of this paper.
3.5. Verification of conductivity models proposed
The results of fitting σ = f(T, PO2) datasets for Pr1−xYxBaCo2−yNiyO6−δ solid solutions using both theoretical models are given in Fig. 5 by solid lines (the respective functional dependencies of Co defect species’ concentrations are presented in Fig. 3). As can be seen, both models excellently reproduce experimental points (R2 > 0.994 for all cases considered); fitting parameters obtained are supplied within Table 3.One can notice that the obtained transport and thermodynamic parameters change in a quite complex manner with doping concentrations which makes it difficult to elucidate the crucial role of a particular factor in the observed overall conductivity decrease with increasing x and y. Nevertheless, both models work perfectly and some additional data are needed in order to define which of them is more correct. At this point it is reasonable to return to effective magnetic moments derived earlier (see Table 1). As discussed previously, model I imposes the presence of only HS Co3+ in CoO6 octahedra while model II partially corrects this statement assuming that there can be some fraction of IS Co3+ at the same sites. Evidently, these models will give different μeff values. Hence, the magnetic susceptibility of Pr1−xYxBaCo2−yNiyO6−δ cobaltites can be considered as an indicator for choosing an adequate model of electronic conduction. The respective equations can be derived on the basis of the general formula for paramagnetic materials:
 | (14) |
 term in eqn (12) can be approximated simply as fractions ω and 1 − ω of HS and IS Co3+ in CoO6 octahedra, respectively. Utilizing equations for magnetic moments of ions with frozen angular momenta68 along with the abovementioned considerations one can derive the following formula (see ref. 37 for more details) for μeff:
term in eqn (12) can be approximated simply as fractions ω and 1 − ω of HS and IS Co3+ in CoO6 octahedra, respectively. Utilizing equations for magnetic moments of ions with frozen angular momenta68 along with the abovementioned considerations one can derive the following formula (see ref. 37 for more details) for μeff: | (15) |
3.6. Assessment and discussion of modeling results
In order to define the actual influence of different parameters on conductivity values in Pr1−xYxBaCo2−yNiyO6−δ solid solutions it is instructive to evaluate the respective transference numbers tk (which are defined in a standard way69). These data are presented in the lower panel of Fig. 5 for all studied samples. As can be seen, external conditions (i.e. temperature and oxygen partial pressure) strongly influence the dominating conducting mechanism in Pr1−xYxBaCo2−yNiyO6−δ while doping does not. As a consequence, some general trends can be outlined. For instance, the increase of temperature under oxidative conditions leads to soft transition from p- to n-type conductivity which is in accordance with changes of respective carrier concentrations (see Fig. 3 for more details). To add, the reduction process strongly promotes the fraction of electrical current carried by Co2+ ions. Interestingly, the simultaneous increase of T and decrease of PO2 lead to a pronounced increase of semiconducting conductivity over the metallic one. Still, the contribution of the metallic subsystem remains dominant at T < 1000 K for all compounds considered. The obtained dependencies may also help to understand the qualitative reasons of Seebeck coefficient changes with T and PO2, reported earlier.35 In particular, at temperatures below ∼900 K and PO2 = 0.21 atm the thermopower for LnBaCo2O6−δ is negative and very small in absolute values which coincides with the dominant metallic type of conductivity. When the oxygen partial pressure starts to decrease, the thermopower becomes positive and grows up (heating the sample also promotes the increase of Seebeck coefficient). This behavior is consistent with a decline of p-type carriers’ concentration. Nevertheless, more studies on monocrystalline samples are needed in order to elucidate the actual contribution of different carriers in the total thermopower of layered cobaltites.Keeping in mind the distribution of transference numbers in Pr1−xYxBaCo2−yNiyO6−δ solid solutions it is interesting to evaluate the respective mobility terms for each particular type of conduction. The corresponding estimations for the k-th carrier can be made using the general formula for mobility which reads as
 | (16) |
 | (17) |
 | (18) |
 | (19) |
 | ||
| Fig. 8 Calculated isobaric temperature dependencies of k-th charge carrier mobility for Pr1−xYxBaCo2−yNiyO6−δ layered cobaltites. | ||
One can notice that n-type mobility for all studied compounds slightly increases with temperature almost regardless of actual PO2 values which is a natural consequence of the inner structure of eqn (19). The respective magnitude of un values is close to 0.1 cm2 V−1 s−1 – the commonly accepted limit of polaronic-type mobility.70 In contrast to this, the up parameter for each cobaltite considered tends to strongly vary with both T and PO2: the reduction and/or heating of a sample leads to a sufficient decrease of its p-type mobility. Obviously, this effect indicates the sufficient role of octahedrally coordinated IS Co3+ sites in providing energy states for p-type carriers’ migration through the lattice. Finally, the mobility of metallic carriers is significantly higher as compared to the semiconducting subsystem and furthermore, following eqn (17), almost temperature-independent, which is in full accordance with the propositions made during the formulation of model II.
At this point it should be stressed that although transference numbers and mobilities provide useful information regarding the actual contribution of each particular carrier to the overall charge transport, one cannot elucidate the role of doping in this process. This is especially remarkable when considering the clearly observed trend for lowering temperature dependencies of conductivity in a PBC → PYBC → PBCN → PYBCN row (see Fig. 5). At the same time, Co species’ concentrations, tk and uk values for all studied specimens are essentially similar as can be seen from the data given in Fig. 3, 5 and 8. Therefore, it is instructive to analyze the distribution of Co3+ spin states as these play a crucial role in providing transport channels for electrical current. The respective dependencies of Co3+IS(Δ), Co3+IS(⋄) and Co3+HS(⋄) concentrations in the crystalline lattice on external conditions are shown in Fig. 9 for PBC, PYBC, PBCN and PYBCN.
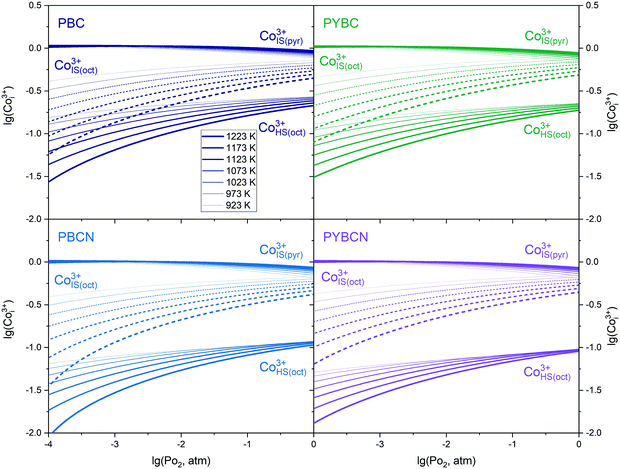 | ||
| Fig. 9 The concentration of Co3+ ions in different spin states as a function of the crystallographic environment, temperature and oxygen partial pressure for Pr1−xYxBaCo2−yNiyO6−δ layered cobaltites. | ||
By analyzing the data presented one can conclude that doping PBC with different ions consequently enlarges the difference between the amount of HS and IS Co3+ in the CoO6 octahedral environment. As a result, the competition between p-type semiconducting and metallic transport increases with increasing x and y due to the respective mobility difference (see Fig. 8). Thus, p-type conductivity for PYBCN is sufficiently higher under reducing conditions as compared to pristine PBC (see the lower panel of Fig. 5). Hence, the influence of temperature on σ values should decline with doping amount which is in full accordance with the uncovered trends. In their turn, the concentrations of pyramidally coordinated IS Co3+ remain almost unaffected by T or PO2 in the studied range of external conditions for all cobaltites considered. Consequently, the contribution of n-type carriers to the overall conductivity values is approximately the same regardless of the magnitude of dopants’ content. To add, the data in Fig. 9 also coincide with the earlier discussed low-temperature distribution of Co3+ ions in different spin states. For instance, ω values presented in Table 1 decrease as the dopant content increases. Similarly to that, Y and Ni substitution leads to the consequent increase of the  fraction in the Pr1−xYxBaCo2−yNiyO6−δ crystalline lattice. Therefore, the assumptions made at formulating model II provide a reasonable linkage between high- and low-temperature properties’ variations with the actual cation composition of compounds considered.
fraction in the Pr1−xYxBaCo2−yNiyO6−δ crystalline lattice. Therefore, the assumptions made at formulating model II provide a reasonable linkage between high- and low-temperature properties’ variations with the actual cation composition of compounds considered.
3.7. Testing the derived model on external data
Despite the essentially ad hoc character of the model formulated it is interesting to consider the possibility of describing high-temperature transport properties for other cobaltites from the LnBaCo2O6−δ oxide family. One should keep in mind though that only combined non-stoichiometry and conductivity data can be used for the respective analysis. Also, the ceramics density should be specified so as to correct measured resistivity on porosity. Among all studies presented only a small number of works can be distinguished30,33,34,71,72 which reported all of the necessary data. Actually, simultaneous conductivity and oxygen non-stoichiometry dependencies on PO2 and T are known only for EuBaCo2O6−δ (EBC),33 GdBaCo2O6−δ (GBC)34 and Gd0.8La0.2Ba1−xLaxCo2O6−δ with x = 0.1, 0.2, 0.3 or 0.5 (GLBC),30 respectively. Accordingly, fitting procedures using the developed theoretical approach were performed in PO2–T domains available. To be precise, applying the proposed defect chemistry model for description of EBC, GBC and GLBC oxygen content dependencies and substituting the obtained thermodynamic parameters in eqn (13) one arrives at reasonably good description of the respective datasets as shown in Fig. 10 (the obtained R2 values during the fitting procedure were no less than 0.992).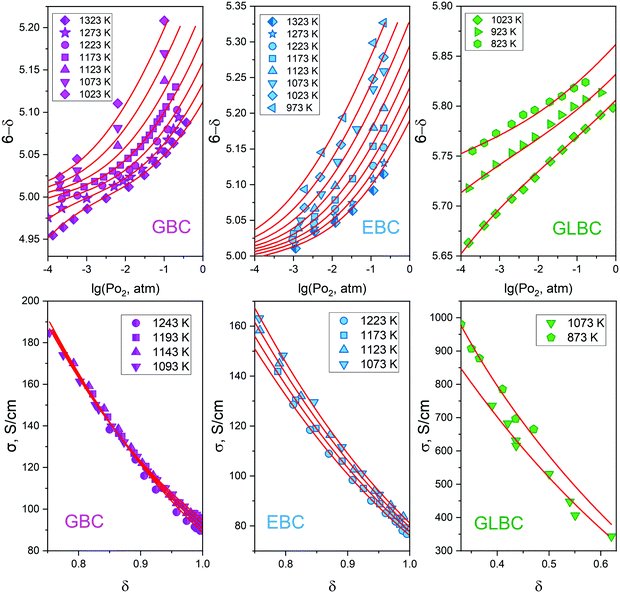 | ||
| Fig. 10 Oxygen non-stoichiometry (upper panel) and electrical conductivity (lower panel) for different cobaltites with a layered double perovskite structure. Experimental results taken from ref. 30, 33, 34 and 71 are shown with symbols, and the respective theoretical description is given with red lines. | ||
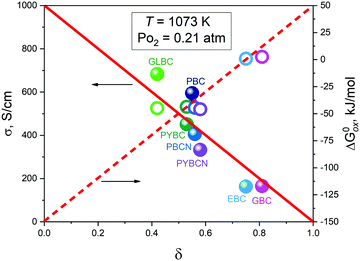
As can be seen, the different composition of A-sublattice heavily influences the magnitude of conductivity in LnBaCo2O6−δ cobaltites. Nevertheless, the derived model accurately reproduces the observed curvatures of σ = f(δ) isotherms for EBC, GBC and GLBC. Note that the actual values of δ somehow correlate with the reported magnitude of σ. The obtained transport parameters (the respective data are presented in supplementary materials), however, do not reveal any clearly visible correlations with cation composition/defect formation enthalpies/ionic radii, etc. Perhaps, it is a consequence of too many parameters involved. Hence, in order to find any interrelations between the data obtained one should fix some variables and see how others start to depend on each other. For instance, it is reasonable to assign identical external conditions, and compare how conductivity of different cobaltites is related to their oxygen non-stoichiometry. The respective data at T = 1073 K and PO2 = 0.21 atm (these conditions can be met for all samples considered) are presented in Fig. 11.
It is easy to see that there is a clear correlation between achieved values of δ and the resulting magnitude of σ. The trend observed is likely to be linked with an increasing role of metallic conduction when the respective increase of oxygen content in a particular sample takes place. It is therefore of special interest to compare how thermodynamic functions governing oxygen equilibration in cobaltites vary with δ. By analyzing the data obtained in the scope of defect chemistry modeling (see Table 2 and Table S1 in the ESI†) one can conclude that the only representative quantity here is oxidation enthalpy and entropy which can be combined so as to calculate the standard Gibbs energy change for oxidation reaction –  . The resulting
. The resulting  values were also plotted in Fig. 11versus δ. Again, certain correlation between
values were also plotted in Fig. 11versus δ. Again, certain correlation between 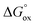 and δ (at fixed T and PO2) is observed. Similarly to the conductivity case the result achieved is reasonable: the more the exothermic oxidation energy is, the less non-stoichiometric will be the sample. It is therefore another confirmation of deep interconnections between thermodynamic and transport properties in LnBaCo2O6−δ-based materials. However, the exact quantum-mechanical explanations of trends observed are lacking at the moment. Accordingly, further studies are needed in order to elucidate whether the existing dependencies can be reasonably rationalized.
and δ (at fixed T and PO2) is observed. Similarly to the conductivity case the result achieved is reasonable: the more the exothermic oxidation energy is, the less non-stoichiometric will be the sample. It is therefore another confirmation of deep interconnections between thermodynamic and transport properties in LnBaCo2O6−δ-based materials. However, the exact quantum-mechanical explanations of trends observed are lacking at the moment. Accordingly, further studies are needed in order to elucidate whether the existing dependencies can be reasonably rationalized.
3.8. General aspects and further outlook
The nature of the derived dependencies partly contradicts both our earlier published results35,36 and those obtained by other authors.24,30,34 Therefore it is instructive to underline the key arguments standing behind the proposed model and suggest further research directions in the area. Firstly, the high-temperature conduction of materials considered cannot be adequately described either in purely metallic or in only semiconducting models. As a result, the combination of these two models in a single one seems reasonable with the actual spin state of cobalt ions acting as a main descriptor between them. The respective proposition is supported by numerous data sources including high temperature magnetic susceptibility,36,50 DFT calculations,27,58 conductivity and Hall coefficient measurements30 along with thermodynamics of oxygen dissolution and defect formation.40 What is important is that the proposed theoretical approach successfully integrates all this data complex providing unambiguous description of the respective properties. As a result, earlier proposed models of conduction mechanisms in LnBaCo2O6−δ are easily derived as a special case of more general equations (eqn (10) and (13)). Secondly, there is no admissible agreement on various aspects of cobaltites’ electronic band structure such as band gap width, the degree of carriers’ localization and the role of crystalline anisotropy in charge transport. All these issues were shown to be entirely resolved if a number of reasonable assumptions were taken into account. For instance, the band gap of cobaltites considered was unequivocally ascribed to the values obtained in the scope of DFT simulations and thermodynamic modeling of the defect structure. Earlier reported UV-Vis values of 1.528 and 3.3 eV29 should be considered corresponding to intraband transitions. In its turn, the problem with carriers’ localization can be resolved by attracting magnetic data as a control method, while the influence of anisotropy can be essentially neglected thus reducing LnBaCo2O6−δ 3D conductivity to the quasi-2D case. However, the latter procedure cannot be made for thermopower and all earlier published theoretical descriptions of it should be carefully revised. Finally, the huge data array collected within this research allowed one to find another confirmation to the model proposed. In particular, the role of doping was partly uncovered, and the respective temperature dependencies of conductivity with increasing dopant concentration were explained. Also, several previously published experimental results were confirmed to satisfy the model equations derived. On the overall one can conclude that the validity of the theoretical approach proposed is strongly supported by numerous data sources and methods. Consequently, additional experiments are needed in order to clarify some unclear points. We suppose that thermopower and conductivity measurements performed on monocrystalline LnBaCo2O6−δ samples in different crystallographic directions and variable temperature/gaseous atmospheres would help a lot in estimating actual direction-resolved contributions of different carriers to thermoelectric and conducting properties of materials considered. Also, high-temperature XPS measurements would appear quite useful in determining the true band structure of layered cobaltites above the MI transition point. Finally, there is a need for more detailed theoretical studies aimed at explaining the revealed correlations between cation composition, defect formation thermodynamics and transport properties of LnBaCo2O6−δ compounds.4. Conclusion
Solid solutions with the general composition Pr1−xYxBaCo2−yNiyO6−δ (x = 0, 0.1, y = 0, 0.2) were successfully synthesized by means of organo-metallic precursors’ combustion. The obtained specimens were shown to be single-phase possessing tetragonal symmetry (S.G. P4/mmm) which corresponds to the layered double perovskite structure. The prepared PrBaCo2O6−δ, Pr0.9Y0.1BaCo2O6−δ, PrBaCo1.8Ni0.2O6−δ and Pr0.9Y0.1BaCo1.8Ni0.2O6−δ powders were sintered so that to obtain ceramics dense enough for conductivity measurements. The respective quantity (σ) was determined in a wide range of temperatures and oxygen partial pressures in gaseous phase for all studied samples. It was found that the obtained dependencies σ = f(T, PO2) cannot be properly described in the framework of any previously suggested model of electronic conduction in LnBaCo2O6−δ layered cobaltites. Therefore, two theoretical models were formulated which accounted for the anisotropic character of the Pr1−xYxBaCo2−yNiyO6−δ crystalline structure, its actual non-stoichiometry δ, defect formation reactions at elevated temperatures, different Co coordination and spin states, the degree of charge carriers’ localization and the coexistence of metallic and semiconducting channels of conductivity. The main difference between the suggested models was linked with the actual mechanisms of p-type charge transport. Still, both derived approaches were found to be in reasonable agreement with thermodynamic and structural data for the materials considered. Moreover, the fitting of the proposed models to experiment resulted in excellent description of huge σ = f(T, PO2) data arrays collected within this work. Hence, a comparison between the models was made additionally involving magnetic data which suggested that p-type conductivity is more likely to be delocalized in nature. The obtained transport parameters enabled one to conclude that the main contribution to cobaltites’ conductivity under oxidative conditions is linked with the metallic subsystem formed by HS Co3+ in CoO6 octahedra. At the same time, the high-temperature reduction of studied compounds was found to promote the n-type conductivity dominance over other types of charge transport mostly due to the large concentration of the respective carriers resting in CoO5 pyramids. In its turn, doping of PrBaCo2O6−δ with either Y or Ni was found to lower the absolute conductivity value and its temperature dependency as well. The observed trends were explained as due to the increasing competition between semiconducting and metallic subsystems with the respective increase in dopants’ concentration. Accordingly, conductivity data for other LnBaCo2O6−δ oxides published previously were also successfully interpreted in terms of the suggested theoretical approach. The obtained results indicate the complex influence of actual chemical composition on thermodynamic and transport properties in layered cobaltites, although the versatility of the conduction model proposed appears to be verified with some interesting correlations found. Based on the collected data several new experiments and research directions are suggested.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. V. P. acknowledges the Russian Science Foundation for the support under grant no. 21-79-30051. A. Yu. S. is grateful to government assignment AAAA-A19-119110190048-7.References
- K. Takada, H. Sakurai, E. Takayama-Muromachi, F. Izumi, R. A. Dilanian and T. Sasaki, Nature, 2003, 422, 53–55 CrossRef CAS PubMed.
- A. I. Waidha, L. Ni, J. Ali, M. Lepple, M. Donzelli, S. Dasgupta, S. Wollstadt, L. Alff, U. I. Kramm and O. Clemens, J. Mater. Chem. A, 2020, 8, 616–625 RSC.
- X. Li, Z. Ju, F. Li, Y. Huang, Y. Xie, Z. Fu, R. J. Knize and Y. Lu, J. Mater. Chem. A, 2014, 2, 13366–13372 RSC.
- A. P. Ramirez, J. Phys. Conens. Matter, 1997, 9, 8171–8199 CrossRef CAS.
- S. Li and J. T. S. Irvine, Solid State Ionics, 2021, 361, 115571 CrossRef CAS.
- Y. Dou, Y. Xie, X. Hao, T. Xia, Q. Li, J. Wang, L. Huo and H. Zhao, Appl. Catal., B, 2021, 297, 120403 CrossRef CAS.
- J. H. Kim and A. Manthiram, J. Mater. Chem. A, 2015, 3, 24195–24210 RSC.
- A. A. Taskin and Y. Ando, Phys. Rev. Lett., 2005, 95, 2–5 CrossRef PubMed.
- A. Grimaud, K. J. May, C. E. Carlton, Y. L. Lee, M. Risch, W. T. Hong, J. Zhou and Y. Shao-Horn, Nat. Commun., 2013, 4, 1–7 Search PubMed.
- F. Dong, M. Ni, Y. Chen, D. Chen, M. O. Tadé and Z. Shao, J. Mater. Chem. A, 2014, 2, 20520–20529 RSC.
- E. Coulaud, G. Dezanneau and G. Geneste, J. Mater. Chem. A, 2015, 3, 23917–23929 RSC.
- A. Y. Suntsov, B. V. Politov, I. A. Leonidov, M. V. V. Patrakeev and V. L. Kozhevnikov, Solid State Ionics, 2016, 295, 90–95 CrossRef CAS.
- D. Parfitt, A. Chroneos, A. Tarancon and J. A. Kilner, J. Mater. Chem., 2011, 21, 2183–2186 RSC.
- D. Garcés, C. F. Setevich, A. Caneiro, G. J. Cuello and L. Mogni, J. Appl. Crystallogr., 2014, 47, 325–334 CrossRef.
- A. A. Taskin, A. N. Lavrov and Y. Ando, Phys. Rev. Lett., 2003, 90, 227202 CrossRef PubMed.
- I. D. Seymour, A. Tarancón, A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, Solid State Ionics, 2012, 216, 41–43 CrossRef CAS.
- Y. C. Chen, M. Yashima, J. Peña-Martínez and J. A. Kilner, Chem. Mater., 2013, 25, 2638–2641 CrossRef CAS.
- A. Y. Suntsov, S. N. Marshenya, A. A. Markov and V. L. Kozhevnikov, Mater. Lett., 2021, 295, 129818 CrossRef CAS.
- Y. Hu, O. Hernandez, T. Broux, M. Bahout, J. Hermet, A. Ottochian, C. Ritter, G. Geneste and G. Dezanneau, J. Mater. Chem., 2012, 22, 18744–18747 RSC.
- V. P. Zhukov, B. V. Politov, A. Y. Suntsov, I. A. Leonidov, I. R. Shein and V. L. Kozhevnikov, Solid State Ionics, 2020, 347, 115230 CrossRef CAS.
- V. P. Zhukov, E. V. Chulkov, B. V. Politov, A. Y. Suntsov and V. L. Kozhevnikov, Phys. Chem. Chem. Phys., 2021, 23, 2313 RSC.
- M. Søgaard, P. V. Hendriksen, M. Mogensen, F. W. Poulsen and E. Skou, Solid State Ionics, 2006, 177, 3285–3296 CrossRef.
- T. Miruszewski, W. Skubida, A. Dawczak, K. Dzierzgowski, S. Wachowski, A. Mielewczyk-Gryń and M. Gazda, J. Eur. Ceram. Soc. DOI:10.1016/j.jeurceramsoc.2021.07.018.
- D. Garcés, A. G. Leyva and L. Mogni, Solid State Ionics, 2020, 347, 115239 CrossRef.
- Z. Gao, L. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602–1644 RSC.
- R. Pelosato, G. Cordaro, D. Stucchi, C. Cristiani and G. Dotelli, J. Power Sources, 2015, 298, 46–67 CrossRef CAS.
- A. A. Makhnev, L. V. Nomerovannaya, S. V. Strel’Tsov, V. I. Anisimov, S. N. Barilo and S. V. Shiryaev, Phys. Solid State, 2009, 51, 525–531 CrossRef CAS.
- X. Zhang, X. M. Wang, H. W. Wei, X. H. Lin, C. H. Wang, Y. Zhang, C. Chen and X. P. Jing, Mater. Res. Bull., 2015, 65, 80–88 CrossRef CAS.
- I. Szpunar, R. Strandbakke, M. H. Sørby, S. L. Wachowski, M. Balaguer, M. Tarach, J. M. Serra, A. Witkowska, E. Dzik, T. Norby, M. Gazda and A. Mielewczyk-Gryn, Materials, 2020, 13, 4044 CrossRef CAS PubMed.
- E. Vøllestad, M. Schrade, J. Segalini, R. Strandbakke and T. Norby, J. Mater. Chem. A, 2017, 5, 15743–15751 RSC.
- A. Grimaud, K. J. May, C. E. Carlton, Y. L. Lee, M. Risch, W. T. Hong, J. Zhou and Y. Shao-Horn, Nat. Commun., 2013, 4, 1–7 Search PubMed.
- P. Yasodha, M. Premila, A. Bharathi, M. C. Valsakumar, R. Rajaraman and C. S. Sundar, J. Solid State Chem., 2010, 183, 2602–2608 CrossRef CAS.
- S. V. Telegin, A. Y. Zuev, S. V. Naumov, E. I. Patrakov and D. S. Tsvetkov, J Chem, 2017, 1–6 Search PubMed.
- D. S. Tsvetkov, V. V. Sereda and A. Y. Zuev, Solid State Ionics, 2011, 192, 215–219 CrossRef CAS.
- A. Y. Suntsov, I. A. Leonidov, M. V. Patrakeev and V. L. Kozhevnikov, J. Solid State Chem., 2011, 184, 1951–1955 CrossRef CAS.
- B. V. Politov, A. Y. Suntsov, D. G. Kellerman, I. A. Leonidov and V. L. Kozhevnikov, J. Magn. Magn. Mater., 2019, 469, 259–263 CrossRef CAS.
- E. A. Antipinskaya, S. N. Marshenya, B. V. Politov and A. Y. Suntsov, Solid State Ionics, 2019, 339, 115002 CrossRef CAS.
- S. N. Marshenya, B. V. Politov, A. Y. Suntsov, I. A. Leonidov, S. A. Petrova, M. V. Patrakeev and V. L. Kozhevnikov, J. Alloys Compd., 2018, 767, 1041–1047 CrossRef CAS.
- A. Y. Suntsov, I. A. Leonidov, M. V. Patrakeev and V. L. Kozhevnikov, Solid State Ionics, 2015, 274, 17–23 CrossRef CAS.
- B. V. Politov, A. Y. Suntsov, I. A. Leonidov, M. V. Patrakeev and V. L. Kozhevnikov, J. Alloys Compd., 2017, 727, 778–784 CrossRef CAS.
- S. N. Marshenya, B. V. Politov, D. A. Osinkin, A. Y. Suntsov, I. A. Leonidov and V. L. Kozhevnikov, J. Alloys Compd., 2019, 779, 712–719 CrossRef CAS.
- M. D. Abràmoff, P. J. Magalhães and S. J. Ram, Biophotonics Int., 2004, 11, 36–41 Search PubMed.
- I. A. Leonidov, V. L. Kozhevnikov, E. B. Mitberg, M. V. Patrakeev, V. V. Kharton and F. M. B. Marques, J. Mater. Chem., 2001, 11, 1201–1208 RSC.
- L. Vasylechko, V. Vashook, D. Savytskii, A. Senyshyn, R. Niewa, M. Knapp, H. Ullmann, M. Berkowski, A. Matkovskii and U. Bismayer, J. Solid State Chem., 2003, 172, 396–411 CrossRef CAS.
- J. L. García-Muñoz, C. Frontera, A. Llobet, A. E. Carrillo, A. Caneiro, M. A. G. Aranda, C. Ritter and E. Dooryee, Phys. B: Condens. Matter, 2004, 350, 277–279 CrossRef.
- G. Kim, S. Wang, A. J. Jacobson, L. Reimus, P. Brodersen and C. A. Mims, J. Mater. Chem., 2007, 17, 2500–2505 RSC.
- A. S. Urusova, V. A. Cherepanov, O. I. Lebedev, T. V. Aksenova, L. Y. Gavrilova, V. Caignaert and B. Raveau, J. Mater. Chem. A, 2014, 2, 8823–8832 RSC.
- H. Zhao, Y. Zheng, C. Yang, Y. Shen, Z. Du and K. Świerczek, Int. J. Hydrogen Energy, 2013, 38, 16365–16372 CrossRef CAS.
- P. Miao, X. Lin, S. Lee, Y. Ishikawa, S. Torii, M. Yonemura, T. Ueno, N. Inami, K. Ono, Y. Wang and T. Kamiyama, Phys. Rev. B, 2017, 95, 1–12 Search PubMed.
- Y. Xin, L. Shi, J. Zhao, X. Yuan, S. Zhou, L. Hou, R. Tong and S. Pan, J. Alloys Compd., 2020, 819, 153001 CrossRef CAS.
- K. Tomiyasu, S. I. Koyama, M. Watahiki, M. Sato, K. Nishihara, Y. Takahashi, M. Onodera, K. Iwasa, T. Nojima, H. Nojiri, J. Okamoto, D. J. Huang, Y. Yamasaki, H. Nakao and Y. Murakami, J. Phys. Soc. Jpn., 2016, 85, 1–7 CrossRef.
- V. S. Kudyakova, A. M. Shalamova, B. V. Politov and A. Y. Suntsov, J. Alloys Compd., 2021, 886, 161133 CrossRef CAS.
- F. A. Kroger and H. J. Vink, Solid State Phys., 1956, 3, 307–435 CAS.
- M. U. Gutowska, J. Wieckowski, A. Szewczyk, S. Kolesnik, B. Dabrowski, M. Kowalczyk, J. Pietosa, N. Nedelko and R. Minikayev, J. Alloys Compd., 2016, 670, 175–181 CrossRef CAS.
- J. Pietosa, K. Piotrowski, R. Puzniak, A. Wisniewski, S. Kolesnik and B. Dabrowski, J. Alloys Compd., 2015, 645, 223–229 CrossRef CAS.
- S. S. Pramana, A. Cavallaro, C. Li, A. D. Handoko, K. W. Chan, R. J. Walker, A. Regoutz, J. S. Herrin, B. S. Yeo, D. J. Payne, J. A. Kilner, M. P. Ryan and S. J. Skinner, J. Mater. Chem. A, 2018, 6, 5335–5345 RSC.
- L. Mogni, F. Prado, C. Jiménez and A. Caneiro, Solid State Ionics, 2013, 240, 19–28 CrossRef CAS.
- V. P. Zhukov and E. V. Chulkov, Phys. Solid State, 2021, 63, 395–404 CrossRef CAS.
- E. Chavez, M. Mueller, L. Mogni and A. Caneiro, J. Phys.: Conf. Ser., 2009, 167, 012043 CrossRef.
- S. Streule, A. Podlesnyak, D. Sheptyakov, E. Pomjakushina, M. Stingaciu, K. Conder, M. Medarde, M. V. Patrakeev, I. A. Leonidov, V. L. Kozhevnikov and J. Mesot, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 3–7 Search PubMed.
- C. Lim, A. Jun, H. Jo, K. M. Ok, J. Shin, Y. W. Ju and G. Kim, J. Mater. Chem. A, 2016, 4, 6479–6486 RSC.
- S. V. Naumov, V. I. Voronin, I. F. Berger, M. S. Udintseva, V. V. Mesilov, B. A. Gizhevskii, S. V. Telegin and V. R. Galakhov, J. Alloys Compd., 2020, 817, 152775 CrossRef CAS.
- S. S. Nikitin, E. N. Naumovich, O. V. Merkulov, I. A. Leonidov and M. V. Patrakeev, Acta Mater., 2021, 203, 116489 CrossRef CAS.
- J. B. Goodenough, Mater. Res. Bull., 1967, 6, 967–976 CrossRef.
- A. Sergeev and V. Mitin, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 6041–6047 CrossRef CAS.
- A. J. Freeman and R. E. Watson, Phys. Rev., 1962, 127, 2058–2075 CrossRef CAS.
- H. Sözeri, H. Deligöz, H. Kavas and A. Baykal, Ceram. Int., 2014, 40, 8645–8657 CrossRef.
- P. W. Selwood, Magnetochemistry, Interscience, New York, 1956 Search PubMed.
- R. W. Vest and N. M. Tallan, J. Appl. Phys., 1965, 36, 543–547 CrossRef CAS.
- A. J. Bosman and H. J. van Daal, Adv. Phys., 1970, 19, 1–117 CrossRef CAS.
- A. Tarancón, D. Marrero-López, J. Peña-Martínez, J. C. Ruiz-Morales and P. Núñez, Solid State Ionics, 2008, 179, 611–618 CrossRef.
- D. S. Tsvetkov, I. L. Ivanov, D. A. Malyshkin, A. L. Sednev, V. V. Sereda and A. Y. Zuev, Pure Appl. Chem., 2019, 91, 923–940 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04624a |
| This journal is © the Owner Societies 2022 |