Dramatic differences in the conformational equilibria of chalcogen-bridged compounds: the case of diallyl ether versus diallyl sulfide†
Tamanna
Poonia
 ,
Weslley G. D. P.
Silva
,
Weslley G. D. P.
Silva
 and
Jennifer
van Wijngaarden
and
Jennifer
van Wijngaarden
 *
*
Department of Chemistry, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada. E-mail: vanwijng@cc.umanitoba.ca; Fax: +204474-7608; Tel: +204474-8379
First published on 3rd December 2021
Abstract
The conformational landscapes of diallyl ether (DAE) and diallyl sulfide (DAS) were investigated for the first time using rotational spectroscopy from 6–20 GHz supported by quantum mechanical calculations. A significant difference in the conformational distribution of these chalcogen-bridged compounds is predicted by theory at the B3LYP-D3(BJ)/aug-cc-pVTZ level as DAS has only one low energy conformer while DAE has up to 12 energy minima within 5 kJ mol−1. This was confirmed by rotational spectroscopy as only transitions corresponding to the global minimum of DAS were observed while the spectrum of DAE was much richer and composed of features from the nine lowest energy conformers. To understand the effects that govern the conformational preferences of DAE and DAS, natural bond orbital and non-covalent interaction analyses were done. These show that unique orbital interactions stabilize several conformers of the ether making its conformational landscape more competitive than that of the sulfide. This is consistent with a bonding model involving decreased hybridization of the bridging atom as one moves down the periodic table which is confirmed by the experimental ground state structures of the lowest energy forms of DAE and DAS, derived using spectra of the 13C and 34S substituted species in natural abundance.
Introduction
It is well-established that organic molecules can adopt different conformers by rotating about single bonds and that their tertiary structure is central to many chemical and biological processes. In most environments, it is difficult to isolate individual conformers and thus relate bulk properties to underlying molecular-level phenomena which leaves chemists to empirically screen many compounds for a desired reactivity. In this sense, modern rotational spectroscopy offers great promise in informing the design of new chemical processes as it allows the unambiguous identification of conformers that are isolated in a collision-free jet.1–3 The conformer geometries, relative energies and dynamics extracted from a rotational spectrum provide deeper insights into the attractive and repulsive interactions that govern physical and chemical properties.4–6While various allyl containing compounds are found to play an important role in processes in diverse fields such as medicine,7 polymer science,8 catalysis9,10 and atmospheric chemistry,11,12 from a fundamental perspective, these species also serve as interesting test cases for conformational studies. This is due to the flexibility of the side chain and the presence of an unsaturated region (vinyl substituent) that can introduce additional stabilizing interactions compared with aliphatic side chains. The rich conformational landscape of allylic compounds was recently highlighted in microwave spectroscopic characterizations of molecules containing one (allyl isothiocynate,13 allyl isocyanate14 and allyl methyl amine5) and two allyl (diallyl amine4 and diallyl disulfide15) moieties. For each, a highly molecule-specific balance of stereoelectronic effects (e.g. steric hindrance, orbital interactions, hydrogen bonding, etc.) was found to govern the observed conformational preferences. For the diallyl molecules in particular, the electronegative bridging group (NH in diallyl amine or the disulfide linkage in diallyl disulfide) plays a key directing role in the conformational equilibria giving rise to an unusually complex and non-intuitive distribution of conformer energies and shapes. This is seen, for example, by the significant differences in the conformational equilibria of diallyl amine (DAA)4 and diallyl disulfide (DADS).15 While DAA is smaller and has one fewer dihedral angle, its rotational spectrum contains transitions from four prominent conformers compared with the spectrum of DADS which features only one conformer.
The chalcogen-bridged analogs of the amine, diallyl ether (DAE) and diallyl sulfide (DAS), provide a more prescriptive case study of the role of the central atom on directing the conformational preferences as a function of its size and electronic properties. There are no prior rotational spectroscopic studies of either DAE or DAS, however, the latter has been investigated by theory and vibrational spectroscopy (liquid, solid and gas phase and Ar-matrix infrared, and Raman).12,16 The vibrational spectrum of DAS suggests the presence of four stable conformers with the global minimum accounting for about 52% of the total conformational population. This competition seems rather surprising in light of the results for the related disulfide (DADS) for which only one geometry was observed experimentally.15 As chalcogen-substitution has received substantial attention in the materials science community17 as a means to tune the optoelectronic properties of organic materials used in photovoltaics,18 light emitting diodes19 and sensors,20 there is great value in deriving deeper understanding of the energy states of organochalcogens through detailed studies of their underlying potential energy surfaces.
Herein, we report the first investigation of the conformers of DAE and DAS using Fourier transform microwave (FTMW) spectroscopy supported by B3LYP-D3(BJ)/aug-cc-pVTZ predictions. A drastic reduction in the conformational competition was found when moving to the heavier organochalcogen with spectra attributable to nine unique conformers found for DAE and only one for DAS. To explain this surprising difference, we used natural bond orbital (NBO) and non-covalent interaction (NCI) analyses to characterize their electronic structures as a function of the bridging atom and to identify preferential orbital interactions that promote stability in conformers of the ether.
Experimental methods
DAS (97%, bp: 138 °C) and DAE (98%, bp: 94 °C) are commercially available from Sigma-Aldrich Canada and were used without further purification in this study. As both samples are liquid at room temperature, a gas mixture containing either ∼1% of DAS or ∼1% of DAE in neon (100–200 kPa) was prepared at room temperature. The gas mixture was then expanded into the high vacuum chamber of the spectrometers through a pulsed nozzle (1 mm diameter) resulting in a supersonic jet expansion. The rotational spectra of DAS and DAE were measured using both a chirped-pulse (cp)21 and a cavity-based Balle-Flygare (BF)22 type Fourier transform microwave (FTMW) spectrometer, both of which have been described in detail previously.23,24 A survey cp-FTMW spectrum was initially measured in 2 GHz segments from 8–18 GHz from which the most intense rotational transitions of the conformers were identified. Next, final frequency measurements were done using the BF-FTMW instrument from 6–20 GHz which features higher resolution and sensitivity. In the BF-FTMW instrument, due to the collinear arrangement of the molecular beam and the resonator axis, all rotational transitions recorded appear as two Doppler split components. In the cavity-based instrument, the transitions have line widths of ∼7 kHz (FWHM) and the uncertainty in the measurement of line positions is typically ±2 kHz.Computational methods
The presence of four dihedral angles γ, θ, δ and ϕ in the heavy atom backbones of DAS and DAE makes their conformational landscapes complex as different conformers may arise from internal rotations around these single bonds as shown in Fig. 1. For both molecules, an automated conformational search was first carried out to identify potential conformers using the Conformer-Rotamer Ensemble Sampling Tool (CREST) at the GFN2-xTB25 level of theory as available in the extended tight binding (xTB) program package.26,27 The automated search led to 53 and 55 possible geometries for DAS and DAE, respectively. Next, all these 53 and 55 starting geometries were fully optimized using the dispersion-corrected density functional theory (DFT) B3LYP28-D3(BJ)29,30 method with Dunning's aug-cc-pVTZ31 basis set. Upon comparing the optimized DFT structures with those from CREST, it was noted that both methods predict similar global minimum geometries for DAE and DAS but different relative energy orderings of the remaining conformers. Vibrational frequency calculations within the harmonic approximation were performed for all optimized geometries at the same level of theory to verify the nature of the stationary points and to obtain electronic energies with zero-point corrections (ZPE) and quartic centrifugal distortion constants. All optimization and frequency calculations were done using the Gaussian 16 software.32 Natural bond orbital (NBO)33 and non-covalent interaction (NCI)34 calculations were carried out using the NBO 7.035 and NCIPLOT36 programs, respectively, to investigate the stereoelectronic effects responsible for the observed conformational preferences.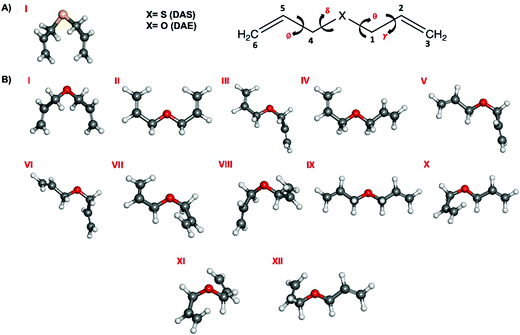 | ||
| Fig. 1 Lowest energy conformers of (A) DAS and (B) DAE that fall within 5 kJ mol−1 of the global minimum at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory. | ||
Results
Conformational space of DAS and DAE
A surprisingly rich conformational equilibrium was predicted for DAS and DAE. The geometry optimization calculations identified 24 unique geometries of DAS within ∼26 kJ mol−1 and 23 for DAE within 15 kJ mol−1. Those found within 5 kJ mol−1 of the global minimum are shown in Fig. 1 for DAS (one conformer) and DAE (12 conformers) while the energetic and spectroscopic parameters of all minima are given in Table 1. The Cartesian coordinates of the DAS and DAE conformers are provided in the ESI,† file in Tables S1–S13 and the dihedral angles for all conformers are provided in Tables S14 and S15 (ESI†). Roman numerals were used to label the conformers to reflect their stability ordering, based on the ΔE0, with conformer I predicted to be the most stable.| DAS | ΔEea | ΔE0b | P | A/B/Cd | |μa|/|μb|/|μc|e |
|---|---|---|---|---|---|
| a Relative total electronic energy in kJ mol−1. b Zero-point energy (ZPE) corrected relative total energies in kJ mol−1. c Boltzmann population at 298 K in %. These populations do not account for the degeneracy of the conformers due to symmetry (see text). d Rotational constants in MHz. e Magnitude of the electric dipole moment components in Debye. | |||||
| I | 0.00 | 0.00 | 83.0 | 2449/1781/1186 | 0.0/1.2/0.0 |
| II | 7.06 | 6.58 | 4.8 | 2833/1545/1257 | 0.4/1.3/0.2 |
| III | 7.80 | 7.11 | 3.6 | 3215/1310/1044 | 0.4/1.3/0.1 |
| IV | 8.22 | 7.57 | 3.0 | 4192/1083/924 | 0.7/1.1/0.6 |
| V | 9.28 | 8.42 | 2.0 | 3949/1106/932 | 0.6/1.0/0.7 |
| VI | 10.04 | 9.27 | 1.4 | 2925/1420/1049 | 0.7/1.0/0.7 |
| VII | 12.42 | 11.34 | 0.6 | 2272/1938/1151 | 0.1/1.1/0.6 |
| VIII | 13.99 | 12.82 | 0.3 | 4397/1133/973 | 0.9/1.1/0.6 |
| IX | 14.22 | 13.13 | 0.3 | 2534/1745/1265 | 0.6/1.0/0.9 |
| X | 15.69 | 14.55 | 0.1 | 4486/1098/977 | 0.6/0.5/1.4 |
| XI | 16.02 | 14.84 | 0.1 | 4187/1125/980 | 0.5/0.4/1.4 |
| XII | 16.27 | 14.94 | 0.1 | 10163/775/765 | 0.0/1.6/0.1 |
| XIII | 16.37 | 15.04 | 0.1 | 10484/775/764 | 0.0/1.6/0.0 |
| XIV | 16.25 | 15.07 | 0.1 | 5626/912/849 | 0.3/0.8/1.2 |
| XV | 16.21 | 15.15 | 0.1 | 3659/1268/1245 | 0.0/1.4/0.0 |
| XVI | 16.55 | 15.39 | 0.1 | 4129/1118/1058 | 0.2/1.3/0.7 |
| XVII | 16.96 | 15.61 | 0.1 | 6600/874/832 | 0.2/0.9/1.1 |
| XVIII | 17.47 | 16.52 | 0.1 | 4396/1056/950 | 0.0/1.4/0.0 |
| XIX | 17.95 | 16.82 | 0.1 | 2860/1532/1139 | 0.1/0.5/1.4 |
| XX | 18.23 | 17.02 | 0.1 | 3408/1191/964 | 0.3/0.7/1.3 |
| XXI | 20.56 | 19.12 | 0.0 | 4220/1182/1076 | 0.8/0.5/1.4 |
| XXII | 21.38 | 19.65 | 0.0 | 8387/860/809 | 0.1/1.7/0.0 |
| XXIII | 21.89 | 20.22 | 0.0 | 6238/935/889 | 0.5/1.3/0.9 |
| XXIV | 26.06 | 23.98 | 0.0 | 6829/974/861 | 0.0/1.9/0.0 |
| DAE | ΔEea | ΔE0b | P | A/B/Cd | |μa|/|μb|/|μc|e |
|---|---|---|---|---|---|
| I | 0.00 | 0.00 | 15.8 | 3784/1817/1396 | 0.0/1.2/0.0 |
| II | 2.01 | 0.42 | 13.3 | 5842/1379/1131 | 0.0/1.6/0.0 |
| III | 1.70 | 0.75 | 11.6 | 7505/1208/1129 | 1.1/0.9/0.5 |
| IV | 3.27 | 1.59 | 8.3 | 8059/1104/1010 | 0.3/1.3/0.0 |
| V | 2.78 | 1.76 | 7.7 | 6276/1198/1078 | 0.6/0.7/0.7 |
| VI | 3.03 | 1.95 | 7.2 | 7493/1125/1055 | 0.7/0.9/0.4 |
| VII | 2.84 | 2.16 | 6.6 | 5214/1501/1352 | 0.7/0.6/1.1 |
| VIII | 2.65 | 2.39 | 6.0 | 5204/1422/1380 | 0.5/1.1/0.2 |
| IX | 4.61 | 2.73 | 5.2 | 11535/932/924 | 0.0/1.1/0.4 |
| X | 4.48 | 3.61 | 3.7 | 5328/1421/1198 | 0.3/0.2/1.2 |
| XI | 4.24 | 3.84 | 3.3 | 6726/14191290 | 0.0/0.0/1.3 |
| XII | 5.18 | 4.20 | 2.9 | 6730/1270/1140 | 0.4/0.2/1.2 |
| XIII | 6.37 | 5.67 | 1.6 | 3941/1780/1510 | 0.8/0.5/1.0 |
| XIV | 7.10 | 6.46 | 1.2 | 6041/1267/1164 | 0.5/1.2/0.1 |
| XV | 7.93 | 6.69 | 1.1 | 8112/1112/1087 | 0.7/1.3/0.1 |
| XVI | 7.90 | 6.84 | 1.0 | 3379/2041/1411 | 0.1/0.9/0.6 |
| XVII | 7.43 | 6.90 | 1.0 | 4524/1533/1255 | 0.6/0.8/0.8 |
| XVIII | 8.79 | 7.48 | 0.8 | 8192/1062/998 | 0.3/0.2/1.2 |
| XIX | 9.47 | 8.02 | 0.6 | 11167/994/973 | 0.3/0.3/1.2 |
| XX | 8.92 | 8.08 | 0.6 | 7714/1220/1144 | 0.0/0.2/1.3 |
| XXI | 9.70 | 8.97 | 0.4 | 4136/1781/1382 | 0.2/0.1/1.3 |
| XXII | 13.85 | 12.61 | 0.1 | 1187/1011/1000 | 0.0/0.0/1.3 |
| XXIII | 15.34 | 14.99 | 0.0 | 7732/1176/1134 | 0.0/1.3/0.0 |
Spectral analysis
As the rotational spectra of DAS and DAE have not been previously reported, the calculated parameters from Table 1 were used as guides for the spectral analysis. Preliminary assignment of the observed patterns in the cp-FTMW spectra identified the lowest energy conformer for DAS and the first nine conformers for DAE (I–IX) in Fig. 1. Fig. 2 shows a region of the cp-FTMW spectrum of DAE featuring transitions for these nine assigned conformers to demonstrate the spectral complexity. For the lowest energy forms of DAS and DAE, the spectral intensity was sufficient to allow transitions from singly-substituted minor isotopologues to be observed in natural abundance. These include transitions for the three unique 13C isotopologues of each as well as the 34S isotopologue for DAS. For conformer I of DAE and DAS, the relative intensity of the 13C transitions were ∼2% that of the parent lines due to symmetry which yields two equivalent sites for each carbon atom. Following preliminary assignment of the patterns from the broadband spectrum, the observed transitions for all conformers were re-measured using the higher resolution BF-FTMW instrument and additional lower intensity features were measured to expand the data set. Although the rotational constants and dipole components (Table 1) were good guides for the spectral assignments, the intensities of the observed transitions for DAE were not fully consistent with the predicted populations in Table 1. For a better reproduction of the experimental intensities, the symmetry and resulting degeneracies of the conformers were considered. For example, conformer I of DAE has C2 symmetry with two equivalent minima, while conformer II with C2v symmetry exists as a single geometry. On the other hand, conformer III has C1 symmetry which leads to four equivalent conformations. Once the symmetry of all assigned conformers of DAE is considered, the calculated populations are: I: 15.5%, II: 6.5%, III: 22.9%, IV: 16.4%, V: 7.6%, VI: 7.1%, VII: 13.0%, VIII: 5.9%, IX: 5.1% rather than the values given in Table 1. The new values are consistent with the observed spectral intensities.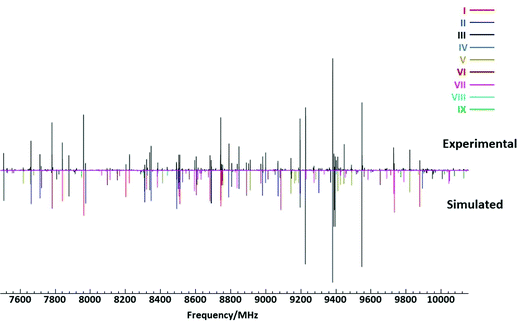 | ||
| Fig. 2 Portion of the broadband cp-FTMW spectrum (average of 1.5 million free induction decays) of DAE showing rotational transitions observed for the nine lowest energy conformers. The top portion is the experimental spectrum and the lower is the simulated spectrum using the fitted parameters from Tables 3 and 4. Intensities are dependent on the calculated dipole moment components and the relative populations from Table 1. | ||
The transition frequencies of each species from the BF-FTMW measurements were least-squared fit with Pickett's SPFIT program37 using Watson's A-reduced Hamiltonian38 in the Ir representation to obtain experimental rotational and quartic centrifugal distortion constants which are summarized in Tables 2–4. Line lists containing all assigned rotational transitions and their residuals are given in Tables S18–S34 of the ESI.† Despite careful searches, transitions attributable to higher energy conformers of DAS and DAE were not observed.
| Parameter | I | 13C1 | 13C2 | 13C3 | 34S |
|---|---|---|---|---|---|
| a Rotational constants. b Quartic centrifugal distortion constants. c Electric dipole moment components (“y” if observed and “n” if not observed). d Range of observed rotational quantum number for the upper state (J′). e Total number of lines (N) in the fit. f Root-mean-square deviation of the fit (σ). A complete list of the calculated rotational parameters at the B3LYP-D3(BJ)/aug-cc-pVTZ is provided in Table S16 (ESI). | |||||
| A/MHza | 2447.825367(51) | 2438.40000(15) | 2445.98277(11) | 2414.296667(93) | 2394.45055(14) |
| B/MHz | 1783.279427(47) | 1771.27288(26) | 1759.05341(17) | 1758.70686(14) | 1783.30467(15) |
| C/MHz | 1180.778463(45) | 1177.021037(77) | 1169.802141(59) | 1162.645711(50) | 1168.200759(62) |
| Δ J/kHzb | 1.67263(47) | 1.6344(41) | 1.6250(21) | 1.6495(19) | 1.6625(21) |
| Δ JK/kHz | −4.6702(10) | −4.505(14) | −4.5602(74) | −4.5739(63) | −4.6773(89) |
| Δ K/kHz | 5.4083(12) | 5.223(15) | 5.3600(58) | 5.2663(50) | 5.3463(70) |
| δ J/kHz | 0.70110(16) | 0.6838(20) | 0.6794(10) | 0.69231(92) | 0.7030(10) |
| δ K/kHz | 0.70125(51) | 0.7187(73) | 0.7086(40) | 0.7064(27) | 0.6078(37) |
| μ a/μb/μcc | n/y/n | n/y/n | n/y/n | n/y/n | n/y/n |
| J′d | 2–10 | 2–8 | 2–8 | 2–8 | 2–8 |
| N | 87 | 35 | 37 | 37 | 37 |
| σ/kHzf | 1.0 | 1.1 | 0.9 | 0.8 | 0.9 |
| Parameter | Conformer I | 13C1 | 13C2 | 13C3 |
|---|---|---|---|---|
| a Rotational constants. b Quartic centrifugal distortion constants. c Electric dipole moment components (“y” if observed and “n” if not observed). d Range of observed rotational quantum number for the upper state (J′) e Total number of lines (N) in the fit. f Root-mean-square deviation of the fit (σ). Values in brackets were fixed to those determined for the parent species. A complete list of the calculated rotational parameters at the B3LYP-D3(BJ)/aug-cc-pVTZ is provided in Table S17. | ||||
| A/MHza | 3783.26132(19) | 3756.61996(76) | 3782.29381(82) | 3731.21601(66) |
| B/MHz | 1815.02675(18) | 1806.04406(39) | 1791.78164(49) | 1786.36659(38) |
| C/MHz | 1392.94239(14) | 1387.99557(33) | 1379.30819(38) | 1369.12820(29) |
| Δ J/kHzb | 3.7222(22) | 3.6924(56) | 3.6918(65) | 3.7003(50) |
| Δ JK/kHz | −17.7190(49) | −17.563(56) | −17.555(58) | −17.527(46) |
| Δ K/kHz | 29.3613(93) | 28.98(11) | 29.21(11) | 28.703(92) |
| δ J/kHz | 1.34698(82) | [1.34698] | [1.34698] | [1.34698] |
| δ K/kHz | 3.2401(88) | [3.2401] | [3.2401] | [3.2401] |
| μ a/μb/μcc | n/y/n | n/y/n | n/y/n | n/y/n |
| J′d | 2–9 | 2–6 | 2–6 | 2–6 |
| N | 46 | 16 | 14 | 15 |
| σ/kHzf | 1.6 | 2.3 | 2.2 | 1.8 |
| Parameter | II | III | IV | V | VI | VII | VIII | IX |
|---|---|---|---|---|---|---|---|---|
| a Rotational constants. b Quartic centrifugal distortion constants. c Electric dipole moment components (“y” if observed and “n” if not observed). d Range of observed rotational quantum number for the upper state (J′). e Total number of lines (N) in the fit. f Root-mean-square deviation of the fit (σ). Values in brackets were fixed to the predicted values obtained at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory. A complete list of the calculated rotational parameters at the B3LYP-D3(BJ)/aug-cc-pVTZ is provided in Table S17 (ESI). | ||||||||
| A/MHza | 5778.39751(83) | 7474.59182(36) | 7983.34964(53) | 6196.70156(13) | 7433.27031(24) | 5196.26139(43) | 5268.65716(22) | 11414.02484(47) |
| B/MHz | 1392.06750(11) | 1214.02905(52) | 1110.32576(76) | 1208.265554(39) | 1129.15749(33) | 1511.415694(91) | 1415.96699(26) | 934.64344(26) |
| C/MHz | 1139.27067(14) | 1133.29913(52) | 1015.20606(74) | 1083.339960(48) | 1057.78776(32) | 1359.856187(94) | 1378.23179(26) | 926.73986(26) |
| Δ J/kHzb | 0.25929(93) | 0.40733(98) | 0.1835(14) | 0.50571(27) | 0.26314(53) | 1.81536(76) | 1.13564(90) | 0.1490(66) |
| Δ JK/kHz | −1.4672(72) | −10.9365(62) | −5.2452(93) | −9.0581(18) | −4.7302(33) | −14.1707(54) | −12.9628(30) | −14.5608(83) |
| Δ K/kHz | 7.93(18) | [162.9582] | 21.01(14) | 77.203(13) | [71.538104] | 55.543(87) | 55.693(20) | [535.86204] |
| δ J/kHz | 0.06735(44) | 0.00922(55) | 0.02392(28) | 0.11361(14) | 0.05348(17) | 0.53599(48) | 0.17603(51) | 0.01438(19) |
| δ K/kHz | 0.835(23) | 4.57(26) | −1.02(37) | 1.365(10) | 0.42(16) | 4.892(31) | −3.61(12) | [−6.4307101] |
| μ a/μb/μcc | n/y/n | y/y/y | y/y/n | y/y/y | y/y/y | y/y/y | y/y/y | n/y/y |
| J′d | 1–10 | 1–9 | 1–11 | 1–11 | 1–11 | 1–9 | 1–9 | 1–11 |
| N | 30 | 67 | 40 | 110 | 74 | 71 | 67 | 28 |
| σ/kHzf | 1.5 | 1.5 | 1.1 | 1.1 | 1.0 | 1.3 | 1.4 | 1.5 |
Structural determination
With the measurement of the spectra of minor isotopic species for conformer I of both compounds, the geometries of the heavy atom skeletons were determined using the complete sets of experimental rotational constants from Tables 2 and 3 for DAS and DAE, respectively. Accounting for symmetry, the atomic coordinates of the substituted atoms and their Costain39 errors were estimated by solving Kraitchman's equations40 as implemented in Kisiel's KRA program.41 These are summarized in Table S35 of the ESI.† The signs of the coordinates were inferred by comparison with the computational geometries and the imaginary c-coordinate for sulfur in the case of DAS was set to zero in the subsequent analysis as it lies in the ab-plane of the molecule. The resulting sets of coordinates were used to estimate the internal geometric parameters involving the heavy atoms using the EVAL program41 which are summarized in Tables 5 and 6 for DAS and DAE, respectively, under the rs headings. Overall, fewer structural elements were determined for DAE due to absence of 18O data and the uncertainty in the derived bond lengths is about three times larger than in the sulfur containing analog. This is likely a consequence of the relatively large Costain error in the position of C2 (Fig. 1) in DAE which lies only 0.065(23) Å from the ac-plane.| r e | r s | r 0 | |
|---|---|---|---|
| S–C1 | 1.838 | 1.823(3) | 1.826(5) |
| C1–C2 | 1.490 | 1.489(7) | 1.490(10) |
| C2–C3 | 1.328 | 1.347(4) | 1.349(9) |
| ∠C4–S–C1 | 100.1 | 99.3(2) | 99.6 (3) |
| ∠S–C1–C2 | 112.1 | 111.9(3) | 111.9(6) |
| ∠C1–C2–C3 | 124.3 | 122.5(5) | 122.6(13) |
| ∠C2–C1–S–C4 | 68.7 | 69.5(2) | 69.4(4) |
| ∠C3–C2–C1–S | −115.5 | −119.4(6) | −119.0(15) |
| r e | r s | r 0 | |
|---|---|---|---|
| C1–C2 | 1.499 | 1.507(12) | 1.487(8) |
| C2–C3 | 1.326 | 1.340(23) | 1.309(17) |
| ∠C1–O–C4 | 114.2 | — | 113.8(6) |
| ∠C2–C1–O | 112.6 | — | 113.0(3) |
| ∠C1–C2–C3 | 124.2 | 122.6(10) | 125.1(9) |
| ∠C2–C1–O–C4 | −69.1 | — | −69.4(5) |
The ground state effective geometries, r0, of DAS and DAE were then derived using Kisiel's STRFIT program41 to fit the effective moments of inertia to a set of internal parameters. This procedure was carried out by fixing the equilibrium internal coordinates of hydrogen atoms to those derived at the B3LYP-D3(BJ)/aug-cc-pVTZ level of theory. Accounting for symmetry, there are eight internal parameters needed to define the arrangement of the allyl side chains (three bond lengths, three angles and two dihedral angles) relative to the central atom. With 15 rotational constants determined from fitting transitions arising from five isotopologues of DAS, all eight structural parameters were well-determined and these are listed in Table 5. For DAE, with data from one fewer isotopologue, several combinations of parameters were considered as the fit was not particularly sensitive to the C–O bond length. In the end, six structural parameters were determined for DAE in the fit after keeping the C–O bond length and the C–C–C–O dihedral angle fixed at the computed values. The results are provided in Table 6. Overall, the derived r0 parameters are an excellent model of the geometries as this procedure successfully reproduced the experimental rotational constants of conformer I of DAS and DAE to within 0.004% and 0.013% or better.
Discussion
The surprising differences in the conformational landscape of DAS and DAE, both in terms of the conformer geometries and relative energies predicted by DFT calculations, are confirmed by the FTMW measurements. The ground state spectroscopic constants obtained from fitting the experimental spectrum of both molecules are well-determined and in good agreement with the calculated values for conformer I of DAS and conformers I through IX of DAE at the B3LYP-(D3)BJ/aug-cc-pVTZ level of theory shown in Tables 1–4. Although additional conformers for both molecules are populated at 298 K (Table 1), the absence of features from higher energy structures in the rotational spectrum may be justified by insufficient population in the supersonic jet which is likely exacerbated by conformational cooling. This process allows higher energy conformers to interconvert to lower energy forms through collisions with the carrier gas at the beginning of the expansion. For small molecules and complexes, interconversion barriers less than ∼5 kJ mol−1 are known to allow for relaxation in the molecular beam.42 Modelling the interconversion pathways for the conformer relaxation of DAE and DAS is complex as it requires simultaneous changes for up to four dihedral angles, but the observation of nine conformers for DAE affirms that relaxation involving movement of the heavy alkyl chains is not facile. In general, for both DAS and DAE, conformers with relative energies within 3 kJ mol−1 of the global minimum were observed, which is coincidentally the same energy cut-off reported in the previous microwave study of the related diallyl amine (DAA) compound.4Based on the relative energies from Table 1 and the number of species identified in the supersonic jet for DAS and DAE, it is evident that the conformational landscape of DAE is highly competitive compared to that of DAS. Interestingly, although conformational changes upon replacing oxygen with sulfur in organic molecules were predicted from theoretical studies of a series of analogs of alcohols, thiols, ethers and sulfides,43 with the oxygen compounds showing a more competitive equilibrium, these large differences in conformational equilibria have not been widely explored spectroscopically. This makes DAE and DAS excellent prototypes to test whether these phenomena are observed experimentally. By analyzing the geometries corresponding to the minima of DAE and DAS (Fig. 1), it is readily apparent that many of the low energy conformers of DAE have one or both vinyl groups in the plane of the (C–X–C) link and pointed up (dihedral angles 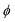 and
and  = 0°), such as in conformer II in which the orientation of the allyl moieties form a “W-shaped” structure. The analogous geometries are not stable in DAS or are much higher in energy which provides an important clue towards understanding why the conformational distribution is so unique for these two organochalcogens.
= 0°), such as in conformer II in which the orientation of the allyl moieties form a “W-shaped” structure. The analogous geometries are not stable in DAS or are much higher in energy which provides an important clue towards understanding why the conformational distribution is so unique for these two organochalcogens.
According to NBO calculations, this marked difference in conformational stability can be rationalized in terms of orbital interactions through their second order perturbation energies. Conformers of DAE with a W-shaped or with a V-shaped side chain (only one allyl group pointing up, e.g. conformer III) favour LP1(O) → σ*C–C orbital interactions involving donation from the lone pair LP1 on oxygen to the antibonding σ* orbital of the neighbouring C1–C2 and/or C4–C5 bond, whereas in the DAS analogs, these hyperconjugative interactions are largely absent. This is illustrated in Fig. 3 and Table S36 (ESI†) using the NBO results for conformer II of DAE and conformer XXIV of DAS, which have comparable dihedral angles. The greater stabilizing orbital interactions in the DAE geometries are possible because of better overlap between the donor and acceptor orbitals compared with that in the heavier congener. The enhanced orbital interactions in the ether are responsible for its competitive conformational landscape. A similar observation was noted for oxygen versus sulfur compounds in the case of 1-butanol and 1-butanethiol and for iso-butanol and iso-butanethiol44 in which the alcohols exhibited LP(O) → σ*C–H and LP(O) → σ*C–C interactions and the thiols did not. The increased favourability of orbital interactions is also consistent with the natural charges on oxygen (−0.56) and sulfur (+0.19) from conformer I in DAE and DAS, respectively, as expected based on their relative intrinsic electronegativities. These results are illustrative of how sensitive molecular potential energy surfaces are to subtle changes in non-covalent interactions as one moves down the periodic table and how this gives rise to measurable differences in molecular properties such as structure.
 | ||
| Fig. 3 NBO plots for conformers II of DAE (left) and XXIV of DAS (right) showing the LP1(X) and σ*C–C orbitals. | ||
Although the richness of the conformational distributions of DAE and DAS are surprisingly different, the orientation of the two allyl groups in the lowest energy structure of each is somewhat similar as seen in Fig. 1. Upon closer inspection of the geometric parameters in Tables 5 and 6, the most notable difference is that the bridging angle C–S–C is ∼14° smaller than the corresponding C–O–C angle which brings the allyl groups closer to each other in DAS. This is consistent with the hybridization of the central atoms from the NBO calculations with the sulfide C–S bonding orbitals showing larger p-character on sulfur (84.8% for both) compared to those on oxygen (72.5–78.7%) in DAE. This confirms that hybridization models of bonding used to understand molecular geometry around lighter elements (O) cannot be extrapolated to heavier analogs (S).
To further investigate the origin of the high stability of conformers I of DAE and DAS, we carried out NCI analysis. While one might think that conformer I is favoured by interactions between the two allyl groups as this is the main effect governing the stability of other allyl containing molecules such as diallyl disulfide (DADS)15 and from the structures shown in Fig. 1, no strong interactions (represented by blue-coloured isosurfaces) are found in the NCI graphs (Fig. 4). Rather, a green-coloured surface indicative of a weak contact (either attractive or repulsive) is present suggesting that interactions between the allyl groups are not a substantial stabilizing effect. Indeed, based on the NBO output, neither conformer I of DAE nor DAS show charge transfer between the two allyl groups. Instead, this arrangement of the two allyl fragments appears to optimize other charge transfer interactions (summarized in Table S36, ESI†), including electron donation from the lone pair on the bridge atom LP2(S)/LP2(O) to the antibonding π* orbitals of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of both allyl side chains and thus stabilizes conformer I relative to others.
C bonds of both allyl side chains and thus stabilizes conformer I relative to others.
 | ||
| Fig. 4 NCI isosurfaces (s = 0.05, color scale for −0.02 < ρ < +0.02 a.u.) for conformer I of DAS and DAE. | ||
The dramatic differences in the conformational equilibria of DAE and DAS through the observed species and their geometries reinforces the fact that even substitution of heteroatoms within a group can completely alter the properties of an organic compound in impactful ways. Although bonding among p-block elements is of critical importance in most branches of chemistry, chemical intuition does not seamlessly extend to molecules with rich conformational landscapes as subtle changes in non-covalent interactions are sufficient to completely alter the relative energies of competing structures. This unexpected conformational complexity is surprising in DAE and DAS as the side chains are small and thus, the identity of the center atom controls the conformer distribution rather than interactions between the side chains.
Conclusions
Using quantum chemical calculations and rotational spectroscopy, the conformational landscapes of DAE and DAS were investigated for the first time. The results revealed a dramatic conformational change upon replacing the central bridging atom from oxygen to sulfur with the ether existing as a rich conformational mixture. This was confirmed by FTMW spectra from which transitions were assigned for nine stable conformers of DAE but for only one of DAS. A NBO analysis contributed new physical insights by identifying unique orbital interactions involving one lone pair on oxygen that stabilize specific geometries of DAE. By comparison, these interactions are absent in DAS because the lone pairs on sulfur do not adopt a favourable spatial arrangement. The larger p-character on S is consistent with less hybridization in the bonding between sulfur and carbon which is also manifested in the C–X–C angle of DAS which is 14° smaller than that of the ether. The surprising conformational differences of DAE and DAS highlight that the electronic properties of the bridging atom have a dramatic effect on the arrangement of the organic side chains. This re-affirms that models of bonding, dynamics and reactivity based on carbon and its neighbours cannot be automatically extrapolated as one moves down the periodic table. Our results lay the foundation for the development of improved models of chemical bonding, dynamics and reactivity in organochalcogens for better design of main group and organometallic compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Natural Sciences and Engineering Research Council of Canada (NSERC) through the Discovery Grant program. T. P. acknowledges the graduate student stipend support from the GETS program of the Faculty of Graduate Studies at the University of Manitoba. W. G. D. P. S. is grateful for the financial support provided by the Faculty of Graduate Studies (FGS) of the University of Manitoba through a UM Graduate Fellowship (UMGF).References
- S. R. Domingos, C. Pérez, C. Medcraft, P. Pinacho and M. Schnell, Phys. Chem. Chem. Phys., 2016, 18, 16682–16689 RSC.
- F. Xie, N. A. Seifert, M. Heger, J. Thomas, W. Jäger and Y. Xu, Phys. Chem. Chem. Phys., 2019, 21, 15408–15416 RSC.
- S. I. Murugachandran, J. Tang, I. Peña, D. Loru and M. E. Sanz, J. Phys. Chem. Lett., 2021, 12, 1081–1086 CrossRef CAS PubMed.
- W. G. D. P. Silva, G. Daudet, S. Perez, S. Thorwirth and J. van Wijngaarden, J. Chem. Phys., 2021, 154, 1–25 CrossRef PubMed.
- W. G. D. P. Silva, T. Poonia and J. van Wijngaarden, ChemPhysChem, 2020, 21, 2515–2522 CrossRef CAS PubMed.
- W. G. D. P. Silva, T. Poonia and J. van Wijngaarden, Phys. Chem. Chem. Phys., 2021, 23, 7368–7375 RSC.
- K. C. Lai, C. L. Kuo, H. C. Ho, J. S. Yang, C. Y. Ma, H. F. Lu, H. Y. Huang, F. S. Chueh, C. C. Yu and J. G. Chung, Phytomedicine, 2012, 19, 625–630 CrossRef CAS PubMed.
- Z. Jian and S. Mecking, Angew. Chem., Int. Ed., 2015, 54, 15845–15849 CrossRef CAS PubMed.
- P. Wu, Y. Liu, M. He and T. Tatsumi, J. Catal., 2004, 228, 183–191 CAS.
- K. H. Dragnev, R. W. Nims and R. A. Lubet, Biochem. Pharmacol., 1995, 50, 2099–2104 CrossRef CAS PubMed.
- A. R. Oliaey, A. Shiroudi, E. Zahedi and M. S. Deleuze, Monatshefte fur Chemie, 2018, 149, 1389–1400 CrossRef CAS.
- B. E. Arango Hoyos and R. M. Romano, J. Mol. Struct., 2019, 1182, 54–62 CrossRef CAS.
- J. Stitsky, W. G. D. P. Silva, W. Sun and J. van Wijngaarden, J. Phys. Chem. A, 2020, 124, 3876–3885 CrossRef CAS PubMed.
- W. Sun, O. P. Sogeke, W. G. D. P. Silva and J. van Wijngaarden, J. Chem. Phys., 2019, 151, 194304 CrossRef PubMed.
- J. Demaison, N. Vogt, R. T. Saragi, M. Juanes, H. D. Rudolph and A. Lesarri, Phys. Chem. Chem. Phys., 2019, 21, 19732–19736 RSC.
- M. T. Devlin, V. F. Kalasinsky and I. W. Levin, J. Mol. Struct., 1989, 213, 35–50 CrossRef CAS.
- G. C. Hoover and D. S. Seferos, Chem. Sci., 2019, 10, 9182–9188 RSC.
- J. G. Manion, J. R. Panchuk and D. S. Seferos, Chem. Rec., 2019, 19, 1113–1122 CrossRef CAS PubMed.
- T. Gneuß, M. J. Leitl, L. H. Finger, N. Rau, H. Yersin and J. Sundermeyer, Dalton Trans., 2015, 44, 8506–8520 RSC.
- Z. Lou, P. Li and K. Han, Acc. Chem. Res., 2015, 48, 1358–1368 CrossRef CAS PubMed.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer and B. H. Pate, J. Mol. Spectrosc., 2006, 238, 200–212 CrossRef CAS.
- T. J. Balle and W. H. Flygare, Rev. Sci. Instrum., 1981, 52, 33–45 CrossRef CAS.
- L. Evangelisti, G. Sedo and J. van Wijngaarden, J. Phys. Chem. A, 2011, 115, 685–690 CrossRef CAS PubMed.
- G. Sedo and J. van Wijngaarden, J. Chem. Phys., 2009, 131, 044303 CrossRef PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- A. D. Becke, J. Chem. Phys., 1998, 109, 2092–2098 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 1–19 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 (Revision C.01), Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- F. Weinhold, C. R. Landis and E. D. Glendening, Int. Rev. Phys. Chem., 2016, 35, 399–440 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0., Theoretical Chemistry Institute, University of Wisconsin, Madison, 2018 Search PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS.
- J. K. G. Watson, J. Chem. Phys., 1968, 48, 4517–4524 CrossRef CAS.
- C. C. Costain, Am. Crystallogr. Assoc., 1966, 2, 157–164 CAS.
- J. Kraitchman, Am. J. Phys., 1953, 21, 17–24 CrossRef CAS.
- Z. Kisiel, in Spectroscopy from Space, ed. J. Demaisonet al., Kluwer Academic Publishers, Dordrecht, 2001, pp. 91–106 Search PubMed.
- R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150 CrossRef CAS.
- P. Vansteenkiste, E. Pauwels, V. Van Speybroeck and M. Waroquier, J. Phys. Chem. A, 2005, 109, 9617–9626 CrossRef CAS PubMed.
- Y. Kawashima, Y. Tanaka, T. Uzuyama and E. Hirota, J. Phys. Chem. A, 2021, 125, 1166–1183 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Appendix 1: cartesian coordinates for the energy minima of DAS and DAE; Appendix 2: dihedral angle values for the conformers of DAS and DAE; Appendix 3: calculated energetic and spectroscopic parameters for conformer I of DAS and conformers I–IX of DAE; Appendix 4: assigned transitions for the observed species of conformer I of DAS and conformers I–IX of DAE; Appendix 5: non-covalent interaction (NCI) isosurfaces for the conformers of DAS and DAE; Appendix 6: kraitchman coordinates of conformer I of DAS and DAE; Appendix 7: natural bond orbitals (NBO) results for conformers I of DAS and DAE and conformer XXIV and II of DAS and DAE, respectively.; Appendix 8: geometries of conformers XXIV of DAS and conformer II of DAE. See DOI: 10.1039/d1cp04591a |
| This journal is © the Owner Societies 2022 |
