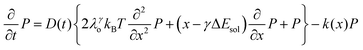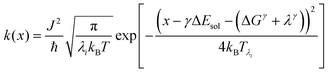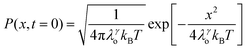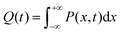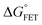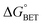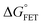Ultrafast nonequilibrium dynamics of short-range protein electron transfer in flavodoxin†
Received
28th September 2021
, Accepted 18th November 2021
First published on 18th November 2021
Abstract
Short-range protein electron transfer (ET) is ubiquitous in biology and is often observed in photosynthesis, photoreceptors and photoenzymes. These ET processes occur on an ultrafast timescale from femtoseconds to picoseconds at a short donor–acceptor distance within 10 Å, and thus couple with local environmental fluctuations. Here, we use oxidized Anabaena flavodoxin as a model system and have systematically studied the photoinduced redox cycle of the wild type and seven mutant proteins by femtosecond spectroscopy. We observed a series of ultrafast dynamics from the initial charge separation in 100–200 fs, subsequent charge recombination in 1–2 ps and final vibrational cooling process of the products in 3–6 ps. We further characterized the active-site solvation and observed the relaxations in 1–200 ps, indicating a nonergodic ET dynamics. With our new ET model, we uncovered a minor outer (solvent) reorganization energy and a large inner (donor and acceptor) reorganization energy, suggesting a frozen active site in the initial ultrafast ET while the back ET couples with the environment relaxations. The vibronically coupled back ET dynamics was first reported in D. vulgaris flavodoxin and here is observed in Anabaena flavodoxin again, completely due to the faster ET dynamics than the cooling relaxations. We also compared the two flavodoxin structures, revealing a stronger coupling with the donor tyrosine in Anabaena. All ultrafast ET dynamics are from the large donor–acceptor couplings and the minor activation barriers due to the reaction free energies being close to the inner reorganization energies. These observations should be general to many redox reactions in flavoproteins.
Introduction
Short-range electron transfer (ET) is often a critical step in biological photomachinery such as in photoenzymes1–4 and photoreceptors,5–8 as well as in long-range biological electron transport processes.9–13 Unlike long-range ET, short-range ET occurs ultrafast in a time range from femtoseconds (fs) to picoseconds (ps).14–18 On such short timescales, hydration water and local proteins fluctuate and couple with the ET dynamics, resulting in a nonequilibrium process of electron tunneling.19–21 Several theoretical models, such as the Sumi-Marcus two-dimensional model22 and the nonergodic approach,23–25 have been used to elucidate the ET mechanism. We have recently extended these models and analyzed a series of ultrafast short-range protein ET,26–28 unveiling the significant interplay between the ET process and environmental fluctuation. The appearance of ET dynamics highly depends on their coupling, showing different non-exponential behaviors. We have used a model protein, flavodoxin from Desulfovibrio vulgaris (D. vulgaris) to examine the coupled ET processes.17,18 In this work, we use another flavodoxin from Anabaena PCC7119 (Anabaena) to fully characterize the photoinduced ET redox cycle, as well as the active-site relaxation, to better understand such ultrafast nonequilibrium ET processes in flavodoxin.
Flavodoxin contains five parallel β-sheet strands and five α-helices and noncovalently binds a cofactor flavin mononucleotide (FMN) at the active site,29,30 as shown in Fig. 1. The cofactor FMN is mainly recognized by two 50's and 90's loops and sandwiched by two aromatic residues of tryptophan (W57) and tyrosine (Y94) at a close van der Waals distance, respectively (Fig. 1B). Upon excitation of FMN, both W57 and Y94 are excellent electron donors as observed in many flavoproteins.2,14 Here, we will systematically characterize both forward and backward ET dynamics, measure the local environment relaxations, examine the effects of critical mutations at the active site, analyze the data with our new developed ET model28 and finally compare the dynamics with those obtained from D. vulgaris flavodoxin.17 By using femtosecond spectroscopy, site-directed mutations, and theoretical analyses, we map out these various ET dynamics and provide a molecular picture of ultrafast nonequilibrium short-range protein ET dynamics.
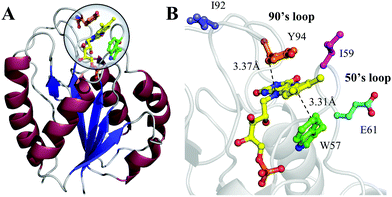 |
| | Fig. 1 (A) X-ray crystal structure of oxidized Anabaena PCC7120 flavodoxin (PDB: 1FLV). The sequence of Anabaena PCC7119 that we used is similar to that of Anabaena 7120. (B) Close-up view of the active FMN-binding site. The FMN (yellow) cofactor is sandwiched between W57 (green) and Y94 (orange). The positions of I59, E61 and I92 are also shown. | |
Results and discussion
Femtosecond electron transfer and frozen active site
Fig. 2A shows the steady-state absorption spectra of Anabaena WT with three representative mutants and the fluorescence spectrum of ET-inert mutant W57FY94F. Compared with the optical properties of D. vulgaris flavodoxin (Fig. S1, ESI†), the current absorption spectra are red-shifted by about 30 nm and also more sensitive to various mutants, particularly with the Y donor, indicating more favorable interactions of the Y donor with the ground state of FMN. Although flavodoxin is considered to be a non-fluorescent protein, we were still able to detect the excited-state fluorescence dynamics using the sensitive fluorescence up-conversion method. Fig. 2B shows several fluorescence transients of WT and four mutants. Specifically, for WT and W57R, their dynamics are not fully resolved but the timescale must be less than 100 fs. The ultrafast ET dynamics by the single donor Y94 is clearly favored by the stabilization of the positively charged residue R with the negative FMN− after ET. For W57E and W57F, the dynamics occur in about 100 fs, slower than the previous mutant W57R due to the unfavorable negative charge E and the hydrophobic F. For Y94F, the transient becomes relatively slower in 200 fs due to the single donor W57 with an unfavorable orientation structure even with a short distance and a favorable potential. The faster ET by the donor Y than W is clearly due to the perfect parallel stacking structure with the FMN (Fig. 1). This observation is opposite to the trend observed in D. vulgaris flavodoxin;17 there the W donor shows much faster ET reactions (also see discussion below). Nevertheless, the forward ET dynamics is ultrafast, much faster than the cooling processes of the excited- or ground-state of oxidized FMN,17,31 and probably leaves FMN− in its vibrationally excited states. The observed ET dynamics shows a single-exponential decay on such ultrafast timescale, indicating a possible frozen active site and relatively slow local fluctuations. Otherwise, we would observe a coupled, non-exponential decay of ET dynamics.2,18 The single-exponential dynamics also indicates a well-defined, less flexible donor–acceptor configuration.
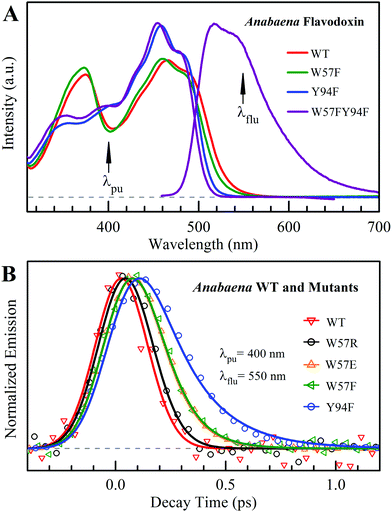 |
| | Fig. 2 (A) Steady-state spectra of Anabaena flavodoxin. Absorption spectra of WT (red), W57F (black), Y94F (blue) and W57FY94F (purple) and fluorescence spectrum of W57FY94F (purple). The pump wavelength and the gated fluorescence wavelength are marked with arrows. (B) Normalized femtosecond-resolved fluorescence transients of Anabaena flavodoxin WT and several mutants gated at 550 nm. | |
Femtosecond emission spectra and active-site solvation
To better understand such ultrafast single-exponential ET dynamics, we need to characterize the active-site relaxation. We used mutant W57FY94F to eliminate the ET donor and directly mapped out the femtosecond-resolved emission spectra (FRES) of excited FMN*. Fig. 3A shows the reconstructed plots of FRES and Fig. 3B shows several snapshots at certain delay times with the steady-state fluorescence emission spectrum at the bottom. Clearly, the spectral shape changes with time, especially at the blue side. Fig. 3C shows three typical fluorescence transients gated from the blue to red side. These transients show a typical solvation signature with a gradual decay at the blue side and an increase on the red side. Similar to that observed for the double F mutant of D. vulgaris flavodoxin,32 the emission spectra do not show significant Stokes shifts instead of a shape change with time, reflecting the active-site heterogeneous relaxations confined within the limited nanospace inside the protein.32,33 As treated in the previous work, we can calculate the average frequency (![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) changes with time and the derived stabilization energies (ΔE = ν − ν0) are shown in Fig. 3D, relative to the initial energy at time zero (ν0). The resulting energies ΔE(t) can be fitted by the following equation.
) changes with time and the derived stabilization energies (ΔE = ν − ν0) are shown in Fig. 3D, relative to the initial energy at time zero (ν0). The resulting energies ΔE(t) can be fitted by the following equation.
| ΔE(t) = ΔE1e−t/τ1 + ΔE2e−t/τ2 + ΔE3e−t/τ3 + ΔE∞, |
| | | ΔE1 + ΔE2 + ΔE3 + ΔE∞ = 0 | (1) |
We observed the relaxations occurring on the timescales of 1 ps (80%), 28 ps (11%), and 267 ps (9%). The total stabilization energy is 182 cm−1. We performed MD simulations and Fig. 3E shows the 5 ns trajectory with a snapshot shown in Fig. 3F. The FMN in a shallow binding site is partially exposed to the protein surface. We found about 120 water molecules around the isoalloxazine (ISO) ring within a distance of 10 Å. About 90% of the hydration water molecules are near the protein surface within 7 Å, about two hydration layers of water. According to our earlier extensive hydration studies,34–36 the relaxation in 1 ps is the initial hindered rotation of hydration water; the 28 ps dynamics reflects the water-sidechain coupled relaxation; and the long relaxation in 267 ps could be from the water-loop collective fluctuation, given the loop nature of the binding site. Similar relaxations are also observed in D. vulgaris flavodoxin32 with a slightly larger value of stabilization energy of 209 cm−1 relative to 182 cm−1 observed here, probably due to its more exposed binding sites (Fig. S2, ESI†).
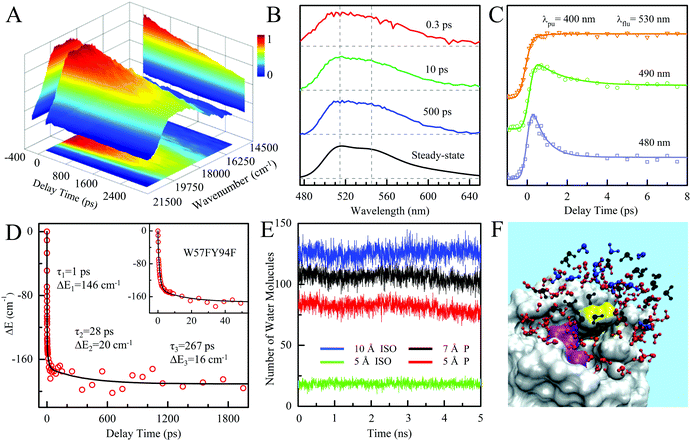 |
| | Fig. 3 (A) Three-dimensional representation of FRES of W57FY94F mutant. (B) Three snapshots of the normalized FRES at typical delay times with the corresponding steady-state emission spectrum. (C) Normalized, femtosecond-resolved fluorescence transients with a series of gated fluorescence emissions from the blue to red side. (D) Solvation responses at the active site of flavodoxin represented by stabilization energy changes (ΔE) with time. The inset shows the responses at short timescale. (E) Five nanosecond snapshots of 50 ns MD simulation on W57FY94F mutant. Total water molecules at a distance of ≤5 Å and ≤10 Å to the center of the ISO ring are plotted in green and blue, respectively. Water molecules within 10 Å of the ISO ring and ≤7 Å and 5 Å of the protein surface are plotted in black and red, respectively. (F) All the water molecules within 10 Å of the ISO ring are plotted with the protein shown as gray surface structures. Water molecules within 10 Å of the ISO ring and greater than 7 Å from the protein surface are plotted in blue. Water molecules between 5 and 7 Å of the surface are plotted in black. Water molecules closer than 5 Å to the surface are plotted in red. Note that the ISO is marked in yellow and the other part of the FMN is marked in magenta. | |
The observed relaxation dynamics at the active site are important and clearly show the fluctuations around the FMN on the picosecond timescales, much slower than the above ET reactions in femtoseconds. Thus, the driving force and strong coupling enable the ET to occur on an ultrafast timescale within such a short distance, leaving the surrounding environment nearly frozen. The hydration water and nearby sidechains would not make noticeable rearrangements even though the system is in nonequilibrium upon excitation. As shown below, the solvent reorganization energy (λo) would be minor.
Back electron transfer and subsequent vibrational cooling
To follow the dynamic processes after initial ET, we employed femtosecond TA to detect all intermediates and final products. We first used broadband TA to scan the overall absorption evolution ranging from 470 nm to 770 nm. Fig. 4 shows the two-dimensional contour plots of the two typical mutants of W57F, Y94F and the WT with different ET donors. Specifically, Fig. 4A shows the spectral evolution of W57F with only Y94 as the electron donor. Clearly, the positive signal from the long wavelength such as 680–770 nm must have originated from the excited FMN* and disappeared quickly. The signals in the range of 500–680 nm include the initial excited FMN*, intermediates containing possible FMN−† (<640 nm) after initial ET, and FMN† (<570 nm) by backward ET, and ground-state FMN formation (<550 nm) through vibrational cooling. At 470–500 nm, the signal becomes negative because of the dominant ground-state bleaching. Fig. 4B exhibits the ET dynamics of Y94F with only one ET donor W57. Compared with Fig. 4A, a new absorption band was observed for tryptophan cation (W+) that peaked at 580–620 nm, extending to 700 nm. For WT with dual ET donors, Fig. 4C shows a pattern similar to that shown in Fig. 4B. These broadband spectra show the clear time evolution of each species in such ultrafast photoinduced redox cycles.
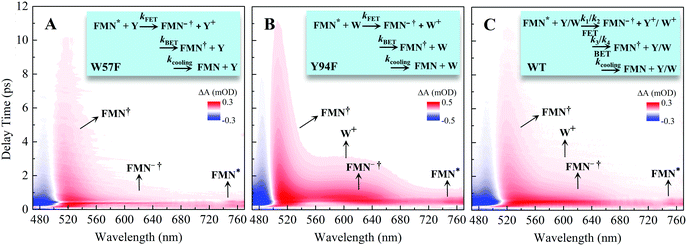 |
| | Fig. 4 Broadband TA spectra of (A) W57F (B) Y94F, and (C) WT with 400 nm excitation. Also shown are the three complete ET reactions in the panels as well as the marked absorption species by arrows. Note that k1 and k2 are the forward ET rates for the donors Y and W, and k3 and k4 are their back ET rates, respectively. | |
To precisely determine the timescales of these ET dynamics, we detected various species and related dynamics with different single probe wavelengths. Fig. 5–7 show the different transients at several typical probe wavelengths for W57F, Y94F and WT. The results of other mutants (W57E, W57R, Y94A, E61K, and I59AI92A) are shown in Fig. S3–S5 (ESI†). Specifically, for the Y donor of Y94 (W57F/E/R) in Fig. 5 and Fig. S3 (ESI†), the forward ET dynamics detected at 800 nm is ∼300 fs, longer than that obtained by fluorescence detection, a phenomenon often observed in many molecules and probably related to different configurations detected by the two methods.37 For the transients around 500–540 nm, we can derive the back ET dynamics in 1.3–1.5 ps and the resulting ground state is vibrationally hot. The subsequent vibrational cooling takes about 3–6 ps. At 480 nm, the transient exhibits a faster recovery due to the cancellation of vibrational cooling signals, and at 410 nm, the transient mainly showed the forward ET dynamics. For the W donor of W57 (Y94F/A) in Fig. 6 and Fig. S4 (ESI†), similarly we obtained the forward ET dynamics also in ∼300 fs, longer than that determined by the fluorescence detection and similar to the ET dynamics by the Y donor. At 580 nm, we mainly detected the FMN−†/W+ dynamics and unambiguously determined the back ET in 0.8–1.0 ps, faster than that of the Y donor. From the transients around 500–540 nm, besides the signal of FMN* and FMN−†/W+, we mainly observed the cooling dynamics in a similar timescale of ∼3–5 ps. However, for WT and two mutants of E61K and I59AI92A, we have two ET donors of Y and W. According to the ET scheme in Fig. 4C, two ET pathways coexist. The forward ET is the sum of two ET rates (k1 + k2); the back ET has two separate pathways (k3 and k4). The transient probed at 800 nm gives an ultrafast decay time of 170 fs, similar to the sum of two independent rates for Y (380 fs) and W (330 fs). At 580 nm, the transient represents the dynamics of the forward ET and intermediates FMN−†/W+ and we derived their back ET in 1.02 ps. In the range of 500–540 nm, we detected a series of intermediates and by the overall fitting, we obtained the back ET of Y+ in about 1.70 ps. These two back ET rates for W+ and Y+ are similar to their individual back ET dynamics. We also obtained the cooling dynamics in 4–6 ps. Similarly, at 480 nm and 410 nm, the transients mainly reflect the recovery of the ground state and excited ET dynamics, respectively. We also studied another two mutants of E61K and I59AI92A (Fig. S5, ESI†) and similar patterns were observed. Table 1 lists all the results of Anabaena flavodoxin WT and the mutants along with those obtained from D. vulgaris flavodoxin for comparison.
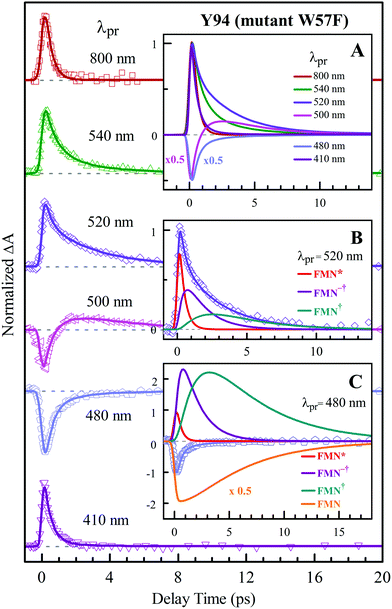 |
| | Fig. 5 Normalized TA spectra of mutant W57F flavodoxin probed from 800 to 410 nm for the ET reaction with one donor Y94. Inset A shows the entire evolution of the dynamics with probe wavelengths. Insets B and C show the deconvolution of the transients into various species probed at 520 and 480 nm, respectively. | |
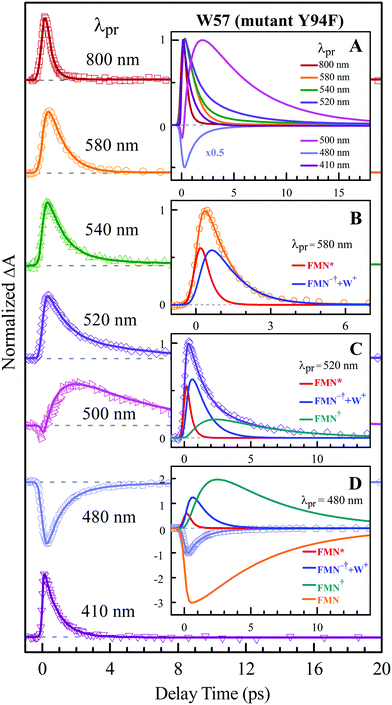 |
| | Fig. 6 Normalized TA spectra of mutant Y94F flavodoxin probed from 800 to 410 nm for the ET reaction with one donor W57. Inset A shows the entire evolution of the dynamics with probe wavelengths. Insets B–D show the deconvolution of the transients into various species probed at 580, 520 and 480 nm, respectively. | |
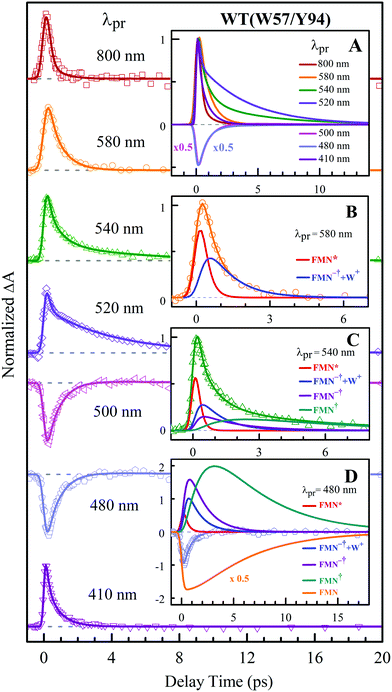 |
| | Fig. 7 Normalized TA spectra of WT flavodoxin probed from 800 to 410 nm for the ET reaction with dual donors of Y94 and W57. Inset A shows the entire evolution of the dynamics with probe wavelengths. Insets B–D show the deconvolution of the transients into various species probed at 580, 540 and 480 nm, respectively. | |
Table 1 Redox potentials and timescales of ET and cooling dynamics.a
|
|
Mutants |
Donor |
E(FMN/FMN−)b |
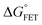
|
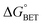
|
τ
FET
|
τ
FET
|
τ
BET
|
τ
cooling
|
|
All energies in electron volt and times in picosecond.
These data are from ref. 40 and 44–46. E(FMN/FMN−) could be calculated from Em,7(FMN/FMNH) + 0.06 × log[(1 + [H+]/Kox)(1 + [H+]/Kred)] with known values of 10−7 for [H+], 1 for Kox, and 10−10.5 for Kred.
From fluorescence detection.
From TA detection.
For the dual donors Y and W, the first column for Y and the second for W.
The data are from ref. 17.
|
|
Anabaena flavodoxin |
W57E |
Y94 |
−0.41 |
−0.62 |
−1.88 |
0.10 |
0.31 |
1.33 |
3.4–5.2 |
| W57F |
Y94 |
−0.36 |
−0.67 |
−1.83 |
0.10 |
0.38 |
1.51 |
3.0–5.0 |
| W57R |
Y94 |
−0.38 |
−0.65 |
−1.85 |
<0.10 |
0.32 |
1.46 |
3.1–5.6 |
| Y94A |
W57 |
−0.41 |
−0.94 |
−1.56 |
|
0.31 |
0.87 |
3.9–5.1 |
| Y94F |
W57 |
−0.40 |
−0.95 |
−1.55 |
0.20 |
0.33 |
1.02 |
4.4–5.2 |
| WT |
Y94,W57 |
−0.42 |
|
|
<0.10 |
0.17 |
1.70, 1.02 |
4.2–5.8 |
| E61K |
Y94,W57 |
−0.45 |
|
|
|
0.18 |
1.62, 1.02 |
3.6–5.8 |
| I59AI92A |
Y94,W57 |
−0.49 |
|
|
|
0.17 |
1.63, 1.02 |
3.6–5.5 |
|
D. vulgaris flavodoxinf |
W60A |
Y98 |
−0.37 |
−0.66 |
−1.84 |
0.34 |
0.49 |
0.95 |
3.7–4.0 |
| W60F |
Y98 |
|
|
|
0.30 |
0.49 |
0.95 |
3.7–4.0 |
| Y98A |
W60 |
−0.40 |
−0.95 |
−1.54 |
0.25 |
0.37 |
1.00 |
2.5–3.5 |
| Y98F |
W60 |
−0.36 |
−0.99 |
−1.51 |
0.26 |
0.37 |
1.61 |
3.3–3.8 |
| WT |
Y98,W60 |
−0.36 |
|
|
0.16 |
0.18 |
0.95, 1.56 |
3.0–4.3 |
Fig. 8A and Table 1 show the comparison of two flavodoxins from Anabaena and D. vulgaris. Both proteins show the similar ultrafast ET dynamics. However, in Anabaena flavodoxin, the ET dynamics for the Y donor is faster than that of the W donor while in D. vulgaris the trend is the opposite and the ET dynamics of the W donor is faster and the Y donor shows slower. Fig. 8B shows the X-ray structures of the two binding sites and clearly, for Anabaena flavodoxin, the cofactor FMN is bent toward the donor Y, leading to a stronger coupling between FMN* and Y and resulting in the fastest ET around 100 fs. The ET channel by the W donor becomes slower while in D. vulgaris flavodoxin, the ET by W is faster, around 250 fs. Also, the alignments of the ISO ring with the Y donor in Anabaena (Fig. S6, S7 and Table S1, ESI†) are favorable for better overlap of the molecular orbitals. Also, the driving force for the ET by Y94 with an equilibrium reaction has the potential of −0.65 eV, less than that for W57 with a potential of −0.95 eV. Clearly, the coupling is a determinant for the final ET time with similar distances. Interestingly, the faster the forward ET, the slower the back ET. We observed a slow back ET for the Y donor in Anabaena flavodoxin but in D. vulgaris the slow one is from the W donor. Overall, the forward ET is ultrafast and the ET system is nearly in a frozen active site. For the back ET to the ground state, the ET dynamics is in 1–2 ps, heavily coupled to the environment relaxation. Generally, such nonequilibrium back ET dynamics appears as a nonexponential behavior, and typically, it can be described by a single stretched exponential decay [e−(t/τ)β, β < 1]. However, such stretched behaviors strongly overlap with the subsequent cooling dynamics. For simplicity, we only treat the back ET in a single exponential decay and probably the stretched tails were included in the cooling process; but such treatment should not affect our general conclusion here.
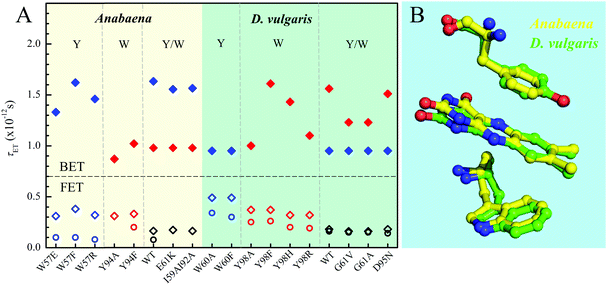 |
| | Fig. 8 (A) Comparison of various τET of Anabaena and D. vulgaris flavodoxin. The τFET and τBET detected from TA are marked in diamonds. The τFET detected from fluorescence up-conversion is marked in circles. (B) X-ray structures of the two binding sites of Anabaena and D. vulgaris flavodoxin for comparison of local conformations. Note that the ISO ring is bent toward the Y donor in Anabaena flavodoxin. | |
Model analysis and nonergodic dynamics
We recently extended the reaction-diffusive Sumi-Marcus model to analyze ultrafast ET reactions. In our new model,28 we introduced a dynamic factor, γ, to describe the coupling between environmental fluctuations and ET dynamics. If the ET is much faster than the environment relaxation, γ is close to 0; while when the ET is much slower than the environmental fluctuation, γ is equal to 1. For most short-range ET processes in proteins, the ET is coupled with the environment and the γ is between 0 and 1; the clear appearance is the stretched exponential behavior of the ET dynamics. We have used the new model to analyze the ultrafast ET dynamics in D. vulgaris flavodoxin and elucidated the molecular mechanism of the ET reactions.28 Here, with all determined ET timescales, we used the model to further examine the nonergodic dynamics of the ET processes. By knowing the environmental relaxation of 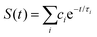 above, the dynamic factor γ can be obtained by
above, the dynamic factor γ can be obtained by 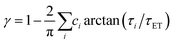 . Then, the excited-state population Q(t) and ET rate k(x) can be expressed as follows:38,39
. Then, the excited-state population Q(t) and ET rate k(x) can be expressed as follows:38,39| | 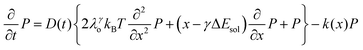 | (2) |
| | 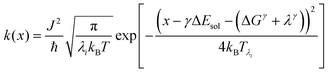 | (3) |
| | | λγo = γλeqo, λγ = λi + λγo | (4) |
| | | ΔGγ = ΔG° + (1 − γ)λeqo | (5) |
| | 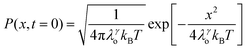 | (6) |
| | 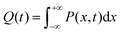 | (7) |
x is the solvent coordinator, P(x) is the distribution of the reactants, D(t) is a diffusion coefficient, calculated from -1/S(t)⋅dS(t)/dt, λo is the outer (solvent) reorganization energy, λi is the inner (donor and acceptor) reorganization energy, ΔEsol is the total stabilization energy of solvation, ΔG° is the equilibrium free energy change of the ET reaction, i.e., reaction driving force, and J is the electronic coupling constant. With the above equations, we simulated the forward electron-transfer dynamics as shown in Fig. 9A. The derived constants are listed in Table 2. Clearly, the solvent reorganization energies for the mutants are close to 0, a characteristic of ET reactions in a frozen region with γ being extremely small. The ultrafast ET dynamics is the result of negligible activation energy determined by the large driving force |ΔGγ|, as well as a fairly large inner reorganization energy λi. The unusual value of λi is from the significant structural alternation from planar FMN* to anionic semiquinone FMN− with a bent structure. Besides FMN, the electron donors Y and W also contribute to the change of λi during forward ET as the value of Y94F (0.86 eV) is larger than that of W57E/F/R (0.78 eV). As shown in Table 2, the calculated reaction free energy ΔGγ deviates significantly from its equilibrium value of ΔG° due to the frozen environment on the ultrafast ET timescale of about 100 fs. Thus, from the nonergodic model, we found that on such ultrafast ET processes, the environment nearly freezes and the free energy release compensates the inner reorganization energy, leading to a minor activation energy and a downhill ET reaction. Fig. 9B shows the complete photoinduced redox cycle in Anabaena flavodoxin with all resolved elementary dynamics and their timescales. During electron hopping from Y/W to FMN*, both the electron donor and acceptor experience a structural change while the environment cannot respond fast enough in time. As expected, during the back electron transfer in 1–2 ps, the environmental fluctuations couple with the back ET reaction.
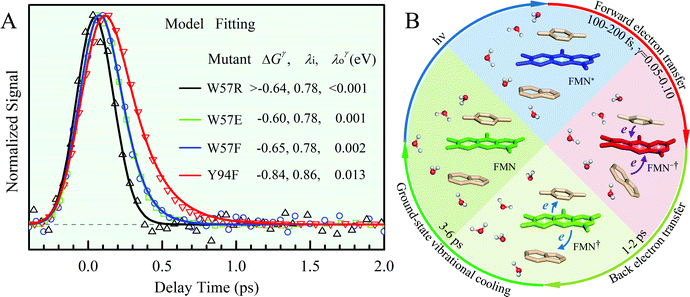 |
| | Fig. 9 (A) Simulations (solid lines) for different mutants are compared with fluorescence up-conversion data (symbols). The derived active-site correlation function is S(t) = 0.80e−t/1.0 + 0.11e−t/28 + 0.09e−t/267; the unit for t in ps. (B) The complete photoinduced redox cycle in Anabaena flavodoxin with all resolved elementary dynamics and their timescales. Note the configurations of the active-site water molecules around the donor (Y/W) and acceptor (ISO) on different stages. Specifically, during the forward ET process, the water molecules only have slight rotations, and during the back ET and cooling process, the water molecules have time to fluctuate in translational motions. | |
Table 2 Energetics of forward electron transfer reactions in Anabaena flavodoxina
| Mutants |
Donor |
τ
FET
|
J
|
γ
|
λ
i
|
λ
γ
o
|
λ
γ
|
ΔGγFET |
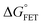
|
|
All energies in eV.
Fitting data from fluorescence up-conversion.
|
| W57E |
Y94 |
0.10 |
0.024 |
0.05 |
0.78 |
0.001 |
0.781 |
−0.60 |
−0.62 |
| W57F |
Y94 |
0.10 |
0.024 |
0.05 |
0.78 |
0.002 |
0.782 |
−0.64 |
−0.67 |
| W57R |
Y94 |
<0.10 |
0.024 |
<0.05 |
0.78 |
<0.001 |
<0.781 |
>−0.63 |
−0.65 |
| Y94F |
W57 |
0.20 |
0.017 |
0.10 |
0.86 |
0.012 |
0.872 |
−0.84 |
−0.95 |
Conclusion
We reported here the complete studies of ultrafast electron-transfer reactions of a photoinduced redox cycle in Anabaena flavodoxin. We first characterized the active-site solvation and observed multiple relaxations in 1–206 ps. Upon excitation, the forward ET between the cofactor FMN and neighbouring amino-acid tryptophan or tyrosine occurs on an ultrafast timescale in 100–200 fs, much faster than the environment response. On such an ultrafast timescale, the active-site motion is minor and the solvent reorganization is negligible. The resulting FMN−† proceeds to charge recombination in 1–2 ps, one order of magnitude slower than charge separation. The back electron transfer couples with the environmental fluctuations, leading to a convoluted process of two dynamics of the electron hopping and solvent motions. The typical appearance of such ET dynamics is a stretched exponential behavior. Significantly we observed the vibrational cooling after the back ET and the ground-state FMN is vibrationally excited. The hot ground state relaxes in 3–6 ps. The cooling dynamics can be general to flavoproteins and only ultrafast forward and back ET enables to observe such an ultrafast cooling process, otherwise this process is immersed in the slow ET dynamics, probably in most flavoproteins.
With various mutations of the donor tryptophan or tyrosine as well as environmental modifications, we observed a slight change in the ET dynamics. By careful examination of the X-ray structure, we found the distance and orientation favor the Y donor and thus, its ET dynamics is faster than that of the W donor. This observation is opposite to the trend observed in D. vulgaris flavodoxin, given by a very similar protein architecture with a very similar active site having both W and Y sandwiching the cofactor FMN. Combining both the results of Anabaena and D. vulgaris flavodoxin proteins, we conclude that the ultrafast forward ET results from the strong coupling and the minor activation barriers. Using our recently developed nonergodic ET model, we clearly showed the negligible outer (solvent) reorganization energy but a large inner (donor and acceptor) reorganization energy. Such similar large reaction free energy and reorganization energy result in the minor activation energy. Our new model elucidates the molecular mechanism of the ultrafast ET dynamics and the role of environmental fluctuations.
Materials and methods
Site-directed mutations
We have designed seven mutations to change donors and the related environments. The pTrc99a plasmid encoding the Anabaena flavodoxin was used to modify various mutations. At the W57 position, three mutants of W57F, W57E and W57R were made with hydrophobic, negative and positive charge residues to leave Y94 as the only ET donor. For Y94, we mutated Y94A and Y94F with hydrophobic residues to leave W57 as the only ET donor. We also modified the environment by mutations of E61K with switching charge from negative to positive and I59AI92A with a more negative redox potential.40 Finally, we mutated both W and Y donors to phenylalanine F as a control without any ET reactions.
Protein purification
Anabaena flavodoxin wild type (WT) and various mutants have been expressed and purified as reported.41,42,45 Briefly, the plasmid was transformed into E. coli JM101 cells for expression and cultured in LB at 37 °C. When the OD value of cells reached 1.0 per cm, isopropyl β-D-1-thiogalactopyranoside (IPTG) was added to induce protein expression and then cells allowed to grow for another 6 hours. Cells were harvested by centrifugation and lysed by ultra-sonication to release apo-flavodoxin into the supernatant. Holo-flavodoxin was obtained by incubating FMN with the supernatant for 2 hours. Then, the supernatant was purified using DE52 column and Sephacryl S-100 column. The purity of each holo-flavodoxin was confirmed by SDS-polyacrylamide gel electrophoresis. Circular dichroism (CD) spectra were measured by Chirascan (Applied Photophysics, UK) for all mutant proteins to confirm their correct structures (Fig. S8, ESI†). The steady-state UV-Vis spectra were recorded using a UV2600 UV-Visible Spectrophotometer (Shimadzu Corporation, Japan). Right before ultrafast spectroscopic measurements, the protein sample was eluted through a mini desalting column (Sephadex G-25 medium) to remove any free FMN in the sample solution. The flavodoxin samples with a concentration of 60–250 μM, dissolved in a 50 mM phosphate buffer solution at pH 7, were used for ultrafast spectroscopic measurements under aerobic conditions.
Ultrafast methods
The experimental setups for the fluorescence up-conversion and transient absorption (TA) measurements have been reported previously.43 The wavelength of the pump pulse was set at 400 nm with an attenuated energy of ∼100–150 nJ. For the fluorescence up-conversion measurements, the fluorescence emission at 550 nm was mixed with the 800 nm gating pulse in a 0.5 mm thick β-barium borate crystal (type I BBO). The fluorescence up-conversion system has an instrument response of 250–300 fs. For the TA measurements, probe pulses with wavelengths scanning from 410 nm to 800 nm were generated via an optical parametric amplifier (TOPAS). The TA system has an instrument response of ∼200 fs. Broadband TA spectra were also measured using a femtosecond transient-absorption spectrometer (Helios fire, Ultrafast System). All the measurements were taken under the magic angle (54.7°) conditions, and the samples were stirred constantly to avoid photobleaching.
Author contributions
D. Z. designed the project; T. H., J. Y., Y. Z., L. W. and B. D. conducted the experiments and analyzed the data; Y. L. provided the help for nonergodic analysis. J. Y., B. D. and D. Z. wrote the paper.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgements
We acknowledge the Plant Bioscience Limited in England for providing us the plasmid pTrc99a encoding Anabaena flavodoxin. We thank Ms Yukti Aggarwal for her critical work in collecting data during the initial phase of this project. We thank the National Natural Science Foundation of China (Grant No. 21733007 and 21903052) for supporting this work and providing for the summer stays of D. Z. in Shanghai Jiao Tong University to finish this work.
Notes and references
- D. Sorigué, B. Legeret, S. Cuiné, S. Blangy, S. Moulin, E. Billon, P. Richaud, S. Brugière, Y. Couté, D. Nurizzo, P. Müller, K. Brettel, D. Pignol, P. Arnoux, Y. Li-Beisson, G. Peltier and F. Beisson, Science, 2017, 357, 903–907 CrossRef PubMed.
- Z. Liu, C. Tan, X. Guo, J. Li, L. Wang, A. Sancar and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12966–12971 CrossRef CAS PubMed.
- J. Li, Z. Liu, C. Tan, X. Guo, L. Wang, A. Sancar and D. Zhong, Nature, 2010, 466, 887–890 CrossRef CAS PubMed.
- D. Sorigué, K. Hadjidemetriou, S. Blangy, G. Gotthard, A. Bonvalet, N. Coquelle, P. Samire, A. Aleksandrov, L. Antonucci, A. Benachir, S. Boutet, M. Byrdin, M. Cammarata, S. Carbajo, S. Cuiné, R. B. Doak, L. Foucar, A. Gorel, M. Grünbein, E. Hartmann, R. Hienerwadel, M. Hilpert, M. Kloos, T. J. Lane, B. Légeret, P. Legrand, Y. Li-Beisson, S. L. Y. Moulin, D. Nurizzo, G. Peltier, G. Schirò, R. L. Shoeman, M. Sliwa, X. Solinas, B. Zhuang, T. R. M. Barends, J. P. Colletier, M. Joffre, A. Royant, C. Berthomieu, M. Weik, T. Domratcheva, K. Brettel, M. H. Vos, I. Schlichting, P. Arnoux, P. Müller and F. Beisson, Science, 2021, 372, eabd5687 CrossRef PubMed.
- M. Gauden, I. H. van Stokkum, J. M. Key, D. C. Lührs, R. Van Grondelle, P. Hegemann and J. T. Kennis, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10895–10900 CrossRef CAS PubMed.
- E. R. Sayfutyarova, J. J. Goings and S. Hammes-Schiffer, J. Phys. Chem. B, 2018, 123, 439–447 CrossRef PubMed.
- N. Ozturk, C. P. Selby, Y. Annayev, D. Zhong and A. Sancar, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 516–521 CrossRef CAS PubMed.
- K. S. Conrad, C. C. Manahan and B. R. Crane, Nat. Chem. Biol., 2014, 10, 801 CrossRef CAS PubMed.
- H. B. Gray and J. R. Winkler, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3534–3539 CrossRef CAS PubMed.
- C. C. Moser, J. M. Keske, K. Warncke, R. S. Farid and P. L. Dutton, Nature, 1992, 355, 796–802 CrossRef CAS PubMed.
- T. R. Prytkova, I. V. Kurnikov and D. N. Beratan, Science, 2007, 315, 622–625 CrossRef CAS PubMed.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 811, 265–322 CrossRef CAS.
- J. Lin, I. A. Balabin and D. N. Beratan, Science, 2005, 310, 1311–1313 CrossRef CAS PubMed.
- D. Zhong and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 11867 CrossRef CAS PubMed.
- Y.-T. Kao, C. Saxena, L. Wang, A. Sancar and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16128–16132 CrossRef CAS PubMed.
- H. Wang, S. Lin, J. P. Allen, J. C. Williams, S. Blankert, C. Laser and N. W. Woodbury, Science, 2007, 316, 747–750 CrossRef CAS PubMed.
- T.-F. He, L. Guo, X. Guo, C.-W. Chang, L. Wang and D. Zhong, Biochemistry, 2013, 52, 9120–9128 CrossRef CAS PubMed.
- M. Kundu, T.-F. He, Y. Lu, L. Wang and D. Zhong, J. Phys. Chem. Lett., 2018, 9, 2782–2790 CrossRef CAS PubMed.
- C. C. Page, C. C. Moser, X. Chen and P. L. Dutton, Nature, 1999, 402, 47–52 CrossRef CAS PubMed.
- A. Yartsev, Y. Nagasawa, A. Douhal and K. Yoshihara, Chem. Phys. Lett., 1993, 207, 546–550 CrossRef CAS.
- Z. Liu, X. Guo, C. Tan, J. Li, Y.-T. Kao, L. Wang, A. Sancar and D. Zhong, J. Am. Chem. Soc., 2012, 134, 8104–8114 CrossRef CAS PubMed.
- H. Sumi and R. A. Marcus, J. Chem. Phys., 1986, 84, 4894–4914 CrossRef CAS.
- D. V. Matyushov, J. Chem. Phys., 2009, 130, 164522 CrossRef PubMed.
- D. N. LeBard and D. V. Matyushov, Phys. Chem. Chem. Phys., 2010, 12, 15335–15348 RSC.
- D. V. Matyushov, J. Chem. Phys., 2013, 139, 07B606 CrossRef PubMed.
- Y. Lu and D. Zhong, J. Phys. Chem. Lett., 2019, 10, 346–351 CrossRef PubMed.
- Y. Lu and D. Zhong, J. Chem. Phys., 2020, 152, 065102 CrossRef CAS PubMed.
- Y. Lu, M. Kundu and D. Zhong, Nat. Commun., 2020, 11, 2822 CrossRef CAS PubMed.
- S. T. Rao, F. Shaffie, C. Yu, K. A. Satyshur, B. J. Stockman, J. L. Markley and M. Sundaralingam, Protein Sci., 1992, 1, 1413–1427 CrossRef CAS PubMed.
- J. Sancho, Cell. Mol. Life Sci., 2006, 63, 855–864 CrossRef CAS PubMed.
- M. Kondo, J. Nappa, K. L. Ronayne, A. L. Stelling, P. J. Tonge and S. R. Meech, J. Phys. Chem. B, 2006, 110, 20107–20110 CrossRef CAS PubMed.
- C.-W. Chang, T.-F. He, L. Guo, J. A. Stevens, T. Li, L. Wang and D. Zhong, J. Am. Chem. Soc., 2010, 132, 12741–12747 CrossRef CAS PubMed.
- C.-W. Chang, L. Guo, Y.-T. Kao, J. Li, C. Tan, T. Li, C. Saxena, Z. Liu, L. L. Wang, A. Sancar and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2914–2919 CrossRef CAS PubMed.
- D. Zhong, Adv. Chem. Phys., 2009, 143, 83–149 CrossRef CAS.
- L. Zhang, L. Wang, Y.-T. Kao, W. Qiu, Y. Yang, O. Okobiah and D. Zhong, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18461–18466 CrossRef CAS PubMed.
- L. Zhang, Y. Yang, Y.-T. Kao, L. Wang and D. Zhong, J. Am. Chem. Soc., 2009, 131, 10677–10691 CrossRef CAS PubMed.
- C. Wan, T. Xia, H.-C. Becker and A. H. Zewail, Chem. Phys. Lett., 2005, 412, 158–163 CrossRef CAS.
- S. A. Adelman, J. Chem. Phys., 1976, 64, 124–130 CrossRef CAS.
- D. Zhong, S. K. Pal and A. H. Zewail, Chem. Phys. Lett., 2011, 503, 1–11 CrossRef CAS.
- S. Frago, G. Goni, B. Herguedas, J. R. Peregrina, A. Serrano, I. Perez-Dorado, R. Molina, C. Gomez-Moreno, J. A. Hermoso, M. Martínez-Júlvez, S. G. Mayhew and M. Medina, Arch. Biochem. Biophys., 2007, 467, 206–217 CrossRef CAS PubMed.
- S. G. Mayhew and V. Massey, J. Biol. Chem., 1969, 244, 794–802 CrossRef CAS.
- C. G. Genzor, C. Gómez-Moreno, J. Sancho, A. Beldarraín, J. L. López-Lacomba and M. Cortijo, Protein Sci., 1996, 5, 1376–1388 CrossRef CAS PubMed.
- L. Zhang, Y.-T. Kao, W. Qiu, L. Wang and D. Zhong, J. Phys. Chem. B, 2006, 110, 18097–18103 CrossRef CAS PubMed.
- J. J. Pueyo, C. Gomez-Moreno and S. G. Mayhew, Eur. J. Biochem., 1991, 202, 1065–1071 CrossRef CAS PubMed.
- A. Lostao, C. Gómez-Moreno, S. G. Mayhew and J. Sancho, Biochemistry, 1997, 36, 14334–14344 CrossRef CAS PubMed.
- G. Goñi, B. Herguedas, M. Hervás, J. R. Peregrina, M. A. De la Rosa, C. Gómez-Moreno, J. A. Navarro, J. A. Hermoso, M. Martínez-Júlvez and M. Medina, Biochim. Biophys. Acta, 2009, 1787, 144–154 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp04445a |
|
| This journal is © the Owner Societies 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab
*ab

![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) ) changes with time and the derived stabilization energies (ΔE = ν − ν0) are shown in Fig. 3D, relative to the initial energy at time zero (ν0). The resulting energies ΔE(t) can be fitted by the following equation.
) changes with time and the derived stabilization energies (ΔE = ν − ν0) are shown in Fig. 3D, relative to the initial energy at time zero (ν0). The resulting energies ΔE(t) can be fitted by the following equation.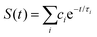 above, the dynamic factor γ can be obtained by
above, the dynamic factor γ can be obtained by 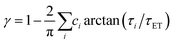 . Then, the excited-state population Q(t) and ET rate k(x) can be expressed as follows:38,39
. Then, the excited-state population Q(t) and ET rate k(x) can be expressed as follows:38,39