Rotational analysis of naphthol-aromatic ring complexes stabilized by electrostatic and dispersion interactions

Abstract

For complexes involving aromatic species, substitution effects can influence the preferred geometry. Using broadband rotational spectroscopy, we report the structures of three naphthol-aromatic ring complexes with different heteroatoms (furan and thiophene) and alkyl groups (2,5-dimethylfuran). The aim was to analyze the influence of the presence of heteroatoms or alkyl groups on the structure of the complex and the kind of intermolecular forces that control it. Face or edge arrangements can take place in these complexes via π–π or O–H⋯O/O–H⋯π interactions, respectively. All the experimentally observed complexes present O–H⋯O/O–H⋯π interactions with the hydroxyl group, with different structures and intermolecular interactions depending on the heteroatom present in the five-membered aromatic rings, yielding different symmetries in the experimental structure. Structures are experimentally identified through the use of planar moments of inertia. Further results from SAPT calculations show that dispersion and electrostatic interactions contribute similarly to the stabilization of all the studied complexes. These new spectroscopic results shed light on the influence of dispersion and hydrogen bonding in molecular aggregation of systems with substituted aromatic residues.

---

I. Introduction

The competition or reinforcement of different intermolecular interactions governs the properties and structural preferences in biochemistry,^1–3 reactivity,^3,4 catalysis^3,5 and even in the design of new materials.^2,3,6 The insight into the interplay of these interactions at a molecular level is paramount to be able to design structurally related systems, or just to predict molecular recognition events.^7,8 In this respect, the importance of non-covalent interactions, especially dispersion, in the stabilization of biochemical systems and materials has been underrated for some time.⁷ As a consequence, there is a demand for more knowledge about the performance of these interactions on a quantitative scale both theoretically and experimentally.^7–9 The study of molecular complexes isolated in the gas phase provides the conditions to investigate their structural changes and interactions without any external influence and the possibility of benchmarking the results directly with theoretical calculations.^9–12

The presence of a polar functional group along with an aromatic ring within a complex can influence its preferred arrangement.¹³ Examples of this are the phenol dimer and trimer, where π–π interactions and substituent effects enable the stabilization through their hydrogen bonded structures.^14–19 The consideration of dispersion interactions in the theoretical calculations was crucial to simulate correctly the experimental phenol dimer structure.¹⁹ This structural situation changes when another aromatic ring is fused to that of phenol, turning into 1-naphthol (1-NpOH), a naphthalene analogue of phenol. The 1-NpOH dimer features a partially overlapping π–π structure with, surprisingly, no hydrogen bonds.^20,21

1-NpOH presents a planar, aromatic, bicyclic ring structure bridged along a carbon–carbon bond, which has two possible binding sites: the aromatic “face” with two π-rings and the “edge” hydroxyl group. The aromatic rings give a relatively large surface for dispersion-dominated interactions to form, while the hydroxyl group would tend to favor an electrostatic interaction. This molecule is thus an attractive model to test its complexation preferences with molecules with different functional groups.

The range of face vs. edge interactions available to 1-NpOH was already tested in the gas phase by three different studies. The first was a rotational spectroscopy study that looked at the homodimer of 1-NpOH formed in a molecular beam.²¹ The authors found this to favor the π–π stacked geometry, a result of the large surface interaction between the two bicyclic aromatic systems having increased dispersive interactions. A complement to this rotational spectroscopy work are two studies by the Leutwyler group. The first focuses on single-ring complexes with 1-NpOH using the stimulated emission pumping-resonant two-photon ionization (SEP-R2PI) technique and a cold, supersonic molecular beam.²² The second uses the same technique, but with small linear molecules.²³ In both studies, experimental dissociation energies are compared to vibrational zero point corrected energies obtained from quantum-chemical calculations. The authors found different agreements between experimental and theoretical values of dissociation energy for the different complexes. This work extends these studies, where we contribute detailed structural information about the complexes, with a focus on the small ring complexes with 1-NpOH.²² A rotational-spectroscopy study of the linear–molecule complexes will follow in a future work.

The small-ring SEP-R2PI study of Knochenmuss et al. combined new experimental data on complexes of 1-NpOH with furan, 2,5-dimethylfuran (DMF), tetrahydrofuran (THF), and thiophene, with previously published data on the 1-NpOH complexes with cyclopropane²⁴ and benzene.²⁵ All experimental results were compared against three dispersion corrected DFT methods, B97-D3, B3LYP-D3, and ωB97X-D. Of the six measured complexes, computed D₀ values for thiophene and DMF had the largest errors relative to the SEP-R2PI results. The experimental D₀ of the 1-NpOH–thiophene complex was 26.56 ± 0.57 kJ mol⁻¹, with the range of computed values from 20.77 to 24.15 kJ mol⁻¹. In the DMF complex, the observed value is 36.5 ± 2.5 kJ mol⁻¹, with a range of theoretical values from 29.69 to 32.41 kJ mol⁻¹. While 1-NpOH–furan did have good agreement to the experimental D₀, the authors observed two isomers of the complex contributing to the observed spectrum. Overall, of the three DFT methods used there was no clear optimal method for the prediction of binding energy across all six complexes.

To better understand the differences between the experimental D₀ values and the quantum-chemically calculated ones, we examine observed structures used to make the comparison. The assignment of vibrational-band shifts in the SEP-R2PI study confirmed that all six 1-NpOH complexes with small rings preferred the edge interaction to the π–π dominated structures by 7–12 kJ mol⁻¹ according to their computational results. The technique cannot discern the absolute geometries of the measured structures. Rotational spectroscopy can determine the planar moments of inertia to confirm absolute symmetries of these complexes. A recent double-blind benchmark study on the furan–methanol complex²⁶ has many computational methods predicting equilibrium geometries of C₁ symmetry, while experimental structures were found to be similar in general, but with an observed C_s symmetry. At first glance, these appear to be small differences in structure, but the subsequent comparisons between theory and experiment were ultimately complicated by the two different geometries.

To this end, we employ chirped-pulse Fourier transform microwave (CP-FTMW) spectroscopy in the 2–8 GHz region to measure the pure rotational spectrum of 1-NpOH complexes with DMF and thiophene. Rotational spectroscopy will determine the relative symmetry of each complex, C_s or C₁, and also give insight to intermolecular distance of each complex in the ground vibrational and electronic state. We also include the 1-NpOH complex with furan. While for 1-NpOH–furan good agreement between experimental and theoretical dissociation energies were determined in the SEP-R2PI study, the authors observed two over-lapping isomers of the complex and had to consider both contributing to the measured dissociation energy together. Microwave spectroscopy will discern the relative favorability of the two isomers with the inherent fingerprint character of the technique.

These three complexes are also good candidates to test the influence of different heteroatoms and alkyl groups in the respective preferred geometries, which reinforces the inclusion of the furan complex to the study. Their structures present a five-membered aromatic ring with a heteroatom that can be oxygen (furan and DMF) or sulfur (thiophene). A structural difference between furan and DMF is the addition of two methyl groups. Thus, two possible arrangements (face or edge) with different interaction possibilities can ensue between them and 1-NpOH.

II. Methods

A. Experimental

The broadband rotational spectra were recorded with the Hamburg broadband chirped-pulse Fourier-transform microwave (CP-FTMW) spectrometer COMPACT in the frequency range 2–8 GHz.²⁷ Three separate experiments were run, in the order of furan, 2,5-dimethyl furan (DMF), and thiophene. In all three experiments, 1-naphthol (1NpOH) was heated in a small reservoir built into the nozzle head to a temperature of 80–90 °C. The samples of furan, DMF, and thiophene were introduced into the neon carrier gas via an external reservoir further upstream, which was not heated. The absolute pressure of neon was 3.5 bars in all experiments. As the seeded neon was pulsed (at 8 Hz) into the chamber in an adiabatic expansion, a microwave chirp from 2.0–8.0 GHz and with 4 μs duration was broadcast into the cold, expanding jet using a horn antenna. The microwave chirps were created by an arbitrary waveform generator (AWG) and amplified with a 300 W traveling wave tube amplifier. The resulting free-induction decay (FID) was then collected and averaged between 2.7 and 4.0 million averages, which is subsequently Fourier transformed into the frequency domain to produce rotational spectra. The experimental setup is described in detail in ref. 27. The “fast frame” option of the digital oscilloscope was used for these experiments.²⁸ Eight back-to-back excitation chirps were performed per gas pulse, and the subsequent eight FID acquisitions were co-added and averaged. In this way, the measurement time and sample consumption were decreased, resulting in an effective repetition rate of 64 Hz for the experiment. The FID was recorded for 40 μs, which generated a frequency resolution of 25 kHz in our Fourier transformed microwave spectrum.

The resulting spectra were then analyzed, concentrating first on the species for which rotational transitions are already reported to clean and simplify the spectra. These include trans-naphthol,²⁹cis-naphthol,²⁹ naphthol dimer,¹⁹ furan,^30,31 thiophene,^32,33 and dimethyl furan.³⁴ The remaining, unassigned rotational transitions are then considered as potential transitions for the desired complexes. Graphical assignment and interface programs, JB95³⁵ and SPFIT/SPCAT³⁶ programs with AABS package interface,³⁷ were used to make the initial assignments of the rotational spectra. All final fits were done in SPFIT/SPCAT using a rigid-rotor and centrifugal distortion Hamiltonian in I^r representation with a Watson S reduction. The XIAM program was used to analyze the internal dynamics of 1NpOH–DMF.³⁸ XIAM is a least squares fitting program employing the combined axis method of Woods,^39,40 which is used to analyze the internal rotation features of molecules containing up to three internal rotors.

B. Theoretical

The minima structures of the 1NpOH–furan, 1NpOH–DMF, and 1NpOH–thiophene complexes were taken from ref. 22, where they were optimized at three different levels of theory: B97-D3⁴¹/def2-TZVPP,⁴² B3LYP-D3⁴³/def2-TZVPP, and wB97X-D⁴⁴/6-311++G(d,p). B97-D3 and B3LYP-D3 calculations yielded very similar geometries for all the complexes. The two DMF isomers and thiophene isomer I optimized with the wB97X method resulted in different geometries than those obtained with B97-D3 and B3LYP-D3. More details of the calculations can be found in ref. 22. The molecular electric dipole moments were predicted using single-point calculations of each previously reported structure and its respective calculation level and basis set using the ORCA program package.^45,46 The relative energies presented herein have been calculated at the PBE0-D3/def2-TZVPP level of theory and are harmonically zero point corrected relative energies to ensure real minima on the potential energy surface. The theoretical calculations were carried out using Gaussian16.⁴⁷ For clarity we use roman numerals to identify the isomers of the complexes. The equivalent structures of ref. 22 are given in the ESI† (Table S1).

We used Non-Covalent Interactions (NCI) analysis⁴⁸ to characterize the non-covalent interactions present in the complexes and the Symmetry-Adapted Perturbation Theory (SAPT)⁴⁹ calculations to gain insight into the different contributions to the binding energy. The lowest-energy complexes optimized at the B97-D3⁴¹/def2-TZVPP level of theory were used as inputs for the SAPT2+3/aug-cc-pVDZ-RI⁴⁹ calculations and the NCI plots.⁴⁸ The SAPT analysis was carried out using the PSI4 package.⁵⁰

III. Results and discussion

A. Rotational spectra analysis

In Fig. 1 portions of the experimental broadband rotational spectra of 1NpOH–furan (a), 1NpOH–DMF (b), and 1NpOH–thiophene (c) are shown, in comparison with simulations based on their fitted rotational parameters (Tables 1–3). Similar to the SEP-R2PI study, we identified two 1NpOH–furan complexes, one 1NpOH–DMF cluster, and one complex of thiophene interacting with the 1NpOH system (Fig. 2).

Fig. 1 Sections of the broadband rotational spectra of 1NpOH–furan (a), 1NpOH–DMF (b), and 1NpOH–thiophene (c) complexes. The upper traces depict the experimental spectra, while the lower traces are simulations of the experimentally identified complexes (rotational temperatures of 0.7 K) based on fitted rotational parameters.

Table 1 Experimental and predicted rotational parameters calculated at the B97-D3/def2-TZVPP, B3LYP-D3/def2-TZVPP, and wB97X-D/6-311++G(d,p) levels of theory for the lowest-energy 1NpOH–furan isomers

Rotational parameters	Exp. 1NpOH–furan(I)	Exp. 1NpOH–furan(II)	Theor. isomer I			Theor. isomer II
			B97-D3	B3LYP-D3	wB97X-D	B97-D3	B3LYP-D3	wB97X-D
a A, B and C are the rotational constants. DJ, DJK, DK, d1 and d2 are the quartic centrifugal distortion constants. μα (α = a, b or c) are the electric dipole moment components (n: α-type transition is not observed, y: α-type transition is observed). N is the number of fitted transitions. σ is the root-mean square deviation of the fit. b Planar moments are calculated via the moments of inertia, Paa = (Ib + Ic − Ia)/2. c ΔEZPE is the energy relative to the most stable isomer with the zero point energy correction calculated at the PBE0-D3/def2-TZVPP level of theory. d Numbers in parentheses give standard errors (1σ, 67% confidence level) in units of the least significant figure. e Values in square-brackets fixed during fitting. f Predicted dipole moment components calculated at the B3LYP-D3/def2-TZVPP level of theory.
A (MHz)	1380.68437(21)^d	1283.024(27)	1370.6	1396.1	1394.2	1276.7	1282.0	1287.9
B (MHz)	251.312253(73)	259.67161(16)	254.2	252.7	255.5	261.4	263.3	266.8
C (MHz)	222.926429(57)	226.55088(16)	224.7	224.1	226.2	228.3	230.0	233.2
D J (kHz)	0.02797(12)	0.01801(31)		—			—
D JK (kHz)	0.3916(12)	0.238(12)		—			—
D K (kHz)	[0]^e	[0]		—			—
d 1 (kHz)	−0.003065(84)	[0]		—			—
d 2 (kHz)	0.001056(55)	0.00220(26)		—			—
P aa (amu Å^2)	1955.97341(38)	1891.5397(43)	1934.3	1946.5	1924.9	1875.6	1861.2	1834.5
P cc (amu Å^2)	54.98706(38)	54.6838(43)	53.9	53.4	53.1	57.8	58.2	59.7
P aa , furan (amu Å^2)	54.6785(15)
μ a/μb/μc (D)	y/y/n	y/n/n	2.8/1.1/0.0^f			2.2/−0.1/0.3^f
ΔEZPE^c (kJ mol^−1)	—	—		0.0			0.7
N	191	62		—			—
σ (kHz)	4.3	5.7		—			—

---

Table 2 Experimental and predicted rotational parameters calculated at the B97-D3/def2-TZVPP, B3LYP-D3/def2-TZVPP and wB97X-D/6-311++G(d,p) levels of theory for the lowest-energy 1NpOH–DMF isomers

Rotational parameters	Exp. 1NpOH–DMF (SPFIT)	Exp. 1NpOH–DMF (XIAM)^f	Theor. Isomer I			Theor. Isomer II
			B97-D3	B3LYP-D3	wB97X-D	B97-D3	B3LYP-D3	wB97X-D
a A, B and C are the rotational constants. DJ, DJK, DK, d1 and d2 are the quartic centrifugal distortion constants. μα (α = a, b or c) are the electric dipole moment components (n: α-type transition is not observed, y: α-type transition is observed). N is the number of fitted transitions. σ is the root-mean square deviation of the fit. b Planar moments are calculated via the moments of inertia, Paa = (Ib + Ic − Ia)/2. c ΔEZPE is the energy relative to the most stable isomer with the zero point energy correction calculated at the PBE0-D3/def2-TZVPP level of theory. d Numbers in parentheses give standard errors (1σ, 67% confidence level) in units of the least significant figure. e Values in square-brackets fixed during fitting. f Using initial internal-rotation parameters from B3LYP-D3/def2-TZVPP levels of theory (see text). g Predicted dipole moment components calculated at the B3LYP-D3/def2-TZVPP level of theory.
A (MHz)	887.366(19)^d	887.219(37)	878.1	891.3	905.0	876.6	914.8	909.4
B (MHz)	209.95454(11)	209.95482(18)	211.5	211.0	216.6	220.2	219.6	241.1
C (MHz)	201.75474(11)	201.75412(18)	202.8	202.7	207.4	192.1	195.0	215.9
D J (kHz)	0.01132(24)	0.012868(38)		—			—
D JK (kHz)	1.5683(14)	1.5613(21)		—			—
D K (kHz)	276.(18)	119(36)		—			—
d 1 (kHz)	[0]^e	−0.00040(20)		—			—
d 2 (kHz)	[0]	0.00157(26)		—			—
V 3 (cm^−1)	—	480.0(12)		—			—
V 3 (kJ mol^−1)	—	5.742(14)		—			—
ε (rad)	—	[1.97]^f
δ (rad)	—	[1.30]^f
P aa (amu Å^2)	2171.2391(62)	2171.192(12)	2153.0	2160.7	2105.8	2174.7	2170.3	1940.6
P cc (amu Å^2)	235.8486(62)	235.896(12)	236.5	234.5	227.5	120.4	131.1	155.5
P aa , DMF (amu Å^2)	233.994101(10)	234.037309(64)
μ a/μb/μc (D)	y/y/n	y/y/n		2.5/−0.7/0.0^g			2.4/0.2/0.1^g
ΔEZPE,rel^c (kJ mol^−1)	—	—		0.0			1.2
N	230	276		—			—
σ (kHz)	9.5	8.6		—			—

---

Table 3 Experimental and predicted rotational parameters calculated at the B97-D3/def2-TZVPP, B3LYP-D3/def2-TZVPP and wB97X-D/6-311++G(d,p) levels of theory for the lowest-energy 1NpOH–thiophene isomers

Rotational parameters	Exp. 1NpOH–thiophene	Theor. isomer I		Theor. isomer II
		B97-D3	B3LYP-D3	B97-D3	B3LYP-D3	wB97X-D
a A, B and C are the rotational constants. DJ, DJK, DK, d1 and d2 are the quartic centrifugal distortion constants. μα (α = a, b or c) are the electric dipole moment components (n: α-type transition is not observed, y: α-type transition is observed). N is the number of fitted transitions. σ is the root-mean square deviation of the fit. b Planar moments are calculated via the moments of inertia, Paa = (Ib + Ic − Ia)/2. c ΔEZPE is the energy relative to the most stable isomer with the zero point energy correction calculated at the PBE0-D3/def2-TZVPP level of theory. d Numbers in parentheses give standard errors (1σ, 67% confidence level) in units of the least significant figure. e Values in square-brackets fixed during fitting. f From ref. 63 and 64, no errors reported. g Predicted dipole moment components calculated at the B3LYP-D3/def2-TZVPP level of theory.
A (MHz)	1166.603(32)^d	1155.0	1184.6	1158.4	1166.7	1177.1
B (MHz)	220.65946(19)	230.7	223.8	223.7	223.6	223.1
C (MHz)	198.52431(18)	204.4	197.5	201.6	201.5	201.5
D J (kHz)	0.01332(21)	—			—
D JK (kHz)	0.2440(47)	—			—
D K (kHz)	46.7(49)	—			—
d 1 (kHz)	−0.00060(18)	—			—
d 2 (kHz)	[0]^e	—			—
P aa (amu Å^2)	2201.3923(61)	2112.8	2195.2	2164.9	2167.6	2172.0
P cc (amu Å^2)	88.9197(61)	77.8	63.0	94.3	92.6	93.2
P bb,thio (amu ·Å^2)	62.8768^f
μ a/μb/μc (D)	y/n/n		−2.6/1.0/0.0^g		2.4/−0.4/0.4^g
ΔEZPE,rel^c (kJ mol^−1)	—	2.8			0.0
N	102	—			—
σ (kHz)	5.4	—			—

---

Fig. 2 NCI plots overlayed on the predicted geometries for the experimentally observed 1NpOH–furan(I), 1NpOH–furan(II), 1NpOH–DMF, and 1NpOH–thiophene complexes. Blue color represents strong attractive interactions, green indicates weak attractive interactions, and red shows repulsive interactions.

According to the quantum-chemical calculations carried out in ref. 22 as described in the Theoretical methods section, the lowest-energy structures of these complexes correspond to edge isomers (Fig. 3 and Tables 1–3). The face structures were predicted to be 7–12 kJ mol⁻¹ higher in energy than the edge ones. By comparison of the calculated and experimentally determined rotational parameters, we can unambiguously assign the identified complexes to edge structures (see below), in agreement with the results obtained using SEP-R2PI.

Fig. 3 Predicted molecular structures of the lowest-energy 1NpOH–furan, 1NpOH–DMF, and 1NpOH–thiophene complexes optimized at the B97-D3/def2-TZVPP level of theory, except for thiophene isomer I, which was optimized at the B3LYP-D3/def2-TZVPP level. The theoretical distances are given in Å. Relative energies are given in kJ mol⁻¹ at the PBE0-D3/def2-TZVPP level in parentheses. See ESI† for the numbering of the isomers compared to ref. 22.

For the 1NpOH–furan system, quantum-chemical calculations²² predicted two low energy edge isomers with relative energies below 0.7 kJ mol⁻¹ (Fig. 3 and Tables 1–3). The calculated isomers I and II could be unambiguously assigned to the experimentally observed 1NpOH–furan(I) and 1NpOH–furan(II), respectively, due to the good agreement between their experimental and computed rotational constants as well as an evaluation of the predicted/calculated dipole moment components (Fig. 2 and Table 1). In the 1NpOH–furan(I) spectrum, we observe a- and b-type rotational transitions, whereas in 1NpOH–furan(II) only a-type features are observed, in good agreement with the theoretical calculations where 1NpOH–furan(II) has a small predicted μ_b component.

In the 1NpOH–DMF case, two isomers with an energy difference of 1.2 kJ mol⁻¹ were computationally identified (see Fig. 3). The experimentally observed 1NpOH–DMF complex showed a- and b-type rotational transitions, and its rotational constants and dipole moment components agree quite well with those calculated for the lowest-energy 1NpOH–DMF structure (see Fig. 2 and Table 2), especially its (B and C) difference. In this respect, it is important to note that differences between the B and C rotational constants, i.e., relative values, are often predicted better by quantum-chemical calculations than absolute values of any of the constants.⁵¹ The predicted μ_b of isomer II is close to zero, so no b-type rotational transitions would be observed in the spectrum if isomer II was the one present in the supersonic expansion, which supports the assignment of the experimentally observed isomer as the lowest-energy one, isomer I. There is no indication of further 1NpOH–DMF isomers in the spectrum.

In the 1NpOH–DMF spectrum, splittings of the respective rotational transitions into three components were observed for a few transitions (14) with K_c = 3, which could be due to internal rotation of the methyl groups. A prediction of the expected internal rotation splitting was generated using the published internal rotation barrier for DMF⁵² as an initial guess and the angles from the r_e structures provided by Knochenmuss et al.²² Fitting the internal rotation parameters with an internal rotation Hamiltonian was carried out with XIAM, with all appropriate values taken from the SPFIT fit as an initial guess. Both SPFIT and XIAM fits are presented in Table 2. As only some transitions showed partially resolved internal rotation splitting (not all internal rotation states were observed for each transition), we present both fits to show the limits of the rotational constants obtained when (i) ignoring the splitting and fitting only the AA transitions (SPFIT), and (ii) fitting the internal rotation states when they are observed/resolved (XIAM). The barrier was determined to be 480.0(12) cm⁻¹, which is higher than that of the monomer reported value, 439.1461(83) cm⁻¹. For this barrier, it is expected that some transitions will not have fully resolved internal rotation splitting. As there are two tops in DMF, this partial resolution can lead to different amounts of transitions being resolved for different transitions.

Unlike the furan and dimethylfuran complexes with 1NpOH, the 1NpOH–thiophene complex does not have a plane of symmetry in the ground state as observed by experiment. This can be directly deduced from our experimental parameters via the large difference between the planar moment of the monomer of thiophene that is in the C_s plane, P_aa = 62.8768 amu Ų, and the complex P_cc = 88.9197(61) amu Ų. Different axis labels for the planar moments are used in the comparison because they both represent the axis that would be in the C_s plane of symmetry. This comparison is valid as long as the correct planes are chosen to match the symmetry elements being compared with the molecules and complexes.

The lowest-energy isomers correspond to two edge structures with an energy difference of about 2.8 kJ mol⁻¹ (Fig. 3). As mentioned, one 1NpOH–thiophene complex was observed under the cold conditions of our molecular jet, and it showed a weak spectrum with only a-type rotational transitions (see Table 3). The good agreement between the experimentally determined and calculated B − C difference supports that isomer II is the one present in our experiment. Additionally, the fact of observing only a-type rotational transitions further supports this assignment of the experimental complex as isomer II. For isomer I, we would have expected to also record b-type transitions because of a predicted μ_b value of 1.0 D for isomer I compared to 0.4 D for isomer II. After removing the transitions of the known species, some lines remained in the 1NpOH–thiophene spectrum. We tried to identify isomer I, but we did not observe a rotational pattern that could belong to it. Isomer I could have been present in the jet, but only at concentrations smaller than 4–5% of that of isomer II. Additional transitions were observed, some belonging to other known systems. We observed the 1NpOH–1 water and 1NpOH–neon complexes,^29,53 however this does not account for all the unassigned transitions, which we attribute to other complexes containing water, neon, and thiophene.⁵⁴

B. Structure determination

Structural information based on isotopic information is not available for these structures as only the parent isotopologues were observed in the microwave spectra, and the signal to noise ratios of the spectra of these weakly bound complexes were not sufficient to record singly-substituted isotopologues. For benchmarking theory with experiment, it was recently shown that comparisons of the intermolecular planar moments can be used to evaluate the predicted structures of different methods when isotopic data is limited,²⁶ and we have chosen to follow this approach. Planar moments are represented by P_gg, where g is the respective principal axis a, b, or c and describes the mass coordinate of that respective axis. It is defined in two equivalent ways, shown here for the a-axis term, where i is an index for each atom, a_i is the atom's distance from the bc-plane, and I_g are the moments of inertia determined from the rotational constants. From experimental data, determination from the moments of inertia is the only possible method of planar moment determination without extensive isotopic studies.

Planar moments can be used to confirm certain symmetries in molecules when compared to other molecules, as was reviewed by Bohn et al.⁵⁵ We extend this methodology here to include complexes. In this study, edge complexes that are C_s symmetric will have mass out of the ab-plane from only the smaller ring-binding partner. Assuming no large structural changes upon complexation, this will have a similar P_gg to the equivalent planar moment of the monomer. The out-of-plane planar moments, P_cc, for each complex are given in their respective Tables 1–3, along with the equivalent planar moment of the monomer.

In furan, P_aa is used to compare the mass out of the plane of symmetry perpendicular to the furan ring. It was determined from experimental values⁵⁶ to be P_aa,Fu = 54.6785(45) amu Ų. Comparing this for both isomer exp(I), 54.9872(42) amu Ų, and isomer exp(II), 54.6838(43) amu Ų, to the monomer P_aa,Fu, it is clear that these complexes have C_s symmetry with furan in an edge configuration perpendicular to 1-naphthol. Like the 1NpOH–furan complex, the 1NpOH–DMF complex has C_s symmetry in the ground vibrational state confirmed by similar planar moments between the out-of-plane P_cc of the complex, 235.896(12) amu Ų, with the P_aa,DMF = 234.039001(75) amu Ų.

As the planar moments confirm the C_s symmetry of the dimethyl furan complex, they also confirm the C₁ symmetry of the thiophene complex: The respective planar moment of the complex, P_cc = 88.9197(61) amu Ų, is much larger than in the monomer thiophene value, P_bb,thio = 62.8768 amu Ų. This large increase suggests that the sulfur is no longer in any symmetry plane and that the complex cannot contain any planes of symmetry, which agrees with the relative orientation of the 1-naphthol and thiophene subunits predicted by DFT methods.

In addition to the overall symmetry of each complex, we can also gauge the balance of intermolecular forces as predicted by ab initio methods. We compare the predicted planar moments of each complex to the experiment, focusing on P_aa. In these complexes, the inertial a-axis is nearly collinear with the line connecting the center-of-mass for the two binding partners. It becomes sensitive to changes in the intermolecular distance, thus providing a good benchmark value for ab initio methods that focus mainly on the accuracy of the intermolecular forces. While the value of P_aa will not reveal which specific forces are better predicted, it will gauge the overall accuracy of the quantum-chemical method. This method is similar to the pseudo-diatomic model first used by Novick and Millen,^57,58 except that information on the force constant between the two molecules is not predicted, so no binding energy approximation can be made.

Even as some of the complexes do not share the same overall symmetry, this approximation has been valid in the past.²⁶Table 4 summarizes this comparison. For each of the predicted complexes, using the three previously published structures, it is found that the errors are all positive. As they are all related in sign to obs-pred (Table 4), a positive error indicates that the two molecules are closer together in the predicted structure than in the experimentally observed one. A negative error would indicate a predicted structure where the two binding partners are further apart than in the experimental case. As the predicted geometries are from optimizations to equilibrium structures, and as we are approximating a pseudo diatomic system in the complex, methods that produce a slightly positive error are better than those that produce a negative error.

Table 4 The predicted vs. experimental planar moments that contain the intermolecular mass distribution information for each observed complex

Species	Exp. Paa	B97-D3/def2-TXVPP		B3LYP-D3/def2-TZVPP		wB97X-D/6-311++G(d,p)
		Pred. Paa	% err	Pred. Paa	% err	Pred. Paa	% err
1NpOH–furan(I)	1955.9732(42)	1934.3	1.1	1946.5	0.5	1924.9	1.6
1NpOH–furan(II)	1891.5397(43)	1875.6	0.8	1861.2	1.6	1834.5	3.0
1NpOH–DMF	2171.192(12)	2153	0.8	2160.7	0.5	2105.8	3.0
1NpOH–thiophene	2201.3923(61)	2164.9	1.7	2167.6	1.5	2172	1.3
Average error		1.1%		1.0%		2.2%

---

While all three methods have positive errors, it is clear that the calculations done at the wB97x-D level of theory have large errors along with a large range of errors for the individual complexes. Predictions using B3LYP-D3 have only a slightly better error than B97-D3, over all observed complexes. As both do better than the wB97x-D, these results highlight the better performance of DFT methods using Grimme's D3 correction.⁴³

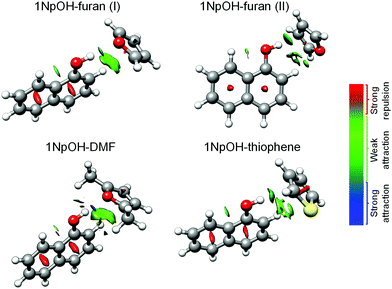
C. Intermolecular interactions

In the following, we summarize the rotational analyses and provide a structural comparison of the different complexes and their intermolecular interactions. Adding the structural information in this work allows for a deeper analysis of the dissociation energy (D₀) results of the SEP-R2PI study. Our focus in this comparison is the consistency and agreement of the three DFT-D predictions with two different sets of high-resolution, gas-phase experimental results. We further compliment the comparison study by including Non-Covalent Interaction (NCI) analysis.⁴⁸ The NCI analysis provides a characterization and visualization of the different interactions present as hydrogen bonds (strong attraction, blue color), van der Waals (weak attraction, green color), and steric (strong repulsion, red color) interactions (Fig. 2). Also included are Symmetry-Adapted Perturbation Theory (SAPT) calculations, which provide more quantitative information of the non-covalent interactions. Specifically the SAPT2+3/aug-cc-pVDZ-RI method was employed, following the results of a recent benchmark study on SAPT methods.⁵⁹ The results are given in Table 4. To keep the comparison consistent, only the geometries identified experimentally in our work and the SEP-R2PI study were used in the NCI and SAPT analysis.

Table 5 The SAPT2+3/aug-cc-pVDZ-RI equilibrium energies (kJ mol⁻¹) for the experimentally identified 1NpOH complexes. The percentages relative to the overall attractive interactions are given for the electronic, induction, and dispersion components. The experimental dissociation energies determined in ref. 22 are given for comparison

Complex	Exp. D0	ΔEtot,eq	ΔEelect (%)	ΔEind (%)	ΔEdisp (%)	ΔEexch
1NpOH–furan(I)	21.82 ± 0.29	−24.5	−26.8 (43.2)	−10.9 (17.5)	−24.3 (39.3)	37.5
1NpOH–furan(II)		−21.1	−20.3 (38.2)	−9.6 (18.1)	−23.3 (43.8)	32.1
1NpOH–DMF	36.5 ± 2.3	−33.7	−38.8 (43.1)	−16.3 (18.1)	−34.8 (38.8)	56.2
1NpOH–thiophene	26.56 ± 0.57	−21.8	−22.5 (37.5)	−11.4 (19.0)	−26.1 (43.5)	38.2

---

a. 1-Naphthol·furan. Both this microwave and the previous SEP-R2PI experiments observed two different isomers of the furan moiety. In the SEP-R2PI study, there was significant overlap between the observed signals in the hole-burning experiment, meaning the different dissociation energies between the two isomers could not be determined. The assumption of that study was that the observation came from structures similar to the equilibrium geometry predictions where 1NpOH–furan(I) has C_s and 1NpOH–furan(II) has C₁ symmetry. The structural difference between the two experimentally identified 1NpOH–furan complexes results from the arrangement of the furan moiety within the complex (Fig. 2 and 3).

The spectrum of 1NpOH–furan(I) showed more intense a-type transitions than 1NpOH–furan(II), pointing to a higher population in the experiment. Determining the abundances of the different species present, based on the intensities of rotational transitions, can be a challenging task (see ref. 60 for a complete discussion). We focused our analysis on a rather narrow frequency range (5–6 GHz) where the frequency dependence of the various components of the broadband spectrometer should be negligible. We did a relative intensity comparison of selected transitions that provided the estimated abundances of the different 1NpOH–furan isomers to be 1NpOH–furan(I) > 1NpOH–furan(II) (see Tables S2 and S3, ESI†). This abundance estimation was done following the steps reported in ref. 60, and it is based on the proportionality of the relative intensities of the a-type transitions with respect to the square of the corresponding dipole-moment component in the CP-FTMW experiment. In the absence of experimental dipole moments theoretical values are used. Theoretical calculations also predict the 1NpOH–furan(I) isomer to be the most abundant (PBE0-D3).

As we have discussed the differences between the symmetries of the 1NpOH–furan(I) and 1NpOH–furan(II) when comparing the experiment and theoretical structures, we can also examine possible origins of the differences in structure. As can be seen, and as confirmed by the NCI analysis displayed in Fig. 2, 1NpOH–furan(I) is stabilized through an O–H⋯O hydrogen bond and a weak attractive C–H⋯π interaction. However, the attractive intermolecular interactions present in 1NpOH–furan(II) are O–H⋯π and C–H⋯O. Only the O–H⋯π interaction of 1NpOH–furan(II) is predicted to be bifurcated, even though a similar bifurcation is possible in the C–H⋯π interaction of 1NpOH–furan(I).

Comparing the intermolecular planar moment, P_aa, all the predictions do relatively well by predicting the complexes to have a smaller r_cm than in the experiment. This is expected of accurate calculations, as in a pseudo-diatomic model of a potential energy well, the distance between two atoms (molecules) should increase going from the equilibrium structure to the ground state. The wB97X prediction seems to do the worst at predicting the intermolecular distances for both 1NpOH–furan(I) and 1NpOH–furan(II). This difference between prediction and experiment is larger for 1NpOH–furan(II) than for 1NpOH–furan(I), with 1NpOH–furan(II) also being the isomer that was incorrectly predicted with C₁ symmetry.

b. 1-Naphthol·DMF. The structure and intermolecular interactions of the identified 1NpOH–DMF complex are like those of 1NpOH–furan(I), with additional weak attractive C–H⋯O interactions between the methyl groups of DMF and the 1NpOH oxygen. The O–H⋯O distance (1.92 Å) in this complex is shorter than in 1NpOH–furan(I), whereas C–H⋯π shows a similar value (2.42 Å). This shortening of the hydrogen bond might arise from the additional C–H_methyl⋯O_1NpOH attractions, which could contribute to the approach of O_furan to the hydrogen of O–H_1NpOH. This attractive contribution is seen in the NCI plots for 1NpOH–DMF in Fig. 2. It is likely that this interaction is what raises the methyl internal rotation barrier in the 1NpOH–DMF complex with respect to the monomer of DMF. In addition, the DMF is slightly more basic than furan because of the two additional methyl groups, which are electron donating to the ring. Another similar situation was observed in a recent rotational spectroscopy study of diadamantyl ether (DAE) and alcohol aggregates.⁶¹ The O–H⋯O distance was longer for the DAE-tertbutanol (tBuOH) complex than for the ethanol or water analogues. This was attributed to the existence of weak attractive C–H⋯H–C interactions between the methyl groups of tBuOH and the methylenes of DAE. The P_aa values of the 1NpOH–DMF are again better for the B3LYP-D3 and B97-D3 predictions, and worse for the wB97X-D prediction.

c. 1-Naphthol·thiophene. The structure of the experimentally observed 1NpOH–thiophene complex represents an intermediate position between 1NpOH–furan(I) and 1NpOH–furan(II). It has weak attractive O–H⋯π (2.3 Å) and C–H⋯π (2.7 Å) interactions with lengths similar to those of 1NpOH–furan(II). However, thiophene is tilted in isomer I, with longer O–H⋯S (2.57 Å) and C–H⋯π (2.89 Å) distances.

It is notable how the presence of a different heteroatom and the addition of two methyl groups can change the structural preferences in these 1NpOH complexes. 1NpOH–furan(I) and 1NpOH–DMF present an O–H⋯O hydrogen bond, whereas in the experimentally identified 1NpOH–furan(II) and 1NpOH–thiophene complexes the O–H⋯π interactions prevail. No thiophene complex with an O-H⋯S hydrogen bond, i.e., isomer I, is observed experimentally. The O–H⋯π isomer for the 1NpOH–DMF (isomer II) is likewise not present in our experiment. All the 1NpOH complexes are further stabilized by C–H⋯π interactions. These experimental findings are supported by the computational results, which predict higher energies for the non-experimentally observed complexes. In looking at the wB97X-D prediction of P_aa, the prediction of 1NpOH–thiophene is the only instance of being better than the B3LYP-D3 and B97-D3 methods.

d. SAPT analysis. In the hydrogen bonded O–H⋯O complexes (1NpOH–furan(I) and 1NpOH–DMF), electrostatic interactions are slightly larger than dispersion, amounting to 43% of the overall attractive interaction, compared to 39% of dispersion (Table 5). An inverted situation is observed in the O–H⋯π complexes (1NpOH–furan(II) and 1NpOH–thiophene), where dispersion increases (43%) and the electrostatic contribution decreases (38%) in comparison with the hydrogen bonded O–H⋯O complexes. These results confirm the importance of dispersion interactions for the stabilization of these complexes. Dispersion drives at about 40% of the overall attractive energy and presents a similar SAPT energy contribution to the electrostatic contribution. This is true even for the O–H⋯O complexes, where it would be expected to find an electrostatic interaction to dominate dispersion.

It is important to remark that 1NpOH–DMF shows the highest value for the total interaction SAPT energy, followed by 1NpOH–furan(I), 1NpOH–thiophene, and 1NpOH–furan(II). This result is in agreement with the experimentally determined dissociation energies (D₀) and with the calculated binding energies (D_e) obtained in ref. 22, which were larger for the classically H-bonded complexes than for the non-classically H-bonded ones.

IV. Conclusions

We report a high-resolution rotational spectroscopic study of dimers between 1NpOH and a series of aromatic rings with different heteroatoms and the addition of alkyl groups, that is, furan, DMF, and thiophene. In the complexes where the aromatic ring has been derivatized with an oxygen (furan(I) and DMF), an O–H⋯O hydrogen bond is formed. However, when a sulfur atom replaces the oxygen (thiophene) the O–H⋯π interaction prevails. No O–H⋯S thiophene isomer is observed in our experiment. The O–H⋯π arrangement is also observed in the furan(II) complex, but it is less populated than furan(I) (O–H⋯O). Weak attractive C–H⋯π interactions further stabilize the structures. Dispersion and electrostatic forces contribute almost equally to the overall attractive energy in all of them.

This work illustrates how the derivatization of an aromatic ring within a complex can drastically change its preferred arrangement and the main interactions that control it, i.e., O–H⋯O or O–H⋯π interactions. The results presented here contribute to better understand the subtle interplay between dispersion and hydrogen bonding in derivatized aromatic species and to predict molecular recognition events between chemical entities that contain functional groups similar to those treated herein.

Results from the planar moments identify that all quantum-chemical methods fail to predict the correct symmetry of 1NpOH–furan(II). In comparing the overall results of all three methods, wB97X-D is overall the worst method at predicting the intermolecular distance as compared to P_aa, although it was the better method in the case of the thiophene complex. This method of analysis has proven a quick and useful method for comparing to computationally predicted geometries when there is limited isotopic information.

Having two sets of observables (structures and binding energies) presents a useful tool for further benchmarking studies. The subtle difference in the observed structures demonstrates the usefulness of these three complexes in benchmarking. It is clear that they require a more careful exploration of DFT and ab initio methods in order to find a more accurate method overall. However, this search can prove computationally expensive as these systems are on the edge of what is tractable for larger calculations.

Additional comparisons could also be made to the OH stretch region of naphthol, which has been shown to be a good detector of van der Waals interactions in naphthol–water clusters.⁶² Line shifts in the presented naphthol complexes would provide a third set of experimental data to benchmark against ab initio and DFT methods.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Deutsche Forschungsgemeinschaft (SCHN1280/4-2, Project number 271359857) in the context of the priority program SPP 1807 “Control of London dispersion interactions in molecular chemistry,” where it was first introduced to us by W. Klopper. M. M. Q. M. thanks Fundación Alfonso Martín Escudero for a postdoctoral grant and Ministerio de Ciencia, Innovación y Universidades for a Juan de la Cierva formación contract (ayuda FJC2018-035709-I financiada por MCIN/AEI/10.13039/501100011033). Parts of the computations were performed using the European XFEL and DESY funded Maxwell computational resources operated at Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany. We acknowledge N. A. Seifert and W. Jäger for providing us the rotational constants of the 1NpOH–1 water and 1NpOH–neon complexes. We also acknowledge C. Holzer for the relative energies calculated at the PBE0-D3/def2-TZVPP level of theory.

References

1. J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, W. H. Freeman, New York, 5th edn, 2002.
2. T. P. Knowles, A. W. Fitzpatrick, S. Meehan, H. R. Mott, M. Vendruscolo, C. M. Dobson and M. E. Welland, Science, 2007, 318, 1900.
3. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
4. D. V. Vranken and G. A. Weiss, Introduction to Bioorganic Chemistry and Chemical BiologyGarland Science, New York and London, 2018, ch. 2, The Chemical Origins of Biology.
5. A. J. Neel, M. J. Hilton, M. S. Sigman and F. D. Toste, Nature, 2017, 543, 637.
6. S. Yamada, Molecular Interactions (Molecular and Surface Forces), in Encyclopedia of Polymeric Nanomaterials, ed. S. Kobayashi and K. Müllen, Springer, Berlin, Heidelberg, 2014.
7. J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274.
8. M. Fatima, A. L. Steber, A. Poblotzki, C. Pérez, S. Zinn and M. Schnell, Angew. Chem., Int. Ed., 2019, 58, 3108.
9. C. Pérez, I. León, A. Lesarri, B. H. Pate, R. Martínez, J. Millán and J. A. Fernández, Angew. Chem., Int. Ed., 2018, 57, 15112.
10. C. Puzzarini, Computational Approach to Rotational Spectroscopy, in Computational Strategies for Spectroscopy: from Small Molecules to Nano Systems, ed. V. Barone, John Wiley & Sons, New Jersey, 2011, ch. 6, pp. 285–286.
11. S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031.
12. N. O. C. Winter, N. K. Graf, S. Leutwyler and C. Hättig, Phys. Chem. Chem. Phys., 2013, 15, 6623.
13. S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854.
14. K. Fuke and K. Kaya, Chem. Phys. Lett., 1982, 91, 311.
15. K. Fuke and K. Kaya, Chem. Phys. Lett., 1983, 94, 97.
16. T. Ebata, T. Watanabe and N. Mikami, J. Phys. Chem., 1995, 99, 5761.
17. A. Weichert, C. Riehn and B. Brutschy, J. Phys. Chem. A, 2001, 105, 5679.
18. M. Schmitt, M. Böhm, C. Ratzer, D. Krügler, K. Kleinermanns, I. Kalkman, G. Berden and W. L. Meerts, ChemPhysChem, 2006, 7, 1241.
19. N. A. Seifert, A. L. Steber, J. L. Neill, C. Pérez, D. P. Zaleski, B. H. Pate and A. Lesarri, Phys. Chem. Chem. Phys., 2013, 15, 11468.
20. M. Saeki, S. Ishiuchi, M. Sakai and M. Fujii, J. Phys. Chem. A, 2007, 111, 1001.
21. N. A. Seifert, A. S. Hazrah and W. Jäger, J. Phys. Chem. Lett., 2019, 10, 2836.
22. R. Knochenmuss, R. K. Sinha, A. Poblotzki, T. Den and S. Leutwyler, J. Chem. Phys., 2018, 149, 204311.
23. R. Knochenmuss, R. K. Sinha and S. Leutwyler, J. Chem. Phys., 2019, 150, 234303.
24. S. Maity, R. Knochenmuss, C. Holzer, G. Féraud, J. Frey, W. Klopper and S. Leutwyler, J. Chem. Phys., 2016, 145, 164304.
25. C. Wickleder, T. Droz, T. Bürgi and S. Leutwyler, Chem. Phys. Lett., 1997, 264, 257.
26. H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. Mogren Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, J. Chem. Phys., 2020, 152, 164303.
27. D. Schmitz, V. Alvin Shubert, T. Betz and M. Schnell, J. Mol. Spectrosc., 2012, 280, 77.
28. C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1.
29. N. A. Seifert, A. Hazrah and W. Jäger, 73rd International Symposium on Molecular Spectroscopy, at The University of Illinois at Urbana-Champaign (IL, USA), 18–22 June 2018, Talk WE04, π–π Stacking in Competition with Hydrogen Bonding in the 1-Naphtol Dimer: a CP-FTMW Spectroscopy Study.  DOI:10.15278/isms.2018.WE04.
30. F. Mata, M. C. Martin and G. O. Sørensen, J. Mol. Struct., 1978, 48, 157.
31. B. Bak, D. Christensen, W. B. Dixon, L. Hansen-Nygaard, J. Rastrup Andersen and M. Schottländer, J. Mol. Spectrosc., 1962, 9, 124.
32. B. R. Bak, D. Christensen, J. Rastrup-Andersen, E. Tannenbaum, B. Bak and E. Tannenbaum, J. Chem. Phys., 1956, 25, 892.
33. B. Bak, D. Christensen, L. Hansen-Nygaard and J. Rastrup-Andersen, J. Mol. Spectrosc., 1961, 7, 58.
34. V. Van, J. Bruckhuisen, W. Stahl, V. Ilyushin and H. V. L. Nguyen, J. Mol. Spectrosc., 2018, 343, 121.
35. D. F. Plusquellic, JB95, 2016, https://www.nist.gov/services-resources/software/jb95-spectral-fitting-program.
36. H. M. Pickett, J. Mol. Spectrosc., 1991, 148, 371.
37. Z. Kisiel, L. Pszczółkowski, I. R. Medvedev, M. Winnewisser, F. C. De Lucia and E. Herbst, J. Mol. Spectrosc., 2005, 233, 231.
38. H. Hartwig and H. Dreizler, Z. Naturforsch., A: Phys. Sci., 1996, 51, 923.
39. R. C. Woods, J. Mol. Spectrosc., 1966, 21, 4.
40. R. C. Woods, J. Mol. Spectrosc., 1967, 22, 49.
41. S. Grimme, J. Comput. Chem., 2004, 25, 1463.
42. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
43. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
44. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
45. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73.
46. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
48. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498.
49. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887.
50. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. Eugene DePrince, E. G. Hohenstein, U. Bozkaya, A. Y. Sokolov, R. D. Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185.
51. W. Gordy and R. L. Cook, Microwave Molecular Spectra, Wiley Interscience, New York, 1984, vol. 11.
52. V. Van, J. Bruckhuisen, W. Stahl, V. Ilyushin and H. V. L. Nguyen, J. Mol. Spectrosc., 2018, 343, 121.
53. N. A. Seifert, A. Hazrah and W. Jäger, (private communication).
54. J. G. Wasserman, K. J. Murphy and J. J. Newby, J. Phys. Chem. A, 2019, 123, 10406.
55. R. K. Bohn, J. A. Montgomery, H. H. Michels and J. A. Fournier, J. Mol. Spectrosc., 2016, 325, 42.
56. P. B. Liescheski and D. W. H. Rankin, J. Mol. Struct., 1989, 196, 1.
57. S. E. Novick, S. J. Harris, K. C. Janda and W. Klemperer, Can. J. Phys., 1975, 53, 2007.
58. D. J. Millen, Can. J. Chem., 1985, 63, 1477.
59. T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106.
60. M. M. Quesada-Moreno, A. Krin and M. Schnell, Phys. Chem. Chem. Phys., 2019, 21, 26569.
61. M. M. Quesada-Moreno, P. Pinacho, C. Pérez, M. Šekutor, P. R. Schreiner and M. Schnell, Chem. – Eur. J., 2020, 26, 10817.
62. R. Yoshino, K. Hashimoto, T. Omi, S.-I. Ishiuchi and M. Fujii, J. Phys. Chem. A, 1998, 102, 6227.
63. U. Kretschmer, W. Stahl and H. Dreizler, Z. Naturforsch., A: Phys. Sci., 1993, 48, 733.
64. U. Kretschmer, H. Hartwig and H. Dreizler, J. Mol. Spectrosc., 1995, 174, 137.

---

Footnotes

† Electronic supplementary information (ESI) available: For NCI scatter graphs, numbering of the isomers, intensity analysis for the calculation of the ratio (1NpOH-furan(I) : 1NpOH-furan(II)), and line lists with all fitted rotational transitions. See DOI: 10.1039/d1cp04337d

‡ Present address: Departamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, Avda. Fuentenueva s/n, 18071, Granada, Spain.

§ Present address: Institut für Physikalische Chemie, Universität Göttingen, Tammannstr. 6, 37077 Göttingen, Germany.

---