 Open Access Article
Open Access ArticleMartini 3 coarse-grained force field for poly(para-phenylene ethynylene)s†
Matthias
Brosz
 ab,
Nicholas
Michelarakis
a,
Uwe H. F.
Bunz
c,
Camilo
Aponte-Santamaría
a and
Frauke
Gräter
ab,
Nicholas
Michelarakis
a,
Uwe H. F.
Bunz
c,
Camilo
Aponte-Santamaría
a and
Frauke
Gräter
 *ab
*ab
aHeidelberg Institute for Theoretical Studies, Am Schlosswolfsbrunnenweg 35, 69118 Heidelberg, Germany. E-mail: frauke.graeter@h-its.org
bInterdisciplinary Center for Scientific Computing, Heidelberg University, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany
cInstitute of Organic Chemistry, Heidelberg University, Im Neuenheimer Feld 270, 69120 Heidelberg, Germany
First published on 12th April 2022
Abstract
Poly(para-phenylene ethynylene)s, or short PPEs, are a class of conjugated and semi-flexible polymers with a strongly delocalized π electron system and increased chain stiffness. Due to this, PPEs have a wide range of technological applications. Although the material properties of single-chains or mixtures of few PPE chains have been studied in detail, the properties of large assemblies remain to be fully explored. Here, we developed a coarse-grained model for PPEs with the Martini 3 force field to enable computational studies of PPEs in large-scale assembly. We used an optimization geometrical approach to take the shape of the π conjugated backbone into account and also applied an additional angular potential to tune the mechanical bending stiffness of the polymer. Our Martini 3 model reproduces key structural and thermodynamic observables of single PPE chains and mixtures, such as persistence length, density, packing and stacking. We show that chain entanglement increases with the expense of nematic ordering with growing PPE chain length. With the Martini 3 PPE model at hand, we are now able to cover large spatio-temporal scales and thereby to uncover key aspects for the structural organization of PPE bulk systems. The model is also predicted to be of high applicability to investigate out-of-equilibrium behavior of PPEs under mechanical force.
1 Introduction
Poly(para-phenylene ethynylene)s, or short PPEs, are a class of conjugated and semi-conductive polymers with a strong delocalized π electron system extending over the entire backbone.1,2 Due to the π conjugation of the carbon atoms, PPEs exhibit unique optical and optoelectronic properties,3–6 and therefore have a wide range of applications, ranging from the printing of electronic devices (e.g. organic transistors, organic light emitting diodes, and organic photovoltaic cells) to the fabrication of biological and chemical sensors.7–11 The backbone of PPEs is composed of aromatic rings and stiff triple bonds, which are linked by single carbon bonds (Fig. 1). Based on the alternation of single and multiple bonds, the orbitals of the carbon atoms overlap and the π electrons are delocalized from one end of the polymer to the other. The delocalization of the π electrons is the reason for the planar structure of monomers and the linear backbone together with its increased mechanical bending stiffness.12 Therefore, PPEs can be classified as semi-flexible polymers and the bending stiffness can be characterized by the persistence length of a single polymer.13 Previous studies determined the persistence length of PPEs through a combination of light scattering experiments or electron paramagnetic resonance spectroscopy and computational methods. Cotts et al. obtained a persistence length of 13.5–16 nm and Godt et al. obtained an estimate of 14.3–19.1 nm.14,15 PPEs thus are roughly 10 to 50-fold stiffer than most polymers with non-conjugated backbones, such as polyethylene (0.45 ± 0.1 nm)16,17 or polymethyl methacrylate (1.2 ± 0.1 nm),18,19 a feature that could be exploited in the development of composite materials with tunable elasticity resulting in unique mechanical properties.20,21Computational simulation is a reliable technique to determine the material properties of conjugated polymers, such as PPEs.22,23 The molecular origin of the high stiffness has been addressed with high-level-of-accuracy quantum mechanical calculations. In fact, both the excited states and the energy barrier of the torsion angle for the backbone rotation of di(para-phenylene ethynylene)s or bis(phenyl ethynyl) benzenes were determined using density functional theory (DFT) simulations.23,24 Bagheri et al. combined molecular dynamics (MD) with DFT simulations to improve the Optimized Potential for Liquid Simulation (OPLS) force field to ensure the planarity of the PPE backbone.12,23 Several studies performed all-atom (AA) MD simulations, using this developed OPLS force field, to simulate the conformation of single PPE chains to thereby examine the rigidity and side-chain aggregation in different solvents.12,25,26 However, DFT calculations and AA-MD simulations are limited to small PPE systems, since both are computationally costly and sample the conformational space inefficiently.27 Alternatively, coarse-grained MD is a well-established approach to cover larger spatio-temporal scales compared to AA-MD by reducing the atomistic degrees of freedom.28 Godt et al. developed a simplified freely rotating chain model for PPE backbones by substituting the phenylene ring, the bond between the phenylene and ethynylene unit and the triple bond with one single bead each.15 Although this model reproduces the global stiff nature of PPEs, it lacks the chemical and thermodynamic distinction between aromatic rings and triple bonds giving rise to the π stacking. Hence, there exists no CG model that considers atomistic structure on the one hand and enables the simulation of large semi-flexible PPE networks on long timescales, capturing their thermodynamic behavior appropriately, on the other hand.
To address this question, we developed a CG model for PPEs based on the Martini 3 force field.29 The Martini force field is one of the most commonly applied CG models in the field of biomolecules or materials science.30–33 Martini 3 is based on reparameterised small and tiny beads with improved solute–solvent interactions to better reproduce stacking properties, like the bulk density and the oil–water partitioning behavior.34 The force field offers the advantage of capturing larger spatio-temporal scales of molecular systems while adjusting the level of resolution of their molecular components. In particular, Martini 3 is very suitable to model long PPE chains, and even mixtures of them, while still taking the essential chemical details of the aromatic rings and the triple bond, giving rise to the enhanced chain stiffness, into account. In detail, the Martini force field is based on a building block principle.35 Each building block is parameterised separately to cover a diverse spectrum of chemical moieties.36 The parameterisation of the building blocks relies on reproducing experimentally determined thermodynamic properties, like the partitioning free energies of a broad range of chemical substances between polar and apolar solvents.37 Besides this top–down approach, the parameterisation of the bonded interactions relies on a bottom–up method through the use of AA simulations.38 For PPEs, we used a geometrical model to consider the shape of the conjugated backbone and an additional harmonic bond angle potential to fine-tune its mechanical bending stiffness. We analyzed the structural organization within the bulk material by characterizing the nematic alignment of PPEs. We find that the degree of alignment decreases with increasing chain length, showing how the dynamics of long-chain semi-flexible PPEs is increasingly driven by entropic effects. Hence, our Martini 3 PPE model adequately reproduces the transition from the rigid rod to random coil like behavior of semi-flexible polymers. It thus enables the study of large bulk systems of such polymers close to atomistic resolution, and together with backmapping and multi-scale approaches allows characterization of the intriguing structural, mechanical and electronic properties of this remarkable material.
2 Methods
For Martini 3, on average, four heavy atoms plus the associated hydrogens are replaced by one CG interaction site.27 To take more complex structures into account (e.g. especially aromatic rings as in the case of PPE), higher resolution mapping is recommended, where three or two heavy atoms plus the associated hydrogens are substituted by one small or tiny bead.28,34 For PPEs, we followed the standardized bottom-up top-down Martini philosophy and defined four tiny beads as our main building block (Fig. 2A). Next, we compared the octanol-/water partitioning free energy of di(para-phenylene ethynylene) to experimental measurements reported in the literature to select the respective bead type of each building block.39,40 For the optimization of bonded interactions, we used a bottom-up strategy by matching the probability densities, describing the bonded potentials, from CG to AA reference simulations.29 We performed all simulations, both Martini 3 and AA, with the GROMACS 2020 molecular dynamics simulations package.41 A detailed protocol regarding the setup of each simulation is described in the following sections. | ||
| Fig. 2 Mapping scheme and geometrical modeling. (A) Mapping from AA (black) to CG (orange) resolution. The dotted lines represent the bonded potentials of the CG model. (B) The geometrical model takes the shape of the PPE backbone into account. PPEs are represented as a linear chain of regular triangles with side length dB and spacing dM. The remaining equilibrium values are calculated by trigonometrical relations (eqn (8)–(10)). | ||
2.1 All-atom simulation protocol
For the AA simulations of PPEs we used a modified version of the OPLS force field. The modification is implemented by converting parameters from the Polymer Consistent Force Field to OPLS and applying a Rickaert–Bellemanns torsion potential to keep the backbone of the polymer planar.23 Bagheri et al. performed DFT simulations to determine an energetic barrier of 4 kJ mol−1 for the rotation of phenylene units, slightly above the experimental values of approximately 2 to 2.5 kJ mol−1 from fluorescence spectroscopy.42–44 The setup of the AA force field for PPEs is described in more detail by Bagheri et al.12,232.2 Coarse-grained simulation protocol
To develop a CG model of PPEs, we chose the Martini 3 force field.29 We used the Martini PolyPly package to generate the topology and coordinate files for PPEs with a different polymerization degree.36 We applied the common Martini 3 MD simulation parameters to calculate the neighbor list and to consider the electrostatics or van der Waals interactions.29 The Verlet neighbor search algorithm updated the neighbor list every 20 to 40 steps with a buffer tolerance of 0.005 kJ mol−1 ps−1. For electrostatics, the reaction-field cut off the coulomb potential at rc = 1.1 nm with a relative permittivity of εr = 15. We modeled the van der Waals interactions with the Lennard-Jones potential, a cutoff at rc = 1.1 nm and the potential-shift with the Verlet scheme.33,53 If not stated otherwise, we selected the common Martini 3 MD parameter set from the Martini webportal (https://www.cgmartini.nl)54 for the equilibration and production run simulations.29,34,552.3 Free energy calculations
The partitioning free energy of tolane, short for di(para-phenylene ethynylene), in an octanol-/water system forms the basis for selecting the Martini 3 bead types. We performed umbrella sampling of tolane in an octanol-/water simulation box to determine the free energy of transfer together with the potential of mean forces and the partition coefficient. The partition coefficient describes the distribution of solute between two immiscible solvents and can be compared to experiments.61 For the umbrella sampling, we defined a reaction coordinate pointing from the center of the hydrophilic solvent towards the center of the hydrophobic one with a 0.05 nm window spacing. Next, we restrained the solute for 100 ps with a force constant of 1000 kJ mol−1 nm−2, energy minimized each window with the steepest descent algorithm and equilibrated the system for 3 ns with a 10 fs timestep. We applied the velocity rescaling thermostat to stabilize the temperature at 300 K with τT = 1 ps and the Parrinello–Rahman barostat to keep the pressure at 1 bar with τP = 12 ps and a compressibility of 3 × 10−4 bar−1. To ensure appropriate sampling of the free energy landscape, we simulated each window for 500 ns with a 25 fs timestep. We applied the weighted histogram analysis method,62 as implemented in gmx wham,63 to estimate the potential of mean forces (PMF) and derive the partition coefficient:61 | (1) |
2.4 Methods for validation
The validation of the developed CG model followed a mixed bottom–up top–down strategy by comparing the properties of interest with experimental data or AA simulations. In particular, we focused on reproducing the mechanical bending stiffness of the polymer by identifying the persistence length, and on its packing properties, by calculating the bulk density and the orientation of packed chains. For this purpose, we imported the trajectory into Python using the Molecular Dynamics Analysis software package (MDAnalysis) and determined the properties with the Numerical Python package (NumPy).65–67 In the case of the packing analysis, we not only calculated the orthogonal distances between aligned chains, but also projected the center-of-mass of each polymer onto the main center-of-mass (COM) axis of the polymer bundle.〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕij〉 = 〈 ϕij〉 = 〈![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) j· j·![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) i〉/〈LM2〉 = exp(−NM〈LM〉/LP) i〉/〈LM2〉 = exp(−NM〈LM〉/LP) | (2) |
![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) i and
i and ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) j are the unit tangent vectors of segment i or j, respectively; ϕij is the angle spanned between
j are the unit tangent vectors of segment i or j, respectively; ϕij is the angle spanned between ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) i and
i and ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) j; NM is the number segments between i and j, and 〈LM〉 is the average length of one segment. To get an estimate for the persistence length, we loaded the CG trajectory into Python and applied the scalar product function of NumPy to determine the angle between each pair of segments along the backbone ϕij. More specifically, we defined the CG beads representing the triple bonds as the segments of the polymer chain, linked adjacent segments by a vector, and then normalized each vector to obtain the unit tangent vector. Hence, we received a chain of unit tangent vectors following the backbone of the polymer. From this chain, we calculated the pair-wise scalar product
j; NM is the number segments between i and j, and 〈LM〉 is the average length of one segment. To get an estimate for the persistence length, we loaded the CG trajectory into Python and applied the scalar product function of NumPy to determine the angle between each pair of segments along the backbone ϕij. More specifically, we defined the CG beads representing the triple bonds as the segments of the polymer chain, linked adjacent segments by a vector, and then normalized each vector to obtain the unit tangent vector. Hence, we received a chain of unit tangent vectors following the backbone of the polymer. From this chain, we calculated the pair-wise scalar product ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) i,
i, ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) j to estimate the cosines of the angles ϕij enclosed by two segments i and j. Next, we averaged the cosines of the angles over the number of segments NM = |j − i| before averaging over time. We also applied the worm-like chain theory to estimate the persistence length.71 For this purpose, as proposed by Doi et al., the square of the orientation correlations (eqn (2)) was integrated along the curvature of the chain,72
j to estimate the cosines of the angles ϕij enclosed by two segments i and j. Next, we averaged the cosines of the angles over the number of segments NM = |j − i| before averaging over time. We also applied the worm-like chain theory to estimate the persistence length.71 For this purpose, as proposed by Doi et al., the square of the orientation correlations (eqn (2)) was integrated along the curvature of the chain,72 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕij〉 and squared end-to-end distances 〈Re2〉 as a function of the count of segments NM. To estimate the persistence length of semi-flexible PPEs, we fitted eqn (2) and (3) to the trajectory obtained from CG simulations using the curve fitting function from the Scientific Python package.73
ϕij〉 and squared end-to-end distances 〈Re2〉 as a function of the count of segments NM. To estimate the persistence length of semi-flexible PPEs, we fitted eqn (2) and (3) to the trajectory obtained from CG simulations using the curve fitting function from the Scientific Python package.73
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) e, and linked the COM of all the other polymers to one end of the end-to-end vector
e, and linked the COM of all the other polymers to one end of the end-to-end vector ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) p. From the norm of the vector product between
p. From the norm of the vector product between ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) e and
e and ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) p, we computed the area content spanned by both vectors and divided the normalized vector product by the length of the end-to-end vector |
p, we computed the area content spanned by both vectors and divided the normalized vector product by the length of the end-to-end vector |![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) e| to estimate the orthogonal distances between adjacent polymer chains:
e| to estimate the orthogonal distances between adjacent polymer chains: | (4) |
In addition, we determined the axial displacement describing the movement of parallelly aligned polymers. We estimated the axial displacement of chains by projecting the COM for each polymer orthogonally onto the main COM axis of the bundle. More precisely, we defined the main COM axis as the vector between the COMs at both ends of the bundle ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) b, linked one end of the COM axis to the COM of any other polymer
b, linked one end of the COM axis to the COM of any other polymer ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) k and projected the COM of each polymer onto the main COM axis, according to74
k and projected the COM of each polymer onto the main COM axis, according to74
 | (5) |
![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) Rb(Rk) denotes the vector projection of the COM of the polymer onto the COM axis of the bundle. We normalized the projected vector |
Rb(Rk) denotes the vector projection of the COM of the polymer onto the COM axis of the bundle. We normalized the projected vector |![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) Rb(Rk)| and subtracted half the length of the main COM axis |
Rb(Rk)| and subtracted half the length of the main COM axis |![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) b| to obtain the axial displacement for the COM of each polymer with regard to the COM of the bundle. In the end, we used the kernel density estimator from the Seaborn package to compute the respective probability density.75
b| to obtain the axial displacement for the COM of each polymer with regard to the COM of the bundle. In the end, we used the kernel density estimator from the Seaborn package to compute the respective probability density.75
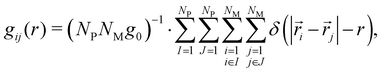 | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i and
i and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j denote the position vectors of bead i and j from polymer I and J and with i ∈ I and j ∈ J, respectively; r is the distance from a reference bead i; δ corresponds to the Dirac delta function and g0 = 4ρπr2dr represents a factor used to normalize the RDF with respect to a uniform system.
j denote the position vectors of bead i and j from polymer I and J and with i ∈ I and j ∈ J, respectively; r is the distance from a reference bead i; δ corresponds to the Dirac delta function and g0 = 4ρπr2dr represents a factor used to normalize the RDF with respect to a uniform system.
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j| with the absolute value of the dot product of their tangent vectors
j| with the absolute value of the dot product of their tangent vectors ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) i and
i and ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) j, as defined in eqn (7):
j, as defined in eqn (7): | (7) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i −
i − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) j|.
j|.
3 Results
The development of the CG model included the mapping of the AA structure to CG resolution, the identification of bead types for the non-bonded interactions and the parameterisation of bonded terms, along with an experimental or AA based validation. By an iterative process we validated our parametrization against experimental data, such as the mechanical bending stiffness, partitioning free energies, the π stacking or bulk density. In the supplementary information, we provided a flow chart showing each step of the force field parameterization (Fig. S1, ESI†) and a table summarising the properties used for validation (Table S1, ESI†).3.1 Mapping scheme for PPE
We followed the building block principle of Martini to identify the mapping scheme for PPE that properly resembles its chemistry and shape of its π conjugated backbone.29,69 The PPE backbone consists of alternating phenyl rings and triple bonds, interconnected by single carbon bonds as shown in Fig. 1. Due to the alternation of single and multiple bonds, the π orbitals of the carbon atoms overlap and the electrons are delocalized from one end of the backbone to the other. To adequately represent the π conjugated backbone of PPEs, we divided the monomer into two building blocks, using similar but different bead types for each (Fig. 2). We substituted the phenyl ring with three apolar TC5 beads forming a triangle with constrained bond lengths to mimic the rigidity of the aromatic ring. For the triple bond between the phenyl rings, we chose one slightly less polar TC4 bead.3.2 Parameterisation of the bonded potentials for PPE
The parameterisation of the bonded potentials followed a bottom-up strategy based on both the identification of bond potentials between Martini 3 beads and the fine tuning of them through comparison to AA simulations or by taking the shape of the molecule into account.29 This methodology has been previously outlined for modeling non-complex molecular structures with Martini and has been partly automated for high-throughput applications.31,78–80 To begin with, we mapped the AA trajectory to CG resolution by placing each CG bead at the center-of-geometry of the underlying AA structure (Fig. 2A). From the mapped trajectory, we computed the probability densities for the bonded terms and performed CG simulations to determine the exact same distribution functions. Next, we iterated over the force constants and equilibrium values of the Martini 3 force field to match the resultant probability densities to the mapped AA ones (Fig. S2, ESI†).However, due to the planar structure of the monomers, we underestimated the volume of the phenyl rings and thus overestimated the PPE bulk density compared to the AA one by roughly 5% (Fig. S4, ESI†). Accordingly, our method required further optimization to consider the shape and volume of the π conjugated backbone as explained in the following section.
 . Based on these assumptions, we finally derived the following equations for the unknown bond length dBT and bond angles ϕAn with n = (1,2), ϕ01= 180° and ϕ02= 120°:
. Based on these assumptions, we finally derived the following equations for the unknown bond length dBT and bond angles ϕAn with n = (1,2), ϕ01= 180° and ϕ02= 120°: | (8) |
 | (9) |
As shown in Fig. 2B, the equation for the equilibrium bond length (eqn (8)) and angles (eqn (9)) only depends on the side length dB and spacing dM of the triangles. To identify each unknown, we set the distance between monomers dM to 0.7 nm in agreement with the AA simulations (0.7 nm) and experiments (0.69 nm).15,56 In addition, we estimated the side length of the regular triangle dB by matching the solvent accessible surface area (SASA) of PPEs from Martini 3 to AA simulations.29,81 We retrieved the SASA from AA simulations of one small four-monomer long PPE chain (ASASA = 13.22 nm2). By setting the side length of the triangle to dB = 0.325 nm, the SASA with our Martini 3 model was ASASA = 13.20 nm2 (Fig. S5, ESI†), a value which is in very close agreement with the AA prediction. The equilibrium values obtained from this optimized geometric model are summarized in Table 1.
| Selected beads for bonded potentials | Reference value [nm or °] | Force constant [kJ mol−1 nm−2 or kJ mol−1] |
|---|---|---|
| a Extra harmonic bond angle potential models the π conjugated backbone. Force constant is identified by matching the persistence length from Martini 3 simulations to experiments reported in the literature.14,15 b Extra harmonic bond angle potential extends over both polymer ends. | ||
| BB1–BB2 | 0.325 | Constraint |
| BB1–BB3 | 0.325 | Constraint |
| BB2–BB3 | 0.325 | Constraint |
| BB3–BB4 | 0.234 | 9000 |
| BB1–BB3–BB4 | 143 | 550 |
| BB–BB3–BB4 | 83 | 650 |
| BB4–BB8–BB12a | 180 | 50 |
| BB1–BB4–BB8ab | 165 | 50 |
| BB4–BB8–BB11ab | 165 | 50 |
| BB4–BB2–BB1–BB3 | 0 | 50 |
 | (10) |
3.3 Partitioning free energy for tolane
The selected Martini 3 bead types, namely, TC5 for the rings and TC4 for the triple bonds, specify the non-bonded interactions. We validated the non-bonded interactions by comparing the solubility of such-chosen CG beads obtained in simulations with that from experiments. We estimated the partitioning free energy in a biphasic octanol-/water system to compute the distribution of the solute between the hydrophilic and hydrophobic solvent. Due to the absence of experimental data regarding the solubility of PPEs, we chose tolane, short for di(para-phenylene ethynylene), as a reference for validation purposes. We estimated the free energy of transfer of tolane from water towards octanol and validated the partition coefficient with experiments from the literature.39,40For this purpose, we calculated the PMF, using the weighted histogram analysis method, and the resultant partitioning free energy for tolane ΔΔGOct−H2O = 27.69 kJ mol−1 in an octanol-/water system. Based on a cumulative simulation of 6 microseconds per umbrella, we performed Bayesian bootstrapping to obtain an absolute error below 0.10 kJ mol−1, and backward block averaging to show convergence within 200 ns (Fig. S6, ESI†).64 For the partition coefficient of tolane logPOct−H2O = 4.82 ± 0.02, calculated with eqn (1), we observed good agreement with experiments reported in the literature 4.78.40 Beyond this, we suggest that similar chemical moieties, such as bibenzyl or trans-stilbene, could be equally considered with our Martini 3 model due to a comparable partition coefficient of 4.70 ± 0.20 and 4.81 ± 0.40, respectively.39Table 2 gives the literature values of experimentally measured partition coefficients for tolane, bibenzyl and trans-stilbene.39,40
3.4 Mechanical bending stiffness for PPE
We further improved our CG model by fine-tuning the bending stiffness of a single chain backbone such that the experimental persistence length is reproduced. The π conjugated backbone is known to induce increased mechanical bending stiffness for a single PPE which classifies PPEs as semi-flexible polymers. To estimate the persistence length LP for the PPE backbone, we performed simulations of a single chain in solution, and fitted both the unit tangent vector auto-correlation between pair-wise segments (eqn (2)) and the squared end-to-end distance (eqn (3)) to the Martini 3 trajectory, as two independent measures for LP.We simulated single PPEs of various chain lengths ranging from 20 to 100 monomers with an increment of 10 in both water and toluene. For each increment, we performed 10 replicas to adequately sample the free energy landscape and obtain a significant estimate for the persistence length. To model the π conjugated backbone and fine-tune the chain stiffness, we introduced an extra harmonic bond angle potential between adjacent TC4 beads (see section 3.2.3) and adjusted the force constant to match the experimental persistence lengths.14,15Fig. 3 shows the resulting persistence length for a single PPE chain for chains of size ranging from 20 to 100 monomers, obtained when choosing a spring constant of 50 kJ mol−1 for the additional bond angle potential of the CG model. The persistence length obtained from the unit tangent vector auto-correlation (14.8 nm) and from the squared end-to-end distances (14.6 nm) were comparable. A detailed summary of the persistence lengths for each replica is provided in Fig. S7 and S8 (ESI†) for water and in Fig. S9 and S10 (ESI†) for toluene. The calculated persistence lengths are largely independent of the chain length and solely depend on the chemical nature of the repetition unit.15 The covered range as well as the obtained average from both estimation methods and solvents of 14.7 nm (with a standard error of 1.3 nm) is in very good agreement with the experimental values reported from Cotts et al. (13.5–16 nm). We thus chose this parametrization for the extra harmonic bond angle potential for all subsequent Martini 3 simulations.
 | ||
Fig. 3 Persistence length of PPEs obtained from Martini 3. Average and standard error for the persistence length of a single PPE chain as a function of the polymerization degree was computed both in water and toluene. Estimated with the unit tangent vector auto correlation ![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) j· j·![[t with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0074_20d1.gif) i (blue) and squared end-to-end distance Re2 (orange). Experimental estimates by Cotts et al., using light scattering experiments (LP = 13.5–16 nm),14 and by Godt et al., performing electron paramagnetic resonance spectroscopy (LP = 14.3–19.1 nm)15 are shown in green. i (blue) and squared end-to-end distance Re2 (orange). Experimental estimates by Cotts et al., using light scattering experiments (LP = 13.5–16 nm),14 and by Godt et al., performing electron paramagnetic resonance spectroscopy (LP = 14.3–19.1 nm)15 are shown in green. | ||
3.5 Packing within a bundle of PPEs
We next evaluated the properties of systems containing multiple PPE chains. To validate the Martini 3-based CG model presented here, we analyzed the local structural organization of PPE chains, and compared it to AA reference simulations and experimental measurements. To this end, we constructed and equilibrated a finite bundle of short PPE chains (10 chains, each 4 monomers in length), and monitored two major degrees of freedom, the radial arrangement of aligned polymers, and their axial displacement within the polymer bundle. These observables jointly tested the bonded and non-bonded interactions defined in the Martini 3 force field potential.First, we characterized the radial displacement between PPE chains by computing the orthogonal distances between aligned polymer chains (eqn (4)). We determined the probability density for π stacking (Fig. 4A). The π stacking obtained from the AA and CG trajectories exhibits a similar behavior. In particular, we observed three distinct peaks of the distribution, at ∼ 0.5 nm, 0.8–0.9 nm and 1.2–1.3 nm. Both the AA and CG simulations show good agreement with the experimentally observed interchain distances.82,83 Both models slightly overestimated the π stacking distances with reference to the experimental value (∼0.4 nm) by 15% for the first and 5% for the second and third peak. In contrast to the AA case, for Martini 3, the probability distribution did not drop to zero between the peaks, the second and third peaks were hardly separated, and finer structural features seen in the AA model were lost. This reflects an overall less ordered packing, which is expected, given the loss of resolution upon coarse-graining. To resolve the second and third peak in more detail, a finer resolution, i.e. mapping a ring of six heavy atoms to a rhombus of four beads, would be suitable at the expense of the performance. Still, the CG simulations capture the major features of radial packing of chains and, thus, yield the expected local structure of PPEs.
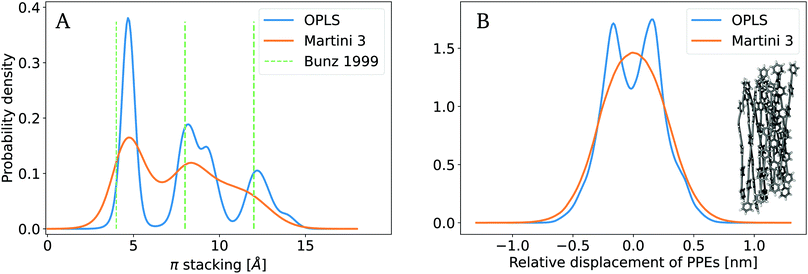 | ||
| Fig. 4 Packing of aligned PPE molecules. (A) Radial orientation of aligned chains within the bundle estimated with the π stacking distance. Experimental measurements reported in the literature used for comparison.82,83 (B) Axial displacement or side-by-side sliding of single chains within the polymer bundle. Both packing properties are validated with reference to OPLS atomistic data.23 | ||
Second, we characterized the axial degree of freedom by computing the horizontal displacement of each chain relative to the centre of the polymer bundle. To this end, we projected the COM of each polymer onto the main COM axis of the bundle using eqn (5). We compared the probability densities from both AA and CG simulations as shown in Fig. 4B. Both the CG and AA models exhibit distributions around zero displacements with highly similar width. They both strongly disfavor chains from displacing relative to each other by more than 0.5 nm. Again, the CG model is unable to reproduce a finer Angstrom-scale structure of the PPEs, namely a bimodal distribution with peaks at ±0.13 nm. Aromatic rings slightly prefer an axial shift relative to one another by this length, a low-energy π stacking mode also known for benzene rings that the AA force field is able to capture.34,84–86 In contrast, the probability density from Martini is unimodal and centered around mode zero. This deviation is due to the flattened free energy surface resulting from mapping the AA structure to the CG resolution, that is, a ring of six heavy atoms to a triangle of three beads. Yet, on the coarser scale beyond 1–2 Å, the CG data closely follows the AA data. Within the expected level of resolution of Martini, we conclude that our CG model accurately represents both the axial and radial degree of freedom within a bundle of aligned polymer chains.
3.6 Structural organization in PPE bulk systems
We next moved from finite PPE systems to a mid-size bulk PPE simulation system with full periodicity of the polymer material and absence of a solvent. The system size was chosen such that simulations at the atomistic scale are still feasible, and comprised 300 chains of 4 monomers each. To characterize the structural organization within a PPE bulk, we focused on properties at both the macroscopic and microscopic length scale, namely global packing by measuring the densities, and the local packing to short-range structural parameters. First, we evaluated the bulk densities from CG with AA simulations and obtained a bulk density of ρAA = 1092 kg m−3 and ρCG = 1098 kg m−3 for the AA and CG models, respectively (Fig. S4, ESI†). This agreement is satisfying, and suggests that the coarse-grained model largely reproduces the inter-PPE distances. Note that experimental densities for solid-state PPEs between 997 and 1118 kg m−3, obtained from X-Ray powder diffraction, depend strongly on the side-chain concentration, and are therefore not suited for validation purposes.87,88On the microscopic scale, we characterized the local organization within the bulk by computing the radial distribution function (RDF) for the assembly of 300 PPEs with a length of four monomers each. Fig. 5 shows a snapshot of the PPE bulk obtained from an AA system in A, from a backmapped CG system in C together with their respective RDF in B. For direct comparison, we mapped the AA and CG trajectory to a one-bead-per aromatic ring resolution and computed the RDF from the mapped trajectories to analyze the packing of 300 PPEs. Due to the symmetry along the backbone, the RDF between the triple bonds as well as the one between the aromatic and the ethynylene groups are very similar (Fig. S11, ESI†). For the mapped AA system, the RDF exhibits a first peak around 0.57 nm, a minimum at 0.73 nm, and a second and third peak at 0.92 and 1.13 nm, respectively. Hence, the PPE assembly, obtained from AA reference simulations, possesses a high degree of local order as shown in Fig. 5A. The RDF computed from the mapped Martini 3 trajectory exhibits a first peak at 0.58 nm, in close agreement with the AA force field. Its second maximum at 0.74 nm is broader and covers the second and third peaks of the RDF from the mapped AA trajectory. Thus, the Martini 3 model broadly shows a similar packing geometry also at such large distances. As expected and as also seen for finite bundles (Fig. 4), it is evident that the PPE assembly obtained on the CG scale is less locally ordered (Fig. 5C). As a consequence of this, the CG model for PPEs did not resolve features beyond the second peak. Still, overall, the packing of the first and second neighbors (i.e. first and second peaks in the RDF) is reproduced by the Martini 3 force field.
3.7 Nematic alignment in large-scale bulk systems
The Martin 3 model now opens the route towards analyzing PPE assemblies at a larger length and time scale. We set out to construct simulation systems of 300 to 800 chains, with 20 to 60 monomers, resulting in box sizes of 10 nm3 to 20 nm3. In the largest system, around 200,000 CG beads represent approximately 600,000 atoms, and have been simulated for 5 microseconds (Fig. 6). Note that these spatial and temporal scales are already difficult to assess at the all-atom level of resolution.Fig. 6A shows snapshots for a bulk system containing 500 PPEs consisting of 20, 40 and 60 monomers each. It is evident that short-chains mostly align in parallel, while this alignment is lost across larger distances when the chain length grows. To quantify this nanometer-scale alignment of polymers within the network, we calculated the nematic correlation function (NCF). The NCF describes the decay in structural order with increasing radial distance from a reference monomer, as defined in eqn (7). More precisely, the lower limit of the NCF (with 0.5) defines randomly oriented polymers and the upper one (with 1.0) parallelly oriented ones. Fig. 6B shows the results of the NCF analysis for different polymer chain lengths ranging from 20 to 60 monomers. We computed the average and standard deviation for the NCF from 8 replicas. The averaged NCF increases sharply at the beginning and decreases with increasing distance until the curve asymptotically approaches the lower limit of 0.5. As reflected by the standard deviations, the variations in nematic ordering reached after independent assembly simulations varied strongly for a given chain length and system size, as the ordering extends across length scales comparable to the system sizes.
Notwithstanding these fluctuations, the extensive sampling aided by the efficient Martini model allowed us to reveal significant differences when modifying the PPE chain length. Most importantly, we observe a steady decrease in ordering with increasing polymer chain length, across the whole range of radial distances. PPEs with a chain length in the range of their persistence length (20 monomers) show a higher degree of alignment in comparison to longer-chain PPEs (40 or 60 monomers). The latter are less parallel and rather assemble through entanglement as opposed to alignment. In this case, parallel alignment is maintained on a length scale of up to ∼5 nm, beyond which a nano-domain forms comprising PPE chains aligned along a different direction. The decrease in alignment with increase in polymer chain length can be attributed to the competition between entropic and enthalpic effects. The influence of the entropic effects on the polymer dynamics increases with the polymer length, thus long-chain PPEs exhibit a random coil-like behaviour with less ordering.
To exclude effects from the limited system size, we also examined the influence of the number of polymer chains on the NCF (Fig. 6B, lighter colors). We compared networks consisting of 300, 500 and 800 chains (e.g. system sizes of 12.1 nm3, 14.3 nm3 and 16.9 nm3 for a 40-monomer long chain), and found that the alignment of PPEs within a bulk system is constant with the increasing number of polymers, and hence independent of the box size. Starting from the equilibrated bulk structures, we confirmed our observation regarding the decrease in order with increasing chain length through annealing simulations of PPE networks (Fig. S12, ESI†).
Taken together, we observe a decay in nematic alignment of PPE chains on the nanometer length scale, resulting in the formation of nano-crystalline domains. The loss of interchain alignment is more pronounced for long-chain PPEs which form nano-domains on the ∼5 nm scale and are independent from the system size. Longer chains show more chain fluctuations and thus entanglement, which impedes the preferred interchain alignment observed for PPE chains with shorter chain lengths, i.e. lengths in the range of their persistence length.
4 Conclusions
In this paper, we have developed a Martini 3 model for the π conjugated backbone of PPEs which we validated against experimental properties for single chains and bulk mixtures, such as solvation and inter-chain packing. The CG model reproduced the stacking and axial displacement of polymers in a bundle as observed in AA reference simulations.82,83 With the Martini 3 model at hand, we shed light on the structural properties of PPEs at larger length scales. As a proof of concept, we here found that the overall high nematic ordering is partly lost for longer chains (Fig. 6B). In addition, the assembly of polymers with chain lengths in the range of the persistence length exhibits parallel alignment across up to ∼6 nm.We recommend the usage of the PPE Martini 3 model for understanding the bulk properties of PPEs, that is MD simulations compromising dozens of polymer chains, for which we observe a pronounced performance boost at the expense of structural detail. We compared the performance obtained with a single NVIDIA GeForce RTX 2080 Super GPU and a 20-core Intel Xeon Gold 6230 processor for the smallest bulk system, consisting of 300 polymers with 20 monomers each, for a total of 26,100 coarse-grained beads. Equilibration for this system, on a timescale of 5 microseconds, would take about 150 days at the AA level as opposed to 60 hours at the CG one. Obviously, the applicability of the AA or CG model depends on the dynamics the user wants to study. In general, the dynamics from Martini 3 simulations will allow the user to study larger polymer systems at longer timescales at the expense of loss on the atomistic accuracy.
The Martini 3 force field can be extended in a straightforward way to comprise side-chains of different chemistry (R in Fig. 1) to thereby analyze the packing of PPEs in detail. Future refinement of the already satisfying packing properties might involve a finer mapping scheme, a desolvation barrier potential, although no solvent molecule was found within the bundle of parallelly aligned polymer chains, or generic labels from Martini 3 to optimize self-interactions between phenyl rings.34 Besides, backmapping the Martini 3 bulk systems to AA resolution allows an advanced analysis on different length scales depending on the required degree of detail. Therefore, our Martini 3 PPE model opens the pathway to elucidate the mechanical stress–strain response of PPE bulk systems under mechanical force as well as the microscopic interactions along the backbone. Finally, the CG model in combination with the backmapping routine and QM/MM methods could, e.g. help in understanding the electronic properties, conductance, or excited states in the environment found in bulk PPE networks.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for fruitful discussions with Peter Gumbsch and Florian Franz. We acknowledge funding through the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – 2082/1 – 390761711, the Klaus Tschira Foundation, the state of Baden-Württemberg through bwHPC and the DFG through grant INST 35/1134-1 FUGG.References
- U. H. F. Bunz, Acc. Chem. Res., 2001, 34, 998–1010 CrossRef CAS PubMed.
- H. Schnablegger, M. Antonietti, C. Göltner, J. Hartmann, H. Cölfen, P. Samori, J. P. Rabe, H. Häger and W. Heitz, J. Colloid Interface Sci., 1999, 212, 24–32 CrossRef CAS PubMed.
- T. M. Swager, C. J. Gil and M. S. Wrighton, J. Phys. Chem., 1995, 99, 4886–4893 CrossRef CAS.
- R. Deans, J. Kim, M. R. Machacek and T. M. Swager, J. Am. Chem. Soc., 2000, 122, 8565–8566 CrossRef CAS.
- Y. Jiang, D. Perahia, Y. Wang and U. H. F. Bunz, Macromolecules, 2006, 39, 4941–4944 CrossRef CAS.
- U. H. F. Bunz, K. Seehafer, M. Bender and M. Porz, Chem. Soc. Rev., 2015, 44, 4322–4336 RSC.
- D. Perahia, R. Traiphol and U. H. F. Bunz, Macromolecules, 2001, 34, 151–155 CrossRef CAS.
- F. Markl, I. Braun, E. Smarsly, U. Lemmer, N. Mechau, G. Hernandez-Sosa and U. H. F. Bunz, ACS Macro Lett., 2014, 3, 788–790 CrossRef CAS.
- E. Smarsly, D. Daume, R. Tone, L. Veith, E. R. Curticean, I. Wacker, R. R. Schröder, H. M. Sauer, E. Dörsam and U. H. F. Bunz, ACS Appl. Mater. Interfaces, 2019, 11, 3317–3322 CrossRef CAS PubMed.
- J. H. Wosnick, C. M. Mello and T. M. Swager, J. Am. Chem. Soc., 2005, 127, 3400–3405 CrossRef CAS PubMed.
- J. H. Moon and T. M. Swager, Macromolecules, 2002, 35, 6086–6089 CrossRef CAS.
- B. Bagheri, M. Karttunen and B. Baumeier, Eur. Phys. J.: Spec. Top., 2016, 225, 1743–1756 CAS.
- C. P. Broedersz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995–1036 CrossRef CAS.
- P. M. Cotts, T. M. Swager and Q. Zhou, Macromolecules, 1996, 29, 7323–7328 CrossRef CAS.
- A. Godt, M. Schulte, H. Zimmermann and G. Jeschke, Angew. Chem., 2006, 118, 7722–7726 CrossRef.
- F. Kienberger, V. P. Pastushenko, G. Kada, H. J. Gruber, C. Riener, H. Schindler and P. Hinterdorfer, Single Mol., 2000, 1, 123–128 CrossRef CAS.
- R. Ramachandran, G. Beaucage, A. S. Kulkarni, D. McFaddin, J. Merrick-Mack and V. Galiatsatos, Macromolecules, 2008, 41, 9802–9806 CrossRef CAS.
- C. Tweedie, G. Constantinides, K. Lehman, D. Brill, G. Blackman and K. Van Vliet, Adv. Mater., 2007, 19, 2540–2546 CrossRef CAS.
- D. Y. Yoon and P. J. Flory, J. Polym. Sci., Polym. Phys. Ed., 1976, 14, 1425–1431 CrossRef CAS.
- M. Das and F. C. MacKintosh, Phys. Rev. Lett., 2010, 105, 138102 CrossRef PubMed.
- M. Das and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 061906 CrossRef PubMed.
- C. J. Zeman and K. S. Schanze, J. Phys. Chem. A, 2019, 123, 3293–3299 CrossRef CAS PubMed.
- B. Bagheri, B. Baumeier and M. Karttunen, Phys. Chem. Chem. Phys., 2016, 18, 30297–30304 RSC.
- M. Hodecker, A. M. Driscoll, U. H. F. Bunz and A. Dreuw, Phys. Chem. Chem. Phys., 2020, 22, 9974–9981 RSC.
- S. Wijesinghe, S. Maskey, D. Perahia and G. S. Grest, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 582–588 CrossRef CAS.
- S. Maskey, J. M. D. Lane, D. Perahia and G. S. Grest, Langmuir, 2016, 32, 2102–2109 CrossRef CAS PubMed.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- P. C. T. Souza, R. Alessandri, J. Barnoud, S. Thallmair, I. Faustino, F. Grünewald, I. Patmanidis, H. Abdizadeh, B. M. H. Bruininks, T. A. Wassenaar, P. C. Kroon, J. Melcr, V. Nieto, V. Corradi, H. M. Khan, J. Domański, M. Javanainen, H. Martinez-Seara, N. Reuter, R. B. Best, I. Vattulainen, L. Monticelli, X. Periole, D. P. Tieleman, A. H. de Vries and S. J. Marrink, Nat. Methods, 2021, 18, 382–388 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801 RSC.
- R. Alessandri, F. Grünewald and S. J. Marrink, Cond. Mat. Mtrl. Sci., 2020, 33, 2008635 Search PubMed.
- N. Michelarakis, F. Franz, K. Gkagkas and F. Gräter, Phys. Chem. Chem. Phys., 2021, 23, 25901–25910 RSC.
- F. Grünewald, R. Alessandri, P. C. Kroon, L. Monticelli, P. C. T. Souza and S. J. Marrink, Nat. Commun., 2022, 13, 68 CrossRef PubMed.
- R. Alessandri, J. Barnoud, A. S. Gertsen, I. Patmanidis, A. H. de Vries, P. C. T. Souza and S. J. Marrink, Adv. Theory Simul., 2021, 2100391 Search PubMed.
- R. Alessandri, P. C. T. Souza, S. Thallmair, M. N. Melo, A. H. de Vries and S. J. Marrink, J. Chem. Theory Comput., 2019, 15, 5448–5460 CrossRef CAS PubMed.
- F. Grunewald, G. Rossi, A. H. de Vries, S. J. Marrink and L. Monticelli, J. Phys. Chem. B, 2018, 122, 7436–7449 CrossRef CAS PubMed.
- H. J. Risselada, Nat. Methods, 2021, 18, 342–343 CrossRef CAS PubMed.
- J. J. Uusitalo, H. I. Ingólfsson, P. Akhshi, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2015, 11, 3932–3945 CrossRef CAS PubMed.
- J. Sangster, J. Phys. Chem. Ref. Data, 1989, 18, 1111–1229 CrossRef CAS.
- C. Hansch, A. Leo and D. Hoekman, Exploring QSAR Vol. 2: Hydrophobic, electronic, and steric constants, American Chemical Society, Washington, DC, 1995 Search PubMed.
- E. Lindahl, M. J. Abraham, B. Hess and D. van der Spoel, GROMACS 2020 Source code (2020), Zenodo, 2020 DOI:10.5281/zenodo.3923645.
- K. Okuyama, T. Hasegawa, M. Ito and N. Mikami, J. Phys. Chem., 1984, 88, 1711–1716 CrossRef CAS.
- C. E. Halkyard, M. E. Rampey, L. Kloppenburg, S. L. Studer-Martinez and U. H. F. Bunz, Macromolecules, 1998, 31, 8655–8659 CrossRef CAS.
- S. Toyota, Chem. Rev., 2010, 110, 5398–5424 CrossRef CAS PubMed.
- E. Lindahl, M. J. Abraham, B. Hess and D. van der Spoel, GROMACS 2020 Manual (2020), Zenodo, 2020 DOI:10.5281/zenodo.3562512.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Pall and H. Berk, Phys. Comp., 2013, 1–17 Search PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- N. Goga, A. J. Rzepiela, A. H. de Vries, S. J. Marrink and H. J. C. Berendsen, J. Chem. Theory Comput., 2012, 8, 3637–3649 CrossRef CAS PubMed.
- G. J. Martyna, D. J. Tobias and M. L. Klein, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- D. H. de Jong, S. Baoukina, H. I. Ingólfsson and S. J. Marrink, Comput. Phys. Commun., 2016, 199, 1–7 CrossRef CAS.
- Martini, General Purpose Coarse-Grained Force Field, 2021, http://www.cgmartini.nl/ Search PubMed.
- P. C. T. Souza, S. Thallmair, P. Conflitti, C. Ramírez-Palacios, R. Alessandri, S. Raniolo, V. Limongelli and S. J. Marrink, Nat. Commun., 2020, 11, 3714 CrossRef CAS PubMed.
- F. Grünewald, P. C. Kroon, P. C. T. Souza and S. J. Marrink, Structural Genomics, Springer US, New York, NY, 2021, vol. 2199, pp. 315–335 Search PubMed.
- S. Kirkpatrick, C. Gelatt and M. Vecchi, Science, 1983, 220, 671–680 CrossRef CAS PubMed.
- R. Alessandri, J. J. Uusitalo, A. H. de Vries, R. W. A. Havenith and S. J. Marrink, J. Am. Chem. Soc., 2017, 139, 3697–3705 CrossRef CAS PubMed.
- R. Alessandri, S. Sami, J. Barnoud, A. H. Vries, S. J. Marrink and R. W. A. Havenith, Adv. Funct. Mater., 2020, 30, 1–11 CrossRef.
- C.-H. Shu, M.-X. Liu, Z.-Q. Zha, J.-L. Pan, S.-Z. Zhang, Y.-L. Xie, J.-L. Chen, D.-W. Yuan, X.-H. Qiu and P.-N. Liu, Nat. Commun., 2018, 9, 2322 CrossRef PubMed.
- C. C. Bannan, G. Calabró, D. Y. Kyu and D. L. Mobley, J. Chem. Theory Comput., 2016, 12, 4015–4024 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720 CrossRef CAS.
- N. Nitschke, K. Atkovska and J. S. Hub, J. Chem. Phys., 2016, 145, 125101 CrossRef PubMed.
- R. Gowers, M. Linke, J. Barnoud, T. Reddy, M. Melo, S. Seyler, J. Domański, D. Dotson, S. Buchoux, I. Kenney and O. Beckstein, MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations, Austin, Texas, 2016, pp. 98–105.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- H.-P. Hsu, W. Paul and K. Binder, Macromolecules, 2010, 43, 3094–3102 CrossRef CAS.
- P. Gutjahr, R. Lipowsky and J. Kierfeld, Europhys. Lett., 2006, 76, 994–1000 CrossRef CAS.
- H.-P. Hsu, W. Paul and K. Binder, Polym. Sci., Ser. C, 2013, 55, 39–59 CrossRef CAS.
- H. Benoit and P. Doty, J. Phys. Chem., 1953, 57, 958–963 CrossRef CAS.
- M. Doi, S. F. Edwards and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1988 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. Millman, N. Mayorov, A. R. Nelson, E. Jones, R. Kern, E. Larson, C. Carey, I. Polat, Y. Feng, E. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. van Mulbregt, Nat Methods, 2020, 17(3), 261–272 CrossRef CAS PubMed.
- J. B. Carrell, Groups, Matrices, and Vector Spaces: A Group Theoretic Approach to Linear Algebra, Springer New York, New York, NY, 2017 Search PubMed.
- M. L. Waskom, Journal of Open Source Software, 2021, 6(60), 3021 CrossRef.
- M. Tuckerman, Statistical Mechanics: Theory And Molecular Simulation, Oxford University Press, Oxford, 2010 Search PubMed.
- R. Fitzpatrick, D. Michieletto, K. R. Peddireddy, C. Hauer, C. Kyrillos, B. J. Gurmessa and R. M. Robertson-Anderson, Condens. Matter, 2018, 257801-1-7 Search PubMed.
- T. Bereau and K. Kremer, J. Chem. Theory Comput., 2015, 11, 2783–2791 CrossRef CAS PubMed.
- J. A. Graham, J. W. Essex and S. Khalid, J. Chem. Inf. Model., 2017, 57, 650–656 CrossRef CAS PubMed.
- C. Empereur-Mot, L. Pesce, G. Doni, D. Bochicchio, R. Capelli, C. Perego and G. M. Pavan, ACS Omega, 2020, 5, 32823–32843 CrossRef CAS PubMed.
- F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284 CrossRef CAS.
- L. Kloppenburg, D. Jones, J. B. Claridge, H.-C. zur Loye and U. H. F. Bunz, Macromolecules, 1999, 32, 4460–4463 CrossRef CAS.
- D. Ofer, T. M. Swager and M. S. Wrighton, Chem. Mater., 1995, 7, 418–425 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200–10207 CrossRef CAS.
- T. M. Cardozo, A. P. Galliez, I. Borges, F. Plasser, A. J. A. Aquino, M. Barbatti and H. Lischka, Phys. Chem. Chem. Phys., 2019, 21, 13916–13924 RSC.
- J. Hermann, D. Alfè and A. Tkatchenko, Nat. Commun., 2017, 8, 14052 CrossRef CAS PubMed.
- U. H. F. Bunz, V. Enkelmann, L. Kloppenburg, D. Jones, K. D. Shimizu, J. B. Claridge, H.-C. zur Loye and G. Lieser, Chem. Mater., 1999, 11, 1416–1424 CrossRef CAS.
- H. Li, D. R. Powell, R. K. Hayashi and R. West, Macromolecules, 1998, 31, 52–58 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Coarse-grained distributions and bulk densities for center-of-geometry or geometrical mapping, potential of mean forces, and persistence length estimation. See DOI: 10.1039/d1cp04237h |
| This journal is © the Owner Societies 2022 |



