Open Access Article
Open Access ArticleImaging of femtosecond bond breaking and charge dynamics in ultracharged peptides†
Ibrahim
Eliah Dawod
 *ab,
Nicusor
Tîmneanu
*ab,
Nicusor
Tîmneanu
 a,
Adrian P.
Mancuso
bc,
Carl
Caleman
a,
Adrian P.
Mancuso
bc,
Carl
Caleman
 ad and
Oscar
Grånäs
ad and
Oscar
Grånäs
 *a
*a
aDepartment of Physics and Astronomy, Uppsala University, Box 516, SE-75120 Uppsala, Sweden. E-mail: ibrahim.dawod@physics.uu.se; oscar.granas@physics.uu.se
bEuropean XFEL, Holzkoppel 4, DE-22869 Schenefeld, Germany
cDepartment of Chemistry and Physics, La Trobe Institute for Molecular Science, La Trobe University, Melbourne, Victoria 3086, Australia
dCenter for Free-Electron Laser Science, Deutsches Elektronen-Synchrotron, Notkestraße 85, DE-22607 Hamburg, Germany
First published on 23rd December 2021
Abstract
X-ray free-electrons lasers have revolutionized the method of imaging biological macromolecules such as proteins, viruses and cells by opening the door to structural determination of both single particles and crystals at room temperature. By utilizing high intensity X-ray pulses on femtosecond timescales, the effects of radiation damage can be reduced. Achieving high resolution structures will likely require knowledge of how radiation damage affects the structure on an atomic scale, since the experimentally obtained electron densities will be reconstructed in the presence of radiation damage. Detailed understanding of the expected damage scenarios provides further information, in addition to guiding possible corrections that may need to be made to obtain a damage free reconstruction. In this work, we have quantified the effects of ionizing photon-matter interactions using first principles molecular dynamics. We utilize density functional theory to calculate bond breaking and charge dynamics in three ultracharged molecules and two different structural conformations that are important to the structural integrity of biological macromolecules, comparing to our previous studies on amino acids. The effects of the ultracharged states and subsequent bond breaking in real space are studied in reciprocal space using coherent diffractive imaging of an ensemble of aligned biomolecules in the gas phase.
1 Introduction
With the development of high-repetition rate X-ray facilities, high resolution imaging of single biological molecules becomes increasingly more achievable.1–5 Previously, structural biology has largely relied on crystallized biomolecules, which can feasibly be investigated using X-rays at synchrotron facilities, since the detected signal is enhanced by the large number of ordered molecules in the crystal.6 The recently introduced X-ray free-electron laser (XFEL) facilities around the globe have enabled using much smaller crystals as well as single particle imaging (SPI), where single, non-crystalline molecules in the gas phase are imaged by an ultrafast X-ray laser operating at femtosecond (fs) timescales, before being destroyed by the extreme radiation damage.7 In order to reconstruct the target, the experiment must be repeated many times to acquire diffraction patterns from all the different orientations of the molecule, which are merged into a 3D volume in reciprocal space, and later used to reconstruct the target in real space.1 Several fundamental processes currently limit the obtainable resolutions in SPI,8 such as radiation damage9 and structural heterogeneity,10 as well as more practical limitations such as experimental background or number of diffraction patterns attainable in a realistic experimental time.11 In serial femtosecond crystallography (SFX) experiments, atomic resolution is achievable using XFELs, since crystalline samples are used.12 Radiation damage is less of a concern here, as the damage is averaged over the crystals, and only the part of the system which is still a crystal will diffract into Bragg spots.13 However, the high intensity pulse will ionize the system and introduce disorder which may limit the obtainable resolutions and thus the interpretation of the retrieved structures.14,15 Furthermore, the interpretation of time-resolved SFX experiments of radiation-sensitive bio-systems might be particularly sensitive to structural changes due to damage. Understanding how biomolecules respond to an intense X-ray pulse in real space and its effects on the signal observed in reciprocal space is therefore vital in order to provide information which can be used to achieve higher resolutions in both SPI and SFX.16 Depending on system sizes and atomic compositions, differences in radiation damage dynamics can be observed. For single molecules, Coulomb explosion is the main factor which drives the dynamics. Here, both high-energy photoelectrons and the slower Auger electrons usually have sufficient kinetic energy such that the electron mean free path is similar to, or larger than the sample.15 For larger systems, such as large proteins and viruses in SPI and crystals in SFX, the system will attain a high positive charge, enabling trapping of free electrons. This will affect the long range interactions in the system through Debye screening, resulting in local interactions driving the dynamics in the system.17, 18 Studying molecules containing heavier atoms is of importance, since the rates at which these atoms will be ionized is different compared to the more common atoms (C, N, O) available in biomolecules.15 They also provide more complicated damage dynamics in the local area of the heavy atoms, which might require one to account for molecular effects in the modeling.17, 19In this work, we simulate damage dynamics and how this affects the electronic structure of the biomolecules. We investigate the effects in reciprocal space (where imaging is done), where we see the dynamics as a function of resolution. Quantifying the effects of damage at atomic resolution using theory can potentially be used to improve the obtained structure in SFX and SPI experiments. The experimentally determined model of a biomolecule can be compared to the theoretically obtained one with damage, in order to confirm that the reconstructed structure is correct. Detailed models such as real-time time-dependent density functional theory (RT-TDDFT) can be used for such cases.20–23 If needed, corrections can then be applied to the experimentally obtained model. Using a combination of damage modeling and experimental data to correct structures is indeed feasible.16 Refinement of obtained structural parameters from X-ray diffraction experiments is commonly done using ab initio theory. An example is the use of combined ab initio and classical molecular (QM/MM) simulations to explore the possible conformations of a metalloprotein and compare to a structure solved at an XFEL source. Heavy metal sites can be significantly more difficult to find the native structure since it can involve searching for oxidation and spin states in addition to the regular structural parameters.23–25 The heavy metal's higher cross section for interaction with light makes these atoms more prone to absorb X-ray photons, and the local environment to be significantly disturbed from its equilibrium structure during the course of the XFEL pulse.14,26,27 By estimating the expected damage at these sites theoretically and quantifying the reproducible damage pathways as done in this work, the information can potentially assist the search for the initial equilibrium states of the desired observables.
2 Method
This work uses ab initio molecular dynamics to study the dynamics of ultracharged biomolecules. By studying the molecules that are the building blocks of larger biological molecules, we aim to find features in the dynamics which can provide transferable information for simulations of larger systems, in particular where local damage is significant for the overall dynamics. Even though the systems we study here are small compared to proteins and viruses, we believe that specific recurring behaviours in the dissociation pathways and charge dynamics that can be distinguished here will be important in larger systems. Following our previous work studying ultrafast bond breaking and charge dynamics of amino acids,28 we turn our attention to larger systems. The same framework is used, however, the target molecules are poly–peptides with a varying number of amino acids. The molecules studied are cystine (C6H12N2O4S2), dialanine (C6H12N2O3) and trialanine (C9H17N3O4) as seen in Fig. 1. They were all built and visualized using the molecular editor AVOGADRO29 in their linear conformations. In the Ramachandran plot, these would correspond to angular values of ϕ = ψ = 180°.30, 31 | ||
| Fig. 1 Images of the four biomolecules studied. The numbering of the atoms is referenced throughout this work and in the ESI.† | ||
In reality, the peptides can occupy other conformations, and we therefore also performed simulations of a different conformation of trialanine (here called alpha helix), with starting angles ϕ = −60° and ψ = −40°. This provides us the opportunity to compare the same structure in different minima on the potential energy surface, and its implications on the subsequent dynamics. The molecules studied have certain important differences that we aim to compare. Cystine contains a disulfide bond, while the alanine peptides contain one and two peptide bonds respectively. The two different types of bonds give us the opportunity to study the dynamics of bond breaking as a function of the particular atoms that have the largest effect on the structural integrity of the entire system. The question of how adding an additional amino acid to a peptide affects the dynamics is answered by comparing di- and trialanine. The structural configurations of the peptides in vacuum will depend on the dynamics due to temperature, as thermal breathing,32 and how they are delivered into the gas phase. The differences in the dynamics due to thermal vibration are investigated by simulating several geometries of the same system, and we also study the effects of different conformations by comparing the linear structure of trialanine to its alpha helix. Finally, it is particularly interesting to compare cystine and trialanine since they contain approximately the same number of electrons (126 for cystine and 124 for trialanine).
In coherent diffractive imaging (CDI), the detected photons are acquired in reciprocal space. The measured signal is dependent on the atoms' electronic occupation numbers and their relative positions. Radiation damage will alter these observables from their equilibrium values such that the detected signal may not reflect the structure of the sample independent of irradiation.16 In order to understand how bond breaking and charge dynamics in real space affects imaging of biomolecules, we have also computed time-resolved scattering from our damage simulations. The time dependent electron density from the ab initio simulation is used as an input to CONDOR,33 in order to calculate the expected scattering signal. Different methods of calculating scattering from molecules are available.33–35 The efficient independent atom approximation (IAM) is commonly applied, where the electron density for each atom is calculated separately. This method ignores the effects of bonding, and the approximation is less accurate for low Z atoms, due to the ratio of bonding to non-bonding electrons.36 Calculating the Fourier transform of the entire molecule accounts for the bonding effects on the resulting diffraction pattern. However, this requires information regarding the electron density of the entire molecule, of which the quality depends on the level of theory used.34
2.1 Density functional theory based ionization simulations
The density functional theory simulations were done using version 4.1 of the SIESTA37 package, where the atomic model is based on pseudopotentials and the Born–Oppenheimer approximation is applied (consult the ESI† for additional details regarding the pseudopotentials used). We modeled the ultrafast dynamics following the photon-matter interaction by focusing on the electrons that are vital to the structural integrity of the molecular system and therefore only ionized electrons involved in bonding, even though we are able to include core hole states.38 Taking into account core hole states would affect the shape of the valence orbitals, since the nuclear charge is less screened.The focus of our study is to specifically compare how different biological molecules respond to comparable degrees of ionization which can be attained at light-sources such as synchrotrons and XFELs. We prepared the molecules for the production simulations by first performing energy minimization using the conjugate gradient algorithm. Molecular dynamics simulations starting at 300 K without temperature coupling were done for 2000 fs, in order to find 10 different starting configurations of each system. pH dependent structural alteration of hydrogen positions was not incorporated for the molecules, due to the simulations being in vacuum. As the chain grows with the number of attached amino acids, the influence of the position of one hydrogen on the pathways of the dynamics will be small. The ionization simulations, which were started at a temperature of 300 K, were done by removing electrons from 0 to the number of atoms available in the system N. In order to compare the charge state of different molecules, the parameter ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = [0, 1] with unit e−/N, was defined. It is the number of electrons removed normalized to the number of atoms in the system N. The highest charge state studied (
= [0, 1] with unit e−/N, was defined. It is the number of electrons removed normalized to the number of atoms in the system N. The highest charge state studied (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1) corresponds to each atom having a net charge of +1 on average. Using nominal XFEL experimental parameters, our collisional-radiative simulations of a Lysozyme crystal exposed to a 100 fs pulse with 9 keV photons and a fluence of 106 J cm−2 show that the average ionization of atoms in the crystal reaches a value of
= 1) corresponds to each atom having a net charge of +1 on average. Using nominal XFEL experimental parameters, our collisional-radiative simulations of a Lysozyme crystal exposed to a 100 fs pulse with 9 keV photons and a fluence of 106 J cm−2 show that the average ionization of atoms in the crystal reaches a value of ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1 within 20 fs.39
= 1 within 20 fs.39
The time step for the simulations was 0.5 fs and the total simulation time was 75 fs. Generalized gradient approximation (GGA) as formulated by Perdew, Burke, and Ernzerhof (PBE)40 was used as the exchange–correlation functional with double-zeta polarized (DZP) basis. To test the importance of incorporating exact exchange we compare the semi-local PBE40 treatment to the hybrid functional PBE041 for a scan along the C–N bond for several degrees of ionization. These results are presented in the ESI.† The behavior of all curves is qualitatively similar independent of the potential energy surface being dissociative or bonding. Furthermore, the Hirshfeld charge partitioning scheme used in this work was also compared for the same functionals and the results are deemed to be qualitatively similar enough to not cause misidentifying different atomic species.
As the Born–Oppenheimer approximation is used, transitions between potential energy surfaces with different spin-states are not well described. However, the spin–orbit coupling is weak due to the low atomic numbers of the atoms treated, and therefore the non-adiabatic coupling between potential energy surfaces corresponding to different spin-states is weak. Further, effects of the spin polarized radicals in homolytic reactions are expected to be much weaker than the Coulomb forces due to ionization.42
The use of polarized basis functions is of great importance for the diffraction calculations, in order to assess the effects of the deformation of the electron density on the observed scattering.37 The structural integrity of the bonds was studied using the chemical bond integrity parameter, first introduced in our previous work,28
 | (1) |
The parameter returns a value in the interval [0,1] at time t, where 0 corresponds to a broken bond and 1 to an intact bond. λ (= 10) is a constant which defines how fast the function decays as the bond length increases, and NMD (= 10) is the number of different trajectories simulated for a specific ionization configuration of a molecule. An example of such a trajectory for cystine at net charge ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1 with its electron density isosurface is shown in Fig. 2.
= 1 with its electron density isosurface is shown in Fig. 2.
 | ||
Fig. 2 Snapshots of a single 30 fs molecular dynamics trajectory for cystine at +26 (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1), with the corresponding electron density isosurface. = 1), with the corresponding electron density isosurface. | ||
The bond integrity gives detailed information regarding the bond breaking of the molecules, but it is difficult to get a global picture of the structural integrity of the system. By analyzing the radius of gyration (Rg) defined as
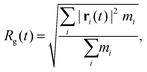 | (2) |
2.2 Coherent diffraction imaging calculations with radiation damage
The damaged ab initio electron densities from the density functional theory simulations were used to compute diffraction patterns in CONDOR,33 by sampling the electron density on a cubic grid with equidistant spacing. Given that we have a charge density on a grid with N points in each dimension with spacing Δx determined from SIESTA, we can use this an input to CONDOR and determine the scattering amplitude which is computed from the Fourier transform of the electron density, making the intensity I(q) ∝ |FT[ρe(x])|2. The number of photons per pixel on the detector is determined as33| I(q) = I0|Ψ(q)|2P(θ)Ω(θ), | (3) |
 | (4) |
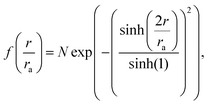 | (5) |
 . We calculated diffraction patterns for 10 geometries where the molecules' backbone was aligned perpendicular to the direction of the X-ray beam. Theoretical studies have suggested that alignment of biomolecules can be done experimentally using an external electric field which interacts with the intrinsic dipole moment of the molecule.45 Other methods exist, for instance using substrates for preferential alignment.46 Furthermore, several experiments have been done on aligned gas phase molecules of sizes similar to the systems studied here.47,48 We assume that the concentration of the molecular ensemble is low, where the distances between the nearest neighbours are larger than the coherence length of the pulse. The scattering patterns from the 10 different geometries with the same
. We calculated diffraction patterns for 10 geometries where the molecules' backbone was aligned perpendicular to the direction of the X-ray beam. Theoretical studies have suggested that alignment of biomolecules can be done experimentally using an external electric field which interacts with the intrinsic dipole moment of the molecule.45 Other methods exist, for instance using substrates for preferential alignment.46 Furthermore, several experiments have been done on aligned gas phase molecules of sizes similar to the systems studied here.47,48 We assume that the concentration of the molecular ensemble is low, where the distances between the nearest neighbours are larger than the coherence length of the pulse. The scattering patterns from the 10 different geometries with the same ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) were added, simulating the incoherent addition of an ensemble of aligned gas phase molecules, thus enhancing the detected signal by 10 times.
were added, simulating the incoherent addition of an ensemble of aligned gas phase molecules, thus enhancing the detected signal by 10 times.
3 Results
3.1 Chemical bond integrity
The following section provides results from the study of the time resolved changes of the structural integrity of all molecules, where the ionization is sequentially increased. Eqn (1) is used to quantify the integrity of a particular intramolecular bond as a function of time and level of ionization. In Fig. 3 we see an example of the bond integrity for several bonds in cystine, averaged over the type of bond. Plots of the bond integrity for each bond is presented in the ESI.†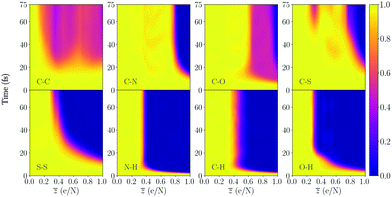 | ||
Fig. 3 Bond integrity as a function of ionization ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) , as described by eqn (1), averaged over the different types of bonds in cystine (seen in the figure). The values correspond to the average of the 10 different trajectories. Yellow (≈1) in the colorbar is an intact bond, while purple (≈0) is a broken bond. The molecule contains a disulfide bond (S–S) and has 26 atoms, which makes , as described by eqn (1), averaged over the different types of bonds in cystine (seen in the figure). The values correspond to the average of the 10 different trajectories. Yellow (≈1) in the colorbar is an intact bond, while purple (≈0) is a broken bond. The molecule contains a disulfide bond (S–S) and has 26 atoms, which makes ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1 correspond to removing 26 valence electrons from the available 126 electrons. The bond integrity for each specific bond is shown in the ESI.† = 1 correspond to removing 26 valence electrons from the available 126 electrons. The bond integrity for each specific bond is shown in the ESI.† | ||
We begin by inspecting Fig. 3, where cystine dissociates into several fragments, and note that specific carbon bonds C14–C15 and C1–C2 are broken for the lowest charge states (shown in Fig. SI.2a and SI.2e in the ESI†). These start to break for charge states around ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0.2 and after approximately 20 fs during the trajectory. The average bond integrity over all C–C bonds in the molecule is around 0.5 (Fig. 3), since the other two carbon bonds (C18–C14 in Fig. SI.2c and C1–C5 in SI.2e, ESI†) are intact. In our previous work on DFT simulations of ultracharged amino acids28 (see Fig. 4a in the article), the carbon bond attached to the carboxyl group COOH was sensitive to bond breaking, which is also the case here. The next non-hydrogen bond that dissociates is the disulfide bond (S–S in Fig. 3), which is the bond that binds the two cysteine amino acids. We see that as the ionization degree increases, the point in time at which the disulfide bond dissociates decreases. For the highest degree of ionization (
= 0.2 and after approximately 20 fs during the trajectory. The average bond integrity over all C–C bonds in the molecule is around 0.5 (Fig. 3), since the other two carbon bonds (C18–C14 in Fig. SI.2c and C1–C5 in SI.2e, ESI†) are intact. In our previous work on DFT simulations of ultracharged amino acids28 (see Fig. 4a in the article), the carbon bond attached to the carboxyl group COOH was sensitive to bond breaking, which is also the case here. The next non-hydrogen bond that dissociates is the disulfide bond (S–S in Fig. 3), which is the bond that binds the two cysteine amino acids. We see that as the ionization degree increases, the point in time at which the disulfide bond dissociates decreases. For the highest degree of ionization (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1), it is the non-hydrogen bond which dissociates first. For this
= 1), it is the non-hydrogen bond which dissociates first. For this ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) , we have removed 26 electrons, and by looking at the average deviation of the neutral charge for the sulfurs in Fig. 9a, one can see that the (S20) sulfur atom acquires a mean of +1.375 and (S7) around +1.0, which can be the reason for the fast dissociation. For higher charge states than
, we have removed 26 electrons, and by looking at the average deviation of the neutral charge for the sulfurs in Fig. 9a, one can see that the (S20) sulfur atom acquires a mean of +1.375 and (S7) around +1.0, which can be the reason for the fast dissociation. For higher charge states than ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1, we see that the timescale for breaking the bond would be even shorter. Interestingly, the two sulfur atoms have different mean charge states, where the deviation increases as more electrons are removed. This might be explained by differences in the geometric configurations of the two ends of the molecule.
= 1, we see that the timescale for breaking the bond would be even shorter. Interestingly, the two sulfur atoms have different mean charge states, where the deviation increases as more electrons are removed. This might be explained by differences in the geometric configurations of the two ends of the molecule.
 | ||
Fig. 4 Bond integrity for the majority of the bonds in dialanine, averaged over the bond types. This molecule contains a single peptide bond (C–N). The number of atoms in the molecule is 23, and ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1 therefore corresponds to removing 23 electrons. The bond integrity for each specific bond is shown in the ESI.† = 1 therefore corresponds to removing 23 electrons. The bond integrity for each specific bond is shown in the ESI.† | ||
Comparing to the only sulfur-containing amino acid methionine (MET) in our previous work28 with the C–S bond here, we notice for the S-side chain that dissociation occurred at about ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0.3 and
= 0.3 and ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0.8, with a stability island between
= 0.8, with a stability island between ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ≈ [0.5, 0.8]. In this work, the stability island is enhanced, and we only see some indication of dissociation at
≈ [0.5, 0.8]. In this work, the stability island is enhanced, and we only see some indication of dissociation at ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0.3, at the end of the simulation. Around
= 0.3, at the end of the simulation. Around ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0.8, we see a similar behaviour for the dissociation, but it happens around 10 fs later. The reason for the increased stability is that the sulfur atom binds to a cysteine fragment, instead of a methyl group in methionine. Furthermore, the two C–S bonds in Fig. SI.2c and SI.2d (ESI†) show similar fragmentation dynamics. Thus, the difference in the charge states between the two sulfur atoms does not seem to be large enough to induce differences in the integrity of this bond type.
= 0.8, we see a similar behaviour for the dissociation, but it happens around 10 fs later. The reason for the increased stability is that the sulfur atom binds to a cysteine fragment, instead of a methyl group in methionine. Furthermore, the two C–S bonds in Fig. SI.2c and SI.2d (ESI†) show similar fragmentation dynamics. Thus, the difference in the charge states between the two sulfur atoms does not seem to be large enough to induce differences in the integrity of this bond type.
In Fig. SI.2b and SI.2f (ESI†), the C–O bonds in the carboxyl group for cystine where the oxygen has a bond to hydrogen is far more stable compared to the case without a hydrogen atom (for a certain range of ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ), which is also the case for the alpha helix (Fig. 7). The result is a range of charge states
), which is also the case for the alpha helix (Fig. 7). The result is a range of charge states ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) where the average over all C-O results are around 0.5 in Fig. 3 and 7. Studying the charge dynamics of cystine in Fig. 9a we note that the carbon bond to the oxygen in the carboxyl group with the largest Hirshfeld charge (O16) breaks for smaller charge states compared to (O24). This also the case for the alpha helix.
where the average over all C-O results are around 0.5 in Fig. 3 and 7. Studying the charge dynamics of cystine in Fig. 9a we note that the carbon bond to the oxygen in the carboxyl group with the largest Hirshfeld charge (O16) breaks for smaller charge states compared to (O24). This also the case for the alpha helix.
In the other alanine peptides however, the two bonds have similar behaviour (see Fig. 4 and 6). The difference between the alanine molecules is likely due to the O–H in the COOH group dissociating at different levels of ionization. The charge of the hydrogen in the carboxyl group seems to be lower in the alpha helix (see in Fig. 9d), compared to the other alanine molecules. This makes the O–H break at a later time in the alpha helix, and therefore makes the dynamics of the C–O bonds in the carboxyl group different. Compared to the amino acids, the C–O bonds in the larger molecules tend to become more sensitive to bond breaking for large charge states.
For all the molecules, we note the C–N bond at the end of the chains to be more unstable compared to the amino acids. This is also what we concluded going from smaller amino acids to larger ones.28 Thus, we can predict that larger poly–peptides will see an increased instability of this bond.
In Fig. 5, the peptide and disulfide bonds are compared. For trialanine and the alpha helix, which have two peptide bonds, the average bond integrity has been calculated (consult the ESI† for results of each peptide bond). We notice that the disulfide bond is far more unstable. For the peptides, only at large degrees of ionization and at much later times than the typical timescales of atomic motion do we see an indication of bond breaking. This shows that the atomic species involved greatly affects the timescales of bond breaking. The heavier sulfur atoms attain larger charges than the atoms in the peptide bonds, which localizes the net charge to the sulfur atoms. Since these atoms are only separated by a single bond, the Coulomb interaction will be strong. Further, we note that the local environment greatly affects the bond breaking, since the two peptide bonds in trialanine do not have the same chemical environment at each side of the peptide, making their bond breaking behaviour different.
 | ||
| Fig. 5 Comparison of the bond integrity for the peptide and disulfide bonds. For trialanine and the alpha helix, the average of the two peptide bonds has been calculated. | ||
Trialanine and dialanine have a similar behaviour for the interval ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ≈ [0.55, 0.75], showing indications of bond breaking for long timescales. For large degrees of ionization close to
≈ [0.55, 0.75], showing indications of bond breaking for long timescales. For large degrees of ionization close to ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1, the peptide bond in dialanine is intact, while the average in trialanine is broken after around 50 fs. For the alpha helix, the bonds are broken after around 30 fs. The local structural integrity of trialanine and the alpha helix is more sensitive to the removal of electrons compared to dialanine for high charge states around
= 1, the peptide bond in dialanine is intact, while the average in trialanine is broken after around 50 fs. For the alpha helix, the bonds are broken after around 30 fs. The local structural integrity of trialanine and the alpha helix is more sensitive to the removal of electrons compared to dialanine for high charge states around ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1. Even though the trialanine molecules contain additional number of bonds which could be deemed as more difficult to break due to the bonds being attached to an additional substructure, the increased Coulomb interaction for the larger molecules contributes more to the local integrity of the molecule.
= 1. Even though the trialanine molecules contain additional number of bonds which could be deemed as more difficult to break due to the bonds being attached to an additional substructure, the increased Coulomb interaction for the larger molecules contributes more to the local integrity of the molecule.
By inspecting the alanine structures in Fig. 4, 6 and 7 we see that several of the bonds have similar behaviour. The averages over the C–N bonds are similar for the molecules, being stable up to high charge states, similar to the amino acids.28 The average of the C–C bonds shows that the more unstable carbon bonds have an interval of re-stabilization. For the amino acids however, the C–C bond was particularly sensitive to bond breaking over the majority of charge states. The induced re-stabilization of the carbon bonds seems to correlate with the breaking of the bonds to hydrogen, which reduces the nuclear charge.28 As this behaviour is present for all alanine peptides, we can conclude that larger chains with alanine residues will have an increased stability of the C–C bonds.
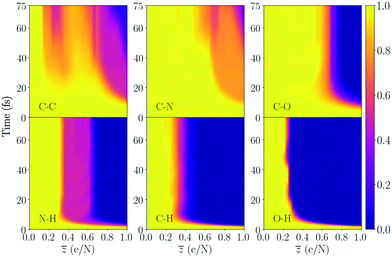 | ||
Fig. 6 Bond integrity for the majority of the bonds in trialanine, averaged over the bond type. This molecule contains two peptide bonds. The molecule has 33 atoms, and ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1 therefore corresponds to removing 33 electrons from the available 124. The bond integrity for each specific bond is shown in the ESI.† = 1 therefore corresponds to removing 33 electrons from the available 124. The bond integrity for each specific bond is shown in the ESI.† | ||
 | ||
| Fig. 7 Bond integrity for the alpha helix, averaged over a particular bond species. The bond integrity result for each specific bond is shown in the ESI.† | ||
For di- and trialanine, the C–C bond attached to the amino acid containing COOH is far more sensitive to bond breaking for lower charge states compared to the other C–C bonds. However, it becomes more robust to ionization when the bonds to the oxygen atoms in the carboxyl group are broken. For the alpha helix, this bond is also re-stabilized at higher charge states due to the dynamics of the carboxyl group, and it also gains stability when bonds to hydrogen are broken.
In Fig. 8, the relative radius of gyration (Rg) is presented, where dialanine and the alpha helix are the molecules which dissociate the fastest compared to cystine and trialanine. Studying the two trialanine conformations, we see that the explosion dynamics of the alpha helix is significantly faster than the linear conformation and one can see that the evolution of Rg is similar to dialanine. The bond integrity results for the two conformations are relatively similar, which means that the more rapid expansion of the alpha helix might be due to the more compact structure. This gives a larger density of positively charged ions compared to trialanine, and therefore makes the Coulomb interaction stronger. Furthermore, the geometric shape, where the alpha helix has a twist with respect to the backbone, can potentially make certain bonds in the backbone break more easily, due to the smaller mass required to be displaced to break the bond. The result gives an indication of the importance of exploring the conformation space of a biomolecule as the differences in the pathways of bond breaking would not have been observed by omitting this in the modeling.
 | ||
Fig. 8 The relative radius of gyration Rg for dialanine, cystine, the alpha helix and trialanine, averaged over all trajectories for ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1. The radius of gyration has been normalized by its value at time = 0 fs. One can conclude from the change of the derivatives of the curves, that the effects of the damage has an effect early in the trajectory. A comparison of the Rg for a wide range of = 1. The radius of gyration has been normalized by its value at time = 0 fs. One can conclude from the change of the derivatives of the curves, that the effects of the damage has an effect early in the trajectory. A comparison of the Rg for a wide range of ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) is shown in the ESI,† which shows a similar trend as presented here. is shown in the ESI,† which shows a similar trend as presented here. | ||
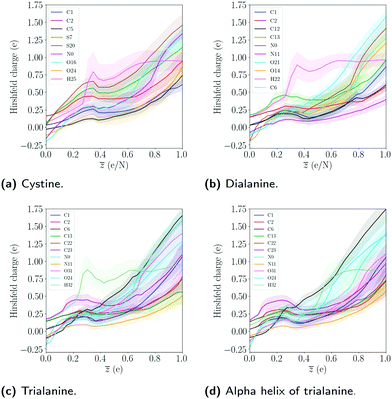
The results of the two conformations of alanine show that the particular fold has a small effect on the bond integrity. The sequence of a poly-peptide is the main contributor to the observed differences in the bond integrity, while the conformation mostly affects the dynamics of the expansion. We note that the size can also affect the explosion dynamics, as dialanine expands on similar timescales as the alpha helix, even though the Hirshfeld charge of dialanine are generally smaller compared to trialanine, as seen in Fig. (9).
3.2 Charge dynamics
In Fig. 9 the Hirshfeld charge has been calculated, which quantifies how much the charge of an atom deviates from its neutral charge state.49 From the Hirshfeld data for the trialanine conformations, there is no significant difference in the average charge, indicating that the differences in the dynamics are due to the geometric configurations. The charge state for dialanine seems to be lower for most atoms compared to the tripeptides for![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1. This might be explained by the fact that in the reference frame of each atom, the attractive Coulomb interaction from the other ions is larger, since there are more atoms in trialanine compared to the smaller system.
= 1. This might be explained by the fact that in the reference frame of each atom, the attractive Coulomb interaction from the other ions is larger, since there are more atoms in trialanine compared to the smaller system.
The charges of the sulfur atoms decrease after around ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ≈ 0.38, where the disulfide bond starts to show instability (see S–S bond in Fig. 3). This is likely due to the breaking of the bonds to hydrogens, which we see start to occur at this level of ionization. The interplay between the dynamics of fragmentation and the bonds to hydrogen is noted in all molecules. For cystine, the disulfide bond is severed after the bonds to hydrogens are broken. In the alanine peptides, carbon bonds are instead stabilized. The particular charge state where this happens will depend on the number of hydrogen atoms in the system. Since a hydrogen atom can easily lose its single electron, it will leave the molecule as a proton, which neutralizes the molecule and the atoms' Hirshfeld charges decrease. The interplay between the stability of the system and the level of ionization where the bonds to hydrogens break was also noted for the amino acids.28 We note that as the net charge is increased, the atoms at the end points of the molecules acquire the largest change in charge (except for the sulfur atoms in cystine). The dependence of Hirshfeld charge with the respect to the center of molecule is evident by the fact that as one moves from the center to the end point of the chain, the Hirshfeld charge increases. This could be due to the self-consistent cycle in the DFT procedure finding a minimum where the Coulomb interaction is minimized. This would correspond to an electronic configuration where the interaction between the largest Hirshfeld charges are minimized, which occurs when the distance between the two charges is maximized.
≈ 0.38, where the disulfide bond starts to show instability (see S–S bond in Fig. 3). This is likely due to the breaking of the bonds to hydrogens, which we see start to occur at this level of ionization. The interplay between the dynamics of fragmentation and the bonds to hydrogen is noted in all molecules. For cystine, the disulfide bond is severed after the bonds to hydrogens are broken. In the alanine peptides, carbon bonds are instead stabilized. The particular charge state where this happens will depend on the number of hydrogen atoms in the system. Since a hydrogen atom can easily lose its single electron, it will leave the molecule as a proton, which neutralizes the molecule and the atoms' Hirshfeld charges decrease. The interplay between the stability of the system and the level of ionization where the bonds to hydrogens break was also noted for the amino acids.28 We note that as the net charge is increased, the atoms at the end points of the molecules acquire the largest change in charge (except for the sulfur atoms in cystine). The dependence of Hirshfeld charge with the respect to the center of molecule is evident by the fact that as one moves from the center to the end point of the chain, the Hirshfeld charge increases. This could be due to the self-consistent cycle in the DFT procedure finding a minimum where the Coulomb interaction is minimized. This would correspond to an electronic configuration where the interaction between the largest Hirshfeld charges are minimized, which occurs when the distance between the two charges is maximized.
In terms of structure determination using X-ray diffraction, averaging the Hirshfeld charge with respect to time can be considered as the average charge which the probe will coherently scatter from. This means that the usual neutral form factors used to fit the molecular model to the experimental data might not yield the best final model, since the fitting is done to data acquired from a different system than the native one. The obtained model, and the subsequent refinement of the structure would then correspond to a structure with a different potential energy surface. This is especially true when XFELs are used, since the atoms can reach high charge states. If one would estimate the expected damage of the molecule in an experiment, the average Hirshfeld charge during the trajectory could be used to quantify the atom with the largest deviation from the neutral state. If this deviation is large enough to be detectable within the variation of the experiment, then fitting the data using a corrected form factor would be needed. These improved form factors can be obtained from the electron density of the atom during the trajectory using the Hirshfeld partitioning scheme and thereafter Fourier transform the density. This would incorporate both the effects of radiation damage, and the molecular bonds on the atomic density.50
3.3 Effects of radiation damage in reciprocal space
In Fig. 10, we compare the resulting diffraction pattern from a 30 fs trajectory of a damaged molecule at the highest degree of ionization![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1 and the undamaged molecule (
= 1 and the undamaged molecule (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0). There is a change in the scattered signal due to bond breaking and charge dynamics where the undamaged patterns have a larger contrast between the maximum and minimum value of the intensity, compared to the damaged one. The structural differences in real space can also be noted in the diffraction data. For instance, the alpha helix provides the smallest contrast between the lowest/largest signal. Comparing to trialanine, which contains the same number of electrons, the differences are due to how the electrons are distributed in space. The electron density of the alpha helix is more localized since the molecule is smaller, which gives smaller contrast between the minimum (usually at high resolutions) and maximum values (at low resolutions). Differences because of the conformation can also be noted by the different shape of the central speckle.
= 0). There is a change in the scattered signal due to bond breaking and charge dynamics where the undamaged patterns have a larger contrast between the maximum and minimum value of the intensity, compared to the damaged one. The structural differences in real space can also be noted in the diffraction data. For instance, the alpha helix provides the smallest contrast between the lowest/largest signal. Comparing to trialanine, which contains the same number of electrons, the differences are due to how the electrons are distributed in space. The electron density of the alpha helix is more localized since the molecule is smaller, which gives smaller contrast between the minimum (usually at high resolutions) and maximum values (at low resolutions). Differences because of the conformation can also be noted by the different shape of the central speckle.
In Fig. 11a and b, the damaged structure provides a different intensity profile at 0 fs, by attaining more signal at larger resolutions. Due to the applied normalization, the number of electrons in the two systems are the same, but the electron density is different. This means that relocation of charge density has occurred, where higher resolutions have acquired a larger density. The relocation at 0 fs corresponds to the effects of damage when the atoms have not moved (compared to the 30 fs result). This is due to the electron density becoming more localized, since the remaining electrons interact more strongly with the nuclear charge, due to the reduced screening from previously bound electrons. This type of damage will always exist independent of how short pulses one uses (i.e. how much the ions move during the pulse). However, there are procedures of retrieving the undamaged electron densities for such cases.16
 | ||
Fig. 11 Comparison of the integrated intensity for the ideal undamaged case (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0) and the damaged case ( = 0) and the damaged case (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1) for cystine in (a) and (b) as a function of resolution q = 1/d Å−1. The intensity has been normalized such that they are equal at q = 0. At 30 fs, the integrated intensity corresponds to the total accumulated signal during the molecular dynamics trajectory. In figure (c) we compare damaged and undamaged time-resolved noiseless intensity for cystine at ( = 1) for cystine in (a) and (b) as a function of resolution q = 1/d Å−1. The intensity has been normalized such that they are equal at q = 0. At 30 fs, the integrated intensity corresponds to the total accumulated signal during the molecular dynamics trajectory. In figure (c) we compare damaged and undamaged time-resolved noiseless intensity for cystine at (![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 1), for the first 30 fs of the molecular dynamics trajectory. The figure depicts the logarithm of the ratio = 1), for the first 30 fs of the molecular dynamics trajectory. The figure depicts the logarithm of the ratio  , where the data has been normalized such that they are equal at q = 0. Since ionization can cause certain bonds to acquire more or less electron density compared to the neutral state,28 certain resolutions will be enhanced while the signal in other will diminish. The observed dynamics of the intensity early in the simulations is dominated by the charge redistribution in the molecules, where the ions occupy approximately the same equilibrium positions. The results for the alanine molecules are shown in the ESI.† , where the data has been normalized such that they are equal at q = 0. Since ionization can cause certain bonds to acquire more or less electron density compared to the neutral state,28 certain resolutions will be enhanced while the signal in other will diminish. The observed dynamics of the intensity early in the simulations is dominated by the charge redistribution in the molecules, where the ions occupy approximately the same equilibrium positions. The results for the alanine molecules are shown in the ESI.† | ||
We note the relocation of the electron density to higher q by inspecting the intensity difference between the neutral and the damaged trajectory in Fig. 11c. The result shows that there is a positive change in higher q before any movement has occurred. This feature is also present during the whole 30 fs trajectory. When there has been significant atomic displacement after approximately 10 fs, lower momentum transfers q acquire a negative change.
A notable feature in Fig. (11) is that the intensity at time 0 and the integrated intensity at 30 fs cross at the same resolution q ≈ 0.21 Å−1 which can roughly be explained through the radius of gyration. In Fig. SI.7 (ESI†), we show the radius of gyration as a function of time for 30 fs. By calculating the average value, we get 5.11 Å for cystine, 5.83 Å for the alpha helix and 6.10 Å for trialanine. These average length scales seem to be largely unaffected by the damage for the first 30 fs, and therefore provide a similar intensity profile between the damaged/undamaged structures.
4 Discussions and conclusions
We have presented the dynamics of highly charged biomolecules in both real and reciprocal space, as a function of chemical composition (amino acid sequence), size and conformation. The real space simulations were done using density functional theory in SIESTA, and the resulting ab initio electron density was Fourier transformed in CONDOR in order to study the expected scattering as a function of resolution.The systems simulated here are relevant to the structural integrity of macromolecules such as proteins and viruses. Our results show that certain fragmentation patterns are reproducible as the peptide chain grows, which could help predict the dynamics of proteins. For instance, by comparing to our previous work on amino-acids, we see for larger molecules that the average bond integrity of the C–C bond becomes more robust to ionization, while the C–O bond becomes more sensitive to bond breaking.
Furthermore, we concluded in our previous work that the hydrogen atoms can provide re-stabilization of certain bonds since they leave the molecule as a proton, neutralizing the rest of the system. This is also true for the results presented in this work. We therefore predict that hydrogen atoms will also have an impact on the structural integrity of larger systems. However, in a molecule such as a protein, the free hydrogens will not always propagate directly into vacuum, but they will likely interact with other molecules. This could lead to additional fragmentation in the system. We have seen that the C–N bond at the end of the chains in the peptides becomes more sensitive to bond breaking for larger systems. For the amino-acids, this bond also had this dependence on the size. Therefore, we will state that this will be seen for larger poly-peptides as well.
We conclude that the Coulomb explosion due to ionization is mainly driven by differences in the geometry, such as conformation and size of the system. Systems that have a greater number of atoms, or heavier atoms relative to a particular system, can have a slower expansion due to the ionization, even though certain bonds in the molecule can be more unstable, as is the case for trialanine and cystine, compared to dialanine. Furthermore, even though the local structural integrity of a system can be similar, the rate of the Coulomb explosion is greatly affected by the conformation since this affects the distribution of the ions in space and therefore the Coulomb interaction. Chemical composition (amino acid sequence) also plays an important role, by determining the local dynamics. This might motivate future studies of radiation damage in biomolecules to investigate different conformations, in order to capture the full damage dynamics. Additionally, gas phase scattering experiments of an ensemble of aligned molecules might be limited by the fact that different conformations will provide different diffraction patterns. If one can not control the conformation space of the ensemble, this may result in a single-shot diffraction pattern which is an incoherent sum of several different conformations.
It is important to note that we have only studied peptides with equivalent residues. However, a protein contains poly–peptides which will have non-equivalent residues. From our conclusions about the dependence of the dynamics on conformation, size and the chemical composition, we can say that changing an alanine molecule with an amino-acid with the same chemical composition should only provide a substantial difference if the angles ϕ and ψ are significantly changed. This would alter the distribution of charges in space and therefore change the explosion dynamics. Introducing a molecule with a different chemical composition, by for instance adding an amino-acid containing a sulfur atom, the local dynamics could be changed. This is because heavier atoms such as sulfur acquire a larger deviation from the neutral charge, compared to light atoms such as carbon, oxygen and nitrogen. This will localize the positive charge, leading to a greater interaction with neighbouring atoms. Since the charge is less spread over the molecule, the rate of expansion should decrease but the local integrity around the sulfur should be more sensitive to bond breaking. Finally, since the bonds to hydrogens are sensitive to bond breaking for relatively small charge states for all molecules studied, this would likely disturb the hydrogen-bond networks in proteins.
We observe the fragmentation patterns to be reproducible for several molecules. This enables imaging of the breaking of these bonds experimentally, since they will not be averaged out. Additionally, we see that ionization alters the equilibrium charge states of the atoms involved and will induce charge transfer, which for radiation-sensitive systems such as metalloproteins can make the reconstruction of structural parameters more difficult. This is especially important to consider when interpreting time-resolved XFEL structures of radiation-sensitive systems, where for instance oxidation states and spin configurations are investigated.51,52 By theoretically calculating the expected damage dynamics, together with possible mass spectrometry/spectroscopy data, information regarding what the probe observes during the pulse can be estimated. This could in combination with experimentally reconstructed electron densities and ab initio theory calculations provide a path toward additional refinement of the structure, and the confirmation that the retrieved structure is closer to the native one.
Finally, the effects of free electrons on the dynamics were not considered in our modeling. This approximation is valid for small molecules in gas phase since the mean free path of the electrons will be larger than the sample.53 For a crystal in a plasma phase, Coulomb interactions will be dominated by small lengths scales, due to Debye screening from the trapped free electron gas.17,18 Future studies using this model could therefore investigate the effects of the free electrons on the fragmentation dynamics, which will be applicable to larger systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the developers of CONDOR for helpful discussions and access to the Davinci computer cluster provided by the Laboratory of Molecular Biophysics, Uppsala University. We thank the biophysics network at Uppsala University for fruitful discussions. The main computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX partially funded by the Swedish Research Council through grant agreement no. 2018-05973. N. T. thanks the Swedish Research Council for financial support (2019-03935). C. C. acknowledges the Swedish Research Council (grant 2018-00740) and the Helmholtz Association through the Center for Free-Electron Laser Science at DESY. O. G. acknowledges the Strategic Research Foundation (SSF) for funding through Grant No. ICA16-0037.Notes and references
- T. Ekeberg, M. Svenda, C. Abergel, F. R. N. C. Maia, V. Seltzer, J.-M. Claverie, M. Hantke, O. Jönsson, C. Nettelblad, G. van der Schot, M. Liang, D. P. DePonte, A. Barty, M. M. Seibert, B. Iwan, I. Andersson, N. D. Loh, A. V. Martin, H. Chapman, C. Bostedt, J. D. Bozek, K. R. Ferguson, J. Krzywinski, S. W. Epp, D. Rolles, A. Rudenko, R. Hartmann, N. Kimmel and J. Hajdu, Phys. Rev. Lett., 2015, 114, 098102 CrossRef PubMed.
- K. Ayyer, P. L. Xavier, J. Bielecki, Z. Shen, B. J. Daurer, A. K. Samanta, S. Awel, R. Bean, A. Barty, M. Bergemann, T. Ekeberg, A. D. Estillore, H. Fangohr, K. Giewekemeyer, M. S. Hunter, M. Karnevskiy, R. A. Kirian, H. Kirkwood, Y. Kim, J. Koliyadu, H. Lange, R. Letrun, J. Lübke, T. Michelat, A. J. Morgan, N. Roth, T. Sato, M. Sikorski, F. Schulz, J. C. H. Spence, P. Vagovic, T. Wollweber, L. Worbs, O. Yefanov, Y. Zhuang, F. R. N. C. Maia, D. A. Horke, J. Küpper, N. D. Loh, A. P. Mancuso and H. N. Chapman, Optica, 2021, 8, 15–23 CrossRef.
- I. V. Lundholm, J. A. Sellberg, T. Ekeberg, M. F. Hantke, K. Okamoto, G. van der Schot, J. Andreasson, A. Barty, J. Bielecki, P. Bruza, M. Bucher, S. Carron, B. J. Daurer, K. Ferguson, D. Hasse, J. Krzywinski, D. S. D. Larsson, A. Morgan, K. Mühlig, M. Müller, C. Nettelblad, A. Pietrini, H. K. N. Reddy, D. Rupp, M. Sauppe, M. Seibert, M. Svenda, M. Swiggers, N. Timneanu, A. Ulmer, D. Westphal, G. Williams, A. Zani, G. Faigel, H. N. Chapman, T. Möller, C. Bostedt, J. Hajdu, T. Gorkhover and F. R. N. C. Maia, IUCrJ, 2018, 5, 531–541 CrossRef CAS PubMed.
- R. P. Kurta, J. J. Donatelli, C. H. Yoon, P. Berntsen, J. Bielecki, B. J. Daurer, H. DeMirci, P. Fromme, M. F. Hantke, F. R. N. C. Maia, A. Munke, C. Nettelblad, K. Pande, H. K. N. Reddy, J. A. Sellberg, R. G. Sierra, M. Svenda, G. van der Schot, I. A. Vartanyants, G. J. Williams, P. L. Xavier, A. Aquila, P. H. Zwart and A. P. Mancuso, Phys. Rev. Lett., 2017, 119, 158102 CrossRef PubMed.
- M. Rose, S. Bobkov, K. Ayyer, R. P. Kurta, D. Dzhigaev, Y. Y. Kim, A. J. Morgan, C. H. Yoon, D. Westphal, J. Bielecki, J. A. Sellberg, G. Williams, F. R. Maia, O. M. Yefanov, V. Ilyin, A. P. Mancuso, H. N. Chapman, B. G. Hogue, A. Aquila, A. Barty and I. A. Vartanyants, IUCrJ, 2018, 5, 727–736 CrossRef CAS PubMed.
- J. C. H. Spence, IUCrJ, 2017, 4, 322–339 CrossRef CAS PubMed.
- R. Neutze, R. Wouts, D. van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752–757 CrossRef CAS PubMed.
- A. Aquila, A. Barty, C. Bostedt, S. Boutet, G. Carini, D. dePonte, P. Drell, S. Doniach, K. H. Downing, T. Earnest, H. Elmlund, V. Elser, M. Gühr, J. Hajdu, J. Hastings, S. P. Hau-Riege, Z. Huang, E. E. Lattman, F. R. N. C. Maia, S. Marchesini, A. Ourmazd, C. Pellegrini, R. Santra, I. Schlichting, C. Schroer, J. C. H. Spence, I. A. Vartanyants, S. Wakatsuki, W. I. Weis and G. J. Williams, Struct. Dyn., 2015, 2, 041701 CrossRef CAS PubMed.
- B. Ziaja, H. N. Chapman, R. Fäustlin, S. Hau-Riege, Z. Jurek, A. V. Martin, S. Toleikis, F. Wang, E. Weckert and R. Santra, New J. Phys., 2012, 14, 115015 CrossRef.
- T. Mandl, C. Östlin, I. E. Dawod, M. N. Brodmerkel, E. G. Marklund, A. V. Martin, N. Timneanu and C. Caleman, J. Phys. Chem. Lett., 2020, 11, 6077–6083 CrossRef CAS PubMed.
- J. Bielecki, F. R. N. C. Maia and A. P. Mancuso, Struct. Dyn., 2020, 7, 040901 CrossRef CAS PubMed.
- H. Chapman, P. Fromme, A. Barty, T. White, R. Kirian, A. Aquila, M. Hunter, J. Schulz, D. DePonte, U. Weierstall, R. Doak, F. Maia, A. Martin, I. Schlichting, L. Lomb, N. Coppola, R. Shoeman, S. Epp, R. Hartmann and J. Spence, Nature, 2011, 470, 73–77 CrossRef CAS PubMed.
- A. Barty, C. Caleman, A. Aquila, N. Timneanu, L. Lomb, T. A. White, J. Andreasson, D. Arnlund, S. Bajt, T. R. M. Barends, M. Barthelmess, M. J. Bogan, C. Bostedt, J. D. Bozek, R. Coffee, N. Coppola, J. Davidsson, D. P. DePonte, R. B. Doak, T. Ekeberg, V. Elser, S. W. Epp, B. Erk, H. Fleckenstein, L. Foucar, P. Fromme, H. Graafsma, L. Gumprecht, J. Hajdu, C. Y. Hampton, R. Hartmann, A. Hartmann, G. Hauser, H. Hirsemann, P. Holl, M. S. Hunter, L. Johansson, S. Kassemeyer, N. Kimmel, R. A. Kirian, M. Liang, F. R. N. C. Maia, E. Malmerberg, S. Marchesini, A. V. Martin, K. Nass, R. Neutze, C. Reich, D. Rolles, B. Rudek, A. Rudenko, H. Scott, I. Schlichting, J. Schulz, M. M. Seibert, R. L. Shoeman, R. G. Sierra, H. Soltau, J. C. H. Spence, F. Stellato, S. Stern, L. Strüder, J. Ullrich, X. Wang, G. Weidenspointner, U. Weierstall, C. B. Wunderer and H. N. Chapman, Nat. Photonics, 2012, 6, 35–40 CrossRef CAS PubMed.
- K. Nass, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2019, 75, 211–218 CrossRef CAS PubMed.
- C. Caleman, F. Junior, O. Granas and A. Martin, Crystals, 2020, 10, 585 CrossRef CAS.
- A. Kozlov, T. E. Gureyev, D. M. Paganin, A. V. Martin, C. Caleman and H. M. Quiney, IUCrJ, 2020, 7, 1114–1123 CrossRef CAS PubMed.
- K. Nass, A. Gorel, M. Abdullah, A. Martin, M. Kloos, A. Marinelli, A. Aquila, T. Barends, F.-J. Decker, R. Doak, L. Foucar, E. Hartmann, M. Hilpert, M. Hunter, Z. Jurek, J. Koglin, A. Kozlov, A. Lutman, G. Kovacs and I. Schlichting, Nat. Commun., 2020, 11, 1814 CrossRef CAS PubMed.
- A. Kozlov, A. Martin and H. Quiney, Crystals, 2020, 10, 478 CrossRef CAS.
- K. Nass, L. Foucar, T. R. M. Barends, E. Hartmann, S. Botha, R. L. Shoeman, R. B. Doak, R. Alonso-Mori, A. Aquila, S. Bajt, A. Barty, R. Bean, K. R. Beyerlein, M. Bublitz, N. Drachmann, J. Gregersen, H. O. Jönsson, W. Kabsch, S. Kassemeyer, J. E. Koglin, M. Krumrey, D. Mattle, M. Messerschmidt, P. Nissen, L. Reinhard, O. Sitsel, D. Sokaras, G. J. Williams, S. Hau-Riege, N. Timneanu, C. Caleman, H. N. Chapman, S. Boutet and I. Schlichting, J. Synchrotron Radiat., 2015, 22, 225–238 CrossRef CAS PubMed.
- M. Amin, A. Badawi and S. Obayya, Sci. Rep., 2016, 6, 36492 CrossRef CAS PubMed.
- G. Kolesov, O. Grånäs, R. Hoyt, D. Vinichenko and E. Kaxiras, J. Chem. Theory Comput., 2016, 12, 466–476 CrossRef CAS PubMed.
- K. A. Omar, K. Hasnaoui and A. de la Lande, Annu. Rev. Phys. Chem., 2021, 72, 445–465 CrossRef CAS PubMed.
- M. Amin, M. Askerka, V. S. Batista, G. W. Brudvig and M. R. Gunner, J. Phys. Chem. B, 2017, 121, 9382–9388 CrossRef CAS PubMed.
- M. Mandal, K. Saito and H. Ishikita, J. Phys. Chem. Lett., 2020, 11, 10262–10268 CrossRef CAS PubMed.
- M. Mandal, K. Saito and H. Ishikita, J. Phys. Chem. Lett., 2021, 12, 4032–4037 CrossRef CAS PubMed.
- K. Nass, L. Foucar, T. R. M. Barends, E. Hartmann, S. Botha, R. L. Shoeman, R. B. Doak, R. Alonso-Mori, A. Aquila, S. Bajt, A. Barty, R. Bean, K. R. Beyerlein, M. Bublitz, N. Drachmann, J. Gregersen, H. O. Jönsson, W. Kabsch, S. Kassemeyer, J. E. Koglin, M. Krumrey, D. Mattle, M. Messerschmidt, P. Nissen, L. Reinhard, O. Sitsel, D. Sokaras, G. J. Williams, S. Hau-Riege, N. Timneanu, C. Caleman, H. N. Chapman, S. Boutet and I. Schlichting, J. Synchrotron Radiat., 2015, 22, 225–238 CrossRef CAS PubMed.
- S. P. Hau-Riege and B. J. Bennion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022705 CrossRef PubMed.
- O. Grånäs, N. Timneanu, I. Eliah Dawod, D. Ragazzon, S. Trygg, P. Souvatzis, T. Edvinsson and C. Caleman, J. Chem. Phys., 2019, 151, 144307 CrossRef PubMed.
- M. Hanwell, D. Curtis, D. Lonie, T. Vandermeersch, E. Zurek and G. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- M. Feig, J. Chem. Theory Comput., 2008, 4, 1555–1564 CrossRef CAS PubMed.
- V. Mironov, Y. Alexeev, V. K. Mulligan and D. G. Fedorov, J. Comput. Chem., 2019, 40, 297–309 CrossRef CAS PubMed.
- R. Pepin, A. Petrone, K. J. Laszlo, M. F. Bush, X. Li and F. Tureček, J. Phys. Chem. Lett., 2016, 7, 2765–2771 CrossRef CAS PubMed.
- M. F. Hantke, T. Ekeberg and F. R. N. C. Maia, J. Appl. Crystallogr., 2016, 49, 1356–1362 CrossRef CAS PubMed.
- T. Northey, N. Zotev and A. Kirrander, J. Chem. Theory Comput., 2014, 10, 4911–4920 CrossRef CAS PubMed.
- T. Northey and A. Kirrander, J. Phys. Chem. A, 2019, 123, 3395–3406 CrossRef CAS PubMed.
- R. Santra, J. Phys. B: At., Mol. Opt. Phys., 2008, 42, 023001 CrossRef.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745 CrossRef CAS.
- O. Grånäs, A. Mocellin, E. S. Cardoso, F. Burmeister, C. Caleman, O. Björneholm and A. N. de Brito, J. Phys. B: At., Mol. Opt. Phys., 2020, 53, 244007 CrossRef.
- H. O. Jönsson, C. Östlin, H. A. Scott, H. N. Chapman, S. J. Aplin, N. Tîmneanu and C. Caleman, High Energy Density Phys., 2018, 26, 93–98 CrossRef.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. R. Schmidt, N. Shenvi and J. C. Tully, J. Chem. Phys., 2008, 129, 114110 CrossRef CAS PubMed.
- M. Bergh, N. Tmneanu and D. van der Spoel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051904 CrossRef PubMed.
- A. P. Mancuso, A. Aquila, L. Batchelor, R. J. Bean, J. Bielecki, G. Borchers, K. Doerner, K. Giewekemeyer, R. Graceffa, O. D. Kelsey, Y. Kim, H. J. Kirkwood, A. Legrand, R. Letrun, B. Manning, L. Lopez Morillo, M. Messerschmidt, G. Mills, S. Raabe, N. Reimers, A. Round, T. Sato, J. Schulz, C. Signe Takem, M. Sikorski, S. Stern, P. Thute, P. Vagovič, B. Weinhausen and T. Tschentscher, J. Synchrotron Radiat., 2019, 26, 660–676 CrossRef CAS PubMed.
- E. G. Marklund, T. Ekeberg, M. Moog, J. L. P. Benesch and C. Caleman, J. Phys. Chem. Lett., 2017, 8, 4540–4544 CrossRef CAS PubMed.
- R. A. Kirian, J. Phys. B: At., Mol. Opt. Phys., 2012, 45, 223001 CrossRef.
- T. Kierspel, A. Morgan, J. Wiese, T. Mullins, A. Aquila, A. Barty, R. Bean, R. Boll, S. Boutet, P. Bucksbaum, H. N. Chapman, L. Christensen, A. Fry, M. Hunter, J. E. Koglin, M. Liang, V. Mariani, A. Natan, J. Robinson, D. Rolles, A. Rudenko, K. Schnorr, H. Stapelfeldt, S. Stern, J. Thøgersen, C. H. Yoon, F. Wang and J. Küpper, J. Chem. Phys., 2020, 152, 084307 CrossRef CAS PubMed.
- J. Küpper, S. Stern, L. Holmegaard, F. Filsinger, A. Rouzée, A. Rudenko, P. Johnsson, A. V. Martin, M. Adolph, A. Aquila, S. C. V. Bajt, A. Barty, C. Bostedt, J. Bozek, C. Caleman, R. Coffee, N. Coppola, T. Delmas, S. Epp, B. Erk, L. Foucar, T. Gorkhover, L. Gumprecht, A. Hartmann, R. Hartmann, G. Hauser, P. Holl, A. Hömke, N. Kimmel, F. Krasniqi, K.-U. Kühnel, J. Maurer, M. Messerschmidt, R. Moshammer, C. Reich, B. Rudek, R. Santra, I. Schlichting, C. Schmidt, S. Schorb, J. Schulz, H. Soltau, J. C. H. Spence, D. Starodub, L. Strüder, J. Thøgersen, M. J. J. Vrakking, G. Weidenspointner, T. A. White, C. Wunderer, G. Meijer, J. Ullrich, H. Stapelfeldt, D. Rolles and H. N. Chapman, Phys. Rev. Lett., 2014, 112, 083002 Search PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- E. K. Wieduwilt, G. Macetti, L. A. Malaspina, D. Jayatilaka, S. Grabowsky and A. Genoni, J. Mol. Struct., 2020, 1209, 127934 CrossRef CAS.
- C. Kupitz, S. Basu, I. Grotjohann, R. Fromme, N. Zatsepin, K. Rendek, M. Hunter, R. Shoeman, T. White, D. Wang, D. James, J.-H. Yang, D. Cobb, B. Reeder, R. Sierra, H. Liu, A. Barty, A. Aquila, D. Deponte and P. Fromme, Nature, 2014, 513, 261–265 CrossRef CAS PubMed.
- R. Chatterjee, G. Han, J. Kern, S. Gul, F. D. Fuller, A. Garachtchenko, I. D. Young, T.-C. Weng, D. Nordlund, R. Alonso-Mori, U. Bergmann, D. Sokaras, M. Hatakeyama, V. K. Yachandra and J. Yano, Chem. Sci., 2016, 7, 5236–5248 RSC.
- C. Östlin, N. Timneanu, C. Caleman and A. V. Martin, Struct. Dyn., 2019, 6, 044103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp03419g |
| This journal is © the Owner Societies 2022 |