Stability of alkyl carbocations

Abstract

The traditional and widespread rationale behind the stability trend of alkyl-substituted carbocations is incomplete. Through state-of-the-art quantum chemical analyses, we quantitatively established a generally overlooked driving force behind the stability of carbocations, namely, that the parent substrates are substantially destabilized by the introduction of substituents, often playing a dominant role in solution. This stems from the repulsion between the substituents and the C–X bond.

---

Carbocations are ubiquitous reactive intermediates in synthetic chemistry and are involved in many fundamental organic transformations.^1,2 These reactive intermediates generally form through a heterolytic C–X bond dissociation, yielding a carbocation C⁺ and an anionic X⁻. The heterolytic bond dissociation energy (BDE), for simple alkyl halides Me_mH_3−mC–X, decreases upon increasing methyl substitution along the series of H₃C–X (methyl, 0°), MeH₂C–X (primary, 1°), Me₂HC–X (secondary, 2°), Me₃C–X (tertiary, 3°).³ In other words, it is easier to form more substituted carbocations, making them more likely to participate as an intermediate in a chemical reaction.

Currently, the reduced heterolytic bond dissociation energy of the C–X bond is often ascribed to the stabilization of the carbocation, which increases along methyl, primary, secondary, and tertiary substituted carbocations.⁴ This stability trend stems from the stabilizing interactions (hyperconjugation and inductive effects)^1a,5 between the electron-depleted carbon center and the methyl groups. The true definition of structural stability is less straightforward than stated above since, strictly speaking, one cannot directly compare the structural stabilities of non-isomeric species.^6,7 Furthermore, this trend also has been attributed to the relief of steric repulsion, going from the substrate to the carbocation, between the substituents of the C–X bond for more substituted systems (also known as B-strain; back-strain).⁸

Typically, the thermodynamic stability of organic molecules is quantified using hypothetical reactions (e.g., isodesmic or homodesmotic), which are specifically designed to isolate a desired effect.⁹ Recently, in contrast to common textbook knowledge, we found using isodesmic reactions that methyl substitution destabilizes simple organic radicals.¹⁰ In our present study, we partition the energy of the system using the isodesmic reaction shown in eqn (1), which allows us to investigate the effect of the number of methyl groups on the thermodynamic stability of the system. We use the non-substituted H₃C–X as our reference compound. This approach has proven useful for quantifying the stability of organic molecules, however, it does not directly permit one to uncover the true origin of the stability trend.

H₃C–X + Me_mH_3−mC⁺ → H₃C⁺ + Me_mH_3−mC–X (1)

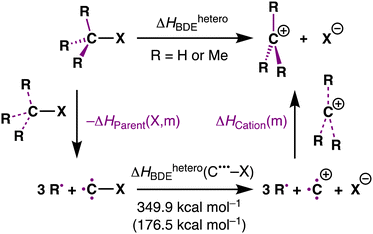
Herein, we reveal the exact source of the stability trend of carbocations by using partial reactions in a thermodynamic cycle quantitatively decomposing the effect of methyl groups on the carbocation species and the parent substrate, as shown in Scheme 1 (purple bonds). We have chosen to study the archetypal Me_mH_3−mC–X model systems with m = 0, 1, 2, 3 and X = F, Cl, Br, I, H, CH₃. The activation strain model (ASM)¹¹ was employed to provide quantitative insight into the driving processes for the carbocation stability.

Scheme 1 Computationally studied heterolytic bond dissociation of the C–X bond (R = H or Me; X = F, Cl, Br, I, H, CH₃).

Here, we focus on the Me_mH_3−mC–I systems as a representative example. However, all model systems we have studied, that is, Me_mH_3−mC–X (m = 0–3; X = F, Cl, Br, H, CH₃), possess similar trends and can be found in Table S1 and Fig. S1 (ESI†). Table 1 presents our computed Me_mH_3−mC–I bond lengths (r (C–I)) and heterolytic bond dissociation enthalpies (ΔH^hetero_BDE). The dissociation of the leaving-group atom, X⁻, from the tetrahedral substrate leads to a Me_mH_3−mC⁺ carbocation. The latter adopts a trigonal planar geometry to optimize the C⁺˙˙˙-substituent bonding overlap between the singly-occupied 2p atomic orbitals of C⁺ and the E-symmetric SOMO of the substituents R₃˙˙˙ (where a dot ˙ represents an unpaired electron; see Fig. S2 for structures, ESI†). The trigonal planar geometry also minimizes steric (Pauli) repulsion between the substituents. Note that, as reported earlier, the ethyl cation adopts a “non-classical” bridged carbocation structure in which the positive charge is delocalized over both carbons (see Fig. S2, ESI†).¹²

Table 1 R₃C–X (R = H or Me; X = I) bond lengths (in Å) and heterolytic bond dissociation energies (ΔH^hetero_BDE), which are decomposed using a thermochemical cycle in ΔH_Parent(X, m), ΔH^hetero_BDE(C˙˙˙–X), and ΔH_Cation(m) (kcal mol⁻¹)^a

System	r (C–X)	ΔH^heteroBDE	ΔHParent(X, m)	ΔHCation(m)
a Computed at ZORA-(U)M06-2X/QZ4P and values in parentheses at COSMO(H2O)-ZORA-(U)M06-2X/QZ4P, at 298.15 K and 1 atm.
H3C–I	2.132 (2.136)	210.7 (66.7)	–321.5 (–320.8)	–453.0 (–440.2)
MeH2C–I	2.150 (2.157)	170.1 (40.1)	–311.5 (–310.3)	–483.5 (–456.3)
Me2HC–I	2.170 (2.181)	152.5 (29.8)	–302.7 (–301.1)	–492.4 (–457.7)
Me3C–I	2.194 (2.209)	137.2 (19.2)	–294.5 (–292.4)	–499.5 (–459.4)

---

As expected, the C–I bond, indeed, significantly weakens as the degree of methyl substitution increases, going from ΔH^hetero_BDE = 210.7 to 170.1 to 152.5 to 137.2 kcal mol⁻¹, along m = 0, 1, 2, and 3 (see Table 1). At the same time, the C–I bond also becomes longer along this series from 2.132 to 2.150 to 2.170 to 2.194 Å. Our computed bond dissociation energies at ZORA-M06-2X/QZ4P are in good agreement with experiments (see Table S2, ESI†).³ Moreover, the same general conclusions are obtained at ZORA-BLYP-D3(BJ)/QZ4P and ZORA-BP86-D3(BJ)/QZ4P, see Fig. S3, S4 and Tables S3, S4 (ESI†).

To analyze how the heterolytic Me_mH_3−mC–X bond dissociation enthalpy depends on both the bonding of the substituents in the carbocation Me_mH_3−mC⁺ and in its parent substrate Me_mH_3−mC–X, we have decomposed the heterolytic bond dissociation enthalpy of the system into three terms: ΔH_Parent(X, m), ΔH^hetero_BDE(C˙˙˙–X), and ΔH_Cation(m) (eqn (2)), associated with the three partial reactions of the thermochemical cycle shown in Table 1. The ΔH_Parent(X, m) is the overall bond enthalpy as the three separate substituents, i.e., Me_mH_3−m˙˙˙ combine with C˙˙˙–X to form the parent substrate Me_mH_3−mC–X. The ΔH^hetero_BDE(C˙˙˙–X) is the heterolytic C–X bond dissociation enthalpy of the completely unsubstituted C˙˙˙–X species into C⁺˙˙˙ and X⁻. The ΔH_Cation(m) is the overall bond enthalpy as the three separate substituents Me_mH_3−m˙˙˙ combine with C⁺˙˙˙ to form the carbocation Me_mH_3−mC⁺. Thus, we have the following relationship of eqn (2):

ΔH^hetero_BDE = ΔH^hetero_BDE(C˙˙˙–X) + ΔH_Cation(m) − ΔH_Parent(X, m) (2)

Consequently, the trend in isodesmic dissociation energy (ΔΔH^hetero_BDE) upon increasing methyl substitution is determined not only by ΔΔH_Cation(m) but by the difference between ΔΔH_Cation(m) and ΔΔH_Parent(X, m) (eqn (3)–(5)). In other words, a less stable parent molecule is more prone to dissociate the leaving-group and hence form a carbocation.

ΔΔH_Cation(m) = ΔH_Cation(m) − ΔH_Cation(m = 0) (3)

ΔΔH_Parent(X, m) = ΔH_Parent(X, m) − ΔH_Parent(X, m = 0) (4)

ΔΔH^hetero_BDE = ΔΔH_Cation(m) − ΔΔH_Parent(X, m) (5)

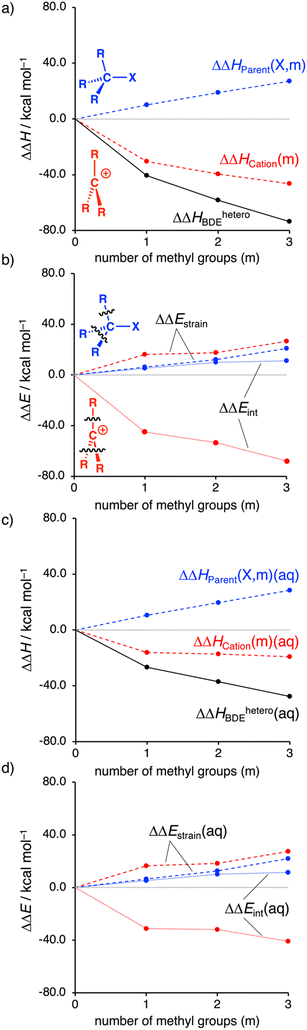
Several trends emerge from our decomposition of ΔH^hetero_BDE using the thermochemical cycle in Table 1 (Fig. 1). As discussed previously, the Me_mH_3−mC–I bonds become weaker by increasing the number of methyl groups, which is illustrated by the increasingly more negative isodesmic dissociation energy (ΔΔH^hetero_BDE) in Fig. 1a (black line). We find that the parent substrate Me_mH_3−mC–I is systematically destabilized by the substituents, as seen in Fig. 1a (blue line) by the positive ΔΔH_Parent(X, m) going from +10.0 to +18.8 to +27.0 kcal mol⁻¹ along m = 1, 2, 3. In contrast, the carbocation is stabilized by the substituents (red line), through, among others, hyperconjugation, as evidenced by the more stabilizing ΔΔH_Cation(m) going from −30.5 to −39.5 to −46.5 kcal mol⁻¹ along the same series.

Fig. 1 Effect of methyl groups on ΔΔH^hetero_BDE, ΔΔH_Parent(X, m), ΔΔH_Cation(m), and the corresponding activation strain analysis (in kcal mol⁻¹) for R₃C–X (R = H or Me; X = I). Computed at ZORA-(U)M06-2X/QZ4P (a and b) and COSMO(H₂O)-ZORA-(U)M06-2X/QZ4P (c and d).

To assess the role of solvation, we have also studied the decomposition of ΔH^hetero_BDE in solution with COSMO. For this purpose, we selected dichloromethane (ε = 9), DMSO (ε = 47), and water (ε = 78), spanning realistic extremes of polarity used in experiments.¹³ For our discussion, we focus on water solvation and note that in all solvents, the same general trends emerge, see Tables S5, S6 and Fig. S5 (ESI†).

Solvation significantly reduces the stabilizing effects of the methyl groups on the carbocation (Fig. 1c, red line) with ΔΔH_Cation(m)(aq) of only −16.1, −17.2, −19.2 kcal mol⁻¹ going from m = 1 to 2 to 3, respectively. This stems from the fact that the less substituted carbocation, with its more localized and less shielded positive charge, enters into a more stabilizing interaction with the solvent. In sharp contrast, the observed systematic destabilization of the parent substrate Me_mH_3−mC–I by the substituents is entirely maintained if we go from the gas phase to solution, as reflected by ΔΔH_Parent(X, m)(aq), which still steeply increases from +10.1, +19.7, +28.4 kcal mol⁻¹ along the same series.

Note that, in solution, the magnitude of stabilization of the carbocation levels off after the addition of more than one methyl group. This saturation effect finds its origin in the aforementioned interaction between the solvated cation and the substituents. Introducing the first substituent stabilizes the cation, reducing the electron depletion on the carbocation. Intuitively, the next substituent can interact less strongly with the less depleted pertinent carbon center. This effect is also observed in the gas phase, although less apparent.

Next, to further understand the effect of the methyl groups on the carbocation stability, we employ our activation strain model (see ESI† for Computational methods; Fig. 1b and d).⁹ Note that the computed trends are the same for both ΔH and ΔE (Table S1, ESI†). We continue with the analysis of ΔE. As discussed, the parent substrate is systematically destabilized by adding methyl groups, which can be traced back to both the destabilizing strain (ΔΔE_strain > 0) and less stabilizing interaction energy (ΔΔE_int > 0; Fig. 1b). The less stabilizing interaction energy stems from the substituents that engage in steric (Pauli) repulsive interactions (see Fig. S6 and S7, ESI†). The larger methyl groups have more repulsion with the C˙˙˙–X bond and have more mutual repulsion than the smaller hydrogen atoms. This type of repulsion is also known as F-strain (front-strain).¹⁴ The destabilizing strain mainly results from the need of the methyl group(s) to deform from their planar methyl radical equilibrium geometry to a pyramidal geometry in the substrate.¹⁵

In contrast, the carbocation becomes more stabilized by the introduction of substituents, which stems from the stabilizing interactions between the substituents and the cationic carbon center (Fig. 1b). Our quantitative MO analyses show that this, indeed, finds its origin in, among others, the stabilizing hyperconjugation (Fig. S8 and S9, ESI†). For the carbocations, a systematically slightly more destabilizing strain compared to the parent substrate is found (Fig. 1b; red versus blue dashed line). This can be traced back to the intrinsically shorter carbon–substituent bonds for the carbocations, which require the methyl groups to deform more. The shorter carbon–substituent bonds of the trigonal planar carbocations are a result of the relief of steric repulsion between the substituents.

Note that the jump in both the interaction and strain energy by going from the methyl to the ethyl cation is the direct effect of the “non-classical” bridged carbocation (see Fig. S6 and S7, ESI†). As discussed above, solvation stabilizes the carbocation and thus reduces the electron-accepting capabilities of this species (attenuates hyperconjugative effects), which leads to a substantial reduction of the substituent–cation interaction going from the gas phase to solution (Fig. 1d). While the destabilizing steric repulsive effects in the systems are maintained.

In conclusion, we find that the heterolytic bond strength of C–X bonds decreases as the degree of alkyl substitution increases. We quantitatively established a commonly overlooked driving force behind this trend, namely, the parent substrate is increasingly destabilized by introducing alkyl substituents. This is the result of destabilizing steric repulsion between the alkyl substituents and the C–X bond (also known as F-strain). This trend is reinforced by the stabilization of the carbocation by the alkyl substituents through, among others, hyperconjugation. We found that the destabilization of the parent substrate often plays a dominant role if the species are in solution.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) D. H. Aue, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 4, 487; (b) R. R. Naredla and D. A. Klumpp, Chem. Rev., 2013, 113, 6905; (c) D. J. Tantillo, Nat. Prod. Rep., 2011, 28, 1035; (d) D. J. Tantillo, Chem. Soc. Rev., 2010, 39, 2847; (e) X. Creary, Chem. Rev., 1991, 91, 1625; (f) M. Saunders and H. A. Jimenez-Vazquez, Chem. Rev., 1991, 91, 375; (g) G. I. Borodkin, I. R. Elanov and V. G. Shubin, Russ. J. Org. Chem., 2021, 57, 301.
2. (a) J. Bah, V. R. Naidu, J. Teske and J. Franzén, Adv. Synth. Catal., 2015, 357, 148; (b) J. P. Richard, T. L. Amyes and M. M. Toteva, Acc. Chem. Res., 2001, 34, 981; (c) T. Hansen, L. Lebedel, W. A. Remmerswaal, S. van der Vorm, D. P. A. Wander, M. Somers, H. S. Overkleeft, D. V. Filippov, J. Désiré, A. Mingot, Y. Bleriot, G. A. van der Marel, S. Thibaudeau and J. D. C. Codée, ACS Cent. Sci., 2019, 5, 781; (d) M. A. Mercadante, C. B. Kelly, T. A. Hamlin, K. R. Delle Chiaie, M. D. Drago, K. K. Duffy, M. T. Dumas, D. C. Fager, B. L. C. Glod, K. E. Hansen, C. R. Hill, R. M. Leising, C. L. Lynes, A. E. MacInnis, M. R. McGohey, S. A. Murray, M. C. Piquette, S. L. Roy, R. M. Smith, K. R. Sullivan, B. H. Truong, K. M. Vailonis, V. Gorbatyuk, N. E. Leadbeater and L. J. Tilley, Chem. Sci., 2014, 5, 3983; (e) S. van der Vorm, T. Hansen, E. R. van Rijssel, R. Dekkers, J. M. Madern, H. S. Overkleeft, D. V. Filippov, G. A. van der Marel and J. D. C. Codée, Chem. – Eur. J., 2019, 25, 7149; (f) E. S. Stoyanov, I. V. Stoyanova, F. S. Tham and C. A. Reed, Angew. Chem., Int. Ed., 2012, 51, 9149; (g) J. M. Madern, T. Hansen, E. R. van Rijssel, H. A. V. Kistemaker, S. van der Vorm, H. S. Overkleeft, G. A. van der Marel, D. V. Filippov and J. D. C. Codée, J. Org. Chem., 2019, 8, 1218.
3. (a) Y. R. Luo and P. D. Pacey, J. Phys. Chem., 1991, 95, 9470; (b) H. M. Rosenstock, R. Buff, M. A. Ferreira, S. G. Lias, A. C. Parr, R. L. Stockbauer and J. L. Holmes, J. Am. Chem. Soc., 1982, 104, 2337; (c) E. M. Arnett and N. J. Pienta, J. Am. Chem. Soc., 1980, 102, 3329–3334.
4. (a) F. A. Carey and R. J. Sundberg, Advanced Organic Chemistry Part A: Structure and Mechanisms, Springer, 5 edn, 2007, pp. 300–310; (b) M. B. Smith, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, 6th edn, Wiley, New York, 2013, pp. 234–245; (c) F. P. Lossing and J. L. Holmes, J. Am. Chem. Soc., 1984, 106, 6917.
5. (a) E. S. Stoyanov and G. dos Passos Gomes, J. Phys. Chem. A, 2015, 119, 8619; (b) I. V. Alabugin, G. dos Passos Gomes and M. A. Abdo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, e1389; (c) I. V. Alabugin, K. M. Gilmore and P. W. Peterson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 109.
6. (a) M. L. Coote, A. Pross and L. Radom, Org. Lett., 2003, 5, 4689; (b) M. Swart, E. Rösler and F. M. Bickelhaupt, Eur. J. Inorg. Chem., 2007, 3646; (c) C. Rüchardt, Angew. Chem., Int. Ed. Engl., 1970, 9, 830; (d) K. B. Clark and D. D. M. Wayner, J. Am. Chem. Soc., 1991, 113, 9363; (e) S. Gronert, J. Org. Chem., 2006, 71, 1209; (f) S. Gronert, J. Org. Chem., 2006, 71, 7045; (g) S. Gronert, Org. Lett., 2007, 9, 2211; (h) M. Swart and F. M. Bickelhaupt, J. Chem. Theory Comput., 2006, 2, 281; (i) F. M. Bickelhaupt, H. L. Hermann and G. Boche, Angew. Chem., Int. Ed., 2006, 45, 823.
7. (a) A. A. Zavitsas, J. Chem. Educ., 2001, 78, 417; (b) J. L. M. Abboud, I. Alkorta, J. Z. Davalos, P. Müller, E. Quintanilla and J. C. Rossier, J. Org. Chem., 2003, 68, 3786; (c) P. de, A. M. Nicholas and D. R. Arnold, Can. J. Chem., 1984, 62, 1850.
8. (a) T. Sorrell, Organic Chemistry, 2 edn, 2006, pp 186–188; (b) K. Takeuchi, Y. Ohga and T. Kitagawa, J. Org. Chem., 1991, 56, 5007; (c) K. T. Liu, S. J. Hou and M. L. Tsao, J. Org. Chem., 1998, 63, 1360; (d) K. T. Liu, S. J. Hou and M. L. Tsao, J. Chin. Chem. Soc., 2009, 56, 425; (e) K. I. Takeuchi, Y. Ohga, M. Yoshida, K. Ikai, T. Shibata, M. Kato and A. Tsugeno, J. Org. Chem., 1997, 62, 5696; (f) K. Takeuchi, Y. Ohga, T. Ushino and M. Takasuka, J. Phys. Org. Chem., 1997, 10, 717.
9. (a) D. A. Ponomarev and V. V. Takhistov, J. Chem. Educ., 1997, 74, 201; (b) R. Fuchs, J. Chem. Educ., 1984, 61, 133; (c) S. E. Wheeler, K. N. Houk, P. v R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547.
10. E. Blokker, W.-J. van Zeist, X. Sun, J. Poater, J. M. van der Schuur, T. A. Hamlin and F. M. Bickelhaupt, Angew. Chem., Int. Ed., 2022, 61, e202207477.
11. (a) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649; (b) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chem. Commun., 2021, 57, 5880.
12. (a) H. S. Andrei, N. Solcà and O. Dopfer, Angew. Chem., Int. Ed., 2007, 47, 395; (b) B. G. Oliveira, M. L. Vasconcellos and R. R. Olinda, Struct. Chem., 2009, 20, 81.
13. (a) T. A. Hamlin, B. van Beek, L. P. Wolters and F. M. Bickelhaupt, Chem. – Eur. J., 2018, 24, 5927; (b) T. Hansen, J. C. Rooze, F. M. Bickelhaupt and T. A. Hamlin, J. Org. Chem., 2022, 87, 1805.
14. (a) H. C. Brown, J. Am. Chem. Soc., 1945, 67, 374; (b) J. S. Lomas, M. J. D'Souza and D. N. Kevill, J. Am. Chem. Soc., 1995, 117, 5891; (c) K. Takeuchi, Y. Ohga and T. Kitagawa, J. Org. Chem., 1991, 56, 5007.
15. W.-J. van Zeist and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2009, 11, 10317.

---

Footnote

† Electronic supplementary information (ESI) available: Additional computational results; Cartesian coordinates, energies, and the number of imaginary frequencies of all stationary points. See DOI: https://doi.org/10.1039/d2cc04034d

---