Prediction of pH in multiphase multicomponent systems with ePC-SAFT advanced

Abstract

Proton activity, which is usually expressed as a pH value, is among the most important properties in the design of chemical and biochemical processes as it determines the dissociation of species in aqueous mixtures. This article addresses the prediction of pH values in multiphase systems based on the IUPAC definition via proton activity. The required proton activity coefficients were predicted using the thermodynamic equation of state ePC-SAFT advanced. The developed framework considers reaction equilibria and phase equilibria (vapor–liquid and liquid–liquid) to predict pH in the equilibrated liquid phases.

---

Designing unit operations for chemical and biochemical processes requires incorporating predictive computational technologies. These reduce the experimental effort, ultimately leading to a model-supported decision for process optimization.¹ For this, molecular thermodynamics, especially equations of state and activity-coefficient models, have been emerging as a vital tool in the industry.² Still, these models have been mainly applied in a correlative way, although many among them have a high predictive power, as shown recently for pharmaceuticals, polymers, biofuels, and electrolytes.³ In many of these research areas, species distribution plays an essential role for the behavior of the mixtures, and pH is the primary quantitative indicator of the degree of dissociation of ionizable components, given that their pK_a values are known. The pH definition has recently been revised by IUPAC, cf. ref. 4, and it is a single ion quantity that accounts for the proton activity on a molality scale. Thus, pH is accessible from molecular thermodynamic models that are capable of calculating activity coefficients, providing a helpful approach towards phase-equilibrium relations in reactive systems that contain electrolytes.⁵ pH plays a vital role in different areas, e.g., reaction kinetics, the activity of biomolecules, or salting-out effects, and thus, pH is important to know in applications such as seawater desalination, amino-acid purification, fermentation, CO₂ capture, or injection of CO₂ into groundwater with large amounts of salts.⁶ However, pH measurements are challenging, especially for in situ processes where application-specific sensors are needed, for geological applications where access is limited, or for water-poor media where pH is not well-defined.¹ The characterization of electrolyte mixtures has been considered in the literature. Austgen and coworkers applied an electrolyte non-random two-liquid model (eNRTL) to the vapor–liquid equilibrium of H₂S and CO₂ aqueous solutions in monoethanolamine.⁷ A significant drawback of eNRTL and other models is the high number of adjustable parameters, and most of the models are highly correlative. To overcome these issues, equations of state based on statistical associating fluid theory (SAFT) have been used extensively to model electrolyte systems.⁸ Recently, Kohns and coworkers used variable range SAFT to successfully model vapor–liquid equilibria in nitric acid, sulfuric acid, and carbonic acid reactive systems and other properties such as osmotic coefficients.⁹ That approach includes Coulombic ion–ion interactions and electrostatic ion–solvent interactions to describe correctly free energies of solvation. Dufal et al. applied the same framework using SAFT-γ-Mie to model phase equilibria in aqueous solutions of CO₂ and NH₃.¹⁰ Electrolyte Perturbed-Chain SAFT (ePC-SAFT) has followed a similar development. It is based on PC-SAFT¹¹ and an extended Debye–Hückel term for electrolytes,⁸ and it can be applied up to high salt concentrations.¹² The most recent development includes a concentration-dependent dielectric constant within Debye–Hückel and Born terms.¹³ It was validated by sour gas solubility in reactive systems,¹⁴ salt solubility in organic solvents,¹⁵ and prediction of the salting-out in liquid–liquid two-phase systems.¹⁶ In this work, this newest ePC-SAFT development (‘ePC-SAFT advanced’) was used to predict pH values for aqueous systems CO₂ + water (+ salt) and carboxylic acid + water + organic solvents. The considered systems form two phases (one liquid and one vapor L–V, or one liquid aqueous and one liquid organic phase L–L), and they involve dissociation of the present electrolytes. Both, phase equilibria and dissociation were considered in this work, and the pH was predicted at V–L or L–L phase equilibrium of the respective systems with ePC-SAFT advanced.

Thermodynamic modeling of equilibrated multiphase aqueous electrolyte solutions requires simultaneously solving phase equilibria and reaction equilibria. The reactions that may take place in the liquid phases of the systems under consideration (CO₂ + water + salt and carboxylic acid HA + water + organic solvents) are summarized in eqn (1)–(3).

2H₂O ⇌ OH⁻ + H₃O⁺ (1)

2H₂O + CO₂ ⇌ HCO₃⁻ + H₃O⁺ (2)

HA + H₂O ⇌ A⁻ + H₃O⁺ (3)

These reactions (1)–(3) are highly affected by a change in pH and by the amount of dissolved CO₂. Thus, knowledge of pH is crucial for the dissociation degree of the acids and whether chemical equilibria take place besides physical interactions. pH is defined based on the thermodynamic activity of the proton in solution according to eqn (4).¹⁷

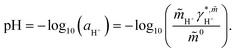In eqn (4) the quantity is the molality-based activity of the proton, which can be calculated from the molality-based activity coefficient (accessible using a thermodynamic model) at the given composition and the molality 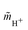of the proton in the investigated system and m̃⁰ = 1 mol kg⁻¹. Please note, that H₃O⁺ exists in aqueous solution as the proton does not exist without hydration water. Therefore, by H⁺ we refer to H₃O⁺ in this manuscript; a differentiation between H⁺ and H₃O⁺ was not considered. was calculated using eqn (5) according to Thomsen et al.¹⁸

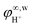Here denotes the proton fugacity coefficient at infinite dilution in water. Eqn (5) was used then in eqn (4) for the proton activity coefficient. Please note that eqn (5) was also used for all other charged reaction participants in the systems under study 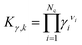(see ESI†).

The required fugacity coefficients and activity coefficients were predicted with ePC-SAFT advanced, which expresses the residual Helmholtz energy a^res as the sum of energy contributions caused by repulsion and attraction. It is important to state that ion–solvent interactions are captured by electrostatic ion–dipolar forces within a modified Born term and by non-electrostatic ion–solvent effects (van der Waals dispersion), while Coulombic interactions between point charges are accounted for by the Debye–Hückel theory, which ignores solvent effects (primitive theory). Based on the so-obtained a^res, the residual chemical potential μ^res_i can be accessed by derivations of a^res with respect to density and mole fraction. This allows modeling fugacity coefficients and thus, modeling pH and phase equilibria using the φ–φ concept. More details on the modeling procedure and parameters used can be found in the ESI.† For technical details regarding the multiphase equilibria calculations, please refer to ref. 26.

The pH of the binary system CO₂ + water for temperatures up to 423 K and pressures up to 150 bar was found to be in the range 3.0 < pH < 4.0 depending on the amount of dissolved CO₂ and thus, on temperature and pressure.²⁰Fig. 1 represents pH values in the system CO₂ + water at various temperatures.

Fig. 1 pH of the binary system CO₂ + water as a function of the pressure at equilibrium CO₂ concentrations. Experimental data from Peng et al.¹⁹ (circles: 432 K, stars: 368 K, and triangles: 323 K). Lines are modeling results obtained with ePC-SAFT advanced using the parameters listed in Tables S1–S3 in the ESI.† The underlying CO₂ solubilities were modeled using the same approach, cf. ref. ²⁰

Fig. 1 shows that ePC-SAFT advanced is able to predict the pH of the binary system CO₂ + water over a broad temperature range and pressure range with an excellent agreement with available data from the literature. The dependence of pH on temperature and pressure is interrelated to CO₂ solubility. The higher the pressure, the more CO₂ is soluble in water, which makes the aqueous solution more acidic and decreases the pH. In addition, the pH increases with an increase in temperature. This is again caused by CO₂ solubility that decreases with increasing temperature and produces a less acidic solution. The underlying CO₂ solubility was predicted as well, cf. ref. ²⁰.

Fig. 2 shows the pH in the pseudo-ternary system CO₂ + water + salt as a function of the salt molality m̃_salt for the salts KCl, NaCl, and NaHCO₃. Fig. 2 illustrates that predictions obtained with ePC-SAFT advanced are in excellent agreement with the available literature data. This is an outstanding result since the ePC-SAFT parameters for all ionic species were used from the literature, and binary fitting parameters between CO₂ and ions were not used. Note, the binary fitting parameters within SAFT models are a correction for the short-range forces and thus, not related to electrostatics (the electrostatic potentials as applied by us do not include adjustable parameters). As no binary dispersion parameters between CO₂ and ions were applied, the shown results are fully predictive. This also applies to the CO₂ solubilities that were predicted as well and the corresponding results are shown in Fig. S1, S2 and S4 in the ESI.† A strong increase in pH is visible in Fig. 2 for the system CO₂ + water upon the addition of NaHCO₃.

Fig. 2 pH of the ternary system CO₂ + water + salt as a function of salt molality m̃_salt at equilibrium CO₂ concentrations. Symbols are experimental data from the literature (stars:²¹ NaHCO₃ at T = 308 K and p = 9.2 bar, hexagons:²¹ NaHCO₃ at T = 308 K and p = 43 bar, circles:²¹ NaCl T = 343 K and p = 10 bar, and triangles:²² KCl at T = 298 K and p = 9 bar). Lines are modeling results obtained with ePC-SAFT advanced using the parameters listed in Tables S1–S3 in the ESI.† The underlying CO₂ solubilities were modeled using the same approach, see ESI† Fig. S1 and S2. A low-concentration regime is shown in ESI† Fig. S3.

The addition of bicarbonate (HCO₃⁻) salts drastically shifts the dissociation equilibrium of eqn (2) to the left-hand side, which explains the subsequent shift of pH. Thus, ePC-SAFT advanced is able to predict the influence of salts containing a reactive species on the pH. Furthermore, Fig. 2 shows that the pH stays almost constant upon addition of NaCl or KCl. The chloride salts are not involved directly in the dissociation equilibrium. However, the presence of ions (e.g., Na⁺ or Cl⁻) indirectly affects the dissociation equilibrium via salting-out effects. Thus, a small effect of such salts on the resulting pH might have been expected. As the chloride salts cause a decrease in CO₂ solubility (see Fig. S2 and S4 in ESI†), the pH is expected to increase upon chloride addition. However, according to experimental measurements shown in Fig. 2, the pH slightly decreases upon adding NaCl or KCl. ePC-SAFT advanced is able to account for these effects and is able to correctly predict the resulting pH. This effect is caused by the proton activity that decreases upon chloride addition. Anyway, this effect is not pronounced and the pH of CO₂ + water + chloride salt remains in the range of 3.0 < pH < 4.0 as already found for the binary system CO₂ + water. This observation has already been stated in previous works (cf. ref. ²⁰) where the influence of dissociated carbonic acid was found to be negligible in the systems CO₂ + water + chloride salts.

Furthermore, the predictive capabilities of ePC-SAFT advanced were tested against experimental pH values in demixed aqueous/organic systems. The equilibrated aqueous phase that originates from a phase split of a two-phase liquid–liquid system formed by water and an organic solvent, with a weak organic acid dissolved into that system, was considered. ePC-SAFT advanced prediction results of pH are displayed in Fig. 3. These pH values were predicted at liquid-phase compositions of the aqueous phase that were also modeled with ePC-SAFT advanced (using the same model parameters). These are shown in Fig. S5 in the ESI.†

Fig. 3 pH of ternary systems carboxylic acid + water + organic solvent. pH plotted against the acid mole fraction x_acid in the aqueous phase of the biphasic aqueous/organic liquid–liquid equilibrium. Symbols are experimental data from the literature at T = 298 K and p = 1 bar (stars:²³ acetic acid, triangles:²⁴ citric acid, and circles:²⁵ oxalic acid). Lines are predicted results obtained with ePC-SAFT advanced. The underlying liquid–liquid equilibria were modeled using the same approach, see ESI,† Fig. S5.

The considered pseudo-ternary systems carboxylic acid + water + organic solvent comprise one of the acids acetic acid, citric acid, and oxalic acid. The biphasic systems are formed by water and an organic solvent. The systems with acetic acid and oxalic acid contain toluene as the solvent, whereas the system with oxalic acid contains methyl isobutyl ketone (MIBK) as the solvent. As shown in Fig. 3, ePC-SAFT advanced is able to predict the pH value in the aqueous phase of the ternary systems carboxylic acid + water + organic solvent with an excellent agreement with the literature data. The pure-component parameters were inherited from the literature. Binary interaction parameters k_ij between the acid and the organic solvent were fitted to experimental partition coefficients from the literature.^23–25 Binary interaction parameters between water and the organic solvent were fitted to the respective binary liquid–liquid equilibria, which were partly inherited from previous works. It is important to note that no binary interaction parameters were fitted for pairs that involve ionic species; such k_ij values were all set to zero according to experiences from previous publications.^16,26 Most importantly, no parameters were fitted to the experimental pH values considered in this work. The input data were the pK_a values and dielectric constants (Tables S4 and S5 in ESI†). All results of the considered systems (Table S6 in ESI†) are summarized by deviations between predictions and experimental data in Tables S7–S16 in ESI.† These results open the door for determining pH also in non-aqueous phases, since the isofugacity φ–φ concept requires that proton activity must be equal in the aqueous and the organic phase at phase equilibrium.

To sum up, this work suggests following the IUPAC definition for pH towards pH prediction in aqueous phases. A proton-activity-based calculation framework was developed to predict pH values in reactive phase equilibria coupled with dissociation reactions of water, CO₂, or a carboxylic acid. It was suggested to use the equation of state ePC-SAFT advanced for the estimation of the required fugacity coefficients and activity coefficients of the dissolved components and especially of the proton. The studied systems were CO₂ + water + salt and carboxylic acid + water + organic solvent. All pure-component parameters for ePC-SAFT advanced were inherited from the literature. Binary interaction parameters (if any) were fitted to phase diagrams of binary systems of the molecular species present in the system, while no binary interaction parameters were used between any pair ion–molecular species. Thus, the pH values calculated in this work were obtained fully predictively. Despite this, the pH could be predicted in excellent agreement with the literature values, ultimately showing the potential of the developed modeling approach towards accessing pH values and dissociation degrees of the dissolved components. This can be considered as an important step in reducing the experimental effort to optimize reactive biochemical systems and processes for CO₂ capture and processing as well as for downstream processing of carboxylic acids.

The authors acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033 – project number 390677874 and through the project MUST (MicroflUidics for Structure–reactivity relationships aided by Thermodynamics & kinetics) ANR-20-CE92-0002-01 – Project number 446436621. Translation into German required: Gefördert durch die Deutsche Forschungsgemeinschaft (DFG) im Rahmen der Exzellenzstrategie des Bundes und der Länder – EXC 2033 – Projektnummer 390677874 – RESOLV.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. C. Held, Thermodynamic gE Models and Equations of State for Electrolytes in a Water-Poor Medium: A Review, J. Chem. Eng. Data, 2020, 65, 5073–5082.
2. G. M. Kontogeorgis, R. Dohrn, I. G. Economou, J.-C. de Hemptinne, A. ten Kate, S. Kuitunen, M. Mooijer, L. F. Žilnik and V. Vesovic, Industrial Requirements for Thermodynamic and Transport Properties: 2020, Ind. Eng. Chem. Res., 2021, 60, 4987–5013.
3. T. Reschke, S. Naeem and G. Sadowski, Osmotic coefficients of aqueous weak electrolyte solutions: influence of dissociation on data reduction and modeling, J. Phys. Chem. B, 2012, 116, 7479–7491.
4. V. Gold, The IUPAC Compendium of Chemical Terminology, International Union of Pure and Applied Chemistry (IUPAC), Research Triangle Park, NC, 2019.
5. D. Tong, J. P. M. Trusler and D. Vega-Maza, Solubility of CO₂ in Aqueous Solutions of CaCl₂ or MgCl₂ and in a Synthetic Formation Brine at Temperatures up to 423 K and Pressures up to 40 MPa, J. Chem. Eng. Data, 2013, 58, 2116–2124.
6. F. Millero, F. Huang, T. Graham and D. Pierrot, The dissociation of carbonic acid in NaCl solutions as a function of concentration and temperature, Geochim. Cosmochim. Acta, 2007, 71, 46–55.
7. D. M. Austgen, G. T. Rochelle, X. Peng and C. C. Chen, Model of vapor-liquid equilibria for aqueous acid gas-alkanolamine systems using the electrolyte-NRTL equation, Ind. Eng. Chem. Res., 1989, 28, 1060–1073.
8. L. F. Cameretti, G. Sadowski and J. M. Mollerup, Modeling of Aqueous Electrolyte Solutions with Perturbed-Chain Statistical Associated Fluid Theory, Ind. Eng. Chem. Res., 2005, 44, 3355–3362.
9. M. Kohns, G. Lazarou, S. Kournopoulos, E. Forte, F. A. Perdomo, G. Jackson, C. S. Adjiman and A. Galindo, Predictive models for the phase behaviour and solution properties of weak electrolytes: nitric, sulphuric, and carbonic acids, Phys. Chem. Chem. Phys., 2020, 22, 15248–15269.
10. S. Dufal, T. Lafitte, A. J. Haslam, A. Galindo, G. N. Clark, C. Vega and G. Jackson, The A in SAFT: developing the contribution of association to the Helmholtz free energy within a Wertheim TPT1 treatment of generic Mie fluids, Mol. Phys., 2015, 113, 948–984.
11. J. Gross and G. Sadowski, Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules, Ind. Eng. Chem. Res., 2001, 40, 1244–1260.
12. C. Held, T. Reschke, S. Mohammad, A. Luza and G. Sadowski, ePC-SAFT revised, Chem. Eng. Res. Des., 2014, 92, 2884–2897.
13. M. Bülow, M. Ascani and C. Held, ePC-SAFT advanced - Part I: Physical meaning of including a concentration-dependent dielectric constant in the born term and in the Debye-Hückel theory, Fluid Phase Equilib., 2021, 535, 112967.
14. M. Bülow, N. Gerek Ince, S. Hirohama, G. Sadowski and C. Held, Predicting Vapor–Liquid Equilibria for Sour-Gas Absorption in Aqueous Mixtures of Chemical and Physical Solvents or Ionic Liquids with ePC-SAFT, Ind. Eng. Chem. Res., 2021, 60, 6327–6336.
15. D. Pabsch, P. Figiel, G. Sadowski and C. Held, Solubility of electrolytes in organic solvents: Solvent-specific effects and ion-specific effects, Chem. Eng. Data, 2022 DOI:10.1021/acs.jced.0c00704.
16. M. Ascani and C. Held, Prediction of salting-out in liquid–liquid two-phase systems with ePC-SAFT: Effect of the Born term and of a concentration-dependent dielectric constant, Z. Anorg. Allg. Chem., 2021, 647, 1305–1314.
17. S. P. Sørensen and K. Linderstrøm-Lang, C. R. Trav. Lab. Carlsberg, 1924, 15, 1–29.
18. K. Thomsen, Electrolyte solutions: Thermodynamics, crystallization, separation methods, DTU Chemical Engineering, Technical University of Denmark, 2009.
19. C. Peng, J. P. Crawshaw, G. C. Maitland, J. P. Martin Trusler and D. Vega-Maza, The pH of CO₂-saturated water at temperatures between 308 K and 423 K at pressures up to 15 MPa, J. Supercrit. Fluids, 2013, 82, 129–137.
20. D. Pabsch, C. Held and G. Sadowski, Modeling the CO₂ Solubility in Aqueous Electrolyte Solutions Using ePC-SAFT, J. Chem. Eng. Data, 2020, 65, 5768–5777.
21. X. Li, C. Peng, J. P. Crawshaw, G. C. Maitland and J. M. Trusler, The pH of CO2-saturated aqueous NaCl and NaHCO₃ solutions at temperatures between 308 K and 373 K at pressures up to 15 MPa, Fluid Phase Equilib., 2018, 458, 253–263.
22. M. Mutailipu, Y. Liu, Y. Song and J. M. Trusler, The pH of CO2–saturated aqueous KCl solutions at temperatures between 298 K and 423 K at pressures up to 13.5 MPa, Chem. Eng. Sci., 2021, 234, 116434.
23. H. Ziegenfuβ and G. Maurer, Distribution of acetic acid between water and organic solutions of tri-n-octylamine, Fluid Phase Equilib., 1994, 102, 211–255.
24. T. Kirsch, H. Ziegenfuß and G. Maurer, Distribution of citric, acetic and oxalic acids between water and organic solutions of tri-n-octylamine, Fluid Phase Equilib., 1997, 129, 235–266.
25. T. Kirsch and G. Maurer, Distribution of Oxalic Acid between Water and Organic Solutions of Tri-n-octylamine, Ind. Eng. Chem. Res., 1996, 35, 1722–1735.
26. M. Ascani, G. Sadowski and C. Held, Calculation of Multiphase Equilibria Containing Mixed Solvents and Mixed Electrolytes: General Formulation and Case Studies, J. Chem. Eng. Data, 2022 DOI:10.1021/acs.jced.1c00866.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc02943j

---