Open Access Article
Open Access ArticleMachine learning for non-additive intermolecular potentials: quantum chemistry to first-principles predictions†
Richard S.
Graham
 *a and
Richard J.
Wheatley
*a and
Richard J.
Wheatley
 *b
*b
aSchool of Mathematical Sciences, University of Nottingham, Nottingham NG7 2RD, UK. E-mail: richard.graham@nottingham.ac.uk
bSchool of Chemistry, University of Nottingham, Nottingham NG7 2RD, UK
First published on 24th May 2022
Abstract
Prediction of thermophysical properties from molecular principles requires accurate potential energy surfaces (PES). We present a widely-applicable method to produce first-principles PES from quantum chemistry calculations. Our approach accurately interpolates three-body non-additive interaction data, using the machine learning technique, Gaussian Processes (GP). The GP approach needs no bespoke modification when the number or type of molecules is changed. Our method produces highly accurate interpolation from significantly fewer training points than typical approaches, meaning ab initio calculations can be performed at higher accuracy. As an exemplar we compute the PES for all three-body cross interactions for CO2–Ar mixtures. From these we calculate the CO2–Ar virial coefficients up to 5th order. The resulting virial equation of state (EoS) is convergent for densities up to the critical density. Where convergent, the EoS makes accurate first-principles predictions for a range of thermophysical properties for CO2–Ar mixtures, including the compressibility factor, speed of sound and Joule–Thomson coefficient. Our method has great potential to make wide-ranging first-principles predictions for mixtures of comparably sized molecules. Such predictions can replace the need for expensive, laborious and repetitive experiments and inform the continuum models required for applications.
Improvements in computational chemistry mean calculations of intermolecular potentials can be performed accurately for small molecules.1 Such ab initio calculations can lead to first-principles potential energy surfaces (PES), from which molecular simulation2,3 can quantitatively predict useful physical properties. This molecular understanding and predictive ability has potentially transformative applications in many fields. Examples include improved models of CO2 for understanding and mitigating climate change,4–7 molecular models of water to improve treatment and desalination8,9 and the effect of ice structure and behaviour on pollution control and other planetary processes.10 There are also innumerable industrial applications including the molecular design of materials, manufacture and industrial processing.11 The main barrier is the computational cost of evaluating the energy. This cost is significant (often minutes or hours for a single point1), so fitting or interpolating calculated energy data is necessary. This task of bridging between quantum chemistry and statistical mechanics is, in general, difficult for established parametric approaches. A robust and accurate alternative has recently been provided by a machine learning technique, Gaussian Processes (GP).12–19 For example, work on two-body interactions13,14 produced highly accurate GP interpolation for many different chemical systems, without bespoke modification. This led to first-principles predictions for dilute gas mixtures that surpassed those of a leading empirical equation of state.
Despite the above progress, modelling denser fluids requires non-additive interactions. Including three-body non-additive interactions in first-principles approaches, dramatically decreases the deviation from experiments,20 at times by an order of magnitude.21 Non-additive interactions are high-dimensional and vary strongly and unpredictably with molecular position. Consequently, traditional parametric fitting typically requires a bespoke fitting form for each PES, must be fit to an extensive data set22–24 and the resulting fit, even to the training data, is not particularly accurate. Furthermore many applications involve molecular mixtures. Mixtures are especially challenging because each combination of two-body and three-body interactions requires a PES. Therefore, parametric approaches are laborious, insufficiently accurate and may require an unattainable number of high-level quantum chemistry calculations. In this communication we present a comprehensive solution to this long-standing problem. We successfully capture non-additive three-body calculations via an existing GP approach.13,14 The training sets are small enough to allow expensive, high-quality ab initio calculations. Taking CO2–Ar as an exemplar, we produce accurate first-principles predictions for a range of thermophysical properties. Previously, our two-body approach successfully interpolated a wide range of small molecules, comprising 1–4 atoms. This included single atoms, linear and non-linear molecules,13,14 along with dipole–dipole and charge–dipole interactions.25 In each case the same algorithm was successful, despite significant variation in the chemistry. Herein, we successfully capture three different non-additive interactions with the same algorithm. These successes suggest that our approach will be effective for the myriad of mixtures involving such molecules.
CO2–Ar is important to carbon capture, storage and utilization (CCUS). Safe and economical handling of captured CO2 requires accurate knowledge of numerous thermophysical properties, for mixtures of many impurities.6 A recent US Department of Energy report7 highlighted the key role for molecular modelling in CCUS. PES exist for (Ar)226 and (CO2)2,27 along with non-additive PES for (Ar)323 and (CO2)3.24 Thus we produced GP PES for the remaining interactions: CO2–Ar, CO2–(Ar)2 and (CO2)2–Ar. We also modelled (CO2)2 and (Ar)3 to confirm consistency with existing literature.
The CO2–(Ar)2 and (CO2)2–Ar PES were sub-divided into three regions based on the order of the molecular centre-to-centre distances (see Table S2, ESI†). Reference datasets were designed for each region, each containing a list of molecular geometries, specified viax: each element of x is the inverse separation of two atoms on different molecules. The geometries were limited so that no pairwise interaction exceeds 0.005 Eh, where Eh is hartrees, and no molecule pair is separated by more than ∼10 Å (see Section S3.3, ESI†). Within these constraints a space-filling Latin Hyper Cube (LHC) design (see Section S3.6, ESI†) produced reference sets for each region, each of ∼10k geometries. Interaction energy calculations were performed in Molpro,28 using coupled-cluster theory with single, double and non-iterative triple excitations and the counterpoise correction. Moderate accuracy calculations used the augmented correlation-consistent triple-zeta basis set, while high accuracy calculations involved complete basis set extrapolation of the interaction energies from the augmented correlation-consistent triple-zeta and quadruple-zeta basis sets. The interaction potentials were calculated for each reference set geometry at moderate accuracy. These calculations enable selection of the GP training set before this much smaller set is upgraded to high accuracy.
We interpolate via the machine learning technique, Gaussian Processes (GP).29 GPs are non-parametric models, which are effective at creating theory-free models of complex data. GPs require a mean function and a covariance function k(x, x′), expressing the covariance between f(x) and f(x′), where f is the function being interpolated. Training data, namely values of f at various x, update the mean and covariance functions to give a posterior model which predicts f at any x. As previously,13 our GPs are mean-zero with a squared-exponential covariance function, made symmetric under the permutations of x that do not change the interaction. Using inverse interatomic distances as covariates achieves approximate stationarity. GP training involves regression against the training data and estimation of the hyperparameters through the log-likelihood. We capture non-additive data, without varying the covariance function, geometric constraint, covariate choice, covariate transformation, LHC algorithm or sequential learning. Instead our unmodified GP algorithm accurately interpolates the non-additive data, even when the molecule types are varied.
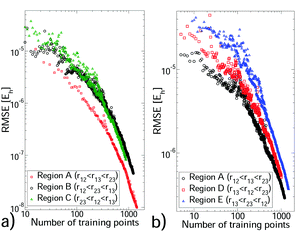
We selected a GP training set from our non-additive data through sequential learning,14 which progressively moves points from the reference set to the training set (see Section S4, ESI†). At each iteration, the current GP predictions were computed for the reference set and the geometry with the largest error was moved to the training set. The root mean square error (RMSE) against the reference set was monitored (see Fig. 1) and these steps were repeated until a sufficiently small RMSE was achieved. In all cases the training set remained significantly smaller than the reference set. We also monitored the root mean square value (RMS) of the reference set to verify that depletion of this set was minimal. The hyperparameter values depend on the triplet being modelled, but were stable during sequential learning once the RMSE was ≲10% of the reference set RMS. Each CO2–(Ar)2 region required 780–1000 training points to achieve an RMSE of 1.1–6.5 × 10−7Eh, which is ∼0.5% of the reference set RMS. (CO2)2–Ar was more challenging, requiring 1000–1400 training points for errors of 1–2%. For (Ar)3 and the two body PES, errors of <0.1% were achieved with 72–337 training points (see Tables S4 and S5 of the ESI†). For the larger systems sequential learning was essential to achieve an acceptable RMSE from a reasonable training set size. For example, for CO2–(Ar)2 in region A our best RMSE from LHC learning13 was ∼10 times larger than that from sequential learning of the same training set size. All PES have sufficiently low RMSEs for first-principles predictions. All training sets were small enough to be upgraded to high accuracy calculations, to which a new GP was trained. This produced, for each PES, a GP with precise interpolation of high-quality quantum chemical calculations. Our calculation data and PES code are available in the ESI.†
Outside the geometric constraint the GP model does not predict the interaction, so alternative forms are required. Configurations of very close molecules are negligibly rare in a thermal ensemble, so we used a strongly repulsive function13 for binary interactions and set the non-additive potential to zero. In contrast, the long range behaviour makes a measurable contribution to the virial coefficients for binary interactions.13 This two-body long-range behaviour can be obtained from a truncated multipole expansion of the interaction energy from intermolecular perturbation theory.13,25 However, this does not generalise readily to three-body interactions, particularly when two molecules are close. Instead, we used carefully chosen interaction calculations to characterise an empirical power law form for the long-range behaviour, by generalising our previous empirical approach25 (see Section S6 of the ESI†).
The total CPU times for ab initio calculations in kiloCPU-hours are 0.99 [(Ar)3], 83 [CO2–(Ar)2] and 689 [(CO2)2–Ar]. Upgrading all calculations to high accuracy, as would be required for traditional parametric fitting, increases these by a factor of 3.5–6. All calculations required <0.5 GB of RAM.
To produce first-principles predictions we use our PES to compute virial coefficients. This produces an equation of state (EoS), valid for densities up to approximately the critical density, 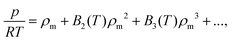 where p is pressure, T is temperature, R is the universal gas constant, ρm is the molar density and Bn(T) is the nth virial coefficient. For binary mixtures the virial coefficients are
where p is pressure, T is temperature, R is the universal gas constant, ρm is the molar density and Bn(T) is the nth virial coefficient. For binary mixtures the virial coefficients are 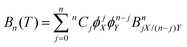 , where nCj is the binomial coefficient, ϕX/Y is the mol fraction of species X/Y and BnjX/(n−j)Y is the nth virial coefficient involving j and n − j molecules of type X and Y, respectively. For pure Ar23 and pure CO224 there are literature calculations up to B7 from non-additive three-body potentials. We computed the remaining cross virial coefficients for (CO2)X–(Ar)Y, up to and including B5, by Monte-Carlo integration.30 We also computed the temperature derivatives of each virial by differentiating the integrand before integrating. Uncertainties due to the integration are negligible for the lower virials, but rise to ∼10% for B5 at 298 K and are larger still at lower temperatures (see Tables S9–S18 of the ESI†). We analytically propagated these uncertainties for all predictions. Finally, for comparison, we computed the cross virials neglecting the non-additive interactions, while retaining full calculations for the pure CO2 and Ar virials. We will show below that this two-body mixture model gives inaccurate predictions.
, where nCj is the binomial coefficient, ϕX/Y is the mol fraction of species X/Y and BnjX/(n−j)Y is the nth virial coefficient involving j and n − j molecules of type X and Y, respectively. For pure Ar23 and pure CO224 there are literature calculations up to B7 from non-additive three-body potentials. We computed the remaining cross virial coefficients for (CO2)X–(Ar)Y, up to and including B5, by Monte-Carlo integration.30 We also computed the temperature derivatives of each virial by differentiating the integrand before integrating. Uncertainties due to the integration are negligible for the lower virials, but rise to ∼10% for B5 at 298 K and are larger still at lower temperatures (see Tables S9–S18 of the ESI†). We analytically propagated these uncertainties for all predictions. Finally, for comparison, we computed the cross virials neglecting the non-additive interactions, while retaining full calculations for the pure CO2 and Ar virials. We will show below that this two-body mixture model gives inaccurate predictions.
Fig. 2 compares measured compressibility factors for CO2–Ar mixtures31 with our first-principles predictions. The virial EoS predictions converge up to a threshold density, with this threshold increasing with Ar fraction. For the two highest Ar fractions predictions converge for the whole density range. Even the most CO2-rich mixture converges up ∼10 kmol m−3, which is approximately the critical density of pure CO2. In the converged region, the uncertainties are negligible. Where converged, the three body predictions closely predict the experiments, confirming that our approach leads to accurate first-principles predictions, entirely free of any need to fit experiments. The disagreement with measured pressure for converged calculations is always <0.6% and is often significantly smaller. Also shown in Fig. 2 are the two-body mixture calculations (dashed lines). Each mixture composition shows a clear window where the model is converged, uncertainties are negligible and the three-body calculations capture the experiments, whereas the two-body mixture model does not. Hence our new mixture PES are essential for accurate prediction.
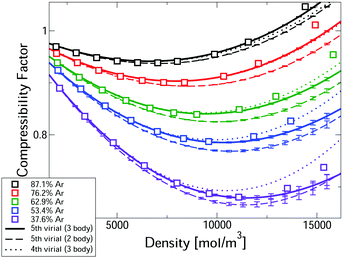 | ||
| Fig. 2 Comparison of the first-principles predictions of the compressibility factor of CO2–Ar mixtures at 323.15 K and measurements.31 | ||
The virial EoS can predict many other thermophysical properties, including the speed of sound and Joule–Thomson coefficient. We derive expressions for these from the virial model in Section S8.2 of the ESI.† Modelling these properties is challenging because they depend on the temperature derivatives of the pressure. Fig. 3 shows accurate prediction for both measurements, except for the Joule–Thomson coefficient in the liquid phase, where predictions do not converge. Uncertainties are negligible in the converged region, except for the Joule–Thomson predictions around 10 MPa, where the uncertainties are somewhat larger due to stronger dependence on the 5th virial coefficient (see Section S8.3 of the ESI†).
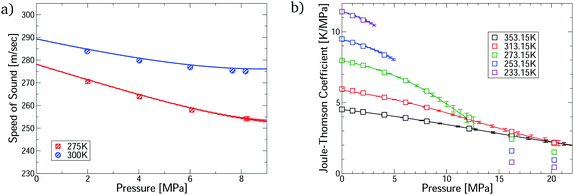 | ||
| Fig. 3 Comparison of the first-principles predictions for CO2–Ar mixtures via our virial calculations. (a) Speed of sound measurements32 at ϕCO2 = 0.5; and (b) Joule–Thomson coefficient measurements33 at ϕCO2 = 0.464. All predictions are converged with respect to number of virial terms. | ||
To conclude, our GP approach produces highly accurate interpolation of the non-additive three-body interaction of small molecules. The method requires relatively few training points, so highly accurate ab initio calculations can be used. This precise interpolation of high-level calculations leads to exceptionally accurate PES. Furthermore, the method requires no adaptation when changing chemical species. This is essential to mixtures as a separate PES is required for each distinct molecular triplet. Taking CO2–Ar mixtures as an exemplar, we achieved interpolation errors of <5.1 × 10−7Eh with <5000 training points per PES. The data can be supplemented progressively if greater accuracy is required. Our method is applicable to many systems of comparable molecules without modification. This contrasts to parametric approaches where PES fitting is laborious, often inaccurate and requires many ab initio calculations, precluding high accuracy calculations. Applying the method to significantly larger molecules would require an impractical number of training points. This may be alleviated by future improvements in computing resources or the GP method.
Our GP approach consistently requires fewer training points than other approaches. A parametric approach to (CO2)3 required ∼9k training points for a non-additive PES,24 achieving a mean error of 1.1 × 10−6Eh. (CO2)3 has the same range of centre-to-centre distances as one region of our non-additive PES, for which our GP used only ∼1 k training points to obtain an RMSE of ∼0.5 × 10−6Eh. Neural networks (NN) are often used for PES interpolation. A NN PES trained to ∼300 (HF)2 calculations34 gave an RMSE in the well region of 6.8 × 10−5Eh. A GP trained to a similar number of points13 gave an RMSE in the same region of 5 × 10−6Eh, ∼10 times smaller. A comparison of NN and GP PES for formaldehyde35 concluded that NN require more bespoke modification and have inferior physical predictions to GPs.
From our CO2–Ar PES we produced new virial coefficients, which led to first-principles predictions for thermophysical properties. We successfully predicted compressibility, speed of sound and the Joule–Thompson coefficient for dense gases. Our predictions are reliable over a wide range of temperatures, densities and mixture compositions. The speed of sound and the Joule–Thompson coefficient are especially challenging for empirical EoS because they depend on the temperature derivatives of the pressure. Empirical fitting of pressure–density measurements for isothermal slices does not guarantee accurate temperature gradients. In contrast our approach enables direct calculation of these temperature gradients from molecular first-principles. Our virial methods are readily extended to predict further equilibrium properties such as heat capacity and critical phenomena. The success of our approach shows the potential to replace expensive, laborious and repetitive experiments with first-principles calculations. Such predictions are particularly useful for mixtures, where many experiments are required to span the relevant density, composition and temperature space for each property of interest.
Our approach enables the generation of PES and gas phase predictions for mixtures of small molecules. Furthermore, implementation of our PES in Monte Carlo (MC) simulations will enable prediction of equilibrium liquid properties, including coexistence. Molecular dynamics (MD) simulations will give access to non-equilibrium properties, such as thermal conductivity, nucleation rates and mixing dynamics. MC simulations require only the GP PES as implemented herein. MD also requires forces, which can readily be obtained from our GPs by direct differentiation. The evaluation cost of the GP PES and forces is proportional to the number of training points and so is considerably more expensive than traditional parametric PES. However, simulation of small molecules with parametric PES are extremely cheap on modern computers.6 Furthermore, the GP PES involves nested sums over training points, suggesting parallelization will be highly effective. The resulting simulation data could replace experiments, particularly where these are difficult or hazardous. Liquid simulations will enable EoS to be derived independently of experiments. This could proceed either via systematically deriving EoS from simulations16,36 or hybrid methods where the virial model provides the gas phase and additional empirical terms are fitted to simulation data in the liquid phase.
The authors are grateful for access to the University of Nottingham high-performance computing facility.
Conflicts of interest
There are no conflicts to declare.References
- F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, 2017 Search PubMed.
- G. A. Cisneros, et al. , Chem. Rev., 2016, 116, 7501–7528 CrossRef CAS PubMed.
- D. Zheng and F. Wang, ACS Phys. Chem. Au, 2021, 1, 14–24 CrossRef CAS PubMed.
- T. Ilyina, Nature, 2016, 530, 426 CrossRef PubMed.
- H. W. Kim, et al. , Science, 2013, 342, 91–95 CrossRef CAS PubMed.
- A. J. Cresswell, et al. , Faraday Discuss., 2016, 192, 415–436 RSC.
- https://www.energy.gov/fecm/downloads/accelerating-breakthrough-innovation-carbon-capture-utilization-and-storage .
- S. B. Grant, et al. , Science, 2012, 337, 681–686 CrossRef CAS.
- C. I. Lynch, S. Rao and M. S.-P. Sansom, Chem. Rev., 2020, 120, 10298–10335 CrossRef CAS.
- T. Bartels-Rausch, Nature, 2013, 494, 27 CrossRef CAS PubMed.
- A. G. Slater and A. I. Cooper, Science, 2015, 348, 8075 CrossRef PubMed.
- A. P. Bartok, et al. , Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- E. Uteva, et al. , J. Chem. Phys., 2017, 147, 161706 CrossRef PubMed.
- E. Uteva, et al. , J. Chem. Phys., 2018, 149, 174114 CrossRef PubMed.
- J. Dai and R. V. Krems, J. Chem. Theory Comput., 2020, 16, 1386–1395 CrossRef CAS PubMed.
- M. Veit, et al. , J. Chem. Theory Comput., 2019, 15, 2574–2586 CrossRef CAS PubMed.
- C. M. Handley, et al. , Phys. Chem. Chem. Phys., 2009, 11, 6365 RSC.
- M. J.-L. Mills, et al. , Phys. Chem. Chem. Phys., 2013, 15, 18249–18261 RSC.
- V. L. Deringer, et al. , Chem. Rev. Rev., 2021, 121, 10073–10141 CrossRef CAS.
- R. Bukowski and K. Szalewicz, J. Chem. Phys., 2001, 114, 9518–9531 CrossRef CAS.
- O. Akin-Ojo and K. Szalewicz, J. Chem. Phys., 2013, 138, 024316 CrossRef PubMed.
- M. T. Oakley and R. J. Wheatley, J. Chem. Phys., 2009, 130, 034110 CrossRef PubMed.
- B. Jäger, et al. , J. Chem. Phys., 2011, 135, 084308 CrossRef PubMed.
- R. Hellmann, J. Chem. Phys., 2017, 146, 054302 CrossRef PubMed.
- J. Broad, et al. , J. Chem. Phys., 2021, 155, 144106 CrossRef CAS PubMed.
- K. Patkowski and K. Szalewicz, J. Chem. Phys., 2010, 133, 094304 CrossRef PubMed.
- R. Hellmann, Chem. Phys. Lett., 2014, 613, 133–138 CrossRef CAS.
- H. J. Werner, et al. , MOLPRO 2012.1, 2012 Search PubMed , https://www.molpro.net.
- C. Rasmussen and C. K.-I. William, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- R. J. Wheatley, et al. , Phys. Rev. E, 2020, 101, 051301 CrossRef CAS PubMed.
- W. H. Abraham and C. O. Bennett, AIChE J., 1960, 6, 257–261 CrossRef CAS.
- R. Wegge, et al. , J. Chem. Thermodyn., 2016, 99, 54–64 CrossRef CAS PubMed.
- J. P. Strakey, C. O. Bennett and B. F. Dodge, AIChE J., 1974, 20, 803–814 CrossRef CAS.
- D. F.-R. Brown, M. N. Gibbs and D. C. Clary, J. Chem. Phys., 1996, 105, 7597 CrossRef CAS.
- A. Kamath, et al. , J. Chem. Phys., 2018, 148, 241702 CrossRef PubMed.
- H. Do, J. D. Hirst and R. J. Wheatley, J. Chem. Phys., 2011, 135, 174105 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cc01820a |
| This journal is © The Royal Society of Chemistry 2022 |