 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Na superionic conductor-type LiZr2(PO4)3 as a promising solid electrolyte for use in all-solid-state Li metal batteries
Masanobu
Nakayama
 *abc,
Koki
Nakano
*abc,
Koki
Nakano
 ab,
Maho
Harada
a,
Naoto
Tanibata
ab,
Maho
Harada
a,
Naoto
Tanibata
 ac,
Hayami
Takeda
ac,
Hayami
Takeda
 ac,
Yusuke
Noda
d,
Ryo
Kobayashi
ac,
Yusuke
Noda
d,
Ryo
Kobayashi
 e,
Masayuki
Karasuyama
f,
Ichiro
Takeuchi
fgh and
Masashi
Kotobuki
i
e,
Masayuki
Karasuyama
f,
Ichiro
Takeuchi
fgh and
Masashi
Kotobuki
i
aDepartment of Advanced Ceramics, Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Aichi 466-8555, Japan. E-mail: masanobu@nitech.ac.jp
bFrontier Research Institute for Materials Science (FRIMS), Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Aichi 466-8555, Japan
cUnit of Elements Strategy Initiative for Catalysts & Batteries (ESICB), Kyoto University, Katsura, Saikyo-ku, Kyoto, 615-8520, Japan
dDepartment of Information and Communication Engineering, Okayama Prefectural University, 111 Kuboki, Soja, Okayama 719-1197, Japan
eDepartment of Applied Physics, Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Aichi 466-8555, Japan
fDepartment of Computer Science, Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Aichi 466-8555, Japan
gRIKEN Center for Advanced Intelligence Project, 1-4-1 Nihonbashi, Chuo-ku, Tokyo, 103-0027, Japan
hFaculty of Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8601, Japan
iBattery Research Center of Green Energy, Ming Chi University of Technology, 84 Gungjuan Rd., Taishan Dist., New Taipei City, 24301, Taiwan
First published on 5th August 2022
Abstract
All-solid-state Li-ion batteries are of considerable interest as safer alternatives to Li-ion batteries containing flammable organic electrolytes. To date, however, achieving sufficient charging and discharging rates, in addition to capacity, at room temperature using these all-solid-state batteries has been challenging. To overcome these issues, material simulations and informatics investigations of a relatively new Na superionic conductor (NASICON)-type LiZr2(PO4)3 (LZP) electrolyte were conducted to elucidate its characteristics and material functions. The following thermodynamic and/or kinetic properties of NASICON-type Li-ion conductive oxides were investigated with respect to the crystal structure mainly using material simulation and informatics approaches: (1) the electrochemical stabilities of LZP materials with respect to Li metal and (2) Li-ion conductivities in the bulk and at the grain boundaries. An efficient materials informatics search method was employed to optimise the material functions of the LZP electrolyte via Bayesian optimisation. This study should promote the application of LZP in all-solid-state batteries for use in technologies such as mobile devices and electric vehicles and enable more complex composition and process control.
1. Introduction
Li-ion batteries, which are employed as power sources in mobile devices and electric vehicles, contain flammable organic electrolytes, which introduce the risks of liquid leakage and explosion. These problems may be resolved using all-solid-state batteries, wherein the flammable organic electrolytes are replaced with non-flammable inorganic solid electrolytes.1,2 However, the diffusion of Li ions is generally much slower in a solid than in a liquid, and charging and discharging at sufficient rates and capacities at room temperature are challenging. Solid electrolyte materials for use in all-solid-state batteries were developed in the 1980s, and various materials have been investigated to date. Recently, Kanno et al. reported a solid electrolyte, Li10GeP2S12, with a Li-ion conductivity rivalling those of liquid systems (10−2 S cm−1 at room temperature).3,4 The discovery of such materials inspires further practical applications, such as an all-solid-state battery that may achieve the energy density and charge/discharge rate required for use as an electric vehicle power source. In addition, the introduction of robust inorganic solid electrolytes should enable the use of Li metal, which exhibits a very large capacity, as the anode.5,6 To date, Li metal has been unusable due to the risk of short-circuiting because of dendrite precipitation following repeated charging and discharging. However, the use of solid electrolytes has yielded drastic increases in battery capacity. Furthermore, all-solid-state batteries enable bipolarised series connections.7,8 Conventional liquid-based batteries require the cell to be packaged prior to connection. However, an all-solid-state battery does not require complex packaging for electrolyte solution leakage, which may considerably improve the volumetric energy density.To date, the highest Li-ion conductivities at room temperature have been reported using Li10GeP2S12 and its derivatives, with values on the order of 10−2 S cm−1, and oxide-based perovskite-type (Li, La)TiO3 materials, with values on the order of 10−3 S cm−1.9,10 Sulphide-based materials exhibit higher ionic conductivities than oxides. Sulfur also displays a higher moldability than oxygen and less grain boundary (GB) resistance, even in green compacts. However, sulfides are chemically unstable, and as shown in Fig. 1, their potential windows are generally very narrow compared to those of oxide-based systems. Furthermore, they exhibit low atmospheric stabilities, with the risk of reactions with atmospheric moisture that generate H2S and concomitant deterioration.11
 | ||
| Fig. 1 Potential windows of typical solid electrolytes, according to convex hull computations based on first-principles calculations. | ||
Oxide ion conductors exhibit large energy gaps between the upper end of the valence band and the lower end of the conduction band and generally display wider potential windows than sulfides (Fig. 1). Furthermore, their atmospheric stabilities are high, and they are less likely to generate toxic gases, such as H2S, rendering them safer than sulfides. Na superionic conductors (NASICONs),12,13 perovskites,9,10 and garnets9,18–20 are oxide materials with high Li-ion conductivities, and various solid electrolytes are proposed based on these structural frameworks. However, perovskites exhibit high reduction potentials, which reduce the operating voltages of all-solid-state batteries.14–23 Furthermore, garnet-type Li7La3Zr2O12 exhibits high stability compared to metallic Li.15,16 However, this material also displays challenges in terms of handling in practical applications, such as its reaction with low amounts of atmospheric moisture, which reduces the conductivity.17,18 NASICON-type oxide was discovered earlier than the perovskite and garnet types. In 1976, Goodenough et al. reported that the Na-ion conductive oxide Na(1+x)Zr2SixP(3−x)O12 generated a high ionic conductivity of ∼5 S cm−1 at 300 °C.19 This material was denoted as NASICON, with the highest Na-ion conductivity at that time. Subsequently, materials wherein the Na ions were substituted with Li or Mg ions have been reported and have exhibited high ionic conductivities.20,21,27Table 1 shows the ionic conductivities of representative NASICON-type solid electrolytes. Examples of NASICON-type oxides that display high Li-ion conductivities include Li1.3Al0.3Ti1.7(PO4)3 (LATP), where the Ti in LiTi2(PO4)3 is partially substituted with Al (∼10−3 S cm−1), and Li1.5Al0.5Ge1.5(PO4)3 (LAGP, ∼10−3 S cm−1).22,23 However, materials containing Ti and Ge exhibit reducing properties, and LATP and LAGP experience the same issue as perovskite-type materials in that they react with metallic Li.24,25 However, stable charging and discharging of LiZr2(PO4)3 (LZP), which is a type of NASICON material, was recently observed in an all-solid-state battery comprising Li/LZP/LiFePO4, where the metallic Li was the anode.28 As in the case of LATP, doping metal cations to stoichiometric LZP significantly improves the Li-ion conductivity. For example, LZP doped with SrO,27,29,38 CaO,31,32 Y2O3,33,39 Al2O3,34 and As2O5 has been reported to show improved Li-ion conductivity up to 100 times that of non-doped LZP. The common feature in these systems with a significant increase in ionic conductivity is when the molar ratio of Li ions to the formula unit (LiZr2(PO4)3) exceeds 1, indicating that the introduction of Li ions at the interstitial site by doping with aliovalent ions is effective. Rossbach et al. conducted a comprehensive study of LATP systems based on a survey of many papers, which showed that introducing an excess of Li rather than inserting Li vacancies contributed more to performance improvement.40 On the other hand, it has also been pointed out that increasing the amount of Li too much can adversely reduce ionic conductivity. This phenomenon is observed even in the single-phase NASICON phase, which suggests that trade-off factors of aliovalent doping may exist. For example, in systems doped with CaO41 and SrO,27 the ionic conductivity reaches a maximum at 1.2 mol of Li in both cases, with conductivity decreasing at higher substitutions. The possible contribution of grain boundaries, such as dopant segregation, to this phenomenon has been pointed out.27 Similarly, a maximum ionic conductivity at 1.15 mol has also been reported for Y2O3-doped LZP;33 Xu et al. have performed a systematic investigation of the factors associated with the ionic conductivity of this Y2O3-doped LZP.42 They pointed out that although the effect of particle size is small, the formation of polymorphs such as monoclinic phases and the formation of impurity layers due to over-doping with Li and P lead to a rapid decrease in conductivity Hence, careful compositional optimization holds considerable potential in the improvement of the performance of all-solid-state batteries. We focused on this NASICON-type LZP material in this study and conducted comprehensive research, including material simulations and informatics investigations, to elucidate its material functions. This article presents these results in the following structure. Section 2 introduces the characteristics of NASICON-type Li-ion conductive oxides in terms of the crystal structure. Section 3 describes the stabilities of LZP materials toward Li metal. Sections 4 and 5 analyse the Li-ion conductivities in the bulk and at the GBs, respectively, in addition to the corresponding mechanisms. Section 6 presents the results of ion conductivity optimisations of LZP materials doped with Ca and Y via experimental and materials informatics approaches. Finally, Section 7 summarises this study.
| Electrolyte | Structure | σ (RT, S cm−1) | Ea (eV) | Ref. |
|---|---|---|---|---|
| LiTi2(PO4)3 | Crystalline | 2 × 10−6 | — | 26 |
| Li1.3Al0.3Ti1.7(PO4)3 | Crystalline | 7 × 10−4 | — | 26 |
| Li1.3Sc0.3Ti1.7(PO4)3 | Crystalline | 7 × 10−4 | — | 26 |
| LiZr2(PO4)3 | Crystalline, rhombohedral | 8.06 × 10−7 | 0.56 | 27 |
| LiZr2(PO4)3 | Crystalline, rhombohedral | 2 × 10−4 | 0.28 | 28 |
| Li1.2Zr1.9Sr0.1(PO4)3 | Crystalline, rhombohedral | 3.44 × 10−5 | 0.43 | 27 |
| Li1.2Zr1.9Sr0.1(PO4)3 | Crystalline, rhombohedral | 0.85 × 10−4 | 0.29 | 29 |
| Li0.91Hf2.022(PO4)3 | Crystalline | 3.2 × 10−7 | 0.47 | 30 |
| Li1.2Zr1.9Ca0.1(PO4)3 | Crystalline, rhombohedral | 1.2 × 10−4 | 0.44 | 31,32 |
| Li1.15Y0.15Zr1.85(PO4)3 | Crystalline, rhombohedral | 1.4 × 10−4 | 0.39 | 33 |
| Li1.275Al0.275Zr1.725(PO4)3 | Crystalline rhombohedral | 3.1 × 10−6 | 0.44 | 34 |
| LiZr2(AsO4)x(PO4)3−x | Crystalline monoclinic | 10−7 | 0.6 | 35 |
| Li1.5Al0.5Ge1.5(PO4)3 | Crystalline, hexagonal, a = 8.25, c = 20.65 | 4.0 × 10−4 | 0.35 | 36 |
| Li1.5Al0.5Ge1.5(PO4)3 | Glass-ceramics, rhombohedral, a = 8.276, c = 20.394 | 1.18 × 10−3 | 37 |
2. Structures of NASICON-type Li-ion conductive oxides
The NASICON-type structure is derived from orthophosphate and represented by the general formula LiM2(PO4)3, with the M site occupied by a tetravalent transition metal (Fig. 2(a)). In 1986, Petit et al. studied the relationship between the Li-ion conductivity and crystal structure in LZP. Long-distance diffusion of Li ions was possible, and a high ionic conductivity was observed at ≥280 °C after the phase transition from the monoclinic to the rhombohedral phase, which is the NASICON phase.43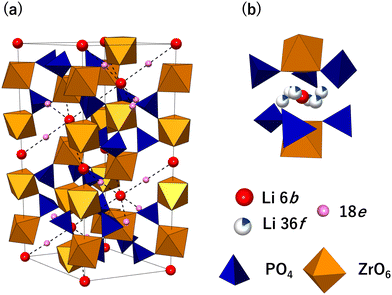 | ||
| Fig. 2 (a) LiZr2(PO4)3 crystal structure. (b) Arrangement of ions and polyhedra around the Li 6b site. | ||
Catti et al. investigated the intralattice Li distribution using neutron diffraction, which has an excellent ability to detect Li.44,45Fig. 2 shows the crystal structure of NASICON-type LiZr2(PO4)3, which was elucidated from these studies. The structure belongs to the space group R3c, and PO4 tetrahedrons and ZrO6 octahedrons share vertices to form a 3D network. There is a relatively large cavity, which may contain Li ions, surrounded by two ZrO6 octahedra and six PO4 tetrahedra. The centre of the cavity is a 6b site, but according to Catti et al., Li ions partially occupy the 36f site, which is a split site around the 6b site at 423 K (Fig. 2(b)).44,45 The ionic conductivity of LZP is low, with values of 10−5–10−7 S cm−1.33,35 Therefore, performance enhancement using methods such as element substitution has been investigated to improve the ionic conductivity. Partial substitution of Zr4+ ions with aliovalent ions generates Li vacancies and interstitial Li ions, but the conductivity is considerably improved, particularly in systems wherein interstitial Li ions are formed. For instance, Li1.2Zr1.9Ca0.1(PO4)3, where Zr4+ is substituted with Ca2+, and Li1.15Y0.15Zr1.85(PO4)3, where Zr4+ is substituted with Y, exhibit high ionic conductivities of ∼10−4 S cm−1.31,33,41,42 Furthermore, according to studies of Y-substituted systems, Li-ion diffusion in LZP occurs via the 18e site at the midpoint between two adjacent 6b sites (∼6.7 Å), and a 3D Li migration network is formed, as indicated by the dashed lines in Fig. 2(a).yst42
3. Stability toward Li metal
Li et al. reported that all-solid-state batteries comprising Li/LZP/LiFePO4 (LFP) exhibited stable charging and discharging.28 Therefore, the LZP solid electrolyte is electrochemically stable with respect to Li metal and thus should be applied in large-capacity all-solid-state batteries with Li metal anodes. Additionally, Li3P and Li8ZrO6 materials were produced during the operation of the all-solid-state battery.28 Therefore, we verified the reactivity between Li metal and LZP using first-principles computations and experimental studies.46Theoretical studies on the electrochemical potential window of solid electrolytes have been reported by several researchers; nowadays, with the availability of comprehensive computational databases for inorganic solid-state materials, such as the Materials Project,47 convex hull calculations have been used for evaluation. For example, Zhu et al. have shown the potential windows of various Li ion-conducting materials and the decomposition products in oxidative or reductive end of the electrochemical potential windows.48 For example, Garnet-type Li7La3Zr2O12, known experimentally not to react with Li metal, was shown to be 0.021 eV per atom unstable with respect to Li metal, and Li2O, Zr3O and La2O3 are the candidates of the decomposition products. Therefore, it is kinetically unreactive with Li metal. Convex hull calculations do not require calculations for complex electrode/electrolyte interface models. The electrochemical potential window at absolute zero Kelvin can be evaluated with a database of total electron energies derived from first-principles calculations for a single phase (bulk) of all compounds comprising the elements in the solid electrolyte of interest.
We reported on the first-principles computations to determine the total energies of the electrons of 110 crystal structures that included Li, Zr, P, or O,46 which were extracted from the Materials Project crystal structure database.47 We evaluated the thermodynamic phase stability by considering a convex hull for the composition and the energy values of the material datasets. This analysis showed that LZP is at the vertex of the convex hull diagram, indicating that this crystal structure was thermodynamically stable. (Notably, the polymorphic monoclinic phase was stable, whereas the NASICON-type rhombohedral phase was slightly unstable. This behaviour is consistent with the stability of the monoclinic phase at low temperatures. Therefore, the monoclinic phase data were excluded.) Furthermore, the potential window ranged from 2.20 to 4.14 V vs. Li+/Li, based on the convex hull diagram. The potential window on the reducing side did not generate 0 V, and, thus, there could be a reaction with the Li metal. Table 2 shows the details of the reduction decomposition reactions at ≤2.20 V as reaction equations D1–D9.46
| Index # | Decomposition reaction | η Li/V vs. E0(Li) |
|---|---|---|
| D1 | 4LiZr2(PO4)3 + 5Li → 3Li3PO4 + 4Zr2P2O9 + P | 2.20–2.15 |
| D2 | LiZr2(PO4)3 + 5Li → 2Li3PO4 + 2ZrO2 + P | 2.15–2.10 |
| D3 | 5LiZr2(PO4)3 + 28Li → 11Li3PO4 + 8ZrO2 + 2ZrP2 | 2.10–1.83 |
| D4 | 11LiZr2(PO4)3 + 84Li → 21Li3PO4 + Li2ZrO3 + 6ZrP2 | 1.83–1.73 |
| D5 | 23LiZr2(PO4)3 + 196Li → 41Li3PO4 + 16Li6ZrO7 + 14ZrP2 | 1.73–1.37 |
| D6 | 4LiZr2(PO4)3 + 56Li → 5Li3PO4 + 4Li6ZrO7 + 7Li3P | 1.37–1.10 |
| D7 | LiZr2(PO4)3 + 24Li → 3Li3P + 2Li8ZrO6 | 1.10–1.02 |
| D8 | 7LiZr2(PO4)3 + 197Li → 84Li2O + Zr14P9 + 12Li3P | 1.02–0.95 |
| D9 | 7LiZr2(PO4)3 + 200Li → 84Li2O + 2Zr7P4 + 13Li3P | 0.95–0.0 |
As the reaction with the highest reaction potential occurs, D1 may ensue. However, the potential window of Li3PO4, which is a product of D1, is 0.71 V, and further continuous reactions are expected. Therefore, in terms of the thermodynamic stabilities of the decomposition products of D1–D9, D9 is the reaction wherein all products are stable with respect to the Li metal. However, the reaction potential of Li8ZrO6, which is a product of D7, with respect to the Li metal is only 0.04 V, and it may be kinetically stable, depending on the temperature.
Moreover, it was reported that LZP was reacted with molten Li metal to investigate these computational results experimentally.46 Images of the LZP sintered body before and after the reaction are shown in Fig. 3(a and b). The material is a white pellet prior to the reaction, but when reacting with the molten Li metal, reduction decomposition proceeds and the interior of the pellet becomes black. The X-ray diffraction (XRD) results for the sample after the reaction confirm the presence of the Li8ZrO6 and Li3P phases, reproducing the results of Li et al. (Fig. 3(c)).28 The products of D7 are stable in the presence of Li metal. A thin film of Li8ZrO6 and Li3P is likely formed at the Li/LZP interface of the Li/LZP/LFP all-solid-state battery reported by Li et al.; thus, this battery may exhibit stable cycling due to the side-reaction products.
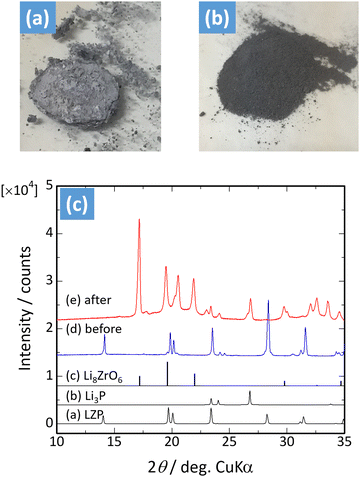 | ||
| Fig. 3 (a) LiZr2(PO4)3 sintered body after reaction with molten Li and (b) after crushing. (c) Powder XRD pattern of LiZr2(PO4)3 before and after reaction with molten Li (reproduced from ref. 46 with the permission of American Chemical Society, copyright 2017). | ||
4. First-principles molecular dynamics simulations of LZP and related materials
The ionic conductivity of stoichiometric LZP is low but improves considerably with aliovalent ion doping, e.g. stoichiometric LZP exhibits a conductivity of 8.06 × 10−7 S cm−1 at room temperature,28 but doping with CaO improves the ionic conductivity to 4.9 × 10−5 S cm−1.41 This improvement may be due to the introduction of interstitial Li sites into the lattice. However, excessive Ca ion doping reduces the ionic conductivity, and the material should be designed while considering trade-off effects. Understanding this complex behaviour of ionic conductivity at an atomic/electronic scale may lead to rational material design. Therefore, we conducted first-principles molecular dynamics (FPMD) simulations to analyse the ion behaviours at finite temperatures sequentially with high accuracies in our previous works.46,49The compositions that were simulated using FPMD were unsubstituted LZP, in addition to Li(1+2x)CaxZr(2−x)(PO4)3 (LCZP) with Ca doped at the Zr site46,49 We created a superstructure and computational model lattice with the composition Li(16+2x)CaxZr(32−x)P48O192. Furthermore, divalent Ca ions replaced tetravalent Zr ions; thus, the Li ions could become excessive and occupy the interstitial sites. The interstitial sites are defined as the 18e sites (Fig. 2), and the Li ions are randomly arranged. FPMD was implemented with a simulation time of >50 ps. The details of the computational conditions were described previously.46,49Fig. 4(a) shows the mean square displacement (MSD) profile of the LCZP material at 1173 K. The Li ions exhibit a diffusion behaviour with the MSD increasing linearly with time, but the MSDs of the constituent ions Ca, P, Zr, and O plateau (≤1 Å2), which corresponds to thermal vibration. Hence, only Li ions contribute to the observed ionic conductivities. The obtained MSD profile was used to calculatethe diffusion coefficient at each temperature, and the migration energy of the Li ions was evaluated using the Arrhenius plot. The Li-ion conductivity at 298 K was also calculated using the Nernst-Einstein equation, which converts the diffusion coefficient into ionic conductivity, and extrapolation to the Arrhenius equation.50Fig. 4(b) shows the Li-ion conductivity with respect to the Ca concentration (x). The activation energy is high at x = 0 in the unsubstituted system and decreases considerably with minimal Ca doping, subsequently becoming constant. The ionic conductivity is improved by approximately two orders of magnitude when a small amount of Ca is doped from x = 0 and gradually decreases at x > 0.13. The same pattern as that obtained via the calculations is observed for the reported changes in the experimental values.28,41 Regarding the ionic conductivity, the calculated values are generally overestimates compared to the experimental values, which may be because aspects such as the GB resistance are not considered in the simulation. Fig. 5(a) shows the population density of the Li ions in the computational grid at 1173 K. The Li ions diffuse linearly along the lines connecting the adjacent 6b (36f) sites, which is consistent with the diffusion pathways proposed in previous studies (Fig. 2(a)).33,45
 | ||
| Fig. 4 Results of FPMD simulations of the Li1+2xCaxZr2−x(PO4)3 material. (a) MSD profiles of constituent ions at 1173 K. (b) Ionic conductivity at room temperature and (c) substitution dependence of activation energy. The solid circles and squares represent the values obtained from the FPMD simulations and the experimental values, respectively (reproduced from ref. 49 with permission of Authors, copyright 2018). | ||
 | ||
| Fig. 5 (a) Population density of Li ions in LiZr2(PO4)3 (yellow isosurface).46 Diffusion pathways linearly connect the Li 6b sites. (b) Left: Site displacement functions around four randomly selected 6b sites in Li1.250Ca0.125Zr1.875(PO4)3. The various colours in the figure represent each individual Li-ion, and the letters on the left indicate the cationic species that occupy the two adjacent octahedral sites. Right: Change over time of the number of Li ions present within 1.77 Å of each 6b site. The number shown on the right is the time-average occupancy of Li ions (reproduced from ref. 49 with permission of Authors, copyright 2018) | ||
We defined the following function Si,j(t) to confirm the ionic conductivity mechanism in more detail:46
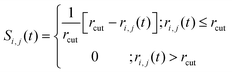 | (1) |
| ri,j(t) = |rj(t) − ri| | (2) |
Furthermore, there are two adjacent Ca/Zr sites at the 6b site (Fig. 2(b)), but when both are occupied by Zr, the rate of simultaneous occupation is low, and Ca frequently occupies one site. The presence of a Ca2+ ion at a Zr4+ site, i.e. a negatively charged defect, attracts mobile Li+ ions; thus, the probability of Li ions at sites adjacent to Ca ions may be selectively increased. The Li-ion trapping effects of Ca ions may cause decreased conductivity with excessive Ca2+ doping, as reported in our previous study.49 This effect is observed for numerous ion-conducting compounds.
5. Grain boundary Li-ion conductivity based on high-throughput force field calculations
LZP-related materials are promising as solid electrolyte materials with high ionic conductivities and electrochemical stabilities, but the effective ionic conductivities are considerably reduced due to the influence of GBs.33 The GBs decrease the ionic conductivities of numerous materials, but improved ionic conductivities have also been observed in several studies.51–56 Therefore, understanding the behaviour of ions at GBs at the atomic level should yield insights into the design of materials with improved ionic conductivities. Numerous material calculations have been performed using ionic conductors with NASICON-type structures, but most of these studies have been focused on bulk conductivity, with very little research conducted regarding GBs.13,46,49,57–63For example, Moriwake et al. evaluated the effect of grain boundaries on electrode material performance for LiCoO2 cathode materials using electron microscopy image analysis and first-principles calculations.63 The lithium insertion/desorption potential decreased by about 0.2 V near the interface. The site-to-site hopping energy of Li ions evaluated by the NEB method is about 0.2 eV in the parallel direction to the grain boundary, while a large change of 0.4 eV is revealed in the perpendicular direction. In battery devices operating at room temperature, a change in the hopping barrier of 0.2 eV leads to a change in the diffusion coefficient of three orders of magnitude. This suggests that an increase in the GB surface, e.g. due to nanoparticulation, has a significant impact on the energy density and charge/discharge rate characteristics of batteries. Several studies have been reported on a quantitative conductivity evaluation of selected GBs in garnet-type Li7La3Zr2O12 materials using classical force-field molecular dynamics.64–66 Yu et al. explain that the diffusion coefficient decreases both parallel and perpendicular to the GB surface, and that changes in the crystal structure in the GB affect the activation energy of ionic conduction, leading to large intergranular conduction changes at room temperature.64 Thus, material simulation evaluations provide important information for GBs, which are directly linked to battery performance. However, due to the complexity of modelling GB structures and limited computational resources, examples of simulation studies are limited thus far. Experimentally determining complicated GB structures is challenging. Furthermore, reproducing a complex grain structure requires the use of large unit cells and increases computational costs. Hopping events at GBs are rare and require extended simulation times when performing MD calculations. Therefore, calculations regarding the GBs of other materials that have been employed to date involved ionic conductivity simulations of the GBs using force fields (FFs) with low computational costs.64,65,67,68 In previous studies, we also utilized FF calculations, in addition to numerous different GB models.69
The calculation of Li-ion diffusion in the LZP GB model employed the BVFF proposed by Adam et al.,70 in addition to a high-throughput FF with the addition of the Stillinger–Weber (SW) type representing the interactions between three bodies.71,72 The screened Coulomb potential ϕCoulAB of a pair with the same charge sign (i.e. cation–cation or anion–anion) was applied to the interaction between the two bodies, along with the Morse potential ϕMorseAB of a pair with different charge signs (i.e. cation–anion). ϕCoulAB may be described as follows using the Coulomb term and error function (erfc), which is a screening term that simulates the electrostatic shielding effect:
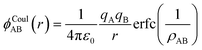 | (3) |
| ϕMorseAB(r) = DAB{exp[−2αAB (r − sAB)] − 2exp[−αAB(r − sAB)]} | (4) |
 | (5) |
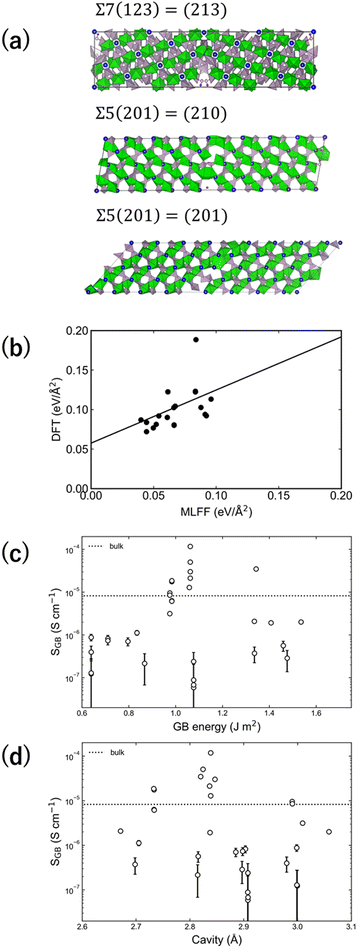 | ||
| Fig. 6 (a) Three representative GB models. (b) Relationship between GB generation energy of each GB model according to first-principles calculations and high-throughput FF calculations. (c) Relationship between GB generation energy and GB Li-ion conductivity based on high-throughput FF calculations. (d) Relationship between cavity size around the 6b site in the GB model and GB Li-ion conductivity (reproduced from ref. 69 with permission of American Chemical Society, copyright 2021). | ||
The FFMD simulations using the NVT ensemble were performed from 773 to 1173 K for 1 ns, with only Li among the constituent particles diffusing in all 32 LZP GB models. The GB formation energy was evaluated for each model, and the GB thickness was set to 1.5 nm to evaluate the Li-ion conductivity of the GB. Fig. 6(c) shows the relationships between the Li-ion conductivities of various GB models with respect to the GB formation energy. Overall, the Li-ion conductivity increases as the GB formation energy increases. This pattern was also observed via GB calculations for garnet-type Li7La3Zr2O12 (LLZ) materials by Siegel et al. and Shiiba et al.64,65 Garnet-type LLZ exhibits lower ionic conductivities in all models than in the bulk model, whereas several GB models of NASICON-type LZP exhibit ionic conductivities higher than that in the bulk model.64,65 This finding suggests that a solid electrolyte with an even higher Li-ion conductivity may be fabricated by designing the GBs.
Fig. 7(a–c) reveal the site potential distributions of individual Li ions at three representative GBs (planes with maximum, minimum, and intermediate GB conductivities) in the direction perpendicular to the interface. The site potential of Li ions is ∼0.35 eV more stable close to the GBs than in the bulk material, indicating a strong trapping effect for Li ions. The potential trapping effect is consistent among the three GB models, although these models exhibit different GB ion conductivities. As the site potential stabilises at approximately 1.5 nm from the GBs, the GB thickness was set to 1.5 nm. Meanwhile, Fig. 7(d) shows the positional dependence of the average concentration of Li ions along the c-axis in each GB model. The Σ7(123) = (213) GB model, which displays the highest Li-ion conductivity, exhibits a flat concentration distribution in the bulk material and at the GBs. However, in the other GB models, large fluctuations in the Li-ion concentrations are observed, potentially due to trapping. Therefore, the hopping frequency should be high in the GB model with a high ionic conductivity (Σ7(123) = (213)).
 | ||
| Fig. 7 Probability density distributions of Li-ion site potentials with respect to fractional coordinates in the c-axis direction obtained via FPMD simulations at 1173 K. (a) Σ7(123) = (213) GB with the highest Li-ion conductivity, (b) Σ5(2−10) = (20−1) GB with the lowest Li-ion conductivity, and (c) Σ5(201) = (210) GB with the smallest cavity. (d) Concentration distributions of Li ions in the c-direction. The Σ7(123) = (213) GB with the highest Li-ion conductivity is shown in red, the [Σ5(2−10) = (20−1)] GB with the lowest Li-ion conductivity in black, and the Σ5(201) = (210) GB with the smallest cavity in blue (reproduced from ref. 69 with permission of American Chemical Society, copyright 2021). | ||
The mechanism of bulk ionic conductivity suggests that the simultaneous presence of two Li ions in the cavity around the 6b site promotes hopping. Such double occupancy of Li ions may be affected by the cavity size. Fig. 6(d) shows the relationship between the cavity size around the 6b site and the Li-ion conductivity. The maximum cavity size in the bulk model is 2.48 Å, which is smaller than the cavities in all GB models. When the cavity size approaches 2.8 Å, in particular, the GB Li-ion conductivity of the GB model increases. Additionally, when the cavity size is smaller or larger than 2.8 Å, the GB Li-ion conductivity generally decreases, suggesting the existence of an optimum cavity size. When the cavity size is <2.8 Å, the double occupancy of Li ions does not occur, and when it is >2.8 Å, the repulsion due to double occupancy may be slow. Guidelines for GB design are required for further quantitative evaluation.
The ionic conductivities related to individual GBs have been evaluated, but for polycrystalline sintered bodies, the ionic conductivities at various GBs should be comprehensively evaluated. A materials informatics approach was used to evaluate the conductivity of the entire GB quantitatively.
Numerous examples of applying materials informatics to the bulk structures of Li-ion conductors have been reported,68,72,75–80 but there are few studies on GBs.81 This gap may be due to the absence of GB-derived datasets and technical difficulties of descriptor building. In this study, the GB formation energies and ionic conductivities of the 32 GB models were used as the objective variables, and the differential RDF and ADF obtained by subtracting the bulk RDF and ADF from the RDF and ADF of the GB model were used as the descriptors. We applied various machine learning regression analysis algorithms to such datasets, with the partial least squares (PLS) regression algorithm after deleting the descriptor using Lasso (Lasso + PLS) exhibiting the lowest root mean square error (RMSE, 0.04 eV Å−2). Even when the objective variable is set as the common logarithm of the GB Li-ion conductivity, the RMSE remains the smallest when using Lasso + PLS regression analysis (RMSE = 0.54 vs. logarithm of Li-ion conductivity/S cm−1). Fig. 8(a and b) show the distributions of the GB energy and logarithm of conductivity. There are interfaces that show conductivities higher than that of bulk LZP, but the conductivities at most of the interfaces are ≤10−5 S cm−1. The Boltzmann distribution was applied to calculate the probability of formation of each GB and evaluate the ionic conductivity, with values of 10−8–10−7 cm−1 obtained, which are much smaller than the bulk conductivity.67Fig. 8(c) shows the change in GB conductivity with respect to the temperature (firing temperature) input to calculate the Boltzmann distribution. A lower (i.e. more stable) GB energy generally results in a higher ionic conductivity; thus, a higher firing temperature results in a lower GB Li-ion conductivity.
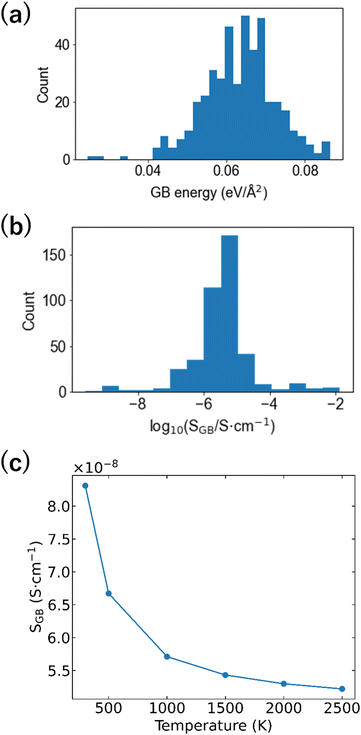 | ||
| Fig. 8 (a) GB formation energy distribution, (b) GB Li-ion conductivity distribution, and (c) firing temperature dependence of GB Li-ion conductivity averaged by applying Boltzmann statistics to the 474 grain interfaces predicted via machine learning regression analysis (Lasso + PLS) (reproduced from ref. 69 with the permission of American Chemical Society, copyright 2021). | ||
Notably, these results are applicable only to coherent GBs. Recently, we revealed that high-throughput FFs are also effective in simulating incoherent GBs.82
6. Composition optimisation using the Bayesian method
Material simulations and informatics may be critical tools in the mechanistic understanding of various physical properties of solid electrolyte materials. However, obtaining direct guidance in exploring novel materials is challenging.Various informatics-aided approaches are proposed for the optimization of functional materials. Various informatics-aided approaches are proposed for the prediction and/or optimization of battery materials.83,84 For example, Joshi et al. predicted the voltage of electrode materials by DFT calculations by machine learning.85 More recently, Louis et al. suggested deep neural network based approach for a prediction of voltage of battery electrode.86 Zhang et al. used unsupervised machine learning approach, clustering of anion framework information, to discover fast Li ion conductors.87 They succeeded to list the new 16 compounds that exhibit fast Li ion conductivity according to DFT-MD calculations. We have also shown the results of high-throughput computational evaluation of ion-conductive materials linked to machine learning analysis.88,89 As well as the discovery of new materials, research is also being conducted to efficiently optimise composition ratios to maximise ionic conductivity in a restricted compositional space. Suzuki et al. used a machine-learning classifier based on the presence or absence in the crystal structure database to discover new ionic conductivity compositions using a recommender that takes synthetic possibilities into account.90 Homma et al. evaluate the optimal composition in the pseudo-ternary Li2SO4–Li3PO4–Li3BO3 system in an efficient experimental step using Bayesian optimisation.91 Therefore, this section introduces our previous research on the search for high-ion-conductivity materials using materials informatics.92 Ionic conductivity may be increased by introducing low-valence ions, such as Ca2+ and Y3+, at the Zr ion sites of LZP and inducing a state of excess Li.33,41,42,49,72 However, only single-element doping has been used in most studies to date, with few examples wherein two elements have been doped simultaneously (i.e. co-doping). We previously synthesised co-doped samples and evaluated the phase stabilities, degrees of sintering, ionic conductivities, etc.92Fig. 9(a and b) present the results of XRD structural analyses when the amounts of Ca2+ and Y3+ dopants are systematically varied. Fig. 9(a) shows the number of impurities, and Fig. 9(b) displays the distribution of the α (NASICON) and β (monoclinic) phases in red and blue, respectively. An impurity phase should be observed with increasing doping. Meanwhile, the α phase is generally stable under Ca2+ doping, whereas the β phase is generally stable under Y3+ doping. The α phase may exhibit a high ionic conductivity; thus, the high-ion-conductivity phase may form in the region with identical substitution amounts of Ca2+ and Y3+ or with more Ca2+. Furthermore, Fig. 9(c) shows the relative density of the sintered body. Ca2+ is effective as a sintering aid, and excessive Ca2+ introduction may improve the relative density, regardless of the Y3+ content.
 | ||
| Fig. 9 (a) α (red) and β (blue) phase distributions, (b) impurity percentage distribution, (c) relative density distribution of the sintered body, and (d) Li-ion conductivity distribution of Li(1+2x+y)Zr(2−xy)CaxYy(PO4)3 at 30 °C (reproduced with from ref. 92 with the permission of Royal Society of Chemistry, copyright 2020). | ||
Fig. 9(d) shows the distribution of the Li-ion conductivity at 30 °C. The ionic conductivity is given by the sum of the intra-particle volume resistance (i.e. bulk) and interfacial resistance between particles (i.e. GBs). Separating the bulk and GB resistances in all samples in the complex impedance plot was challenging in this study; thus, their sum was used to evaluate the ionic conductivity. As shown in the figure, the ionic conductivity is high when the amounts of Ca and Y dopants with respect to Zr are ∼0.13 (molar ratio). The optimum ionic conductivity is improved by a factor of approximately five compared with the optimum value obtained via single-element doping; thus, co-doping is effective. Note that the obtained Li-ion conductivity at 303 K is lower than the previously reported values. For example, the reported Li-ion conductivity of Li1.2Ca0.1Zr1.9(PO4)331,41 is approximately 35 times higher than that of the corresponding composition in this study. This discrepancy is due to the inclusion of the GB resistance in this study (Fig. 9(d)). Indeed, computationally obtained bulk ionic conductivity (∼10−6 S cm−1 at 298 K, Fig. 4(b)) of stoichiometric LZP is approximately 100 times higher than GB ionic conductivity (10−8 S cm−1 at 298 K, Fig. 8(c)). In addition, dopant segregation at GB may increase GB resistance for doped LZP compounds. EDS observations indicated Y2O3 segregation at GB of Y2O3-doped LZP at high dopant concentration region.42 Another example is that the difference between the bulk Li-ion conductivity synthesized by sol–gel reaction is ∼100 times as high as the total conductivity according to the literature.93 As the GB conductivity is strongly dependent on the process of synthesis, various preparation methods have been applied to reduce the GB and/or interface resistance for LZP and related compounds38,94 and the other NASICON-type oxides.95–97
The relationships among the composition, crystal structure, presence of the impurity phase, relative density of the sintered body, and ionic conductivity are quite complex. We infer that Low ionic conductivity at low composition y region owes to large GB resistance because of small relative density. Maybe CaO plays an important role as sintering aid. However, increase of CaO reduces the conductivity owning to the trapping effect as shown in Fig. 4. The large drop of ionic conductivity at high composition x region is the stabilization of β phases. Indeed, the compositional dependence of conductivity at x > 0.2 (Fig. 9(d)) shows strong correlation with that of weight ratio of α-phase (Fig. 9(a)). However, above interpretation is qualitative, and thus intuitive estimation of ionic conductivity and its optimisation are technically challenging. We reported whether a Bayesian optimisation (BO) algorithm, which is a materials informatics method, could efficiently determine the optimum composition with the highest ionic conductivity for such a material composition.91 Although the optimum composition was already known due to exhaustive measurements, all measured ionic conductivity data were intentionally hidden from the computer (Bayesian optimiser), and the data were analysed stepwise, with sampling proceeding as suggested by the Bayesian optimisation algorithm. For sampling in the first step, samples with two compositions were randomly selected. This procedure (loop) was repeated 1000 times to average the discovery rate.
Fig. 10(a and b) respectively present plots of the highest ionic conductivity obtained and discovery probability of the optimum composition in terms of Li-ion conductivity at 30 °C as functions of the number of steps. The results of random sampling (average over 1000 times) are also shown for comparison. As depicted in Fig. 10(a), the maximum ionic conductivity of the sampled material increases with the number of steps, but the random search is superior in the very early stages. However, after seven steps, the Bayesian optimisation-based search is superior in terms of maximum ionic conductivity (Fig. 10(a)). The discovery rate of the random search is a proportional function (i.e. searching half the data results in a discovery rate of 50%), as shown in Fig. 10(a). Meanwhile, for the Bayesian optimisation-based search, the discovery rate is constant at a few percentage points for the first 13 steps but increases sharply from the 14th step onwards, with a discovery rate of 100% at the 16th step. Therefore, Bayesian optimisation based on the expected improvement (EI) strategy applied in this study involves an ‘exploration’ in the early stages, where sampling composition is selected deliberately to obtain a broad perspective of the entire composition. Subsequently, the optimisation is based on ‘exploitation’, prioritising the sections with the highest predicted ionic conductivities. Hence, excellent materials may be identified in the search space of all 47 compositions in 16 steps; thus, the search efficiency is improved by a factor of 47/16, or approximately three. Therefore, BO may be used to obtain the optimum composition in a few steps without obtaining unnecessary data, even in materials with expanded search spaces due to co-doping. The objective in this example was to verify quantitatively the efficiency of BO based on a comprehensively sampled database. Therefore, the optimisation was conducted on a relatively simple dataset of only ∼50 cases. Increasing the search space may generally increase the efficiency. Moreover, the optimal material properties of ∼170 samples may be identified with a high efficiency of ∼20 times that of a random search (90% correct answer rate) by conducting composition optimisation based on the calculated data and adding descriptors other than the composition.58
 | ||
| Fig. 10 Bayesian optimisation of Li-ion conductivity of Li(1+x+2y)Zr(2−x−y)YxCay(PO4)3 at 30 °C. The results of random sampling are also shown for comparison. Changes in the (a) highest ionic conductivity and (b) probability of discovering the material with the highest ionic conductivity as functions of the number of observations (steps). We conducted 1000 trials (reproduced with from ref. 92 with the permission of Royal Society of Chemistry, copyright 2020). | ||
In addition, there are advanced uses linked to the BO algorithm, e.g. multi-objective optimisation may be used to optimise multiple properties, such as ionic conductivity and sintering density (mechanical characteristics of the material). In practice, there is often a trade-off (improving one of the physical properties results in a deterioration in the other); thus, multi-objective optimisation involves the evaluation of a list of candidate materials denoted Pareto-optimal solutions. The materials that constitute the Pareto-optimal solutions are those that cannot replace multiple performances of interest simultaneously. BO may also be used to efficiently search for the entire Pareto-optimal solution. Given the complex condition settings, the efficiency of multi-objective optimisation hardly improved with ∼50 samples. However, for a system wherein the composition was virtually expanded to 225 combinations, we succeeded in obtaining the combination of Pareto-optimal solutions with ≤100 samples, as reported in ref. 92 (search efficiency: ∼2.5 times that of a random search).
It is worthy to note that present optimization only considers the compositional combination of Ca2+ and Y3+ doping. Both dopant ions replace Zr ions with formation of interstitial Li ions. Other possible compositional candidates, which show improved ionic conductivity, are replacement of P5+ ions by tetravalent cations, such as Si4+, and Ge4+. Indeed, Na(1+x)Zr2SixP(3− x)O12, where P ions are partially replaced by Si ions, is known to one of the highest Na ion conductors.12 Also, control of sintering degree and stabilization of α-phase, i.e. process optimization38,94–97 would be effective to improve ionic conductivity as well as composition optimization.
7. Conclusions
In this study, we focused on a NASICON-type LZP solid electrolyte, which was previously applied in an all-solid-state Li metal battery. The reaction stability toward Li metal was evaluated by performing comprehensive material calculations using the crystal structure database, with the LZP solid electrolyte becoming thermodynamically unstable. However, the calculated and experimental results confirmed that the formation of the Li3P and Li8ZrO6 phases, which were generated at the interface of the Li metal by further decomposition reactions with Li, was suppressed. Bulk ionic conductivity evaluations based on MD showed that the high ionic conductivity observed in the NASICON-type material was due to the repulsion of two Li ions, and we analysed the effectiveness of doping strategies that enhanced this repulsion. In addition, we quantitatively evaluated the mechanism of Li-ion conductivity at the GBs using MD, where we predicted that a conductivity exceeding that of the bulk structure could be observed, depending on the GB model. We evaluated the ionic conductivities of various GB models using machine learning regression analysis and performed a total GB conductivity evaluation via statistical mechanics, with performance significantly lower than that of the bulk material. Therefore, various physical properties and performance aspects that are critical in solid electrolytes may be evaluated via material simulation. Furthermore, facile access to atomic-level data led to the elucidation of the composition and structural factors that guide material design. However, reducing the data to just the specific composition and process control parameters to maximise material functions is challenging. To resolve these issues, we introduced an efficient search method using materials informatics. A Ca/Y co-doped LZP material was synthesised, and the total ionic conductivity of the bulk and grain boundaries was evaluated. The ionic conductivity distribution exhibited complex changes with respect to the composition because of complex changes in phase transition and sinterability, but the search cost was reduced by ∼1/3 using BO. This NASICON-type LZP material should be applied in all-solid-state Li metal batteries to enable more complex composition and process control.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computations reported in this paper were performed at the Supercomputer Center at the Institute for Solid State Physics at the University of Tokyo, Japan. English language editing was performed by Editage (http://www.editage.com). The figures illustrating the crystal structures were drawn using VESTA software.98 This work was partially supported by a Grant-in-Aid for Scientific Research (grant numbers 19H05815, 19K15657, 20H02436, 20H05290, 21H01625, 21J14422, 21H03498, and 21K14715) from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT), Japan, the Elements Strategy Initiative to Form Core Research Center of MEXT (grant number JPMXP0112101003), Materials Research by Information Integration Initiative of the Support Program for Starting Up Innovation Hub of the Japan Science and Technology Agency (JST), Program for Promoting Research on the Supercomputer Fugaku (Fugaku Battery & Fuel Cell Project) of MEXT (grant number JPMXP1020200301), and CREST of JST (grant number JPMJCR21O6).Notes and references
- K. Takada, Acta Mater., 2013, 61, 759–770 CrossRef CAS
.
- Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Chem. Rev., 2021, 121, 1623–1669 CrossRef CAS PubMed
.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682–686 CrossRef CAS PubMed
.
- Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama, A. Mitsui, M. Yonemura, H. Iba and R. Kanno, Nat. Energy, 2016, 1, 16030 CrossRef CAS
.
- M. Kotobuki, H. Munakata, K. Kanamura, Y. Sato and T. Yoshida, J. Electrochem. Soc., 2010, 157, A1076 CrossRef CAS
.
- C. Wang, K. Fu, S. P. Kammampata, D. W. McOwen, A. J. Samson, L. Zhang, G. T. Hitz, A. M. Nolan, E. D. Wachsman, Y. Mo, V. Thangadurai and L. Hu, Chem. Rev., 2020, 120, 4257–4300 CrossRef CAS PubMed
.
- S.-H. Kim, J.-H. Kim, S.-J. Cho and S.-Y. Lee, Adv. Energy Mater., 2019, 9, 1901841 CrossRef CAS
.
- Y. Gambe, Y. Sun and I. Honma, Sci. Rep., 2015, 5, 8869 CrossRef CAS PubMed
.
- Y. Inaguma, C. Liquan, M. Itoh, T. Nakamura, T. Uchida, H. Ikuta and M. Wakihara, Solid State Commun., 1993, 86, 689–693 CrossRef CAS
.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS
.
- Y. Zhu and Y. Mo, Angew. Chem., Int. Ed., 2020, 59, 17472–17476 CrossRef CAS PubMed
.
- J. B. B. Goodenough, H.-P. Y. P. Hong and J. A. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS
.
- B. Lang, B. Ziebarth and C. Elsässer, Chem. Mater., 2015, 27, 5040–5048 CrossRef CAS
.
- M. Nakayama, T. Usui, Y. Uchimoto, M. Wakihara and M. Yamamoto, J. Phys. Chem. B, 2005, 109, 4135–4143 CrossRef CAS PubMed
.
- R. Murugan, V. Thangadurai and W. Weppner, Angew. Chem., Int. Ed., 2007, 46, 7778–7781 CrossRef CAS PubMed
.
- W. D. Richards, L. J. Miara, Y. Wang, J. C. Kim and G. Ceder, Chem. Mater., 2015, 28, 266–273 CrossRef
.
- S. Rajendran, N. K. Thangavel, K. Mahankali and L. M. R. Arava, ACS Appl. Energy Mater., 2020, 3, 6775–6784 CrossRef CAS
.
- R. H. Brugge, A. K. O. Hekselman, A. Cavallaro, F. M. Pesci, R. J. Chater, J. A. Kilner and A. Aguadero, Chem. Mater., 2018, 30, 3704–3713 CrossRef CAS
.
- J. B. Goodenough, H. Y.-P. Y. P. Hong and J. A. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS
.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, J. Electrochem. Soc., 1990, 137, 1023 CrossRef CAS
.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, J. Electrochem. Soc., 1989, 136, 590 CrossRef CAS
.
- X. Xu, Z. Wen, X. Wu, X. Yang and Z. Gu, J. Am. Ceram. Soc., 2007, 90, 2802–2806 CrossRef CAS
.
- D. Safanama and S. Adams, J. Power Sources, 2017, 340, 294–301 CrossRef CAS
.
- S. Patoux and C. Masquelier, Chem. Mater., 2002, 14, 5057–5068 CrossRef CAS
.
- C. Delmas and A. Nadiri, Mater. Res. Bull., 1988, 23, 65–72 CrossRef CAS
.
- H. Aono, E. Sugimoto, Y. Sadaoka, N. Imanaka and G. Adachi, Solid State Ionics, 1990, 40–41, 38–42 CrossRef CAS
.
- S. Kumar and P. Balaya, Solid State Ionics, 2016, 296, 1–6 CrossRef CAS
.
- Y. Li, W. Zhou, X. Chen, X. Lü, Z. Cui, S. Xin, L. Xue, Q. Jia and J. B. B. Goodenough, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 13313–13317 CrossRef CAS PubMed
.
- S. Smith, T. Thompson, J. Sakamoto, J. L. Allen, D. R. Baker and J. Wolfenstine, Solid State Ionics, 2017, 300, 38–45 CrossRef CAS
.
- E. R. Losilla, M. A. G. Aranda, M. Martínez-Lara and S. Bruque, Chem. Mater., 1997, 9, 1678–1685 CrossRef CAS
.
- H. Xie, J. B. Goodenough and Y. Li, J. Power Sources, 2011, 196, 7760–7762 CrossRef CAS
.
- A. Cassel, B. Fleutot, M. Courty, V. Viallet and M. Morcrette, Solid State Ionics, 2017, 309, 63–70 CrossRef CAS
.
- Y. Li, M. Liu, K. Liu and C.-A. Wang, J. Power Sources, 2013, 240, 50–53 CrossRef CAS
.
- Y. Zhang, K. Chen, Y. Shen, Y. Lin and C.-W. Nan, Ceram. Int., 2017, 43, S598–S602 CrossRef CAS
.
- V. I. Pet’kov, M. V. Sukhanov, A. S. Shipilov, V. S. Kurazhkovskaya, E. Y. Borovikova, I. Y. Pinus and A. B. Yaroslavtsev, Inorg. Mater., 2014, 50, 263–272 CrossRef
.
- D. Safanama and S. Adams, J. Power Sources, 2017, 340, 294–301 CrossRef CAS
.
- X. Xu, Z. Wen, X. Wu, X. Yang and Z. Gu, J. Am. Ceram. Soc., 2007, 90, 2802–2806 CrossRef CAS
.
- H. Park, E. G. Lee, S.-Y. Kim, S. J. Seong, J. Y. Suh, M. Wu, Y. Kang, S.-Y. Choi, Y. Kim and S. Choi, ACS Appl. Energy Mater., 2021, 4, 13974–13982 CrossRef CAS
.
- Q. Li, C. Xu, B. Huang and X. Yin, Materials, 2020, 13, 1719 CrossRef CAS PubMed
.
- A. Rossbach, F. Tietz and S. Grieshammer, J. Power Sources, 2018, 391, 1–9 CrossRef CAS
.
- H. Xie, Y. Li and J. B. Goodenough, RSC Adv., 2011, 1, 1728 RSC
.
- H. Xu, S. Wang, H. Wilson, F. Zhao and A. Manthiram, Chem. Mater., 2017, 29, 7206–7212 CrossRef CAS
.
- D. Petit, P. Colomban, G. Collin and J. P. Boilot, Mater. Res. Bull., 1986, 21, 365–371 CrossRef CAS
.
- M. Catti and S. Stramare, Solid State Ionics, 2000, 136–137, 489–494 CrossRef CAS
.
- M. Catti, A. Comotti and S. Di Blas, Chem. Mater., 2003, 15, 1628–1632 CrossRef CAS
.
- Y. Noda, K. Nakano, H. Takeda, M. Kotobuki, L. Lu and M. Nakayama, Chem. Mater., 2017, 29, 8983–8991 CrossRef CAS
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 11002 CrossRef
.
- Y. Zhu, X. He and Y. Mo, ACS Appl. Mater. Interfaces, 2015, 7, 23685–23693 CrossRef CAS PubMed
.
- Y. Noda, K. Nakano, M. Otake, R. Kobayashi, M. Kotobuki, L. Lu and M. Nakayama, APL Mater., 2018, 6, 060702 CrossRef
.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef CAS
.
- T. Nakagawa, A. Nakamura, I. Sakaguchi, N. Shibata, K. P. D. Lagerlöf, T. Yamamoto, H. Haneda and Y. Ikuhara, J. Ceram. Soc. Jpn., 2006, 114, 1013–1017 CrossRef CAS
.
- N. R. Williams, M. Molinari, S. C. Parker and M. T. Storr, J. Nucl. Mater., 2015, 458, 45–55 CrossRef CAS
.
- R. A. De Souza, M. J. Pietrowski, U. Anselmi-Tamburini, S. Kim, Z. A. Munir and M. Martin, Phys. Chem. Chem. Phys., 2008, 10, 2067–2072 RSC
.
- L. Sun, D. Marrocchelli and B. Yildiz, Nat. Commun., 2015, 6, 6294 CrossRef CAS PubMed
.
- V. Metlenko, A. H. H. Ramadan, F. Gunkel, H. Du, H. Schraknepper, S. Hoffmann-Eifert, R. Dittmann, R. Waser and R. A. De Souza, Nanoscale, 2014, 6, 12864–12876 RSC
.
- K. McKenna and A. Shluger, Appl. Phys. Lett., 2009, 95, 222111 CrossRef
.
- K. Nakano, Y. Noda, N. Tanibata, M. Nakayama, K. Kajihara and K. Kanamura, RSC Adv., 2019, 9, 12590–12595 RSC
.
- K. Nakano, Y. Noda, N. Tanibata, H. Takeda, M. Nakayama, R. Kobayashi and I. Takeuchi, APL Mater., 2020, 8, 41112 CrossRef CAS
.
- X. Zhao, Z. Zhang, X. Zhang, B. Tang, Z. Xie and Z. Zhou, J. Mater. Chem. A, 2018, 6, 2625–2631 RSC
.
- Z. Zhang, Z. Zou, K. Kaup, R. Xiao, S. Shi, M. Avdeev, Y. Hu, D. Wang, B. He, H. Li, X. Huang, L. F. Nazar and L. Chen, Adv. Energy Mater., 2019, 9, 1902373 CrossRef CAS
.
- Z. Deng, G. S. Gautam, S. K. Kolli, J.-N. Chotard, A. K. Cheetham, C. Masquelier and P. Canepa, Chem. Mater., 2020, 32, 7908–7920 CrossRef CAS
.
- X. Lu, S. Wang, R. Xiao, S. Shi, H. Li and L. Chen, Nano Energy, 2017, 41, 626–633 CrossRef CAS
.
- H. Moriwake, A. Kuwabara, C. A. J. Fisher, R. Huang, T. Hitosugi, Y. H. Ikuhara, H. Oki and Y. Ikuhara, Adv. Mater., 2013, 25, 618–622 CrossRef CAS PubMed
.
- S. Yu and D. J. Siegel, Chem. Mater., 2017, 29, 9639–9647 CrossRef CAS
.
- H. Shiiba, N. Zettsu, M. Yamashita, H. Onodera, R. Jalem, M. Nakayama and K. Teshima, J. Phys. Chem. C, 2018, 122, 21755–21762 CrossRef CAS
.
- N. Zettsu, H. Shiiba, H. Onodera, K. Nemoto, T. Kimijima, K. Yubuta, M. Nakayama and K. Teshima, Sci. Rep., 2018, 8, 1–11 CAS
.
- J. A. Dawson, P. Canepa, T. Famprikis, C. Masquelier and M. S. Islam, J. Am. Chem. Soc., 2018, 140, 362–368 CrossRef CAS PubMed
.
- J. A. Dawson, P. Canepa, M. J. Clarke, T. Famprikis, D. Ghosh and M. S. Islam, Chem. Mater., 2019, 31, 5296–5304 CrossRef CAS
.
- K. Nakano, N. Tanibata, H. Takeda, R. Kobayashi, M. Nakayama and N. Watanabe, J. Phys. Chem. C, 2021, 125, 23604–23612 CrossRef CAS
.
- S. Adams and R. P. Rao, Phys. Status Solidi A, 2011, 208, 1746–1753 CrossRef CAS
.
- R. Kobayashi, J. Open Source Softw., 2021, 6, 2768 CrossRef
.
- R. Kobayashi, Y. Miyaji, K. Nakano and M. Nakayama, APL Mater, 2020, 8, 081111 CrossRef CAS
.
- K. Ishida, N. Tanibata, H. Takeda, M. Nakayama, T. Teranishi and N. Watanabe, Phys. Stat. Sol. B, 2021, 2100526, DOI:10.1002/pssb.202100526
.
- R. Iwasaki, K. Ishida, R. Yasuda, K. Nakano, N. Tanibata, H. Takeda, M. Nakayama and N. Watanabe, Phys. Status Solidi B, 2022, 2100546, DOI:10.1002/pssb.202100546
.
- M. Nakayama, K. Kanamori, K. Nakano, R. Jalem, I. Takeuchi and H. Yamasaki, Chem. Rec., 2019, 19, 771–778 CrossRef CAS
.
- S. K. Kauwe, T. D. Rhone and T. D. Sparks, Crystals, 2019, 9, 1–9 CrossRef
.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef
.
- A. Iglesias, A. Gálvez, P. Suárez, M. Shinya, N. Yoshida, C. Otero, C. Manchado and V. Gomez-Jauregui, Symmetry, 2018, 10, 58 CrossRef
.
- L. Breiman, Mach. Learn., 2001, 45, 5–32 CrossRef
.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K. A. N. Duerloo, Y. Cui and E. J. Reed, Energy Environ. Sci., 2017, 10, 306–320 RSC
.
- C. Hu, Y. Zuo, C. Chen, S. Ping Ong and J. Luo, Mater. Today, 2020, 38, 49–57 CrossRef CAS
.
- R. Kobayashi, K. Nakano and M. Nakayama, Acta Mater., 2022, 226, 117596 CrossRef CAS
.
- C. Ling, npj Comput. Mater., 2022, 8, 33 CrossRef
.
- C. Chen, Y. Zuo, W. Ye, X. Li, Z. Deng and S. P. Ong, Adv. Energy Mater., 2020, 10, 1903242 CrossRef CAS
.
- R. P. Joshi, J. Eickholt, L. Li, M. Fornari, V. Barone and J. E. Peralta, ACS Appl. Mater. Interfaces, 2019, 11, 18494–18503 CrossRef CAS PubMed
.
- S.-Y. Louis, E. M. D. Siriwardane, R. P. Joshi, S. S. Omee, N. Kumar and J. Hu, ACS Appl. Mater. Interfaces, 2022, 14, 26587–26594 CrossRef CAS PubMed
.
- Y. Zhang, X. He, Z. Chen, Q. Bai, A. M. Nolan, C. A. Roberts, D. Banerjee, T. Matsunaga, Y. Mo and C. Ling, Nat. Commun., 2019, 10, 5260 CrossRef PubMed
.
- M. Nakayama, J. Ceram. Soc. Jpn., 2021, 129, 286–291 CrossRef CAS
.
- M. Nakayama, K. Kanamori, K. Nakano, R. Jalem, I. Takeuchi and H. Yamasaki, Chem. Rec., 2019, 19, 771–778 CrossRef CAS
.
- K. Suzuki, K. Ohura, A. Seko, Y. Iwamizu, G. Zhao, M. Hirayama, I. Tanaka and R. Kanno, J. Mater. Chem. A, 2020, 8, 11582–11588 RSC
.
- K. Homma, Y. Liu, M. Sumita, R. Tamura, N. Fushimi, J. Iwata, K. Tsuda and C. Kaneta, J. Phys. Chem. C, 2020, 124, 12865–12870 CrossRef CAS
.
- M. Harada, H. Takeda, S. Suzuki, K. Nakano, N. Tanibata, M. Nakayama, M. Karasuyama and I. Takeuchi, J. Mater. Chem. A, 2020, 8, 15103–15109 RSC
.
- H. El-Shinawi, C. Greaves and J. Janek, RSC Adv., 2015, 5, 17054–17059 RSC
.
- Y. Lai, Z. Sun, L. Jiang, X. Hao, M. Jia, L. Wang and F. Liu, Ceram. Int., 2019, 45, 11068–11072 CrossRef CAS
.
- G. Yang, Y. Zhai, J. Yao, S. Song, W. Tang, Z. Wen, L. Lu and N. Hu, Chem. Commun., 2021, 57, 4023–4026 RSC
.
- S. Yde-Andersen, J. S. Lundsgaard, L. Møller and J. Engell, Solid State Ionics, 1984, 14, 73–79 CrossRef CAS
.
- K. Noi, Y. Nagata, T. Hakari, K. Suzuki, S. Yubuchi, Y. Ito, A. Sakuda, A. Hayashi and M. Tatsumisago, ACS Appl. Mater. Interfaces, 2018, 10, 19605–19614 CrossRef CAS PubMed
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2022 |
