Reactivities of allenic and olefinic Michael acceptors towards phosphines

Abstract

The kinetics of the reactions of tributylphosphine with allenic and olefinic Michael acceptors in dichloromethane at 20 °C was followed by photometric and NMR spectroscopic methods. Combination with DFT-calculated methyl anion affinities revealed the relevance of retroaddition barriers in phosphine-catalysed reactions when mixtures of allenic and olefinic substrates are used.

---

In 1995, the Lu group discovered (3+2)-cycloadditions, in which Bu₃P or Ph₃P are used as Lewis-basic catalysts to furnish cyclopentenes from mixtures of alkyl allenoates and electron-deficient alkenes (Fig. 1).¹ In recent years, the versatility of Lu cycloadditions was expanded by the development of several catalytic asymmetric versions, which were also applied to the synthesis of core units of natural products.² Computational and kinetic studies showed that phosphonium–dienolate formation can be considered to be the rate-determining step in the catalytic cycle.^2a,3

Fig. 1 Mechanism of the phosphine-catalysed Lu cycloaddition (E = ester group, Acc = electron-accepting group).

The rates of adduct formations, in which only one new bond is formed between an electrophile and a nucleophile, can be discussed in a broader context and beyond the limitations of structurally analogous compound classes when the Mayr–Patz eqn (1) is used.^4–7 Thus, the nucleophilic reactivity of R₃P catalysts in a certain solvent is described by the two parameters N (nucleophilicity) and s_N (susceptibility) in eqn (1).⁸ The reactivities of Michael acceptors are characterised by electrophilicity parameters E. It has been shown that once E, N and s_N of reaction partners in polar reactions are known the second-order rate constant k₂ for adduct formation can be predicted with an accuracy within two orders of magnitude.^5,6

log k₂(20 °C) = s_N(N + E) (1)

Many of the R₃P-catalysed reactions are performed with mixtures of two competing electrophiles, which are often combined in a way that one of the electrophiles carries an sp-and the other one an sp²-hybridised carbon as the electrophilic centre.^1,2,9 In this work, we set out to determine the kinetics of the adduct formation of R₃P with electron-deficient olefins and a set of alkyl and phenyl allenoates to gain a deeper understanding of the factors that influence the initial step of the related R₃P-catalysed organic reactions.^1,2,9

First, we characterised the vinyl phosphonium triflates 3 obtained by Ph₃P reactions with 1a, 1d, 1f, and 1i (Fig. 2A) by spectroscopic methods (ESI†). It is reasonable to assume that the entire set of R₃P + 1a–1j reactions that we followed kinetically also yield vinyl phosphonium triflates 3. The kinetics of the carbon–phosphorus bond-formations between R₃P and 1a–1j was followed by spectroscopic methods.

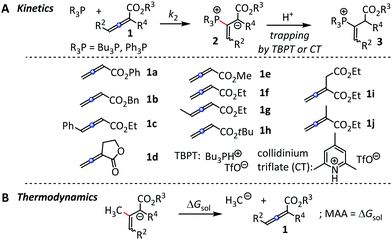Fig. 2 (A) R₃P additions to 1 and (B) reference reaction for the determination of methyl anion affinities (MAA) by quantum-chemical methods.

Reactions of Bu₃P with alkyl allenoates 1a–1i in CH₂Cl₂ at 20 °C were monitored photometrically by following the decrease of the UV absorptions of 1 at or close to their absorption maximum (λ_max = 242–262 nm). The Bu₃P addition reactions to 1 give rise to polymerisation, which can be avoided by trapping the zwitterionic adducts 2 with tributylphosphonium triflate (TBPT) as the proton source ([TBPT]/[1]₀ = 2–3). TBPT is a weak Brønsted acid in CH₂Cl₂ and does not activate the electrophiles 1 by hydrogen-bonding to an oxygen of the ester group (as shown for the combination of 1f + TBPT, ESI,† Fig. S7). To simplify the kinetic evaluation of the second-order reactions, we used the Bu₃P in at least 10-fold excess relative to the initial electrophile concentrations [1]₀. Hence, the decrease of absorptions A of 1 could be fitted by the mono-exponential decay function A = A₀ exp(−k_obst) + C to determine the (pseudo) first-order rate constants k_obs (s⁻¹).

For each Bu₃P + 1 pair, k_obs was determined at four or five different Bu₃P concentrations, which made it possible to calculate the second-order rate constants k₂ (M⁻¹ s⁻¹) from the slope of the linear correlation of k_obs with [Bu₃P]₀. Fig. 3 visualises this procedure for the Bu₃P addition to 1f.

Fig. 3 (A) Kinetics of the reaction of Bu₃P with 1f: mono-exponential decay of the absorbance A in the reaction of Bu₃P (12.3 mM) with 1f (0.121 mM); (B) linear correlation of observed rate constants k_obs with [Bu₃P]₀.

Rate constants of the reactions of Ph₃P with 1a–1j were determined by ¹H NMR spectroscopy using mesitylene as an internal integration standard and collidinium triflate (CT) as a proton source ([CT]/[1]₀ = 2). Generally, Ph₃P additions to 1 are endergonic with retroadditions being faster than the addition reactions. Trapping of the zwitterionic intermediates 2 by CT is thus necessary to observe the kinetics of the addition (forward) reaction. By obeying the conditions for (pseudo)first-order kinetics, that is [Ph₃P]₀/[1]₀ > 9, the time-dependent decrease of [1] could be fitted by the mono-exponential decay function to yield the rate constants k_obs. NMR experiments at four different [Ph₃P]₀ made it possible to determine the second-order rate constants k₂ for the Ph₃P additions to the electrophiles 1a–1j from the slope of the linear correlation of k_obs with [Ph₃P]₀. Rate constants (k₂) for the reactions of Bu₃P with 1j were determined analogously. Data of the individual kinetic measurements for the nucleophilic attack of Bu₃P and Ph₃P at the allenoates 1 are given in the ESI.† The experimentally determined second-order rate constants k₂ are compiled in Table 1.

Table 1 Second-order rate constants (k₂, in M⁻¹ s⁻¹) for the additions of Bu₃P and Ph₃P to phenyl or alkyl allenoates 1 in dichloromethane at 20 °C

Electrophiles 1	k 2(Bu3P)^a	k 2(Ph3P)^b	MAA^c	PA^d
a Photometry, CH2Cl2, 20 °C. b ^1H NMR spectroscopy, CD2Cl2, 20 °C. c MAA as defined in Fig. 2B [in kJ mol^−1 at SMD(DMSO)/B3LYP/6-311++G(3df,2pd)//B3LYP/6-31G(d,p) level of theory, with Truhlar quasi-harmonic treatment]. d Phosphine affinities, PA, as defined in ESI, Table S42 [in kJ mol^−1 at PCM(DCM,ua0)/B3LYP-D3/6-31+G(d,p) level of theory, with Truhlar quasi-harmonic treatment]. e MAA values from ref. 10.
1a	5.52	1.19 × 10^−1	182.5^e	−15.0
1b	1.16	1.70 × 10^−2	163.1^e	−22.6
1c	1.10	1.90 × 10^−2	165.5	−23.7
1d	9.55 × 10^−1	2.33 × 10^−2	171.2	−15.9
1e	8.40 × 10^−1	1.10 × 10^−2	167.6^e	−26.5
1f	6.35 × 10^−1	7.67 × 10^−3	163.4^e	−29.8
1g	5.00 × 10^−1	8.05 × 10^−3	152.7	−29.5
1h	2.47 × 10^−1	2.39 × 10^−3	153.9	−33.3
1i	2.01 × 10^−1	4.59 × 10^−3	142.5	−26.0
1j	1.96 × 10^−2^b	3.49 × 10^−4	133.6	−38.3

---

The Bu₃P-based reactivity scale (log k₂) for 1a–1j is depicted in Fig. 4A. The phenyl ester 1a is the strongest electrophile of the studied allenoates without further substituents at the cumulated π-system and reacts about 5 to 9 times faster with Bu₃P than the analogous benzyl (1b), methyl (1e), or ethyl esters (1f).¹¹ Replacement of the ethyl by a t-butyl group (1f→1h) attenuates reactivity by a factor of 3. An additional methyl group (1g) at the 4-position of the alkyl allenoate has almost no influence on the reactivity of the electrophilic π-system, which remains at the level of the γ-unsubstituted 1f. Extending the π-system by a terminal phenyl group enhances the reactivity of 1c only slightly if compared to that of 1f, probably because the phenylvinyl moiety in 1c is perpendicular to the reactive π-system. In contrast, substituents in 2-position of 1 have a greater effect, and Bu₃P reacts slower by a factor of 32 with 1j than with the parent 1f. This reactivity gap can be reduced by attaching an electron-accepting group to the C-2 substituent. Thus, 1i reacts 10-fold faster with Bu₃P than 1j and is only 3 times less electrophilic (towards Bu₃P) than 1f.

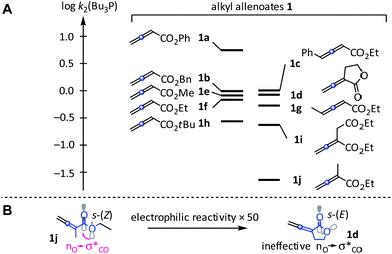Fig. 4 (A) Relative reactivities of 1a–1j in reactions with Bu₃P (in CH₂Cl₂, 20 °C). (B) Different stereoelectronic effects in 1d and the open-chain analogue 1j.

Consistent with previous work on the relative reactivity of open chain esters and lactones,¹² α-allenic γ-butyrolactone 1d is a significantly more reactive electrophile than 1j. The increase in electrophilic reactivity is explained by the different conformations of the CO–OR bonds, which is preferably in the s-(Z) conformation in 1j but fixed in the unfavourable s-(E) conformation in 1d (Fig. 4B).^12,13 Ineffective n_O→σ*_CO interactions enhance the electron-deficiency of the reacting π-system, which enables the versatile use of allenic lactones in organic synthesis.¹⁴

Reactivity of 1 towards Bu₃P is transferrable to other R₃P as shown by the linear correlation (r² = 0.9636, n = 10) with a slope (1.02) close to unity for the Ph₃P vs. Bu₃P comparison (Fig. 5).

Fig. 5 Linear relation of log k₂(Bu₃P) and log k₂(Ph₃P) for reactions with 1.

To gain a better understanding of R₃P-catalysed Lu reactions it is crucial to compare the R₃P reactivities of 1 with those of competing electrophiles, which are typically olefinic Michael acceptors. It was previously shown that MAAs of olefinic Michael acceptors correlate linearly with their Mayr E parameters.¹⁵ MAA values have also been applied to rationalise R₃P-catalysed (3+2) annulations of 1a, 1b, 1e, and 1f with 2-aminoacrylates.¹⁰ The data in Table 1 now show that the DFT-calculated MAA values for 1 (Table 1) are linearly related with their electrophilic reactivities towards the investigated R₃P nucleophiles, that is, Bu₃P and Ph₃P (ESI,† Fig. S1 and S2). A linear correlation of similar quality was obtained when log k₂ for 1 + Ph₃P reactions were plotted against phosphine affinities, PA, which are defined analogously to MAA but use Ph₃P instead of the methyl anion as the Lewis base (Fig. S3, ESI†).

The nucleophilic reactivity of Bu₃P has previously been characterised by N = 15.49 (s_N = 0.69) on the basis of the kinetics of its additions to benzhydrylium ions (E > −10.04).¹⁶ To avoid long range extrapolations for predicting reaction rates with Michael acceptors, we determined the kinetics of further reactions of Bu₃P with the structurally diverse neutral and positively charged electrophiles 4a–4r of known Mayr E.⁷ Second-order rate constants k₂ (CH₂Cl₂, 20 °C) were determined by applying the photometric methods described above for the 1 + Bu₃P reactions (see ESI† for individual rate constants). Fig. 6 shows that log k₂ for the additions of Bu₃P to 4a–4r follow a linear correlation (r² = 0.9635, n = 18) over a range of 16 units on the Mayr E scale, which gives N(Bu₃P) = 19.11 and s_N = 0.48. Applying the k₂ values for reactions of 1 (Table 1) in the correlation depicted in Fig. 6 indicates that 1a–1j are located in the reactivity range −22.7 < E < −17.5.

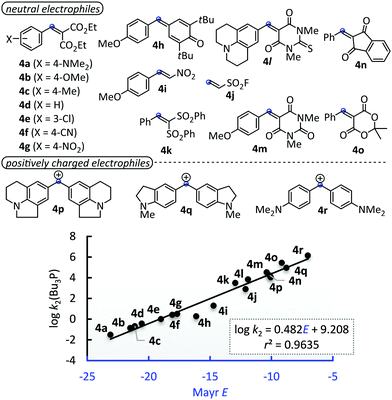Fig. 6 Linear correlation of log k₂(Bu₃P) with the Mayr E parameters of structurally diverse Michael acceptors 4a–o and benzhydrylium ions 4p–r (k₂ in dichloromethane at 20 °C, see ESI† for details of the kinetic measurements, Table S1 (ESI†) gathers the data used to construct the correlation).

In classical Lu reactions, the R₃P catalyst first attacks the alkyl allenoate. The catalytic cycle continues with the reaction of a C-nucleophilic zwitterion with the second Michael acceptor in the reaction mixture. If the kinetics of the R₃P reactions with the two competing electrophiles would be the decisive factor, Lu reactions could be expected to occur only if 1 is more reactive towards the R₃P catalyst than the competing Michael acceptor (e.g., 4). This is not always the case, however. Already in the first publication on the R₃P-catalysed cycloaddition, the Lu group¹ used electrophiles with Mayr E < −16.8, that is, with comparable or even slightly higher electrophilicity than for 1. This indicates that the thermodynamics for R₃P adduct formation is another crucial factor for the success of Lu reactions.

For reactions of vinyl cations with nucleophiles it has been observed that sp/sp² rehybridisation occurs via higher Marcus intrinsic barriers than for reactions that involve sp²/sp³ rehybridisations.^17,18 Analogously, in this work the higher MAA for 1 than for equally reactive olefinic Michael acceptors^15a (Fig. 7) along with the experimental kinetic data indicate that the main difference between 1 and Michael acceptors, such as 4, are the Marcus intrinsic barriers for the R₃P addition at the differently hybridised electrophilic centres.

Fig. 7 (A) Separate linear relationships between the electrophilicities E of acceptor-substituted olefins M1–M44 and allenes 1 with the calculated methyl anion affinities (MAA) (molecular structures of M1–M44 and data used to construct the linear correlation are given in ESI,† Table S2; electrophilicities E for allenoates 1 estimated by applying the k₂(Bu₃P) values from Table 1 in the correlation equation for Bu₃P additions to Michael acceptors in Fig. 6). (B) MAA values and electrophilicities E for Michael acceptors 4s–4v.

Even if the rate constants for the electrophile/R₃P additions are of the same order of magnitude, the MAA values show that allenoates 1 are considerably stronger Lewis acids than olefinic Michael acceptors or imines, such as 4t. As a consequence, the differences in the barriers for the retroadditions differentiate the two competing classes of electrophiles. Owing to their higher energetic barrier for retroaddition, only the allenic electrophiles 1 generate sufficiently high concentrations of reactive zwitterions, which are the pivotal intermediates for the subsequent ring-forming reactions. Thus, allenoates 1 are capable to compete with much stronger electrophiles. For example, 1f (MAA = 163 kJ mol⁻¹) can be used as a partner for the more electrophilic yet less Lewis acidic 4s, 4t, or 4u in Lu cycloadditions.^19–21 Benzylidenemalononitrile (4v) seems to be an exception. However, despite of its high MAA, 4v reacts reversibly with Bu₃P and does not form an adduct with Ph₃P (ESI†). Yet, free 4v traps efficiently the zwitterion generated by Ph₃P and 1f to yield cyclopentenes.^22,23

The reactivities of allenic and olefinic Michael acceptors have been calibrated towards P-nucleophiles through determining the kinetics of their reactions with Bu₃P. Allenoates 1 are weaker electrofuges as well as weaker electrophiles than Michael acceptors 4 of similar Lewis acidity because of the higher intrinsic barriers for sp/sp² rehybridisation. The kinetic and thermodynamic data in this work will be instrumental for the design of novel R₃P-catalysed reactions with alkyl allenoates.

This work was funded by the Deutsche Forschungsgemeinschaft (DFG), project number 410831260, and the National Natural Science Foundation of China (NSFC) 21861132014.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) C. Zhang and X. Lu, J. Org. Chem., 1995, 60, 2906; (b) X. Lu, C. Zhang and Z. Xu, Acc. Chem. Res., 2001, 34, 535; (c) Y. Wei and M. Shi, Org. Chem. Front., 2017, 4, 1876.
2. (a) Y. C. Fan and O. Kwon, in Lewis Base Catalysis in Organic Synthesis, ed. E. Vedejs and S. E. Denmark, Wiley-VCH,Weinheim (Germany), 1st edn, 2016, ch. 15, p. 715; (b) H. Guo, Y. C. Fan, Z. Sun, Y. Wu and O. Kwon, Chem. Rev., 2018, 118, 10049; (c) M. Shi, Y. Wei, M.-X. Zhao and J. Zhang, Organocatalytic Cycloadditions for Synthesis of Carbo- and Heterocycles, Wiley-VCH, Weinheim, 2018; (d) Y. Huang, J. Liao, W. Wang, H. Liu and H. Guo, Chem. Commun., 2020, 56, 15235; (e) Y. Wei and M. Shi, Chin. J. Chem., 2020, 38, 1395; (f) C. Xie, A. J. Smaligo, X.-R. Song and O. Kwon, ACS Cent. Sci., 2021, 7, 536.
3. (a) Y. Liang, S. Liu, Y. Xia, Y. Li and Z.-X. Yu, Chem. – Eur. J., 2008, 14, 4361; (b) G.-T. Huang, T. Lankau and C.-H. Yu, J. Org. Chem., 2014, 79, 1700.
4. H. Mayr and M. Patz, Angew. Chem., Int. Ed. Engl., 1994, 33, 938.
5. (a) H. Mayr and A. R. Ofial, Pure Appl. Chem., 2005, 77, 1807; (b) H. Mayr, Angew. Chem., Int. Ed., 2011, 50, 3612.
6. (a) H. Mayr and A. R. Ofial, SAR QSAR Environ. Res., 2015, 26, 619; (b) H. Mayr, Tetrahedron, 2015, 71, 5095.
7. For a freely accessible database of E, N, and s_N parameters, see: https://www.cup.lmu.de/oc/mayr/DBintro.html.
8. S. Lakhdar, in Lewis Base Catalysis in Organic Synthesis, ed. E. Vedejs and S. E. Denmark, Wiley-VCH, Weinheim (Germany), 1st edn, 2016, ch. 4, p. 85.
9. B. J. Cowen and S. J. Miller, Chem. Soc. Rev., 2009, 38, 3102.
10. X.-Y. Wu, H.-Z. Gui, H. Jangra, Y. Wei, H. Zipse and M. Shi, Catal. Sci. Technol., 2020, 10, 3959.
11. A ratio of k(1a)/k(1f) = 8 was reported for the reactions with pyrrolidine (in CHCl₃): C. Kiattisewee, A. Kaidad, C. Jiarpinitnun and T. Luanphaisarnnont, Monatsh. Chem., 2018, 149, 1059.
12. (a) R. J. Mayer, P. W. A. Allihn, N. Hampel, P. Mayer, S. A. Sieber and A. R. Ofial, Chem. Sci., 2021, 12, 4850; (b) P. M. Jüstel, A. Stan, C. D. Pignot and A. R. Ofial, Chem. – Eur. J., 2021, 27, 15928.
13. I. V. Alabugin, L. Kuhn, M. G. Medvedev, N. V. Krivoshchapov, V. A. Vil’, I. A. Yaremenko, P. Mehaffy, M. Yarie, A. O. Terent’ev and M. A. Zolfigol, Chem. Soc. Rev., 2021, 50, 10253 ; 10700; and ref. cited therein.
14. (a) W. Yao, X. Dou, S. Wen, J. Wu, J. J. Vittal and Y. Lu, Nat. Commun., 2016, 7, 13024; (b) B. Mao, W. Shi, J. Liao, H. Liu, C. Zhang and H. Guo, Org. Lett., 2017, 19, 6340; (c) W. Shi, B. Mao, J. Xu, Q. Wang, W. Wang, Y. Wu, X. Li and H. Guo, Org. Lett., 2020, 22, 2675 ; 6600.
15. (a) D. S. Allgäuer, H. Jangra, H. Asahara, Z. Li, Q. Chen, H. Zipse, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2017, 139, 13318; (b) A. Mood, M. Tavakoli, E. Gutman, D. Kadish, P. Baldi and D. L. Van Vranken, J. Org. Chem., 2020, 85, 4096.
16. B. Kempf and H. Mayr, Chem. – Eur. J., 2005, 11, 917.
17. P. A. Byrne, S. Kobayashi, E.-U. Würthwein, J. Ammer and H. Mayr, J. Am. Chem. Soc., 2017, 139, 1499.
18. (a) R. A. Marcus, J. Phys. Chem., 1968, 72, 891; (b) W. J. Albery, Annu. Rev. Phys. Chem., 1980, 31, 227.
19. Q. Zhao, X. Han, Y. Wei, M. Shi and Y. Lu, Chem. Commun., 2012, 48, 970–972.
20. X.-F. Zhu, J. Lan and O. Kwon, J. Am. Chem. Soc., 2003, 125, 4716.
21. L. Birbaum, L. Gillard, H. Gerard, H. Oulyadi, G. Vincent, X. Moreau, M. De Paolis and I. Chataigner, Chem. – Eur. J., 2019, 25, 13688.
22. X. Lu, Z. Lu and X. Zhang, Tetrahedron, 2006, 62, 457.
23. For [4+2] cycloadditions of 4v with 1i and 1j, see: Y. S. Tran and O. Kwon, J. Am. Chem. Soc., 2007, 129, 12632.

---

Footnote

† Electronic supplementary information (ESI) available: Additional tables and figures, procedures for the synthesis and spectroscopic characterisation of 1, product studies, details of the kinetic experiments and DFT calculations. See DOI: 10.1039/d1cc06786a

---