Infrared micro-spectroscopy coupled with multivariate and machine learning techniques for cancer classification in tissue: a comparison of classification method, performance, and pre-processing technique

Abstract

The visual detection, classification, and differentiation of cancers within tissues of clinical patients is an extremely difficult and time-consuming process with severe diagnosis implications. To this end, many computational approaches have been developed to analyse tissue samples to supplement histological cancer diagnoses. One approach is the interrogation of the chemical composition of the actual tissue samples through the utilisation of vibrational spectroscopy, specifically Infrared (IR) spectroscopy. Cancerous tissue can be detected by analysing the molecular vibration patterns of tissues undergoing IR irradiation, and even graded, with multivariate and Machine Learning (ML) techniques. This publication serves to review and highlight the potential for the application of infrared microscopy techniques such as Fourier Transform Infrared Spectroscopy (FTIR) and Quantum Cascade Laser Infrared Spectroscopy (QCL), as a means to improve diagnostic accuracy and allow earlier detection of human neoplastic disease. This review provides an overview of the detection and classification of different cancerous tissues using FTIR spectroscopy paired with multivariate and ML techniques, using the F1-Score as a quantitative metric for direct comparison of model performances. Comparisons also extend to data handling techniques, with a provision of a suggested pre-processing protocol for future studies alongside suggestions as to reporting standards for future publication.

---

Introduction

Infrared spectroscopy, a specific method of vibrational spectroscopy, is the quantitative interrogation of a sample using infrared radiation to stimulate transitions between molecular vibrational energy states. These vibrations are characteristic of the molecule itself, giving molecules their own spectral fingerprint.¹ This means that, in theory, chemical compositions of complex biological samples, with their unique molecular make-up, can be identified as a superposition of all the individual spectral fingerprints, unique for each chemical composition.² In layman terms, this is achieved by directing an infrared beam through a biological sample and measuring the signal that transmits through it. In principle, cancerous tissue will have a different superposition of spectral fingerprints to that of normal tissue. These spectra have been shown to be sufficiently different for a machine learning algorithm to differentiate between, not only cancerous and non-cancerous tissue, but also between the cancer types, the grade of cancer, and the stage of cancer.^3–5 This enables researchers to informatively analyse tissue samples for the quantitative detection and classification of a range of diseases and cancers.^6–9

Infrared spectroscopy applied to tissue is normally conducted using a Fourier transform infrared (FTIR) spectrometer coupled to an infrared microscope and covers the wavenumber range 4000–800 cm⁻¹. This range encompasses the vibrational frequencies of numerous organic functional groups that are key in differentiating chemical compounds. More recently specially designed infrared microscopes using tuneable Quantum Cascade Laser sources have been used that span a more limited region of the infrared spectrum, typically ∼1900–900 cm⁻¹ that covers the, so-called, fingerprint region.¹⁰ The QCL based systems, while limited in spectral range, offer the possibility of discrete frequency imaging whereby just a few key wavenumbers can be probed, potentially allowing very rapid sampling.¹¹ The choice of technique, therefore, will come with certain experimental biases that may also restrict the information obtained from a biological sample.

Effective application of IR spectroscopy can also be limited due to the substrate or slide upon which samples are loaded. While most tissue samples used in cancer diagnoses are processed from formalin-fixed, paraffin-embedded (FFPE) tissues onto glass slides, the opacity of glass over much of the mid-IR range limits the data obtainable,^12–15 causing many studies to require the use of the expensive and fragile IR transparent substrates such as calcium or barium fluoride (CaF₂ and BaF₂ respectively) crystal slides. This increased cost has serious ramifications for those wishing to apply IR spectroscopy on a large scale in a clinical setting. Infrared spectroscopic classification studies upon haematoxylin and eosin (H&E) stained tissue samples on glass slides have started to be evaluated but it remains to be seen whether conducting multivariate and ML analyses on the current standard of biological tissue samples will become more widely applicable.^16,17

There are many drivers for the application of IR spectroscopy coupled with analytical techniques such as multivariate analysis or ML, in the classification of cancers. Primarily, pathologist concordance has been observed to vary greatly across different stages of cancer, with concordances amongst single pathologist diagnoses ranging from 48–90%, and concordance rates of about 80% in expert pathologist consensus studies,^18–22highlighting the beneficial impact of machine learning to reduce inter and intra pathologist variability. In cases where lesions are detected, IR spectroscopy can measure the chemical presence of these lesions before they become visible histologically, providing the possibility of early-stage cancer detection.²³ The scalability of many of the methods mentioned also provide a cost-effective method for cancer detection in studies with large sample numbers.

Multivariate analysis refers to techniques/models that primarily utilise multivariate statistics for discrimination, such as principal component analysis (PCA) and linear discriminant analysis (LDA).^24,25 Alternatively, machine learning loosely refers to techniques that utilise learning algorithms to build models that are then used for discrimination/decision making processes.²⁶ While there are many studies on the detection and classification of cancerous tissue using the pairing of IR with multivariate and Machine Learning (ML) techniques, there is very little comparative evaluation of these methods.⁷ There also exists low levels of concordance between publications for performance metric presentation and data handling and pre-processing techniques applied. A well-trained machine learning classifier works continuously without supervision, with the potential for hardware upgrades. The model can be exported/replicated to multiple machines which can run in parallel. Simple diagnoses can be recorded by the machine learner, allowing the human pathologist to direct resources towards complex diagnoses with ambiguous probabilities thus saving both time and money.

While IR instrumentation and data collection are well established, there is no “gold standard” for the chemometric technique used when attempting to tackle classification problems encountered with FTIR (or QCL based) spectral datasets. It could be argued that there can be no true set-defined “gold standard”, given that the best suited analytical techniques can vary depending on the underlying data being analysed and the purpose of the study. This is not to say however that there cannot be structured guidance on how best to approach certain research problems. There is also no general agreement on the preparation protocol of the samples for IR spectroscopy, the slides upon which samples are processed, the collection method of the spectral datasets, the specific data to be analysed and their respective handling, and the classification algorithms best suited for the relevant study. This lack of consistency might be caused by the varying suitability of the preparation protocol dependent on the study tissue samples and research objective. For example, the spectral “fingerprint” region found below 1800 cm⁻¹ absorbance is not measurable for tissue samples presented on common silica glass, whereas this region is measurable for tissues on other slides such as calcium/barium fluoride. Studies conducted on either slide type will differ in their analyses. In addition, the spectra of different tissues may also be impacted by distortion scattering effects such as resonant Mie scattering that require treatment before analysis.²⁷

While developing a standard for the chemometric techniques may prove difficult, the development of a “gold standard” for the presentation of model/algorithm results and performance metrics is a reasonable endeavour. All classification studies share commonality in the use of models to predict specific class memberships, with the same measures of performance available, irrespective of the classification method, or data being classified. With adequate labelling of samples, be it at a pixel level or overall tissue assignment, the study authors have the capacity to produce quantitative metrics that can be used as a basis of model validation internally, and comparison between alternative studies externally. While authors have access to all these common performance metrics, they vary in how they report the performance of their models and which of the metrics to use. This has knock on effects for the comparison of models in this area of research. It is common for authors to favour the production of visually pleasing graphs to present model performance metrics, foregoing any quantitative presentation of results. To directly compare the models presented in current literature, a single performance metric can be computed from the studies’ results. This metric is the F₁-Score, which has been applied in the field of query classification, machine learning, and natural language processing.^28–31

The F₁-Score can be calculated directly from a confusion matrix, or through rebuilding a confusion matrix using the sensitivity and specificity metrics. This can be an effortless process in instances of two class classifications, or more complex in multiple class problem areas. The scope of this comparative study is twofold: to conduct cancer classification using spectroscopic techniques across different tissues, concisely summarising key study information such as targeted wavenumber ranges (hereby referred to as a range in cm⁻¹), and how each study measured relative performance metrics to review their work. In addition, this review will provide a method of direct model comparison through the calculation of the F₁-Score for each study. In instances where an F₁-Score calculation is not possible, due to insufficient data or inadequate reporting within the study, a note will be placed in lieu of a score. This review will highlight the importance of establishing a common standard for the reporting of model performance metrics, providing examples of high and low tier reporting, to encourage future authors to report in ways that can be directly compared, without the need of such metric calculations such as the F1 score.

Many of the studies in this review focus on the classification between healthy and cancerous tissue sample groups. While this approach may be suitable for high throughput screening or indeed post diagnosis, quality control, it might not be sufficient to assist in diagnosis beyond simply indicating the presence of diseases such as cancer. It can be argued that the classification between cancerous and healthy samples is too simple, and that classifying the complexity of the unhealthy tissue types is of greater importance e.g., the distinction between inflammation and necrosis in a particular tissue. With regards to the F₁-Score, akin to other performance metrics, a simpler classification problem will often obtain high scores. The problem simplicity must also be considered alongside performance metrics. Classifying the subclasses such as disease type and cancer grading within the sample can provide much greater information for the users of the classifiers. While studies that report on the correct classification of cancer compared to healthy patient tissues showcase the potential of spectroscopy and ML techniques, studies that progress beyond two group classifications are more challenging but will be useful to augment diagnosis in a clinical setting. It is expected therefore, that future studies will focus on the classification of disease subtypes and grading beyond the presence of the disease alone.

The studies have been tabulated in Table 1 to summarise several features including the method(s) used, the different types of cancerous tissue(s) being classified, the original performance metric utilised when reporting results, alongside the paper's relevant F₁-Scores. Performance metrics are reported as either a confusion matrix (CM), sensitivity and specificity metrics (S&S), or percentage of correct classification (%CC). The prediction methods were tabulated to reflect what method is being scored: “Main” denoted a single classification level, in example cancerous against non-cancerous, with other labels reflecting which model/level is used as reported in the relevant study. Additionally, Table 2 is provided to highlight key data handling steps for each study including the data range analysed and key pre-processing steps. Many levels of model performance are reported in our review, indicating that machine learners are very apt at detecting cancerous tissues. However, some studies tackle two group classification problems between non-cancerous and cancerous tissues which are two distinctly different sets of tissue. These high-performance metrics can therefore be misleading, as they result in a simple classification problem. There are alternative studies that showcase very effective classifiers that can differentiate between cancerous tissues within entire tissue sections, by sub-categorising tissue constituents.

Table 1 Collated list of studies conducting classification of cancers in tissue samples

Method used	Author	Classification classes	Performance metric	Cancer type	Prediction method	Macro – F1	Micro – F1	Median – F1
RF	Mittal et al.^36	Malignant epithelium, noncancerous epithelium, stroma, others	CM	Breast	Main	0.9514	0.9509	0.9583
SVM, CNN	Berisha et al.^37	Adipocytes, blood, collagen, epithelium, necrosis, myofibroblasts	S&S	Breast	SVM (HD)	0.7443	0.7575	0.7396
					CNN (HD)	0.9169	0.9294	0.9404
					SVM (SD)	0.5746	0.5478	0.6251
					CNN (SD)	0.8015	0.7868	0.7987
RF	Mayerich et al.^38	Blood, epithelium, collagen, fibroblasts, myofibroblasts, lymphocytes, necrosis	S&S	Breast	Main	Insufficient information available
PLS-DA	Verdonck et al.^39	Epithelial cells, lymphocytes, connective tissue, vascular tissue, erythrocytes	S&S	Breast	Cell/tissue type	0.8521	0.8492	0.8813
					Epithelial phenotype	0.9125	0.9125	0.9125
AdaBoost	Tang et al.^40	Cancerous epithelium, cancerous stroma, normal associated tissue epithelium, normal associated tissue stroma	CM	Breast	Main	0.8877	0.8890	0.8745
RF	Piling et al.^42	Model 1: epithelium, stroma, blood, necrosis	CM	Breast	Model 1	0.9644	0.9640	0.9650
		Model 2: malignant stroma, non-malignant stroma			Model 2	0.8958	0.896	0.8958
RF	Kuepper et al.^3	Level 1: Tissue classification	S&S	Colon	Level 1	0.9700	0.9700	0.9700
		Level 2: colon cancer grade (1, 2, 3)			Level 2	0.8852	0.8837	0.8557
SVM	Hughes et al.^44	Transitional cell carcinoma, stroma, micro-papillary, lymphocyte rich cells, clear cells	%CC	Bladder	Main	Insufficient information available
RF	Großerueschkamp et al.^46	Level 1: healthy, pathologic. Level 2: tumour classes. Level 3: subtypes of lung adenocarcinoma.	S&S	Lung	Main	Only accuracy values given.
ANN	Bird et al.^45	Level 1: normal, not normal. Level 2: small cell lung cancer (SCLC), not SCLC. Level. 3a/b: squamous cell carcinomas (SqCCs), not SqCC Level 4: adenocarcinomas (ADC), not bronchiolo-alveolar carcinomas(BAC)	S&S	Lung	Main	0.9116	0.9043	0.9441
SVM	Akalin et al.^47	Normal, small cell lung cancer (SCLC), non-small cell lung cancer (NSCLC), squamous cell carcinomas (SqCCs), and adenocarcinomas (ADCs).	CM	Lung	Full spot (a)	0.9219	0.9521	0.9219
					Full spot (b)	0.9461	0.9681	0.9461
PCA-LDA, SPA-LDA, GA-LDA	Theophilou et al.^5	Grouping 1: benign tissue, borderline tumours, ovarian carcinoma. Grouping 2: carcinoma subtypes	CM	Ovarian	Main	Only accuracy values given.
PLS-DA	Wald et al.^48	Level 1: epithelial cells, erythrocytes, lymphocytes, connective tissues.	CM, S&S	Skin	Level 1	0.9144	0.9130	0.9069
		Level 2: melanoma cells, endothelial cells			Level 2	0.9450	0.9450	0.9450
PLS- DA	Wald and Goormaghtigh^49	Melanoma, erythrocytes, lymphocytes, connective tissues, necrotic cells, keratinocytes	CM	Skin	Cell type	0.9671	0.9667	0.9701
PLS-DA	Wald et al.^50	Dacarbazine responders, dacarbazine non-responders	CM	Skin	Dacarbazine response	0.9565	0.9565	0.9565
KNN, SVM	Ghassemi et al.^51	Normal adjacent vs cancerous tissue	CM	Gastric cancer	Unknown	0.8137	0.8137	0.8137

---

Table 2 Key data properties and pre-processing steps of collated studies conducting classification of cancers in tissue

Author	Wavenumber range(s) analysed	Scan co-additions	Scan resolution	Quality test	Baseline/scattering correction	Noise reduction	Normalisation	Derivative conversion	Dimensionality reduction
Mittal et al.^36	950–3800 cm^−1	32	4 cm^−1	Absorbance threshold	✗	Minimum noise Fraction	✗	✗	✗
Berisha et al.^37	1000–3801 cm^−1	SD: 4 HD: 32	4 cm^−1	✗	Rubber band subtraction (non-linear)	✗	Feature normalised (Amide I)	✗	PCA – 16 components
Mayerich et al.^38	750–4000 cm^−1	4	4 cm^−1	✗	Not stated	✗	✗	✗	152 specialist chosen metrics
Verdonck et al.^39	900–3795 cm^−1	256	8 cm^−1	Water correction, absorbance threshold, outlier detection	Linear baseline subtraction	✗	Does not state	✗	✗
Tang et al.^40	2500–3700 cm^−1	96	5 cm^−1	Absorbance threshold	✗	✗	✗	1st derivative	✗
Piling et al.^42	912–1800 cm^−1	QCL (not required)	4 cm^−1	Absorbance threshold	✗	PCA noise reduction	Vector normalised	1st derivative	✗
Kuepper et al.^3	950–1800 cm^−1	Not stated	4 cm^−1	Signal to noise ratio & absorbance threshold	RMies correction	✗	✗	2nd derivative	✗
Hughes et al.^44	1000–1760 & 2800–3000 cm^−1	128	4 cm^−1	Absorbance threshold	RMies correction	PCA noise reduction	Vector normalised	1st derivative	PCA – 10 components
Großerueschkamp et al.^46	950–1800 cm^−1	32 & 128	4 cm^−1	Signal to noise ratio	RMies correction	✗	✗	2nd derivative	✗
Bird et al.^45	778–1800 cm^−1	4	4 cm^−1	Spectral quality test	✗	PCA noise reduction	Vector normalised	2nd derivative	✗
Akalin et al.^47	800–1800 cm^−1	4	2 cm^−1	✗	Phase correction	Phase correction	✗	2nd derivative	✗
Theophilou et al.^5	900–1800 cm^−1	32	8 cm^−1	✗	✗	✗	✗	✗	✗
Wald et al.^48	1000–3100 cm^−1	256	8 cm^−1	Signal to noise ratio	Water & linear baseline subtraction	✗	Feature normalised	✗	✗
Wald and Goormaghtigh^49	1000–3100 cm^−1	256	8 cm^−1	Signal to noise ratio	Water & linear baseline subtraction	✗	Feature normalised	✗	✗
Wald et al.^50	1000–3100 cm^−1	256	8 cm^−1	Signal to noise ratio	Water & linear baseline subtraction	✗	Feature normalised	✗	✗
Ghassemi et al.^51	600–4000 cm^−1	100	4 cm^−1	✗	Air removal & baseline correction	Spectral smoothing	Standard normal variate normalization & min-max normalization	2nd derivative	✗

---

The criterion for inclusion in this meta-analysis was cancer studies that employed the application of ML classification methods on tissue samples scanned using infrared spectroscopy, specifically FT-IR and QCL, with a minimal aim to discriminate between key constituents, including the cancer(s). The cancers targeted in the studies summarised in this paper are breast, colon, bladder, liver, lung, ovarian, gastric, and skin.

The F₁-Score

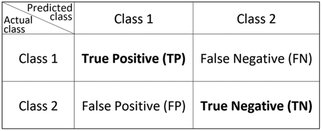
The F₁-Score, alternatively called the traditional F-measure, is defined as the harmonic mean of a model's positive predictive value (precision) and the recall (sensitivity), considering the true positive counts alongside that of false positives and false negatives.^32–34 The F₁-Score is highest when a model obtains low false positive and low false negative predictions, reflecting the model's accuracy. A comparative worked example of this is provided in the ESI.† There are extensions of the F₁-Score to provide weights that award more importance to either the precision or recall, however this is not considered in this review. From the simplest form of confusion matrix (Fig. 1) the F₁-Score can be predicted as in eqn (1) with the true and false positive and negative values (TP, FP, TN, FN respectively), or with the precision and recall given by eqn (2) and (3).where:and

Fig. 1 Simple confusion matrix denoting true and false classification classes.

Calculation of the F₁-Score is possible when provided with sensitivity and specificity, in both simple two class and multiclass problems. This is done by rebuilding a confusion matrix that corresponds to those two metrics. In the more complex multiclass problem areas, Microsoft Excel's Solver³⁵ is used to find combinations of predictions that produce the sensitivity and specificity metrics, as illustrated in Fig. 2. A worked example of this process is provided as ESI.†

Fig. 2 Illustration of how to calculate sensitivity and specificity metrics in a multi-class problem for a confusion matrix of four classes (1). The sensitivity and specificity calculations for class A (2 & 3) and class B (4 & 5) are shown. In each instance the metric is calculated as a division of the sum of upper shaded/greyed confusion matrix value(s) by the sum of the divisor shaded/greyed confusion matrix value(s).

In problems with more than two classes, there are multiple ways of presenting the F₁-Score either individually as numerous scores, or a single score across all groups. Typically, the micro and macro averaging can be used to produce a score that is either biased by class frequency or takes all classes as having equal importance by calculating a total F₁-Score across all classes or averaging the individual scores obtained at each class. Additionally in this study the median-F₁-Score is proposed, taking the median score across all classes, combatting the impact of outlier scores overall. The weighted average F₁-Score, an already established and commonly used metric, was not used because each study allocates different importance to their type I and II errors (false positive and negatives respectively), meaning a set value for the positive real factor β (a user defined weighting) could not be decided upon.

The F₁-Score is criticised as being misleading for unbalanced classes because the metric ignores the instances of True Negatives.³² While the impact of the unbalanced classes is minimised in multi-class problems, it may be combatted in two-class problems through calculation of a secondary F₁-Score that incorporates the True Negatives in the score calculation as opposed to the True Positives, an example of which is provided in the ESI.† This criticism is of importance especially in cases where instances of misclassification have varied levels of impact. Additionally, it can be combatted by incorporating the standard practices proposed in this study i.e. by presenting specificity metrics alongside the F₁-Score to account for the True Negatives.

Classification of cancer in tissue

Reporting of modelling techniques applied to breast cancer data were generally of a high standard, allowing for calculation of F₁-Scores in all but one instance. The classification of and differentiation between noncancerous and malignant epithelium is noted as being a potential measure or indicator of the presence of cancer in humans, resulting in the development of a four class Random Forests (RF) classifier to classify breast tissue sample cells into one of four groups: non-cancerous epithelium, malignant epithelium, stroma, and others.³⁶ The model attained a high range of correct classification rates (94.17–96.09%) with few instances of false positive/negatives, corresponding to a high level of F₁-Scores.

The use of a Support Vector Machine (SVM) and Convolutional Neural Network (CNN) were used to determine whether six major cellular and acellular constituents of breast biopsy cores could be differentiated i.e. adipocytes, blood, collagen, epithelium, myofibroblasts, and necrosis.³⁷ Applied to both standard definition (SD) and high definition (HD) datasets which differ in the number of co-additions in scanning, the CNN model outperformed the SVM overall, with the differences in performance across groups highlighting the beneficial impact of higher quantity data (at the expense of acquisition time).

In a similar vein, a RF method was trained to characterise breast tissue biopsies for use in supplementing pathologist diagnostic activities, classifying groups of tissue types that could be useful for differentiating biomarkers of breast cancer: blood, epithelium, collagen, fibroblasts, myofibroblasts, lymphocytes, and necrosis.³⁸ Unfortunately some details are omitted in this study, such as the pre-processing techniques utilised and the training and test split quantities for model training. Results are also not provided in a quantifiable form to be used in the calculation of F₁-Scores, with the sensitivity and specificity results having to be determined visually. While class receiver operating characteristic curves are overlaid in a plot, they do not aid in the interpretation of the results nor the study's comparability.

Two separate Partial Least Squares Discriminant Analysis (PLS-DA) models were trained to classify five main cell types present in breast tissue sections, and to differentiate between normal and breast tumour epithelial cell phenotypes.³⁹ While the phenotype method of the study produced better F₁-Scores than the five cell type differentiation, this is because of the easier problem being addressed (tumour versus normal). While the cell type differentiation model obtained reasonable scores, the results of ML methods from other studies provide weight to the argument that the more complex modelling techniques are more apt for the problem of tissue classification.

Given the fragility and high cost of CaF₂ and BaF₂ slides, it was rational to determine whether these ML techniques can still be applied to haematoxylin and eosin (H&E) stained tissues on glass slides, to differentiate cancerous and non-cancerous epithelium and stroma using the AdaBoost method.^40,41 Even with the restricted wavenumber range of 2500–3600 cm⁻¹ high levels of correct classification were obtained, alongside high F₁-Scores. The performance of this technique was limited by high levels of incorrect classification for the normal epithelium class, with a 21% misclassification of total normal epithelium spectra being classified as cancerous.

The acquisition of spectra using Quantum cascade laser (QCL) infrared imaging, limited to the lower wavenumber range of the spectrum (1800–912 cm⁻¹), paired with a RF classifier was used to accurately differentiate four different histological classes contained within breast cancer tissue microarrays: epithelium, stroma, blood, and necrosis. Additionally, the successful discrimination between malignant and non-malignant stroma spectra was demonstrated using the same methodology.⁴² In classifying the four histological classes, exceptional F₁-Scores were obtained, with the minimum true positive proportion of classifications being 94.33%. In discriminating between malignant and non-malignant stroma, a lower F₁-Score was obtained. This is due to a higher level of misclassification at the non-malignant level, bringing down the overall score.

In the studies listed in Table 1, there exists only one focussed on classification of colon cancers, removing the ability to conduct comparisons within the same tissue type. The study acts as a continuation of previous works, which included the development of a RF model to discriminate between colon tissue tumours and noncancerous tissue constituents such as crypts, lumen of crypts, mucus, mucosal cells, supporting cells, submucosa, muscle, adipocytes, blood, lymph follicles, inflammation, and connective tissue.⁴³ The reported study extends this RF model to include a second RF classifier to determine the grading of the tumour, from well-differentiated, moderately differentiated, and poorly differentiated.³ The first level of the model separating the colon tumour tissue from the non-cancerous constituents achieved the highest average F₁-Score across all three metrics, with no false positives of tumour tissue reported. The second level is measured by the congruence between the model output and the pathologist's annotations, with the F₁-Scores obtained still being of a high level. It can be argued that the differentiation of tumour grades is a more difficult endeavour than differentiation between tissue types, leading to a greater appreciation of the model's performance.

Similar to the colon cancer group, there is only a single study focussed on classification of bladder cancer data, and the results are not presented in a form that can be used to calculate relevant F₁-Scores. Five sub-variants of transitional cell carcinoma (TCC) were subjected to classification by a SVM method: conventional TCC, stroma, microcapillary, lymphocyte rich, and clear cell.⁴⁴ While achieved overall accuracy was very high (98.36%), there are no quantified performance metrics beyond group classification accuracies, and visual plots detailing the method's decision boundaries for each prediction. It is suspected that the study would have achieved very high F₁-Scores.

In a study directed at the development of an automated histopathological annotation of lung tumour subtypes, a three-tiered RF classifier was used to separate healthy and cancerous regions, followed by the identification of tumour classes, with a final subtyping of adenocarcinoma.⁴ While the study mentions that improved standards of sample collection and characterization result in higher accuracy and reproducibility, the results presented were not sufficient to calculate any F₁-Scores. The only quantified results were overall classification accuracy metrics, with no tabulated results, nor sensitivity or specificity metrics. While false positive rates are mentioned in the discussion of results for the second RF level, the full confusion matrix detailing all classifications and distribution of these false positives, are omitted from the paper. While the modelling approach appears very promising, without adequate result metrics there is no basis from which these results can be verified/compared to other modelling techniques in the same tissue group.

In an alternative study on lung tissue a multi-level Artificial Neural Network (ANN) diagnostic algorithm was constructed to distinguish between normal and cancerous tissue, while also classifying small cell lung carcinomas (SCLCs), squamous cell carcinomas (SqCCs), and also adenocarcinomas/bronchiolo-alveolar carcinomas (ADCs/BACs).⁴⁵ The structure of all levels were set up as binary classifiers, with the first tier discriminating between normal and non-normal tissue subtypes which is equivalent to a cancer against non-cancer classifier. From the non-normal tissue subtypes the second tier separated SCLC from non-SCLC spectra, consisting of the SqCC, ADC, and BAC. The third tier then classified SqCC from non-SqCC data, containing the remaining ADC and BAC data. This third tier is conducted twice with two different feature selection methods, one employed the second derivative of spectra, the second used feature selection based on PCA scores. Finally, the fourth tier distinguishes between the ADC and BAC data. Overall the F₁-Scores obtained were exceptional, with the overall scores being lowered by the final tier, which had a low specificity metric. It can be concluded that breaking down the classification of the tissues into tiers of two class problems is a more effective method than attempting to train a classifier to discriminate between multiple classes at once.

An SVM approach was also trialled to differentiate a number of different cancer types most frequently encountered within lung cancer: small-cell carcinoma (SCLC), squamous cell carcinomas (SqCCs), and adenocarcinomas (ADCs), as well as normal tissue and regions of necrosis.⁴⁷ The study was divided into two main classification problems, firstly the tissue microarrays were classified at a pixel level, with each pixel being classed as one of the aforementioned groups. The second set of classifications were conducted at a full spot level, providing diagnoses of either normal or cancerous samples. Unfortunately, it was not possible to rebuild a confusion matrix for the pixel-based classifications and this could either be a result of rounding differences in reporting, or problems with the presentation of sensitivity and specificity metrics. At the spot level however, the modelling achieved the highest F₁-Scores in the lung tissue studies, albeit potentially due to the simplicity associated with a binary classification problem.

Of the sole study conducted on ovarian tissue samples, results were not reported to a standard where F₁-Scores could be calculated and compared. The first of the two listed studies set out to develop a technique to discriminate between normal, borderline, and malignant ovarian tumours, while classifying the ovarian carcinoma subtypes.⁵ The methods employed were a collection of different chemometric analyses in the form of PCA, successive projection algorithm (SPA), and genetic algorithm (GA). All of these methods were then followed by a linear discriminant analysis (LDA). The results of these techniques are presented in a large table of accuracy measurements for each carcinoma subtype, with the lowest scoring predictions coloured green, and highest scoring predictors coloured in red, causing interpretability issues. Of the reported results however, some accuracy levels were as high as 100%, indicating that if reported to the same standard as other papers, the F₁-Scores obtained would be expected to be very high.

All studies on skin cancer classification were conducted by the same key author using the same modelling technique. This allows an insight as to how a single modelling technique's effectiveness ranges when tackling different classifications. The classes in each of the works are either conducting cell type classification, or predicting treatment responses. In developing a method for the identification of melanoma cells and lymphocyte subpopulations in lymph node metastasis, cell type recognition models were trialled in order to classify the four main histological classes of the tissue samples: epithelial cells, erythrocytes, lymphocytes, and connective tissue. Following the identification, the endothelial cells were then sub-classed into melanoma and endothelial cell groups.⁴⁸ In discriminating between the four main histological groups and between the melanoma and endothelial cells, the PLS-DA method achieved high performance metrics and F₁-Scores. The four-level histological group was limited by a high level of false negatives associated with lymphocyte and connective tissue pixels being predicted as epithelial cells. In prior works by the same author, six cell types commonly found in melanoma tumours were the subject of classification: melanoma cells, erythrocytes, connective tissues (including blood vessel walls, dermis, and collagen), keratinocytes, lymphocytes, and necrotic cells.⁴⁹ Unlike the later study, melanoma cells are not separated from endothelial cells at a second classification level. The study reports that over 98% of melanoma cells are correctly identified using this method, as opposed to the ∼92% identified in the later study. This is reflected in the F₁-Scores, with the earlier study achieving higher scores across all metrics.

The third study reported on skin cancer deviates from the standard classification groupings seen in previous studies and instead of classifying disease presence/state on a pixel level or providing diagnosis predictions the study frames the groups as dacarbazine responders and non-responders (chemotherapy drug used in the treatment of metastatic melanomas).⁵⁰ This study examined the melanoma histological sections to identify clinical responsiveness to treatment. The PLS-DA discriminates between responders and non-responders at a high level, achieving some of the highest F₁-Scores of the report.

Finally, both SVM and KNN methods of classification were tested on gastric cancer tissue samples scanned using attenuated total reflectance Fourier Transform Infrared (ATR-FTIR) spectroscopy.⁵¹ Classes were split into normal and malignant groups, with the samples being classified on a sample level. While two classification methods are mentioned in the paper only one set of prediction results are presented, with no indication as to whether these results belong to the SVM or KNN method. The superior method of prediction cannot be determined. This is unfortunate as this study would have been able to compare the classification methods directly, with the underlying data going through the same pre-processing steps.

Data acquisition and pre-processing techniques for the classification of cancer in tissue

A major aspect of any quantitative study is the handling, structure, and pre-processing of the data being analysed. Transformations applied to spectral datasets can have a profound impact upon the performance of multivariate and ML techniques applied to the data. In that regard, identifying and highlighting the key sources of variability between the studies in relation to their data handling techniques can assist in the better understanding of each study's model(s) performance. It also assists in the development of guidelines and best practices for future research that can aid in the standardisation of data handling techniques for future research. Beyond the comparison of study types, their ML models, and comparative F₁-Scores, key study information pertaining to their data and handling is presented in Table 2. With key insight as to how prior researchers have handled their data, a guideline of important and optional pre-processing steps can be formulated for use in future studies. The wavenumber ranges analysed is one of the first key sources of variance between the studies. While FTIR spectrometers collect absorbance readings across both the near and mid IR range, typically 900–3800 cm⁻¹, many studies restrict their analyses to the “fingerprint” region of 900–1800 as this complex region contains many of the absorbance bands key in identifying molecular structures.¹³ This is key when trying to discriminate between tissue constituents whose chemical structures are largely similar.

Additional variability between studies can occur due to differences in scan parameters in the choice of scan co-additions and resolution. A higher number of scan coadditions provides better quality data, as it combines multiple readings of the same region to provide an average, minimising the signal to noise ratio of the data. Scan resolution impacts the number of absorbance readings taken between the wavenumber range, for example a resolution of 4 cm⁻¹ will result in twice as many data points as 8 cm⁻¹. While the quality of the data is improved, each collection setting will impact the time taken to acquire a spectral dataset, requiring a compromise if time is a limiting factor. Across the studies, the number of co-additions has ranged from 4 to 256, with scan resolution ranged from 2–8 cm⁻¹.

Quality testing is a key pre-processing step when preparing data for classification. Confounding factors such as stray hair or dust may be present within the sample scanned image, alongside saturated spectra and generally unusable data that all must be removed to improve the quality of the overall analyses. The quality testing across the studies differs, ranging from visual removal of saturated spectra, to signal to noise ratio considerations, even applications of thresholds to certain absorbance bands/values such as the Amide I signal, removing any spectra deemed to be abnormal.^52,53 While most studies employ at least one form of quality testing, there are still some that do not. It may be argued that initial quality testing of data is a fundamental pre-processing step that should be done in all future studies.

Certain baseline distortions and scattering artefacts caused by Mie scattering may also be treated for, prior to analysis.^27,54,55 Both baseline subtraction, linear or non-linear, and resonant-Mie scattering (RMies) correction methods correct for warped absorbance profiles without removing any relevant chemical information. It is important to note that RMies correction also applies baseline correction when used, meaning both methods need not be applied. While both methods improve the quality of the data, these pre-processing steps are not always required. For example, the effect of consistent baseline shifts can be nullified by converting data to the second derivative, removing the need to conduct baseline subtraction, and Mie scattering occurrence is improbable within large sections of FFPE tissue that has not been dewaxed. Although wax embedding reduces scattering artefacts, it does not eradicate it. While most of the studies have either employed baseline subtraction or RMies correction, there are still several studies that have not.

While the signal to noise ratio of the data can be improved through certain collection criteria, noise within the datasets can still be present and therefore treated. Noise reduction, also referred to as smoothing, can be considered an optional treatment step as high quality data would have little to no noise present. Regardless, noise correction can be an important tool to improve spectral data quality when users are unable to commit to large acquisition timeframes. The main noise reduction method used in the tabulated studies is Principal Component Analysis (PCA) noise reduction.² This method is different from PCA dimensionality reduction, as the data dimensions are not changed ref. The severity of the noise reduction/smoothing is influenced by the number of components that are selected. A reasonable number of components are user defined and are chosen to ensure that the key aspects of the data, which is assumed to be the chemical information, is retained.

Normalisation of data is an integral step in spectral pre-processing, providing a scale commonality between different spectral datasets to ensure comparability between data. Beyond accounting for differences in thickness across a sample, some ML methods also require data to be normalised, as certain methods require the data to be valued within a [0,1] range. The three main forms of normalisation are vector normalisation, which converts each absorbance spectrum to a unit vector (dividing the spectrum by its highest absorbance value), min-max normalisation, which transfers all the minimum and maximum values to 0 and 1 respectively. There is also feature normalisation, which divides each spectrum based on a user defined feature. Just over half of the studies tabulated apply some form of normalisation technique. As this technique provides that commonality between samples, it is suggested that all future studies apply some form of normalisation of data. However, it is important to note that any discussions regarding features of the data following normalisation must be done in relative terms.

Data transformations to derivatives of the data have also been used in the studies, with the second derivative being a popular choice. Transformations of data to a derivative is an alternative representation of the data. In layman terms, converting data to the first derivative maps the rate of change of the spectroscopic absorbance profiles across a wavenumber range, while conversion to the second derivative maps the gradient of the gradient of the underlying absorbance profile. When converting data to the first derivative, feature maximums become zero intercepts. In the second derivative a feature maximum will be negative, reflecting the concave down form of the feature. Second derivative spectroscopy enhances the separation of subtly differing spectra, reducing the effective linewidth while simultaneously reducing contributions from broad and structureless elements, allowing for greater differentiation of tissue constituents and better performance of multivariate and ML methods.^56–58 Conversion to the second derivative also negates any linear baseline shifts within the data. Of the studies listed, three utilise the first derivative and three use the second.

An alternative way to transform the data is to perform dimensionality reduction techniques. This technique can be applied in combination with derivative transformations. This technique transforms data into a lower dimensional representation of that data, ideally retaining the most important aspects of the original data. The most commonly used technique is PCA dimensionality reduction, reducing the original dataset to a user-specified set dimension. The theory implies that the variance captured in the key initial components will be those which separate the key tissue constituents most, which may be true when analysing two distinctly different samples such as cancerous tumours and healthy tissue. However, this may not be the case, in practice, within tissue samples that are mainly homogenous, where a lot of the main variation within the dataset may not be attributable to the miniscule differences that exist between the mainly similar tissue constituents. For example, a small increase in an absorbance peak that denotes tyrosine protein kinase activity resulting from a survival response to tissue damage, is much smaller in absolute terms than the difference in absorbance peaks that reflect tissue thickness. Caution is advised when using this method, as important chemical information can be lost when reducing data dimensions. A secondary criticism of the PCA technique is that it is a linear mapping of data, and spectroscopic data reflecting tissue change are not necessarily linear, requiring the utilisation of non-linear and more complex methods such as kernel principal component analysis to map the non-linearity using kernels, which no tabulated study has done.^59,60 Creating user specified metrics such as key absorbance ratios is also a possibility, as one study conducted,³⁸ however, this requires extensive prior knowledge of the datasets being analysed, which is not always the case in practice.

With regards to the impact of pre-processing upon obtained F₁-Scores, direct comparison would require a study that builds two identical classification methods trained on raw (unprocessed) and pre-processed spectra respectively. The comparison could then provide F₁-Scores to be directly compared. However, given pre-processing of spectra is an integral step of all studies utilising spectroscopic techniques, converting data to a format that may best be discriminated by ML/multivariate models, by implication pre-processing techniques will always improve obtained F₁-Scores.²

Each study's collection and ordering of pre-processing steps are all selected relative to the study itself, meeting the requirements of each model and study objective. The order of these steps will have a direct impact upon the study results. It is clear from Table 2 that while there is no unanimous agreement on any form of pre-processing protocol, there does appear to be some trending across studies, even in the presence of already published pre-processing protocols.² In contrast to a general protocol for biological samples, a data pre-processing protocol for multivariate and ML classification studies on tissues will be suggested in line with the trends captured in the tabulated studies. It is important that this suggested protocol be considered alongside the aforementioned pre-processing protocol, to ensure full understanding of the data handling options available to the user.

Data pre-processing protocol for tissue classification

An important note for this proposed workflow is that not all steps are mandatory, however their order is important. In example normalisation should never be implemented prior to baseline correction or smoothing. Judgment must be exercised for studies that do not conform to the tabulated studies analysed. These steps can be conducted irrespective of wavenumber range(s) analysed.

1. Apply quality testing to the collected spectra. Researchers should consider using either signal to noise or absorbance thresholding to remove inappropriate data.

2. Researchers should conduct either baseline or scattering correction depending on the conditions below:

(i) If the baseline shift appears consistent across spectra and linear in nature, apply linear baseline subtraction through interpolation of a straight line through key spectral points (optional).

(ii) If the baseline shift appears consistent across spectra but non-linear in nature, apply non-linear rubber band baseline subtraction^61,62 (optional).

(iii) If the baseline shifts appear warped and are inconsistent across spectra, apply RMies scattering correction.^27,54,55 The number of iterations required are dependent on the severity of scattering.

Steps i and ii are deemed optional as transformation of data to the second derivative removes impact of any consistent baseline shift.

3. Apply Eigenvalue decomposition techniques such as PCA for noise reduction to further improve data quality.^63,64 For PCA noise reduction a large component number (∼50) is recommended to avoid removal of subtle absorbance peaks (optional).

This step is optional and dependent on signal to noise ratio of the spectra at this stage.

4. Perform vector normalisation of the data, feature normalisation and min-max normalisation are viable alternatives.

5. Transform data using Savitzky–Golay differentiation (second derivative is recommended).⁶⁵

Discussion

In applications of multivariate and ML techniques, interpretations of the results presented by the comparative F₁-Score require consideration. A key aspect of any study is the framing of the classification problem. The classification problems addressed in the tabulated studies can be split into two key groups: the number of classes, separated as two class or multi-class, and the number of classification levels, split across single and multi-level classification. Two-class classification is concerned with discriminating between two groups of data and is arguably the simplest classification problem for ML application. Regarding cancer classification within tissue, the two classes consist of a control set of healthy tissue and the cancerous tissue. The high levels of performance metrics reported for these two group classification problems are misleading. This is due to the two groups’ absorbance profiles being distinctly different, resulting in a very simple classification problem for a machine learner.

Multi-class classification is more complex, requiring multiple tissue constituents to be differentiated. The homogenous nature of tissue samples would imply that a classification method that can distinguish between the many different constituents of tissue, as well as highlighting the cancerous regions and determining their grade, would be of much greater impact, given it is a much more difficult endeavour, irrespective of whether it obtains lower performance metrics. This type of classification can be conducted at once with a single model, or a tiered set of models that focus on separating specific groups. Having multiple sets of classifiers with different targets is more desirable, as each model can specialise in key spectral separations, improving the overall performance. Großerueschkamp and colleagues applied tiered classifications, separating healthy tissue from tumorous tissue of pathological interest, followed by classifying these tumours, and finally subtyping the lung adenocarcinoma.⁴ In light of this complexity variance, F₁-Scores must be considered on a case-by-case basis when comparing studies, as the framing of the classification problem could have profound impacts on the final metric. To mitigate this limitation, the difficulty of the classification problem should be highlighted where applicable, with results reported in a way so that the relative complexity of the approach can be deduced by the reader. This can be achieved with confusion matrices, as the numbers and size of the matrices are proportional to the classification complexity.

When selecting the best classification method each technique comes with it its own advantages and disadvantages, and needs to be well understood before application. For example, SVMs require more computational time for both model training and prediction than an ensemble RF method but are very good at finding high-dimensional hyperplanes for class separation. Many of the papers, possibly in the interests of length, do not articulate the influencers in the choice of machine learners or the author's process for method selection and application. In addition to this, many studies do not provide adequate discussion about the hyper-parameters used in each of their methods, even when a selected method may have multiple setups. For example, kernel choice is a major decision criterion when applying a SVM classifier, however there is very rarely a mention of what kernel was selected or why the decision was made. The addition of model structure information and model selection influences within future studies would be a positive contribution to the research community, improving the reproducibility and comparability of studies. There is at least one instance of each reported method achieving an F₁-Score above 0.90, making it difficult to objectively rank the techniques. For example, in studies involving breast tissue samples, the RF method appears to be the best relative classifier, however there are limited studies using alternative techniques, so the statement cannot be made with confidence. Additionally, the pre-processing steps applied to the data have direct impact upon model performances. Given that there is no concordance among the studies in this regard, directly comparing the multivariate and ML methods becomes difficult.

As to the comparison of technique, both FTIR and QCL techniques were employed in the collated studies, however it is difficult to directly compare the two techniques in terms of the F₁-Score. Key differences between the two methods restrict concise comments without first a larger discussion on the differences inherent in the spectroscopic methods, such as the impact of discrete wavenumber frequency choices or restricted wavenumber range collection under the QCL method and how these choices impact the F₁-Score metric.^2,10 In example, discrete wavenumber selection may not be apt for tissue classification studies without adequate knowledge of the key tissue constituents, potentially resulting in ineffective classifications. While difficult to address this issue through a meta-analysis, the improved reporting standards recommended in this article would assist in providing a better overview and in-depth analysis of the field.

All authors have the capacity to produce their performance metrics to the same standard, which would allow for greater levels of comparability across the research. Some studies do not have access to fully labelled data, so performance metrics of predictions on independent datasets may not be calculated, however there will still be internal model metrics that can be reported, given that the training datasets must have been labelled. The importance of adequate reporting of results for these classification techniques cannot be understated, especially given the developing trend towards workflows that give more weight to the outputs of the computational methods within a medical context. While the F₁-Score allowed for a new comparison to be made between studies with varying reporting of results, providing an additional representation of a technique's ability to perform its function, it was not always possible to calculate this performance metric. If all tabulated studies were consistent in their reporting standards, the calculation of this F₁-Score would not be necessary as direct comparisons could have been made between the results.

The data collection, handling, and pre-processing steps employed by each study are another key source of variability and direct influencers of model performance. At the collection level there exists a trade-off between the quality of the data acquired and the time to completion for each collection. Increasing the number of scan co-additions reduces the signal to noise ratio of the acquired spectra through the power of averaging, while better scan resolution increases the number of absorbance readings taken across a specified range. While the former decreases the impact of noise, the latter can provide more defined absorbance peaks, capturing changes to peak shape and position, possibly even breaking apart peaks that would otherwise appear as a sole broad absorbance peak. When considering the homogeneity of tissue samples, preference may be given to better scan resolution to best capture the slight changes in absorbance profiles, especially as there are existing pre-processing steps to combat noise contributions.

In certain instances, the choice of wavenumber range(s) for use can be restricted because of the scanning technique or sample substrate employed. When unrestricted, the user is free to target specific wavenumber ranges to best suit their study. While the full IR wavenumber range has been used in some studies, many elect to focus on the complex “fingerprint” region containing many of the absorbance bands key in identifying molecular structures.¹³ Focussing on a specific wavenumber range removes unnecessary data, decreases the computational complexity of applied techniques and increases the effectiveness of multivariate and ML methods in discriminating between spectral profiles. Restricting the spectral range is the first of many pre-processing steps available to users to assist in classification problems. Additional pre-processing steps can be conducted to combat issues such as baseline distortions and scattering artefacts, improvement of signal to noise ratios through noise reduction, normalisation of data, differentiation and dimensionality reduction of data.

To assist future researchers, a specific pre-processing protocol is proposed for the classification of biological tissue samples using ML methods. The protocol covers fundamental and optional data transformations to improve both data quality and overall classification performance. One form of data transformation that is included in the tabulated studies, but not considered for the protocol, is dimensionality reduction techniques. While helpful in many other aspects of data analytics, the commonly used PCA technique is inclined to ignore important chemical information that, while important in discrimination, may not capture enough variance to be captured as a key component. While applying this technique upon two distinctly different tissue samples such as healthy control and cancerous tumours may produce good class separation across key components, the miniscule chemical differences that exists within homogenous tissue samples may not be captured by this method.

Conclusions

The comparisons conducted in this study, where possible, consisted of two main categories: the multivariate and ML classification types employed on the data returned by FTIR spectroscopy of tissues, alongside the performance metrics achieved and the key data attributes, handling, and pre-processing steps of each study. Both categories provided key insights into the current practices employed in the research community, while simultaneously highlighting the lack of concordance across both categories. It is noted that the studies differ in their techniques, from pre-processing steps to classification technique, and the classification problem being addressed. Classification model performances were compared through the calculation of a directly comparable F₁-Score, determined through reported metrics of either sensitivity and specificity, or confusion matrices. Data handling and pre-processing techniques were also compared across the studies, resulting in the development of a pre-processing protocol which can be utilised by future researchers employing classification techniques on biological tissue samples. In the literature examined, both pixel level and tissue wide classification problems have been addressed to varying levels of success, allowing for the discrimination of both key tissue constituents and unhealthy tissue regions of interest, with many of the studies originally reporting high levels of performance metrics, while also obtaining reasonably high F₁-Scores. This highlights the overall effectiveness of classification of tissue cancers through the application of multivariate and ML techniques on FTIR spectroscopy datasets. In conclusion, IR microscopy has been developed to be a useful adjunct to histopathological diagnosis of human cancer, particularly of the breast, colon, prostate, urinary bladder, liver, lung, ovary, and skin. With early studies focused on basic classification of healthy from cancerous tissues, while recent work has further developed the methods to classify cancerous grades, subtypes, and tissue variants. The studies indicate that while the choice of ML techniques is not consistent, with ensemble methods providing the best results on average, the workflows are moving towards tiered modelling approaches that capture tissue complexity.

In future it would be beneficial to the research community for authors to present their results in a similar standard that allows for the effective comparison and reproducibility of those publications. This can be achieved by a mandatory minimum reporting of classification results in a confusion matrix form, with supplementary sensitivity and specificity metrics. These standards would eliminate the need to produce the F₁-Score. Additionally, further levels of research concordance and comparability can be achieved through the following of the proposed pre-processing protocol, establishing a set standard for the type of data being analysed by multivariate and ML techniques.

Author contributions

Dougal Ferguson: conceptualization, methodology, formal analysis, investigation, writing – original draft, visualization. Alex Henderson: conceptualization, supervision. Elizabeth F. McInnes: writing – review & editing, supervision. Rob Lind: conceptualization. Jan Wildenhain: conceptualization, writing – review & editing. Peter Gardner: conceptualization, writing – review & editing, supervision.

Data availability statement

This publication is supported by multiple datasets which are openly available at locations cited in the ‘References’ section of this paper.

Conflicts of interest

The authors of this paper declare no conflicts of interest.

Acknowledgements

Partial funding is provided by a bloc grant from the Engineering and Physical Sciences Research Council (EPSRC).

Notes and references

1. B. C. Smith, Fundamentals of Fourier transform infrared spectroscopy, CRC press, 2011.
2. M. J. Baker, J. Trevisan, P. Bassan, R. Bhargava, H. Butler, K. M. Dorling, P. R. Fielden, S. W. Fogarty, N. J. Fullwood, K. Heys, C. Hughes, P. Lasch, P. L. Martin-Hirsch, B. Obinaju, G. D. Sockalingum, J. Sulé-Suso, R. Strong, M. J. Walsh, B. R. Wood, P. Gardner and F. L. Martin, Nat. Protoc., 2014, 9, 1171.
3. C. Kuepper, F. Großerueschkamp, A. Kallenbach-Thieltges, A. Mosig, A. Tannapfel and K. Gerwert, Faraday Discuss., 2016, 187, 105–118.
4. F. Großerueschkamp, T. Kallenbach-Thieltges, T. Behrens, T. Brüning, M. Altmayer, G. Stamatis, D. Theegarten and K. Gerwert, Analyst, 2015, 140, 2114–2120.
5. G. Theophilou, K. M. Lima, P. L. Martin-Hirsch, H. F. Stringfellow and F. L. Martin, Analyst, 2016, 141, 585–594.
6. C. A. Meza Ramirez, M. Greenop, L. Ashton and I. U. Rehman, Appl. Spectrosc. Rev., 2020, 56(8–10), 733–763.
7. I. U. Rehman, R. S. Khan and S. Rehman, Expert Rev. Mol. Diagn., 2020, 20, 749–755.
8. M. Piling and P. Gardner, Chem. Soc. Rev., 2016, 45, 1935–1957.
9. M. J. Baker, H. J. Byrne, J. Chalmers, P. Gardner, R. Goodacre, A. Henderson, S. G. Kazarian, F. L. Martin, J. Moger, N. Stone and J. Sulé-Suso, Analyst, 2018, 143, 1735–1757.
10. M. J. Piling, A. Henderson, B. Bird, M. D. Brown, N. W. Clarke and P. Gardner, Faraday Discuss., 2016, 187, 135–154.
11. P. Bassan, M. J. Weida, J. Rowlette and P. Gardner, Analyst, 2014, 139, 3856–3859.
12. P. Bassan, J. Mellor, J. Shapiro, K. J. Williams, M. P. Lisanti and P. Gardner, Anal. Chem., 2014, 86, 1648–1653.
13. C. N. Banwell, Fundamentals of molecular spectroscopy, 1972.
14. H. Günzler and H. U. Gremlich, IR spectroscopy. An introduction, 2002.
15. B. Straughan, Spectroscopy: Volume Three, Springer Science & Business Media, 2012.
16. M. J. Piling, A. Henderson, J. H. Shanks, M. D. Brown, N. W. Clarke and P. Gardner, Analyst, 2017, 142, 1258–1268.
17. J. Tang, D. Kurfürstová and P. Gardner, Clin. Spectrosc., 2021, 100008.
18. J. G. Elmore, G. M. Longton, P. A. Carney, B. M. Geller, T. Onega, A. N. Tosteson, H. D. Nelson, M. S. Pepe, K. H. Allison, S. J. Schnitt and F. P. O'Malley, J. Am. Med. Assoc., 2015, 11, 1122–1132.
19. J. G. Elmore, R. L. Barnhill, D. E. Elder, G. M. Longton, M. S. Pepe, L. M. Reisch, P. A. Carney, L. J. Titus, H. D. Nelson, T. Onega and A. N. Tosteson, Br. Med. J., 2017, 357, 1–11.
20. M. G. Crespo-Leiro, A. Zuckermann, C. Bara, P. Mohacsi, U. Schulz, A. Boyle, H. J. Ross, J. Parameshwar, M. Zakliczynski, R. Fiocchi and J. Stypmann, Transplantation, 2012, 94, 1172–1177.
21. D. A. Cohen, D. J. Dabbs, K. L. Cooper, M. Amin, M. W. Jones, M. Chivukula, G. A. Trucco and R. Bhargava, Am. J. Clin. Pathol., 2012, 138, 796–802.
22. A. Z. Mahmoud, T. I. George, D. R. Czuchlewski, Q. Y. Zhang, C. S. Wilson, C. E. Sever, A. G. Bakhirev, D. Zhang, N. L. Steidler, K. K. Reichard and H. Kang, Mod. Pathol., 2015, 28, 545–551.
23. M. J. Baker, E. Gazi, M. D. Brown, J. H. Shanks, N. W. Clarke and P. Gardner, J. Biophotonics, 2009, 2, 104–113.
24. S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37–52.
25. S. J. Prince and J. H. Elder, Probabilistic linear discriminant analysis for inferences about identity, In 11th International Conference on Computer Vision, 2007, ICCV 2007, Issue: 1–8.
26. M. I. Jordan and T. M. Mitchell, Science, 2015, 349, 255–260.
27. P. Bassan, H. J. Byrne, F. Bonnier, J. Lee, P. Dumas and P. Gardner, Analyst, 2009, 134, 1586–1593.
28. C. Goutte and E. Gaussier, A probabilistic interpretation of precision, recall and F-score, with implication for evaluation, In European conference on information retrieval 2005, Springer, Berlin, Heidelberg, 2005, pp. 345–359.
29. S. M. Beitzel, On understanding and classifying webqueries, Illinois Institute of Technology, 2006.
30. X. Li, Y. Y. Wang and A. Acero, Learning query intentfrom regularized click graphs, 2008.
31. Y. Sasaki, Teach. Tutor. Mater., 2007, 1, 1–5.
32. D. M. Powers, 2020, arXiv preprint arXiv:2010.16061.
33. W. Siblini, J. Fréry, L. He-Guelton, F. Oblé and Y. Q. Wang, in International Symposium on Intelligent Data Analysis, Springer, Cham., 2020, pp. 457–469.
34. A. Tharwat, Applied Computing and Informatics, 2020.
35. Microsoft Corporation, Microsoft Excel, 2016. Available: https://office.microsoft.com/excel.
36. S. Mittal, T. P. Wrobel, L. S. Leslie, A. Kadjacsy-Balla and R. Bhargava, Medical Imaging 2016: Digital Pathology, 2016, vol. 9791, p. 18.
37. S. Berisha, M. Lotfollahi, J. Jahanipour, I. Gurcan, M. Walsh, R. Bhargava, H. Van Nguyen and D. Mayerich, Analyst, 2019, 144, 1642–1653.
38. D. M. Mayerich, M. Walsh, A. Kadjacsy-Balla, S. Mittal and R. Bhargava, in Medical Imaging 2014: Digital Pathology, 2014, vol. 9041, p. 107.
39. M. Verdonck, A. Denayer, B. Delvaux, S. Garaud, R. De Wind, C. Desmedt, C. Sotiriou, K. Willard-Gallo and E. Goormaghtigh, Analyst, 2016, 141, 606–619.
40. J. Tang, A. Henderson and P. Gardner, Analyst, 2021, 146, 5880–5891.
41. R. E. Schapire, in Empirical inference, Springer, Berlin, 2013, pp. 37–52.
42. M. J. Piling, A. Henderson and P. Gardner, Anal. Chem., 2017, 89, 7348–7355.
43. A. Kallenbach-Thieltges, F. Großerüschkamp, A. Mosig, M. Diem, A. Tannapfel and K. Gerwert, J. Biophotonics, 2013, 6, 88–100.
44. C. Hughes, J. Iqbal-Wahid, M. Brown, J. H. Shanks, A. Eustace, H. Denley, P. J. Hoskin, C. West, N. W. Clarke and P. Gardner, J. Biophotonics, 2013, 6, 73–87.
45. B. Bird, M. Miljković, S. Remiszewski, A. Akalin, M. Kon and M. Diem, Lab. Invest., 2012, 92, 1358–1373.
46. F. Großerueschkamp, A. Kallenbach-Thieltges, T. Behrens, T. Brüning, M. Altmayer, G. Stamatis, D. Theegarten and K. Gerwert, Analyst, 2015, 140, 2114–2120.
47. A. Akalin, X. Mu, M. A. Kon, A. Ergin, S. H. Remiszewski, C. M. Thompson, D. J. Raz and M. Diem, Lab. Invest., 2015, 95, 406–421.
48. N. Wald, N. Bordry, P. G. Foukas, D. E. Speiser and E. Goormaghtigh, Biochim. Biophys. Acta Mol. Basis Dis., 2016, 1862, 202–212.
49. N. Wald and E. Goormaghtigh, Analyst, 2015, 140, 2144–2155.
50. N. Wald, Y. Le Corre, L. Martin, V. Mathieu and E. Goormaghtigh, Biochim. Biophys. Acta Mol. Basis Dis., 2016, 1862, 174–181.
51. M. Ghassemi, S. Barzegari, P. Hajian, H. Zham, H. R. Mirzaei and F. H. Shirazi, J. Mol. Struct., 2021, 129493.
52. P. Lasch, Chemom. Intell. Lab. Syst., 2012, 117, 100–114.
53. D. Naumann, FT-IR spectroscopy of microorganisms at the Robert Koch Institute: experiences gained during a successful project, Biomedical Optical Spectroscopy, 2008, vol. 6853, pp. 95–106.
54. P. Bassan, A. Kohler, H. Martens, J. Lee, H. J. Byrne, P. Dumas, E. Gazi, M. Brown, N. Clarke and P. Gardner, Analyst, 2010, 135, 268–277.
55. P. Bassan, A. Sachdeva, A. Kohler, C. Hughes, A. Henderson, J. Boyle, J. H. Shanks, M. Brown, N. W. Clarke and P. Gardner, Analyst, 2012, 137, 1370–1377.
56. M. R. Whitbeck, Appl. Spectrosc., 1981, 35, 93–95.
57. L. Rieppo, S. Saarakkala, T. Närhi, H. J. Helminen, J. S. Jurvelin and J. Rieppo, Osteoarthr. Cartil., 2012, 20, 451–459.
58. H. Susi and D. M. Byler, Biochem. Biophys. Res. Commun., 1983, 115, 391–397.
59. S. Mika, B. Schölkopf, A. Smola, K. R. Müller, M. Scholz and G. Rätsch, Adv. Neural Inf. Process. Syst., 1998, 11.
60. L. Van Der Maaten, E. Postma and J. Van den Herik, J. Mach. Learn. Res., 2009, 10, 13.
61. S. Wartewig, IR and Raman spectroscopy: fundamental processing, John Wiley & Sons, 2006.
62. M. Pirzer and J. Sawatzki, U.S Pat., 7359815, 2008.
63. M. Člupek, P. Matějka and K. Volka, J. Raman Spectrosc., 2007, 38(9), 1174–1179.
64. R. Bhargava, S. Q. Wang and J. L. Koenig, Appl. Spectrosc., 2000, 54, 1690–1706.
65. P. A. Gorry, Anal. Chem., 1990, 62, 570–573.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2an00775d

---