Open Access Article
Open Access ArticleCreating water-in-salt-like environment using coordinating anions in non-concentrated aqueous electrolytes for efficient Zn batteries†
Dario
Gomez Vazquez
 a,
Travis P.
Pollard
a,
Travis P.
Pollard
 b,
Julian
Mars
c,
Ji Mun
Yoo
a,
Hans-Georg
Steinrück
b,
Julian
Mars
c,
Ji Mun
Yoo
a,
Hans-Georg
Steinrück
 d,
Sharon E.
Bone
e,
Olga V.
Safonova
d,
Sharon E.
Bone
e,
Olga V.
Safonova
 f,
Michael F.
Toney
f,
Michael F.
Toney
 cg,
Oleg
Borodin
b and
Maria R.
Lukatskaya
cg,
Oleg
Borodin
b and
Maria R.
Lukatskaya
 *a
*a
aDepartment of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland. E-mail: mlukatskaya@ethz.ch
bBattery Science Branch, DEVCOM Army Research Laboratory, Adelphi, MD 20783, USA
cDepartment of Chemical and Biological Engineering, University of Colorado Boulder, Boulder, CO 80309, USA
dDepartment Chemie, Universität Paderborn, Paderborn, Germany
eStanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
fPaul Scherrer Institute, Villigen PSI, 5232, Switzerland
gRenewable and Sustainable Energy Institute, University of Colorado Boulder, Boulder, CO 80309, USA
First published on 13th March 2023
Abstract
Rechargeable aqueous Zn metal batteries are promising systems for grid storage because of their high energy density, low cost, and non-flammability. However, Zn metal anodes have major limitations due to dendrite formation and concurrent water splitting during charge–discharge cycling. Both processes negatively affect coulombic efficiency (CE) and long-term cycling stability. Water-in-salt (WIS) electrolytes were previously proposed to address these challenges, yielding improvements in the cycling stability of Zn metal anodes. While WIS electrolytes help increase CE, they require high amounts of salt (often toxic) and have dramatically increased viscosity, which in turn limit their transport properties, charge–discharge rates, and usability in advanced Zn batteries. In this manuscript, we propose a strategy for simultaneously achieving high CE (>99%), high rate, low cost and reduced environmental footprint. Specifically, we show that by using coordinating anions like acetate a WIS-like Zn coordination environment can be achieved even in relatively dilute conditions, enabling prolonged cycling of Zn metal anodes. Such electrolytes have an order of magnitude higher conductivity and lower viscosity than traditional WIS electrolytes, thus enabling lower overpotentials and higher rate of Zn plating/stripping.
Introduction
Increasing the utilization of renewable energy sources such as wind and solar is necessary to reduce carbon emissions to the atmosphere.1,2 However, due to the intermittent nature of these energy sources, it is critical to develop low-cost, safe, and reliable grid-level energy storage.3–5 While Li-ion batteries are a mature technology, concerns over the usage of flammable electrolytes, their relatively high cost as well as projected supply shortages for Li6 make them suboptimal for grid storage.7 Rechargeable aqueous batteries offer a promising alternative for grid energy storage due to their lower cost and improved safety enabled by the use of non-flammable and environmentally benign electrolytes.8,9 Among these, Zn metal batteries are of great interest due to the high theoretical gravimetric (∼820 mA h g−1) and volumetric (∼5800 mA h cm−3) capacities of Zn metal anodes as well as the high abundance, mature recycling infrastructure and low toxicity of Zn.10–12 However, the commercialization of Zn metal anodes faces several critical challenges. First, concurrent hydrogen evolution reaction (HER) during Zn plating negatively affects coulombic efficiency (CE) and leading to continuous electrolyte consumption and pressure-build-up in a battery cell, thereby reducing cycling stability.10,11,13–15 Another major problem for Zn metal anodes is dendrite formation during plating that can lead to short-circuiting of the cells.16,17Several approaches involving electrolyte engineering were proposed to address these challenges.15–20 For example, the replacement of relatively dilute, salt-in-water electrolytes with highly concentrated ones (water-in-salt electrolytes, WIS) was shown effective in suppressing both HER and dendrite formation.21–23 In WIS electrolytes, the fraction of salts is higher than water by weight and/or volume.24 As a result, at such high salt concentrations, there are not enough water molecules to fully solvate ions of the electrolyte, leading to disruption of hydrogen bonding and increased ion–ion interactions (ion pair and ion aggregate formation). This leads to increased participation of anions in Zn-ion solvation22,25 that together with disrupted hydrogen bonding is assumed to suppress HER, yielding improved coulombic efficiencies and cycle life.26,27 For example, the use of 1 m ZnTFSI2 + 20 m LiTFSI WIS or 30 m K acetate (KOAc) + 3 m Li acetate (LiOAc) + 3 m Zn acetate (ZnOAc2) electrolytes leads to an increase in Zn plating-stripping CE up to 99.9%22 and 99.6%,28 respectively, compared to single salt dilute electrolytes.
In this work, we examine whether the WIS regime for electrolytes is always the most advantageous for cycling Zn anodes or if equivalent or even more promising performance can be achieved with non-WIS electrolytes. Prior research indicates that Zn plating and stripping efficiency is strongly affected by the Zn-ion coordination environment that is influenced by electrolyte speciation.14,29 However, the primary parameter considered in much of the literature relates to electrolyte concentration, where at WIS conditions anions are forced into coordination sphere of Zn. Meanwhile, it is known that anion-rich, water-deficient coordination can be achieved for cations even in salt-in-water solutions if anion coordination ability is higher than that of water.30–32 Herein, we investigate how electrolyte concentration affects the local coordination of Zn ions in mixed-cation acetate solutions and how modified electrolyte speciation affects the physicochemical characteristics of electrolytes and the Zn plating/stripping efficiency. Acetate salts were chosen due to the acetate anion's strong coordination ability towards transition metal ions (relative to water), their low cost, and environmental friendliness.33–35 We show that the use of WIS systems per se does not necessarily increase the efficiency of Zn batteries and that the role of the anion and supporting cation should be considered in electrolyte engineering for Zn batteries. For the examined solution series (Zn0.2K0.8OAc1.2nH2O), we demonstrate that a WIS-like coordination environment is already observed around Zn for a water-to-cation ratio of n = 10, allowing us to achieve both high CE (99.8%), rate performance compared to both more dilute or concentrated (WIS) regimes. Importantly, we provide comprehensive electrolyte characterization linking its structure and physicochemical properties to electrochemical performance. In addition to extensive validation of the modeling results, we uncover and discuss quantitative differences with the previous reports for WIS bisalt Zn aqueous acetate-based electrolytes.36
Results and discussion
Zn-ion solvation, electrolyte structure, and physicochemical properties
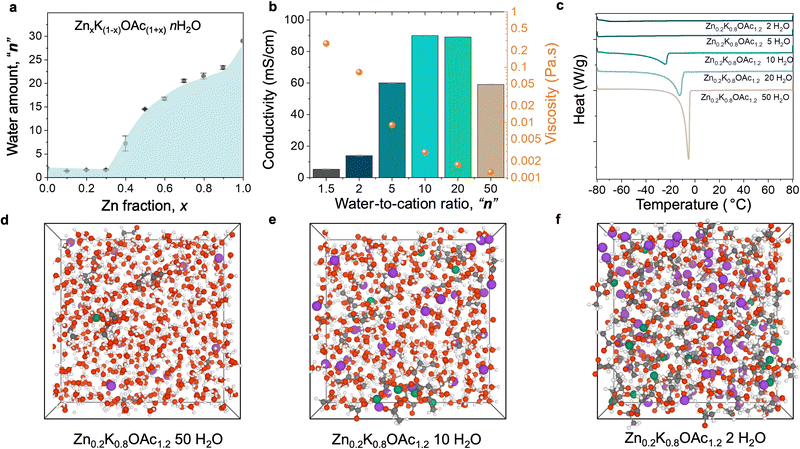
Achieving the WIS regime for Zn2+-based electrolytes is challenging due to insufficient solubility of most Zn salts and often requires the use of a supporting salt. In this work, we study environmentally friendly zinc and potassium acetate electrolytes, where potassium acetate is a supporting salt that enables WIS conditions.33 First, we evaluated the solubility of Zn and K acetate (OAc) mixtures ZnxK1−xOAc1+xnH2O, where “x” is a molar fraction of Zn salt and “n” is the number of water molecules per cation (Zn2+ and K+). The measured liquidus line (Fig. 1(a)) shows that the maximum solubility is achieved when the Zn fraction is 0.1–0.3, which corresponds to a WIS electrolyte (1.5 water molecules per cation). Because we observe a dramatic increase in viscosity for x = 0.3 that negatively affects ion transport (Fig. S1a, ESI†), we select the composition series with x = 0.2 (Zn0.2K0.8OAc1.2nH2O, with n varying from 1.5 (WIS) to 50 (relatively dilute)).Table S1 (ESI†) summarizes the physicochemical properties of the Zn0.2K0.8OAc1.2nH2O electrolytes. The presence of K+ results in an increased conductivity of the electrolyte compared to pure Zn(OAc)2 (Table S1, ESI†). Conductivity of mixed-cation electrolytes reaches a maximum of 90 mS cm−1 at n = 10 (Fig. 1(b)). When the electrolyte enters WIS regime (n < 5), conductivity rapidly decreases while viscosity dramatically increases, reaching a maximum at n = 1.5 (lowest value tested). The Walden plot analysis shows that the behavior of studied Zn–K acetate electrolyte series can be characterized as “good ionic” or moderately “associated”37 (Fig. S1b, ESI†). Further, we analyzed thermal properties of the solution series using differential scanning calorimetry (DCS). Fig. 1(c) depicts the corresponding differential scanning thermograms. The most dilute electrolyte (n = 50) displays normal melting/freezing at temperatures −4.9 °C. Upon increasing the electrolyte concentration from n = 50 to n = 10, the melting drops to −24 °C at n = 10. Further increases in electrolyte concentration (n ≤ 5) are characterized by the suppression of the electrolyte melting/freezing transition and drop in heat capacities (Fig. S2, ESI†). Similar behavior was observed for Li-KOAc33 and other38–41 WIS electrolytes.
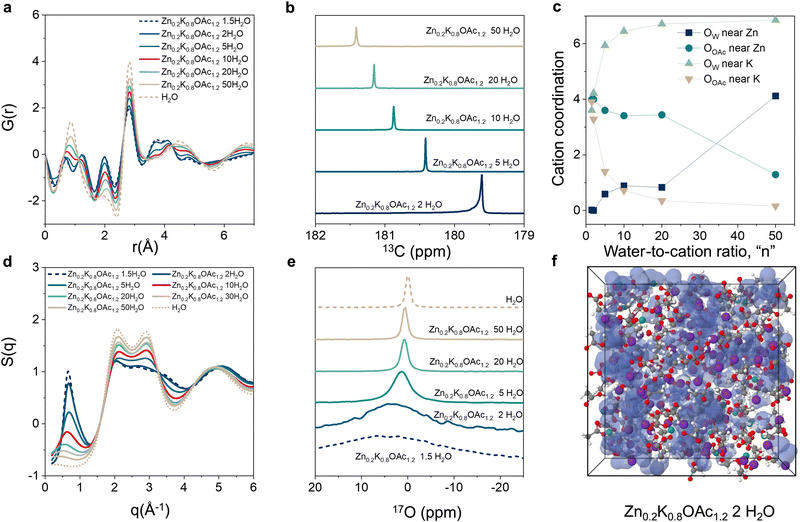
Next, we studied the changes in electrolyte structure and speciation (MD generated electrolyte visualization, Fig. 1(d)–(f)). From pair distribution function (PDF) measurements (Fig. 2(a)) we observe that a concentration increase leads to an increase in ion pair formation between Zn2+ and OAc− as signified by increased intensity of the peak at ∼3.6 Å (Zn–C). This is also in agreement with molecular dynamics (MD) simulations results (see the radial distribution function (RDF) analysis, Fig. S3, ESI†). Similarly, 13C NMR data shows upfield shift of the carbon of carboxylate group (acetate anion) with concentration (Fig. 2(b)) as a result of ion shielding due to increased number of OAc− coordinating to the same cation.42
MD simulations show that K+ has stronger affinity to water vs acetate while the reverse is true for Zn2+. Even in dilute conditions (n = 50), simulations suggest Zn2+ is already partially coordinated by acetate while K+ is fully coordinated by water (Fig. 2(c)). Starting from intermediate concentrations (n = 10), Zn2+ becomes mainly coordinated by acetate while K+ remains coordinated mostly by water molecules (Fig. 2(c) and Fig. S4, ESI†). Upon further increase in concentration (n ≤ 5) the electrolyte enters the WIS regime and K+ starts to be partially coordinated by acetate (Fig. 2(c)). Changes in electrolyte structure at the nanoscale are reflected in the X-ray scattering data S(q). As concentration increases, a progressive increase in the intensity of the low-q peak (0.3 Å−1 < q < 1.5 Å−1), as well as its shift towards larger q values, is observed (Fig. 2(d)).43 This peak can be attributed to the nanoscale compositional segregation.34 It is important to note that experimental and MD-calculated structure factors, S(q), are in good agreement with each other (Fig. S5–S7, ESI†), indicating sufficient accuracy of the MD predictions.
We also observe that the increase in concentration results in a disruption of the hydrogen bonding network and decreases the prevalence of “free” water.17O NMR shows increased interaction of the water molecules with cations in WIS regime (n = 2) as can be seen from the peak shift by 4 ppm compared to pure water (Fig. 2(e)).33 Moreover, MD simulations indicate formation of the water-rich and water-deficient domain at n < 10 (Fig. 2(f) and Fig. S8a–c, ESI†).
Zn2+ solvation environment
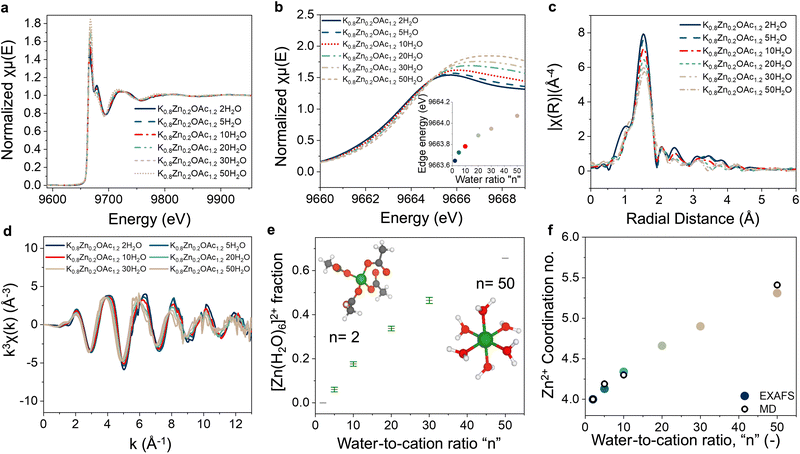
The coordination environment of Zn2+ was studied using XAS (Fig. 3(a)). X-ray absorption near-edge structure (XANES) of Zn2+ shows a gradual decrease in the edge energy with increasing concentration (Fig. 3(b)). We speculate that this can be explained by the increased electron density on Zn2+ when water molecules are displaced by acetate anions in the solvation shell (acetate anion has a higher Lewis basicity than water30,44,45). This explanation also agrees with the 13C NMR results (discussed above, Fig. 2(b)) and MD-generated RDF (Fig. 2(c) and Fig. S4, ESI†) where the acetate interactions with cations and RDF peak for Zn–OOAc relative to Zn–OW increase with concentration.Next, evolution of the Zn2+ coordination environment in electrolytes as a function of concentration was examined using extended X-ray absorption fine structure (EXAFS). All studied electrolytes display a prominent peak at ∼1.5 Å that can be attributed to Zn–O (Fig. 3(c)). Increasing concentration leads to an increasing intensity in the peak shoulder at ∼2.5 Å and the peak at 3–4 Å indicative of a change in the Zn2+ coordination environment. As NMR, PDF, and XANES data suggest, the displacement of water from the coordination sphere of Zn2+ takes place when concentration is increased. The presence of isosbestic points in the EXAFS spectra indicates co-existence of two coordination environments of Zn2+ in each electrolyte of the series, from dilute (n = 50) to the most concentrated (n = 2) (Fig. S9a, ESI†). As a result, for each electrolyte in the series, we can generate high quality fitting of the EXAFS spectra using a linear combination of the experimental spectra of most diluted (n = 50) and most concentrated electrolytes (n = 2) (Fig. S9b–f, ESI†).
To obtain a more quantitative understanding of the Zn coordination environment at different concentrations, we compared the quality of fits of the EXAFS spectra for the electrolytes with density functional theory (DFT) generated Zn2+ coordination models (Table S2, ESI†). In dilute conditions, the best fit was obtained using a linear combination of the two DFT models, [Zn(H2O)6]2+ and [Zn(OAc)4]2− with respective fractions of 0.66 and 0.34 (Fig. S10a–c, ESI†), which improved the goodness of fit (Tables S2 and S3, ESI†). These results are also in agreement with MD simulations that suggest co-presence of acetate and water molecules in the coordination sphere of Zn2+ in dilute conditions (n = 50) (Fig. 2(c)). For the most concentrated electrolyte (n = 2), the best fit was generated using solely the [Zn(OAc)4]2− DFT model (Fig. S10e–f, ESI†). Since the intermediate concentrations (n = 5, 10, 20, and 30) can be fitted well using linear combination of the spectra for most concentrated (n = 2) and most diluted (n = 50) electrolytes (Fig. S9b–f, ESI†) good fits were obtained using a linear combination of the [Zn(H2O)6]2+ and [Zn(OAc)4]2− DFT models (Table S3, ESI† and Fig. 3(e)). The resulting averaged coordination numbers are in good agreement with the predicted values from MD (Fig. 3(f)). It is important to note, that our experimental and MD simulations data, revealing [Zn(OAc)4]2− as the main Zn coordination environment for electrolytes with n < 10, are in contrast to the previous reports36 that predicted formation of multiple 6-coordinated complexes including [Zn(OAc)6]4− as well as the partially hydrated [Zn(OAc)3 (H2O)2]− for 30 m KOAc + 3 m LiOAc + 3 m ZnOAc2 in water and a Zn2+ coordination number >5.1 oxygens.36
Electrochemical characterization
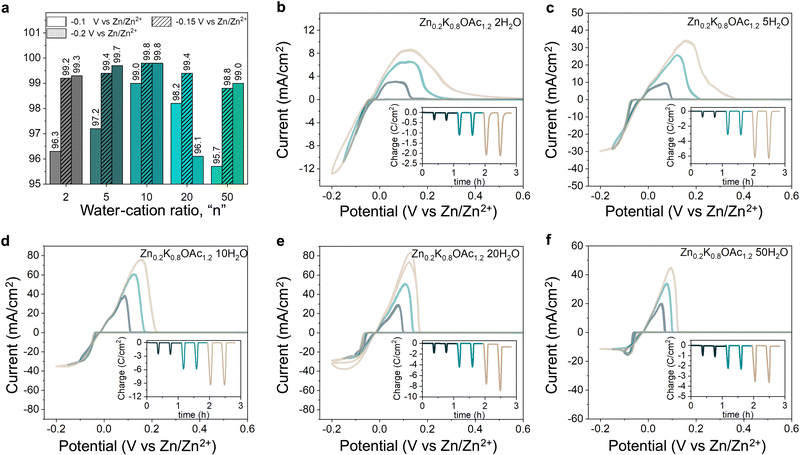
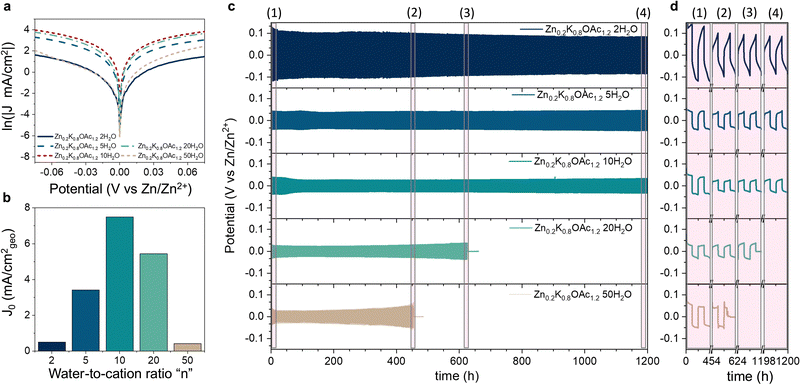
Electrolyte speciation strongly affects reversibility and morphology of Zn plating/stripping as well as parasitic currents associated with processes such as hydrogen evolution. Using cyclic voltammetry (CV), we evaluated effects of electrolyte composition on Zn plating/stripping efficiency at different cut-off plating potentials (−0.1, −0.15 and −0.2 V vs. Zn/Zn2+, see Fig. 4). The CE can be seen following a bell shape with electrolyte concentration for all cut-offs, reaching a maximum of 99.8% (Fig. 4(a)) at intermediate water-to-cation ratios (n = 10). This improvement in CE can be attributed to favorable Zn plating kinetics over HER as a result of the change in the Zn2+ coordination environment from water-containing to acetate-rich (Fig. 2(C) and Table S3, ESI†).46 Further increase in concentration leads to the decrease in CE, which can be ascribed to the high stripping overpotentials due to more sluggish ion transport and low conductivities (Table S1 and Fig. S11, ESI†). Generally, we observed higher CE for higher cut-off potentials (Fig. 4(a)) in agreement with previous reports.47 The only exception was the electrolyte Zn0.2K0.8OAc1.2 20H2O, where the CE drops from 99.4% at −0.15 V to 96.1% at −0.2 V (see Fig. 4(a)), this could be attributed to dendrite formation (and hence electrochemical area increase) as can be seen from higher charge associated with plating during the last CV cycle. Same bell shape CE trend with concentration is observed in a cell configuration with a limited electrolyte amount where the highest CE (99.9%) is obtained in Zn0.2K0.8OAc1.2 10H2O (see Fig. S12, ESI†). Additionally, we characterized CE of Zn plating/stripping using a modified “Aurbach” protocol. The same CE trend was observed with the highest CE (99.1%) for Zn0.2K0.8OAc1.2 10H2O electrolyte (see Fig. S13, ESI†). Further, since DSC results demonstrate a dramatically suppressed freezing point (Fig. 1(c)), for the optimal electrolyte composition (Zn0.2K0.8OAc1.2 10H2O) we performed CV plating-stripping at −5 °C and observed similarly high CE of Zn plating/stripping (99.8%) (see Fig. S12a and d and S14, ESI†).To gain further insights into the effect of electrolyte speciation on the kinetics of Zn plating/stripping process, Tafel slopes were analyzed (Fig. 5(a)) and exchange current density, j0, values were estimated for each electrolyte (Fig. 5(b) and Fig. S15, ESI†). We observe that the exchange current density reaches its highest value for the intermediate water-to-cation ratio (n = 10). Upon further increase in electrolyte concentration, the exchange current drops considerably to its lowest value at n = 2. It is important to note, that two main factors can affect the exchange current density values: the changes in the reaction constant and the activity of the ions in the solution. To decouple individual contribution of both factors, the real activity would need to be quantified, which is challenging.48
Finally, we performed long-term galvanostatic cycling at 1 mA cm−2 of Zn–Zn symmetric cells to assess affinity to dendrite formation as a function of electrolyte speciation. The best cycling stability coupled with low plating/stripping overpotentials is observed for electrolytes at n = 5 and n = 10, where >1000 h of continuous cycling without short-circuiting can be achieved (Fig. 5(c) and (d)). In contrast, cells with electrolytes in the salt-in-water regime (n = 50, n = 20) fail due to dendrite-induced short-circuit after ∼450 and 620 h of cycling, respectively. The lower cycling stability may be related to co-presence of Zn2+ solvated by water that is known to promote dendritic deposits49,50 or the formation of stronger concentration gradients and therefore favorable conditions for dendritic growth.51–53 In electrolytes with the lowest water-to-cation ratio of n = 2 high overpotentials (∼200 mV vs. 50 mV for n = 10) were observed due to dramatically increased viscosities and lower ionic conductivities (Fig. 1(b)), resulting in sluggish Zn2+ transport (Fig. S11, ESI†). Finally, the cycled Zn electrodes were characterized using SEM revealing a conformal deposit morphology for n = 10, in contrast to rough and flakey deposits observed for n = 50 and n = 2 (Fig. S16, ESI†).
Conclusions
In conclusion, we demonstrate that coordinating anions such as acetate can create a WIS-like coordination environments in electrolytes that are relatively dilute. Using XAS and MD simulations we show that in a non-concentrated state, the Zn2+ coordination environment is already WIS-like, with Zn2+ ions being predominantly coordinated by acetate rather than water. These electrolytes can enable Zn plating/stripping with a high CE > 99% and long-term cyclability without a considerable increase in viscosity (which is typical of WIS electrolytes). The best performance is achieved when water-to-cation ratios are 10 and 5 (non-WIS conditions). Overall, we conclude that WIS electrolytes do not always represent an optimal medium for efficient Zn plating/stripping and can result in lower CE and slower kinetics. We suggest that the coordination strength of anion towards Zn is an important parameter in electrolyte engineering determining Zn coordination and plating/stripping efficiency.Materials and methods
Materials
Zn foil (>99.95%) was purchased from Goodfellow. Zn acetate dihydrate (>99%), Potassium acetate (>99%), and other chemicals were purchased from Sigma Aldrich. The salts were stored and weighed inside the glovebox to avoid water uptake from the atmosphere.Liquidus line measurements
To obtain liquidus curve depicted in Fig. 1(a), the mixtures of ZnOAc2 and KOAc salts were prepared inside the Ar-filled glovebox and sealed in vials with septa to avoid water uptake from the atmosphere. Water was added to each vial in small increments using a volumetric glass syringe, and the vials were sonicated for ∼3 hours at 50 °C after each water addition. After cooling to room temperature, water was added after each heating/sonication process until the salt mixture was entirely dissolved. To ensure that the salts stayed dissolved, the vials were kept at room temperature for at least 7 days.Conductivity was measured using an Oakton 2700 benchtop meter.
Electrolyte viscosities were measured using an oscillatory rheometer (ARES-G2, TA Instruments). The measurements were performed in the cone-cup and cone-plate (for viscous electrolytes) geometries. The shear rate was variated from 10 to 1000 Hz.
Differential scanning calorimetry (DSC) measurements were carried out using DSC 2500 (TA Instruments). Prior to the measurements, the samples were cycled once from −80 °C to 80 °C and again to −80 °C at a rate of 10 °C min−1. Data was then collected from −80 °C to 80 °C at a rate of 1 °C min−1.
Scanning electron microscopy (SEM)
The SEM images of the cycled electrodes were collected using Hitachi S-4800 microscope.Nuclear magnetic resonance (NMR)
13C and 17O NMR measurements were acquired on a Bruker ASCEND 400 and 500, respectively. For 13C NMR, 1 mL of each solution were prepared using D2O (Sigma Aldrich, 99.9%) to dissolve the respective salt mixtures. The samples were prepared with the same methodology described for the liquidus line (i.e. salts were weighted inside Ar filled glovebox, vials were sealed with septa, D2O was added using syringe). After preparation, 700 μL of the electrolytes was transferred to NMR tubes (Duran Wheaton Kimble) and tightly closed with a plastic cap and parafilm. For 17O NMR measurement, 700 μL of the respective electrolytes Zn0.2K0.8OAc1.2nH2O were transferred to NMR tubes, to improve 17O signal, 10 μL of 7.7% 17O enriched H2O (Sigma Aldrich) was added to each sample. The samples were measured at 25 ± 0.1 °C. The collected data was processed using MestReNova X64.X-Ray absorption spectroscopy (XAS)
XAS was measured in the Swiss Light source at PSI in the Line X10DA-SuperXAS using a Si (111) monochromator and an ionization chamber for transmission detection. The XAS collection was done in Quick EXAFS (QEXAFS) mode54 around the Zn K-edge (9450–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 eV), using Zn metal foil for energy calibration (Edge at 9659 eV). To avoid beam damage, during measurement the electrolyte was pumped at a rate of 100 μL min−1 through a microfluidic channel from TOPAS (ChipShop, Germany) with a channel depth of 400 μm. The data was collected for 5 minutes and processed using the ProXAS GUI55 (averaging of QEXAFS collected data, calibration) and the Demeter software package56 (post processing, and fitting). The XAS data processing was done in Athena, edge energy was defined as the energy at which the 2nd derivate is zero. The EXAFS data were extracted from normalized XAS spectra and by fitting a spline to the data region between k = 3–12 Å−1. The resulting EXAFS data sets were then plotted using a k3 weighting. For the fitting, the amplitude reduction factor S02 was assumed to be unity based on prior literature.57
800 eV), using Zn metal foil for energy calibration (Edge at 9659 eV). To avoid beam damage, during measurement the electrolyte was pumped at a rate of 100 μL min−1 through a microfluidic channel from TOPAS (ChipShop, Germany) with a channel depth of 400 μm. The data was collected for 5 minutes and processed using the ProXAS GUI55 (averaging of QEXAFS collected data, calibration) and the Demeter software package56 (post processing, and fitting). The XAS data processing was done in Athena, edge energy was defined as the energy at which the 2nd derivate is zero. The EXAFS data were extracted from normalized XAS spectra and by fitting a spline to the data region between k = 3–12 Å−1. The resulting EXAFS data sets were then plotted using a k3 weighting. For the fitting, the amplitude reduction factor S02 was assumed to be unity based on prior literature.57
Total X-ray scattering
Total X-ray scattering was acquired at the Advanced Photon Source (APS) at Argonne National Laboratory (ANL) at beamline 11-ID-B with an X-ray Energy of 58.66 keV (λ = 0.213 Å). A PerkinElmer XRD 1621 detector was placed at a distance of 0.296 m from the sample. The data ranged from q = 0.26–17 Å−1, corresponding to length scales of 24 Å and 0.37 Å, respectively. Samples were filled into 2 mm quartz X-ray capillaries with a wall thickness of 0.01 mm (WJM-Glass) and sealed with Master Bond EP 30-2 low outgassing epoxy resin. Data were recorded for a total of 690 s on a total of 3 different positions on the capillary.Data with q ≳ 2 Å−1 originates in inter- and intra-molecular correlations, which are also represented in the real space pair distribution (PDF). In contrast, data with q ≲ 2 Å−1 corresponds to scattering originating from longer length scales such as nanoscale phase segregation in the form of ion clusters.43 The data reduction and analysis were performed using PyFAI and PDFGetX258,59 to extract S(q) and PDF in G(r) space. The background was subtracted and scaled with the sample transmission. We corrected our data for standard geometric detector corrections, polarization, sample self-absorption, oblique incidence, and Compton scattering. A Lorch function was applied before the Fourier transformation to reduce termination ripples.
Electrochemical characterization
CV plating/stripping was performed in a 3-electrode cell using a 2 mm Au disk working electrode (CH Instruments) and a Zn foil as counter, and a separate Zn foil as reference electrodes. Additional experiments were performed using a Swagelok cell in a 3-electrode configuration, where 2 mm Au disk served as working electrode, 6 mm Zn disk as counter electrode, additional Zn foil was used as reference. Electrolyte volume was kept at 150 μL and working and counter electrodes were separated using a 380 μm Teflon spacer. To collect CVs at −5 °C, electrochemical cell was placed into Binder KB 53 environmental chamber with temperature set at −5 °C.The modified Aurbach protocol was performed using 2 electrode Swagelok cell with Cu disk working electrode (∅12.5 mm) and Zn foil disk counter electrode, glass fiber was used as a separator, 100 μl of electrolyte was added during assembly. The detailed experimental sequence was the following: first, plating, stripping and re-deposition of excess amount of Zn was performed with a current density of 3 mA cm−2 and a specific areal capacity of 5 mA h cm−2, second Zn stripping and plating sequences were performed for 10 times with a current density of 0.5 mA cm−2 and a specific areal capacity of 1 mA h cm−2. Finally, Zn stripping was carried out with current density of 3 mA cm−2 with a cut off voltage set at 0.5 V.
To reduce effect of mass transfer limitations, exchange current measurements were performed using rotating disk electrode (RDE) set-up at 2000 rpm. The working electrode was a 4 mm Au disk with electrodeposited layer of Zn that was polished with 300 nm alumina powder (CH instruments) and cleaned and sonicated in Milli-Q water before the experiment. The counter electrode was a Zn foil placed at ∼5 mm from the working electrode, the reference electrode was Ag/AgCl in 1M KCl (CH instruments). The linear fitting of the Tafel slopes was done in the negative overpotential range from −25 to −50 mV (Fig. S13, ESI†).
Zn–Zn symmetric cells cycling test was performed in 2-electrode Swagelok cell with Zn foil disk electrodes (6 mm in diameter), a 1 mm thick glass fiber separator (∼0.5 mm after compression) and 75 μL of electrolyte. The cells were aged for 1 day and afterwards were cycled in a constant current program at 1 mA cm−2 for a specific areal capacity of 0.5 mA h cm−2 (30 min). The cut off voltages were fixed at ±0.5 V.
Molecular dynamics simulations – density functional theory calculations
Molecular dynamics simulations using the AMOEBA polarizable force field were performed using a locally-modified version of Tinker HP v1.2 to output the stress tensor at the desired frequency.60,61 Two parameterizations of the force field were considered, the first of which (force field 1, FF1) produced results that compared favorably against experimental conductivity data (Table S1, ESI†) and a second (force field 2, FF2) which lowered the average error in the binding energies between the force field prediction and density functional theory with an assortment of solvate species composed of K+ or Zn2+ with differing amounts of OAc− and water. Due to FF2 systematically overestimating conductivities, the analysis presented here focuses on results extracted from simulations with FF1. A detailed discussion of the workflow for the simulation and analysis methodologies is expanded upon in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. R. L., D. G. V. acknowledge support from ReMaP project funded by the Swiss Federal Office of Energy under contract SI/501810-01 and the ETH Foundation. J. M. Y. acknowledges support from Schmidt Science Fellowship funded by Schmidt Futures in partnership with the Rhodes Trust (Oxford, United Kingdom). D. G. V. acknowledges the Paul Scherrer Institute, Villigen, Switzerland for provision of synchrotron radiation beamtime at beamline X10DA Super-XAS of the SLS. Support for the X-ray PDF (M. F. T., J. M.) and computation (T. P. P., O. B.) studies was provided by the Joint Center for Energy Storage Research, an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under contract no. DE-AC02-06CH11357. The use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515.References
- J. P. Barton and D. G. Infield, IEEE Trans. Energy Convers, 2004, 19, 441–448 CrossRef.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
- D.-S. Kourkoumpas, G. Benekos, N. Nikolopoulos, S. Karellas, P. Grammelis and E. Kakaras, Appl. Energy, 2018, 231, 380–398 CrossRef.
- A. Mamen and U. Supatti, 2017.
- Z. Yang, J. Zhang, M. C. W. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef CAS PubMed.
- C. Curry, 2017.
- Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Chem. Rev., 2021, 121, 1623–1669 CrossRef CAS PubMed.
- J. Zhang, X. Yao, R. K. Misra, Q. Cai and Y. Zhao, J. Mater. Sci. Technol., 2020, 44, 237–257 CrossRef CAS.
- H. Wang, R. Tan, Z. Yang, Y. Feng, X. Duan and J. Ma, Adv. Energy Mater., 2021, 11, 2000962 CrossRef CAS.
- H. Jia, Z. Wang, B. Tawiah, Y. Wang, C.-Y. Chan, B. Fei and F. Pan, Nano Energy, 2020, 70, 104523 CrossRef CAS.
- K. Hu, X. Guan, R. Lv, G. Li, Z. Hu, L. Ren, A. Wang, X. Liu and J. Luo, Chem. Eng. J., 2020, 396, 125363 CrossRef CAS.
- M. Kaya, S. Hussaini and S. Kursunoglu, Hydrometallurgy, 2020, 195, 105362 CrossRef CAS.
- M. B. Lim, T. N. Lambert and B. R. Chalamala, Mater. Sci. Eng. R Rep., 2021, 143, 100593 CrossRef.
- W. Lu, C. Zhang, H. Zhang and X. Li, ACS Energy Lett., 2021, 6, 2765–2785 CrossRef CAS.
- V. Verma, S. Kumar, W. Manalastas and M. Srinivasan, ACS Energy Lett., 2021, 6, 1773–1785 CrossRef CAS.
- X. Guo, Z. Zhang, J. Li, N. Luo, G.-L. Chai, T. S. Miller, F. Lai, P. Shearing, D. J. L. Brett, D. Han, Z. Weng, G. He and I. P. Parkin, ACS Energy Lett., 2021, 6, 395–403 CrossRef CAS.
- Q. Zhang, J. Luan, Y. Tang, X. Ji and H. Wang, Angew. Chem., Int. Ed., 2020, 59, 13180–13191 CrossRef CAS PubMed.
- L. Ma, M. A. Schroeder, T. P. Pollard, O. Borodin, M. S. Ding, R. Sun, L. Cao, J. Ho, D. R. Baker, C. Wang and K. Xu, Energy Environ. Mater., 2020, 3, 516–521 CrossRef CAS.
- L. Cao, D. Li, T. Pollard, T. Deng, B. Zhang, C. Yang, L. Chen, J. Vatamanu, E. Hu, M. J. Hourwitz, L. Ma, M. Ding, Q. Li, S. Hou, K. Gaskell, J. T. Fourkas, X.-Q. Yang, K. Xu, O. Borodin and C. Wang, Nat. Nanotechnol., 2021, 16, 902–910 CrossRef CAS PubMed.
- M. Yan, N. Dong, X. Zhao, Y. Sun and H. Pan, ACS Energy Lett., 2021, 3236–3243, DOI:10.1021/acsenergylett.1c01418.
- Y. Zhang, G. Wan, N. H. C. Lewis, J. Mars, S. E. Bone, H.-G. Steinrück, M. R. Lukatskaya, N. J. Weadock, M. Bajdich, O. Borodin, A. Tokmakoff, M. F. Toney and E. J. Maginn, ACS Energy Lett., 2021, 6, 3458–3463 CrossRef CAS.
- F. Wang, O. Borodin, T. Gao, X. Fan, W. Sun, F. Han, A. Faraone, J. A. Dura, K. Xu and C. Wang, Nat. Mater., 2018, 17, 543–549 CrossRef CAS PubMed.
- T. F. Burton, R. Jommongkol, Y. Zhu, S. Deebansok, K. Chitbankluai, J. Deng and O. Fontaine, Curr. Opin. Electrochem., 2022, 35, 101070 CrossRef CAS.
- V. A. Azov, K. S. Egorova, M. M. Seitkalieva, A. S. Kashin and V. P. Ananikov, Chem. Soc. Rev., 2018, 47, 1250–1284 RSC.
- S. B. Pillai, R. J. Wilcox, B. G. Hillis, B. P. Losey and J. D. Martin, J. Phys. Chem. B, 2022, 126, 2265–2278 CrossRef CAS PubMed.
- W. Yang, Y. Yang, H. Yang and H. Zhou, ACS Energy Lett., 2022, 7, 2515–2530 CrossRef CAS.
- A. Bayaguud, Y. Fu and C. Zhu, J. Energy Chem., 2022, 64, 246–262 CrossRef CAS.
- J. Han, A. Mariani, A. Varzi and S. Passerini, J. Power Sources, 2021, 485, 229329 CrossRef CAS.
- W. Sun, F. Wang, B. Zhang, M. Zhang, V. Küpers, X. Ji, C. Theile, P. Bieker, K. Xu, C. Wang and M. Winter, Science, 2021, 371, 46 CrossRef CAS PubMed.
- S. Alvarez, Chem. – Eur. J., 2020, 26, 4350–4377 CrossRef CAS PubMed.
- J. Jorne and W. T. Ho, J. Electrochem. Soc., 1982, 129, 907–912 CrossRef CAS.
- X. Wu, Y. Xu, C. Zhang, D. P. Leonard, A. Markir, J. Lu and X. Ji, J. Am. Chem. Soc., 2019, 141, 6338–6344 CrossRef CAS PubMed.
- M. R. Lukatskaya, J. I. Feldblyum, D. G. Mackanic, F. Lissel, D. L. Michels, Y. Cui and Z. Bao, Energy Environ. Sci., 2018, 11, 2876–2883 RSC.
- J. Han, A. Mariani, M. Zarrabeitia, Z. Jusys, R. J. Behm, A. Varzi and S. Passerini, Small, 2022, 18, 2201563 CrossRef CAS PubMed.
- P. L. Stigliano, N. Pianta, S. Bonizzoni, M. Mauri, R. Simonutti, R. Lorenzi, B. Vigani, V. Berbenni, S. Rossi, P. Mustarelli and R. Ruffo, Phys. Chem. Chem. Phys., 2021, 23, 1139–1145 RSC.
- J. Han, A. Mariani, A. Varzi and S. Passerini, J. Power Sources, 2021, 485, 229329 CrossRef CAS.
- C. Austen Angell, Y. Ansari and Z. Zhao, Faraday Discuss., 2012, 154, 9–27 RSC.
- Q. Zhang, Y. Ma, Y. Lu, L. Li, F. Wan, K. Zhang and J. Chen, Nat. Commun., 2020, 11, 4463 CrossRef CAS PubMed.
- J. Holoubek, H. Liu, Z. Wu, Y. Yin, X. Xing, G. Cai, S. Yu, H. Zhou, T. A. Pascal, Z. Chen and P. Liu, Nat. Energy, 2021, 6, 303–313 CrossRef CAS PubMed.
- T. Sun, X. Yuan, K. Wang, S. Zheng, J. Shi, Q. Zhang, W. Cai, J. Liang and Z. Tao, J. Mater. Chem. A, 2021, 9, 7042–7047 RSC.
- Q. Zhang, K. Xia, Y. Ma, Y. Lu, L. Li, J. Liang, S. Chou and J. Chen, ACS Energy Lett., 2021, 6, 2704–2712 CrossRef CAS.
- Y. Zhu, J. Yin, X. Zheng, A.-H. Emwas, Y. Lei, O. F. Mohammed, Y. Cui and H. N. Alshareef, Energy Environ. Sci., 2021, 14, 4463–4473 RSC.
- H. V. R. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 9507–9508 CrossRef CAS.
- W. Linert, Y. Fukuda and A. Camard, Coord. Chem. Rev., 2001, 218, 113–152 CrossRef CAS.
- I. P. Oliveri and S. Di Bella, Dalton Trans., 2017, 46, 11608–11614 RSC.
- J. Cao, D. Zhang, X. Zhang, Z. Zeng, J. Qin and Y. Huang, Energy Environ. Sci., 2022, 15, 499–528 RSC.
- L. Ma, M. A. Schroeder, O. Borodin, T. P. Pollard, M. S. Ding, C. Wang and K. Xu, Nat. Energy, 2020, 5, 743–749 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, 2nd edn, 2001 Search PubMed.
- P. Sun, L. Ma, W. Zhou, M. Qiu, Z. Wang, D. Chao and W. Mai, Angew. Chem., Int. Ed., 2021, 60, 18247–18255 CrossRef CAS PubMed.
- Z. Cao, P. Zhuang, X. Zhang, M. Ye, J. Shen and P. M. Ajayan, Adv. Energy Mater., 2020, 10, 2001599 CrossRef CAS.
- Y. Zuo, K. Wang, P. Pei, M. Wei, X. Liu, Y. Xiao and P. Zhang, Mater. Today Energy, 2021, 20, 100692 CrossRef CAS.
- K. Wang, P. Pei, Z. Ma, H. Chen, H. Xu, D. Chen and X. Wang, J. Mater. Chem. A, 2015, 3, 22648–22655 RSC.
- C. Brissot, M. Rosso, J. N. Chazalviel and S. Lascaud, J. Power Sources, 1999, 81–82, 925–929 CrossRef CAS.
- O. Muller, M. Nachtegaal, J. Just, D. Lutzenkirchen-Hecht and R. Frahm, J. Synchrotron Radiat., 2016, 23, 260–266 CrossRef PubMed.
- A. H. Clark, J. Imbao, R. Frahm and M. Nachtegaal, J. Synchrotron Radiat., 2020, 27, 551–557 CrossRef PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- P. D'Angelo, V. Barone, G. Chillemi, N. Sanna, W. Meyer-Klaucke and N. V. Pavel, J. Am. Chem. Soc., 2002, 124, 1958–1967 CrossRef PubMed.
- X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37, 678 CrossRef CAS.
- G. Ashiotis, A. Deschildre, Z. Nawaz, J. P. Wright, D. Karkoulis, F. E. Picca and J. Kieffer, J. Appl. Crystallogr., 2015, 48, 510–519 CrossRef CAS PubMed.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht and R. A. DiStasio Jr, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- L. Lagardère, L.-H. Jolly, F. Lipparini, F. Aviat, B. Stamm, Z. F. Jing, M. Harger, H. Torabifard, G. A. Cisneros, M. J. Schnieders, N. Gresh, Y. Maday, P. Y. Ren, J. W. Ponder and J.-P. Piquemal, Chem. Sci., 2018, 9, 956–972 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ee00205e |
| This journal is © The Royal Society of Chemistry 2023 |