Open Access Article
Open Access ArticleY2(Ge,Si)O5:Pr phosphors: multimodal temperature and pressure sensors shaped by bandgap management†
Małgorzata
Sójka
 a,
Marcin
Runowski
a,
Marcin
Runowski
 *b,
Przemysław
Woźny
b,
Luis D.
Carlos
*b,
Przemysław
Woźny
b,
Luis D.
Carlos
 c,
Eugeniusz
Zych
c,
Eugeniusz
Zych
 *a and
Stefan
Lis
*a and
Stefan
Lis
 b
b
aFaculty of Chemistry, University of Wroclaw, 14. F. Joliot-Curie Street, 50-383 Wroclaw, Poland. E-mail: eugeniusz.zych@chem.uni.wroc.pl
bFaculty of Chemistry, Adam Mickiewicz University, Uniwersytetu Poznańskiego 8, 61-614 Poznań, Poland. E-mail: runowski@amu.edu.pl
cPhysics Department, Phantom-g, CICECO-Aveiro Institute of Materials, University of Aveiro, 3810-193 Aveiro, Portugal
First published on 22nd September 2021
Abstract
Luminescence thermometers and manometers are among the most paramount emerging applications of phosphors nowadays, and remote reading is not the only attractive advantage they offer. Presently, truly encouraging examples offering both a wide operating range and appreciating thermal sensitivity are still limited. Double-mode sensors are especially attractive but pose additional problems to design them and control their properties. In this paper, we investigate Y2(Gex,Si1–x)O5:0.05 mol%Pr powder phosphors methodically varying the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si molar ratio to design their properties both in optical thermometry and manometry. We show that activation energy for thermal quenching of the 5d → 4f luminescence may be tuned and the mechanism of this process controlled. Consequently, fine-tuning of the luminescent properties important in thermometry may be managed. Specific properties of the 5d → 4f luminescence allow dual-mode thermometry to be executed using either luminescence intensity ratio or the emission decay kinetics for that purpose. The highest values of the thermometric relative sensitivity depend on the Ge
Si molar ratio to design their properties both in optical thermometry and manometry. We show that activation energy for thermal quenching of the 5d → 4f luminescence may be tuned and the mechanism of this process controlled. Consequently, fine-tuning of the luminescent properties important in thermometry may be managed. Specific properties of the 5d → 4f luminescence allow dual-mode thermometry to be executed using either luminescence intensity ratio or the emission decay kinetics for that purpose. The highest values of the thermometric relative sensitivity depend on the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si molar ratio and range from ∼2.5 to 3.5% K−1. The temperature range of the best performance may also be effectively tuned by adjusting the Ge
Si molar ratio and range from ∼2.5 to 3.5% K−1. The temperature range of the best performance may also be effectively tuned by adjusting the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si molar ratio. Controlling the Ge
Si molar ratio. Controlling the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si proportion also allows the sensitivity of these phosphors in manometry to be improved. The Y2(Ge0.10,Si0.90)O5:0.05%Pr material presents the second-best ever reported sensitivity of 1.28 nm GPa−1. Consequently, the Y2(Gex,Si1–x)O5:0.05%Pr phosphors are useful for both temperature and pressure monitoring, and their performance in both functionalities may be effectively tuned by means of the Ge
Si proportion also allows the sensitivity of these phosphors in manometry to be improved. The Y2(Ge0.10,Si0.90)O5:0.05%Pr material presents the second-best ever reported sensitivity of 1.28 nm GPa−1. Consequently, the Y2(Gex,Si1–x)O5:0.05%Pr phosphors are useful for both temperature and pressure monitoring, and their performance in both functionalities may be effectively tuned by means of the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si molar ratio. Our findings may serve as a guide for researchers searching for novel optical thermometers and manometers.
Si molar ratio. Our findings may serve as a guide for researchers searching for novel optical thermometers and manometers.
1. Introduction
Apart from such applications as modern lighting solutions,1,2 persistent phosphors3,4 or scintillators,5,6 photocatalysis7 and others, luminescence thermometry and manometry belong to the most intensely developing research areas of luminescent materials.8–11 Both these physical quantities greatly affect chemical, physical, geological, and biological processes. Thus, their monitoring is crucial in research and technology. Luminescence thermometry presents great potential in in vitro and in vivo bio- and medical imaging and treatment but also appears attractive in such fields as micro- and nano-electronics, aviation industry, space research, measurements of temperature distribution over (large) surfaces.12–15 Emerging applications involve e.g. catalysis or the protection of structural materials.16,17 The reader may find more comprehensive information on these topics in numerous reviews or books published in recent years.10,14,18–23 Measuring very high pressure is necessary for many technological and scientific processes, among them in such sophisticated circumstances as simulating the conditions of stars and planet formation or geological processes.24The common requirement of all considered applications of luminescent thermometers and manometers is their high thermal sensitivity, low inaccuracy of temperature/pressure readouts, good repeatability, as well as chemical and physical stability when used. In luminescence thermometry, the required temperature operating range is entirely defined by the application considered. In bio- or medical uses, only a narrow range of physiological temperatures is of interest. On the other hand, catalysis, aerospace, or surface temperature distribution may easily require measuring temperature over wide ranges, at least several hundred degrees, and often even above 1000 °C. For luminescent thermometers, it is a great challenge and it is known that only a few phosphors are able to satisfy such requirements.25,26 On the other hand, the search for phosphors that can serve as luminescent thermometers with such rigorous requirements is a fantastic challenge.
We have recently shown that bandgap engineering in Pr3+-activated phosphors offers the possibility to accurately control important thermometric parameters – mainly (relative) thermal sensitivity, temperature uncertainty, and the operating range of luminescent thermometers.27–30 Upon UV 4f → 5d excitation, a number of Pr3+-activated materials exhibit three emissions showing different dependence on temperature: (i) 5d → 4f broad-band luminescence in the UV part of the spectrum, (ii) narrow-line luminescence due to the 3P0 → 3HJ transition which appears mainly around 500 nm (3P0 → 3H4), and (iii) narrow-line 1D2 → 3HJ emission in the red part of the spectrum, which partly overlaps with the 3P0 → 3H6/3F2 luminescence. We have previously shown that the luminescence intensity ratio may be used to measure temperature with very high relative sensitivity.27–29 On the other hand, the ratio of the (ii) and (iii) transition intensities may be useful to extend the operating range of luminescence thermometers using Pr3+ emissions.
Furthermore, we have shown that also decay time of the Pr3+ 5d → 4f emission offers the possibility of temperature measuring in the range of several hundred degrees.29 This finding proved that the Pr3+-activated luminescent thermometers may be used as dual-mode temperature sensors. This enhances the versatility of such sensors.
In the present paper, we examine the performance of the Y2(Gex,Si1–x)O5:Pr family of luminescent thermometers varying the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge ratio. We also discuss in depth the important changes of spectroscopic properties resulting from this change. Fig. 1 presents a vacuum referred binding energy (VRBE) diagram together with Pr3+ levels for the investigated phosphors.
Ge ratio. We also discuss in depth the important changes of spectroscopic properties resulting from this change. Fig. 1 presents a vacuum referred binding energy (VRBE) diagram together with Pr3+ levels for the investigated phosphors.
 | ||
Fig. 1 The effect of the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio on the bandgap structure of the Y2(Gex,Si1–x)O5 host lattices and the relative position of the electronic levels of Pr3+. Si ratio on the bandgap structure of the Y2(Gex,Si1–x)O5 host lattices and the relative position of the electronic levels of Pr3+. | ||
The reader may find such VRBE diagrams with the levels of all Ln3+ and Ln2+ ions for these hosts in Fig. S1a–f (ESI†). Analogously, the required parameters to construct such a diagram are in Table S1 (ESI†). This may be useful for many researchers. As the Ge content increases in the Y2(Gex,Si1–x)O5:Pr phosphors, the bandgap of the host decreases. This strongly affects the properties of the 5d → 4f luminescence, especially its thermal quenching. This, in turn, affects strongly the temperature dependence of the intensity ratio of the above-mentioned luminescence features of the dopant. It also appeared interesting to test the effect of pressure on the Y2(Gex,Si1–x)O5:Pr phosphor luminescent properties. To the best of our knowledge, the effect of pressure on the 5d → 4f luminescence of Pr3+ was previously investigated only in Y3Al5O12:Pr.31 One can, however, find a number of Pr-activated luminescent materials in which the impact of pressure on the intra-configurational 4f → 4f transitions was tested.32–35 However, as we already mentioned above, in contrast to the very sensitive 5d → 4f transition, the 4f → 4f transitions are by their very nature not strongly affected by the external compression.
2. Experimental
Y2(Gex,Si1–x)O5:Pr luminescent powders were prepared via Li2SO4 flux-aided synthesis.29 To prevent any cross-relaxation processes between the Pr3+ ions the low concentration of the dopant, 0.05 mol% with respect to Y3+, was chosen. Ge was assumed to replace Si forming Y2(Gex,Si1–x)O5:Pr solid solutions where x = 0, 0.1, 0.25, 0.5, 0.75, 1 (0%, 10%, 25%, 50%, 75%, 100%). Y2O3 (Stanford Materials, 99.999%), SiO2 (Umicore, 99.99%), GeO2 (Alfa Aesar, 99.999%), and Pr6O11 (Stanford Materials, 99.99%) were used as the starting reagents. They were thoroughly ground in an agate mortar and mixed with Li2SO4 (Alfa Aesar, 99.9%) flux. Then the mixture was placed in a platinum crucible and transferred to a chamber furnace. The samples were heated at 1300 °C for 5 hours. The heating rate was 5 °C per min up to 800 °C and 3 °C per min above this temperature. After cooling, the powders were recovered by washing out the flux a few times with hot deionized water. Afterward, the white phosphor powders were dried at 80 °C for 10 h at a reduced pressure of a vacuum laboratory dryer.Measurements
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol
ethanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water (16
water (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) pressure transmitting medium (hydrostatic up to ∼10 GPa). The high-pressure values were determined using ruby R1 fluorescence line shift, excited with a 532 nm laser, and using a ruby calibration curve available elsewhere.36 For technical reasons, i.e., naturally low PL signal intensity from the tiny amount of the compressed material loaded into the DAC (sample size ≈200 μm), large slits had to be used. This necessarily resulted in significantly broader bands, compared to the PL temperature measurements.
1) pressure transmitting medium (hydrostatic up to ∼10 GPa). The high-pressure values were determined using ruby R1 fluorescence line shift, excited with a 532 nm laser, and using a ruby calibration curve available elsewhere.36 For technical reasons, i.e., naturally low PL signal intensity from the tiny amount of the compressed material loaded into the DAC (sample size ≈200 μm), large slits had to be used. This necessarily resulted in significantly broader bands, compared to the PL temperature measurements.
3. Results
3.1. Structural properties of Y2(Gex,Si1–x)O5:Pr materials
The oxyorthosilicates crystallize in two types of monoclinic structures, X1 and X2. The large rare earth (RE) ions (with the ionic radius >0.92 Å, e.g. La2SiO5, Tb2SiO5) form a monoclinic X1 type of structure in the space group P21/c (#14), whereas smaller ions give the X2 type of structure with the space group C2/c (#15).37 Yet, in the case of Y2SiO5 (YSO) the type of structure is strongly dependent on the fabrication temperature. Below 1190 °C it can form an X1 type of structure, and at higher temperatures of synthesis – X2.38 On the other hand, it was found that isostructural oxyorthogermanate crystallizes only in the monoclinic X2 type of structure in the space group of C2/c (#15), regardless of the preparation temperature.39 The present research was conducted on phosphors showing the X2 structure. Table S2 (ESI†) presents the crystallographic data for the Y2SiO5 and Y2GeO5 host lattices.In the monoclinic C2/c Y2(GexSi1–x)O5:Pr, there exist two crystallographically different Y3+ sites, Y1 and Y2, showing different coordination numbers, CN = 7 and 6, respectively (see Fig. S2a and b, ESI†). As the ionic radius of Pr3+ is ∼8.5% larger compared to Y3+ it is expected and spectroscopically confirmed that Pr3+ (as well as Ce3+) occupy mainly the Y1 site whose coordination number and the RE-O distances are larger compared to Y2.38,40,41 At low concentrations, the occupancy of the Y2 is negligible.
The phase purity of the examined solid solutions with different Ge content was verified by means of powder XRD and the results are presented in Fig. S3 (ESI†). The simulated patterns of X2-Y2SiO5 (ICSD#291362) and Y2GeO5 (ICSD#260425) are given as well. Crystallographically, all the synthesized compounds are high-quality products. Only in the case of Y2GeO5, was a minimal amount of GeO2 found giving a diffraction line at 28.6° (ICSD #59639). Along with the incorporation of Ge into the host lattice, one can observe a shift of diffraction lines towards lower angles. This was expected, since the Ge4+ ionic radius is larger than Si4+, and the interplanar distances in the unit cell increase accordingly.42 Additionally, in the case of the (Ge, Si) solid solutions, broadening of the diffraction lines can be observed. This is a direct consequence of distortion in the local structure of the solid solutions and disturbance of the overwise flat lattice planes. This proves that the (Ge, Si) mixed phosphors are indeed solid solutions. The previously published EDS analysis of Ge and Si confirmed that the Y2(Gex,Si1–x)O5:Pr phosphor compositions agree with the nominal formulas.43
The FTIR spectra of the investigated samples are presented in Fig. 2. In the Ge-free Y2SiO5:Pr sample, the spectrum shows only the bands of typical rare earth oxyorthosilicates.44 The bands between 1150–850 cm−1 are attributed to the asymmetric and symmetric stretching vibrational modes within the SiO4 tetrahedra. The bands around 450 cm−1 are assigned to the bending vibrations of the O–Si–O bonds.45 They overlap with vibrations of the YOx (x = 6, 7) polyhedra (600–400 cm−1). With the increase of germanium content, a new structured absorption band appears with a maximum of around 770 cm−1. As expected, its intensity grows together with the Ge incorporation into the host lattice. These features are assigned to the stretching symmetric and asymmetric vibrations in the GeO4 unit.29,46 With the varying Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio, some small changes in the positions of the various features of the IR spectra can be noted, which reflect small changes in the bond lengths.44 The IR spectroscopic data show that the replacement of (a fraction of) Si with Ge (to engineer the host bandgap), also affects the phonon energies of the host lattice. These have important consequences on the material's photoluminescence properties affecting the nonradiative processes experienced by the excited electron.47 Consequently, thermometric parameters are also expected to be influenced through such effects.
Si ratio, some small changes in the positions of the various features of the IR spectra can be noted, which reflect small changes in the bond lengths.44 The IR spectroscopic data show that the replacement of (a fraction of) Si with Ge (to engineer the host bandgap), also affects the phonon energies of the host lattice. These have important consequences on the material's photoluminescence properties affecting the nonradiative processes experienced by the excited electron.47 Consequently, thermometric parameters are also expected to be influenced through such effects.
3.2. Luminescence properties
Fig. 3 presents the PLE spectra of the 611 nm Pr3+ luminescence (from the 1D2 level) in the Y2(Gex,Si1–x)O5 phosphors, taken at 11 K. | ||
| Fig. 3 Excitation spectra of the Y2(Gex,Si1–x)O5:0.05%Pr phosphors taken at 11 K monitoring the red luminescence from the 1D2 level (∼611 nm). | ||
The broadband located in the UV part is assigned to the inter-configurational 3H4 → 5d (4f → 5d) transition of Pr3+. Its peak locates around 248–250 nm, and it is hardly affected by the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio. The narrow lines in the blue and orange part of visible radiation are attributed to the intra-configurational 4f → 4f transitions. Due to the low C1 symmetry of the dopant, the number of observed lines is large.47–49 It is striking that the relative intensity of the 4f → 4f transitions compared to the 4f → 5d one decreases strongly when the Ge content increases. Qualitatively, this is expected taking into account the data presented in Fig. 4. Namely, increasing the Si concentration leads to intense 5d → 4f emission, and then not much energy is left for the 4f → 4f luminescence. Consequently, when the less-energetic radiation excites electrons through the 4f → 4f transitions, relatively high-intensity luminescence is generated. In the PLE spectra this gives the observed effect. Fig. 4 presents the PL spectra of all the Y2(Gex,Si1–x)O5:0.05%Pr investigated phosphors, recorded in the 11–700 K temperature range, under excitation at the respective maxima of the 4f → 5d excitation bands (Fig. 3). The broadband located in the UV part of the spectra results from the 4f15d1 → 3H4–6,3F2–4 transition of Pr3+. A series of narrow lines is seen in the visible part of the spectra. They correspond to the 3P0 → 3H4,5,6,3F2,3,4 (spreading from bluish-green to red) and 1D2 → 3H4,5 (red) intra-configurational transitions. The latter partially overlap with a fraction of the luminescence from the 3P0 level which will be discussed later. The corresponding diagram of the energy levels of Pr3+ with the assignment of the various transitions is presented in Fig. S4a and b (ESI†).
Si ratio. The narrow lines in the blue and orange part of visible radiation are attributed to the intra-configurational 4f → 4f transitions. Due to the low C1 symmetry of the dopant, the number of observed lines is large.47–49 It is striking that the relative intensity of the 4f → 4f transitions compared to the 4f → 5d one decreases strongly when the Ge content increases. Qualitatively, this is expected taking into account the data presented in Fig. 4. Namely, increasing the Si concentration leads to intense 5d → 4f emission, and then not much energy is left for the 4f → 4f luminescence. Consequently, when the less-energetic radiation excites electrons through the 4f → 4f transitions, relatively high-intensity luminescence is generated. In the PLE spectra this gives the observed effect. Fig. 4 presents the PL spectra of all the Y2(Gex,Si1–x)O5:0.05%Pr investigated phosphors, recorded in the 11–700 K temperature range, under excitation at the respective maxima of the 4f → 5d excitation bands (Fig. 3). The broadband located in the UV part of the spectra results from the 4f15d1 → 3H4–6,3F2–4 transition of Pr3+. A series of narrow lines is seen in the visible part of the spectra. They correspond to the 3P0 → 3H4,5,6,3F2,3,4 (spreading from bluish-green to red) and 1D2 → 3H4,5 (red) intra-configurational transitions. The latter partially overlap with a fraction of the luminescence from the 3P0 level which will be discussed later. The corresponding diagram of the energy levels of Pr3+ with the assignment of the various transitions is presented in Fig. S4a and b (ESI†).
The emission spectra of the investigated materials present significant changes when the temperature increases from 11 to 700 K (Fig. 4a–f). The variations are also dependent on the Ge content in the host. In the Ge-free Y2SiO5:Pr, the parity-allowed 5d → 4f transition intensity decreases as the temperature increases until 500 K. At this point this luminescence gets completely quenched. Simultaneously, the intensities of the intra-configurational 4f → 4f features increase at the expense of the inter-configurational one. This effect is primarily seen in the case of luminescence from the 1D2 level compared to the 5d → 4f emission. Hence, when the luminescence from the 5d level gets thermally quenched, at least a fraction of the energy migrates to the lower-lying 3P0 and (more effectively) to the 1D2 level. The results are in good agreement with the previously published data for the YSO:Pr single crystal,50,51 which is indirect proof that the powder phosphors are of good quality.
As the Ge content increases, the 5d → 4f luminescence becomes more susceptible to temperature quenching. In the material with 50% of Si replaced with Ge it lasts till ∼300 K, whereas in the Si-free Y2GeO5:Pr there is no trace of this luminescence, even at the lowest temperature (11 K) we could achieve. This is the expected effect of the bandgap engineering. Replacing Si by Ge has to reduce the forbidden energy gap of the host lattice. This is mostly caused by the lowering of the CB, which decreases the distance between the band and the (potentially) emitting 5d1 level. When the CB and 5d1 overlap no luminescence from the latter can be produced. It is noteworthy that for higher Ge contents (25–75%), quenching of the 5d → 4f luminescence hardly exerts any effect on the 4f → 4f transition intensities. This indicates that in the Ge-rich phosphors, the energy from the 5d1 is mostly converted into heat, instead of being used to produce luminescence. The fraction of electrons from the 5d1 level, which does not produce the 5d → 4f emission, relaxes nonradiatively by-passing the lower-lying 3P0 and 1D2 levels.
Fig. S5a–e (ESI†) presents the temperature-dependence of the decay traces of the Pr3+ 5d1 → 4f luminescence in the investigated compositions. All decay traces can be fitted using a single-exponential function. Fig. 5a presents the dependence of the derived decay times on temperature for the Y2(Gex,Si1–x)O5:Pr phosphors. In each case, the low-temperature (11 K) lifetime is very similar and reaches τ ∼20 ns. This meets the literature data for Y2SiO5:Pr single crystals.50,52 With increasing temperature, the 5d1 → 4f luminescence decay time shortens, yet in each composition at a different temperature range. The quenching temperature (T50%) (defined as the temperature at which the luminescence decay time is two-fold shorter than at the lowest temperature53) in Y2SiO5:Pr occurs at 360 K, whereas in Y2(Ge0.75,Si0.25)O5:Pr at 125 K. These data reflect the changes observed in the emission spectra (see Fig. 4), and they were already discussed above. Thus, with the increasing Ge content, a decreasing energy barrier for the 5d1 → 4f luminescence thermal quenching is proved. This is exactly what we expected from the bandgap engineering and is discussed in the Introduction section.
 | ||
| Fig. 5 (a) Temperature dependence of the 5d → 4f PL decay time of the Y2(Gex,Si1–x)O5:Pr phosphors, under 250 nm excitation. The inset is a magnification of the low-temperature range of the curves to better reveal the complex shape of the curves in the low range of temperature. (b) Dependence of the activation energies, ΔEa1 and ΔEa2, of the 5d → 4f emission thermal quenching, derived using eqn (1). | ||
To further investigate and better understand the temperature quenching of the 5d → 4f luminescence and find the values of energy barrier(s) for the process, we fitted the data presented in Fig. 5a with eqn (1):29,54
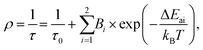 | (1) |
The ΔEa2 values represent the energy barrier of the main process responsible for the thermal quenching of the 5d → 4f luminescence. In general, this may occur as a result of thermally induced photoionization, which transfers the excited electron from the 5d level to the host conduction band. Direct evidence for such a mechanism could be provided by measurements of photoconductivity of the materials, which we are not able to perform at present (and they are hardly possible to perform with powders, in fact). However, van Der Kolk showed experimentally that in Y2SiO5:Pr single crystals this photoionization is inefficient.56 This infers that the thermal quenching of the 5d → 4f emission occurs through a cross-over mechanism, in which the thermal energy is used by the excited electron to overcome the energetic barrier generated by the crossing parabolas of the 5d and 4f levels of Pr3+. Fig. S6 (ESI†) presents schematically the difference between both mechanisms of thermal quenching of the intra-configurational luminescence. The thermally activated cross-over process is often observed in Pr3+ compounds.55,57,58 This requires that the energetic separation of the 4f15d1 and the next-lower-lying level of the 4f2 configurations is not significant, and the former is well below the host conduction band.47
The concluded cross-over mechanism of the 5d → 4f luminescence quenching in Y2SiO5:Pr is consistent with the temperature-induced changes in the PL spectra of Ge-free Y2SiO5:Pr phosphor and the one containing 10% Ge (see Fig. 4a and b). With temperature elevation, the 4f → 4f luminescence intensity in these two phosphors increases at the expense of the decreasing 5d → 4f luminescence. Yet, when the Ge content is higher than 10%, the intensities of the 4f → 4f transitions hardly change, and the 5d → 4f luminescence weakens. This indicates that for the Ge-rich samples the photoionization mechanism dominates when the 5d → 4f luminescence undergoes quenching. Recently, Ueda et al.55 reported similar results for the Y3Al5–xGaxO12:Pr garnet materials. They also concluded that replacing Al by Ga changes the mechanism of the 5d → 4f luminescence thermal quenching from a thermally activated cross-over process into the thermally activated photoionization mechanism.
While thermally activated photoionization is a fairly widely accepted luminescence quenching mechanism,54,55,59,60 it may not be entirely intuitively obvious, at first. Namely, one might suppose that an electron thermally raised to the conduction band should be capable of returning to the level it has just escaped and possibly produce a photon of light. In fact, in scintillation, an electron which happened to get to the conduction band after absorption of gamma-particles indeed falls onto the activator excited level to produce a photon of light, afterwards. However, this happens when the conduction band and the excited (emitting) level below it are not thermally coupled. If they are, scintillation becomes ineffective–the electron is not able to localize on the excited/emitting level for a time long enough to relax radiatively from it. This is true even for high-performance scintillators such as YAG:Ce, LuAG:Ce, LSO:Ce and their Pr-activated versions.61–64 For example, YAG:Ce shows efficient photoluminescence (∼90% of quantum yield61) and efficient scintillation. Each of the emissions is resistant to thermal quenching up to about 600 K65 and only above this temperature both the photoluminescence and scintillation get quenched rapidly.66,67 It is a thermally induced coupling of the wave functions of the conduction band and the excited electronic level of the emitting center, which prevents the radiative relaxation of the excited electron. At elevated temperatures, the just mentioned thermal coupling disperses the electron cloud greatly within the conduction band precluding its bounding to the emitting level and making the luminescent transition unworkable. The effect of Ge content on the decay time was also analyzed for the blue-green luminescence from the 3P0 level and the red one from the 1D2 of Pr3+. Fig. S7a and b (ESI†) presents decay traces of the two emissions in all the Y2(Gex,Si1–x)O5:Pr phosphors under 250 nm (4f → 5d) excitation at 300 K. The kinetics of the emission from the 1D2 level is not affected by the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge ratio. However, the decay time of the 3P0 luminescence prolongs systematically from 2.5 to 8.6 μs between Y2SiO5:Pr and Y2GeO5:Pr, respectively (see Table S3, ESI†). This is understandable taking into account the lower-energy phonons appearing in the hosts with the incorporation of Ge, at the expense of the higher-energy vibrations of Si–O bonds. Consequently, with the increase of Ge content, the 3P0 level is continuously less-efficiently coupled with the next-lower-lying 1D2 level by means of multiphonon relaxation. The same does not apply to the kinetics of the 1D2 emission, as the next-lower-lying 1G4 level is separated from the emitting one by much higher energy (∼0.9 eV/7000 cm−1), compared to the energy spanning 3P0 and 1D2 (∼0.5 eV/4000 cm−1), see Fig. 1 and Fig. S4a (ESI†).
Ge ratio. However, the decay time of the 3P0 luminescence prolongs systematically from 2.5 to 8.6 μs between Y2SiO5:Pr and Y2GeO5:Pr, respectively (see Table S3, ESI†). This is understandable taking into account the lower-energy phonons appearing in the hosts with the incorporation of Ge, at the expense of the higher-energy vibrations of Si–O bonds. Consequently, with the increase of Ge content, the 3P0 level is continuously less-efficiently coupled with the next-lower-lying 1D2 level by means of multiphonon relaxation. The same does not apply to the kinetics of the 1D2 emission, as the next-lower-lying 1G4 level is separated from the emitting one by much higher energy (∼0.9 eV/7000 cm−1), compared to the energy spanning 3P0 and 1D2 (∼0.5 eV/4000 cm−1), see Fig. 1 and Fig. S4a (ESI†).
3.3. Thermometric analysis of Y2(Gex,Si1–x)O5:Pr
The potential of the phosphor systems as optical thermal sensors was initially assessed by analyzing the temperature dependence of their PL spectra in the 11–700 K range (see Fig. 4a–f). For this purpose, three luminescence bands related to transitions from the 5d1, 3P0, and 1D2 levels were taken into account (see Fig. S4a, ESI†). It should be pointed out that the luminescence of Pr3+ in the red part of the spectrum has a mixed origin – besides the emission from the 1D2 level, also transitions from the 3P0 one occur there. Distinguishing between them is thus crucial to maximizing the sensitivity of a given thermometer. Fortunately, differentiating these two emissions can be accomplished by employing time-resolved emission spectroscopy (TRES). The luminescence from the 3P0 level, being spin-allowed, decays much faster, than the emission from the 1D2 level. The decay time of the latter is typically up to two orders of magnitude longer. Fig. S8 (ESI†) presents results of the TRES measurements for the investigated compositions recorded at 11 K. It appears that, independently of the composition, in the 600–615 nm range only the long-decaying (∼100–120 μs) luminescence from the 1D2 level is observed. At longer wavelengths, approximately up to 645 nm, a mixture of both the 4f → 4f transitions is observed. Finally, above 645 nm only luminescence from the 3P0 level occurs. Accordingly, Fig. S9 (ESI†) presents three luminescence bands selected for the thermometric analysis. Their integrated intensities are denoted A1, A2, and A3. The integration ranges are listed in Table S4 (ESI†) and the values of the related band intensities as a function of temperature are presented in Fig. S10a–f (ESI†).Consequently, the luminescence intensity ratio (LIR) was calculated according to the following equations:
 | (2) |
Firstly, we shall focus on the temperature dependence of LIR1 and LIR2–both contain the 5d → 4f luminescence intensity (A1). The temperature dependence of LIR1 and LIR2 could be fitted using the Mott-Seitz68,69 equation for two independent non-radiative channels:28,29
 | (3) |
Upon the spectroscopic analysis presented above, one has to realize that feeding the 3P0 level is somewhat complex, and with increasing temperature it is further complicated. In the case of 1D2, it is even more tangled. This, in turn, makes the physics behind the temperature dependence of LIR3 quite multifarious and problematic. Therefore, in the absence of a good physical model to rationalize the observed evolution of LIR3 with temperature we used polynomial empirical functions. The results are presented in Fig. S12a–f (ESI†) and the fitting parameters are listed in Table S6 (ESI†). It appears that using intra-configurational transitions of Pr3+ in Y2(Ge0.75,Si0.25)O5:Pr allows measuring temperature over the whole accessible range – from 11 to 675 K. This is an important advantage of the solid-solution luminescence thermometers. Adjusting the Ge![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si ratio one may find a phosphor offering what a stoichiometric silicate or germanate cannot.
Si ratio one may find a phosphor offering what a stoichiometric silicate or germanate cannot.
The repeatability of the temperature readouts for each analyzed material, as well as the stability of the temperature-dependent intensity ratios (LIR1, LIR2, and LIR3) were examined during 10 consecutive cycles of heating–cooling (Fig. S13a–f, ESI†). The calculated repeatability (eqn S5, ESI†1) does not fall below 99% which proves the excellent thermal stability of the luminescence generated by the investigated phosphors.
In order to compare the performance of the temperature sensing based on the three luminescence intensity ratios (LIR1, LIR2, LIR3) quantitatively, their relative sensitivities, Sr (% K−1), were determined using eqn (4):19
 | (4) |
 | ||
| Fig. 6 Temperature dependence of the relative thermal sensitivity (eqn (4)) based on (a) LIR1, (b) LIR2, and (c) LIR3. | ||
It is striking that the Sr(LIR3) values are noticeably lower than those based on LIR1 or LIR2 (dependent very much on the 5d → 4f luminescence). They vary from nearly 0 to 0.74% K−1. The highest Sr(LIR3) was obtained for Y2GeO5 at 600 K. Thus, also when the 4f → 4f emissions are exploited, the performance of the luminescence thermometers may be tailored by means of non-stoichiometry of the host lattice.
Corresponding temperature resolution, δT, of the investigated thermometers, was calculated using eqn S7 (ESI†), and the results are presented in Fig. S14a–c (ESI†). For LIR1 and LIR2 the temperature uncertainty varies from 0.01 K to 4 K. At the lowest temperature values (<30 K), the uncertainty exceeds 4 K. This reflects the low Sr values in this region. Then, when the temperature increases, δT decreases accordingly to again increase at the high-temperature part of the operating range. In the case of the samples containing 50% and 75% of Ge, the thermometer deficiency is that δT drastically increases above 250 K and 150 K, respectively. This is understandable, as the 5d → 4f luminescence is severely quenched in these compositions (see Fig. 4 and 5). Such an effect enlarges the δLIR/LIR values accordingly for these phosphors, which directly leads to the larger δT values. Since the uncertainty is a function (somewhat complex) of the signal to noise ratios, whenever one of them is low this parameter is expected to increase. This anticipation is perfectly mirrored by the T-dependences of the uncertainties presented in Fig. S14 (ESI†). They indeed increase at the limits of the operating range when one of the emissions used for calculations shows indeed low intensity.
Among the investigated compositions, the very good candidate for temperature sensing is Y2Ge0.10,Si0.90O5:Pr. It offers the best combination of high accuracy, high sensitivity, and a wide operating T-range (11–500 K). Temperature uncertainty based on the 4f → 4f (Fig. S14c, ESI†) varies from 0.01 to 1 K, which is excellent accuracy, especially at high temperatures. In the Si-fee Y2GeO5:Pr phosphor, δT is as low as 0.1 K, within its whole operating T-range, i.e., 200–600 K (Fig. S14c, ESI†), which is an impressive achievement. This results from the fact that in this phosphor, the excitation energy delivered to the 5d level is used to generate only the 4f → 4f luminescence, resulting in high intensity of the emission features and consequently high signal-to-noise ratio.
Due to significant temperature dependence, it was tempting to exploit the decay time of the 5d → 4f luminescence for temperature measuring as well (see Fig. 5). To analyze the performance quantitatively, the relative thermal sensitivities, Sr, were calculated (using eqn (2), and replacing LIR by τ) for the phosphors showing the 5d → 4f luminescence. Fig. 7 presents how the Sr changes with temperature for each of the examined compositions when the decay time of the intra-configurational transition is used. Importantly, the range of the temperature reading, as well as the temperature at which the Sm is achieved may be effectively tuned by varying the Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ge ratio. The general trend is that with the increasing Ge content the Sm continuously shifts to lower temperature values. This echoes the decreasing temperature of the 5d → 4f luminescence quenching (see Fig. 4 and 5a). In the Ge-free Y2SiO5:Pr sample, Sm reaches a respectable value of 2.67% K−1 at 417 K.
Ge ratio. The general trend is that with the increasing Ge content the Sm continuously shifts to lower temperature values. This echoes the decreasing temperature of the 5d → 4f luminescence quenching (see Fig. 4 and 5a). In the Ge-free Y2SiO5:Pr sample, Sm reaches a respectable value of 2.67% K−1 at 417 K.
 | ||
| Fig. 7 Relative thermal sensitivity (Sr) based on the 5d → 4f decay traces of the Y2(Gex,Si1–x)O5:Pr materials. | ||
As the Ge content increases, both the operating T-range and the temperature of Sm continuously shifts towards lower temperature values. This enables effective tuning of the thermometer performance when the 5d → 4f luminescence decay time is exploited. Furthermore, the temperature resolution (δT) of the measurements was calculated using eqn (S11) (ESI†) and the results are presented in Fig. S15 (ESI†). The resulting uncertainties of the temperature readouts are very low and vary in the range of 0.1–0.001 K. Thus, reading the temperature by means of the 5d → 4f luminescence decay time allows achieving exceptionally high accuracy of the readout. The important source of the impressive accuracies is the fact that the decay traces are single-exponential and this allows for a low standard deviation of the decay time values derived from their fits.
3.4. High-pressure response
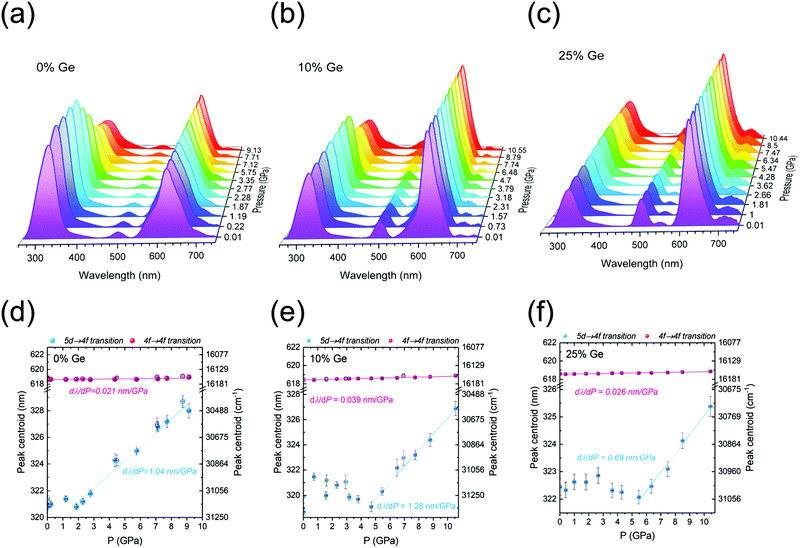
The response of the following three samples, Y2(Gex,Si1–x)O5:Pr3+, where x = 0, 0.10, and 0.25 of Ge, to external high pressure was investigated by their compression in a diamond anvil cell (DAC). The selected samples show a relatively intense 5d → 4f luminescence. Compression of the materials was performed within the hydrostatic pressure range, i.e., up to about 10 GPa. The excitation and emission spectra were recorded for λem = 320 nm and λex = 248 nm, respectively. The results are presented in Fig. 8 and 9. We focused on the inter-configurational 5d → 4f transition of Pr3+, which is much more sensitive to external stimuli (e.g., pressure or temperature), compared to the intra-configurational 4f → 4f transitions.70–73Fig. 8a–c shows the pressure dependence of the (normalized) emission spectra for the investigated phosphors.The 5d → 4f emission feature around 300 nm shows the pressure-induced spectral shift to longer wavelengths (Fig. 8d–f), as well as the non-monotonic variations in the relative intensities of the 5d → 4f bands with respect to the 4f → 4f ones. The latter effect is plausibly caused by a different pressure-induced quenching effect for the intra- and inter-configurational transitions. As expected, similarly to emissions, the excitation spectra presented in Fig. 9a–c also showed a spectral shift with the increasing pressure values. The spectral positions of the peak centroids are presented in Fig. 8d–f and 9d–f, for the emission and excitation spectra, respectively.
The data reveal very significant linear shifts of the Pr3+ f → d transitions. For the emission spectra, the dλPL/dP = 1.04, 1.28 and 0.69 nm GPa−1, and for excitation ones the dλPLE/dP = 0.49, 0.43 and 0.56 nm GPa−1, for the samples containing 0, 10 and 25% of Ge, respectively. These values are by more than an order of magnitude higher than in the case of the 4f → 4f of Pr3+ (1D2 → 3H4/3P0 → 3H6) emission transitions, see Table 1. Such difference between the intra-and inter-configurational transitions is typical for lanthanide ions.70,71,74 Consequently, the 4f → 4f transitions offer a much lower sensitivity in pressure measuring than the intra-configurational ones. It is noteworthy that in the case of the pressure-dependent emission spectra, the position of the 5d → 4f band peak centroid is relatively constant at the low-pressure range. It does not shift at the initial stage of the compression (up to ∼2 GPa for the Ge-free sample, and up to ∼5 GPa for the Ge-doped samples), as can be observed in Fig. 8d–f. It should be emphasized that there are several pressure-induced effects, which may lead to a shift of the bands in excitation and/or emission spectra. These are: (i) enhanced splitting of the multiplets, caused by the increased crystal-field strength due to the shortening of the interionic distances upon compression; (ii) a more pronounced nephelauxetic effect, i.e., decreased spin–orbit interactions and ionic character of bonding (bonds become more covalent); (iii) larger Stokes shift, due to the enhanced electron–phonon coupling, associated with increased phonon energies with pressure.70–74 Raman spectroscopy confirmed pressure-induced structural distortion of the structure in isostructural Lu1.8Y0.2SiO5 single crystals.75 The coincidence of the mentioned effects may account for the initial fluctuations/deviations in the spectral position of the Pr3+ 5d → 4f emissions.
| Sensor | Dopant ion | Line shift (nm GPa−1) | Transition | λ (nm) | Ref. |
|---|---|---|---|---|---|
| Y2SiO5 | Pr3+ | 1.04 | 5d → 4f | 320 | This work |
| 0.49 | 4f → 5d | 248 | |||
| 0.021 | 4f → 4f | 618 | |||
| Y2Ge0.10Si0.90O5 | Pr3+ | 1.28 | 5d → 4f | 320 | |
| 0.43 | 4f → 5d | 248 | |||
| 0.039 | 4f → 4f | 618 | |||
| Y2Ge0.25Si0.75O5 | Pr3+ | 0.69 | 5d → 4f | 320 | |
| 0.56 | 4f → 5d | 248 | |||
| 0.026 | 4f → 4f | 618 | |||
| Al2O3 (ruby) | Cr3+ | 0.365 | 2E → 4A2 | 694 | 76 |
| YAlO3 | Cr3+ | 0.70 | 2E → 4A2 | 723 | 78 |
| CeN-PVDF | Ce3+ | 0.28 | 5d → 4f | 327 | 79 |
| Y6Ba4(SiO4)6F2 | Ce3+ | 0.63 | 5d → 4f | 466 | 73 |
| BaLi2Al2Si2N6 | Eu2+ | 1.58 | 5d → 4f | 532 | 72 |
| EuPO4 | Eu3+ | ∼0.27 | 5D0 → 7F0 | 580 | 80 |
| NaBiF4 | Er3+ | −0.80 | 4I13/2 → 4I15/2 (stark) | 1503 | 81 |
| YPO4 | Er3+ | 0.539 | 4I13/2 → 4I15/2 (stark) | 1589 | 82 |
| Gd3Sc2Ga3O12 | Nd3+ | ∼0.632 | 4F3/2 → 4I9/2 (stark) | 935 | 83 |
| Y3Al5O12 | Sm3+ | 0.30 | 4G5/2 → 6H7/2 (stark) | 618 | 84 |
| SrFCl | Sm2+ | 1.11 | 5D0 → 7F0 | 690 | 85 |
| SrB4O7 | Sm2+ | 0.255 | 5D0 → 7F0 | 685 | 77 |
| SrB2O4 | Sm2+ | 0.244 | 5D0 → 7F0 | 685 | 86 |
One of the most important properties of pressure sensing is the reversible character of the observed spectral shifts. It is perfectly proved by the decompression data (empty symbols in Fig. 8d–f and 9d–f), which converge with the results of the compression runs. In Table 1, the performance of the investigated materials, i.e., their shift rates for the 5d → 4f emission and 4f → 5d excitation bands were compared with other highly-sensitive luminescent manometers reported up to now. It is noteworthy that the determined shift rates for the presently developed Pr3+-doped Y2(Gex,Si1–x)O5:Pr luminescent manometers are much larger, compared to the commonly used ruby (Al2O3:Cr3+; dλ/dP ∼0.36 nm GPa−1) and Sm2+-based (SrB4O7:Sm2+; dλ/dP ∼0.25 nm GPa−1) pressure sensors.76,77 The sample containing 10% of Ge is the second most sensitive luminescent pressure sensor based on the emission band shift (dλ/dP ∼1.28 nm GPa−1) ever reported. The leading composition is the recently published BaLi2Al2Si2N6:Eu2+ sensor excitable in a visible spectral range (dλ/dP ∼1.58 nm GPa−1).72
4. Conclusions and summary
This paper explored the effect of bandgap engineering on the spectroscopy of the Y2(Gex,Si1–x)O5:0.05%Pr powder phosphors, and – more importantly – on their performance as luminescence thermometers and manometers. These are among the most paramount emerging technological applications of phosphors nowadays. It was demonstrated that – when the Ge content increases (at the expense of Si) – the energetic position of the bottom of the host conduction band lowers, and some other effects take place simultaneously. Very important among them is the lowering of the energy of available phonons, from about 850–1150 cm−1 in Y2SiO5 to ∼770 cm−1 in Y2GeO5. This, in turn, affects the rates of radiative/non-radiative relaxation processes experienced by the electrons raised to the Pr3+ 5d excited level by the ∼250 nm excitation radiation.Despite the interplay of different effects, when the Ge:Si ratio changes, fairly systematic variations in the luminescence properties are observed when Ge replaces Si in the host lattice. Accordingly, monotonic changes of thermometric parameters of the phosphors occur then. Consequently, the properties and quality of the Y2(Gex, Si1–x)O5:%Pr luminescent thermometers may be tuned and managed by changing the Ge content (x value).
In the Si-rich materials, the cross-over mechanism of the 5d → 4f luminescence quenching dominates, while in the Ge-rich phosphors the thermally-induced photoionization prevails. This difference has further consequences, as in the latter the ionized electrons have little chance to produce any luminescence. They dissipate their excessive energy mostly non-radiatively. Yet, in the cross-over mechanism of quenching of the 5d → 4f emission, the excited electron is conveyed directly to the lower-lying 3PJ (and possibly further to 1D2 by multiphonon relaxation) levels. It is clear that all these effects are reflected in thermometric properties of the investigated phosphors. In consequence, it may be taken as a universal “rule of thumb”, that the properties of luminescent thermometers may be deliberately designed by means of non-stoichiometry of the host lattices.
We confirmed that luminescence of Pr3+ is attractive for luminescence thermometry using all its three emissions, from 5d, 3P0 and, 1D2 levels. Since each of them shows different dependences on temperature, accurate temperature measurements over the T-range from 11 to 600–700 K can be executed. Furthermore, the temperature range of their highest sensitivity may be intentionally tuned making use of the bandgap engineering. Since both the Pr3+ luminescence intensity ratio and the decay time of its 5d → 4f emission are strongly temperature-dependent, these phosphors may easily serve as dual-mode sensitive thermometers, which makes them even more versatile. This is adequately shown in Fig. 10a, which compares the highest relative thermal sensitivities achievable using the four different thermometric parameters we tested for the series of Y2(Gex,Si1–x)O5:0.05%Pr phosphors. Those of them which use the properties of the 5d → 4f luminescence beat the one based on the 4f → 4f emissions.
 | ||
| Fig. 10 Histogram displaying the (a) maximal thermal relative sensitivity, and (b) pressure absolute sensitivity of the investigated phosphors. | ||
The manageable thermometric capabilities of the Y2(Gex,Si1–x)O5:0.05%Pr powders are complemented by a commendable functioning of these phosphors in manometry. At least up to about 10 GPa (and plausibly even higher) the sensitivity of the Y2(Ge0.10,Si0.90)O5:0.05%Pr phosphor is the second best reported up to now (1.28 nm GPa−1), when the pressure-induced shift of the emission band is employed. Also, in this case, a very good result was achieved exploiting the 5d → 4f luminescence of Pr3+, which is highly-sensitive to the changes in the ion coordination sphere, due to the good exposure of the excited 5d orbitals to their external environment. The comparison of the sensitivity in pressure measurements using the spectral shift of the 5d1 → 4f excitation and emission transitions and the 4f → 4f luminescence band is given in Fig. 10b. The latter effect is much less significant than any of the two transitions involving the 5d orbitals. Indeed, the 5d → 4f electronic transitions of the Pr3+ ions may be very useful for designing sensitive luminescence thermometers and manometers.
Author contributions
MS: conceptualization, data curation, formal analysis, investigation, methodology, project administration, visualization, writing – original draft. MR: funding acquisition, formal analysis, methodology, writing – original draft (manometry). PW: investigation, methodology. LDC: funding acquisition, validation, writing – review & editing. EZ: funding acquisition, conceptualization, supervision, writing – review & editing. SL: writing – review & editing, validation.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was developed within the scope of the project financed by the National Science Centre (NCN), Poland, under grants #UMO-2017/25/B/ST5/00824 (EZ) and 2016/23/D/ST4/00296 (MR), and the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020 & UIDP/50011/2020 (LDC), financed by Portuguese funds through the Portuguese Foundation for Science and Technology (FCT)/MCTES. Financial support from FCT (PTDC/CTM-NAN/4647/2014, NANOHEATCONTROL – POCI-01-0145-FEDER-031469) is also acknowledged. Publication partially financed by the program “Excellence Initiative - Research University”.References
- P. Du, W. Ran, W. Li, L. Luo and X. Huang, J. Mater. Chem. C, 2019, 7, 10802–10809 RSC.
- M. H. Fang, K. C. Chen, N. Majewska, T. Leśniewski, S. Mahlik, G. Leniec, S. M. Kaczmarek, C. W. Yang, K. M. Lu, H. S. Sheu and R. S. Liu, ACS Energy Lett., 2021, 6, 109–114 CrossRef CAS.
- J. Xu, J. Ueda and S. Tanabe, Opt. Mater. Express, 2015, 5, 963 CrossRef.
- P. F. Smet, K. Van den Eeckhout, O. Q. De Clercq and D. Poelman, Persistent Phosphors, Elsevier B.V., 1st edn, 2015, vol. 48 Search PubMed.
- C. L. Melcher, L. A. Eriksson, M. Aykac, F. Bauer, C. Williams, M. Loope and M. Schmand, Radiation Detectors for Medical Applications, Springer, Netherlands, 2006, pp. 243–257 Search PubMed.
- Q. Chen, J. Wu, X. Ou, B. Huang, J. Almutlaq, A. A. Zhumekenov, X. Guan, S. Han, L. Liang, Z. Yi, J. Li, X. Xie, Y. Wang, Y. Li, D. Fan, D. B. L. Teh, A. H. All, O. F. Mohammed, O. M. Bakr, T. Wu, M. Bettinelli, H. Yang, W. Huang and X. Liu, Nature, 2018, 561, 88–93 CrossRef CAS PubMed.
- L. Luo, W. Ran, P. Du, W. Li and D. Wang, Adv. Mater. Interfaces, 2020, 7, 1–10 Search PubMed.
- M. D. Dramićanin, J. Appl. Phys., 2020, 128, 040902 CrossRef.
- A. Bednarkiewicz, L. Marciniak, L. D. Carlos and D. Jaque, Nanoscale, 2020, 12, 14405–14421 RSC.
- C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2019, 7, 1801239 CrossRef.
- J. K. Zareba, M. Nyk, J. Janczak and M. Samoć, ACS Appl. Mater. Interfaces, 2019, 11, 10435–10441 CAS.
- W. Liu and B. Yang, Sens. Rev., 2007, 27, 298–309 CrossRef.
- T. P. Jenkins, C. F. Hess, S. W. Allison and J. I. Eldridge, Meas. Sci. Technol., 2020, 31, 044003 CrossRef CAS.
- C. Zaldo, Lanthanide-based luminescent thermosensors: From bulk to nanoscale, 2018 Search PubMed.
- M. Back, J. Ueda, J. Xu, D. Murata, M. G. Brik and S. Tanabe, ACS Appl. Mater. Interfaces, 2019, 11, 38937–38945 CrossRef CAS PubMed.
- R. G. Geitenbeek, A. E. Nieuwelink, T. S. Jacobs, B. B. V. Salzmann, J. Goetze, A. Meijerink and B. M. Weckhuysen, ACS Catal., 2018, 8, 2397–2401 CrossRef CAS PubMed.
- A. M. Kaczmarek, H. S. Jena, C. Krishnaraj, H. Rijckaert, S. K. P. Veerapandian, A. Meijerink and P. Van Der Voort, Angew. Chem., 2021, 133, 3771–3780 CrossRef.
- D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301 RSC.
- C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millán, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799–4829 RSC.
- C. D. S. Brites, A. Millán and L. D. Carlos, Handbook on the Physics and Chemistry of Rare Earths, 2016, vol. 49, pp. 339–427 Search PubMed.
- M. D. Dramićanin, Methods Appl. Fluoresc., 2016, 4, 042001 CrossRef PubMed.
- M. Dramićanin, Luminescence thermometry: Methods, materials, and applications, Woodhead Publishing Series in Electronic and Optical Materials, 2018 Search PubMed.
- M. Suta and A. Meijerink, Adv. Theory Simul., 2020, 3, 2000176 CrossRef CAS.
- M. Runowski, Handbook of Nanomaterials in Analytical Chemistry, Elsevier, 2020, pp. 227–273 Search PubMed.
- M. L. Debasu, D. Ananias, I. Pastoriza-Santos, L. M. Liz-Marzán, J. Rocha and L. D. Carlos, Adv. Mater., 2013, 25, 4868–4874 CrossRef CAS PubMed.
- G. Gao, D. Busko, S. Kauffmann-Weiss, A. Turshatov, I. A. Howard and B. S. Richards, J. Mater. Chem. C, 2018, 6, 4163–4170 RSC.
- C. D. S. Brites, K. Fiaczyk, J. F. C. B. Ramalho, M. Sójka, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2018, 1701318 CrossRef.
- M. Sójka, J. F. C. B. Ramalho, C. D. S. Brites, K. Fiaczyk, L. D. Carlos and E. Zych, Adv. Opt. Mater., 2019, 7, 1901102 CrossRef.
- M. Sójka, C. D. S. Brites, L. A. D. Carlos and E. Zych, J. Mater. Chem. C, 2020, 3, 12167–12168 Search PubMed.
- P. Bolek, J. Zeler, C. D. S. Brites, J. Trojan-Piegza, L. D. Carlos and E. Zych, Chem. Eng. J., 2021, 421, 129764 CrossRef CAS.
- R. S. Meltzer, H. Zheng, J. W. Wang, W. M. Yen and M. Grinberg, Phys. Status Solidi C, 2005, 2, 284–288 CrossRef CAS.
- A. M. Srivastava, C. Renero-Lecuna, D. Santamaría-Pérez, F. Rodríguez and R. Valiente, J. Lumin., 2014, 146, 27–32 CrossRef CAS.
- R. Turos-Matysiak, H. R. Zheng, J. W. Wang, W. M. Yen, R. S. Meltzer, T. Łukasiewicz, M. Świrkowicz and M. Grinberg, J. Lumin., 2007, 122–123, 322–324 CrossRef CAS.
- S. Mahlik, F. Diaz and P. Boutinaud, Opt. Mater., 2017, 74, 41–45 CrossRef CAS.
- Ł. Marek and M. Sobczyk, Mater. Lett., 2021, 290, 3–5 CrossRef.
- K. Syassen, High Pressure Res., 2008, 28, 75–126 CrossRef CAS.
- K. A. Denault, J. Brgoch, S. D. Kloß, M. W. Gaultois, J. Siewenie, K. Page and R. Seshadri, ACS Appl. Mater. Interfaces, 2015, 7, 7264–7272 CrossRef CAS PubMed.
- V. Babin, V. V. Laguta, M. Nikl, J. Pejchal, A. Yoshikawa and S. Zazubovich, Opt. Mater., 2020, 103, 109832 CrossRef CAS.
- E. M. Rivera-Muñoz and L. Bucio, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, i60 CrossRef PubMed.
- N. L. Jobbitt, S. J. Patchett, Y. Alizadeh, M. F. Reid, J. P. R. Wells, S. P. Horvath, J. J. Longdell, A. Ferrier and P. Goldner, Phys. Solid State, 2019, 61, 780–784 CrossRef CAS.
- N. L. Jobbitt, J. P. R. Wells and M. F. Reid, J. Lumin., 2020, 224, 117302 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. Sójka, J. Zeler and E. Zych, J. Alloys Compd., 2021, 858, 1–8 CrossRef.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part A: Theory and Applications in Inorganic Chemistry, 6th edn, 2008, pp. 1–419 Search PubMed.
- M. Handke and M. Urban, J. Mol. Struct., 1982, 79, 353–356 CrossRef CAS.
- A. Shah, A. Tyagi, B. S. Naidu, V. Sudarsan, R. K. Vatsa and V. K. Jain, RSC Adv., 2013, 3, 23172 RSC.
- G. Blasse and B. Grabbmaier, Luminescent Materials, Springer-Verlag, Berlin Heidelberg, 1994 Search PubMed.
- P. A. Tanner and Y. Y. Yeung, J. Phys. Chem. A, 2013, 117, 10726–10735 CrossRef CAS PubMed.
- J. G. Bunzli and S. V. Eliseeva, Springer Ser. Fluoresc., 2011, 1–45 CAS.
- J. Pejchal, M. Nikl, E. Mihokova, A. Novoselov, A. Yoshikawa and R. T. Williams, J. Lumin., 2009, 129, 1857–1861 CrossRef CAS.
- J. Pejchal, M. Nikl, E. Mihóková, J. A. Mareš, A. Yoshikawa, H. Ogino, K. M. Schillemat, A. Krasnikov, A. Vedda, K. Nejezchleb and V. Múčka, J. Phys. D: Appl. Phys., 2009, 42, 055117 CrossRef.
- A. Zych, M. de Lange, C. de Mello Donegá and A. Meijerink, J. Appl. Phys., 2012, 112, 013536 CrossRef.
- S. K. Sharma, Y.-C. Lin, I. Carrasco, T. Tingberg, M. Bettinelli and M. Karlsson, J. Mater. Chem. C, 2018, 6, 8923–8933 RSC.
- K. Fiaczyk, S. Omagari, A. Meijerink and E. Zych, J. Lumin., 2018, 198, 163–170 CrossRef CAS.
- J. Ueda, A. Meijerink, P. Dorenbos, A. J. J. Bos and S. Tanabe, Phys. Rev. B, 2017, 95, 1–8 Search PubMed.
- E. van der Kolk, P. Dorenbos, C. W. E. van Eijk, S. A. Basun, G. F. Imbusch and W. M. Yen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165120 CrossRef.
- R. Shi, L. Lin, P. Dorenbos and H. Liang, J. Mater. Chem. C, 2017, 5, 10737–10745 RSC.
- S. W. Long, M. M. Yang, D. C. Ma, Y. Z. Zhu, S. P. Lin and B. Wang, Opt. Mater. Express, 2019, 9, 1062 CrossRef CAS.
- J. Ueda, S. Tanabe and T. Nakanishi, J. Appl. Phys., 2011, 110, 053102 CrossRef PubMed.
- V. Jarý, E. Mihóková, J. A. Mareš, A. Beitlerová, D. Kurtsev, O. Sidletskiy and M. Nikl, J. Phys. D: Appl. Phys., 2014, 47(36), 365304 CrossRef.
- V. Bachmann, C. Ronda and A. Meijerink, Chem. Mater., 2009, 21, 2077–2084 CrossRef CAS.
- E. Zych, C. Brecher and J. Glodo, J. Phys.: Condens. Matter, 2000, 12, 1947–1958 CrossRef CAS.
- K. V. Ivanovskikh, J. M. Ogiegło, A. Zych, C. R. Ronda and A. Meijerink, ECS J. Solid State Sci. Technol., 2013, 2, R3148–R3152 CrossRef CAS.
- A. Vedda, M. Nikl, M. Fasoli, E. Mihokova, J. Pejchal, M. Dusek, G. Ren, C. R. Stanek, K. J. McClellan and D. D. Byler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 1–8 CrossRef.
- Z. Xia and A. Meijerink, Chem. Soc. Rev., 2017, 46, 275–299 RSC.
- M. Moszyński, T. Ludziejewski, D. Wolski, W. Klamra and L. O. Norlin, Nucl. Instrum. Methods Phys. Res., 1994, 345, 461–467 CrossRef.
- M. Nikl and A. Yoshikawa, Adv. Opt. Mater., 2015, 3, 463–481 CrossRef CAS.
- N. F. Mott, Proc. R. Soc. London, Ser. A, 1938, 167, 384–391 Search PubMed.
- F. Seitz, Trans. Faraday Soc., 1939, 35, 74 RSC.
- K. L. Bray, M. Glasbeek, H. Kunkely, A. Vogler, in Transition Metal and Rare Earth Compounds Excited States, Transitions, Interactions I, ed. H. Yersin, Springer, New York, 2001 Search PubMed.
- T. Tröster, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, North-Holland, 2003, vol. 33, pp. 515–589 Search PubMed.
- Y. Wang, T. Seto, K. Ishigaki, Y. Uwatoko, G. Xiao, B. Zou, G. Li, Z. Tang, Z. Li and Y. Wang, Adv. Funct. Mater., 2020, 30, 2001384 CrossRef CAS.
- M. Runowski, P. Woźny, N. Stopikowska, Q. Guo and S. Lis, ACS Appl. Mater. Interfaces, 2019, 11, 4131–4138 CrossRef CAS PubMed.
- M. Runowski, A. Shyichuk, A. Tymiński, T. Grzyb, V. Lavín and S. Lis, ACS Appl. Mater. Interfaces, 2018, 10, 17269–17279 CrossRef CAS PubMed.
- P. C. Ricci, D. Chiriu, C. M. Carbonaro, S. Desgreniers, E. Fortin and A. Anedda, J. Raman Spectrosc., 2008, 39, 1268–1275 CrossRef CAS.
- H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., 1986, 91, 4673 CrossRef CAS.
- F. Datchi, R. LeToullec and P. Loubeyre, J. Appl. Phys., 1997, 81, 3333–3339 CrossRef CAS.
- J. D. Barnett, S. Block and G. J. Piermarini, Rev. Sci. Instrum., 1973, 44, 1–9 CrossRef.
- C. Hernandez, S. K. Gupta, J. P. Zuniga, J. Vidal, R. Galvan, M. Martinez, H. Guzman, L. Chavez, Y. Mao and K. Lozano, Sens. Actuators, A, 2019, 298, 111595 CrossRef CAS.
- G. Chen, J. Hölsä and J. R. Peterson, J. Phys. Chem. Solids, 1997, 58, 2031–2037 CrossRef CAS.
- M. A. Antoniak, S. J. Zelewski, R. Oliva, A. Żak, R. Kudrawiec and M. Nyk, ACS Appl. Nano Mater., 2020, 3, 4209–4217 CrossRef CAS.
- M. Runowski, P. Woźny and I. R. Martín, J. Mater. Chem. C, 2021, 9, 4643–4651 RSC.
- S. F. León-Luis, J. E. Muñoz-Santiuste, V. Lavín and U. R. Rodríguez-Mendoza, Opt. Express, 2012, 20, 10393 CrossRef PubMed.
- N. J. Hess and G. J. Exarhos, High Press. Res., 1989, 2, 57–64 CrossRef.
- Y. R. Shen and W. B. Holzapfel, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 15752–15762 CrossRef CAS PubMed.
- M. Runowski, P. Woźny, V. Lavín and S. Lis, Sens. Actuators, B, 2018, 273, 585–591 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: VRBE diagrams of the Y2(Gex,Si1–x)O5 host lattices, structural X-ray diffraction measurements, energy level diagram of Pr3+, decay traces of the 5d → 4f and 4f → 4f emissions, configuration coordinate diagram for Pr3+ ions, time-resolved spectroscopic measurements, schematic presentation of energies for luminescence intensity integrations (A1, A2, and A3), thermal evolution of the integrated areas of the three emissions with temperature, calibration curves for the LIR1, LIR2, and LIR3, repeatability measurements, temperature uncertainty for LIR1–3 and based on 5d → 4f decay traces. See DOI: 10.1039/d1tc03202j |
| This journal is © The Royal Society of Chemistry 2021 |