Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of dinuclearity in promoting thermally activated delayed fluorescence (TADF) in cyclometallated, N^C^N-coordinated platinum(II) complexes†
Piotr Pander *a,
Andrey V. Zaytsev
*a,
Andrey V. Zaytsev b,
Amit Sil
b,
Amit Sil c,
J. A. Gareth Williams
c,
J. A. Gareth Williams *c,
Pierre-Henri Lanoe‡
*c,
Pierre-Henri Lanoe‡
 b,
Valery N. Kozhevnikov
b,
Valery N. Kozhevnikov *b and
Fernando B. Dias
*b and
Fernando B. Dias a
a
aDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: piotr.h.pander@durham.ac.uk
bDepartment of Applied Sciences, Northumbria University, Ellison Building, Newcastle upon Tyne, NE1 8ST, UK. E-mail: valery.kozhevnikov@northumbria.ac.uk
cDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: j.a.g.williams@durham.ac.uk
First published on 16th July 2021
Abstract
We present the synthesis and in-depth photophysical analysis of a di-Pt(II) complex with a ditopic bis-N^C^N ligand. The complex exhibits a dual luminescent behaviour by emitting simultaneously delayed fluorescence and phosphorescence. By comparing with the mono-Pt(II) analogue, we demonstrate that thermally activated delayed fluorescence (TADF) is turned on in the di-Pt(II) complex due to the occurrence of three main differences relative to the mono-Pt(II) analogue: a larger singlet radiative rate constant (kSr), a smaller singlet–triplet energy gap (ΔEST) and a longer phosphorescence decay lifetime (τPH). We observe similar trends among other di-Pt(II) complexes and conclude that bimetallic structures promote conditions favourable for TADF to occur. The diplatinum(II) complex also shows a long wavelength-emissive excimer which yields near infrared electroluminescence, λel = 805 nm, in a solution-processed OLED device with EQEmax = 0.51%. We believe this is the highest efficiency reported to date for an excimer Pt(II) emitter with λel > 800 nm in a solution-processed OLED device.
Introduction
The high phosphorescence quantum yield associated with appropriately designed cyclometallated iridium(III) and platinum(II) complexes has led to their widespread incorporation into OLED devices.1–9 The triplet radiative rate constants (kTr) of such complexes are four to five orders of magnitude higher than those of typical conjugated organic molecules, thanks to the spin–orbit coupling (SOC) interactions induced by the metal.10 Yet for red and near-infrared (NIR) emitting molecular materials, the strategy of incorporating heavy metal ions with high SOC constants is compromised by the diminished metal character in the excited states as conjugation increases. This leads to lower kTr and hence to reduced quantum yields and exciton-quenching processes in OLED devices, causing increased efficiency roll-off.11 The problem is compounded by the effect of the well-known “energy gap law”, whereby non-radiative decay processes that involve electronic to vibrational energy transfer are enhanced as the excited electronic states fall in energy.12 There is, therefore, a strong case for seeking ways to accelerate kTr in narrow energy-gap emitters. Recently, a number of results have shown that the incorporation of a second metal centre into such cyclometallated complexes seems to enhance kTr with respect to mononuclear analogues.13–17 Nevertheless, the radiative rate still remains heavily dependent upon the SOC induced by the metal centres.Meanwhile, an alternative approach for harvesting of triplet states in OLED devices has become increasingly popular, namely the thermally-activated delayed fluorescence (TADF) that can be brought about by using molecules with small gaps (ΔEST) between their S1 and T1 states. Such a scenario allows the triplet states to re-populate the singlets – which then emit – rather than relying on promotion of the direct T1 → S0 rate constant. The phenomenon is widely studied in purely organic molecules with charge-transfer (CT) states.19–23 A number of examples that contain metals have also been studied in recent years, including Cu(I),24 Ag(I),25 Au(I)26 and Pd(II)27–29 complexes. Amongst the vast number of phosphorescent Ir(III) and Pt(II) complexes, however, there are almost no reported examples of TADF: they are normally considered exclusively phosphorescent. Photophysical behaviour reminiscent of TADF was recently reported in mono- and dinuclear Ir(III) complexes,30 whilst a single case of a Pt(0) delayed fluorescent complex was described before the area had become of such contemporary interest.31 In a recent study of dinuclear cyclometallated Pt(II) complexes, we discovered what appears to be the first example of a Pt(II) complex that emits through TADF at ambient temperature (Chart 1).18
 | ||
| Chart 1 The structure of the dinuclear Pt(II) complex 1 recently discovered to show TADF,18 and of the dinuclear bis-tridentate complex 2 reported in this work as well as its mononuclear analogue 3. | ||
TADF complexes are less reliant on the heavy atom effect, such that large radiative rates can be obtained without strong SOC from the metal. For example, the dinuclear Pt(II) complex 1 mentioned above that emits through a TADF mechanism (Chart 1) shows a radiative rate constant that is comparable to that of state-of-the-art phosphorescent Ir(III) complexes.18,31 We believe that in the particular case of 1, the rates of intersystem crossing (ISC) and reverse intersystem crossing (RISC) are several orders of magnitude larger than the observed radiative rate. Such an assumption is general to many organometallic delayed fluorescence emitters.32,33 The definitive limit for radiative rates is governed by the singlet (S1 → S0) decay rate, which is a spin-allowed process, often orders of magnitude larger than the rate of the spin-forbidden phosphorescence (T1 → S0).
In this work we address the critical role of di-nuclearity as a strategy to induce TADF in platinum(II) complexes by comparing a newly prepared dinuclear complex 2 with its mononuclear analogue 3 (Chart 1). It has already been observed that bimetallic structures may show smaller ΔEST than their monometallic analogues.18,34–36 However, this and other aspects concerning the TADF phenomenon in this group of organometallic compounds have not been fully explored. The new dinuclear Pt(II) complex 2 of a ditopic, bis-N^C^N-chelating ligand shows a small ΔEST and yields TADF properties as a result of decreasing HOMO–LUMO overlap through a hybrid CT state19,23 and the so-called multiple resonance37 orbital pattern. Interestingly, in addition to TADF, 2 also forms emissive excimers, a property in common with mononuclear Pt(II) complexes of related N^C^N ligands.38 In this case, the excimer emits in the near infrared (NIR) with an emission maximum of 810 nm in the solid state.
Results and discussion
Synthesis
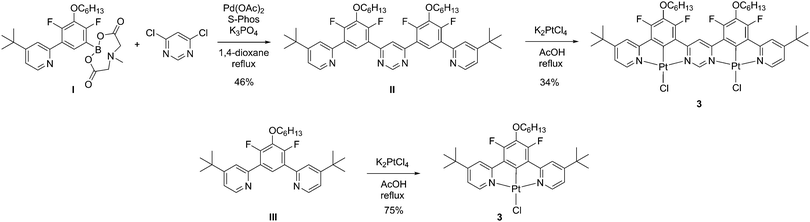
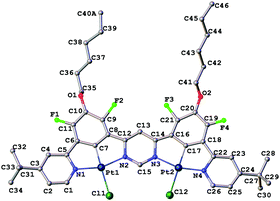
Given the impressive luminescence characteristics of many mononuclear Pt(II) complexes of N^C^N-coordinating ligands, based on 1,3-di(2-pyridyl)benzene, we sought to prepare a ditopic, bis-N^C^N-coordinating proligand in which the two N^C^N units are rigidly linked via a shared pyrimidine ring, i.e. of the form N^C^N–N^C^N (Scheme 1). Such a proligand, similar to II but lacking the tert-butyl groups, was described previously by some of the current authors.39 However, the reaction of that proligand with potassium tetrachloroplatinate, in the hope of obtaining the corresponding dinuclear Pt(II) complex, gave a very insoluble product. The low solubility prevented the unequivocal confirmation of the identity and purity of the material and its photophysical characterisation. In order to improve the solubility, we introduced two tert-butyl groups into the para-positions of the pyridine rings. Thus, proligand II was prepared in 46% yield by the Suzuki reaction of the known MIDA-protected boronic acid I40 with 4,6-dichloropyrimidine. The desired dinuclear platinum complex was then prepared in 34% yield by heating under reflux the mixture of the proligand and two equivalents of potassium tetrachloroplatinate in acetic acid. In a similar manner, the model mononuclear complex 3 was prepared in 75% yield from the known39 proligand III. The identity and purity of the complexes were confirmed through the combination of 1H and 19F NMR spectroscopy, mass spectrometry, elemental analysis and, for 2, X-ray crystallography.The molecular structure of 2 in the crystal (Fig. 1) confirms the presence of two Pt(II) ions in roughly square-planar geometries, each coordinated by a tridentate N^C^N unit and a monodentate chloride ligand. The entire structure (barring the substituents) is close to planarity. The platinum–ligating atom bond lengths are very similar for both Pt(II) centres. The molecules pack in the crystal in off-centre, head-to-tail slanted stacks, with no significant intermolecular metal–metal interactions. The shortest intermolecular Pt···Pt distance is 4.464(2) Å. Planar cores of the adjacent complexes in stacks are separated by a distance of 3.970 Å, typical for aromatic π⋯π interactions.
DFT and TD-DFT calculations
Density functional theory (DFT) calculations leading to optimised ground state geometries were carried out on 2 and 3 using B3LYP41,42 functional and def2-TZVP43 basis set while time-dependent DFT (TDDFT) single point calculations were performed using zeroth-order regular approximation (ZORA44,45)-corrected def2-TZVP43,46 basis sets and the same functional (details of the methods used are described in the ESI†). Their optimised ground-state geometries are found to be roughly planar, favoured by the preferred square arrangement of the Pt(II) centres with d8 electron configuration. The lowest singlet excitation (S0 → S1) has HOMO → LUMO character in 2 (Fig. 2) and is associated with a shift of electron density from both of the Cl–Pt axes into the bridging pyrimidine ring. The transition is of mixed character, with significant contributions from the Pt dxz orbitals and Cl py orbitals: dPt1|Pt2 + pCl1|Cl2 + πph → πpyrim*. Such orbital parentage implies a charge-transfer (CT) character to this transition. Interestingly, there is very little overlap between the frontier MOs in 2, which is attributed to the presence of a strong electron withdrawing pyrimidine unit in the middle, which consequently makes little contribution to the HOMO. The HOMO–LUMO pattern in 2 is thus a combination of multiple resonance37 and charge transfer orbital geometries. In the mono-Pt(II) analogue 3, a very similar HOMO pattern is observed but the LUMO is more uniformly distributed over the π system of the tridentate ligand. The HOMO–LUMO overlap is larger due to the absence of the electron-withdrawing pyrimidine. | ||
| Fig. 2 HOMO and LUMO orbital contour plots at the B3LYP/dev2-TZVP/ZORA/CPCM(CH2Cl2) level for 2 and 3. | ||
Younker and Dobbs47 have demonstrated that a good correlation exists between experimental and theoretical singlet and triplet energies, and other excited state parameters, calculated from the ground state (S0) geometry instead of the excited state. We believe such an approach to be appropriate in rigid structures such as 2 and 3, and it is therefore used in this work. Results obtained for the T1 geometry are in the ESI† for reference. The excited state parameters are analysed at the two theory levels: routine time-dependent density functional theory (TDDFT) and TDDFT including spin–orbit coupling (SOC-TDDFT). In the description of the excited states the former will be referred to as TDDFT or zero-order states (Sn, Tn), while the latter as SOC-TDDFT states (Γn).
The calculated excited state properties of 2 and 3 are summarised in Table 1. TDDFT and SOC-TDDFT calculated excited state energies in 2 and 3 are close to the experimental values recorded in CH2Cl2 (Table 2). However, the SOC-corrected energies show better correlation with the experimental values. The calculated ΔEST in 2 is approximately half of that in 3, which correlates well with the larger HOMO–LUMO overlap of the latter. In contrast, the zero-field splitting calculated as an energy difference between triplet excited states Γ3 and Γ1 in the mono-Pt(II) 3 complex is double that of the di-Pt(II) analogue 2. Note the SOC-TDDFT excited states Γ1–3 refer to the three substates of the lowest triplet state (T1) observed experimentally in metal complexes.33,48 The oscillator strength of the lowest triplet transitions (Γ1, Γ2, Γ3 → Γ0) is also overall larger in 3, leading to a calculated kT−1r = 9.7 μs as opposed to kT−1r = 28 μs for 2. We use  so the reciprocal radiative rate as a representation of the natural triplet lifetime if all non-radiative processes are neglected. The very low S1–T1 SOCME values in both cases do not fully explain the predicted phosphorescent properties of these complexes. A closer analysis indicates that a strong coupling between T1 and upper singlet states influences the triplet oscillator strength in both compounds, i.e. S3–S6 in 3 and S2–S7 in 2 (Fig. S4.4, ESI†). Overall the mononuclear complex 3 is predicted to show superior phosphorescent properties to its di-nuclear analogue 2 due to a larger calculated kTr of the former (if non-radiative processes were neglected). This can be explained with the increased role of the extended ditopic ligand in the excited state in 2, despite the introduction of a second metal centre. Importantly, 2 shows a larger singlet oscillator strength than 3 which stands in an apparent contradiction with the HOMO–LUMO overlap being larger in the latter. However, results (Table S4.4, ESI†) suggest a significant loss of singlet character of the excited states in 3 due to the strong SOC from the metal, which results in lower oscillator strength despite larger frontier molecular orbital overlap. These findings are in agreement with those presented in our earlier work.18
so the reciprocal radiative rate as a representation of the natural triplet lifetime if all non-radiative processes are neglected. The very low S1–T1 SOCME values in both cases do not fully explain the predicted phosphorescent properties of these complexes. A closer analysis indicates that a strong coupling between T1 and upper singlet states influences the triplet oscillator strength in both compounds, i.e. S3–S6 in 3 and S2–S7 in 2 (Fig. S4.4, ESI†). Overall the mononuclear complex 3 is predicted to show superior phosphorescent properties to its di-nuclear analogue 2 due to a larger calculated kTr of the former (if non-radiative processes were neglected). This can be explained with the increased role of the extended ditopic ligand in the excited state in 2, despite the introduction of a second metal centre. Importantly, 2 shows a larger singlet oscillator strength than 3 which stands in an apparent contradiction with the HOMO–LUMO overlap being larger in the latter. However, results (Table S4.4, ESI†) suggest a significant loss of singlet character of the excited states in 3 due to the strong SOC from the metal, which results in lower oscillator strength despite larger frontier molecular orbital overlap. These findings are in agreement with those presented in our earlier work.18
| 2 | 3 | ||
|---|---|---|---|
| a Singlet TDDFT state (S1) energy. b Triplet TDDFT state (T1) energy. c Energy difference between lowest TDDFT singlet and triplet states. d Oscillator strength of lowest TDDFT singlet state. e Reciprocal decay rate of the lowest excited TDDFT singlet state. f Lowest triplet SOC-TDDFT state energy (equivalent of the energy of the lowest substate of the T1 state). g Energy of lowest SOC-TDDFT state with dominant S1 character. h Energy difference between SOC-TDDFT states attributed as lowest singlet and triplet. i Energy difference between the first and third lowest SOC-TDDFT triplet states also referred to as zero-field splitting (ZFS). j S1–T1 spin–orbit coupling matrix element (SOCME). k Oscillator strength of the lowest singlet SOC-TDDFT state. l Reciprocal decay rate of the lowest excited SOC-TDDFT singlet state. m Reciprocal average triplet state lifetime at 295 K calculated using methods reported earlier.51,52 n Properties of the lowest singlet SOC-TDDFT state are not shown for 3 due to a low singlet character. | |||
| TDDFT | S1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/eV (nm) a/eV (nm) |
2.404 (516) | 3.142 (395) |
T1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b/eV (nm) b/eV (nm) |
2.115 (586) | 2.679 (463) | |
ΔEST![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c/eV c/eV |
0.289 | 0.463 | |
f (S1)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
0.21 | 5.8 × 10−3 | |
k S−1r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e/s e/s |
9.5 × 10−9 (9.5 ns) | 2.0 × 10−7 (200 ns) | |
| SOC-TDDFT | Γ 1 (triplet)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f/eV (nm) f/eV (nm) |
2.102 (590) | 2.727 (455) |
Γ n (singlet)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g/eV (nm) g/eV (nm) |
2.338 (530) [Γ7] | ||
ΔEST![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) h/eV h/eV |
0.236 | ||
ΔE(Γ3–Γ1), (ZFS)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i/cm−1 i/cm−1 |
42.7 | 80.1 | |
S1–T1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j SOCME/cm−1 j SOCME/cm−1 |
13 | 1.3 | |
f (Γn) (singlet)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k k |
0.14 [Γ7] | ||
k S−1r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) l/s l/s |
1.5 × 10−8 (15 ns) | ||
| k T−1r /s | 2.8 × 10−5 (28 μs) | 9.7 × 10−6 (9.7 μs) | |
| Complex | Solvent | λ abs /nm (ε M−1 cm−1) | λ em /nm | Φ PL | τ /μs | k r /105 s−1 | k nr /105 s−1 |
|---|---|---|---|---|---|---|---|
| a Absorption maxima and molar absorption coefficients. b Emission maxima. c Photoluminescence quantum yield recorded against rhodamine 6G (ΦPL = 0.9158) or Coumarine 153 (ΦPL = 0.5358) in air-equilibrated absolute ethanol solutions. Details of the experimental procedure for determination of photoluminescence quantum yields are given in the ESI. d Photoluminescence lifetime at room temperature. e Observed radiative rate constant, kr = ΦPL/τ. f Observed non-radiative rate constant, knr = (1 − ΦPL)/τ. | |||||||
| 2 | Toluene | 522 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), 403 (16 000), 403 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800), 350 (23 800), 350 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100), 337 (22 100), 337 (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600), 306 (33 600), 306 (33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200) 200) |
579 sh, 617 | 0.16 | 1.2 | 1.3 | 7.1 |
| Chlorobenzene | 525 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), 450 (7600), 401 (16 200), 450 (7600), 401 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300), 373 (17 300), 373 (17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100), 351 (25 100), 351 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500), 336 (23 500), 336 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400), 306 (31 400), 306 (31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800) 800) |
578 sh, 635 | 0.51 | 5.0 | 1.0 | 1.0 | |
| CH2Cl2 | 515 (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), 443 (8200), 393 (16 200), 443 (8200), 393 (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500), 370 (23 500), 370 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400), 345 (29 400), 345 (29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200), 329 (25 200), 329 (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400), 303 (34 400), 303 (34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900) 900) |
568 sh, 641 | 0.34 | 3.9 | 0.9 | 1.7 | |
| 3 | Toluene | 478 (200), 406 sh (5900), 381 (9900), 366 sh (6100), 329 (5800) | 495 sh, 514 | 0.82 | 5.3 | 1.6 | 0.3 |
| Chlorobenzene | 478 (200), 406 sh (5400), 379 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), 362 sh (6300), 331 (6800) 000), 362 sh (6300), 331 (6800) |
514 | 0.85 | 5.7 | 1.5 | 0.3 | |
| CH2Cl2 | 478 (100), 398 sh (5000), 375 (9000), 358 sh (6100), 329 (7600), 317 (7300) | 512 | 0.73 | 6.4 | 1.1 | 0.4 | |
Considering RISC/ISC in 2, where it is more relevant due to the smaller S–T gap, the SOC matrix was analysed for possible strong S1–Tn couplings, as the direct S1–T1 coupling is relatively weak (13 cm−1). The SOCME for S1–T2 and S1–T3 combinations are significantly larger, 345 cm−1 and 847 cm−1, respectively (Fig. S4.5, ESI†). The T2 state involves HOMO−1 → LUMO transition while the T3 HOMO−2 → LUMO, with the latter involving different d orbitals of Pt(II) centres from those of S1, thus explaining the very large SOC constant in this case (Fig. S4.1, ESI†). The T2 (2.25 eV) and especially T3 (2.47 eV) states are located energetically relatively close to the S1 state (2.40 eV). These findings strongly support the RISC/ISC process being mediated through upper T2, T3 states rather than being direct T1 ↔ S1 exchange, i.e. T1 ↔ (T2,T3) ↔ S1. In this respect the mechanism is similar to the three-state model proposed for RISC/ISC in metal-free systems.49,50
Solution state photophysics
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1) shows about 50% stronger absorption than the respective band in 3, ≈ 380 nm (ε ≈ 10
000 M−1 cm−1) shows about 50% stronger absorption than the respective band in 3, ≈ 380 nm (ε ≈ 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1), in agreement with calculations, indicating a larger oscillator strength for the S0 → S1 transition in the former. The photoluminescence of 2 shows positive solvatochromism as opposed to 3. This is consistent with the HOMO–LUMO distributions of the respective complexes and indicates a charge-transfer character to the transition in 2. The photoluminescence spectrum of 2 consists of two bands: λmax = 617–641 nm (varying with solvent) and a shoulder at 570–580 nm. Notably, the high energy shoulder of the photoluminescence spectrum overlaps with the low energy part of the absorption spectrum, leading to some self-absorption at higher concentrations, as observed in CH2Cl2 at c = 5 × 10−4 M (Fig. S5.1, ESI†). Such overlap and consequent self-absorption are highly indicative of the high energy photoluminescence shoulder originating from the S1 → S0 transition, thus attributed to fluorescence and not to phosphorescence as would normally be anticipated in purely phosphorescent emitters. Indeed, the photoluminescence spectrum of 3 shows a pronounced Stokes shift with no self-absorption at high concentrations (Fig. S5.1, ESI†).
000 M−1 cm−1), in agreement with calculations, indicating a larger oscillator strength for the S0 → S1 transition in the former. The photoluminescence of 2 shows positive solvatochromism as opposed to 3. This is consistent with the HOMO–LUMO distributions of the respective complexes and indicates a charge-transfer character to the transition in 2. The photoluminescence spectrum of 2 consists of two bands: λmax = 617–641 nm (varying with solvent) and a shoulder at 570–580 nm. Notably, the high energy shoulder of the photoluminescence spectrum overlaps with the low energy part of the absorption spectrum, leading to some self-absorption at higher concentrations, as observed in CH2Cl2 at c = 5 × 10−4 M (Fig. S5.1, ESI†). Such overlap and consequent self-absorption are highly indicative of the high energy photoluminescence shoulder originating from the S1 → S0 transition, thus attributed to fluorescence and not to phosphorescence as would normally be anticipated in purely phosphorescent emitters. Indeed, the photoluminescence spectrum of 3 shows a pronounced Stokes shift with no self-absorption at high concentrations (Fig. S5.1, ESI†).
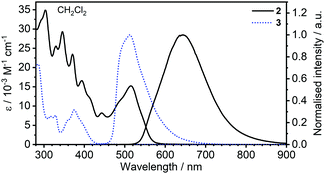 | ||
| Fig. 3 Comparison of absorption and photoluminescence spectra of 2 and 3 in CH2Cl2, c = 10−5 M for absorption and c = 5 × 10−7 M for emission spectra. | ||
 | ||
| Fig. 4 Absorption and photoluminescence spectra of 2 (a) and 3 (b) in the three solvents indicated in figure legend, c ≈ 10−5 M for absorption and c = 5 × 10−7 M for emission spectra. | ||
In general, Pt(II) complexes show large ISC rates to the triplet manifold, such that examples of fluorescent complexes are rare.34 On the other hand, organometallic complexes may exhibit delayed fluorescence properties when ΔEST is small enough to allow sufficient re-population of S1 states in thermal equilibrium with the T1 state. The calculated ΔEST in 2 is larger than the value of ≈ 70 mV in the previously reported complex 1 (Table 1), thus it is reasonable to expect a lesser contribution of TADF to the overall emission, so that delayed fluorescence and phosphorescence may both be contributing to the luminescence spectrum. With this in mind, we have recorded photoluminescence spectra of 2 at temperatures above the ambient in two solvents of high boiling point: chlorobenzene (Fig. 5) and toluene (Fig. S5.2, ESI†). It is evident that the high energy photoluminescence band at 570–580 nm is favoured over the band at λ = 617–641 nm (varies with solvent) at higher temperatures. The ratio of these two bands follows the well-known relation proposed by Parker and Hatchard in the early studies of TADF, then referred to as E-type fluorescence.53 This allows the activation energy to be determined: Ea = 157 ± 4 meV in toluene and Ea = 195 ± 3 meV in chlorobenzene. The photoluminescence spectra obtained from this experiment in chlorobenzene show a clear iso-emissive point at 685 nm (Fig. S5.13, ESI†) indicating that the two emissive bands emanate from the same population of T1 excited states or species formed from them. This finding is indicative of the TADF mechanism being at work. Similar experiments conducted with 3 in chlorobenzene reveal the absence of any thermally activated fluorescence bands up to 364 K (Fig. S5.5, ESI†). Such behaviour indicates a significantly larger ΔEST of the mono-Pt(II) complex.
Solid state photophysics
Solid films of 2 dispersed in polystyrene matrix, and similarly neat films, (Fig. 6) show clear contributions from a NIR-emitting excimer, λem = 810 nm, with the monomolecular emission band, λem = 640 nm, only present at lower concentrations. This is in contrast with the behaviour in solution, where no excimer emission was detectable. The reason for this behaviour is likely related to the suppression of non-radiative processes affecting the excimer emission in the NIR – in this way, the excimer lifetime lengthens and the emission becomes visible in the photoluminescence spectrum. Moreover, concentrations of the Pt(II) complex in film are significantly larger than in solution, facilitating intermolecular interactions, allowing more excimer states to be produced. The ΦPL in film is significantly lower than in solution, decreasing from 0.11 ± 0.02 at 0.1% load to only 0.03 ± 0.01 in neat film. Such photoluminescence quenching is directly related to the larger ability of 2 to produce low-emissive excimers in solid film.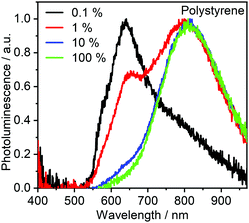 | ||
| Fig. 6 Photoluminescence spectra of 2 dispersed in polystyrene at the various concentrations shown in the figure legend, 100% denotes neat film. | ||
The photoluminescence decay lifetime of the λem = 640 nm band is significantly longer than that of the excimer band at λem = 810 nm (Fig. S5.20, ESI†). As demonstrated before, the kinetic relationship between bimolecular and unimolecular photoluminescence lifetimes in solution is not preserved in solid film (Fig. S5.13, ESI†).57 This is likely due to molecules showing a significantly lower mobility in solid film than in solution. Such behaviour results in only those excited molecules that are located at relatively close distance to a nearest neighbour being able to form bimolecular excited states, while molecules emitting unimolecular luminescence are “isolated”, and in principle unable to come into contact with any of the other molecules. This situation results in a static-quenching like behaviour, as opposed to the dynamic quenching observed in solution. Static quenching might be also an indication of dimer formation in the ground state but, in the case of 2, the excitation spectra recorded in solid film not only agree for both the 640 nm and 810 nm bands but are also very similar to the absorption spectra in solution (Fig. S5.19, ESI†). It is, therefore, likely that some molecules remain at close distances in solid matrix, sufficiently so to migrate and form excimers, but too far apart for clear ground-state interactions to be present.
The photoluminescence spectrum of the lowest concentration film (0.1% w/w) resembles those recorded in solution, featuring two bands: the main one at λem = 640 nm and a shoulder at 580 nm. The shoulder at 580 nm diminishes at lower temperatures, from 300 to 160 K (Fig. 7a). The high energy band at 580 nm behaves in a similar manner to the shoulders in the solution photoluminescence spectra (Fig. 5). The photoluminescence lifetime increases from 5.3 μs at 300 K to 7.5 μs at 160 K. Such simultaneous change in photoluminescence spectrum and lifetime is typical of organometallic TADF emitters.59
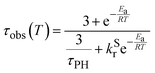 | (1) |
 | ||
| Fig. 7 Photoluminescence of 2 in polystyrene matrix at 0.1% (w/w). (a) Emission spectra at temperatures from 300 to 160 K. (b) Photoluminescence decay lifetime at temperatures from 300 to 80 K, showing the experimental data points and the best fit according to eqn (1). Note the ΔEST figure is obtained from onsets of phosphorescence at 160 K (T1 energy) and TADF at 300 K (S1 energy). | ||
The variation of the photoluminescence lifetime in the temperature region from 300 to 160 K can be described by eqn (1),32,33 where τobs(T) is the observed emission lifetime (s); Ea is the activation energy of the reverse intersystem crossing process in J mol−1; τPH is the phosphorescence lifetime (s); kSr is the radiative rate constant of singlet state (s−1); R is the universal gas constant, 8.314 J mol−1 K−1; and T is the temperature in K. Eqn (1) is used for fitting the photoluminescence lifetime as a function of temperature giving Ea = 159 ± 20 meV and kSr = 9 × 107 s−1. Note the latter figure is very close to the calculated value of ≈ 108 s−1. The energy barrier Ea in polystyrene is very close to the singlet–triplet gap ΔEST = 199 ± 23 meV determined from the onsets of the phosphorescence and fluorescence bands and identical to the Ea value determined in toluene, 157 ± 4 meV. Further increase in the photoluminescence lifetime at temperatures below 160 K is attributed to suppression of non-radiative processes affecting the T1 state. This is in agreement with the behaviour of phosphorescence spectra in this temperature range, which show a simultaneous blue shift and spectral narrowing as the temperature decreases (Fig. S5.15, ESI†). Time-resolved photoluminescence spectra recorded at various temperatures (Fig. S5.16, ESI†) indicate the TADF and phosphorescence bands have the same decay lifetime. This is consistent with the TADF mechanism as S1 and T1 remain in an equilibrium.54
ΔEST: Fig. 8a shows simulations of the luminescence lifetime obtained using eqn (1) as a model for different values of the energy barrier Ea. It is shown that the reduction of Ea favours TADF and reduces τobs at room temperature. With Ea > 0.3 eV, TADF is not present at room temperature and its effect remains negligible up to 400 K. Such a situation is found in 3 (Fig. S5.5, S5.17 and S5.18, ESI†). Reducing the energy barrier for RISC T1 → S1 increases the population of singlet states in equilibrium with the T1.
k sr: Engineering a low ΔEST has been a long standing design target for metal-free TADF molecules where the RISC rate is important for the overall delayed fluorescence lifetime.61 In organometallic emitters, the RISC rate may no longer be considered a limiting factor and the S1 radiative rate becomes the important aspect.32,33 The model (Fig. 8b) shows that increasing ksr helps TADF in a less straightforward way. In this case an increase in ksr leads to a greater contribution of TADF and shorter decay lifetime despite Ea being maintained constant.
τ PH: Longer phosphorescence lifetime, τPH may increase the overall decay lifetime, but will also increase the contribution of TADF due to the T1 → S0 transition being slower, thus allowing TADF to out-compete triplet decay (Fig. 8c). However, in cases where Ea is small, vide infra, longer τPH does not have a significant effect on the overall luminescence lifetime. This is the case in the previously reported delayed fluorescent complex 1, where τPH does not seem to affect the luminescence lifetime given the fact that the TADF complex exhibits a small ΔEST. In fact, it can be demonstrated that if 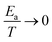 (so that the Boltzmann term
(so that the Boltzmann term  ), the observed decay lifetime is independent of Ea and only depends on the decay rates of the S1 and the T1 state. Since, often τPH−1 ≪ ksr, therefore
), the observed decay lifetime is independent of Ea and only depends on the decay rates of the S1 and the T1 state. Since, often τPH−1 ≪ ksr, therefore  (lower limit for τobs). In practical terms this means that an emitter with a very small ΔEST will show photoluminescence lifetime approaching the value of four times the S1 decay lifetime around room temperature. We find therefore no need for the SOC to be very strong in the TADF complex in order to obtain a large radiative rate and hence a short τobs. We believe even a weak effect of the metal centre and the associated increase in SOC interaction is sufficient for sufficiently fast RISC and ISC processes to occur.34
(lower limit for τobs). In practical terms this means that an emitter with a very small ΔEST will show photoluminescence lifetime approaching the value of four times the S1 decay lifetime around room temperature. We find therefore no need for the SOC to be very strong in the TADF complex in order to obtain a large radiative rate and hence a short τobs. We believe even a weak effect of the metal centre and the associated increase in SOC interaction is sufficient for sufficiently fast RISC and ISC processes to occur.34
Given the analysis based on Fig. 8, it is clear that dinuclear Pt(II) complexes are significantly more likely to exhibit TADF than their mononuclear Pt(II) analogues. Their excited state properties move in exactly the right direction to promote the phenomenon.
OLED devices
Complex 2 forms a NIR-emitting excimer, λem = 810 nm in solid film. Given the scarcity of solution-processed OLEDs with electroluminescence λEL > 800 nm we decided to produce devices taking advantage of the excimer's long emission wavelength. Since 2 is only marginally soluble in toluene at room temperature (≈10 μg mL−1), but much more so in chloroform (≈10 mg mL−1), the most feasible is a simple OLED device structure based on a single emissive layer deposited directly onto PEDOT:PSS. In such a case, it is desirable to control the charge balance in the emitting layer and to increase the device current by using two-component hosts comprising a hole-transport and electron-transport material.62–65 The OLED device structure used in this work is based on a previously reported architecture using a mCP:PO-T2T host (1,3-bis(carbazol-9-yl)benzene and 2,4,6-tris[3-(diphenylphosphinyl)phenyl]-1,3,5-triazine, respectively) that was optimised for excimer-forming mono-Pt(II) complexes with pyridyltriazole ligands.57 For the use of 2 as an emitter, the device structure ITO|PEDOT:PSS Al4083 (30 nm)|mCP:PO-T2T (n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m) co x% 2 (y nm)|PO-T2T (50 nm)|LiF (0.8 nm)|Al (100 nm) comprises commonly used PEDOT:PSS Al4083 as a hole injection layer and a solution-processed emissive layer based on mCP:PO-T2T host (Fig. 9). A thermally-deposited layer of PO-T2T serves as the electron transport layer, while LiF/Al serve as electron injection layer and metallic contact. Note the proportion of mCP and PO-T2T (n
m) co x% 2 (y nm)|PO-T2T (50 nm)|LiF (0.8 nm)|Al (100 nm) comprises commonly used PEDOT:PSS Al4083 as a hole injection layer and a solution-processed emissive layer based on mCP:PO-T2T host (Fig. 9). A thermally-deposited layer of PO-T2T serves as the electron transport layer, while LiF/Al serve as electron injection layer and metallic contact. Note the proportion of mCP and PO-T2T (n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m) in the blend as well as doping concentration (x) are presented in Table 3. Devices 1 and 2 were produced with an emissive layer of 65 ± 5 nm thickness. Thick emissive layer accounts for the simplicity of the OLED structure, minimising recombination on layer interfaces. Due to limited solubility of 2, device 3 was fabricated with a slightly thinner emissive layer of, 40 ± 5 nm. Given the electrical behaviour of 2 in OLED, it is reasonable to believe it acts as an electron transport material. Therefore, in device 3 the contribution of hole-transporting mCP was increased in the host to compensate for the added electron transport ability in the emissive layer. Thinner emissive layer in device 3 increases device current, thus effectively reducing the optical turn-on voltage, VON at 0.1 mW cm−2, to ≈ 9 V while VON ≈ 15–16 V in devices 1 and 2 with the thicker emissive layer.
m) in the blend as well as doping concentration (x) are presented in Table 3. Devices 1 and 2 were produced with an emissive layer of 65 ± 5 nm thickness. Thick emissive layer accounts for the simplicity of the OLED structure, minimising recombination on layer interfaces. Due to limited solubility of 2, device 3 was fabricated with a slightly thinner emissive layer of, 40 ± 5 nm. Given the electrical behaviour of 2 in OLED, it is reasonable to believe it acts as an electron transport material. Therefore, in device 3 the contribution of hole-transporting mCP was increased in the host to compensate for the added electron transport ability in the emissive layer. Thinner emissive layer in device 3 increases device current, thus effectively reducing the optical turn-on voltage, VON at 0.1 mW cm−2, to ≈ 9 V while VON ≈ 15–16 V in devices 1 and 2 with the thicker emissive layer.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PO-T2T (n
PO-T2T (n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m) co x% 2 (y nm)|PO-T2T (50 nm)|LiF (0.8 nm)|Al (100 nm)
m) co x% 2 (y nm)|PO-T2T (50 nm)|LiF (0.8 nm)|Al (100 nm)
| Device | n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ma ma |
x , % | y , nm | λ EL , nm | %λe > 700 nm | Φ PL | EQEmaxg, % | Max. radiosity, mW cm−2 |
|---|---|---|---|---|---|---|---|---|
| a Ratio of mCP to PO-T2T (w/w) in the emissive layer. b Weight doping concentration of 2 in the emissive layer. c Thickness of the emissive layer. d Electroluminescence maxima. e Percent of spectral power at wavelengths above 700 nm. f Photoluminescence quantum yield of the emissive layer in nitrogen. g Device maximum external quantum efficiency. | ||||||||
| Dev 1 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
5 | 65 ± 5 | 637, 730 | 54 | 0.19 ± 0.02 | 2.64 | 3.21 |
| Dev 2 | 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
20 | 65 ± 5 | 651, 787 | 66 | 0.10 ± 0.01 | 0.99 | 1.22 |
| Dev 3 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 20 |
33 | 40 ± 5 | 805 | 87 | 0.07 ± 0.01 | 0.51 | 1.04 |
The electroluminescence spectra of devices 1–3 show the typical increase of excimer contribution to the electroluminescence at higher complex concentrations. At 5% complex load (device 1), there is a clearly noticeable contribution of single molecular emission of 2, with the maximum at 637 nm attributed to phosphorescence and a shoulder at 570 nm attributed to TADF. On the other hand, NIR (λEL = 805 nm) excimer electroluminescence dominates in device 3, with 33% complex load. We recognise that many organometallic complexes show limited solubility in organic solvents and therefore OLED devices benefiting from excimer/aggregate electroluminescence of Pt(II) complexes are preferentially produced using vacuum thermal evaporation.66–71 Examples of such emitters in solution-processed devices are scarce.57,72 Efficient NIR emitters are generally rather uncommon in solution-processed OLEDs and only a very small number of examples exist.73–78 Thanks to alkoxy- and fluoro-substituents in 2, the complex shows extraordinary solubility in chlorinated solvents. In conjunction with the long wavelength excimer electroluminescence, this allows NIR OLEDs to be prepared with EQEmax = 0.51% and λEL > 800 nm. The device reported is among the most efficient solution-processed OLEDs with such long wavelength electroluminescence maxima (see Table S7.1 in the ESI†) being inferior only to a Pt(II) porphyrine complex79 with EQE of 0.75% and λEL = 898 nm.80–82 Notably, device 3 is the first example of an excimer Pt(II)-based solution-processed OLEDs with λel > 800 nm.
Conclusions
In this work we have presented an in-depth study of a TADF diplatinum(II) complex which we believe to be only the second known example of a Pt(II) complex emitting through this mechanism. We demonstrate that the mononuclear analogue 3 is a conventional phosphorescence emitter, as opposed to the diplatinum(II) complex 2 which exhibits delayed fluorescence from the singlet state. The study confirms that dinuclear Pt(II) complexes appear to have smaller ΔEST and larger singlet oscillator strength than their mononuclear analogues. Larger S1 → S0 oscillator strength in 2 than in 3 appears to be due to a larger ligand contribution to the excited state in the former, leading to more defined multiplicity of excited states. These parameters are found to be among the key factors for promoting TADF in Pt(II) complexes. It is also shown that larger phosphorescence (T1 → S0) lifetime will make it more likely that TADF will be observed when ΔEST is larger, i.e. >0.1 eV, while as ΔEST → 0 the value of τPH is no longer important if τPH ≫ kS−1r. Future design strategies should, therefore, probably focus more attention on reducing the S–T gap rather than to increasing the SOC pathways from the metal.RISC/ISC in 2 appears to be mediated through an upper triplet state rather than occurring directly between S1 and T1, given the small SOCME between states of the same orbital geometry. We believe the occurrence of a Tn state involving different d orbitals than those of S1/T1, and energetically close to the latter, is of paramount importance in the design of efficient TADF emitters based on Pt(II) complexes. This strongly indicates that there is no escape from the three-state model proposed20 for metal-free TADF emitters, even in organometallic compounds. Strong singlet–triplet coupling is the key for facilitating large RISC/ISC rates which are shown to be essential in the prospective development of TADF emitters based on organometallic compounds. However, SOC necessary to obtain large RISC/ISC rates is likely to occur even in phosphors demonstrating low metal contributions to the excited state and generally slow triplet radiative decay.34
Finally, 2 forms an NIR excimer with an emission maximum of 810 nm in solid state. When incorporated into a solution-processed OLED, it produces long wavelength electroluminescence, λEL = 805 nm. The EQE of the NIR OLED reaches 0.51% which is, to the best of our knowledge, the second highest efficiency among Pt(II)-based solution-processed devices with such long wavelength electroluminescence > 800 nm and the only OLED with a solution-processed emissive layer using NIR platinum(II) excimer emitter.
Author contributions
P. P. – conceptualization, formal analysis, investigation, visualization, writing – original draft, writing – review & editing; A. V. Z. – investigation; A. S. – investigation; J. A. G. W. – conceptualization, funding acquisition, project administration, supervision, writing – review & editing; P.-H. L. – investigation; V. N. K. – conceptualization, funding acquisition, project administration, writing – original draft, writing – review & editing; F. B. D. – funding acquisition, project administration, resources, validation, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank EPSRC (grant ref. EP/S012788/1 and EP/S01280X) for support of this work. We are grateful to Dr Dmitry Yufit at Durham Chemistry for determining the crystal structure of complex 2 and for his continued assistance with crystallography. This work made use of the facilities of the Hamilton HPC Service of Durham University.Notes and references
- H. Yersin, Highly Efficient OLEDs with Phosphorescent Materials, Wiley, 2008 Search PubMed.
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5051 CrossRef CAS.
- M. A. Baldo, D. F. O’Brien, Y. You, A. Shoustikov, S. Sibley, M. E. Thompson and S. R. Forrest, Nature, 1998, 395, 151–154 CrossRef CAS.
- Y.-L. Chang and Z.-H. Lu, J. Disp. Technol., 2013, 9, 459–468 CAS.
- M.-C. Tang, A. K.-W. Chan, M.-Y. Chan and V. W.-W. Yam, Top. Curr. Chem., 2016, 374, 46 CrossRef PubMed.
- K. T. Kamtekar, A. P. Monkman and M. R. Bryce, Adv. Mater., 2010, 22, 572–582 CrossRef CAS PubMed.
- E. Longhi and L. De Cola, Iridium(III) in Optoelectronic and Photonics Applications, John Wiley & Sons, Ltd, Chichester, UK, 2017, vol. 2, pp. 205–274 Search PubMed.
- C. Cebrián and M. Mauro, Beilstein J. Org. Chem., 2018, 14, 1459–1481 CrossRef PubMed.
- G. Li and Y. She, Light-Emitting Diode – An Outlook On the Empirical Features and Its Recent Technological Advancements, InTech, 2018 Search PubMed.
- M. J. Leitl, V. A. Krylova, P. I. Djurovich, M. E. Thompson and H. Yersin, J. Am. Chem. Soc., 2014, 136, 16032–16038 CrossRef CAS PubMed.
- C. Murawski, K. Leo and M. C. Gather, Adv. Mater., 2013, 25, 6801–6827 CrossRef CAS PubMed.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- Z. Hao, M. Li, Y. Liu, Y. Wang, G. Xie and Y. Liu, Dyes Pigm., 2018, 149, 315–322 CrossRef CAS.
- G. Li, D. Zhu, X. Wang, Z. Su and M. R. Bryce, Chem. Soc. Rev., 2020, 49, 765–838 RSC.
- S. Culham, P.-H. Lanoë, V. L. Whittle, M. C. Durrant, J. A. G. Williams and V. N. Kozhevnikov, Inorg. Chem., 2013, 52, 10992–11003 CrossRef CAS PubMed.
- V. N. Kozhevnikov, M. C. Durrant and J. A. G. Williams, Inorg. Chem., 2011, 50, 6304–6313 CrossRef CAS PubMed.
- M. Z. Shafikov, R. Daniels, P. Pander, F. B. Dias, J. A. G. Williams and V. N. Kozhevnikov, ACS Appl. Mater. Interfaces, 2019, 11(8), 8182–8193 CrossRef CAS PubMed.
- P. Pander, R. Daniels, A. V. Zaytsev, A. Horn, A. Sil, T. J. Penfold, J. A. G. Williams, V. N. Kozhevnikov and F. B. Dias, Chem. Sci., 2021, 12, 6172–6180 RSC.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- F. B. Dias, J. Santos, D. R. Graves, P. Data, R. S. Nobuyasu, M. A. Fox, A. S. Batsanov, T. Palmeira, M. N. Berberan-Santos, M. R. Bryce and A. P. Monkman, Adv. Sci., 2016, 3, 1600080 CrossRef PubMed.
- K.-H. Kim, S.-J. Yoo and J.-J. Kim, Chem. Mater., 2016, 28, 1936–1941 CrossRef CAS.
- M. Chapran, P. Pander, M. Vasylieva, G. Wiosna-Salyga, J. Ulanski, F. B. Dias and P. Data, ACS Appl. Mater. Interfaces, 2019, 11, 13460–13471 CrossRef CAS PubMed.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS PubMed.
- A. S. Romanov, L. Yang, S. T. E. Jones, D. Di, O. J. Morley, B. H. Drummond, A. P. M. Reponen, M. Linnolahti, D. Credgington and M. Bochmann, Chem. Mater., 2019, 31, 3613–3623 CrossRef CAS.
- A. S. Romanov, S. T. E. Jones, L. Yang, P. J. Conaghan, D. Di, M. Linnolahti, D. Credgington and M. Bochmann, Adv. Opt. Mater., 2018, 6, 1801347 CrossRef.
- D. Di, A. S. Romanov, L. Yang, J. M. Richter, J. P. H. Rivett, S. Jones, T. H. Thomas, M. A. Jalebi, R. H. Friend, M. Linnolahti, M. Bochmann and D. Credgington, Science, 2017, 356, 159–163 CrossRef CAS PubMed.
- Z. Q. Zhu, C. Do Park, K. Klimes and J. Li, Adv. Opt. Mater., 2019, 7, 1801518 CrossRef.
- G. Li, Q. Chen, J. Zheng, Q. Wang, F. Zhan, W. Lou, Y. F. Yang and Y. She, Inorg. Chem., 2019, 58, 14349–14360 CrossRef CAS PubMed.
- P. W. Zach, S. A. Freunberger, I. Klimant and S. M. Borisov, ACS Appl. Mater. Interfaces, 2017, 9, 38008–38023 CrossRef CAS PubMed.
- M. Z. Shafikov, R. Martinscroft, C. Hodgson, A. Hayer, A. Auch and V. N. Kozhevnikov, Inorg. Chem., 2021, 60, 1780–1789 CrossRef CAS PubMed.
- Z. Abedin-Siddique, T. Ohno, K. Nozaki and T. Tsubomura, Inorg. Chem., 2004, 43, 663–673 CrossRef CAS PubMed.
- J. R. Kirchhoff, R. E. Gamache, M. W. Blaskie, A. A. Del Paggio, R. K. Lengel and D. R. McMillin, Inorg. Chem., 1983, 22, 2380–2384 CrossRef CAS.
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2011, 255, 2622–2652 CrossRef CAS.
- D. N. Kozhevnikov, V. N. Kozhevnikov, M. Z. Shafikov, A. M. Prokhorov, D. W. Bruce and J. A. G. Williams, Inorg. Chem., 2011, 50, 3804–3815 CrossRef CAS PubMed.
- M. Z. Shafikov, R. Daniels, P. Pander, F. B. Dias, J. A. G. Williams and V. N. Kozhevnikov, ACS Appl. Mater. Interfaces, 2019, 11, 8182–8193 CrossRef CAS PubMed.
- P. K. Chow, C. Ma, W. P. To, G. S. M. Tong, S. L. Lai, S. C. F. Kui, W. M. Kwok and C. M. Che, Angew. Chem., Int. Ed., 2013, 52, 11775–11779 CrossRef CAS PubMed.
- T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777–2781 CrossRef CAS PubMed.
- J. Kalinowski, M. Cocchi, L. Murphy, J. A. G. Williams and V. Fattori, Chem. Phys., 2010, 378, 47–57 CrossRef CAS.
- P.-H. Lanoë, C. M. Tong, R. W. Harrington, M. R. Probert, W. Clegg, J. A. G. Williams and V. N. Kozhevnikov, Chem. Commun., 2014, 50, 6831–6834 RSC.
- R. E. Daniels, S. Culham, M. Hunter, M. C. Durrant, M. R. Probert, W. Clegg, J. A. G. Williams and V. N. Kozhevnikov, Dalton Trans., 2016, 45, 6949–6962 RSC.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- J. M. Younker and K. D. Dobbs, J. Phys. Chem. C, 2013, 117, 25714–25723 CrossRef CAS.
- H. Yersin, Top. Curr. Chem., 2004, 1–26 CAS.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS PubMed.
- K. Nozaki, J. Chin. Chem. Soc., 2006, 53, 101–112 CrossRef CAS.
- K. Mori, T. P. M. Goumans, E. van Lenthe and F. Wang, Phys. Chem. Chem. Phys., 2014, 16, 14523–14530 RSC.
- C. A. Parker and C. G. Hatchard, Trans. Faraday Soc., 1961, 57, 1894 RSC.
- V. Gold, The IUPAC Compendium of Chemical Terminology, International Union of Pure and Applied Chemistry (IUPAC), Research Triangle Park, NC, 2019 Search PubMed.
- S. J. Farley, D. L. Rochester, A. L. Thompson, J. A. K. Howard and J. A. G. Williams, Inorg. Chem., 2005, 44, 9690–9703 CrossRef CAS PubMed.
- D. L. Rochester, S. Develay, S. Záliš and J. A. G. Williams, Dalton Trans., 2009, 1728 RSC.
- M. T. Walden, P. Pander, D. S. Yufit, F. B. Dias and J. A. G. Williams, J. Mater. Chem. C, 2019, 7, 6592–6606 RSC.
- C. Würth, M. Grabolle, J. Pauli, M. Spieles and U. Resch-Genger, Nat. Protoc., 2013, 8, 1535–1550 CrossRef PubMed.
- T. Hofbeck, U. Monkowius and H. Yersin, J. Am. Chem. Soc., 2015, 137, 399–404 CrossRef CAS PubMed.
- M. Z. Shafikov, P. Pander, A. V. Zaytsev, R. Daniels, R. Martinscroft, F. B. Dias, J. A. G. Williams and V. N. Kozhevnikov, J. Mater. Chem. C, 2021, 9, 127–135 RSC.
- F. B. Dias, T. J. Penfold and A. P. Monkman, Methods Appl. Fluoresc., 2017, 5, 012001 CrossRef PubMed.
- M. Huang, B. Jiang, G. Xie and C. Yang, J. Phys. Chem. Lett., 2017, 8, 4967–4973 CrossRef CAS PubMed.
- T. Zhang, B. Zhao, B. Chu, W. Li, Z. Su, L. Wang, J. Wang, F. Jin, X. Yan, Y. Gao, H. Wu, C. Liu, T. Lin and F. Hou, Org. Electron., 2015, 24, 1–6 CrossRef CAS.
- J.-H. Lee, S.-H. Cheng, S.-J. Yoo, H. Shin, J.-H. Chang, C.-I. Wu, K.-T. Wong and J.-J. Kim, Adv. Funct. Mater., 2015, 25, 361–366 CrossRef CAS.
- X. Ban, K. Sun, Y. Sun, B. Huang and W. Jiang, Org. Electron., 2016, 33, 9–14 CrossRef CAS.
- Y.-C. Wei, S. F. Wang, Y. Hu, L.-S. Liao, D.-G. Chen, K.-H. Chang, C.-W. Wang, S.-H. Liu, W.-H. Chan, J.-L. Liao, W.-Y. Hung, T.-H. Wang, P.-T. Chen, H.-F. Hsu, Y. Chi and P.-T. Chou, Nat. Photonics, 2020, 14, 570–577 CrossRef CAS.
- K. Tuong, Ly, R.-W. Chen-Cheng, H.-W. Lin, Y.-J. Shiau, S.-H. Liu, P.-T. Chou, C.-S. Tsao, Y.-C. Huang and Y. Chi, Nat. Photonics, 2017, 11, 63–68 CrossRef.
- X. Yang, H. Guo, X. Xu, Y. Sun, G. Zhou, W. Ma and Z. Wu, Adv. Sci., 2019, 6, 1801930 CrossRef PubMed.
- E. Rossi, L. Murphy, P. L. Brothwood, A. Colombo, C. Dragonetti, D. Roberto, R. Ugo, M. Cocchi and J. A. G. Williams, J. Mater. Chem., 2011, 21, 15501 RSC.
- L. Huang, C. D. Park, T. Fleetham and J. Li, Appl. Phys. Lett., 2016, 109, 233302 CrossRef.
- T. C. Lee, J. Y. Hung, Y. Chi, Y. M. Cheng, G. H. Lee, P. T. Chou, C. C. Chen, C. H. Chang and C. C. Wu, Adv. Funct. Mater., 2009, 19, 2639–2647 CrossRef CAS.
- W. Xiong, F. Meng, H. Tan, Y. Wang, P. Wang, Y. Zhang, Q. Tao, S. Su and W. Zhu, J. Mater. Chem. C, 2016, 4, 6007–6015 RSC.
- J. Yu, M. Li, C. Xu, F. Meng, J. Cao, H. Tan and W. Zhu, Dalton Trans., 2020, 49, 8785–8790 RSC.
- X. Wu, D.-G. Chen, D. Liu, S.-H. Liu, S.-W. Shen, C.-I. Wu, G. Xie, J. Zhou, Z.-X. Huang, C.-Y. Huang, S.-J. Su, W. Zhu and P.-T. Chou, J. Am. Chem. Soc., 2020, 142, 7469–7479 CrossRef CAS PubMed.
- A. J. Pearson, T. Plint, S. T. E. Jones, B. H. Lessard, D. Credgington, T. P. Bender and N. C. Greenham, J. Mater. Chem. C, 2017, 5, 12688–12698 RSC.
- T. Sudyoadsuk, P. Chasing, T. Kaewpuang, T. Manyum, C. Chaiwai, S. Namuangruk and V. Promarak, J. Mater. Chem. C, 2020, 8, 5045–5050 RSC.
- C. You, D. Liu, J. Yu, H. Tan, M. Zhu, B. Zhang, Y. Liu, Y. Wang and W. Zhu, Adv. Opt. Mater., 2020, 2000154 CrossRef CAS.
- C. You, D. Liu, M. Zhu, J. Yu, B. Zhang, Y. Liu, Y. Wang and W. Zhu, J. Mater. Chem. C, 2020, 8, 7079–7088 RSC.
- K. R. Graham, Y. Yang, J. R. Sommer, A. H. Shelton, K. S. Schanze, J. Xue and J. R. Reynolds, Chem. Mater., 2011, 23, 5305–5312 CrossRef CAS.
- Y. Zhang, Q. Li, M. Cai, J. Xue and J. Qiao, J. Mater. Chem. C, 2020, 8, 8484–8492 RSC.
- J. R. Sommer, R. T. Farley, K. R. Graham, Y. Yang, J. R. Reynolds, J. Xue and K. S. Schanze, ACS Appl. Mater. Interfaces, 2009, 1, 274–278 CrossRef CAS PubMed.
- A. Minotto, P. Murto, Z. Genene, A. Zampetti, G. Carnicella, W. Mammo, M. R. Andersson, E. Wang and F. Cacialli, Adv. Mater., 2018, 30, 1706584 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthetic details and characterisation of new materials; X-ray diffraction and crystal data; further information on the equipment and methods for theory, photophysical characterisation, electrochemistry, and OLED devices. CCDC-2088015 (complex 2). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc02562g |
| ‡ Present address: Université Grenoble Alpes, CNRS, DCM, Grenoble, F-38000, France. |
| This journal is © The Royal Society of Chemistry 2021 |