A proposal for using molecular spin qudits as quantum simulators of light–matter interactions

Abstract

We show that molecular spin qudits provide an ideal platform to simulate the quantum dynamics of photon fields strongly interacting with matter. The basic unit of the proposed molecular quantum simulator could be realized by synthesizing a simple dimer of spin 1/2 and spin S ≥ 3/2 transition metal ions, solely controlled by microwave pulses. The spin S ion is exploited to encode the photon field in a flexible architecture, which enables the digital simulation of a wide range of spin-boson models much more efficiently than by using a multi-qubit register. The effectiveness of our proposal is demonstrated by numerical simulations using realistic molecular parameters for each of the two ions and the prerequisites delineating possible chemical approaches for the synthesis of suitable platforms are also discussed.

---

1 Introduction

In the last few years, quantum computers have emerged as a disruptive technology that promises to solve a large class of problems much more efficiently than any classical machine. The first noisy quantum processors¹ are already available and enable the implementation of non-trivial algorithms targeted to specific tasks.^2–5 In particular, thanks to their intrinsic quantum logic,⁶ they can be used already in the short term to simulate the dynamics of classically intractable quantum systems. Understanding the behavior of matter at the nano-scale is a fundamental step in designing new molecules, materials and devices. However, the “wonderful problem” of quantum simulation “doesn't look so easy”.⁷ In fact, many examples of interest for physics and chemistry, such as atoms interacting with light or with thermal baths, are intrinsically difficult to be modeled on current qubit-based architectures.⁸

In this respect, chemistry offers a change of perspective which could overcome the aforementioned difficulties. Indeed, molecular spin systems characterized by a sizeable number of accessible levels can be used to encode multi-level logical units (qudits). Each molecular qudit could replace several distinct two-level units (qubits) in various algorithms,⁹ thus greatly simplifying manipulations of the register. Indeed, since each qudit can host more than two levels, important algorithms can be implemented with a smaller number of computational units, compared to qubit-based realizations. Examples are given by Grover's, Fourier transform or Quantum Phase Estimation algorithms¹⁰ or by quantum-error correction schemes recently put forward.^11–13 Hence, the qudit-route to the physical implementation of quantum computing appears very promising in the current development stage, where the operations are still noisy and full control of complex quantum devices is hard.

Magnetic molecules are the ideal candidate to implement this alternative architecture.¹⁴ Indeed, they are characterized by long coherence times,^15–21 which can be further enhanced by chemically designing the molecular structure^22,23 or targeting protected transitions.^24,25 Moreover, the spin state of these systems can be easily manipulated by microwave or radio-frequency pulses,¹¹ thus implementing single- and two-qubit gates in permanently coupled^26–28 or scalable architectures.^29–33 Recently, it was proposed to exploit the additional levels typical of these systems for implementing quantum error correction within a single object,^11–13 in place of the many qubits required by standard block-codes.³⁴

Here we show how the qudit nature of magnetic molecules could simplify the practical implementation of important quantum simulation algorithms. We focus, in particular, on the simulation of light–matter interaction processes. This problem is generally hard to solve on a classical computer, especially in the ultra-strong coupling regime between light and matter, because it does not generally allow for a perturbative treatment. This class of models is of crucial importance for many fundamental investigations ranging from cavity quantum electrodynamics to photochemistry.^35,36 They have mostly been tackled so far with analog^37–39 or digital-analog^40,41 simulation strategies, i.e. by employing a quantum hardware which directly emulates the target system. Conversely, we pursue here a digital approach, in which the state of the target system is encoded into the qubit or qudit register. This makes the quantum simulator much more flexible with respect to the class of systems which can be simulated, but it implies the necessity to represent radiation modes (characterized in principle by infinite degrees of freedom) as qubit/qudit excitations. This represents a major challenge. Indeed, standard encodings, designed for multi-qubit architectures,⁴² either use a number of qubits equal to the number of simulated photons⁴³ (i.e. an exponentially large Hilbert space) or reduce the number of qubits at the price of much more complex quantum circuits, involving interactions between distant qubits.^42,44

Conversely, here we reduce both the hardware overhead and the complexity of manipulations by mapping each photon mode to a single spin S qudit. The qudit levels are then used to represent the number of photons in each mode (see Fig. 1). Thanks to the power of coordination chemistry, different qudits can be linked together and, e.g., to spin 1/2 units encoding two-level atoms,^45–48 in non-trivial molecular geometries. This, together with the capability of manipulating the state of the hardware by resonant and semi/resonant microwave pulses, would allow us to digitally simulate the atom-photon dynamics involving multi-mode fields and/or multiple atoms.^43,49

Fig. 1 Scheme of the molecular quantum simulator. Left: hardware setup, consisting of a qudit spin S₁ coupled by exchange interaction J to a spin s₂ = 1/2. Right: target spin-photon model. In the bottom part of the figure we qualitatively also sketch the mapping between the qudit, with all the transitions made energetically distinguishable by the combined effect of Zeeman and zero-field splitting interactions, and the boson field.

In particular, we show that very simple molecules consisting of dimers of transition metal ions (a spin 1/2 and a spin S ≥ 3/2) can be used to efficiently simulate atom-photon interactions in a non-trivial range of parameters up to strong and ultra-strong coupling.^35,36 The same approach can be extended to simulate models involving many field excitations,⁴⁴ by exploiting the remarkable capabilities of coordination chemistry in synthesizing multi-center molecules with very large total spin,⁴⁷ or interaction of atoms/spins with any other bosonic field, such as phonons. This allows one to simulate, along the same lines, many other important models, ranging from phonon vibrations,^50–53 to lattice gauge theories⁴⁴ and complex quantum optical setups.⁵⁴

In the following, we design a sequence of pulses allowing us (i) to determine the ground state of the simulated system using the variational quantum eigensolver algorithm (VQE)^3,55–57 and (ii) to follow the time evolution of the system prepared in an out-of-equilibrium initial state. The remarkable performance of the proposed hardware is demonstrated by numerical simulations on hypothetical molecular systems characterized by qudit parameters corresponding to existing coordination compounds,^{17,25,58–62} weakly coupled to a spin 1/2 unit. The effect of decoherence and the full sequence of pulses needed to implement the algorithms are also included, obtaining nevertheless very large fidelities. These results make the here-proposed molecular quantum simulator very promising and pave the way to forthcoming proof-of-principle experiments.

2 Results

2.1 Molecular quantum simulator

The proposed molecular hardware for quantum simulation is sketched in Fig. 1 (left part). It is a dimer consisting of a spin S₁ ≥ 3/2 qudit that we exploit to encode the boson field, and an effective s₂ = 1/2, described by the following Hamiltonian:Here, the first two terms represent the Zeeman interaction of the two spins with an external magnetic field B applied along the z axis and μ_B is the Bohr magneton. The third term is the zero-field splitting on the qudit (important to make all qudit transitions spectroscopically distinguishable) and the last one models an exchange or dipolar interaction between the two ions. To reduce our assumptions, we consider in the following axially anisotropic (J_z = −2J_x,y) coupling, modeling a dipole–dipole interaction between the two centers. We stress, however, that different forms of the spin–spin interaction or of the single-ion anisotropy do not hinder the implementation of our scheme. We have no stringent requirements on the precise values of these parameters, but only on the hierarchy of interactions: the transverse component of the spin–spin coupling must be much smaller than the difference between the excitation energies of the two spins S₁ and s₂. This condition guarantees that the eigenstates of Hamiltonian 1 are practically factorized products of the states of the two spins, and can thus be labeled by S_z1 and s_z2 eigenvalues: |ψ_m1m2〉 ≈ |m₁〉|m₂〉. In this respect, we also note that larger values of J_x,y could be compensated by using larger magnetic fields. At the same time, J_z should be sufficiently large to enable conditional excitations of each of the two spins, depending on the state of the other.

These requirements are easily fulfilled in coordination compounds containing a spin 1/2 ion coupled to a spin S₁ transition metal ion. The latter provides the ideal qudit for the proposed architecture. As shown below, the relatively small number of levels of these qudits (d = 2S₁+ 1 ≤ 6) is already sufficient to simulate light–matter interaction from strong to ultra-strong coupling regimes. In addition, transition metal ion complexes with quenched orbital angular momentum ensure significantly long coherence times,^{17,22,25,58,62} important to achieve a good simulation. We consider, in particular, two paradigmatic cases: Cr^III and Fe^III ions in a distorted octahedral environment, yielding 3d³ and 3d⁵ electronic configurations with a single electron per orbital and thus S = 3/2 and 5/2, respectively.^60,61 Due to the practically complete quenching of the orbital angular momentum, the spectroscopic tensor g is isotropic and close to the free electron value, while single ion anisotropy is typically in the ∼0.2–0.3 cm⁻¹ range.^60,61 As an illustrative example, in the simulations reported below we use d₁= 0.24–0.30 cm⁻¹ and g = 1.98 for Cr^III, as in ref. 22 and 25 and d₁ = −0.30 cm⁻¹ and g = 2.00 for Fe^III, as reported e.g. in ref. 58 and 63. By properly adjusting the static field B, the results do not depend on the sign of d₁.

These single-ion qudits can be weakly coupled through bond or through space to a spin 1/2 ion, such as Cu^II in a distorted octahedral ligand cage,^17,60,61 typically characterized by g ∼ 2.1–2.3 and in some cases also by remarkable coherence times.¹⁷ In the following we assume g_2z = 2.3, significantly different from g_1z = 1.98–2 to ensure factorization of the system wave-function. For the dipolar interaction we assume J_x,y = 0.008 cm⁻¹, which corresponds to a dipolar coupling (in the point dipole approximation) between ions at a distance ∼6 Å. We remark that using a different form of the spin–spin coupling (for instance a weak isotropic super-exchange interaction) does not alter our conclusions. A more extensive discussion on possible physical implementations is provided in Section 3.

These parameters, combined with a static field of ∼0.3–0.5 T ensure that Δm_1,2 = ±1 transitions needed to manipulate the state of the system fall within the 20 GHz range typically explored in coplanar microwave resonators.^64,65

Having described in detail the molecular hardware, we now switch our attention to the target model, the object of our simulation, and on how to map it onto the hardware. The target Hamiltonian is the Rabi model:^66–68

[script letter H]_S = ω_aσ_z + Ωa^†a + 2Gσ_x(a + a^†) (2)

Here σ_z and σ_x are the usual spin 1/2 operators, while a^† (a) are bosonic creation (annihilation) operators, [a, a^†] = 1, G is the atom-photon coupling, Ω (ω_a) is the photon (atom) excitation energy, and we have assumed ħ = 1. Hamiltonian (eqn (2)) describes the interaction between a radiation field and a two-level system, such as an atom or a spin 1/2 particle. Important applications come from the context of quantum computing, where the Rabi Hamiltonian is used to model the coupling of quantized photons in superconducting wave-guide resonators^69,70 with superconducting qubits or spin systems.¹⁴ Behind its apparent simplicity, our target model can reveal interesting physics in different ranges of parameters. For instance, the weak (dispersive) coupling regime is used in quantum computing to read-out the state of the qubit or to induce an effective qubit–qubit coupling mediated by the resonator.⁷¹ Conversely, non-trivial behaviors emerge in the ultra or deep strong coupling regimes,³⁶ in which light and matter strongly mix together and exchange excitations without conserving energy.³⁵ Such a regime can also give insights into fundamental principles of lattice gauge theories.⁷² We fix in the following ω_a = Ω/2 and study the model for increasing values of the G/Ω ratio, the threshold for the ultra-strong coupling regime usually being G/Ω ≳ 0.25.

The molecular processor described by Hamiltonian 1 can be used to compute ground state properties and to mimic the dynamics of the target Hamiltonian 2. To achieve this, we first need to encode the boson field into the spin qudit. Notice that a very good approximation can be obtained by truncating the boson field to a relatively small number of levels. Hence, the d = 2S₁ + 1 levels of the qudit are sufficient to encode the radiation field with negligible error, by truncating it to a maximum number n_M = 2S₁ of bosons. The mapping between S_z1 eigenvalues and number of bosons (n = a^†a) is shown in the bottom part of Fig. 1. In parallel, the two-state atom appearing in the Rabi Hamiltonian can be directly encoded on the hardware spin 1/2 degrees of freedom.

Complete control of the hardware is achieved via microwave pulses resonant (or semi-resonant) with specific excitations of the spin 1/2 or of the qudit. In particular, Δm₂ = ±1 transitions allow us to rotate the state of the qubit, while Δm₁ = ±1 pulses are used to excite the qudit. Moreover, the spin–qudit interaction enables conditioned (entangling) operations.

2.2 Variational quantum eigensolver

The starting point to derive many important properties of the examined systems is the determination of its ground state wave-function. This task can be achieved using the variational quantum eigensolver (VQE) approach.^3,55–57 This is a hybrid quantum-classical algorithm, particularly resilient to noise and therefore well suited for near term quantum processors. It exploits the fact that the energy expectation value is minimum for the ground state of the system. The quantum hardware is used to generate an approximation of the ground state (also known as trial wavefunction or variational ansatz) for the target model, which depends on a set of free parameters θ_i, and to evaluate the energy expectation value. Minimization of the evaluated energy by a classical subroutine allows us to explore the parameter space until convergence to the system ground state. It is worth noticing that this method is typically much less demanding, compared to the digital simulation of real time evolution, in terms of the complexity and length of the required sequences of quantum operations to be implemented.

Here we demonstrate an implementation of the VQE on the proposed qudit architecture applied to the target Rabi Hamiltonian, eqn (2). We construct the trial wavefunction by designing some basic quantum operations achieved in practice via external control microwave pulses. In particular, as shown in Fig. 2a, we assume a (S₁, s₂) = (3/2, 1/2) hardware platform and we combine pulses resonant with transitions of s₂ (green arrows), implementing rotations of the qubit, with Δm₁ = ±1 pulses on the S₁ = 3/2 spin (black). To introduce entanglement in the approximate ground state, the operations on the S₁ = 3/2 spin are actually conditioned by the state of the spin 1/2, i.e. we rotate each pair of qudit levels by ±θ_i depending on the sign of m₂ (see Fig. 2a). In total, the ansatz contains only 4 free parameters, namely the rotation angles {θ_i}, and can be implemented with a sequence of microwave pulses that can be as fast as ≃100–200 ns. We also mention that such variational structure, which can be natively realized on our proposed qudit architecture, is closely related to the so-called polaron ansatz, which was recently implemented on superconducting quantum hardware⁴³ through non-trivial decompositions into elementary qubit operations.

Fig. 2 Qudit-based VQE for the Rabi model. (a) Sequence of pulses for the implementation of the ground state approximation. On the left, we report the (approximate) values m₁ and m₂ for the hardware eigenstates, and on the right the corresponding photon numbers. Black (green) pulses induce transitions on the spin S1 (s2). (b Minimization of the Hamiltonian expectation value for G/Ω = 0.6. Data points converging to the value marked by the blue dashed line are obtained simulating a realistic hardware with T₂ = 10 μs. The red dashed line marks the optimal value achieved in the absence of errors and decoherence, i.e. the best possible approximation of the true ground state energy obtainable with the proposed algorithm in an ideal case. The inset represents schematically the set of quantum operations which are used to approximate the ground state, including R_x,y(δ) = e^−iδs_x,y2 rotations on the spin 1/2 and conditioned Δm = ±1 pulses on the spin S₁ = 3/2. The variational parameters are indicated as θ_i, while we assume an initial state with zero photons and a de-excited atom. (c) Ground state energy and (inset) corresponding average number of photons and atom excitations. Dashed lines represent ideal values with no approximations, solid lines are the exact results obtained by Hamiltonian diagonalization after truncating the photonic Hilbert space to d = 4 levels, dotted lines are numerical VQE results with no errors or dechoherence and diamonds are simulations of the real device. Each expectation value can be measured by inducing Δm_1,2 = ±1 transitions with appropriate microwave pulses. Hardware parameters are g₁ = 1.98, g₂ = 2.3, d₁ = 0.24 cm⁻¹, J_x,y = 0.008 cm⁻¹, B = 0.4 T.

In this demonstration, we combine a classical optimization routine (the Nelder–Mead simplex algorithm⁷³), with numerical simulations of the unitary transformations corresponding to every choice of the variational parameters. In fact, each sequence of microwave pulses can be seen as the series of quantum operations reported in the inset of Fig. 2b. Here the black thick (green narrow) line represents the qudit (qubit). Conditioned qubit–qudit operations are depicted with black boxes, while single qubit rotations are shown in green, in direct correspondence with Fig. 2a.

Simulations are performed according to a realistic hardware setup, including all the required external control pulses and molecular parameters discussed above. The effect of a finite spin coherence time T₂ is included by simulating the dynamics of the hardware density matrix ρ according to the Lindblad master equation⁷⁴

where the time dependent H₁ term in the Hamiltonian indicates the presence of external oscillating control fields. For simplicity, we assume identical T₂ for both spins and values that are consistent with coherence times already observed for individual building blocks.^{17,22,25,58,62} The consequences on T₂ brought by the addition of possible linkers between magnetic ions are discussed in Section 3. It is worth noticing that, similarly to what happens with the structural parameters of our proposed setup, the results presented below do not depend upon stringent choices on the precise values for T₂, particularly in the case of VQE implementations.

In Fig. 2c, we report results of the VQE algorithm simulated by assuming a realistic value of the spin coherence time (10 μs, symbols), compared with exact values (lines) for both the ground state energy and some ground state properties of interest. Notice that, over a wide range of G/Ω values, the proposed ansatz achieves very good approximations of the exact ground state, which in this small-sized example can be computed classically. The limiting factor is essentially the expressibility of the trial wavefunction, i.e. the fact that by using the set of operations reported in Fig. 2a we may not achieve the exact form of the true ground state. This limitation can in principle be overcome by repeating the same basic parametrized structure more than once. It is worth noting that a finite coherence time, similar to small imperfections in the practical realization of quantum gates, only minimally affects the final results. In fact, consistent with the underlying variational principle, noisy ground state energy estimates sometimes converge to values slightly larger than the exact ones.

2.3 Digital quantum simulation of strong light–matter interaction

After investigating ground state properties, we now move on to show how the proposed molecular qudit-based processor can be used to simulate the dynamics of the Rabi model. The digital quantum simulation of the target Hamiltonian [script letter H]_S requires the following transformation to be implemented:

|ψ(0)〉 → |ψ(t)〉 = e^{−i[script letter H]_St}|ψ(0)〉. (4)

This can be approximated to the product of unitary terms e^{−i[script letter H]_St} ≈ (e^{−iω_aσ_zt/N}e^{−iΩa†at/N}e^{−i2Gσ_x(a+a†)t/N})^N by dividing the transformation into small time steps t/N, according to the Suzuki-Trotter decomposition. Each unitary step is then implemented by a sequence of micro-wave pulses. For instance, the effect of the diagonal operator a^†a is obtained by pulses semi-resonant with Δm₁ = ±1 transitions,⁷⁵ while the term σ_x(a + a^†) is simulated by resonant Δm₁ = ±1 transitions conditioned by the state of the qubit and essentially correspond to the similar ones employed in the VQE above.

In Fig. 3 we show the digital quantum simulation of the Rabi model, eqn (2), realized with the spin qudit encoding described above and for increasingly challenging choices of the G/Ω ratio. Large G/Ω values introduce peculiar features in the dynamics of the target system: the rotating wave approximation fails and the total number of excitations is not conserved. This non-trivial behavior emerges in our simulations below, where we report the time evolution of the average number of photons 〈n_photons〉 in the radiation mode and of the atom population 〈σ_z〉, assuming an initial vacuum state with zero photons and the atom in its ground state. This vacuum state (with no excitations) would not be subject to any evolution for small G/Ω ratios. Hence, oscillations in 〈n_photons〉 and 〈σ_z〉 are a direct signature of the ultra-strong coupling regime. In all panels, we compare the reference curves, computed via exact matrix exponentiation, with numerical simulations of a realistic hardware obtained again by integrating eqn (3). A quantitative assessment of the overall quality of the results can be obtained by computing the fidelity 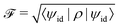between the hardware output ρ and the ideal result |ψ_id〉 of a digital quantum simulation algorithm realized with the same number of Suzuki–Trotter time steps and the same size of the bosonic Hilbert space. The latter can be obtained with standard matrix algebra.

Fig. 3 Digital quantum simulation of the Rabi model on a qudit architecture. In panels (a–f) the solid lines are numerical results taking into account the same digital approximation and space truncation errors to which the hardware sequences are subject, but without decoherence or imperfections in the quantum operations. The data points represent hardware simulations from which we obtain the average number of photons and atom population as 〈n_photons〉 = 〈S_z1〉 + S₁ and 〈σ_z〉 = 〈s_z2〉. (a and b) G/Ω = 0.25 simulated with S₁ = 3/2, s₂ = 1/2, g₁ = 1.98, g₂ = 2.3, d₁ = 0.24 cm⁻¹, and B = 0.4 T. (c and d) G/Ω = 0.5 simulated with S₁ = 3/2, s₂ = 1, g₁ = 1.98, g₂ = 2.18, d₁ = −d₂ = 0.24 cm⁻¹, and B = 0.2 T. (e and f) G/Ω = 0.7 simulated with S₁ = 5/2, s₂ = 1, g₁ = 2, g₂ = 2.18, d₁ ≃ −0.30 cm⁻¹, d₂ = −0.24 cm⁻¹, and B = 0.08 T. (g and h) Exact time evolution (N = ∞) for G/Ω = 0.7, showing the effect of the truncation to a maximum of n_M = 2S₁ photons. In all hardware simulations, we assume J_x,y = 0.008 cm⁻¹.

In the first example, Fig. 3a and b, we show the results of the quantum simulation of the target Hamiltonian [script letter H]_S with G/Ω = 0.25 realized with N = 4 (for t ≤ 5) and N = 6 (for t > 5) Suzuki–Trotter steps. Here, the hardware setup is composed of a spin S₁ = 3/2, encoding a d = 4 photonic space, and a spin s₂ = 1/2 representing the atomic degrees of freedom. The longest pulse sequence requires 1.7 μs, resulting in large average fidelities: [scr F, script letter F] ≃ 0.984 for T₂ = 50 μs and [scr F, script letter F] ≃ 0.951 for T₂ = 10 μs.

Increasing the values of the target G/Ω ratio, Fig. 3c–f, yields larger oscillations in the average number of photons and atom populations. To capture these features we need, on the one hand to increase the number of digital steps (N), and on the other hand to enlarge the bosonic space (n_M). This last step is fundamental to correctly capture the system dynamics at significant G/Ω, as clearly shown in panels (g) and (h), where we compare the time evolution obtained by truncating the number of photons to 3 or 5, for G/Ω = 0.7. Indeed, by slightly increasing n_M, we practically obtain the exact dynamics (continuous line). Given n_M = 2S₁, on the synthetic side, this simply translates in changing the qudit spin from 3/2 to 5/2.

Conversely, increasing N (and hence the length of our manipulations) requires larger T₂ or faster pulses. These can be applied with high fidelity only in the presence of well resolved transitions, a condition which can be achieved, e.g., by properly engineering the molecular spectrum. In this respect, the large degree of chemical flexibility represents a valuable resource. In particular, it is helpful to replace the s₂ = 1/2 with a spin s₂ = 1 system. A promising candidate ion is for example Ni^II, for which coherence times in the regime of microseconds were reported.⁶² While only two consecutive levels, e.g. m₂ = 0,1, are used for the actual encoding of the target model, the presence of an additional zero-field splitting term d₂s_z2² in the hardware Hamiltonian greatly improves the frequency resolution of the relevant transitions, thus allowing for larger operation fidelities with reasonably fast control pulses. For Ni^II, d₂ can be in the 0.1–1 cm⁻¹ range (in the octahedral ligand field).^60,61 In Fig. 3c and d we report a digital simulation for G/Ω = 0.5, obtained with N = 7 on a (S₁, s₂) = (3/2, 1) model hardware. Here, the pulse sequences last approximately 0.9 μs on average, resulting in average fidelities [scr F, script letter F] ≥ 0.92 also for T₂ = 10 μs. Finally, we achieve in Fig. 3e and f a digital simulation well above the ultra-strong coupling threshold (G/Ω = 0.7, N = 8) with a model hardware (S₁, s₂) = (5/2, 1) (i.e. with a bosonic space truncated at d = 6). More demanding pulse sequences are required in this case, with an average duration of ∼1.6 μs and average fidelity around [scr F, script letter F] ≃ 0.84 for the shortest T₂.

3 Possible physical implementations

Let us now explore potential realizations of molecular qudits displaying a set of properties consistent with the ones employed in our calculations. In many cases, we refer to chemical building blocks already discussed or characterized in the literature, which should then be linked together in order to realize the proposed architecture.

To identify a suitable molecular platform, we need to combine requirements on the different units discussed in the previous sections. As already illustrated, a prototypical hardware could consist of a dimer of transition metal ions, respectively with spins S₁ ≥ 3/2 and s₂ ≥ 1/2. In order to ensure factorization of the two-ion wave-function, the two ions should be weakly interacting (no matter if through space, through bond or via super-exchange) and characterized by g factors significantly different along a given direction. Single-ion anisotropy on both S₁ and s₂ (if the latter is ≥1) could help to better resolve different transitions. In particular, the difference between the system energy gaps should be larger than the typical line-width measured in pulse EPR experiments on molecular complexes, which can be in the ∼0.001 cm⁻¹ range for spin 1/2 systems (see, e.g. ref. 76).

Such single constraints do not appear so stringent. For instance, Cr^III and Cu^II have sufficiently different g values g_Cr = 1.98, g_Cu = 2.10–2.3 to allow factorization of the wavefunction. At the same time, the individual spin resonance frequencies are both accessible in the same resonator. d₁ values in the order of the tenth of cm⁻¹ characterize ions that have half-filled valence orbitals, like Mn^II, Fe^III, or Gd^III, as well as half-filled t_2g orbitals in an octahedral ligand field, such as Cr^III. It must be said that in this case the rhombicity and principal directions of the magnetic anisotropy are difficult to predict and control synthetically, but they are not crucial for the feasibility of our scheme.

More demanding is the control of the interaction between the spin qubit and the qudit. In general, weak spin–spin interactions are poorly characterized and hard to predict exactly, only based on the molecular geometry. Indeed, while dipolar couplings can be easily computed and controlled, exchange interactions can depend critically on the choice and orientation of the linkers (see below). It is important to note that this does not hinder the implementation of our scheme. In fact, once the complex has been characterized and even in the presence of an interaction slightly larger than expected, it is possible to tune the external field in order to ensure factorization of the wave-function. This could require the experimental setup to be adapted to work at larger frequencies than commercial resonators, as demonstrated for instance in ref. 65, where superconducting coplanar resonators operating up to 50 GHz were reported. These superconducting resonators could also employ high-T_c superconductors to support large magnetic fields.⁷⁷

We now discuss chemical strategies to obtain the suitable range of interactions. The short distance (∼6 Å) associated with the dipolar coupling used in the simulations reported above (0.01 cm⁻¹) is compatible with compact linkers like oxalate, cyanide, azide etc. These bridging ligands are very efficient in also transmitting exchange interactions, and thus are not ideal for single spin addressing. The optimal choice falls on very weak exchange interactions that are expected to be almost ubiquitous when the two spin centers are embedded in the same molecular scaffold. Single spin addressability in weakly coupled heterometallic species has been recently achieved by combining copper porphyrin with a carboxylate-coordinated Ti^IIICp2 unit.⁷⁸ However, even for the shorter bridge the qubit–qubit interaction is too weak to allow the implementation of the quantum simulator proposed here. An elucidating example of the wide range of achievable interactions is the case of condensed Cu^II porphyrin complexes, which have been attracting increasing interest for the relatively long and robust coherence combined with semiconducting properties and convenient processability.^18,79–81 In a recent study, electron–electron double resonance has been used to investigate the spin–spin interactions in edge-fused coplanar Cu^II dimers and in meso–meso singly linked dimers.⁸² In the latter, the Cu-porphyrin rings are mutually orthogonal and exchange interaction fully suppressed, significantly smaller than the dipolar interaction, estimated to be 0.0028 cm⁻¹. On the contrary, the planarity imposed by the triple link between the two units boosts the antiferromagnetic exchange interaction to −2.64 cm⁻¹. These results demonstrate the wide tuneability of the molecular approach.

The choice of the linkers between the two magnetic ions should also fulfill other constraints. In particular, we need to control the decoherence of the system. A coherence time T₂ above 10 μs at low temperatures can be observed for S = 1/2 transition metal ions, especially if the first coordination sphere is nuclear spin free, e.g. oxygen, sulphur, or carbon donor atoms, and if total or partial deuteration of the ligand is affordable. This requires nitrogen from the first coordination sphere and aliphatic CH_n groups in the molecular scaffold to be eliminated, thus reducing the available library of molecular candidates. Nevertheless, we notice that remarkably good results are already obtained using T₂ in the 10 μs range and even smaller values of a few μs could already be sufficient to achieve the first proof-of-principle demonstrations. Concerning S > 1 metal complexes, coherence times have been less investigated. In the case of Cr^III, T₂ up to 8 μs have been observed in a Cr^III complex with the N,N′-dimethyl-N,N′-dipyridine-2-yl-pyridine-2,6-diamine ligand.⁸³ Interestingly, the longer T₂ compared to other complexes with nuclear spin free donor atoms, such as [Cr(C₃S₅)₃]³⁻ (see ref. 25) or [Cr(C₂O₄)₃]³⁻ (see ref. 15), has been attributed to the weaker single ion anisotropy, d_i = 0.18 cm⁻¹, a value very close to that employed in our simulations. d_i values in the range 0.15–0.25 cm⁻¹ characterize chloro-tetraphenylporphinatochromium(III) complexes with a weakly bound neutral ligand,⁸⁴ suggesting that a heterometallic conjugated porphiryn dimer might satisfy the requirements to implement the protocol described here.

As a final reminder, efficient operation of the simulator requires that the qudit–qubit pairs are well isolated, while still retaining control over the molecular orientation. An isostructural diamagnetic matrix is thus mandatory. While this is usually accessible for single qubits, in the case of a two-spin architecture the co-crystallization of the para- and dia-magnetic molecules must occur without metal scrambling. This can be easily avoided using inert d³/d⁶ ions, as in the case of Cr^III and low spin Co^III. Metal scrambling is however much more common for labile d¹/d⁹ ions, such as Cu^II, requiring the use of polydentate linkers, such as the porphyrin ligands mentioned above, in the design of the molecular architecture.

4 Summary and perspectives

In summary, we have shown that magnetic molecules are very promising quantum simulators for complex physical systems, in particular for target Hamiltonians involving bosonic variables representing e.g. radiation fields. The many degrees of freedom present in this class of target Hamiltonians make their simulation with a multi-qubit register very demanding, both in terms of the number of qubits and sequence of operations. In contrast, the multi-level structure typical of magnetic molecules allows us to encode a boson into a single spin qudit, thus greatly simplifying the architecture of the register and its manipulation. The latter can be achieved solely by sequences of microwave pulses, resonant with specific transitions. As an example, we have reported both ground state calculations, performed with the VQE algorithm, and the digital quantum simulation of real time evolution for the Rabi model up to the ultra-strong coupling regime. In all cases, the outcomes obtained by considering realistic hardware parameters are in very good quantitative agreement with exact predictions. Hence, these results pave the way to proof-of-principle experiments demonstrating the effectiveness of our proposal.

The scheme is flexible and allows one to simulate a wide range of interesting models, thanks to the chemical tunability of the proposed hardware. Indeed, although we have focused here on very simple single ions, much larger S₁ can be obtained by exploiting the total spin ground multiplet of multi-nuclear complexes with tailored interactions.^47,85 With larger S₁, one could for example include more photons in the simulations, thus enabling the treatment of more exotic regimes such as the deep strong coupling for light-matter interactions⁸⁶ or fundamental models such as lattice gauge theories.^44,87,88 The latter require a large number of boson modes and excitations for a detailed description in arbitrary dimension, thus representing a challenging task for both classical devices and near time qubit-based architectures.⁴⁴ Additionally, models involving multiple two-level atoms or boson modes⁴⁹ can be simulated by chemically engineering the structures in order to link together several qudit and/or qubits.^45,46

In conclusion, it is worth stressing that an effort to synthesize molecules satisfying the conditions highlighted in this work would place molecular nanomagnets among the most promising platforms for the realization of effective quantum simulators.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank P. Santini for useful discussions. This work has received funding from the European Union's Horizon 2020 research and innovation programme through FET-OPEN grant 862893 FATMOLS and QUANTERA project SUMO (co-funded by the Italian Ministry of University and Research).

Notes and references

1. J. Preskill, Quantum, 2018, 2, 79.
2. A. Chiesa, F. Tacchino, M. Grossi, P. Santini, I. Tavernelli, D. Gerace and S. Carretta, Nat. Phys., 2019, 15, 455–459.
3. A. Kandala, A. Mezzacapo, K. Temme, M. Takita, M. Brink, J. M. Chow and J. M. Gambetta, Nature, 2017, 549, 242–246.
4. V. Havlíček, A. D. Córcoles, K. Temme, A. W. Harrow, A. Kandala, J. M. Chow and J. M. Gambetta, Nature, 2019, 567, 209–212.
5. F. Arute, et al. , Nature, 2019, 574, 505.
6. F. Tacchino, A. Chiesa, S. Carretta and D. Gerace, Adv. Quantum Technol., 2020, 3, 1900052.
7. R. P. Feynmann, Int. J. Theor. Phys., 1982, 21, 467.
8. R. Somma, G. Ortiz, J. E. Gubernatis, E. Knill and R. Laflamme, Phys. Rev. A, 2002, 65, 042323.
9. B. P. Lanyon, M. Barbieri, M. P. Almeida, T. Jennewein, T. C. Ralph, K. J. Resch, G. J. Pryde, J. L. O'Brien, A. Gilchrist and A. G. White, Nat. Phys., 2009, 5, 134.
10. Y. Wang, Z. Hu, B. C. Sanders and S. Kais, Front. Phys., 2020, 8, 479.
11. R. Hussain, G. Allodi, A. Chiesa, E. Garlatti, D. Mitcov, A. Konstantatos, K. Pedersen, R. D. Renzi, S. Piligkos and S. Carretta, J. Am. Chem. Soc., 2018, 140, 9814–9818.
12. E. Macaluso, M. Rubín, D. Aguilà, A. Chiesa, J. I. M. L. A. Barrios, P. J. Alonso, O. Roubeau, F. Luis, G. Aromí and S. Carretta, Chem. Sci., 2020, 11, 10337.
13. A. Chiesa, E. Macaluso, F. Petiziol, S. Wimberger, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2020, 11, 8610–8615.
14. S. Carretta, D. Zueco, A. Chiesa, Á. Gómez-León and F. Luis, Appl. Phys. Lett., 2021, 118, 240501.
15. M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626.
16. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488.
17. K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304.
18. M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157.
19. M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244.
20. M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341.
21. M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740.
22. C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204.
23. C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685.
24. M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351.
25. M. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344.
26. F. Luis, A. Repollés, M. J. Martínez-Pérez, D. Aguilá, O. Roubeau, D. Zueco, P. J. Alonso, M. Evangelisti, J. S. A. Camón, L. A. Barrios and G. Aromí, Phys. Rev. Lett., 2011, 107, 117203.
27. D. Aguilà, D. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. Alonso, J. Sesé, S. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215.
28. A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, C. R. T. G. A. Timco, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, npj Quantum Inf., 2015, 1, 15012.
29. A. Chiesa, G. F. S. Whitehead, S. Carretta, L. Carthy, G. A. Timco, S. J. Teat, G. Amoretti, E. Pavarini, R. E. P. Winpenny and P. Santini, Sci. Rep., 2014, 4, 7423.
30. J. Ferrando-Soria, E. Moreno-Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. Vitorica-Yrezabal, F. Tuna, E. J. L. McInness and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377.
31. J. Ferrando-Soria, et al. , Chem, 2016, 1, 727–752.
32. M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183.
33. K. Najafi, A. L. Wysocki, K. Park, S. E. Economou and E. Barnes, J. Phys. Chem. Lett., 2019, 10, 7347–7355.
34. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, England, 2000.
35. P. Forn-Díaz, L. Lamata, E. Rico, J. Kono and E. Solano, Rev. Mod. Phys., 2019, 91, 025005.
36. A. F. Kockum, A. Miranowicz, S. De Liberato, S. Savasta and F. Nori, Nat. Rev. Phys., 2019, 1, 19–40.
37. D. Ballester, G. Romero, J. J. García-Ripoll, F. Deppe and E. Solano, Phys. Rev. X, 2012, 2, 021007.
38. A. L. Grimsmo and S. Parkins, Phys. Rev. A, 2013, 87, 033814.
39. J. Braumüller, M. Marthaler, A. Schneider, A. Stehli, H. Rotzinger, M. Weides and A. V. Ustinov, Nat. Commun., 2017, 8, 779.
40. L. Lamata, A. Parra-Rodriguez, M. Sanz and E. Solano, Adv. Phys.: X, 2018, 3, 1457981.
41. L. Lamata, EPL, 2020, 132, 20002.
42. N. P. D. Sawaya, T. Menke, T. H. Kyaw, S. Johri, A. Aspuru-Guzik and G. G. Guerreschi, npj Quantum Inf., 2020, 6, 49.
43. A. DiPaolo, P. K. Barkoutsos, I. Tavernelli and A. Blais, Phys. Rev. Res., 2020, 2, 033364.
44. S. V. Mathis, G. Mazzola and I. Tavernelli, Phys. Rev. D, 2020, 102, 094501.
45. J.-B. Peng, Q.-C. Zhang, X.-J. Kong, Y.-Z. Zheng, Y.-P. Ren, L.-S. Long, R.-B. Huang, L.-S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2012, 134, 3314–3317.
46. W.-P. Chen, J. Singleton, L. Qin, A. Camón, L. Engelhardt, F. Luis, R. E. P. Winpenny and Y.-Z. Zheng, Nat. Commun., 2018, 9, 2107.
47. A. Baniodeh, N. Magnani, Y. Lan, G. Buth, C. E. Anson, J. Richter, M. Affronte, J. Schnack and A. K. Powell, npj Quant. Mater., 2018, 3, 10.
48. F. Luis, P. J. Alonso, O. Roubeau, V. Velasco, D. Zueco, J. I. M. David Aguilá, L. A. Barrios and G. Aromí, Chem. Commun., 2020, 3, 176.
49. R. H. Dicke, Phys. Rev., 1954, 93, 99–110.
50. J. Huh, G. G. Guerreschi, B. Peropadre, J. R. McClean and A. Aspuru-Guzik, Nat. Photonics, 2015, 9, 615–620.
51. S. McArdle, A. Mayorov, X. Shan, S. Benjamin and X. Yuan, Chem. Sci., 2019, 10, 5725–5735.
52. P. J. Ollitrault, A. Baiardi, M. Reiher and I. Tavernelli, Chem. Sci., 2020, 11, 6842–6855.
53. A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. A. Fisher, A. Garg and W. Zwerger, Rev. Mod. Phys., 1987, 59, 1–85.
54. J. S. Kottmann, M. Krenn, T. H. Kyaw, S. Alperin-Lea and A. Aspuru-Guzik, arXiv:2006.03075, 2020.
55. A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. O'Brien, Nat. Commun., 2014, 5, 4213.
56. N. Moll, P. Barkoutsos, L. S. Bishop, J. M. Chow, A. Cross, D. J. Egger, S. Filipp, A. Fuhrer, J. M. Gambetta and M. Ganzhorn, et al. , Quantum Sci. Technol., 2018, 3, 030503.
57. Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, Chem. Rev., 2019, 119, 10856–10915.
58. Y.-S. Ding, Y.-F. Deng and Y.-Z. Zheng, Magnetochemistry, 2016, 2, 40.
59. A. Solano-Peralta, J. P. Saucedo-Vázquez, R. Escudero, H. Höpfl, H. El-Mkami, G. M. Smithd and M. E. Sosa-Torres, Dalton Trans., 2009, 1668–1674.
60. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Metal Ions, Clarendon, Oxford, England, 1970.
61. F. E. Mabbs and D. Collison, Electron Paramagnetic Resonance of d Transition Metal Compounds, Elsevier, Amsterdam-London-New York-Tokyo, 1992.
62. M. K. Wojnar, D. W. Laorenza, R. D. Schaller and D. E. Freedman, J. Am. Chem. Soc., 2020, 142, 14826–14830.
63. J. Zadrozny and D. E. Freedman, Inorg. Chem., 2015, 54, 12027–12031.
64. D. I. Schuster, A. P. Sears, E. Ginossar, L. DiCarlo, L. Frunzio, J. J. L. Morton, H. Wu, G. A. D. Briggs, B. B. Buckley, D. D. Awschalom and R. J. Schoelkopf, Phys. Rev. Lett., 2010, 105, 140501.
65. D. S. Rausch, M. Thiemann, M. Dressel, D. Bothner, D. Koelle, R. Kleiner and M. Scheffler, J. Phys. D: Appl. Phys., 2018, 51, 465301.
66. I. I. Rabi, Phys. Rev., 1936, 49, 324–328.
67. I. I. Rabi, Phys. Rev., 1937, 51, 652–654.
68. D. Braak, Phys. Rev. Lett., 2011, 107, 100401.
69. J. Román-Roche, E. Sánchez-Burillo and D. Zueco, Phys. Rev. A, 2020, 102, 023702.
70. I. Gimeno, W. Kersten, M. C. Pallarés, P. Hermosilla, M. J. Martínez-Pérez, M. D. Jenkins, A. Angerer, C. Sánchez-Azqueta, D. Zueco, J. Majer, A. Lostao and F. Luis, ACS Nano, 2020, 14, 8707–8715.
71. A. Blais, R.-S. Huang, A. Wallraff, S. M. Girvin and R. J. Schoelkopf, Phys. Rev. A, 2004, 69, 062320.
72. S. Savasta, O. D. Stefano, A. Settineri, D. Zueco, S. Hughes and F. Nori, arXiv:2006.06583, 2020.
73. J. C. Lagarias, J. A. Reeds, M. H. Wright and P. E. Wright, SIAM J. Optim., 1998, 9, 112–147.
74. W. Zhong, Z. Sun, J. Ma, X. Wang and F. Nori, Phys. Rev. A, 2013, 87, 022337.
75. A. Chiesa, P. Santini, D. Gerace, J. Raftery, A. A. Houck and S. Carretta, Sci. Rep., 2015, 5, 16036.
76. L. C. de Camargo, M. Briganti, F. S. Santana, D. Stinghen, R. R. Ribeiro, G. G. Nunes, J. F. Soares, E. Salvadori, M. Chiesa, S. Benci, R. Torre, L. Sorace, F. Totti and R. Sessoli, Angew. Chem., Int. Ed., 2021, 60, 2588–2593.
77. A. Ghirri, C. Bonizzoni, D. Gerace, S. Sanna, A. Cassinese and M. Affronte, Appl. Phys. Lett., 2015, 106, 184101.
78. S. von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2021, 143, 8069–8077.
79. M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508.
80. K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626.
81. A. Urtizberea, E. Natividad, P. J. Alonso, M. A. Andrés, I. Gascón, M. Goldmann and O. Roubeau, Adv. Funct. Mater., 2018, 28, 1801695.
82. N. Wili, S. Richert, B. Limburg, S. J. Clarke, H. L. Anderson, C. R. Timmel and G. Jeschke, Phys. Chem. Chem. Phys., 2019, 21, 11676–11688.
83. S. Lenz, H. Bamberger, P. P. Hallmen, Y. Thiebes, S. Otto, K. Heinze and J. van Slageren, Phys. Chem. Chem. Phys., 2019, 21, 6976–6983.
84. D. A. Summerville, R. D. Jones, B. M. Hoffman and F. Basolo, J. Am. Chem. Soc., 1977, 99, 8195–8202.
85. A. M. Ako, I. J. Hewitt, V. Mereacre, R. Clérac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 4926–4929.
86. J. Casanova, G. Romero, I. Lizuain, J. J. García-Ripoll and E. Solano, Phys. Rev. Lett., 2010, 105, 263603.
87. M. Dalmonte and S. Montangero, Contemp. Phys., 2016, 57, 388–412.
88. M. C. Bañuls and K. Cichy, Rep. Prog. Phys., 2020, 83, 024401.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tc00851j

---