 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nonlinear optical probes of nucleation and crystal growth: recent progress and future prospects
Ahmet R.
Dok†
a,
Thibaut
Legat†
 a,
Yovan
de Coene
a,
Yovan
de Coene
 b,
M. A.
van der Veen
b,
M. A.
van der Veen
 c,
T.
Verbiest
b and
Stijn
Van Cleuvenbergen
c,
T.
Verbiest
b and
Stijn
Van Cleuvenbergen
 *a
*a
aDepartment of Chemistry, Molecular Imaging and Photonics, KULAK – KU Leuven, E. Sabbelaan 53, 8500 Kortrijk, Belgium. E-mail: stijn.vancleuvenbergen@kuleuven.be
bDepartment of Chemistry, Molecular Imaging and Photonics, KU Leuven, Celestijnenlaan 200D, 3001 Heverlee, Belgium
cCatalysis Engineering, Department of Chemical Engineering, Delft University of Technology, 2629 Delft, The Netherlands
First published on 2nd August 2021
Abstract
In situ experimental studies have been key in uncovering the often elusive pathways of nucleation and crystal growth. In the field of material science and medicine this offers the prospect of controlling crystallization processes to fight disease or tailor materials towards specific applications. To further advance this quest there is a need for flexible techniques mapping the different stages of crystallization with maximal sensitivity. This article reviews the benefits of nonlinear optical techniques to take on this challenge. We provide a perspective on various nucleation and crystal growth studies that were carried out by nonlinear optical probing techniques. A theoretical background is established, different relevant nonlinear optical phenomena are defined, and optical setups that have been used by various authors are summarized. A primary focus is demonstrating the benefits of nonlinear optical techniques for the in situ study of crystallization. These benefits include low detection limits, complementary information by combining second- and third-order techniques, as well as relatively simple bench-top setups. Through microscopy, high contrast imaging of concomitant formations can moreover be achieved. The discussion outlines several studies involving ionic compounds, noble metal nanoparticles, polymers, metal organic frameworks and pharmaceutical compounds. Finally, we discuss future evolutions in nonlinear optical probing that are expected to further advance the field.
Introduction
Crystalline materials are ubiquitous in all realms of science, industry and nature. They are essential components of modern technologies, and determine the performance and processing of pharmaceuticals, catalysts, molecular sieves, and so on. Crystal structure, size and morphology govern physicochemical properties such as birefringence, band structure and solubility, as well as downstream processing in industry. Although crystalline materials tend towards their thermodynamically most stable configuration, crystal growth processes are typically under kinetic control. This can result in the formation of metastable crystals with distinct crystal structure and properties, a phenomenon called polymorphism. For the advancement of many technologies, precise control over crystal phase and morphology is crucial. Currently, this ambition is still undermined by a lack of understanding of the mechanisms governing crystallization processes.Nucleation, the first step in the formation of a new phase, is considered of key importance since it determines crucial parameters such as polymorph outcome, crystal size distribution, and morphology.1,2 Since the formation of a nucleus results in an interfacial energy penalty, it presents a critical barrier to the crystallization process. The height of this barrier depends on the molecular arrangement of the nucleus in interaction with its environment. In recent years, theoretical and experimental findings have opened a window into the complexity of nucleation processes.3–7 It has for instance been established that classical nucleation theory, the paradigmatic framework developed by Gibbs, does not always adequately describe nucleation processes in solution. Molecular dynamics simulations and experimental observations in a wide range of materials suggest more complex routes, involving amorphous or liquid-like precursors that subsequently re-arrange to form the crystal phase.
Competition between different phases can result in structural transformations involving transient intermediates or metastable phases.8 This is the basis of Ostwald's rule of stages. This empirical rule states that crystallization may proceed through different metastable phases. The metastable phase with the lowest interfacial energy is expected to form first. Subsequently, a stepwise transformation to the most stable polymorph can take place. If this transformation process is incomplete, metastable phases can become kinetically trapped. The latter opens routes to metastable materials with entirely new properties. Detection of intermediates during the growth process can be a first step towards isolating new phases.
Characterization of the complex dynamical pathways of crystallization requires sensitive in situ measurement techniques.9 Such techniques should give insight in the evolution of physical parameters such as crystal structure, morphology, size and concentration. The chemistry of the system often plays a vital role as well. X-Ray or neutron based techniques, offering structural information at atomic length scales, are still considered as the gold standard for crystallization studies. However, for diffraction based techniques, crystalline domains of a certain size need to be formed to be able to deduce the internal structure, while scattering based techniques can only deduce size and shape. This means that for the initial stage of nucleation, information on the internal structure can hardly be attained with these techniques. Moreover, to study fast processes such as nucleation a subsecond time resolution is preferred. Yet, to reach sufficient time resolution it is generally necessary to measure at synchrotron facilities. Since access to such facilities is limited, more flexible probes are required for practical multi-parameter studies. In situ spectroscopic techniques like Raman, Infrared (IR) and nuclear magnetic resonance (NMR) have been applied to study crystal growth in a lab setting.10–13 Microscopic techniques such as atomic force microscopy (AFM), cryo-transmission electron microscopy (TEM) and liquid cell TEM have provided important insights into nucleation and growth processes due to their high spatial resolution, but their broad applicability is limited.14–16
Nonlinear optical (NLO) techniques have only been explored sporadically, but have potential to bridge the gap between synchrotron and the lab. NLO processes are inherently sensitive to symmetry and are able to probe the supramolecular organization of aggregates, clusters and crystals, hence they can probe the internal structure at a much earlier stage then diffraction techniques.17–21In situ NLO scattering measurements are able to extract information about concentration, size and morphology of crystallites in solution at high time resolution.22 While scattering techniques offer an average picture, NLO microscopy allows imaging concomitant pathways with optimal contrast between different polymorphs.23 In this review we will discuss the application of NLO techniques to study crystallization in situ. We will lay out the basic theoretical and technical aspects, and present an overview of selected studies highlighting the potential of NLO measurements. We will limit the discussion to time-resolved studies of crystallization processes. We will focus on techniques based on harmonic light generation, which has hitherto been the focus of the great majority of NLO studies of crystallization processes. These techniques are relatively straightforward and ideally suited to derive structural information during the crystal growth process. In the Prospects section of this review we will discuss potential advantages of using nondegenerate NLO techniques such as sum frequency generation or stimulated Raman scattering.
Theoretical aspects
When electromagnetic radiation interacts with molecules or atoms the induced dipole moment is most accurately described by a Taylor expansion in the electrical field E:21,24| μ = μ(1) + μ(2) + μ(3) + ⋯ = α·E + β:EE + γ⋮EEE + ⋯ | (1) |
| P = P(1) + P(2) + P(3) + ⋯ = χ(1)·E + χ(2):EE + χ(3)⋮EEE + ⋯ | (2) |
As mentioned, we will limit the discussion to processes where the excitation beams have the same frequency, resulting in harmonic light generation. Interaction of beams with different frequencies results in generation of light at sum and difference frequencies, which can be used to probe resonances of specific chemical species. Up until now this possibility has not been widely explored for the in situ study of phase transformations. We will discuss this possibility in the final section of this paper.
To retrieve structural information in terms of symmetry and orientation through NLO experiments, the tensorial nature of χ(2) and χ(3) becomes relevant
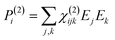 | (3) |
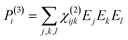 | (4) |
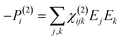 | (5) |
By comparing eqn (3) and (5) it becomes clear that all tensor components of χ(2) must be zero for centrosymmetric materials (within the electric-dipole approximation). Remark that this is also the case for the highly symmetric cubic O (432) point group, although it is in fact non-centrosymmetric. Analogously χ(2) and χ(3) transform in a predictable manner for different symmetry elements and point groups. In this manner discrimination between crystals of different symmetry becomes possible by employing polarimetric analysis.20,26 This principle is particularly useful when applied to crystallization studies. Several excellent articles and books discuss this topic in more detail.21,27–29
Depending on the nature of the interacting light and the probed material different phenomena arise, we will discuss the different possibilities below.
Hyper-Rayleigh scattering of molecules
For molecules or particles much smaller than the wavelength the NLO interaction results in hyper-Rayleigh scattering (HRS).30 In fact, HRS is the nonlinear equivalent of the Rayleigh regime in linear scattering. Exactly like Rayleigh scattering, HRS is isotropic, which means that for vertically polarized incident light, the scattered light intensity is identical for all scattering angles.Within the electric dipole approximation, β-induced HRS can only occur for noncentrosymmetric molecules, while γ-induced HRS is allowed for species of all symmetries. For uncorrelated scatterers, the second and third harmonic intensity depend linearly on the number of scatterers n.
| I2ω ∼ n〈|βHRS|2〉Iω2 | (6) |
| I3ω ∼ n〈|γHRS|2〉Iω3 | (7) |
Polarimetric measurements can provide information about the molecular symmetry. In principle a combination of linear, elliptical and circular polarization for the incoming and outgoing light is necessary to achieve full polarization resolved data.31 Alternatively, the depolarization ratio ρ can serve as a simple measure to interrogate symmetry.32,33 The depolarization ratio is usually defined as the ratio of the intensity of vertically to horizontally polarized scattered light, for vertically polarized incident light:
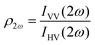 | (8) |
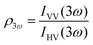 | (9) |
In these equations the first subscript refers to the polarization of scattered light, the second to the polarization of the incident light. Since the symmetry rules for β- and γ-induced HRS are different, both processes provide complementary information.31,34,35 For high molecular symmetries the depolarization ratio can be calculated exactly: ρ2ω is 1.5 for an octupolar scatterer, and 5 for a dipolar scatterer with a dominant βzzz component, while ρ3ω is infinite for an isotropic scatterer and can be as low as 1.6 for more ordered scatterers.31,34 In general the depolarization ratio does not unambiguously point to a specific symmetry, since it is a function of all nonvanishing tensor components. However, both quantities are very sensitive to symmetry and can be taken as a qualitative measure of structural changes. By using polarizing prisms, the evolution of ρ2ω and ρ3ω can be recorded in a single measurement, which makes it convenient for dynamic measurements.
Before the onset of crystallization, the solute molecules are present in high concentration. In a crystallization experiment, this signal can be considered as the background that needs to be overcome in order to detect the presence of aggregates or the formation of nuclei and crystallites. The solvent molecules will also contribute to this background signal, both through second- and third-order NLO effects. At the third harmonic wavelength it has been demonstrated by Shelton et al. that the main contribution stems from Rayleigh scattered coherent THG.36 However, by using circularly polarized light as excitation this contribution can be avoided, as THG becomes symmetry forbidden in isotropic media in this case.24
Hyper-Rayleigh scattering of small particles
For ensembles of molecules with fixed relative positions, specific phase relations result in the appearance of coherent effects within the structure. As long as these ensembles are small compared to the scattered wavelength, they can still be considered as point sources. The resulting scattering is isotropic, and termed HRS. When particles become large compared to the wavelength, phase differences between light generated at different points within the structure result in constructive and destructive interference, and the scattered intensity becomes angle dependent. At that point the Rayleigh limit is surpassed and scattering is termed harmonic light scattering. This threshold is taken to be around λ/50, with λ the wavelength of the scattered light. This corresponds to a diameter of about 5–10 nm for excitation wavelengths typically used in NLO experiments.17For small particles within the Rayleigh limit, the HRS response of the ensemble can be described as:
| I2ω ∼ n′〈|χ(2)HRS|2〉Iω2 | (10) |
| I3ω ∼ n′〈|χ(3)HRS|2〉Iω3 | (11) |
Under the assumption that intermolecular electronic interactions can be neglected, the bulk response of molecular crystals corresponds to the coherent sum of the molecular contributions:37
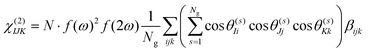 | (12) |
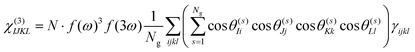 | (13) |
In these equations I, J, K and L refer to the macroscopic (laboratory) framework, i, j, k and l refer to the microscopic (crystallographic) framework. f are local field factors. N is the number density, Ng the number of molecules in the unit cell. In case no clear unit cell can be defined N equals the concentration and Ng = 1. Remark that these relations assume fixed positions and that for dynamical species such as clusters and even nuclei orientational and positional fluctuations can exist. In these cases the overall correlation can be described more adequately by a statistical distribution.38,39 For small species the surface contribution can become important as well. Surface susceptibilities can be introduced to account for this contribution.40 Since centrosymmetry is broken by default at interfaces, a second-order surface response is present even for centrosymmetric particles.
Coherent harmonic light scattering of extended particles
Once particles become larger than around 5–10 nm (λ/50), detectable coherent effects emerge. The respective scattering processes are now termed second and third harmonic scattering (SHS, THS). In order to include the angle-dependence it is convenient to introduce an effective susceptibility Γ for the ensemble:40| I2ω ∼ n′|Γ(2)[F(θ,ϕ,R),χ(2)]|2Iω2 | (14) |
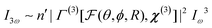 | (15) |
The intensity depends linearly on the particle concentration n′. F and 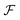 are form factors, analogous to linear scattering. They relate the size and shape of the particle to the in-plane and out-of-plane scattering angles θ and ϕ. Through analysis of the scattered intensity at different angles information about shape, size and dispersity can be derived. Usually only the in-plane scattering angle is considered. The nonlinear optical properties of the crystallites, governed by χ(2) and χ(3), have a strong influence on the polarization dependence of the scattering pattern. Polarimetric measurements hence give insight into the structure of the ensemble. Since χ(2) exclusively probes noncentrosymmetric domains and surfaces while χ(3) probes all symmetries, complementary information about domain sizes or concomitant processes can be extracted by combining both techniques. Moreover, since the bulk response depends on R6 (or V2), information about crystallinity can be extracted during growth processes by comparing the fitted particle radius and the intensity. In absence of a bulk response, surface and quadrupolar contributions can become important sources of SHS for centrosymmetric species. These contributions can be included in the effective susceptibility Γ as well.40
are form factors, analogous to linear scattering. They relate the size and shape of the particle to the in-plane and out-of-plane scattering angles θ and ϕ. Through analysis of the scattered intensity at different angles information about shape, size and dispersity can be derived. Usually only the in-plane scattering angle is considered. The nonlinear optical properties of the crystallites, governed by χ(2) and χ(3), have a strong influence on the polarization dependence of the scattering pattern. Polarimetric measurements hence give insight into the structure of the ensemble. Since χ(2) exclusively probes noncentrosymmetric domains and surfaces while χ(3) probes all symmetries, complementary information about domain sizes or concomitant processes can be extracted by combining both techniques. Moreover, since the bulk response depends on R6 (or V2), information about crystallinity can be extracted during growth processes by comparing the fitted particle radius and the intensity. In absence of a bulk response, surface and quadrupolar contributions can become important sources of SHS for centrosymmetric species. These contributions can be included in the effective susceptibility Γ as well.40
Harmonic light generation of large particles
When particles become substantially larger than the wavelength, full phase matching occurs.41 The size-dependent angular scattering pattern collapses and emission tends towards the phase-matched directions in reflection and transmission.42 At this point the processes are termed second and third harmonic generation (SHG, THG). The threshold for full phase matching to occur can be as large as 20 micrometers, however already for micrometer sized particles scattering at higher angles becomes negligible.17 For particles in this size range, size information can be extracted directly from SHG and THG imaging techniques. The intensity per particle is related to the NLO properties of the material as:| I2ω ∼ |χ(2)|2Iω2 | (16) |
| I3ω ∼ |χ(3)|2Iω3 | (17) |
The orientation of large particles is normally fixed and orientational averaging is not required. In this case the number of experimentally accessible observables increases significantly.27,29 Since the signal for large particles is significantly higher, full polarimetric analysis during crystallization becomes realistic at high time resolution.43,44 Even when full characterization of the χ(2) and χ(3) tensor is not possible, techniques such as Fourier or principle component analysis can be applied to discriminate between crystal structures or to probe local order, with the added advantage that these techniques are significantly faster in terms of data analysis.43–45
Experimental aspects
Since HRS is isotropic there is no additional information to be gained by measuring at multiple angles, and in general detection is performed at 90°. Classically, β-induced HRS was measured by introducing an optical bandpass filter at the second harmonic wavelength in front of a photomultiplier tube.30 However, multiphoton emission (MPE) at the same wavelength often results in an overestimation of the HRS response. In order to discriminate between both contributions several schemes aimed at separation in the spectral, temporal and frequency domain have been developed.46–49 While experimentally equivalent, γ-induced HRS was only first measured two decades later.35 In order to measure both β- and γ-induced HRS simultaneously it is convenient to detect the scattered light with a spectrometer-CCD combination (Fig. 1a). In this manner both contributions can be detected simultaneously and potential MPE can be accounted for by subtracting the broader fluorescent background. This way of measuring has the additional advantage that MPE signal can provide additional information about aggregation, molecular configuration, crystal packing and polymorphism.50 By introducing a Wollaston prism in the detection path, the scattered light can be separated in its horizontal and vertical components and the depolarization ratio can be determined in a single measurement.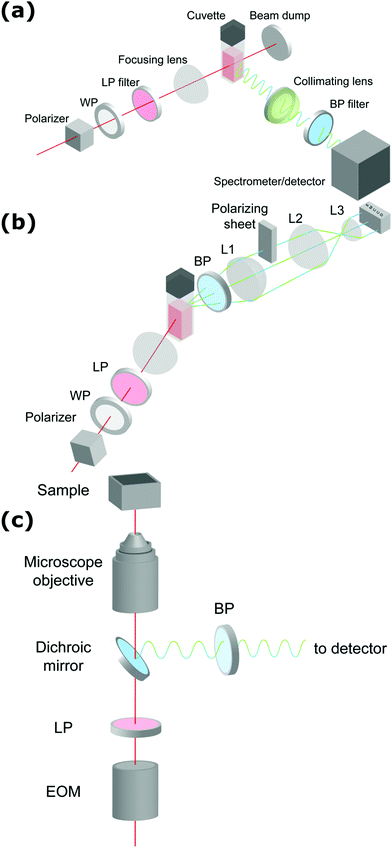 | ||
| Fig. 1 Schematic representation of setups measuring (a) hyper-Rayleigh scattering, (b) angle-dependent second harmonic scattering through Fourier imaging (ref. 52), (c) polarimetric NLO microscopy (ref. 43). WP = wave-plate, LP = long pass filter, BP = band pass filter, L = lens, EOM = electro-optic modulator. The fundamental beam is depicted in red, the second and third harmonic light in green and blue respectively. | ||
Once particles grow larger than λ/50 size and shape information becomes available through measurement at different angles. Classically angle-dependent scattering patterns are measured by rotating a single detector around the sample on a goniometer arm. Since this way of measuring is time-consuming, alternative measurement schemes are preferable. Some of us have implemented a Fourier imaging scheme which allows simultaneous measurement of harmonic light scattering at multiple angles over a wide angular range, significantly improving acquisition times.51 By introducing polarizing sheets in the detection path multiple polarization combinations can be detected simultaneously, giving insight in crystal symmetry (Fig. 1b). A disadvantage of this way of measuring is that potential MPE at the second harmonic wavelength cannot be separated from harmonic light scattering. However, since the fluorescence signal is isotropic, the angle dependence of the detected signal can be attributed unambiguously to the harmonic light scattering contribution. Alternatively, measurement at different angles with multiple detectors can measure angle-dependent scattering for dynamical processes. Coupled to a spectrometer, this way of measuring moreover allows simultaneous detection of second and third harmonic light scattering.
For particles larger than the diffraction limit, microscopy techniques provide information about size, shape, local orientation and structure (Fig. 1c). An advantage of microscopy techniques is that concomitant processes can be imaged directly, where scattering techniques measure an averaged signal. Simultaneous detection of SHG, THG and MPE can be implemented by making use of multiple detectors or by implementing microspectroscopy schemes. For polarimetric analysis electro-optic modulators enable high-frequency modulation of the polarization state, providing temporal resolution in the millisecond range, while at the same time significantly reducing 1/f noise.43–45 The great majority of multiphoton microscopes make use of high frequency (typically 80 MHz) laser sources and scanning schemes, but recent developments in biological imaging highlight some advantages in implementing wide-field multiphoton microscopy. In wide-field microscopy images are captured in a single shot, greatly improving image throughput.52 Moreover, coupled to lower frequency (kHz) sources, gated detection becomes possible and thermal effects can be avoided.53 This holds great promise for measurement of photosensitive samples. In crystallization studies this approach might also help minimizing unwanted effects such as laser-induced nucleation.
Discussion
NLO characterization techniques have been used in a wide range of in situ crystallization studies. These techniques are not limited to specific classes of materials and can be found in the fields of inorganic, organic and hybrid metal–organic chemistry. In this review, some key articles have been selected and the key takeaway points were summarized. The aim was to highlight the benefits that harmonic scattering can bring in characterizing the complex dynamical pathways of crystallization. The discussion will include ionic compounds, noble metal nanoparticles, polymers, metal organic frameworks, proteins, as well as a section dedicated to SHG microscopy in organic materials.Inorganics
Senapati et al. used SHS complemented with real-time TEM to monitor the formation of star shape gold nanocrystals synthesized using a seed-mediated growth process. The synthesis of the gold nanoparticles was performed by addition of ascorbic acid, cetryltrimethylammonium bromide (CTAB) and silver nitrate, following the preparation of gold nanoseeds from a gold tetrachloride solution. In situ SHS at 90° (without polarization analysis) enabled measuring the kinetics and shape evolution during synthesis. Due to the sensitivity of SHS towards shape and size, different hyperpolarizabilities could be derived for each shape. From the derived kinetic models, the transient number densities of the various intermediates could be obtained. In conjunction with TEM and time dependent absorption spectroscopy, the formation of star shaped structures from gold nanoseeds was found to evolve through nano-flower and crown shape configurations. The results showed several steps controlling the shape and size of star shaped gold nanoparticles. Initial formation and accumulation of nanoseeds was followed by Ostwald ripening forming the nano-flowered structures. Next, through control of CTAB, an intraparticle ripening process directed the final form to star shaped particles via the nanocrown structure.54
Sauerbeck et al. exploited the surface sensitivity of the SHS technique to study the seeded growth of gold nanoshells on silica surfaces using a scattering angle of 20° with vertical in and out polarizations. Following adsorption, ripening took place through formaldehyde reduction of a dark-aged solution of gold tetrachloride and potassium carbonate. In situ SHS measurements were combined with vis-NIR extinction spectroscopy and scanning electron microscopy (SEM). In comparison, SHS was strikingly sensitive to growth processes at the particle surface. This can be explained by the quadratic dependence between the second harmonic- and fundamental field. When gold structures grow bigger on the surface, plasmonic coupling between different gold islands occurs, leading to strong field enhancements. This was further confirmed by finite-difference time-domain simulations. Indeed, SHS showed a maximum during shell growth which was not observed with extinction spectroscopy. Next, as the gaps between gold islands on the surface closed, degeneration of local field enhancements resulted in a strong decrease in SHS intensity.55
Khoury et al. employed SHS to study the growth kinetics and the evolution of surface roughness for the seed-mediated growth process of gold nanoparticles in water for different synthesis conditions.56 Gold nanoparticles were prepared by using hydroquinone as a reducing agent, while the gold seeds were synthesized using sodium citrate and gold tetrachloride. Different sizes of particles were prepared by adding various amounts of seeds to the gold tetrachloride solution. The system was monitored in situ by SHS in transmission (180°), without polarization analysis, and with in situ extinction spectroscopy and TEM. These measurements revealed a two-step growth mechanism. The first stage was attributed to inhomogeneous growth of particles with rough surfaces giving rise to plasmonic hotspots, resulting in a peak of SHS intensity. In the second stage, an exponential decay of the SHS response corresponded to smoothening of the particle surface resulting in a decrease in hotspots. The resulting SHS data were fitted with an exponential function to retrieve nanoparticle growth lifetimes. In accordance with previous reports, it was found that the growth rate was proportional with the amount of precursor seeds used during synthesis.56
Ranasinghe et al. used the same technique to interrogate the growth dynamics of colloidal gold–silver core–shell nanoparticles.59 Nanoparticles with varying sizes were prepared in solution by reducing Ag+ onto the surface of a gold core with ascorbic acid. Unlike the previous study for gold nanoparticles, a three-step model was proposed for the growth dynamics of the gold–silver core–shell nanoparticles. Again, a peak in SHS intensity was attributed to the rapid and inhomogeneous growth of the shell resulting in rough surfaces. A biexponential decay of the SHS response then followed the initial stage. The associated growth lifetimes were correlated to a fast and slow SHS lifetime through complementary extinction spectra. The fast SHS lifetime corresponded with the second step of the model leading to a complete and smooth silver shell resulting in a decrease of SHS intensity. The third step, associated with the slow SHS lifetime was the result of a decreasing surface charge density, in agreement with zeta potential measurements.59
de Coene et al. performed an extensive investigation on the mechanisms behind the classic Turkevich reduction with an emphasis on the poorly understood earliest stages and the onset of plasmonic effects.57 The study showed that the Turkevich synthesis proceeds through a state of reversible aggregation of liquid domains forming loose aggregates. The gold nanoparticle growth process was tracked dynamically through SHS and THS (without polarization analysis) and MPE at 90°. SHS provided information on symmetry breaking at the particle surface and surface roughness, while THS probed the bulk response for particles and intermediates of all symmetries. Spectrally resolved MPE was used to pinpoint the transition between molecular and metallic behavior resulting in a shift in emission wavelength. Through simultaneous detection of SHS, THS and MPE, in conjunction with ex situ dynamic light scattering (DLS) and TEM measurements, a complete picture of the growth mechanism appeared. The reaction stages are illustrated in Fig. 2.
 | ||
| Fig. 2 Schematic representation of the different stages of nanoparticle formation during the first 5 minutes of the Turkevich synthesis. T = 0 marks the moment where both reactants (HAuCl4 and Na3Ct) were mixed. Blue, black and red dots show MPE, SHS and THS intensities respectively. The formation of the dense liquid domains in stage I is followed by nucleation, after which agglomeration to superclusters leads to plasmonic particle aggregates in stage II. Particle repulsion and ripening in stage III and IV respectively lead to the final product. The excitation wavelength was 1260 nm, with 0.5 s integration time. Adapted with permission from ref. 57. Copyright 2020 American Chemical Society. | ||
In stage I, a steady increase in SHS and THS indicated the formation of the first scattering sites with the solution going from colorless to light gray (1–3 minutes). A steep initial increase in MPE intensity corresponded to the formation of gold nanoclusters. Interestingly, DLS showed signatures of much larger particles, which was attributed to the formation of dense liquid droplets, preceding the nucleation of the smaller nanoclusters in a two-step nucleation process. In stage II, a fast increase in all signals was ascribed to coalescence of nuclei within the dense droplets forming plasmonic particles. This was further supported by spectral deconvolution of the MPE indicating a red shift in emission due to the transition from gold clusters to metallic particles. A comparatively fast increase in SHS signal indicated surface roughness, resulting in plasmonic hotspots as discussed earlier. In stage III (see Fig. 2), the solution went from dark to red upon formation of individual gold nanoparticles following particle repulsion, while stage IV was marked by further particle ripening. A more rapid decrease in SHS, compared to THS, points towards dramatic changes at the surface during this stage and is most likely due to particle smoothening.
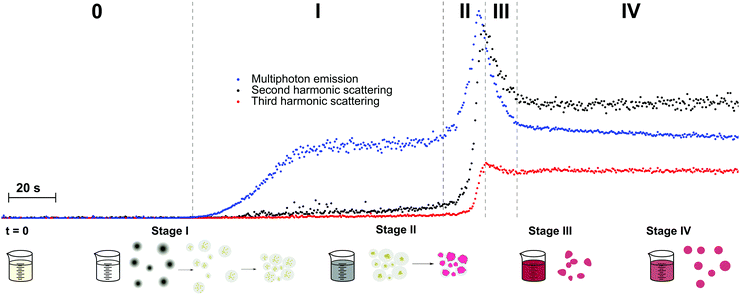
ZnO semiconductor quantum dots have unique electrical and optical properties and find potential applications in electronic devices such as solar cells and light emitting diodes. Aimed at applications, the formation of particles with well-defined properties is essential. However, studies into the mechanisms of nucleation and crystal growth remain rare, due to the fast kinetics of ZnO. Segets et al. used HRS to monitor the different stages in the synthesis of sub-10 nm ZnO nanoparticles.62 Compared to the other methods available for monitoring nanoparticle formation in liquids, HRS appeared as a superior technique to resolve the underlying kinetics, providing a millisecond time resolution (Fig. 3a).
 | ||
| Fig. 3 (a) HRS intensities during the early stages of precipitation of ZnO monitored for three different time resolutions (blue circles, 100 ms; green squares, 50 ms; red crosses, 20 ms). Four different regions can be discerned (I) only one reactant (II) nucleation (III) growth and (IV) ripening. (b) Relation between hyperpolarizability, βZnO, and particle size in nm is in line with a bulk response. Reprinted with permission from ref. 62. Copyright 2009 American Chemical Society. | ||
The authors distinguished four stages in the crystallization process based on the HRS time trace. These corresponded to (I) only one reactant (before mixing) (II) nucleation (III) growth and (IV) ripening regions. The data were treated with classical homogenous growth models and quantitative nucleation, growth and ripening rates could be determined. Furthermore, realistic estimates of size-dependent surface energies could be obtained, which would otherwise be experimentally inaccessible.62
By combining 90° HRS with UV-VIS measurements, a relation between the hyperpolarizability βZnO and the particle diameter could moreover be established. A power law with an index approaching the value of three was a good indication that the measured intensities were predominantly volume signals. These results are provided in Fig. 3b. Four different regions of the particle evolution could be monitored with millisecond time resolution from the HRS intensity signals.
Time resolved SHS measurements at 90° angle were performed by El-Kass et al. to monitor the kinetics and crystal growth of iron iodate nanorods from initial reverse microemulsions prepared in a Triton/cylcohexane/1-hexanol/water quaternary system.60 In this study SHS was used to determine two specific transitions in the crystallization process, which were measured at two different temperatures (RT and 80 °C). The HRS intensities of the reactions at temperatures RT and 80 °C are provided in Fig. 4a and b respectively. The transition times correspond to (A) the appearance of 10–20 nm agglomerates and (B) the onset of crystal growth, and were found to be very reproducible. At the respective transition times determined by SHS, the crystallization process was later quenched by centrifugation, and analyzed by TEM and XRD. The formation of crystalline nanorods was attributed to an aggregation-induced mechanism, and it was found that the kinetics of the transformations was strongly temperature-dependent. The overall HRS response for both crystallization temperatures was similar, but the crystallization time decreased from ∼3000 to ∼75 min when the temperature was raised from RT to 80 °C (Fig. 4b). The authors observed that shorter nanorods were obtained at 80 °C.60
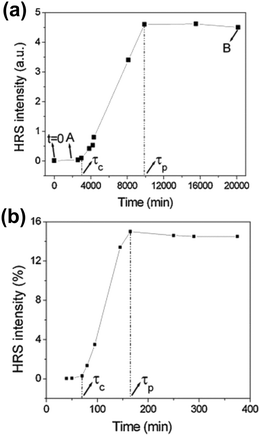 | ||
| Fig. 4 HRS intensity during the crystallization of iron iodate nanorods at (a) RT and (b) 80 °C. Specific transitions for both reaction were identified and labelled τc and τp. τc is defined as the crystallization time once a rapidly growing HRS response is detected. A quasi linear increase in the HRS response is then observed. τp is defined as the onset of a final stage where a plateau is reached. Note that the authors use the term HRS, while strictly speaking SHS is the appropriate term due to the size of the nanorods. Adapted with permission from ref. 60. Copyright 2011 American Chemical Society. | ||
In another study performed by Mugnier et al., the formation of iron iodate nanorods water-in-oil microemulsions were investigated with SHS.61 Similarly to the article by El-Kass et al.,60 the SHS intensity trace was used to identify transitions between different steps in the crystallization process. Hence, four different steps (A–D) of the crystallization process of iron iodate could be identified, and were further analyzed by DLS, TEM and XRD. It was found that nanorods were formed by oriented aggregation of 10–20 nm amorphous nanoparticles. The intermicellar exchange of reactants and the aggregation mechanism were found to depend on the microemulsion composition.
The authors concluded that SHS appears as a fast and non-destructive technique to probe the real-time crystallization and formation dynamics of acentric nanoparticles in microemulsions.
Organics
In a first study, regioregular P3AT polymer aggregation was initiated either by lowering the quality of the solvent (chloroform) by addition of a non-solvent (methanol), or by decreasing the temperature when dissolved in hexanol. Upon addition of non-solvent, self-assembly into micro-crystalline aggregates was triggered at a threshold concentration of 33% (v/v) methanol. This transition resulted in clear changes in UV-vis, MPE, CD, SHS and THS. Remarkably, the authors observed an increase in SHS intensity even before the phase transition was triggered. In this region, the classical spectroscopic techniques could not detect any significant change. In the absence of clusters, a linearity should exist between the monomer concentration and SHS intensity (see eqn (10)). Here, strong deviations from linearity indicated the formation of clusters (see eqn (12)).63 A similar kinetic trace was found for the THS signal. In conjunction with DLS measurements this increase could be attributed to equilibrium clusters, several hundreds of nm in size, preceding crystallization. Additional insight into the structure of these clusters was gained through depolarization measurements for SHS and THS. Along with the absence of electronic coupling corroborated by electronic spectroscopy, the results were in line with loosely structured polymer–solvent clusters of octupolar symmetry. After the phase transition, electronic spectroscopy and circular dichroism indicated planarization of the polymer backbone and aggregation into microcrystalline structures. This also explained the strong increase in THS intensity, due to the planarized polymer backbone resulting in increased conjugation. During aggregation and planarization of the system no sizeable change in depolarization ratios for SHS and THS was observed. This indicated a similarity between the symmetry of the clusters in the low methanol regime and the final aggregate. In DLS a reduction in size was observed, pointing to the expulsion of solvent molecules upon transition from the loosely bound clusters to the microcrystallites. These results are in line with the nonclassical prenucleation cluster model proposed by Gebauer et al.7
A second study by Moris et al. unraveled the aggregation mechanism for chiral star shaped P3AT.64 In line with earlier results, a rise of SHS in the low methanol region up to 35% (v/v) indicated the appearance of prenucleation clusters with octupolar structure (ρ2ω ∼ 2), as shown in Fig. 5. A second region shows a steep decrease of SHS, as the THS intensity starts to increase slightly, attributed to the planarization of the polymer backbone. Additional CD data showed no electronic coupling between the polymer chains in the cluster in this second stage. A third region above 45% (v/v) addition of the non-solvent resulted in a steep increase of THS, while SHS continued to decrease slightly. These results were attributed to the further planarization of the backbone and increased conjugation. This was confirmed by UV/vis, CD and MPE spectra. Unlike the P3AT system from the first study, some peculiar changes occurred for the depolarization ratios. While this stayed constant for SHS throughout the different regions, the THS ratio dropped significantly in value indicating a structural switch.64
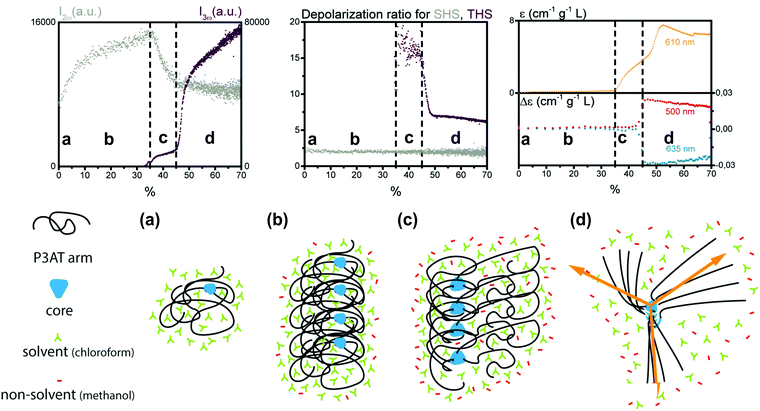 | ||
| Fig. 5 Schematic representation of the aggregation process of the star shaped P3AT polymer in a solvent/non-solvent system shown in function of the SHS intensity (I2ω at 430 nm), THS intensity (I3ω at 433 nm) and depolarization ratio for percentage of non-solvent added. The SHS and THS data were obtained with an acquisition time of 2 s. The electronic spectroscopy of the aggregation process is also shown: at 610 nm dynamic UV/Vis absorption and CD at 460 and 510 nm. The different stages represent (a) isolated polymer; (b) randomly coiled polymer clusters and (c) partially planarized clusters, to (d) final structure with the arrows showing the octupolar character. Adapted with permission form ref. 64. Copyright 2020 American Chemical Society. | ||
Both studies by Moris et al. discussed above demonstrated the formation of polymer–solvent clusters acting as pre-organized micro-environments preceding crystallization upon addition of non-solvent. Hence, the interaction between the solute/solvent and solvent/non-solvent system should play an important role during the aggregation process. In a third study, the effect of the solvent on the self-assembly process of the P3AT system has been investigated as well, by using thiophene and tetrahydrofuran (THF) as solvent with methanol as the non-solvent.65 For the thiophene system a three-step process occurred, from the pre-organization of polymers and solvent into clusters, through a reorganization of an intermediate structure which is not fully assembled yet, to the final structure. In THF an even different assembly process was witnessed. Initially small amounts of comparatively much smaller clusters were observed. At higher concentrations of non-solvent, planarization of the polymer background is accompanied by the formation of large aggregates that are structurally different from the initial clusters. Finally, rearrangements in structure lead to better stacking, followed by a breakage of aggregates in smaller assemblies.
The studies of Moris et al. demonstrate a remarkable influence of experimental conditions on the self-assembly mechanism of polythiophene compounds, both in terms of mechanism and final structure. This is indicative of a complex free-energy landscape with many kinetically accessible close-lying states.
The possibility of probing formation of aggregates and clusters in solution, which are thought to play a vital role in crystallization processes, had been explored earlier in other systems. Ward et al. measured the SHS intensity of urea solutions as a function of concentration.66 Although the measurements were performed by SHS microscopy without selection of polarization state, similar conclusions were drawn. At higher concentrations, deviations of SHS intensity were observed from the expected model which were attributed to semi-ordered urea clusters in the solution.66 In earlier studies by Mukhopadhyay et al. the SHS response was varied through the formation and dissociation of supramolecular complexes.67 Here a titration experiment was performed by addition of a complementary cryptand to the aza cryptands functionalized with π-acceptor groups. The resulting SHS response was measured at a 90° scattering angle. Complexes formed through hydrogen bonding resulted in an increase of SHS intensity. The results showed a linear increase of the intensity with a maximum being reached at a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Addition of methanol to the solution lead to dissociation of the complexes due to competition to form H-bonds, resulting in a decrease of SHS.67 Similar effects were studied earlier by Ray et al. through the self-assembly of melamine and cyanuric acid complexes.68
1. Addition of methanol to the solution lead to dissociation of the complexes due to competition to form H-bonds, resulting in a decrease of SHS.67 Similar effects were studied earlier by Ray et al. through the self-assembly of melamine and cyanuric acid complexes.68
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group (Td) of ZIF-8 (Fig. 6c). Through the same RGD model the particle concentration could be retrieved (Fig. 6b). Initially a sharp decrease of the number of particles with growth was observed, after which growth slowed down and plateaued. These observations are in line with a nucleation model where particle growth initially occurs by coalescence followed by monomer addition.51 Finally, the data were treated with a classical homogenous growth model, giving insight into nucleation, growth and ripening rates.
3m space group (Td) of ZIF-8 (Fig. 6c). Through the same RGD model the particle concentration could be retrieved (Fig. 6b). Initially a sharp decrease of the number of particles with growth was observed, after which growth slowed down and plateaued. These observations are in line with a nucleation model where particle growth initially occurs by coalescence followed by monomer addition.51 Finally, the data were treated with a classical homogenous growth model, giving insight into nucleation, growth and ripening rates.
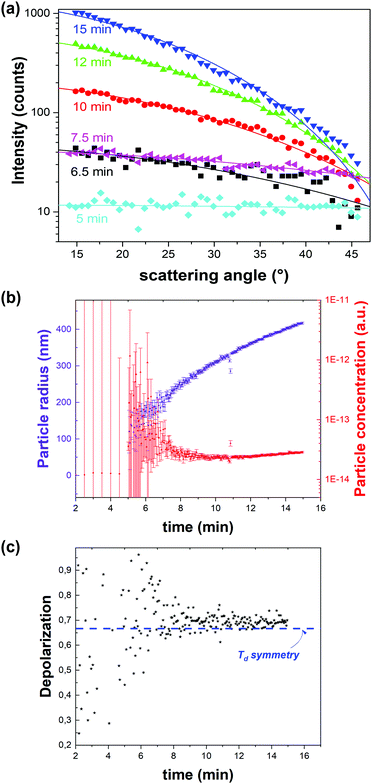 | ||
| Fig. 6 Dynamic angle-resolved SHS of ZIF-8 crystallization process measured at an excitation wavelength of 1030 nm. (a) Angle-resolved SHS pattern at different time intervals during the crystal growth were fitted to a Rayleigh–Gans–Debye model for monodisperse spheres rendering particle radius and concentration. (b) Particle radius (purple) and concentration (red) as a function of time indicate growth by coalescence followed by monomer growth. The time resolution is 3 seconds. (c) Depolarization ratio as a function of time is in line with the formation of phase-pure ZIF-8 (Td). The blue dotted line indicates the depolarization ratio for Td symmetry. Adapted with permission from ref. 51. Copyright 2018 Springer Nature. | ||
Although this was the first study that made use of angle-dependent SHS to study a fast crystallization process, Clays et al. had used the technique earlier to study solubilization of purple membrane consisting of patches of the protein bacteriorhodopsin. This was possible by rotating a detector in discrete steps around the sample during the slow process taking up to 117 hours. Contrary to the crystallization of ZIF-8 discussed above, the scattering patterns showed a broadening of the coherent contribution in the forward direction over time, caused by a decrease of particle size or coherence length.75
Xie et al. performed similar solubilization studies on 4-dimethylamino-4′-nitro-azobenzene (DNAB) particles by sodium dodecyl sulfate (SDS) micelles. Although only a single angle was measured, the evolution of the HRS intensity could be followed.76 To understand the structural changes during the solubilization process of DNAB in the water/SDS system, polarization resolved HRS was measured at 90°. Until the critical micellar concentration (CMC) was reached, a very low HRS response was observed due to the formation of H-aggregates of DNAB molecules. An incremental increase of the SDS concentration caused a steep increase of the HRS signal until a maximum was reached. The change in HRS response was attributed to the formation of J-aggregates, after dispersion into smaller particles and detachment of DNAB molecules from the particle surface. In the last stage, at high SDS concentrations, the HRS intensity decreased to a final value of half the maximum intensity. This response was purely attributed to the DNAB molecules, after all particles were dissolved. This was further confirmed by the depolarization ratio, showing C2V type symmetry typical for DNAB molecules.76
Hall et al. were able to directly observe transient polymorph changes according to Ostwald's rule of stages in amino acid solutions by SHG microscopy.77 For racemic DL-serine solutions, SHG enabled the detection of homochiral microcrystals which only lasted a few seconds before being converted to more stable racemic polymorphic forms. In this case polarimetric analysis was not required since the contrast was provided by the (non)centrosymmetry of both phases. The homochiral serine crystal (space group P212121) has non-vanishing SHG tensor elements while racemic DL-serine crystal (space group P21/n) has a null SHG tensor due to inversion symmetry. Upon onset of crystallization, both the enantiopure and racemic solutions showed increasing SHG signals but these signals were localized in the case of the racemic DL-serine. The SHG signal from the homochiral L-serine solution continued to grow until reaching a plateau while the racemic signal dropped back down to zero after a few minutes. The data indicated that the racemic cocrystal was energetically favored over conglomerates of homochiral crystals under ambient conditions.77
SHG microscopy was also used by Wanapun et al. to characterize early stages of nucleation and growth of pharmaceutical compounds griseofulvin and chlorpropamide. Their work demonstrated that low detection limits were improved by eight orders of magnitude relative to macroscopic averaging techniques as well as five orders of magnitude relative to optical microscopy. The detection limit was documented to be approximately 1 in 10 billion by volume. Due to the high contrast and low background noise of the SHG microscopy images, real-time quantitative monitoring of nucleation and growth rates as well as overall crystallization kinetics were achievable. These quantities were obtained by using a threshold-based imaging and particle counting software. Differences in monitoring of crystal growth by SHG and standard optical microscopy are illustrated in Fig. 7.78
 | ||
| Fig. 7 SHG microscopy at 800 nm (left) images of chlorpropamide crystallization showing the large improvement in sensitivity compared to optical microscopy (right). A time resolution of 25 seconds between captured images was used to observe the relatively fast kinetics of the reaction. Reprinted with permission from ref. 78. Copyright 2010 American Chemical Society. | ||
Also in the field of pharmaceuticals, Sarkar et al. studied amorphous solid dispersions (ASDs) and poorly soluble active pharmaceutical ingredients (APIs) by SHG microscopy. The understanding of the stability of the active ingredient plays a crucial part for optimizing final dosage forms of the drug. X-Ray powder diffraction (PXRD) is usually considered as the pharmaceutical industry standard for detecting trace crystallinity however this technique does not allow quantification at low crystallinity and requires several milligrams of material for analysis. In this work, the authors tracked single particles of ritonavir ASDs by SHG microscopy. The high selectivity of SHG provided high contrast imaging over a wide dynamic range. The same field of view could be monitored over time and this also provided heterogeneity information in crystal growth rates, which would not be possible with other API analysis methods. The sample volume used was also reduced substantially (∼50 fold).79
Sherman et al. integrated differential scanning calorimetry (DSC) with SHG microscopy. In the pharmaceutical industry, there is a need for thoroughly mapping the phase space of different drug candidates. DSC enables the detection of phase transitions with good sensitivity. However, phase transitions in crystals are stochastic and the nucleation needs to be studied on a per-particle basis. The integration of a SHG microscope with DSC would allow to monitor phase transitions of individual particles and the combination of both instruments was referred to as Stochastic differential scanning calorimetry (SDSC).80
The authors measured phase transitions of supersaturated solutions of urea and D-(+) trehalose dihydrate for benchmarking the technique. The SHG imaging was sensitive to the packing arrangements of the crystals and this would not be observable with conventional microscopy. By coupling the structural data of the SHG, it was shown that the DSC data can be disentangled from its ensemble-averaged thermal response on a single-particle basis. SDSC is proposed as a novel technique for the characterization of single-particle transformations.
Conclusion and prospects
Although the majority of crystallization studies still rely on characterization of the final product, the number of in situ studies has soared over the last two decades. This has led to important new insights in the pathways of nucleation and crystallization of biominerals, ionic compounds, organics, polymers and proteins. Only through a detailed understanding of the mechanisms driving crystal formation, rational exploration of the crystal phase space becomes attainable. Recent theoretical and experimental developments in the field of nonlinear optics highlight the potential for these techniques to advance this endeavor.A major advantage lays in the accessibility of sensitive structural information in all stages of the crystallization process. Through structural, size, concentration and morphological information, a comprehensive picture into the complex dynamical pathways leading to crystalline solids arises. In the earliest stages the role and structure of clusters, which are thought to affect nucleation and growth, can be probed by NLO scattering. Nucleation events can be detected early on and can be studied directly for processes involving burst nucleation. In later stages SHS becomes surface-sensitive for centrosymmetric species, providing unique insight in surface processes during growth. For noncentrosymmetric crystals the combination of second- and third-order scattering, with totally different symmetry sensitivity, can provide insight in competing processes, and intraparticle domain size and crystallinity. For larger particles, SHG and THG microscopy allow determination of local symmetry and lattice orientation, and discrimination of polymorphic forms during growth.
NLO techniques are relatively simple bench-top techniques that lend themselves perfectly to multi-parameter studies. This opens perspectives for coupling with machine-learning driven material discovery. This approach is bound to substitute trial-and-error experimental exploration.81–83 Since this requires fast and accessible characterization methods with access to structural information, classical X-ray or neutron based diffraction techniques at synchrotron facilities are however impractical due to the limited time slots. The remarkable sensitivity of NLO techniques to symmetry, definitely when second- and third-order processes are combined, has strong potential for characterizing structural changes in all stages of crystallization. Even when precise structural characterization is not feasible, e.g. due to limited information content in scattering studies, qualitative detection is possible. Coupled to X-ray studies or techniques such as cryo-TEM, this can aid in the identification of transient phases or unknown polymorphs.
While crystallization studies based on harmonic light generation give insight in the evolution of physical parameters such as size, shape and structure, chemistry often play a vital role as well. In some of the studies we discussed, MPE gave insight in chemical changes. Recently, multimodal imaging studies based on sum-frequency generation (SFG) and coherent anti-Stokes Raman scattering (CARS) elucidated surface crystallization and dissolution phenomena in pharmaceutical formulations.84–86 Together with stimulated Raman scattering (SRS), which does not have the problems with nonresonant backgrounds that tend to plague CARS, these NLO techniques probe molecular vibrational modes and can hence provide key chemical information during phase transformations. Just like for sum-frequency scattering, theoretical studies indicate that size information can be retrieved from angle-dependent SRS measurements in solution.87,88 This offers the possibility of simultaneously measuring size distributions for different solution species by spectroscopic discrimination at different angles.
For all these exciting prospects, a potential drawback that needs to be investigated more thoroughly is the effect of intense laser light on the crystallization process. Several studies have shown that the use of intense nanosecond pulsed laser light, even in the absence of photochemical effects, can influence nucleation and even polymorph outcome for small organic compounds.89–94 It should be noted that in NLO studies femtosecond pulses are typically used. Recent work of the group of Sylvie Roke has demonstrated that, by judicious choice of laser frequency and pulse power, photodamage and thermal effects can be avoided in biological systems, but it remains an open question whether these observations are transferable to crystallization studies.52,53 One has to remark that similar effects play for other techniques (e.g. X-ray, TEM) as well, and that useful mechanistic information can still conceivably be extracted, even if some influence is present. Given their high potential, we foresee a bright future for NLO techniques to study crystallization processes, which will be of interest for the entire crystal growth community.
Author contributions
A. R. D., T. L. and Y. d. C. wrote the discussion part of the paper and adapted the figures where appropriate. S. V. C. wrote the introduction, theoretical background and conclusions and prospects. S. V. C., T. V. and M. V. D. V. selected the relevant research to be included, composed the general structure and proofread the document.Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. V. acknowledges financial support from the KU Leuven via a C1 project (C16/16/003) and IDN project (IDN/19/014) and the Fund for Scientific Research Flanders (research project G099319N). S. V. C. is grateful for financial support from the KU Leuven via a C1 project (C14/19/079) and IDN project (IDN/19/014) and the Fund for Scientific Research Flanders (research project G099319N).Notes and references
- R. J. Davey, K. Allen, N. Blagden, W. I. Cross, H. F. Lieberman, M. J. Quayle, S. Righini, L. Seton and G. J. T. Tiddy, CrystEngComm, 2002, 4, 257–264 RSC.
- D. Gebauer and S. E. Wolf, J. Am. Chem. Soc., 2019, 141, 4490–4504 CrossRef CAS PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007–5019 CrossRef CAS PubMed.
- J. J. De Yoreo, MRS Bull., 2017, 42, 525–536 CrossRef CAS.
- J. J. De Yoreo and P. G. Vekilov, Rev. Mineral. Geochem., 2003, 54, 57–93 CrossRef CAS.
- M. Sleutel and A. E. S. Van Driessche, Nanoscale, 2018, 10, 12256–12267 RSC.
- D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371 RSC.
- J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349 Search PubMed.
- N. Pienack and W. Bensch, Angew. Chem., Int. Ed., 2011, 50, 2014–2034 CrossRef CAS PubMed.
- K. D. M. Harris, C. E. Hughes and P. A. Williams, Solid State Nucl. Magn. Reson., 2015, 65, 107–113 CrossRef CAS PubMed.
- F. Ito, Symmetry, 2020, 12, 1–13 Search PubMed.
- P. R. Carey, Annu. Rev. Phys. Chem., 2006, 57, 527–554 CrossRef CAS PubMed.
- G. Févotte, Chem. Eng. Res. Des., 2007, 85, 906–920 CrossRef.
- R. Tang, B. Jin, B. Jin and Z. Liu, CrystEngComm, 2020, 22, 4057–4073 RSC.
- Y. Gao, J. Wang, J. Zhong, Y. Wang, Q. Yin, B. Hou and H. Hao, Sci. Adv. Mater., 2017, 9, 89–101 CrossRef CAS.
- J. Xing, L. Schweighauser, S. Okada, K. Harano and E. Nakamura, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- S. Roke and G. Gonella, Annu. Rev. Phys. Chem., 2012, 63, 353–378 CrossRef CAS PubMed.
- D. J. Kissick, D. Wanapun and G. J. Simpson, Annu. Rev. Anal. Chem., 2011, 4, 419–437 CrossRef CAS PubMed.
- M. A. van der Veen, T. Verbiest and D. E. De Vos, Microporous Mesoporous Mater., 2013, 166, 102–108 CrossRef CAS.
- M. A. Van Der Veen, F. Vermoortele, D. E. De Vos and T. Verbiest, Anal. Chem., 2012, 84, 6378–6385 CrossRef CAS PubMed.
- T. Verbiest, K. Clays and V. Rodriguez, Second-order Nonlinear Optical Characterization Techniques: An Introduction, 2009 Search PubMed.
- N. Gomopoulos, C. Lütgebaucks, Q. Sun, C. Macias-Romero and S. Roke, Opt. Express, 2013, 21, 815 CrossRef CAS PubMed.
- P. D. Schmitt, E. L. Dewalt, X. Y. Dow and G. J. Simpson, Anal. Chem., 2016, 88, 5760–5768 CrossRef CAS PubMed.
- R. W. Boyd, Nonlinear optics, Academic Press, 2003 Search PubMed.
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef.
- S. Van Cleuvenbergen, G. Hennrich, P. Willot, G. Koeckelberghs, K. Clays, T. Verbiest and M. A. Van Der Veen, J. Phys. Chem. C, 2012, 116, 12219–12225 CrossRef CAS.
- X. Y. Dow, E. L. DeWalt, J. A. Newman, C. M. Dettmar and G. J. Simpson, Biophys. J., 2016, 111, 1553–1568 CrossRef CAS PubMed.
- G. J. Simpson, Nonlinear Optical Polarization Analysis in Chemistry and Biology, Cambridge University Press, 2017 Search PubMed.
- M. Samim, S. Krouglov and V. Barzda, Phys. Rev. A, 2016, 93, 033839 CrossRef.
- K. Clays and A. Persoons, Phys. Rev. Lett., 1991, 66, 2980–2983 CrossRef CAS PubMed.
- R. Bersohn, Y. Pao and H. L. Frisch, J. Chem. Phys., 1966, 45, 3184–3198 CrossRef CAS.
- S. Kielich and M. Kozierowski, Acta Phys. Pol., 1970, A38, 271–273 Search PubMed.
- S. Kielich, Classical Theory of Nonlinear Molecular Light Scattering, 1962 Search PubMed.
- V. Rodriguez, J. Phys. Chem. C, 2017, 121, 8510–8514 CrossRef CAS.
- N. Van Steerteghem, K. Clays, T. Verbiest and S. Van, Cleuvenbergen, Anal. Chem., 2017, 89, 2964–2971 CrossRef CAS PubMed.
- D. P. Shelton, J. Chem. Phys., 2018, 149, 224504 CrossRef PubMed.
- P. N. Prasad and D. J. Williams, Introduction to Nonlinear Optical Properties of Molecules and Polymers, 1991 Search PubMed.
- G. Tocci, C. Liang, D. M. Wilkins, S. Roke and M. Ceriotti, J. Phys. Chem. Lett., 2016, 7, 4311–4316 CrossRef CAS PubMed.
- D. P. Shelton, J. Chem. Phys., 2013, 138, 154502 CrossRef PubMed.
- S. Roke, M. Bonn and A. V. Petukhov, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–10 CrossRef.
- A. G. F. F. De Beer and S. Roke, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–8 CrossRef.
- H. B. De Aguiar, R. R. Scheu, K. C. Jena, A. G. F. De Beer and S. Roke, Phys. Chem. Chem. Phys., 2012, 14, 6826–6832 RSC.
- E. L. Dewalt, S. Z. Sullivan, P. D. Schmitt, R. D. Muir and G. J. Simpson, Anal. Chem., 2014, 86, 8448–8456 CrossRef CAS PubMed.
- J. Morizet, G. Ducourthial, W. Supatto, A. Boutillon, R. Legouis, M.-C. Schanne-Klein, C. Stringari and E. Beaurepaire, Optica, 2019, 6, 385 CrossRef.
- N. J. Begue and G. J. Simpson, Anal. Chem., 2010, 82, 559–566 CrossRef CAS PubMed.
- G. Olbrechts, R. Strobbe, K. Clays and A. Persoons, Rev. Sci. Instrum., 1998, 69, 2233–2241 CrossRef CAS.
- J. Campo, F. Desmet, W. Wenseleers and E. Goovaerts, Opt. Express, 2009, 17, 4587 CrossRef CAS PubMed.
- S. F. Hubbard, R. G. Petschek and K. D. Singer, Opt. Lett., 1996, 21, 1774 CrossRef CAS PubMed.
- O. F. J. Noordman and N. F. Van Hulst, Chem. Phys. Lett., 1996, 253, 145–150 CrossRef CAS.
- C. Zheng, Q. Zang, H. Nie, W. Huang, Z. Zhao, A. Qin, R. Hu and B. Z. Tang, Mater. Chem. Front., 2018, 2, 180–188 RSC.
- S. Van Cleuvenbergen, Z. J. Smith, O. Deschaume, C. Bartic, S. Wachsmann-Hogiu, T. Verbiest and M. A. van der Veen, Nat. Commun., 2018, 9, 3418 CrossRef PubMed.
- C. Macias-Romero, M. E. P. Didier, P. Jourdain, P. Marquet, P. Magistretti, O. B. Tarun, V. Zubkovs, A. Radenovic and S. Roke, Opt. Express, 2014, 22, 31102–31112 CrossRef CAS PubMed.
- C. Macias-Romero, V. Zubkovs, S. Wang and S. Roke, Biomed. Opt. Express, 2016, 7, 1458 CrossRef CAS PubMed.
- D. Senapati, A. K. Singh, S. A. Khan, T. Senapati and P. C. Ray, Chem. Phys. Lett., 2011, 504, 46–51 CrossRef CAS.
- C. Sauerbeck, M. Haderlein, B. Schürer, B. Braunschweig, W. Peukert and R. N. Klupp Taylor, ACS Nano, 2014, 8, 3088–3096 CrossRef CAS PubMed.
- R. A. Khoury, J. C. Ranasinghe, A. S. Dikkumbura, P. Hamal, R. R. Kumal, T. E. Karam, H. T. Smith and L. H. Haber, J. Phys. Chem. C, 2018, 122, 24400–24406 CrossRef CAS.
- Y. De Coene, O. Deschaume, S. Jooken, S. Seré, S. Van Cleuvenbergen, C. Bartic, T. Verbiest and K. Clays, Chem. Mater., 2020, 32, 7327–7337 CrossRef CAS.
- Y. de Coene, O. Deschaume, Y. Zhang, A. Billen, J. He, S. Seré, S. Knoppe, S. Van Cleuvenbergen, T. Verbiest, K. Clays, J. Ye and C. Bartic, ChemPhysChem, 2019, 20, 1765–1774 CAS.
- J. C. Ranasinghe, A. S. Dikkumbura, P. Hamal, M. Chen, R. A. Khoury, H. T. Smith, K. Lopata and L. H. Haber, J. Chem. Phys., 2019, 151, 224701 CrossRef PubMed.
- M. El-Kass, R. Ladj, Y. Mugnier, R. Le Dantec, R. Hadji, J. C. Marty, D. Rouxel, C. Durand, D. Fontvieille, E. Rogalska and C. Galez, Mater. Res. Bull., 2013, 48, 4431–4437 CrossRef CAS.
- Y. Mugnier, L. Houf, M. El-Kass, R. Le Dantec, R. Hadji, B. Vincent, G. Djanta, L. Badie, C. Joulaud, J. Eschbach, D. Rouxel and C. Galez, J. Phys. Chem. C, 2011, 115, 23–30 CrossRef CAS.
- D. Segets, L. M. Tomalino, J. Gradl and W. Peukert, J. Phys. Chem. C, 2009, 113, 11995–12001 CrossRef CAS.
- M. Moris, M. P. Van Den Eede, G. Koeckelberghs, O. Deschaume, C. Bartic, S. Van Cleuvenbergen, K. Clays and T. Verbiest, Chem. Commun., 2019, 2, 1–9 CrossRef.
- M. Moris, M. P. Van Den Eede, G. Koeckelberghs, O. Deschaume, C. Bartic, K. Clays, S. Van Cleuvenbergen and T. Verbiest, Macromolecules, 2020, 53, 9513–9520 CrossRef CAS.
- M. Moris, M. P. Van Den Eede, G. Koeckelberghs, O. Deschaume, C. Bartic, K. Clays, S. Van Cleuvenbergen and T. Verbiest, Macromolecules, 2021, 54, 2477–2484 CrossRef CAS.
- M. R. Ward, S. W. Botchway, A. D. Ward and A. J. Alexander, Faraday Discuss., 2013, 167, 441–454 RSC.
- P. Mukhopadhyay, P. K. Bharadwaj, A. Krishnan and P. K. Das, J. Organomet. Chem., 2004, 689, 4877–4881 CrossRef CAS.
- P. C. Ray and P. K. Das, Chem. Phys. Lett., 1997, 281, 243–246 CrossRef CAS.
- M. Jian, B. Liu, R. Liu, J. Qu, H. Wang and X. Zhang, RSC Adv., 2015, 5, 48433–48441 RSC.
- Y. Choi, K. Noh, J. Lee and J. Kim, J. Am. Chem. Soc., 2018, 140, 14586–14589 CrossRef CAS PubMed.
- S. Van Cleuvenbergen, I. Stassen, E. Gobechiya, Y. Zhang, K. Markey, D. E. De Vos, C. Kirschhock, B. Champagne, T. Verbiest and M. A. Van Der Veen, Chem. Mater., 2016, 28, 3203–3209 CrossRef CAS.
- H. Reinsch, M. a. van der Veen, B. Gil, B. Marszalek, T. Verbiest, D. de Vos and N. Stock, Chem. Mater., 2013, 25, 17–26 CrossRef CAS.
- A. Ferguson, L. Liu, S. J. Tapperwijn, D. Perl, F. X. Coudert, S. Van Cleuvenbergen, T. Verbiest, M. A. Van Der Veen and S. G. Telfer, Nat. Chem., 2016, 8, 250–257 CrossRef CAS PubMed.
- S. M. F. Vilela, A. A. Babaryk, R. Jaballi, F. Salles, M. E. G. Mosquera, Z. Elaoud, S. Van Cleuvenbergen, T. Verbiest and P. Horcajada, Eur. J. Inorg. Chem., 2018, 2437–2443 CrossRef CAS.
- K. Clays, S. Van Elshocht and A. Persoons, Opt. Lett., 2000, 25, 1391 CrossRef CAS PubMed.
- H. Xie, L. Liu, W. Wang and L. Xu, Chem. Phys. Lett., 2005, 403, 175–179 CrossRef CAS.
- V. J. Hall and G. J. Simpson, J. Am. Chem. Soc., 2010, 132, 13598–13599 CrossRef CAS PubMed.
- D. Wanapun, U. S. Kestur, D. J. Kissick, G. J. Simpson and L. S. Taylor, Anal. Chem., 2010, 82, 5425–5432 CrossRef CAS PubMed.
- S. Sarkar, Z. Song, S. R. Griffin, N. Takanti, A. D. Vogt, A. Ruggles, G. D. Danzer and G. J. Simpson, Mol. Pharm., 2020, 17, 769–776 CrossRef CAS PubMed.
- A. M. Sherman, A. C. Geiger, C. J. Smith, L. S. Taylor, J. Hinds, P. A. Stroud and G. J. Simpson, Anal. Chem., 2020, 92, 1171–1178 CrossRef CAS PubMed.
- V. Duros, J. Grizou, W. Xuan, Z. Hosni, D. L. Long, H. N. Miras and L. Cronin, Angew. Chem., Int. Ed., 2017, 56, 10815–10820 CrossRef CAS PubMed.
- D. P. Tabor, L. M. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz, H. Tribukait, C. Amador-Bedolla, C. J. Brabec, B. Maruyama, K. A. Persson and A. Aspuru-Guzik, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- P. V. Balachandran, B. Kowalski, A. Sehirlioglu and T. Lookman, Nat. Commun., 2018, 9, 1668 CrossRef PubMed.
- M. Jurna, M. Windbergs, C. J. Strachan, L. Hartsuiker, C. Otto, P. Kleinebudde, J. L. Herek and H. L. Offerhaus, J. Innovative Opt. Health Sci., 2009, 2, 37–43 CrossRef.
- M. Windbergs, M. Jurna, H. L. Offerhaus, J. L. Herek, P. Kleinebudde and C. J. Strachan, Anal. Chem., 2009, 81, 2085–2091 CrossRef CAS PubMed.
- D. Novakovic, A. Isomäki, B. Pleunis, S. J. Fraser-Miller, L. Peltonen, T. Laaksonen and C. J. Strachan, Mol. Pharm., 2018, 15, 5361–5373 CrossRef CAS PubMed.
- W. M. E. Loh, Mod. Phys. Lett. B, 2020, 34, 2050103 CrossRef CAS.
- C. H. R. Ooi, W.-L. Ho and P. Seow, J. Opt. Soc. Am. B, 2013, 30, 2427 CrossRef CAS.
- H. Niinomi, T. Sugiyama, M. Tagawa, K. Murayama, S. Harada and T. Ujihara, CrystEngComm, 2016, 18, 7441–7448 RSC.
- J. Zaccaro, J. Matic, A. S. Myerson and B. A. Garetz, Cryst. Growth Des., 2001, 1, 5–8 CrossRef CAS.
- B. A. Garetz, J. E. Aber, N. L. Goddard, R. G. Young and A. S. Myerson, Phys. Rev. Lett., 1996, 77, 3475–3476 CrossRef CAS PubMed.
- B. a Garetz, J. Matic and A. S. Myerson, Phys. Rev. Lett., 2002, 89, 175501 CrossRef PubMed.
- X. Sun, B. A. Garetz and A. S. Myerson, Cryst. Growth Des., 2006, 6, 684–689 CrossRef CAS.
- T. Sugiyama and H. Masuhara, Chem. – Asian J., 2011, 6, 2878–2889 CrossRef CAS PubMed.
Footnote |
| † Both authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |






