Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A multiaxial electrical switching in a one-dimensional organic–inorganic (pyrrolidinium)2Cd2I6 ferroelectric and photoluminescent crystal†
Magdalena
Rok
 *a,
Bartosz
Zarychta
*a,
Bartosz
Zarychta
 b,
Andrzej
Bil
b,
Andrzej
Bil
 a,
Joanna
Trojan-Piegza
a,
Joanna
Trojan-Piegza
 a,
Wojciech
Medycki
a,
Wojciech
Medycki
 c,
Andrzej
Miniewicz
c,
Andrzej
Miniewicz
 d,
Anna
Piecha-Bisiorek
d,
Anna
Piecha-Bisiorek
 a,
Agnieszka
Ciżman
a,
Agnieszka
Ciżman
 e and
Ryszard
Jakubas
e and
Ryszard
Jakubas
 a
a
aFaculty of Chemistry, University of Wroclaw, 14 F. Joliot-Curie, 50-383 Wroclaw, Poland. E-mail: Magdalena.rok@chem.uni.wroc.pl
bFaculty of Chemistry, University of Opole, Opole PL-45052, Poland
cInstitute of Molecular Physics, Polish Academy of Sciences, Smoluchowskiego 17, 60-179 Poznań, Poland
dAdvanced Materials Engineering and Modelling Group, Faculty of Chemistry, Wroclaw University of Science and Technology, Wybrzeze Wyspianskiego 27, 50-370 Wroclaw, Poland
eDepartment of Experimental Physics, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland
First published on 3rd June 2021
Abstract
Ferroelectric materials exhibiting more than one polar phase are very attractive in terms of application. The advantage of such materials is temperature-dependent switching between two different ferroelectric states. Here we report on the discovery of a unique, continuous ferroelectric – ferroelectric transformation in (C4H10N)2[Cd2I6], PCdI at 220 K. Thermal measurements suggest that phase transition is close to the continuous one. Both phases belong to the same polar monoclinic Cc space group. Temperature-variable X-ray diffraction measurements of single crystals confirm the polar nature of the two phases (I and II). The anionic network is in the form of [Cd2I6]2− 1D chains, with pyrrolidinium cations planted between them. To our knowledge, there are few examples of a structure with chains formed by tetrahedral units. Electrical and dielectric properties were measured for the samples in crystalline and thin-layer film forms. The ferroelectric properties of phases I and II were confirmed by the reversible pyroelectric effect as well as by the polarisation–electric field (P–E) loop tests, and these results were supported by DFT calculations. Strong nonlinear optical properties (NLO) were confirmed by SHG measurements. Additionally, the photoluminescent properties were investigated with the temperature dependence of the spectra of both photoluminescence excitation (PLE) and emission (PL). The broadband luminescence revealed to be thermally quenched from cryogenic temperatures to room temperature.
1. Introduction
The materials based on halide perovskites are of great interest due to their unique properties, resulting from the diversity of components and structures. Organic–inorganic hybrid perovskites (OIHPs) play a crucial role in photovoltaic cells,1–5 photodetectors6,7 and light-emitting diodes.8–11 In particular, these materials exhibit excellent piezoelectric and ferroelectric properties comparable to conventional inorganic oxides.1 The features that make OIHPs so attractive are energy conversion abilities from natural sources such as sunlight, thermal energy, or mechanical energy (due to pressure) into electrical energy.An example of such a hybrid is CH3NH3PbI3 used in solar cells with excellent efficiency.12 Additionally, fabrication of this hybrid requires relatively low production costs compared to inorganic oxide perovskites. The main advantage of OIHPs is the flexibility of their structures. Contrary to the parent oxide-perovskites with 3D-structure, which are relatively rigid, OIHPs from the halide family can form structural units of different architectures: isolated 0D, 1D chain, 2D layered and also 3D elements. The general formulae ABX3 and A2BX4 (A stands for an organic cation, B is a divalent transition metal, X is a halogen atom) describe the most promising 2D-layered structures. Regarding the stability of the perovskite structure, the layered construction allows the incorporation of cations whose size exceeds the limit value of 260 pm.13–16 However, there are no known limits for the length of the cations located between the layered structure composed of inorganic units. A classic examples are: (benzylammonium)2PbCl417 or (cyclohexylammonium)2PbBr418 hybrids. Apart from the semiconducting properties, ferroelectricity was also discovered in these compounds, with the polarization values of about 13 and 5.8 μC cm−2, respectively. Following this, built-in chiral amine R- and S-1-(4-chlorophenyl)ethylammonium embedded between the corner-sharing PbI6 octahedron layers for which polarization value of ca. 14 μC cm−2 was obtained.1,19 Implementation of chiral amines have resulted in the discovery of the first organic–inorganic perovskite enantiomorphic ferroelectrics, (R)- and (S)-3-(fluoropyrrolidinium)MnBr3, which exhibit strong red luminescence.20 Most known piezoelectric materials from the halide perovskites family also indicate ferroelectric properties. Generally, in ferroelectric material, the paraelectric phase can be observed. At the temperature higher than the Curie temperature, spontaneous polarization and sometimes piezoelectric properties vanish to a centrosymmetric point group. Therefore, the phase transition temperature is crucial in applications. In 2017, You et al. discovered an OIHP (trimethylchloromethyl ammonium, TMCM)MnCl3 with excellent piezoelectric property (d33ca. 185 pC N−1).21 However, the doping of trimethylfluoromethyl ammonium (TMFM) in position A, (TMFM)x(TMCM)1−xCdCl3 increased the piezoelectric properties enormously (d33ca. 1540 pC N−1) approaching that of the high-performance piezoelectric ceramics.22
Recently, organic and inorganic materials that emit white light (WL) have evoked much attention.23–25 The first reports concerned hybrids based on layered Pb-halides emitting radiation across the entire visible range when excited with ultraviolet light. These materials have been classified as promising single-source WL phosphors for ultraviolet light-emitting diodes in semiconductor lighting devices.26,27 A very good example is the zero-dimensional (0D) compound of (Ph4P)2Cd2Br6 (tetraphenylphosphonium, Ph4P), for which the results were recently published by Yan et al.28 This new thermal-quenching resistant phosphorescent material shows luminescent stability across a wide temperature range with the room temperature phosphorescence quantum yield of 62.79% and lifetime of 37.85 ms, which exceeds those of other state-of-the-art systems.
Wang et al.29 demonstrated a new organic–inorganic single-component WL emitting material, [C5H9–NH3]4CdBr6. This hybrid exhibits very high values of colour rendering index (CRI of 92.5) and chromaticity coordinates CIE of (0.33, 0.33), resulting in an appropriate correlated colour temperature (CCT) of 5436 K. These parameters are approximately equal to those of natural sunlight, which renders halo-Cd hybrids a potential light source for solid-state lighting (SSL) technologies.
Following this route, we synthesized a new organic–inorganic (C4H10N)2[Cd2I6] (PCdI) hybrid, which undergoes one solid–solid phase transition at about 220 K. The structural phase transition occurs between two polar phases, both showing ferroelectric features. Hence, this work is devoted to the characteristics of PCdI high (I) and low (II) temperature phases, with particular emphasis on exploring the ferroelectric properties. X-ray structural analysis was used to provide complementary evidence of the acentric structure of both phases. In order to verify the ferroelectric nature of phases, the pyroelectric tests and the polarization hysteresis loop observations were undertaken. The electric measurements were scrutinized for three types of the sample: (a) single-crystal, (b) powder pellets and (c) and thin-film layers. For a deeper understanding of the bi-axial ferroelectric property, spontaneous polarisation values have been garnered from DFT theoretical studies. These results allowed for the resolution of structural determinants, which contribute to the direction-dependent polarization values. In the context of emission from organic–inorganic hybrid metal halides, the reported PCdI is expected to serve as an ideal candidate for broadband luminescence that is predominantly ascribed to the self-trapping exciton30 associated with structural deformations.31 Since the structure and its distortions play an essential role in the defects localization and excitons creation it further determines PCdI crystal optical properties. Thus, the temperature-dependent luminescence of PCdI was studied.
2. Experimental
2.1. Sample preparation
4 g of CdI2 (Sigma-Aldrich, 99%, 10 mmol) was dissolved in deionized water, then concentrated hydroiodic acid (1.5 ml, 10 mmol 57% Sigma Aldrich) was added dropwise to the solution. Next, pyrrolidine (Sigma-Aldrich, 99%, 1 ml) was added in part to the solution placed in the ice bath. By slow evaporation at room temperature, light pale-yellow crystals of (C4H10N)2[Cd2I6], PCdI in the shape of the block were obtained (see Fig. 1). The composition of the compound was confirmed by elemental analysis to be C: 8.42% (theor. 8.50%), N: 2.17% (theor. 2.48), H 1.58% (theor. 1.78%). A powder X-ray diffraction verified the phase purity (see Fig. S1, ESI†). XRD was recorded in the range 2θ = 5–80° with the step 2θ = 0.024° and 1 s counting time using a D8 Advance X-ray Diffractometer from Bruker. The Ni-filtered Cu Kα1 radiation (λ = 1.540596 Å) from a Cu X-ray tube was applied.2.2. Thermal analysis
DSC measurements were performed by heating and cooling of the polycrystalline sample in the temperature range of 160–440 K with a ramp rate of 10 K min−1 using a Metler Toledo DSC 3 instrument. The TGA/DSC measurements were performed on a TGA-DSC 3+ instrument between 290 and 900 K with a ramp rate of 5 K min−1. The scan was performed in flowing nitrogen (flow rate: 1 dm3 h−1). The melting point was measured using two methods. First, with a scanning rate of 10 K min−1 using Opti-Melt MPA-100 in the temperature range from 300 to 480 K. Second, the optical microscopy observations were carried out by using an Olympus BX53 combined with a LINKAM THM-600 heating/cooling stage, where the temperature was stabilized with an accuracy of 1 K.2.3. Crystal structure determination
The single crystal of PCdI was mounted on a CCD Xcalibur diffractometer (graphite monochromatic, MoKα radiation, λ = 0.71073 Å). The X-ray diffraction measurements have been done at 100.0 (1) and 300.0 (1) K. The corrections to the Lorentz and polarisation factors were applied to the reflection intensities.32 The structures were solved by direct methods applying SHELX program package.33 The positions of hydrogen atoms were determined from the geometric concepts and refined in a riding model with isotropic temperature factors of 1.2 times the Ueq value of the parent atom. All non-hydrogen atoms were located from difference Fourier synthesis and refined by the least-squares method in the full-matrix anisotropic approximation. The crystallographic data for the compound and details of X-ray experiment are collected in Table S1 in ESI.† Crystal structure figures were constructed using Mercury34 and Olex235 software. The crystallographic data have been deposited with the Cambridge Crystallographic Data Centre no. 2070978 and 2070979 for structure at 100 and 300 K, respectively.2.4. Photoluminescence properties
Photoluminescence excitation (PLE) and emission (PL) spectra were recorded with a double-grating FLS1000 fluorescence spectrometer from Edinburgh Instruments Ltd. using 450 W Xenon arc lamp as a continuous excitation light source. The solid-state sample was mounted with silver glue on the copper holder of a closed-cycle helium cryostat from Lake Shore Cryotronics, Inc. The PL spectra were recorded in the 11–300 K temperature range with 25 K step using Hamamatsu R928P photomultiplier cooled to −20 °C and operating in the range 230–850 nm, while PLE spectrum was measured at 11 K. All spectra were corrected – PL for the wavelength dependence of the spectral response of the recording system and PLE for the incident light intensity. The spectral resolution of all measurements was 0.3 nm.Temperature dependence of PLE and lifetime measurements were performed with an FLS980 Spectrofluorimeter from Edinburgh Instruments equipped with a 450 W Xe lamp (PLE) and 60 W pulse Xe lamp used to measure luminescence decay traces. The solid-state sample was mounted with silver glue on the copper holder of a closed-cycle helium cryostat from Lake Shore Cryotronics, Inc. A Hamamatsu R928P photomultiplier detector operating within 180–870 nm and TMS302-X single grating excitation and emission monochromators of 30 cm focal lengths were used.
2.5. Electric properties
Electrical measurements were performed on different types of the PCdI samples: (a) polycrystalline samples in the form of pressed pellets with geometrical parameters (S = 20–25 mm2, d = 0.8–0.4 mm), (b) single crystal cuts perpendicular to the c-axis (S = 4–8 mm2, d = 0.5–0.8 mm), (c) thin layer (S = 25 mm2, d = 0.06 mm). The complex dielectric permittivity was measured between 200 and 360 K by an Agilent E4980A Precision LCR Meter in the frequency range of 135 Hz–2 MHz. The electric measurements were carried out in a controlled nitrogen atmosphere. The overall error for the complex permittivity real and imaginary parts was less than 5%. The pyroelectric properties were tested with a Keithley 6517D electrometer/high resistance meter between 200 and 360 K, with a temperature ramp of 2 K min−1. The ferroelectric hysteresis loops of polycrystalline powder and single crystals cut in directions perpendicular to the c-axis were obtained by using a Sawyer–Tower circuit Precision Premier II (Radiant Technologies, Inc.) at a frequency of 50 Hz. The surfaces of the pellet were coated with a gold electrode with a mask using a sputter coating system (Quorum Q150T S).2.6. 1H NMR measurements
NMR measurements were performed on an ELLAB TEL-Atomic PS 15 spectrometer working at the frequency of 25 MHz. Spin–lattice relaxation times T1 were measured using a saturation sequence of π/2 pulses followed by a variable time interval τ and a reading π/2 pulse. Single-exponential magnetization recovery was observed in the whole temperature range. The second moment measurements, M2, of 1H NMR line were carried out with a wide-line ELLAB CW spectrometer operating at 26.8 MHz. The second moment values were calculated by numerical integration of the first derivative of an absorption line and corrected for the finite modulation amplitude. The changes of temperature of the sample were obtained using the liquid nitrogen evaporation and were controlled by a UNIPAN 660 temperature controller operating on Pt 100 sensor providing long time-temperature stability better than 1 K. Errors of the measured T1 values were estimated to be lower than 5%. The powder sample for the NMR study was degassed for several hours and sealed in a glass tube under a vacuum.2.7. Second harmonic generation (SHG)
Second-order nonlinear optical properties were measured using Kurtz and Perry method.36 For SHG excitation, we used a Q-switched pulse laser (Nd3+:YAG, Surelite II) delivering 10 ns pulses with a repetition rate of 10 Hz and working at a fundamental wavelength of 1.064 μm. The 5 mm in diameter unfocused beam was incident normally to powdered compound confined in between two microscope glass plates. The typical crystallite size for PCdI was around 100 μm. In the used geometry, the entrance aperture of the optical fiber-end collecting a small portion of the SHG signal was positioned at the angle of 30° with respect to the surface normal. A fiber was connected to spectrometer (Qwave, RGB Photonics) that analyzed the spectrum within the wavelength range 300 to 900 nm.2.8. Computational methods
We performed total-energy calculations using a plane-wave basis set defined by the energy cut-off of 400 eV coupled with Troullier–Martins type pseudopotentials37 and dense Monkhorst–Pack k-point meshes.38 Density functionals applied for the calculations are PBE (Perdew–Burke–Ernzerhof)39 and LDA,40 as implemented in the Abinit software suite.41,42 Polarisation was calculated using the Berry phase method.43,44 The similar approach was successfully applied to study a spontaneous polarisation in organic–inorganic hybrid (Pyrrolidinium)3[Sb2Cl9].453. Results and discussion
3.1. Thermal analysis
PCdI crystals undergo a single structural phase transition (PT) in the solid-state at 220/218 K upon heating/cooling cycle (see Fig. 2). The shape of the thermal anomaly suggests the mixed character of the transition, indicating a second-order PT. The enthalpy change at this transition equals ΔH = 2182 J mol−1, while entropy change ΔS ≅ 10 J mol−1 K−1. Based on Boltzmann equation ΔS = Rln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, the ratio of the respective numbers of microstates N below and above PT can be estimated, and for PCdI equals 3.5, suggesting order–disorder nature of the transition, which can be further confirmed by crystal structure analysis.
N, the ratio of the respective numbers of microstates N below and above PT can be estimated, and for PCdI equals 3.5, suggesting order–disorder nature of the transition, which can be further confirmed by crystal structure analysis.
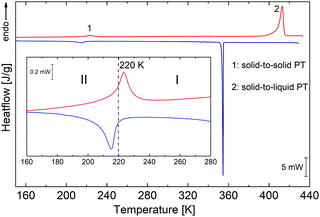 | ||
| Fig. 2 DSC runs obtained upon heating and cooling for PCdI (sample mass m = 9.8940 mg). Blue and red lines show runs (blue-cooling and red-heating at 10 K min−1). | ||
In addition to the transformation in the solid-state, the transition from solid to the liquid phase is observed at 398 K (see TGA-DSC Fig. S2, ESI†), which was also proven by the melting point measurement, and by the observation of the single crystal under the polarised light microscope (Fig. S3, ESI†). However, the complete decomposition of the compound takes place at 527 K.
3.2. Crystal structure
The structure of (C4H10N)2[Cd2I6] was determined at 100 and 300 K. At both temperatures, crystals are monoclinic with the Cc space group. In both phases, the anionic substructure is composed of distorted [CdI4]2− tetrahedra that share two corners with two other neighbours (Fig. 3), forming infinite one-dimensional [{CdI3}−]nzig-zag chains (Fig. 4a). The chains form two different and parallel (110) layers (Fig. S4, ESI†) arranged alternately. These are dissimilar as the chains are extended interchangeably along [110] and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] directions for altered layers. The pyrrolidinium cations are located between the inorganic layers. The crystal data and the structure determination details for (C5H10N)2[Cd2I6] at 300 and 100 K are listed in Table S1 (ESI†). The bond lengths, valence and torsion angles and the hydrogen bond geometries are presented in Tables S2 and S3 (ESI†), respectively.
10] directions for altered layers. The pyrrolidinium cations are located between the inorganic layers. The crystal data and the structure determination details for (C5H10N)2[Cd2I6] at 300 and 100 K are listed in Table S1 (ESI†). The bond lengths, valence and torsion angles and the hydrogen bond geometries are presented in Tables S2 and S3 (ESI†), respectively.
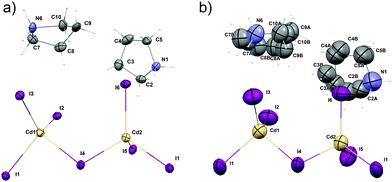 | ||
| Fig. 3 Molecular structure of (PCdI), (a) at 100 K and (b) at 300 K. Hydrogen atoms labels are omitted for clarity. Thermal ellipsoids are drawn at 50% probability level. | ||
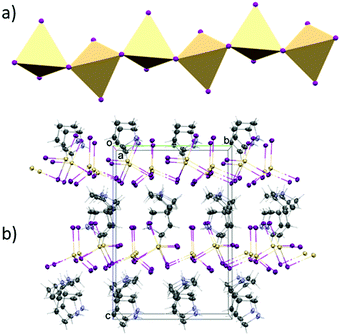 | ||
| Fig. 4 (a) Polyhedral structure of [CdI4]2− moieties. (b) Projection of the unit cell packing of PCdI in phase II. | ||
Structure at 300 K
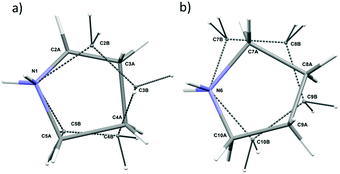
In the asymmetric part of the unit cell, there are two central cadmium(II) atoms which are surrounded by four (Cd1) and three (Cd2) crystallographically independent iodine ligands. The longest Cd–I bonds correspond to bridging iodine atoms and the shortest to terminal ones.The bridging Cd–I distance amounts from 2.8337 (15) Å (Cd2–I4) to 2.8504 (14) Å (Cd1–I4). For the terminal iodine atoms, the bonds lengths do not exceed 1.7261 (19) Å. The I–Cd–I angle range from 96.24 (5)° (I4–Cd1–I1i, (i): x − ½, y − ½, z) to 121.21 (6)° (I3–Cd1–I2). While the bridging ones amount to 101.69 (5)° and 99.48 (4)° respectively for Cd1–I1–Cd2 and Cd1–I4–Cd2. The same anionic substructure, built of [CdI4]2− tetrahedra connected by corners, was found in the structure of benzidine cadmium(II) iodide.46 In the structure, the Cd–I bond lengths are in the same arrangement, i.e. the longest are bridging bonds, while the terminal is noticeably shorter. There are two symmetrically independent pyrrolidinium cations in the asymmetric part of unit cell (Fig. 3 and 4). The type of disorder is similar for both cations as is realized by the presence of two positions of the carbon atoms (Fig. 5) with occupancy factors of 0.5.
The nitrogen atoms, which are hold by the strongest N–H⋯I hydrogen bonds stay ordered. Because of the dynamical disorder, the N–C, C–C bond lengths and N(C)–C(N)–C angles were not determined with high precision. The model of the disorder suggests that the cations dynamics could be described as swinging motion around a positively charged nitrogen atom.
Structure at 100 K
At the low temperature phase (100.0(1) K) there is no change in the space group on cooling from 300 K. The lowering of temperature leads to freezing of reorientational motions of both cations at 100 K. Both molecules adopt the asymmetric envelope conformation. On lowering the temperature, the deformation of [CdI4]2− moieties is also changed. The Cd1–I2, Cd1–I3 and Cd1–I6 terminal bonds become longer. The change in the length of the first one is due to the formation of additional N6–H6B⋯I2v [(V): x, −y + 1, z − ½] hydrogen bond (Fig. 6). In the case of two latter, changes in geometry are connected with the strengthening of existing hydrogen bonds, i.e. N1–H1A⋯I3ii; N6–H6B⋯I3 and N1–H1B⋯I6 [(III): x − ½, y + ½, z] (Table S3, ESI†).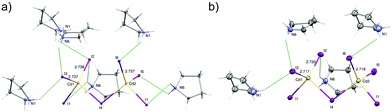 | ||
| Fig. 6 The [Cd2I6]2− bitetrahedra with their N–H ⋯I hydrogen-bonded cations at 100 K (a) and 300 K (b). Displacement ellipsoids are at 10% probability level for clarity. | ||
A measure of tetrahedral coordination distortion from regularity is provided by the distortion parameter for bond length Δ:
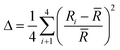 | (1) |
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) is the average Cd–I bond length within the tetrahedron and Ri the individual Cd–I bond length. The parameter amounts for the title structure at 300 K amounts 3.3 × 10−2 and 5.1 × 10−2 for Cd1 and Cd2 tetrahedron, respectively. At 100 K, the Cd1 tetrahedron becomes more distorted as the Δ increases up to 5.5 × 10−2. As pointed above, such an effect is connected with an increase in strength and in the number of the N–H⋯I hydrogen bonds. For Cd2 tetrahedra, the Δ parameter slightly decreases on cooling and amounts 4.6 × 10−2.
is the average Cd–I bond length within the tetrahedron and Ri the individual Cd–I bond length. The parameter amounts for the title structure at 300 K amounts 3.3 × 10−2 and 5.1 × 10−2 for Cd1 and Cd2 tetrahedron, respectively. At 100 K, the Cd1 tetrahedron becomes more distorted as the Δ increases up to 5.5 × 10−2. As pointed above, such an effect is connected with an increase in strength and in the number of the N–H⋯I hydrogen bonds. For Cd2 tetrahedra, the Δ parameter slightly decreases on cooling and amounts 4.6 × 10−2.
3.3. Preparation of thin films of PCdI
Multi-axis ferroelectricity is a highly desirable property because it allows the sample orientation with the electric field along more than one crystallographic axis. In such material, the polar crystal properties utilization does not require samples to be prepared in a specific direction. Thus that samples can be obtained in the form of a thin film or in the form of pressed pellets. There are a limited number of devices made of single ferroelectric crystals. Therefore, the study of ferroelectric properties in thin films is of great importance from the point of application of these crystals. The uncomplicated drop-coating method was employed with the following procedures to prepare thin films of PCdI. Firstly, a homogeneous solution was obtained by dissolving 100 mg of PCdI powder in 1 ml of purified water. The obtained solution (40 ml) was added dropwise to the Cu-substrate and deposited as desirable thin films (see Fig. 1b). Finally, the grown thin films were dried at 340 K for further characterization.3.4. Electric properties
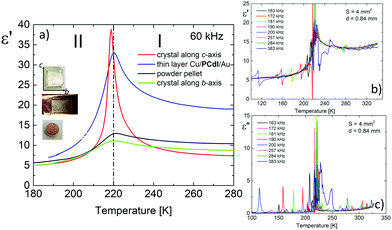
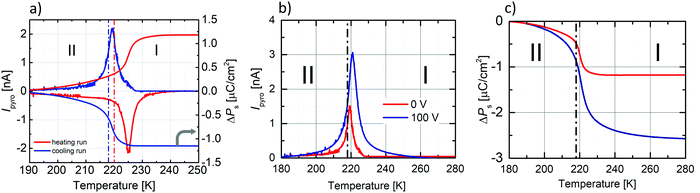
The dielectric response, presented in Fig. 7, was measured on three types of PCdI sample (a) crystallographically oriented single crystal (along the b and c-axis), (b) powder pressed-pellet and c) thin layer with Cu|PCdI|Au configuration. The complex permittivity as a function of temperature was measured in the frequency range between 10 kHz and 2 MHz. In the vicinity of the PT, the dielectric anomaly as a peak was observed for each type of samples, but the greatest change was observed for the crystal along the polar direction (the c-axis). It should be noted that the characteristic anomalies observed in the temperature dependencies of ε′ or ε′′ result from the strong piezoelectric resonance contributions to the electric permittivity. This dielectric behaviour suggests that the low temperature phase II and high temperature (I) are non-centrosymmetric (see Fig. 7b and c).Measurements of pyroelectric current were made on an oriented single crystal along the polar c-axis. The first measurement was made upon heating and cooling runs on a sample not polarised by the external electric field (Fig. 8a). In the vicinity of the PT, we see the pyroelectric current anomaly whose peak maximum occurs in phase I in both cycles. The reversibility of the anomaly indicates the switching of the polarisation sign. The lack of a paraelectric phase somewhat complicates the pyroelectric current measurement.
According to the procedure for crystal with ferroelectric-paraelectric phase transition, an external field must be applied to the sample in the paraelectric phase. Then the field-polarised sample should pass to the ferroelectric phase, where, after a short-circuited of the sample, the change of current amplitude from polar to non-polar phase is measured. We decided to polarise the sample in the lower temperature phase (II). We encountered a similar problem in the case of (diisopropylammonium)2[CdBr4] crystal,47 where the crystal also underwent an isostructural transition from the ferroelectric to the ferroelectric phase around 244 K. First, we applied an external electric field (±1.32 kV cm−1) at 180 K (phase II), then heated the sample to phase I.
After half an hour of short-circuited, the pyroelectric current was measured on the cooling run. Unfortunately, the application of the field greater than ±1.32 kV cm−1 destroys the crystal, which also affected the hysteresis loop measurements. The results of the pyroelectric current measurements are presented in Fig. 8b, whereas temperature dependencies of ΔPs, calculated from the following equation:
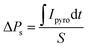 | (2) |
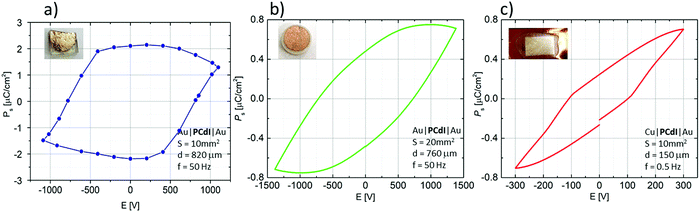
The ferroelectricity was directly confirmed by polarisation–electric field (P–E) hysteresis loop measurements at 298 K. As shown in Fig. 9, P–E hysteresis loops were measured for three different sample forms. Fig. 9a presents the results recorded for crystallographically oriented crystal along the c-axis. The second (Fig. 9b) was recorded for the form of compressed pellets, whereas Fig. 9c present a P–E loop for the form of a thin film. In the case of bulk crystal as well as of pellets the P–E hysteresis loops in phase I of PCdI at 298 K were successfully recorded.
The data collected in Table 1 suggest that, for the reported in the literature, hybrids based on Cd–X and Mn–X metal halides, ferroelectric properties are more pronounced than for the p-electron metals. Additionally, ferroelectric properties have been studied mainly in ABX3 stoichiometry, in which 1D chains of octahedral coordinated MX6 corner-sharing units. In the present case, the anionic network formed by the unique one-dimensional chains created tetrahedral [CdI4]2− corner-sharing moieties.
| Formula | T PT [K] cool./heat. | PT Order | Symmetry change | P s [μC cm−2] | Ref. | |
|---|---|---|---|---|---|---|
| P: pyrrolidinium, 1st: first order PT, 2nd: second order PT.a Theoretical calculation.b This work. | ||||||
| (P)[CdCl3] | 198/218 240/241 | 1st | C2/c ↔ Cmc21 ↔ Cmcm | 3.6 | (210 K) | 48 |
| 2nd | ||||||
| (P)[MnCl3] | 291/295 | 2nd | Cmc21 ↔ Cmcm | 5.5 | (253 K) | 8 |
| (P)[MnBr3] | 215/219 | 2nd | Cmc21 ↔ Cmcm | 6 | (201 K) | 9 |
| (P)2[SbCl5] | 231/236 | 1st | P1121 ↔ P1n1 ↔ Pmn21 ↔ Pmnb | 0.03 | (217 K) | 49 |
| 247/248 | 1st | 0.16 | (235 K) | |||
| 252/255 | 1st | |||||
| (P)3[Sb2Cl9] | 189/197 | 1st | C2 ↔ ? ↔ P31 ↔ R3m | 4 × 10−3 | (220 K) | 45 |
| 214/216 | 1st | |||||
| 216/218 | 1st | |||||
| 241/242 | 1st | |||||
| (P)6[InBr6][InBr4]3·H2O | 227/232 | 2nd | Pna21 ↔ Pbcn | 0.14 | (221 K) | 38 |
| (P)2[Cd2I6] | 218/220 | 2nd | Cc ↔ Cc | 2.2 (5.6a) | (295 K) | |
| 4.6a | (100 K) | |||||
3.5. Elecronic structure calculations
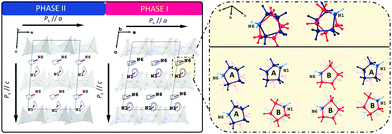
To shed some light on the possible values of the spontaneous polarization of the ferroelectric phases I and II, we performed computational simulations based on the density functional theory (DFT) approach. Electronic structure calculations are complementary to experimental techniques. However, they assume a model representing the studied phenomenon, particularly a well-defined structure of a crystal for which the computations are to be performed. The positions of atoms in the crystallographic cell determined for the disordered phase I are not directly suitable for DFT calculations.As described earlier, the crucial disordered structural motif is related to two independent pyrrolidinium cations in the unit cell swinging around the respective nitrogen atoms. The carbon atoms of each cation may adopt two competing positions with equal probability. Thus, four ordered model structures can be constructed by manual selection of the position of the carbon (and hydrogen) atoms for each of the two disordered cations (Fig. 10). The spontaneous polarisation of the disordered phase I will then be reported as an average of the polarisations obtained for the ordered models. For further details, see ESI.† The atomic coordinates of the ordered models of phase I are available in PCdI_300_AA.cif, PCdI_300_AB.cif, PCdI_300_BA.cif and PCdI_300_BB.cif files appended to ESI.† The atomic coordinates of phase II, the ordered one, were taken directly to perform DFT calculations.
The component of the calculated spontaneous polarisation of LT phase (II) along the ‘a’ crystal axis amounts to 3.22 μC cm−2 while the component along the ‘c’ crystal axis amounts to 4.63 μC cm−2. For HT phase (I), the components of the spontaneous polarisation along a and c crystal axes are 3.64 μC cm−2 and 5.59 μC cm−2, respectively. As already explained, the numbers for phase I represent the values averaged over the four ordered models of the phase. The calculated value of a spontaneous polarisation is immanently accompanied by a so-called polarisation indetermination quantum, which results from a non-periodic character of a position operator r,43,44 (see further details in ESI†).
3.6. Photoluminescence
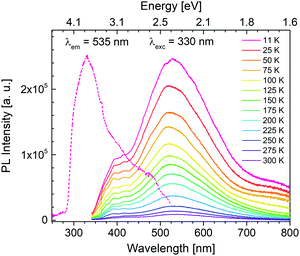
Photoluminescence experiments reveal that for solid-state PCdI only trace of visible emission is observed at room temperature, thus the PL properties were explored at 11–300 K. Photoluminescence excitation (PLE) spectrum (dashed line in Fig. 11) recorded at 11 K shows peak at 330 nm (3.76 eV). As shown in Fig. 11, the material excited with this energy exhibits broadband emission covering the whole visible region. With the increase of temperature, the luminescence disappears that at room temperature (300 K) only traces are visible, as mentioned before, revealing a significant thermal quenching in PCdI. This process is well known for other cadmium halides crystals50–52 and their hybrid compounds.53,54Generally, emission in organic–inorganic hybrid materials originates from both organic and inorganic parts. In the case PCdI emission band maximum is located at 530 nm (2.34 eV). Additional higher-energy shoulder peak is visible at about 390 nm (3.18 eV). The Gaussian deconvolution of the spectrum presented in Fig. S5 (ESI†) confirms that the total emission is a superposition of two broad constituents: at 390 nm (3.18 eV) and 510 nm (2.43 eV) with full width at half-maximum (FWHM) about 80 nm and 180 nm, respectively. Temperature dependence of PLE spectrum (Fig. S6, ESI†) reveals only broad band with intensity systematically decreasing as temperature increases. The position of excitation band remains the same up to 200 K, while above this temperature slight shift occurs towards lower energies. It is known from the results presented above that for PCdI structural phase transition as well as deformation of inorganic layers occurs at about 218–220 K. Thus, band shift in PLE spectra correlates strictly with structural changes.
To probe into the nature of broadband emission of PCdI the decay curves of 535 nm emission were recorded at 11–350 K. Fig. S7 (ESI†) presents the counts at low, high and moderate temperature. To fit the kinetics curves the three-exponential approximation was used which gives the best agreement with experimental results. The nonexponential nature of decay kinetics is most likely determined by the inhomogeneity of the emitting centers. It cannot be excluded that some of them can be formed on the surface of the solid-state, while the others are connected with some defects. The fit results are placed in Table S6 (ESI†). The average lifetime is estimated to be 490 μs at 11 K. An increase of measurement temperature up to 200 K slightly increases the lifetime keeping a value roughly in the range 500–550 μs. Further raising temperature drastically reduces the decay by an order of magnitude at 350 K. The observed variation in emission lifetimes is analogous to the trend in PLE and leads to the conclusion that it is also due to the structural changes in PCdI.
The temperature dependence of the integrated emission and full width at half-maximum (FWHM) values of the emission band are shown in Fig. S8 (ESI†) (brown and blue spheres, respectively). Both features decrease rapidly as the measurement temperature increases. FWHM value changes from 200 nm at 11 K to 180 nm at 200 K. Analogously, the integrated area of emission spectra is reduced at least by the factor of 6, which is the natural effect of the decrease in PL intensity. As evidenced by the crystal structure section, at a lower temperature (100 K), the tetrahedrally coordinated metal is more distorted than at room temperature (300 K). Therefore, the tetrahedral distortion around the metal cation in [CdCl4] influences the emission spectra resulting in further broadening at 11 K, supporting a clear correlation between local structure deformation and the FHWM values. Moreover, due to the deformation, a strong vibronic coupling between emitting centers and the lattice occurs. The results are consistent since more significant distortion induces stronger coupling and broadening of the emission. The PL measurement repeated after one month confirmed the stability of the solid-state specimen.
Summarizing, the observed PL spectra of the Cd-based hybrid iodide are similar to spectra measured for the lead halide perovskites,55–57 alkali halide crystals,58 organic molecular crystals59 and the entire family of inorganic–organic hybrid halide materials such as (C2H5NH3)2CdCl4,24,60 (CH3NH3)2CdX4 (X = Cl, Br, I),61 (2cepiH)CdCl3 (2cepi = 1-(2-chloroethyl)piperidine),53 or (N-MEDA)[PbCl4] (N-MEDA = N1-methylethane-1,2-diammonium).26 The luminescence in these exemplary compounds covers the visible region with peak position depending on the halide and temperature of measurement. In the systems mentioned above, the PLE and PL are of excitonic nature.30,31 It is generally accepted that there are two different types of PL from excitons, called as free exciton (FE) emission and as self-trapped exciton (STE) emission. The former PL is sharp and the latter one is broad. Moreover, FE emission becomes more intensive with temperature decrease since band gap becomes wider. As for PCdI with temperature decrease no formation of higher energetic narrow band is observed, this situation does not apply to the investigated material. Furthermore, since there is no critical change of the PL as a function of temperature (Fig. 11) and the structural rearrangements in the phase transitions are rather subtle we can suspect that both constituents of broad luminesce are of the same origin. Hypothetically, the broadband emission of PCdI could be ascribed to electron–phonon coupling through STE formation since excitons possess high stability at low temperature. This is in fact broadly recognized that in the organic–inorganic metal hybrids the core of broadband emission are excitons (FE and/or STE). In that case, for investigated Cd-based hybrid with increased distortions at lower temperatures (Section 3.2.) PLE band could originates from exciton associates with inorganic [CdI4] moiety,54 and PL could be a result of a self-trapped exciton (STE) emission,53,62 respectively. Especially, considering the PL lifetime of PCdI (Table S6, ESI†), which being relatively long, indicates the occurrence of spin-forbidden triplet exciton emission.28 The appearance of energy transfer from a singlet to a triplet exciton is well known for metal–halide systems.24,63 Furthermore, white emission in PCdI might also originates from other intrinsic or extrinsic trap states or defects. However, the detailed mechanism in PCdI was not undertaken at this stage.
Since PCdI is a source of white light (WL) emission, Fig. 12 pictures the corresponding Commission Internationale de l’Eclairage (CIE) chromaticity coordinates on the diagram. For clarity only points for 11 K and 300 K photoluminescence are marked because coordinates of all temperatures are very close to each other (Table S7, ESI†) and overlap. Correlated colour temperatures (CCT) are in the range of about 6400–7000 K (Table S7, ESI†) providing light that appears “cool” (bluish) according to lighting industry convention.
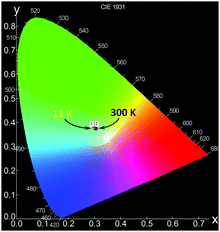 | ||
| Fig. 12 CIE 1931 chromaticity diagram of the emission of PCdI recorded at 11 K (point 1) and 300 K (point 2). | ||
3.7. Nonlinear optical properties
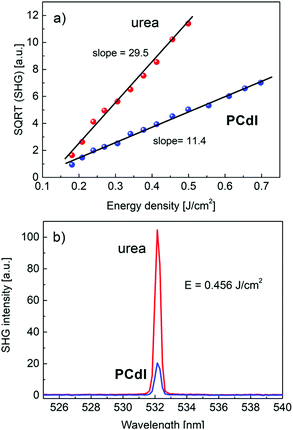
All noncentrosymmetric crystals can exhibit the second-order nonlinear optical properties as nonlinear susceptibility tensor χ(2)ijk contains some nonzero coefficients. The easiest method of evaluating material second-order NLO properties is the measurement of the degenerate process of second harmonic generation of light that could be performed both for single crystals and powdered crystalline material. For the investigated PCdI compound in the powder form, we have performed SHG intensity measurements in the function of incident laser (10 ns pulse) energies in the range of 20 to 400 mJ. Measurements were done at T = 293 K. As expected, the SHG signal generated by 1064 nm excitation wavelength appeared from PCdI at 532 nm wavelength. The dependence of SHG intensity on excitation intensity shows parabolic dependence, in which the tensor coefficients χ(2)ijk are in the power of two, therefore to precisely calculate the values of tensor elements, the square root of SHG intensity is taken. In Fig. 13a, the square root of SHG signal from PCdIvs. input pulse energy density is plotted, showing linear dependence characterized by the slope 11.40.In the same plot, we present SHG measurements results in the reference powder of urea that exhibits a stronger response at identical measurement conditions characterized by the slope equal 29.5. The ratio of the two slopes is proportional to the ratio of NLO average tensor coefficients for respective materials. Basing on known NLO coefficient of urea d14 = 1.4 pm V−1 we can calculate averaged 〈deff〉 = 0.54 pm V−1 for PCdI, which exceeds the value of main nonlinear coefficient d36 = 0.46 pm V−1 of the well-known KDP crystal. The calculated NLO coefficient for PCdI is loaded with ±10% error. The relation between NLO coefficients dil and χ(2)ijk is following: dijk = 1/2χ(2)ijk, where shortened notation for dil was used. In Fig. 13b we directly compared the SHG signal of the investigated PCdI powder with that of urea, both excited with the energy density of 0.456 J cm−2. The second harmonic signal appears exactly at λ = 532.14 nm and no near resonance effects (e.g. SHG induced luminescence) or spurious light were noticed in the spectra (cf.Fig. 13b). Linewidth (FWHM) of the SHG signal for the studied compound amounts to 0.42 nm as follows from fitting the SHG signal with Lorentz line-shape. The high value of the nonlinear optical coefficient for PCdI holds a promise that, if the bulk crystals of PCdI could be grown, this material can be considered as an important one in the field of electrooptic and second-order NLO active materials.
The optical damage threshold for PCdI (cf.Fig. 14) measured in 10 ns pulse regime is moderate and amounts ∼1.0 J cm−2, which is equivalent to power density ∼100 MW cm−2. The damage threshold was determined by observing the departure of SHG intensity from the parabolic behavior and accompanying process of the powder degradation (the grey color that appeared at the beam spot area), leading to the significant and irreversible decrease of the SHG signal.
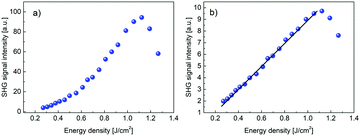 | ||
| Fig. 14 (a) Second harmonic signal in PCdI powder measured in function of the IR laser pulse energy density. Above energy density of ∼1.0 J cm−2 there is the onset of the process of powder optical damage. (b) Square root of the dependence shown in Fig. 14(a) clearly shows linear behavior up to the optical damage threshold. | ||
3.8. 1H NMR studies
Fig. 15 shows the plot of spin–lattice relaxation time (T1vs. 1000/T at Larmor frequency 25 MHz. Between 90 and 230 K two temperature minima spin–lattice relaxation time, the high temperature minimum is cut off by the PT. The fit of the T1 data was done with the BPP-type equation:64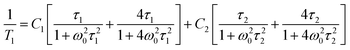 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/RT). The obtained parameters are given in Table S8 (ESI†). Above the PT at 220 K, the activation energies have been estimated to be in three temperature ranges, and it is worthy to conclude that the observed motional barrier has been near twice reduced after the PT. It may suggest that the PT is accompanied by a change in the dynamical state of cations.
exp(Ea/RT). The obtained parameters are given in Table S8 (ESI†). Above the PT at 220 K, the activation energies have been estimated to be in three temperature ranges, and it is worthy to conclude that the observed motional barrier has been near twice reduced after the PT. It may suggest that the PT is accompanied by a change in the dynamical state of cations.
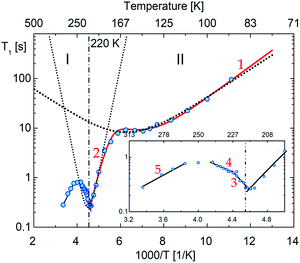 | ||
| Fig. 15 The temperature dependence of the proton spin–lattice relaxation time, T1, measured at 25 MHz. The vertical lines show the transition temperatures determined by the DSC method, numbers corresponds to the possible motional states (more information are in ESI†). | ||
The literature provides data on the dynamics of pyrrolidinium cations in organic–inorganic hybrids,45,49,65,66 where studies show that the following forms of movement of pyrrolidinium cations can be considered:
(i) A small-angle libration of the pyrrolidinium cation,
(ii) A flipping motion of the pyrrolidine ring between twisted and envelope conformations,
(iii) A pseudo-C5 reorientation of the axis perpendicular to the pyrrolidinium ring,
(iv) Isotropic/self-diffusion motion of cation
The (i) type motion is suggested to appear below 200 K, which is assigned to the lowest temperature minima with the Ea = 6.1 kJ mol−1. In turn, the higher temperature minimum is connected with the change in the conformation twisted ↔ envelope with Ea = 32 kJ mol−1.
Comparable values of Ea for these types of motion were encountered in another pyrrolidinium analogue; (C4NH10)2SbCl5,49 (C4NH10)3Sb2Cl9.45 In turn, the (iii)-type of motion takes place over phase I. It is in accord with the T1 and M2 of 1H NMR measurements for (C4NH10)SbCl6,65 for which M2 > 4–5 G2 in its partially ordered phases. It was interpreted as a large-angle libration/pseudo-C5 reorientation of the pyrrolidinium cations. It means that we deal with an analogue dynamical state of cations in PCdI in phase I.
The temperature dependence of the second moment (M2) of the 1H NMR line for PCdI is presented in Fig. S9 (ESI†). The M2 is changing continuously with the temperature between 100 and 290 K. From 230 up to 290 K, the M2 value stabilizes at about 8.4 G2. It indicates that the isotropic motion of the pyrrolidinium cation is not admitted even close to RT.
4. Conclusions
In summary, we designed and synthesized a novel organic–inorganic ferroelectric based on the pyrrolidinium cation (C4H10N)2[Cd2I6] (PCdI). The material exhibits the ferroelectric nature in a broad range of temperatures (from 100 K to the melting point at 398 K) and undergoes one phase transition at 220 K.Variable temperature single-crystal X-ray diffraction measurements confirm acentric layered structure phase I and II. Additionally, the structural analysis presents the unique architecture of the anionic subnetwork in the form of one-dimensional [{CdI3}−]nzig-zag chains. The electric and dielectric properties were studied for samples in crystals and thin-film layers. In both phase I and II, the ferroelectric ordering was confirmed by the polarization reversal process observed via the pyroelectric effect and hysteresis loop measurements (2.2 μC cm−2). DFT calculations were performed to compare the theoretical polarization values for both ferroelectric phases of PCdI. Calculations show that pyrrolidinium cations orientation may contribute to the observed polarization values. 1H NMR measurements confirm the change in the dynamics of organic cations in the phase transition. The high value of the nonlinear optical coefficient for PCdI holds the promise that this material can be considered as a prospective candidate in the field of electrooptic and second-order NLO active materials. Moreover, PCdI exhibits broadband white photoluminescence that is thermally quenched.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research project supported by program “Excellence initiative – research university” for years 2020–2026 for University of Wrocław (BPIDUB.4610.24.2021.KP.B) Author (A. B.) would like to acknowledge Wrocław Center for Networking and Supercomputing (WCSS) for a grant of computer time.References
- H. Park, C. Ha and J. H. Lee, J. Mater. Chem. A, 2020, 8, 24353–24367 RSC.
- S. F. Hoefler, G. Trimmel and T. Rath, Monatshefte fur Chemie, 2017, 148, 795–826 CrossRef CAS PubMed.
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–648 CrossRef CAS PubMed.
- G. Xing, N. Mathews, S. S. Lim, Y. M. Lam, S. Mhaisalkar and T. C. Sum, Science, 2013, 6960, 498–500 Search PubMed.
- J. Burschka, N. Pellet, S. J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316–319 CrossRef CAS PubMed.
- L. Dou, Y. M. Yang, J. You, Z. Hong, W. H. Chang, G. Li and Y. Yang, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- S. A. Veldhuis, P. P. Boix, N. Yantara, M. Li, T. C. Sum, N. Mathews and S. G. Mhaisalkar, Adv. Mater., 2016, 28, 6804–6834 CrossRef CAS PubMed.
- Y. Zhang, W. Q. Liao, D. W. Fu, H. Y. Ye, Z. N. Chen and R. G. Xiong, J. Am. Chem. Soc., 2015, 137, 4928–4931 CrossRef CAS PubMed.
- Y. Zhang, W. Q. Liao, D. W. Fu, H. Y. Ye, C. M. Liu, Z. N. Chen and R. G. Xiong, Adv. Mater., 2015, 27, 3942–3946 CrossRef CAS PubMed.
- Z.-K. Tan, R. S. Moghaddam, M. L. Lai, P. Docampo, R. Higler, F. Deschler, M. Price, A. Sadhanala, L. M. Pazos, D. Credgington, F. Hanusch, T. Bein, H. J. Snaith and R. H. Friend, Nat. Nanotechnol., 2014, 9, 687–692 CrossRef CAS PubMed.
- X. Zhao, J. D. A. Ng, R. H. Friend and Z. K. Tan, ACS Photonics, 2018, 5, 3866–3875 CrossRef CAS.
- X. Lin, D. Cui, X. Luo, C. Zhang, Q. Han, Y. Wang and L. Han, Energy Environ. Sci., 2020, 13, 3823–3847 RSC.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596 CrossRef CAS PubMed.
- D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 1–12 RSC.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- W. Q. Liao, Y. Zhang, C. L. Hu, J. G. Mao, H. Y. Ye, P. F. Li, S. D. Huang and R. G. Xiong, Nat. Commun., 2015, 6, 1–7 RSC.
- H. Y. Ye, W. Q. Liao, C. L. Hu, Y. Zhang, Y. M. You, J. G. Mao, P. F. Li and R. G. Xiong, Adv. Mater., 2016, 28, 2579–2586 CrossRef CAS PubMed.
- C. K. Yang, W. N. Chen, Y. T. Ding, J. Wang, Y. Rao, W. Q. Liao, Y. Y. Tang, P. F. Li, Z. X. Wang and R. G. Xiong, Adv. Mater., 2019, 31, 1–7 Search PubMed.
- J. X. Gao, W. Y. Zhang, Z. G. Wu, Y. X. Zheng and D. W. Fu, J. Am. Chem. Soc., 2020, 142, 4756–4761 CrossRef CAS PubMed.
- Y. M. You, W. Q. Liao, D. Zhao, H. Y. Ye, Y. Zhang, Q. Zhou, X. Niu, J. Wang, P. F. Li, D. W. Fu, Z. Wang, S. Gao, K. Yang, J. M. Liu, J. Li, Y. Yan and R. G. Xiong, Science, 2017, 357, 306–309 CrossRef CAS PubMed.
- W. Q. Liao, D. Zhao, Y. Y. Tang, Y. Zhang, P. F. Li, P. P. Shi, X. G. Chen, Y. M. You and R. G. Xiong, Science, 2019, 363, 1206–1210 CrossRef CAS PubMed.
- G. Zhou, B. Su, J. Huang, Q. Zhang and Z. Xia, Mater. Sci. Eng., R, 2020, 141, 100548 CrossRef.
- M. Li and Z. Xia, Chem. Soc. Rev., 2021, 50, 2626–2662 RSC.
- C. Sun, W. L. He, M. J. Liu, W. J. Pan, L. F. Dong, G. Chen, G. D. Liu and X. W. Lei, Chem. – Asian J., 2020, 15, 3050–3058 CrossRef CAS PubMed.
- E. R. Dohner, E. T. Hoke and H. I. Karunadasa, J. Am. Chem. Soc., 2014, 136, 1718–1721 CrossRef CAS PubMed.
- E. R. Dohner, A. Jaffe, L. R. Bradshaw and H. I. Karunadasa, J. Am. Chem. Soc., 2014, 136, 13154–13157 CrossRef CAS PubMed.
- S. Liu, X. Fang, B. Lu and D. Yan, Nat. Commun., 2020, 11, 1–9 Search PubMed.
- S. Wang, L. Li, Z. Sun, C. Ji, S. Liu, Z. Wu, S. Zhao, A. Zeb, M. Hong and J. Luo, J. Mater. Chem. C, 2017, 5, 4731–4735 RSC.
- R. T. Williams and K. S. Song, J. Phys. Chem. Solids, 1990, 51, 679–716 CrossRef CAS.
- D. Cortecchia, J. Yin, A. Petrozza and C. Soci, J. Mater. Chem. C, 2019, 7, 4956–4969 RSC.
- CrysAlis RED, CrysAlis CCD, Oxford Diffraction, Oxford Diffraction Ltd, Abingdon, England, 2008 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8 CrossRef PubMed.
- C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 8861–8869 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- X. Gonze, J. M. Beuken, R. Caracas, F. Detraux, M. Fuchs, G. M. Rignanese, L. Sindic, M. Verstraete, G. Zerah, F. Jollet, M. Torrent, A. Roy, M. Mikami, P. Ghosez, J. Y. Raty and D. C. Allan, Comput. Mater. Sci., 2002, 25, 478–492 CrossRef.
- X. Gonze, F. Jollet, F. Abreu Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J. M. Beuken, J. Bieder, A. Bokhanchuk, E. Bousquet, F. Bruneval, D. Caliste, M. Cote, F. Dahm, F. Da Pieve, M. Delaveau, M. Di Gennaro, B. Dorado, C. Espejo, G. Geneste, L. Genovese, A. Gerossier, M. Giantomassi, Y. Gillet, D. R. Hamann, L. He, G. Jomard, J. Laflamme Janssen, S. Le Roux, A. Levitt, A. Lherbier, F. Liu, I. Lukačević, A. Martin, C. Martins, M. J. T. Oliveira, S. Ponce, Y. Pouillon, T. Rangel, G. M. Rignanese, A. H. Romero, B. Rousseau, O. Rubel, A. A. Shukri, M. Stankovski, M. Torrent, M. J. Van Setten, B. Van Troeye, M. J. Verstraete, D. Waroquiers, J. Wiktor, B. Xu, A. Zhou and J. W. Zwanziger, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- D. Vanderbilt and R. D. King-Smith, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4442–4455 CrossRef CAS PubMed.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651–1654 CrossRef CAS PubMed.
- M. Wojciechowska, A. Gągor, A. Piecha-Bisiorek, R. Jakubas, A. Ciżman, J. K. Zaręba, M. Nyk, P. Zieliński, W. Medycki and A. Bil, Chem. Mater., 2018, 30, 4597–4608 CrossRef CAS.
- L. Dobrzycki and K. Woźniak, J. Mol. Struct., 2009, 921, 18–33 CrossRef CAS.
- M. Rok, P. Starynowicz, A. Ciżman, J. K. Zaręba, A. Piecha-Bisiorek, G. Bator and R. Jakubas, Inorg. Chem., 2020, 59, 11986–11994 CrossRef CAS PubMed.
- W. J. Xu, C. T. He, C. M. Ji, S. L. Chen, R. K. Huang, R. B. Lin, W. Xue, J. H. Luo, W. X. Zhang and X. M. Chen, Adv. Mater., 2016, 28, 5886–5890 CrossRef CAS PubMed.
- M. Ksiądzyna, A. Gągor, A. Piecha-Bisiorek, A. Ciżman, W. Medycki and R. Jakubas, J. Mater. Chem. C, 2019, 7, 10360–10370 RSC.
- H. Matsumoto and H. Nakagawa, J. Lumin., 1979, 18–19, 19–22 CrossRef CAS.
- S. Kawabata, M. Kitaura and H. Nakagawa, Phys. Status Solidi C, 2005, 2, 53–56 CrossRef CAS.
- S. Kawabata and H. Nakagawa, J. Lumin., 2007, 126, 48–52 CrossRef CAS.
- Z. Qi, Y. Chen, Y. Guo, X. Yang, F. Q. Zhang, G. Zhou and X. M. Zhang, J. Mater. Chem. C, 2021, 9, 88–94 RSC.
- A. Yangui, S. Pillet, E. E. Bendeif, A. Lusson, S. Triki, Y. Abid and K. Boukheddaden, ACS Photonics, 2018, 5, 1599–1611 CrossRef CAS.
- N. Kitazawa, M. Aono and Y. Watanabe, Mater. Chem. Phys., 2012, 134, 875–880 CrossRef CAS.
- N. Kitazawa, T. Ito, D. Sakasegawa and Y. Watanabe, Thin Solid Films, 2006, 500, 133–137 CrossRef CAS.
- G. Zhou, B. Su, J. Huang, Q. Zhang and Z. Xia, Mater. Sci. Eng., R, 2020, 141, 100548 CrossRef.
- T. G. Castner and W. Känzig, J. Phys. Chem. Solids, 1957, 3, 178–195 CrossRef CAS.
- A. Matsui, K. Mizuno, N. Tamai and I. Yamazaki, Chem. Phys., 1987, 113, 111–117 CrossRef CAS.
- A. Ohnishi, T. Yamada, T. Yoshinari, I. Akimoto, K. Kanno and T. Kamikawa, J. Electron Spectrosc. Relat. Phenom., 1996, 79, 163–166 CrossRef CAS.
- R. Roccanova, W. Ming, V. R. Whiteside, M. A. McGuire, I. R. Sellers, M. H. Du and B. Saparov, Inorg. Chem., 2017, 56, 13878–13888 CrossRef CAS PubMed.
- M. S. Lassoued, M. S. M. Abdelbaky, A. Lassoued, A. Gadri, S. Ammar, A. Ben Salah and S. García-Granda, J. Mol. Struct., 2017, 1141, 390–399 CrossRef CAS.
- B. T. Luppi, D. Majak, M. Gupta, E. Rivard and K. Shankar, J. Mater. Chem. A, 2019, 7, 2445–2463 RSC.
- N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712 CrossRef CAS.
- R. Jakubas, B. Bednarska-Bolek, J. Zaleski, W. Medycki, K. Hołderna-Natkaniec, P. Zieliński and M. Gałązka, Solid State Sci., 2005, 7, 381–390 CrossRef CAS.
- H. Ishida, Y. Furukawa, S. Sato and S. Kashino, J. Mol. Struct., 2000, 524, 95–103 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: TGA-DTA results, crystallographic data, hydrogen bonding interaction data, calculation of spontaneous polarisation Ps, 1H NMR and photoluminescence details. CCDC 2070978 and 2070979. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1tc01526e |
| This journal is © The Royal Society of Chemistry 2021 |