Exploring the nature of the fergusonite–scheelite phase transition and ionic conductivity enhancement by Mo⁶⁺ doping in LaNbO₄

Abstract

A number of metal oxides that crystallise in the scheelite structure type are known to be excellent oxide ion conductors. Here we report the synthesis of a series of materials with general formula LaNb_1−xMo_xO_4+0.5x (x = 0, 0.08, 0.12, 0.16, 0.20) and excellent oxide-ionic conductivity for x ≥ 0.16 (7.0 × 10⁻³ S cm⁻¹ at 800 °C). Bond valence energy landscape analysis showing possible facile oxide ion migration pathways give important insights into the local influence of defects on oxide-ionic conductivity in these phases. We also use variable-temperature powder X-ray diffraction data to present, for the first time for any scheelite-type material, a symmetry distortion mode refinement-based analysis of the phase transition between the scheelite and fergusonite structure types. This structural phase transition is known to have implications for both oxide-ionic conductive and ferroelastic properties. We demonstrate that one particular distortion mode, namely the Γ₂⁺ displacive mode of the Nb atoms, is the most significant structural distortion leading to the symmetry-breaking phase transition from the tetragonal scheelite to the monoclinic fergusonite form of the material. Our diffraction data and ab initio lattice dynamics calculations provide evidence that the fergusonite–scheelite transition in these materials exhibits characteristics of a first-order transition.

---

Introduction

The replacement of carbon-emitting energy sources with cleaner alternatives on a massive scale is regarded as a critical research priority in order to limit the detrimental environmental effects of rising atmospheric CO₂ levels. Solid oxide fuel cells (SOFCs) offer a technological alternative to petroleum combustion engines for small vehicle and stationary electricity generation by facilitating safe electrochemical oxidation of hydrogen-rich fuels in an all-solid-state environment. However, commercialisation of these devices has so far been hindered by a lack of solid cathode and electrolyte materials that conduct oxide ions efficiently at economically viable “moderate” operating temperatures (400–650 °C).¹ In particular, development of electronically-insulating solid electrolytes with competitive ionic conductivity (typically ≥10⁻² S cm⁻¹) and acceptable electrode compatibility at these temperatures presents an ongoing challenge.

Several promising oxide-ionic conducting (OIC) materials have been identified among the family of ABO₄ oxides known as scheelites, including (Ca,AM)WO_4−δ (AM = alkali metal),^2,3 (Ca,La)MoO_4+δ,⁴ (Pb,RE)WO_4+δ (RE = rare earth element)^5,6 and La(Nb,W)O_4+δ.⁷ Of these, the PbWO₄-derived materials have achieved the highest OIC performance (4 × 10⁻² S cm⁻¹ for Pb_0.8La_0.2WO_4.1 at 800 °C),⁶ though their commercialisation is undesirable due to the toxic and environmental concerns associated with Pb-containing compounds.

The scheelite structure can be described as a derivative of the cubic fluorite structure, with rock-salt-type alternation of two cations of different size giving rise to a tetragonal network of edge-sharing AO₈ and corner-sharing BO₄ units. At room temperature, many scheelite-type phases adopt a monoclinic ferroelastic structural form known as fergusonite, which converts to the paraelastic scheelite phase upon heating.^8–10 The symmetry relationship between the fergusonite (I2/a) and scheelite (I4₁/a) structures and the apparently continuous evolution of lattice parameters through the transition point have led most authors to consider the phase transition as being of second order.^8–12 Differential scanning calorimetry (DSC) measurements of (Y,Dy,La)NbO₄ (ref. 10) and studies of mode softening in the calculated phonon spectra of YTaO₄ (ref. 11), as well as Raman spectroscopy experiments on pressure-induced scheelite–fergusonite transitions in YVO₄ (ref. 13) and CaMoO₄ (ref. 14), also support this view. However, a few authors have argued that the transition is in fact first-order with “quasi-continuous” character,^15,16 citing fleeting phase coexistence observed near the phase transition in several studies of undoped and Ca-doped LaNbO₄.^10,12,15,17 Structural considerations, such as two very long (∼2.5 Å) Nb–O bonds in the fergusonite phase that increase to effectively non-bonding distance (∼3.1 Å) in the scheelite phase, have also been used to argue that the formation of the fergusonite phase is driven by optimisation of the Nb bonding environment,⁸ and that the transition is reconstructive.¹⁵

The fergusonite–scheelite phase transition is relevant to ionic conductivity in scheelite-based OIC materials because the conductivity of the two phases is predicted to differ, though discrepancies exist in the literature concerning which phase is more desirable. Packer et al.¹⁸ believed the tetragonal phase to be preferable for ionic conductivity, and Bi et al.¹⁹ reported that tetragonal (Ca,La)NbO_4–δ exhibited lower activation energy for ionic diffusion than its monoclinic counterpart. However, oxygen tracer diffusion measurements showed a discontinuous decrease in the diffusion coefficient in CeNbO_4+δ above the transition to scheelite near 850 °C.²⁰ The common strategy of chemically doping scheelite-based OIC phases to enhance their conductivity often alters the temperature of the scheelite–fergusonite phase transition, which may further complicate understanding of the role of the dopant in influencing conductive performance.

One such doped system, LaNb_1−xW_xO_4+δ (LNWO), has attracted recent interest due to its combination of low-toxicity elements, good redox stability and compatibility with candidate electrode materials such as NiO/YSZ (yttria-stabilised zirconia) and (La,Sr)MnO₃.^21,22 The substitution of 8–16% W⁶⁺ for Nb⁵⁺ improves the total conductivity of LaNbO₄ by two orders of magnitude (to ∼10⁻³ S cm⁻¹ at 800 °C) and also suppresses the significant proton conductivity observed in undoped LaNbO₄ in humid atmospheres.^7,21 The fergusonite–scheelite transition temperature is decreased by W⁶⁺ doping, with the x = 0.16 sample appearing almost tetragonal at room temperature.²³ The presence of interstitial oxide ions in LNWO also leads to modulated ordering schemes^24,25 similar to those observed in Ce⁴⁺-doped CeNbO_4+δ.²⁶

Oxide ion mobility is facilitated in LNWO via an interstitialcy mechanism that probably incorporates both interstitial–framework and interstitial–interstitial jumps.^25,27 However, the simulations of Toyoura et al.²⁷ predict a detrimental oxide-ion trapping effect in the vicinity of the W⁶⁺ dopant ions. It was suggested by those authors that doping instead with Mo⁶⁺ might mitigate this effect and further enhance the oxide-ionic transport properties. The synthesis of LaNb_1−xMo_xO_4+δ (LNMO) phases with 0 ≤ x ≤ 0.2 was reported by Cao et al.,²⁸ who found that 20% Mo⁶⁺ doping yielded total conductivity of ∼2.6 × 10⁻² S cm⁻¹ in air at 900 °C – three orders of magnitude higher than undoped LaNbO₄. Electrochemical measurements performed under different atmospheres confirmed that the observed conductivity of LaNb_0.8Mo_0.2O_4.1 in air is dominated by the ionic component (ion transport number t_ion > 0.95). LNMO therefore represents a highly promising system with superior performance characteristics for SOFC electrolyte applications in comparison to LaNbO₄ and LNWO.

Promising conductivity and stable chemical characteristics in air make the LNMO series attractive for further investigation. We present here the results of our detailed variable-temperature structural studies, which are supported by ab initio lattice dynamics calculations to shed light on the nature of the fergusonite–scheelite phase transition, along with new insights into the conductivity-enhancing mechanism of Mo⁶⁺ doping in LaNbO₄ obtained from bond valence energy landscape calculations.

Experimental

Synthetic methods

Polycrystalline samples of LaNb_1−xMo_xO_4+0.5x (x = 0, 0.08, 0.12, 0.16, 0.20, hereafter denoted LNMO00, LNMO08, …, LNMO20) of approximately 2 g each were prepared by solid-state synthesis. Commercially available La₂O₃ (Acros Organics, 99.9%), Nb₂O₅ (Sigma Aldrich, 99.99%) and MoO₃ (Aldrich, 99.97%) were dried overnight (MoO₃ at 400 °C; others at 1000 °C) before being weighed out in appropriate stoichiometric ratios and ground together by hand using an agate mortar and pestle. The powder mixtures were annealed at 1000 °C for 36 h, reground, and annealed again at 1400 °C for a further 36 h. Final regrinding of the resulting dense, fused polycrystalline compacts yielded a series of pale yellow powders.

X-ray diffraction

Room-temperature powder X-ray diffraction (XRD) data were obtained using a Bruker D8 Advance diffractometer operating in reflection mode in Bragg–Brentano geometry with a Cu Kα radiation source and Lynxeye Si strip position-sensitive detector. Samples were mounted on a single-crystal Si wafer sample holder and rotated throughout the measurement to ensure good particle averaging. Data were typically collected in the range 10° ≤ 2θ ≤ 70° using a step size of 0.02° and a total scan time of 55 min, with additional “extended” patterns collected for distortion mode analysis of LNMO00 in the range 15° ≤ 2θ ≤ 120° using a total scan time of 4 h.

Variable-temperature XRD (VT-XRD) data were collected using a Bruker D8 diffractometer with Cu Kα radiation. Powder samples were dispersed on an amorphous silica disc sample holder with Si powder added. The sample disc was positioned on a ceramic pedestal inside a HTK1200 furnace with Kapton windows, and XRD data were collected in the range 10° ≤ 2θ ≤ 70° for each scan, with a scan time of 70 min at each temperature. Measurements were taken over the range 50–1000 °C in 50 °C steps on both heating and cooling with a nominal temperature ramp rate of 30 °C min⁻¹ between steps. A correction was applied to the sample temperature recorded at each step on the basis of a pre-determined furnace calibration curve.²⁹

Rietveld refinements were performed using the Topas Academic software program.^30,31 Initial models of the expected LaNbO₄ tetragonal and monoclinic structures were sourced from the Inorganic Crystallographic Structure Database (ICSD). In all samples, the mixed Nb/Mo site was modelled as containing only Nb due to the lack of X-ray contrast between Nb⁵⁺ and Mo⁶⁺.

For the VT-XRD data, the sequences of XRD patterns collected during each heating–cooling cycle were analysed sequentially in a batch mode utilising macro functionality available in Topas, with parameters from each converged refinement copied as initial values for the next refinement in the sequence. Lattice parameters for Si at each experimental temperature were fixed at values obtained from a quadratic thermal expansion function fitted to the data in ref. 32. Basic peak shape parameters (pseudo-Voigt U, V, W and Y, and asymmetry due to axial divergence) were refined initially against the lowest-temperature LNMO00 pattern and subsequently fixed for all other temperatures and samples. An 8-term spherical harmonic function was then used to model peak shape variations as a function of temperature and composition. The monoclinic fergusonite structure model was converted to the non-standard setting I2/b (long axis c, for comparability with the standard scheelite setting I4₁/a) and used to fit the data collected over the whole temperature range, with the lattice parameters a, b, c and γ refined without constraints. Other refined parameters included scale factors for each phase, sample height, the Nb site z coordinate, and one isotropic atomic displacement parameter for each phase.

In addition to the sequential conventional Rietveld refinements against the VT-XRD data, the data collected on LaNbO₄ (LNMO00) were also analysed using the symmetry-adapted distortion mode refinement approach.^33,34 The Si internal standard was treated as part of the structural model in the conventional way. The monoclinic structure of LaNbO₄ was described via eight freely refinable parameters, amplitudes of displacive distortion modes relative to the tetragonal scheelite-type parent structure, which were derived using ISODISTORT software.³⁵

Conductivity measurements

Samples for conductivity measurements were loaded into latex tubes and pressed at 50 MPa into cylindrical rods approximately 30 mm long and 5 mm in diameter using a hydrostatic press. The rods were sintered at 1615 °C (x = 0–0.12) or 1400 °C (x = 0.16–0.20) for 36 h and then sliced into discs using a rotary cutter with a water-cooled diamond cutting wire. Two or more discs of each sample were then sintered repeatedly at the same temperature until one disc of 0.8–1.9 mm thickness achieved a relative density in the range 90–95% (determined using electronic callipers, a high-precision electronic balance, and the theoretical density of the sample). For each measurement, the sample disc was affixed to a Probostat A-6 cell by attaching Pt wire electrodes to each circular face using a conductive Pt paste. The sample was then inserted into a cylindrical muffle furnace and heated at 10 °C min⁻¹ to 1000 °C, then held at this temperature for at least 30 min in order to cure the Pt paste. Impedance spectra were collected over the range 10⁷ to 10⁰ Hz with an AC amplitude of 2500 mV using a Solartron 1260 frequency response analyser. Spectra were recorded at 10 min intervals as the sample was cooled and heated between 1000 and 250 °C at a constant rate of 2 °C min⁻¹.

Sintered LNMO16 and LNMO20 discs not selected for impedance measurements were analysed by energy-dispersive X-ray spectroscopy (EDX) to confirm that Mo volatilisation had not significantly decreased the expected amount of Mo at the surface of the sample during the repeated sintering. These discs were sputter-coated with graphite (∼20 nm) and grounded using conductive silver paste to prevent surface charging under the electron beam. The EDX analysis was performed using a Hitachi SU70 scanning electron microscope equipped with an Oxford Instruments Aztec 3.3 microanalysis system, with an accelerating voltage of 15 kV. A Co metal standard was used to calibrate the beam intensity prior to recording EDX spectra.

Computational methods

The density functional theory (DFT) calculations were performed with the Castep electronic structure code,^36,37 which uses plane-wave pseudopotential techniques within the density functional formalism. The Perdew–Burke–Ernzerhof (PBE) functional³⁸ was used to describe the electronic exchange and correlation interactions, and Castep's accurate on-the-fly pseudopotentials³⁹ were used for the valence-core terms. The basis set (plane-wave cut-off and k-point sampling for Brillouin Zone integrations) was converged so that total energy differences were less than 1 meV per unit cell. Geometry optimisations of structures for phonon calculations were considered converged when forces were below 1 × 10⁻² eV Å⁻¹ and unit cell residual stresses were below 5 × 10⁻² GPa. Throughout each calculation, the space group was preserved by symmetrising the electron density, forces and stresses. Lattice parameters were fixed to experimental values obtained from the analysis of the VT-XRD data, or, for calculations of the scheelite structure at temperatures below the fergusonite–scheelite phase transition, extrapolated from linear fits to the experimental a and c parameters above the transition temperature.

Phonon calculations were performed using density functional perturbation theory.⁴⁰ To address the hypothesis that the phase transition in LNMO was associated with temperature-dependent phonon softening, calculations were required that accurately described the lowest frequency modes, which are the ones with the largest relative error. Careful consideration of convergence parameters is required.⁴¹ We therefore tested phonon k-point convergence up to grid dimensions of 5 × 5 × 5, finding that a 3 × 3 × 3 grid sufficed. The importance of including the Γ point as part of this grid for accurate interpolation later should be noted. Additionally, in perturbative calculations, grids containing derivatives of quantities are required; given the nature of a plane-wave (Fourier) expansion, finer grids are required to accurately represent derivatives of potential and densities. We found that a grid 2.5 times finer than that for the wavefunction was required to describe the lowest-frequency modes with a small relative error. Finally, for phonon densities of states and dispersion curves, a Fourier interpolation onto a significantly finer grid (for density of states) and path in the Brillouin zone (for dispersion) was used.

An energy envelope around the fergusonite–scheelite phase transition was found by calculating energy as the unit cell was stepped linearly from one structure to the other. Atomic coordinates and lattice parameters were stepped simultaneously as follows: If x₀ and y₀ represent the initial and final parameter values and n is the number of chosen increments on the transition path, the path was defined by

where m lies between 0 and n. At each set of fixed unit cell parameters, geometry optimisation was performed on the atomic positions with no symmetry constraints imposed on the system, allowing movement of atoms as determined by unconstrained forces.

Bond valence energy landscape (BVEL) maps with a grid spacing of 0.2 Å were calculated for O²⁻ ions in LNMO using the 3DBVSMAPPER 2.02 software program.⁴² In order to investigate the local impact of dopant and interstitial defects on BVEL pathways in Mo⁶⁺-doped LaNbO₄, 3 × 3 × 2 supercells of the tetragonal scheelite and monoclinic fergusonite structures were constructed in which two Nb⁵⁺ ions (separated from each other by > 10 Å in every direction) were replaced with Mo⁶⁺ ions. In order to conserve charge balance, one interstitial O²⁻ ion was inserted at coordinates corresponding to a stable interstitial site identified by the DFT calculations of Toyoura et al.,²⁷ resulting in the overall stoichiometry LaNb_0.972Mo_0.028O_4.014 for the simulated material. Lattice parameters for these supercells were obtained by interpolating between values refined for LNMO00 and LNMO08 against XRD data at 323 and 705 °C for the monoclinic and tetragonal structures, respectively. Prior to the calculation of BVEL maps, the constructed superstructures were geometry-optimised without symmetry constraints using Castep with free energy and ionic force convergence criteria of 2 × 10⁻⁵ eV per atom and 5 × 10⁻² eV Å⁻¹, respectively.

All structures and density maps were visualised using VESTA.⁴³

Results and discussion

Phase behaviour of the LNMO series

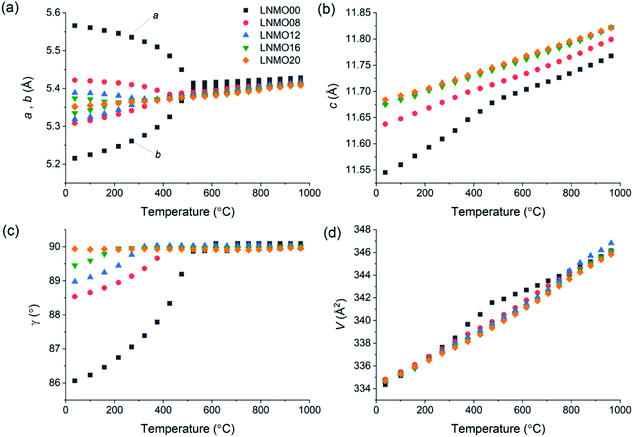
XRD data obtained at room temperature confirmed that pure LNMO fergusonite- or scheelite-type phases could be obtained up to 20% Mo substitution (ESI Fig. S1†), in agreement with the previous findings of Cao et al.²⁸ For all samples except LNMO00, several very weak reflections that could not be indexed using the expected monoclinic or tetragonal unit cells were attributed to modulated superstructures arising from the incorporation of interstitial oxide ions, by analogy to the similar peaks observed in powder XRD patterns of LNWO.²⁵ Despite the difference between the ionic radii of Nb⁵⁺ (0.48 Å) and Mo⁶⁺ (0.41 Å) in tetrahedral coordination environments,⁴⁴ almost no isothermal volumetric expansion with increasing Mo⁶⁺ content was observed in the synthesised LNMO series, suggesting that any contractive effect of including smaller Mo⁶⁺ ions is offset by the expansive effect of the charge-balancing interstitial O²⁻ ions.

Unconstrained lattice parameters obtained for all samples by refining the fergusonite structure against VT-XRD data up to 950 °C are summarised in Fig. 1. Average linear thermal expansion coefficients for the Mo⁶⁺-doped samples are in the range 10.4–15.5 × 10⁻⁶ K⁻¹, suggesting good thermomechanical compatibility with common electrode materials such as Ni-YSZ (10.3–14.1 × 10⁻⁶ K⁻¹)⁴⁵ and lanthanum strontium manganite (LSM, 11.2 × 10⁻⁶ K⁻¹)⁴⁶ (ESI Table S1†). It can be seen from Fig. 1(a and c) that the monoclinic structure of LNMO near room temperature becomes progressively less distorted with increasing Mo⁶⁺ content, with only the LNMO20 sample appearing to maintain the tetragonal structure at the lowest measured temperature (37 °C). However, the room-temperature XRD patterns in Fig. S1† show that pairs of peaks split by the monoclinic distortion appear merged in both LNMO16 and LNMO20, consistent with the findings of Cao et al.²⁸ who also used visual inspection of XRD patterns to assign the tetragonal phase to their 15% and 20% Mo-doped samples.

Fig. 1 Lattice parameters (a) a, b, (b) c, (c) γ, and (d) V obtained for LaNb_1−xMo_xO_4+0.5x (LNMO) samples by refinement of the monoclinic fergusonite structure model against VT-XRD data collected upon heating to 950 °C. Error bars are smaller than the symbols.

Careful examination of the VT-XRD patterns revealed fleeting coexistence of the scheelite and fergusonite phases near the phase transition in several samples, as evidenced by the simultaneous appearance of the intense scheelite (112) reflection and the distinct (112) and (11̄2) reflections of the fergusonite phase (Fig. 2). Although these “triple” peaks were clearly identifiable by eye, the small number of observable reflections from the minor phase were not intense or well-resolved enough in most cases to support simultaneous refinement of both phases during the sequential Rietveld analysis. Coexistence of the fergusonite and scheelite phases has been observed previously in studies of undoped and Ca-doped LaNbO₄,^10,12,15,17 and although some early authors speculatively attributed it to compositional or thermal inhomogeneity in their samples,^12,17 its repeated observation across multiple studies suggests strongly that phase coexistence is an inherent feature of the fergusonite–scheelite transition in LaNbO₄ and its derivatives.

Fig. 2 Section of XRD patterns (Cu Kα radiation) collected while cooling a LNMO00 sample through the fergusonite–scheelite phase transition. Subscripts m and t refer to the monoclinic (fergusonite) and tetragonal (scheelite) phases, respectively.

Further examination of the data collected during repeated heating and cooling cycles also revealed a hysteretic behaviour whereby diffraction patterns nominally recorded at the same temperature near the phase transition sometimes showed different phases to be present, depending on the thermal history of the sample. This was particularly true for LNMO20, for which the refined cell appeared metrically tetragonal at the beginning of the heating cycle recorded in Fig. 1 but showed a measurable monoclinic distortion below 200 °C upon cooling (ESI Fig. S2†). It appears likely that the hysteresis effect is more pronounced in LNMO20 because the high-temperature phase is more readily trapped below its thermodynamically favourable range by slow transition kinetics when the transition temperature is low. The phase coexistence and hysteresis observed in LNMO are both suggestive of an energy barrier associated the fergusonite–scheelite transition, supporting the view that the transition is of first order in this material.

Consideration of the full VT-XRD data set allowed the LNMO phase diagram in Fig. 3 to be constructed. In all cases, phases were assigned up to the highest temperature at which they were observed in any run for a given sample upon either heating or cooling. The temperature of the fergusonite–scheelite phase transition, interpreted as occurring when the refined unit cell becomes metrically tetragonal (a = b and γ = 90°), is observed to decrease with increasing Mo⁶⁺ content. The loss of the structure modulation at high temperatures was determined visually by disappearance of the weak unindexed peak at 2θ ≈ 26.5°. This peak was especially weak in the LNMO20 phase, leading to some difficulty in determining the precise temperature of its disappearance. By comparison to the similar phase diagram published previously for LNWO,²⁴ the fergusonite–scheelite transition occurs in LNMO at lower temperatures for equivalent dopant concentrations, while the modulated tetragonal phase persists to higher temperatures in LNMO and is also observed at all measured doping levels, compared to only ≥12% W⁶⁺ in LNWO.

Fig. 3 Phase diagram of LNMO derived from VT-XRD data.

Phase transition in LaNbO₄: symmetry distortion mode analysis

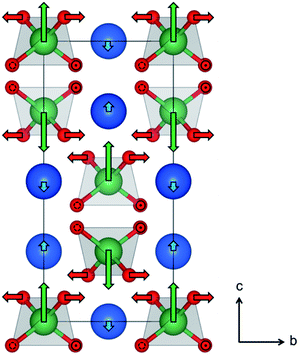
The atomic displacements associated with the structural phase transition in LaNbO₄ were described using symmetry-adapted distortion modes belonging to the irreducible representations of the parent-symmetry group, in this case the tetragonal scheelite structure space group I4₁/a. For brevity, these will be referred to as “distortion modes”. The amplitude of each mode quantifies a structural distortion which may break the symmetry of the parent structure in a particular way; the amplitudes of the symmetry-breaking modes are therefore by definition equal to zero in the parent phase. The use of distortion mode refinements against diffraction data to describe symmetry-reducing phase transitions, both first and second order, has been demonstrated in both extended and molecular systems.^47–50 Here it is used for the first time to analyse and describe the phase transition between the fergusonite and scheelite structures.

Refining eight distortion modes allowed in the monoclinic LaNbO₄ structure against the laboratory XRD pattern collected at room temperature gave an excellent fit with R_wp = 3.66% and R_Bragg = 2.80% (ESI Fig. S3†). The mode amplitudes obtained (ESI Fig. S4†) suggest that one of them, namely the a2 Γ₂⁺ displacive mode of the Nb atoms, is the most significant structural distortion leading to the symmetry-breaking phase transition from the tetragonal scheelite to the monoclinic fergusonite form of LaNbO₄. This is supported by the results of the Rietveld fit in which only this mode amplitude is refined and the remaining seven are fixed to zero, which gives only a small increase in the agreement indices (R_wp = 4.20% and R_Bragg = 3.28%, ESI Fig. S5†). The second- and third-most significant distortion modes are displacements of La and O atoms (Γ₂⁺ modes labelled a1 and a7, with amplitudes of ∼25% and 50% that of a2, respectively). The atomic displacements that these modes represent are illustrated in Fig. 4.

Fig. 4 Representation of atomic displacements associated with the distortion modes denoted a1, a2 and a7, which pertain to the La (blue), Nb (green) and O (red) atomic sites, respectively. The relative lengths of the arrows indicate the relative magnitudes of the displacements in the b–c plane. Dashed circles and solid dot-centred circles represent displacements away from and towards the viewer, respectively, perpendicular to the plane of the image.

The Γ₂⁺ modes labelled a1 and a2 move the La and Nb atoms, respectively, along the scheelite c axis in such a way that the two types cations in the same layer in the structure (i.e. with the same z fractional coordinate) move in opposite directions, and in opposite directions to their counterparts in the layers above and below. This is represented by the blue and green arrows in Fig. 4. The Γ₂⁺ mode labelled a7 causes in-plane displacements of the O atoms bonded to Nb (red arrows in Fig. 4), which result in a twisting of the NbO₄ tetrahedra about the scheelite c axis. The main overall effect of these atomic displacements is the off-centring and partial flattening of the NbO₄ tetrahedra. The bond lengths obtained from the distortion mode refinements against the room temperature XRD data suggest that Nb is best described as having a (4 + 2) coordination number, with three pairs of Nb–O bonds at 1.871(7), 1.924(8) and 2.662(7) Å.

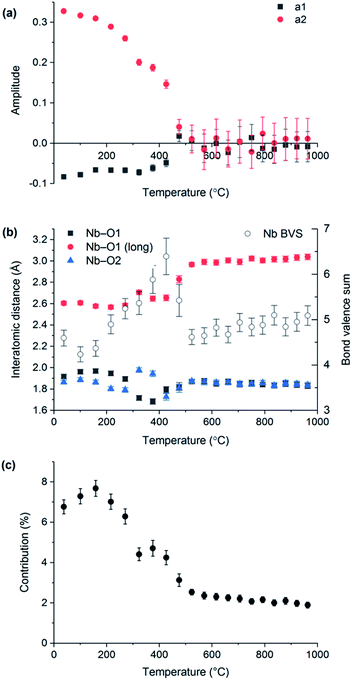
VT-XRD data collected on LaNbO₄ were also analysed using the distortion mode refinement approach. In these refinements, the amplitudes of the three Γ₂⁺ modes representing displacements of the oxygen atoms were set to zero at temperatures above the phase transition (as they must be by definition), since the laboratory XRD data are not very sensitive to them, while the remaining five modes were freely refined. The unit cell parameters obtained agree closely with those from the conventional refinements, shown in Fig. 1. Freely refined Γ₂⁺ distortion mode amplitudes representing the displacements of the Nb and La atoms in the monoclinic fergusonite structure relative to their positions in the high-symmetry tetragonal scheelite structure are shown in Fig. 5(a). Both decrease in magnitude with increasing temperature and reach zero at the phase transition temperature, as expected.

Fig. 5 (a) Refined distortion mode amplitudes of the GM2+ modes a1 (black squares) and a2 (red circles), representing the displacements of La and Nb as a function of temperature. (b) Nb–O bond lengths (filled symbols) and Nb bond valence sum (empty symbols) extracted from distortion mode refinements. (c) Contribution of the long Nb–O bond to the bond valence sum of Nb as a function of temperature.

The Nb–O bond lengths extracted from distortion mode refinements are shown in Fig. 5(b). The bond length trends illustrate the change of the Nb (4 + 2) environment in fergusonite to a four-fold coordination in the scheelite structure (with the next two O nearest neighbours at ∼3.1 Å at 1000 °C). It is worth noting that the long Nb–O distance at 531 °C determined from our distortion mode refinements against XRD data, 2.97(1) Å, is in excellent agreement with 2.971(3) Å reported by David⁸ from neutron diffraction data at 530 °C, and the trend across the observed temperature range is in agreement with that reported by Arulnesan et al. from synchrotron XRD data.¹⁵ The evolution of the longest Nb–O distance with temperature corresponds to its contribution to the Nb bond valence sum decreasing from about 7% at room temperature to only 2% after the phase transition (Fig. 5(c)). Anomalous variations above the level of noise observed for some parameters in Fig. 5(b) and (c) in the temperature region 300–450 °C are attributed to an artefact of the sequential refinement as it approaches the transition temperature, where the small magnitude of the vanishing monoclinic distortion makes reliable determination of the distortion parameters more difficult.

Phonon calculations

Feng et al.¹¹ reported a first principles study of the temperature-induced fergusonite–scheelite phase transition in YTaO₄, which is found experimentally to occur around 1400 °C. The calculated phonon dispersion curves for the monoclinic and tetragonal YTaO₄ indicated their stability in their respective reference states. Phonon calculations for tetragonal scheelite-type YTaO₄ at progressively lower temperatures (1250 °C, 850 °C) revealed imaginary frequencies indicating instability and suggesting that the phase transition is driven by softening of E_u transverse acoustic modes.¹¹ Similar calculations identified phonon mode softening associated with a pressure-induced scheelite–fergusonite transition in CaMoO₄.¹⁴ Soft B_g modes observed by Raman spectroscopy have also been used to support the description of fergusonite–scheelite transitions in BiVO₄ (ref. 51) and YVO₄ (ref. 13) as second-order.

Our phonon calculations confirmed the stability of tetragonal and monoclinic LaNbO₄ in their respective temperature stability ranges above and below ∼500 °C, respectively (Fig. 6(a) and S6†). However, the dispersion curves calculated for tetragonal LaNbO₄ at temperatures as low as 37 °C showed no imaginary frequencies to indicate instability with respect to phonon mode softening (Fig. 6(b) and S7†). This result indicates that the fergusonite–scheelite transition in LaNbO₄ is not a phonon-driven second-order transition but is more likely to be first-order, as the dynamic stability of the scheelite phase below its experimentally-realised temperature range implies that its formation at lower temperatures is inhibited by the presence of an energy barrier.⁵² Transition path energy calculations were therefore performed to probe the possible existence of this barrier. In contrast to the results of similar calculations presented for YTaO₄ by Feng et al.,¹¹ which showed the Landau free energy decreasing monotonically from the scheelite phase to the fergusonite phase, our calculations found a shallow energy maximum between the two phases corresponding to an upper bound of 0.207 eV per unit cell for the transition energy.

Fig. 6 Phonon dispersion curves calculated for scheelite-type LaNbO₄ at (a) 792 °C (in the scheelite stability range), and (b) 37 °C (in the fergusonite stability range). Line colours are assigned independently for each plot and do not necessarily represent corresponding phonon modes in different plots.

Conductivity measurements

Fig. 7 presents total conductivity data measured in air for the LNMO00, LNMO16 and LNMO20 samples. As the objective of this work was to investigate the relationships between the structure and oxide ion conductivity in LNMO materials, we focus here on the samples with high levels of Mo doping. EDX spectra confirmed that Nb : Mo ratios measured at the surfaces of LNMO16 and LNMO20 discs sintered along with the impedance samples did not deviate significantly from the nominal values (ESI Table S2†).

Fig. 7 Total conductivity of selected LNMO samples measured in air. Data collected upon heating and cooling are denoted by filled and open symbols, respectively.

Data published previously for LNMO20 showed that its total conductivity is almost purely ionic with a very small (1–8%) contribution from proton conduction under oxidising conditions, though an order of magnitude increase in total conductivity under a 5% H₂/N₂ atmosphere was attributed to the onset of significant electronic conductivity caused by reduction of Mo⁶⁺.²⁸ The conductivity profiles for our LNMO00 and LNMO20 samples are in excellent agreement with those published elsewhere.^7,28 Doping with Mo⁶⁺ increases the total conductivity of LaNbO₄ by at least 2 orders of magnitude at 600 °C and 3 orders of magnitude at 900 °C, with the conductivity of LNMO16 at 800 °C (7.0 × 10⁻³ S cm⁻¹) being five times higher than that reported²¹ for the analogous W⁶⁺-doped phase. This conductivity is lower than that of La₂Mo₂O₉, (ref. 53) Na_0.5Bi_0.5TiO₃ (ref. 54), La_1.54Sr_0.46Ga₃O_7.27 (ref. 55) and the best Bi₂O₃-based oxide ion conductors⁵⁶ and slightly lower than yttria-stabilised zirconia at the same temperature, and higher than the best performers in the brownmillerite^57,58 structural family.

A decrease of the gradient in the Arrhenius plots, indicating a significant decrease in activation energy (E_a), is observed above ∼600 °C in LNMO00 and above ∼820 °C in LNMO16 and LNMO20. Activation energies determined from linear fitting to data measured above and below these temperatures are given in Table 1. A decrease in activation energy above the fergusonite–scheelite phase transition has been reported for LaNbO₄ previously.¹⁹ Changes in total conductivity activation energies in scheelite-type phases are typically attributed to phase transitions or the onset of contributions from different charge carriers.²¹ However, both LNMO16 and LNMO20 adopt the tetragonal scheelite structure over the whole temperature range represented by the data in Fig. 7, as their corresponding structural phase transition temperatures lie below the range covered by our impedance spectroscopy measurements. One possible explanation for the change observed in LNMO can be found in Fig. 3, which shows that ∼800 °C marks the approximate temperature of the loss of modulated order in LNMO16 (as noted previously, the temperature of the same transition in LNMO20 may occur at a higher temperature than suggested by Fig. 3 due to the weakness of the superstructure reflection used to determine its presence). Although changes in activation energy upon the loss of modulated order have not been reported for LNWO, the phase diagram published by Li et al.²⁴ indicates that such changes would only be expected in LNWO12 at ∼650 °C and in LNWO16 above 850 °C, and we note that these temperatures lie at or beyond the limits of temperature ranges spanned by conductivity data presented for these samples in the literature.^21,25 Subtle changes to the local structure of LNMO, which would influence conductivity locally but cannot be determined from Bragg diffraction alone, present another possible explanation.

Table 1 Activation energies of total conductivity in LNMO samples determined in temperature ranges above and below a change in gradient near T_c. Uncertainties refer to the standard error obtained from the linear regression fit to the data

	T c (°C)	E a below Tc (eV)	E a above Tc (eV)
LNMO00	600	1.09(3)	0.85(4)
LNMO16	830	1.458(4)	0.74(2)
LNMO20	830	1.422(10)	0.77(3)

---

Conductivity mechanisms in LNMO

Bond valence energy landscape (BVEL) maps were calculated for a supercell of LaNbO₄ with a sparse concentration of Mo dopant and O²⁻ interstitial ions (∼2.8% Mo substitution; hereafter LNMO03). BVEL maps use bond valence sum (BVS) calculations to predict energy surfaces for the location of an ionic species within a lattice of other ions,⁴² such as the energy surface for positioning oxide ions within a given array of cations. Although BVS is an empirical quantity and BVEL maps must be interpreted with caution, such maps have been shown to reproduce low-energy ionic conduction pathways determined experimentally or computationally in several ionic-conductive materials.^59–62 BVEL mapping has also been used successfully to screen known database structures for oxide-ionic conductivity which was subsequently confirmed experimentally in several materials for the first time.^63,64 A BVEL map that we calculated for a geometry-optimised undoped LaNbO₄ supercell produced low-energy pathways that show good qualitative agreement with those derived from the nudged elastic band calculations of Toyoura et al.²⁷ (ESI Fig. S8†). This confirms the applicability of BVEL mapping for indicative studies of oxide ion mobility in the LNMO system.

Sections of BVEL maps calculated for the LNMO03 supercell at 705 °C are presented in Fig. 8 and 9. As found in previous studies of LaNbO₄, the low-energy O²⁻ pathways involve the lattice ions (interstitialcy mechanism), and their connectivity permits net ionic transport along all three principal crystal axes. The calculated activation energy barrier (defined as the difference between the minimum energy value in the pathway and the energy value at the saddle point enabling continuous connectivity) is 0.82 eV, in agreement with the experimentally-determined value for undoped LaNbO₄ (Table 1). However, Fig. 8 reveals an absence of low-energy pathways in the vicinity of a Mo⁶⁺ dopant cation, consistent with the higher size/charge ratio of these ions in comparison to Nb⁵⁺. “Trapping” of oxide ions near W⁶⁺ was suggested as a possible impediment to oxide ion mobility in LNWO,²⁷ and our results suggest that similar “trapping” behaviour occurs in LNMO to some extent. Conversely, the relaxation of La³⁺ and Nb⁵⁺ cations near the O²⁻ interstitial defect in the DFT-optimised structure appears to create more energetically-favourable O²⁻ pathways in this region of the structure, especially within the a–b plane (Fig. 9).

Fig. 8 Section of a BVEL map calculated for a lightly-doped supercell of scheelite-type LNMO at 705 °C, shown in the vicinity of a Mo⁶⁺ dopant ion. Atoms are depicted by blue (La), green (Nb), purple (Mo) and red (O) spheres. The yellow surface represents an isolevel corresponding to +0.90 eV above the minimum bond valence energy in the continuously-connected pathway in the BVEL map.

Fig. 9 (a) Sections of the tetragonal LNMO03 supercell viewed along the b and a axes. The inserted interstitial ion is indicated by a black circle. Relaxation of ions near the interstitial after DFT geometry optimisation of the structure can be seen relative to the undistorted positions in the layer behind. Three of the Nb⁵⁺ ions (bright green) near the defect adopt 5-coordinate configurations (bonds drawn where ≤ 2.5 Å). (b) Sections of the calculated BVEL map corresponding to the supercell sections above. The yellow surface represents an isolevel corresponding to +0.90 eV above the minimum bond valence energy in the continuously-connected pathway in the BVEL map. Dashed red lines between approximate lattice and/or interstitial O²⁻ site positions highlight some pathways that appear enhanced (thickened) in the vicinity of the interstitial defect.

Given that the interstitial concentration in synthesised samples is typically much higher than 2.8%, and that local distortions in these samples are likely to be influenced by multiple defects simultaneously, it is difficult to extrapolate the effect of interstitial doping on conduction pathways and their activation barriers under application-relevant conditions. Nevertheless, our results indicate strongly that the significant enhancement of ionic conductivity observed in LaNbO₄ upon doping with M⁶⁺ cations is attributable to the presence of interstitial anions which accompany the dopant cations, rather than to the dopant cations themselves. This anion-induced enhancement probably occurs by two mechanisms: by increasing the total number of mobile charge carriers in the material, and also by distorting the local structure to increase the energetic favourability of the conduction pathway. These two benefits offset the local inhibitory effect of the M⁶⁺ dopant cations, despite the dopant ions being twice as numerous as interstitials. We note that both Mo⁶⁺ and W⁶⁺ dopants introduce the same number of interstitial O²⁻ ions, yet the conductivity enhancement is observed to be greater in Mo⁶⁺-doped LaNbO₄; this is perhaps related to a stronger trapping effect near the W⁶⁺ dopant ions (which our BVEL analysis does not quantify) or to the greater tendency for Mo⁶⁺ to tolerate a variety of coordination geometries and low coordination numbers than W⁶⁺,⁶⁵ which has been identified as a factor contributing to the superior oxide-ionic conductivity of Mo-based analogues of other conductive oxides.⁶⁶

A further consequence of the above finding is that the enhancement of oxide-ionic conductivity in Mo⁶⁺-doped LaNbO₄ is likely to reach an upper limit when the concentration of oxide-trapping dopant cations becomes high enough to disrupt a significant proportion of conduction pathways in the material. The close similarity of the conductivity data recorded for LNMO16 and LNMO20 (Fig. 7) may indicate that such a limit is reached near these levels of Mo⁶⁺ doping.

For the monoclinic form of LNMO03 at 323 °C, BVEL maps show qualitatively similar behaviour of the conduction pathways near the dopant and oxide interstitial defects as in tetragonal LNMO03 discussed above. The calculated activation energy for ionic diffusion in the monoclinic phase is 0.90 eV, this value being higher than that determined for the high-temperature scheelite form but lower than the value obtained from the total conductivity Arrhenius plot for undoped LaNbO₄ below 500 °C (Fig. 7 and Table 1). However, the BVEL surface drawn for monoclinic LNMO03 at the +0.90 eV isolevel reveals continuously connected diffusion pathways along the b axis only (Fig. 10), in contrast to the tetragonal scheelite phase, which exhibits full three-dimensional connectivity at or very near the 0.82 eV barrier in its BVEL map. Three-dimensional connectivity in the monoclinic LNMO03 map is evident only above the +1.31 eV level, suggesting a much higher degree of anisotropy in the ionic conduction pathways of the fergusonite structure. In a polycrystalline sample with random grain orientations, the experimentally-determined activation energy might be expected to lie between the values calculated for the one-dimensional and three-dimensional diffusion barriers; this appears to be consistent with the values reported in Table 1. These findings suggest an oxide-ionic conductive advantage for the scheelite over the fergusonite structure in samples without targeted engineering of grain orientation. Importantly, if suppression of the fergusonite–scheelite phase transition to lower temperatures leads to more facile oxide-ionic conductivity, the stabilisation of the scheelite phase of LaNbO₄ by M⁶⁺ doping may represent an additional mechanism by which ionic conductivity is enhanced in this material by the inclusion of high-valence dopants.

Fig. 10 BVEL maps calculated for the fergusonite phase of LNMO03 (yellow isolevel drawn at +0.90 eV), illustrating the contrasting connectivity of low-energy pathways in the a and b directions. The colours of spheres representing atomic species are as in Fig. 8 and 9.

Conclusions

Analysis of XRD data collected while heating and cooling LNMO samples with various Mo⁶⁺ content suggests that the fergusonite–scheelite transition is of first order in these materials, as the observation of phase coexistence and hysteretic behaviour points to an energy barrier associated with the transition. Transition path energy calculations performed for undoped LaNbO₄ indicate an upper bound for this energy barrier of 0.207 eV per unit cell. The small magnitude of this barrier is consistent with the previously-described “quasi-continuous” nature of the transition in LaNbO₄,¹⁵ which is often reported as second-order due to the apparently continuous evolution of lattice parameters⁹ and the absence of a discernable peak in calorimetry measurements.¹⁰ Calculated phonon dispersion curves for LaNbO₄ also show no evidence for the mode softening that has been reported to justify the second-order description of fergusonite–scheelite phase transitions in other materials such as YVO₄¹³ and CaMoO₄.¹⁴

Symmetry distortion mode analysis of the XRD data was used successfully to describe the fergusonite–scheelite transition for the first time, yielding lattice parameter and interatomic distance trends in close agreement with conventional refinements against variable-temperature diffraction data presented here and elsewhere. The most significant distortion mode contributing to the phase transition involves displacement of Nb from the centre of the tetrahedron, accompanied by a change in coordination from 4 in the high-symmetry scheelite phase to (4 + 2) in the low-symmetry fergusonite phase. This change is further evidenced by a decrease in the contribution of the long O bonds to the calculated BVS of Nb before and after the transition.

Mo⁶⁺ doping levels of 16–20% greatly enhance the oxide-ionic conductivity of LaNbO₄, confirming an earlier report.²⁸ Comparison of BVEL maps calculated for a lightly-doped LNMO material above and below the fergusonite–scheelite phase transition indicate that the diffusion pathways for oxide ions are predominantly one-dimensional in the fergusonite phase but three-dimensional in the scheelite phase, so that the suppression of the fergusonite phase by Mo⁶⁺ doping should be advantageous for moderate-temperature ionic conductivity in the doped materials. In addition, considerable local enhancement of conductivity pathways is attributed to the presence of the charge-balancing O²⁻ interstitials that accompany the dopant ions. In addition to increasing the number of charge carriers, these interstitials introduce local distortions to the cation lattice that appear to facilitate more favourable conduction pathways for the O²⁻ ions. The competition between this effect and an inhibitory local “trapping” effect near the Mo⁶⁺ ions is expected to limit the enhancement of oxide-ionic conductivity due to this effect in LNMO above a certain doping threshold, where the more numerous Mo⁶⁺ defects would come to dominate the local behaviour of the material. Our conductivity data suggest that this limit is reached near the 16–20% Mo⁶⁺ concentration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. E. A. acknowledges the support of a Newton International Fellowship (NF170809) awarded by The Royal Society. L. L.-O. acknowledges the Department of Chemistry and Hatfield College at Durham University for a summer research bursary. We acknowledge Durham's Hamilton high-performance computing (HPC) service, and EPSRC grant EP/P022782/1 for Archer HPC time.

References

1. Z. Gao, L. V. Mogni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602–1644.
2. S. Takai, Y. Morishita, Y. Kondo, T. Yao, T. Yabutsuka and T. Esaka, J. Ceram. Soc. Jpn., 2016, 124, 819–822.
3. S. Takai, S. Shitaune, T. Sano, H. Kawaji, T. Yabutsuka, T. Esaka and T. Yao, Materials, 2018, 11, 1092.
4. J. Cheng, W. Bao, C. Han and W. Cao, J. Power Sources, 2010, 195, 1849–1853.
5. T. Esaka, Solid State Ionics, 2000, 136–137, 1–9.
6. T. Esaka, T. Mina-ai and H. Iwahara, Solid State Ionics, 1992, 57, 319–325.
7. C. Li, R. D. Bayliss and S. J. Skinner, Solid State Ionics, 2014, 262, 530–535.
8. W. I. F. David, Mater. Res. Bull., 1983, 18, 749–756.
9. L. Jian and C. M. Wayman, J. Am. Ceram. Soc., 1997, 80, 803–806.
10. P. Sarin, R. W. Hughes, D. R. Lowry, Z. D. Apostolov and W. M. Kriven, J. Am. Ceram. Soc., 2014, 97, 3307–3319.
11. J. Feng, S. Shian, B. Xiao and D. R. Clarke, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094102.
12. M. Huse, A. W. B. Skilbred, M. Karlsson, S. G. Eriksson, T. Norby, R. Haugsrud and C. S. Knee, J. Solid State Chem., 2012, 187, 27–34.
13. F. J. Manjón, P. Rodríguez-Hernández, A. Muñoz, A. H. Romero, D. Errandonea and K. Syassen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075202.
14. V. Panchal, N. Garg, H. K. Poswal, D. Errandonea, P. Rodríguez-Hernández, A. Muñoz and E. Cavalli, Phys. Rev. Mater., 2017, 1, 043605.
15. S. W. Arulnesan, P. Kayser, J. A. Kimpton and B. J. Kennedy, J. Solid State Chem., 2019, 277, 229–239.
16. Y. Kuroiwa, H. Muramoto, T. Shobu, H. Tokumichi, Y. Noda and Y. Yamada, J. Phys. Soc. Jpn., 1995, 64, 3798–3803.
17. L. Malavasi, C. Ritter and G. Chiodelli, J. Alloys Compd., 2009, 475, L42–L45.
18. R. J. Packer, E. V. Tsipis, C. N. Munnings, V. V. Kharton, S. J. Skinner and J. R. Frade, Solid State Ionics, 2006, 177, 2059–2064.
19. Z. Bi, J. Peña-Martínez, J.-H. Kim, C. A. Bridges, A. Huq, J. P. Hodges and M. P. Paranthaman, Int. J. Hydrogen Energy, 2012, 37, 12751–12759.
20. R. J. Packer and S. J. Skinner, Adv. Mater., 2010, 22, 1613–1616.
21. G. Canu, V. Buscaglia, C. Ferrara, P. Mustarelli, S. Gonçalves Patrício, A. I. Batista Rondão, C. Tealdi and F. M. B. Marques, J. Alloys Compd., 2017, 697, 392–400.
22. M. A. Laguna-Bercero, R. D. Bayliss and S. J. Skinner, Solid State Ionics, 2014, 262, 298–302.
23. C. Ferrara, A. Mancini, C. Ritter, L. Malavasi and C. Tealdi, J. Mater. Chem. A, 2015, 3, 22258–22265.
24. C. Li, S. S. Pramana, R. D. Bayliss, C. P. Grey, F. Blanc and S. J. Skinner, Chem. Mater., 2020, 32, 2292–2303.
25. C. Li, S. S. Pramana and S. J. Skinner, Dalton Trans., 2019, 48, 1633–1646.
26. J. G. Thompson, R. L. Withers and F. J. Brink, J. Solid State Chem., 1999, 143, 122–131.
27. K. Toyoura, Y. Sakakibara, T. Yokoi, A. Nakamura and K. Matsunaga, J. Mater. Chem. A, 2018, 6, 12004–12011.
28. Y. Cao, N. Duan, X. Wang, B. Chi, JianPu and L. Jian, J. Eur. Ceram. Soc., 2015, 35, 1979–1983.
29. S. Allen, PhD thesis, Durham University, 2003.
30. H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
31. A. A. Coelho, J. Evans, I. Evans, A. Kern and S. Parsons, Powder Diffr., 2011, 26, S22–S25.
32. Y. Okada and Y. Tokumaru, J. Appl. Phys., 1984, 56, 314–320.
33. B. J. Campbell, J. S. O. Evans, F. Perselli and H. T. Stokes, Acta Crystallogr., Sect. A: Found. Adv., 2008, 64, C216.
34. S. Kerman, B. J. Campbell, K. K. Satyavarapu, H. T. Stokes, F. Perselli and J. S. O. Evans, Acta Crystallogr., Sect. A: Found. Crystallogr., 2012, 68, 222–234.
35. B. J. Campbell, H. T. Stokes, D. E. Tanner and D. M. Hatch, J. Appl. Crystallogr., 2006, 39, 607–614.
36. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. für Kristallogr. - Cryst. Mater., 2005, 220, 567–570.
37. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys. Condens. Matter, 2002, 14, 2717–2744.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. K. Lejaeghere, G. Bihlmayer, T. Bjoerkman, P. Blaha, S. Bluegel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dulak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Granaes, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iusan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Kuecuekbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordstrom, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunstroem, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
40. K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114.
41. P. U. Jepsen and S. J. Clark, Chem. Phys. Lett., 2007, 442, 275–280.
42. M. Sale and M. Avdeev, J. Appl. Crystallogr., 2012, 45, 1054–1056.
43. K. Momma and F. Izuma, J. Appl. Crystallogr., 2008, 41, 653–658.
44. R. D. Shannon, Acta Crystallogr., Sect. A: Found. Crystallogr., 1976, 32, 751–767.
45. M. Mori, J. Electrochem. Soc., 1998, 145, 1374.
46. S. Srilomsak, ECS Proceedings Volumes, 1989, vol. 11, pp. 129–140.
47. B. J. Campbell, H. T. Stokes, G. L. W. Hart, J. W. Lewis, I. R. Evans and J. S. O. Evans, Acta Crystallogr., Sect. A: Found. Adv., 2017, 73, A328.
48. J. W. Lewis, J. L. Payne, I. R. Evans, H. T. Stokes, B. J. Campbell and J. S. O. Evans, J. Am. Chem. Soc., 2016, 138, 8031–8042.
49. H. Li, W. Zhang, P. S. Halasyamani, H. T. Stokes, B. J. Campbell, J. S. O. Evans and I. R. Evans, J. Am. Chem. Soc., 2018, 140, 13441–13448.
50. H. Liu, M. J. Gutmann, H. T. Stokes, B. J. Campbell, I. R. Evans and J. S. Evans, Chem. Mater., 2019, 31, 4514–4523.
51. A. Pinczuk, G. Burns and F. H. Dacol, Solid State Commun., 1977, 24, 163–165.
52. V. V. Brazhkin, Phys.-Usp., 2006, 49, 719.
53. P. Lacorre, F. Goutenoire, O. Bohnke, R. Retoux and Y. Laligant, Nature, 2000, 404, 856–858.
54. M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35.
55. X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Nat. Mater., 2008, 7, 498–504.
56. X. J. Kuang, J. L. Payne, J. D. Farrell, M. R. Johnson and I. R. Evans, Chem. Mater., 2012, 24, 2162–2167.
57. C. A. Fuller, C. Berrod, B. Frick, M. R. Johnson, S. J. Clark, J. S. O. Evans and I. R. Evans, Chem. Mater., 2019, 31, 7395–7404.
58. C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, M. Avdeev, J. S. O. Evans and I. R. Evans, Chem. Mater., 2020, 32, 4347–4357.
59. M. L. Tate, C. A. Fuller, M. Avdeev, H. E. A. Brand, G. J. McIntyre and I. Radosavljevic Evans, Dalton Trans., 2017, 46, 12494–12499.
60. W. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Nat. Commun., 2020, 11, 1224.
61. X. Yang, S. Liu, F. Lu, J. Xu and X. Kuang, J. Phys. Chem. C, 2016, 120, 6416–6426.
62. J. R. Peet, M. S. Chambers, A. Piovano, M. R. Johnson and I. R. Evans, J. Mater. Chem. A, 2018, 6, 5129–5135.
63. K. Nakamura, K. Fujii, E. Niwa and M. Yashima, J. Ceram. Soc. Jpn., 2018, 126, 292–299.
64. E. Niwa and M. Yashima, ACS Appl. Energy Mater., 2018, 1, 4009–4015.
65. D. Waroquiers, X. Gonze, G.-M. Rignanese, C. Welker-Nieuwoudt, F. Rosowski, M. Göbel, S. Schenk, P. Degelmann, R. André, R. Glaum and G. Hautier, Chem. Mater., 2017, 29, 8346–8360.
66. J. E. Auckett, M. J. Gutmann and I. R. Evans, Inorg. Chem., 2020, 59, 14245–14250.

---

Footnote

† Electronic supplementary information (ESI) available: Additional figures depicting X-ray diffraction data and refined structure parameters; calculated phonon dispersion curves; elemental analysis by EDX spectroscopy. See DOI: 10.1039/d0ta07453e

---