Multiscale simulations of polyzwitterions in aqueous bulk solutions and brush array configurations

Abstract

Zwitterionic polymers are very promising candidates for antifouling materials that exhibit high chemical stability as compared to polyethylene glycol-based systems. A number of simulation and experimental studies have emerged over recent years for the investigation of sulfobetaine-based zwitterionic polymers. Investigating the structural and thermodynamic properties of such polymers requires access to broad time and length regimes, thus necessitating the development of multiscale simulation strategies. The present article advocates a mesoscopic dissipative particle dynamics (DPD) model capable of addressing a wide range of time and length scales. The mesoscopic force field was developed hand-in-hand with atomistic simulations based on the OPLS force field through a bottom-up parameterization procedure that matches the atomistically calculated strand-length, strand-angle and pair distribution functions. The DPD model is validated against atomistic simulations conducted in this work, and against relevant atomistic simulation studies, theoretical predictions and experimental correlations from the literature. Properties examined include the conformations of SPE polymers in dilute bulk aqueous solution, the density profile and thickness of brush arrays as functions of the grafting density and chain length. In addition, we compute the potential of mean force of an approaching hydrophilic or hydrophobic foulant via umbrella sampling as a function of its position relative to the poly-zwitterion-covered surface. The aforementioned observables lead to important insights regarding the conformational tendencies of grafted polyzwitterions and their antifouling properties.

---

1. Introduction

Antifouling, i.e., preventing the accumulation of biomolecules, microorganisms, plants, algae, or even small animals on surfaces, is extremely important in applications ranging from maintaining the separation efficiency of polymeric membranes to excluding pathogens from medical devices.^1–4 Antifouling is typically accomplished by coating the surface of a structure or product with a layer that can eliminate or repel foulants (FLs). Generally, there are two classes of antifouling layers: biocidal^5,6 or non-biocidal.^7–9 Among non-biocidal layers—which are considered to be less toxic⁷—one can find materials that are antifouling because of surface structuration (such as super-slippery sharklet technology),¹⁰ or superhydrophobicity,^11,12 or high surface hydrophilicity.¹³

Among hydrophilic non-biocidal coatings, zwitterionic polymers^14–22 are considered to be one of the two major classes of antifouling materials that are accessible and relatively easy to implement, the other being hydrophilic polymers based on poly(ethylene glycol) (PEG).^23,24 Brushes of zwitterionic polymers terminally grafted to a surface have been found to be effective antifouling agents, exhibiting higher chemical stability than PEG-based layers.²³ A recent review paper highlights the development of biocompatible and bioactive materials for antifouling surfaces as an important and timely topic; it points out that significant efforts have been made for the development of these materials, but “much of the work retains an empirical flavor due to the complexity of experiments and the lack of robust theoretical models”.²³ These systems involve macromolecules of a complex chemical constitution, interfaces, electrolyte solutions, and chemical reactions. Each of these aspects is considered to be a major challenge for molecular simulation.

Promising polyzwitterionic candidates with antifouling properties are carboxybetaine methacrylate (CBMA), 2-methacryloyloxyethyl phosphorylcholine (MPC), and (sulfobetaine methacrylate) (SBMA).²³ The latter, more correctly named 3-[N-(2-methacryloyloxy)ethyl-N,N-dimethyl] ammonio propane-1-sulfonate, is also called SPE. We will use this acronym for both the monomer and its polymer in this work.

During the last decade there have been several atomistic^16,19–22 and a few mesoscopic²⁵ simulations of the antifouling action of zwitterionic membranes. In a series of papers, Shao et al. examine the influence of charged groups¹⁶ and ions²⁰ on polyzwitterions, as well as the effect of the latter on proteins.²² In a recent paper by Xiang et al.,¹⁹ brushes of terminally grafted sulfobetaine polymers were considered at different surface densities. The structure of the brushes, including ion pairs between sulfobetaine zwitterions, was explored. Interactions between two such brushes were computed in vacuo, in water, and in a salt solution. Furthermore, the mean force experienced by a foulant (FL) as a function of its distance from the surface was computed by steered molecular dynamics (SMD).¹⁹ The FL in the work of Xiang et al.¹⁹ was represented as an alginate gel.

The relevant time and length scales governing the thermodynamics and dynamics of long-chain polyzwitterions in solution, their adsorption or chemical grafting onto solid surfaces, and their antifouling action exceed by far the range of microseconds and tens of nanometers that can be addressed by atomistic simulations on readily available computational platforms;^26,27 judicious coarse-graining is thus necessary.

A wide variety of mesoscopic techniques have been developed for addressing the properties of soft matter systems for time scales up to seconds and length scales up to micrometers. A promising technique of this kind for simulating anti-biofouling polyzwitterionic layers is Dissipative Particle Dynamics (DPD), in which beads interact with each other through soft conservative and pairwise dissipative and random forces.^28–33 A definite advantage of DPD is that it correctly represents hydrodynamic interactions. The DPD method has been applied to a variety of problems involving polymers and copolymers,^32,34,35 nanocomposites,³⁴ water–oil interfaces,^36,37 brush arrays,^38,39 liquid/solid⁴⁰ and liquid/vacuum⁴¹ interfaces, bilayers/membranes,^31,42–46 and liquid flow in bulk⁴⁷ and microchannels.⁴⁸

The objective of the present study is to develop a multiscale molecular modeling and simulation methodology that can facilitate the design of polyzwitterionic brush arrays capable of repelling bacteria and other bio-fouling agents from solid surfaces in aqueous environments. The modeling approach is able to predict how the length and concentration of the polymer brushes affect the structure of the layers formed on the surface, and the repulsive potential of mean force experienced by biofoulants due to these layers. Given the chemical complexity of the systems of interest and the broad range of length and time scales governing their physicochemical behavior, a multiscale modeling and simulation methodology is adopted, employing two interconnected representations: (i) a detailed atomistic representation based on a suitable force field, simulated with molecular dynamics (MD); (ii) a mesoscopic representation cast in terms of coarse-grained “beads,” simulated with DPD.

Parameterizing a DPD simulation so as to represent a specific chemical system is not a trivial undertaking.^{30,35–37,42–46,48–50} A common practice is to tune the repulsive parameters of a ramp potential a_ij for each interaction pair ij in a way that reproduces specific Flory–Huggins parameters χ_ij, using the correlation proposed by Groot et al.³⁰ to link χ_ij with the repulsion parameters, a_ij, of the DPD potential. Weiß et al.⁵¹ propose a strategy which initially maps out the surface charge density distribution by quantum chemical methods around each moiety to be coarse-grained into a bead, then invokes the COSMO-RS framework to calculate the residual Gibbs energy of mixing of binary systems of beads, then fits a χ factor to the latter, and finally determines the DPD parameter a so as to match this χ factor. An alternative bottom-up approach to restore the nonbonded interactions is to employ a tabulated pair potential that can be parameterized from the pair-distributions of an MD simulation with iterative Boltzmann inversion^52,53 or with reverse Monte Carlo.^54,55

Given that the estimation of the χ parameters for charged SPEs is not straightforward due to the presence of electric charges, we opted to incorporate a hybrid bottom-up parameterization procedure in which: (i) we retained the usual ramp potential of DPD but, (ii) we optimized the a_ij parameters in a way that best matches the pair-distribution functions between MD and DPD. Optimization of the repulsive coefficients was performed via brute force and machine-learning-based parameterization procedures (Bayesian optimization) which minimized the standard deviation between the pair-distributions from MD and DPD. The effective bonded interactions, on the other hand, were parameterized based on a Monte Carlo optimization scheme which best matches the strand-length and strand-angle distributions between MD and DPD.

Predicted properties include the conformations of long SPE chains in aqueous bulk solutions, the density profiles of brush arrays and the brush dimensions and grafted layer structure by means of the root mean square brush height 〈h_g²〉^0.5 and the span 〈h_99%〉,^53,56,57 and the potential of mean force (PMF) between a solid substrate covered by the brush array and an approaching mock foulant (suspended particle) as a function of the foulant's position relative to the surface. PMF is a direct measure of the layer's effectiveness as an antifouling agent. A repulsive PMF is desirable; the longer the range of repulsion and the steeper the potential of mean force, the better the antifouling properties. The repulsive/attractive tendencies between the foulants and the antifouling brushes are governed by an interplay of brush–solution, brush–foulant and foulant–solution interactions. To discern and validate these tendencies we performed a sensitivity analysis of the PMF in terms of varying the strength of the repulsive foulant–water and foulant–SPE interactions; hence, tuning in that way the hydrophobicity/hydrophilicity of these substances. Extensive validation efforts were performed between the MD and DPD levels of modeling and between simulations¹⁹ and available experimental evidence^14,15 from the literature.

To the authors’ knowledge, this is the first mesoscale study of SPE polyzwitterions that addresses the following aspects in the field of dissipative particle dynamics and antifouling:

• It proposes a hybrid IBI/MC/machine learning approach for the bottom-up parameterization of the DPD model, which does not require knowing the Flory's χ-parameters.

• It provides indirect indications for the transferability of the free energy potential to different concentrations.

• It displays predictions concerning poly-zwitterions of high molar mass, whose simulation exceeds by far the capabilities of atomistic molecular dynamics.

• It assesses the scaling laws of the brush measures over a broad range of molar masses and grafting densities and provides comparisons with theoretical predictions.

• It demonstrates the applicability of umbrella sampling techniques for assessing the antifouling properties of polyzwitterionic layers.

The article is structured as follows: Section 2 presents an introduction to DPD; Section 3 introduces the atomistic and mesoscopic models and discusses the bottom-up parameterization procedure that bridges the atomistic levels of description with the mesoscopic ones. Section 4 includes in-depth details regarding the MD and DPD simulations. Section 5 presents the main findings of this work for bulk solutions and brush arrays. Finally, Section 6 concludes the manuscript.

2. Dissipative particle dynamics

DPD was initially introduced by Hoogerbrugge and Koelman²⁸ and reformulated by Español and Warren.²⁹ In DPD, the dissipative and random forces are related through the fluctuation–dissipation theorem, leading to conservation of the momentum, which is a prerequisite for a correct description of hydrodynamics.⁵⁸ In this model a set of point particles move and interact with each other with three types of pairwise forces:with f^C being a conservative force derived from a potential, f^D being a dissipative force that reduces the radial velocity differences between particles, and f^R being a stochastic force directed along the line joining the centers of the particles. The functional forms of the dissipative and random forces are:

f^D_ij = −γ_ijw_D(e_ij·v_ij)e_ij (2)

f^R_ij = σ_ijw_Rζ_ije_ij (3)

with e_ij = (r_i − r_j)/(|r_i − r_j|) being a unit vector in the direction from particle j to particle i, v_ij = v_i − v_j being the relative velocity of the particles, γ_ij being a pairwise friction factor, and w_D and w_R being the weight functions which are chosen according to the fluctuation–dissipation theorem, σ_ij² = 2γ_ijk_BT and w_D = w_R².

The standard description of nonbonded soft conservative interactions in DPD involves a repulsive ramp force that has a finite value at zero distance and decays linearly with increasing distance to zero at a characteristic cutoff distance, r_c.

The forces vanish beyond the cutoff distance r_c; the total momentum is conserved, and hydrodynamics is respected. We will call this force “dispersive” for short in the following. The magnitude of dispersive nonbonded forces is determined by the coefficients a_ij which tune the pairwise repulsion of the DPD beads.

3. Model systems

3.1 Atomistic model

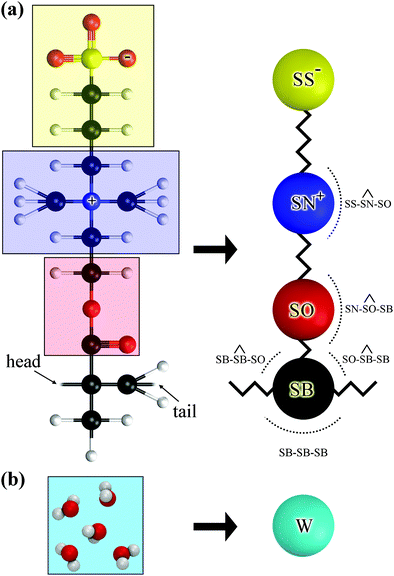
The chemical formula of SPE is illustrated schematically in Fig. 1. The sulfobetaine group contained in SPE is zwitterionic, consisting of a positively charged quaternary ammonium and a negatively charged sulfonate tethered by three methylene units. During the polymerization the double bond opens, connecting the SPEs across the CH₂ into a backbone.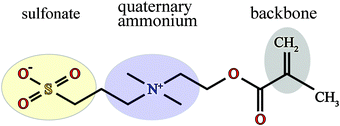

Fig. 1 Chemical structure of an SPE monomer. During the polymerization the double bond at the backbone opens, forming a new bond with the next SPE monomer.

3.1.1 Force fields for SPE. The atomistic SPEs were described using two different force fields for validation and comparison purposes, namely DREIDING⁵⁹ and OPLS.^60,61

DREIDING is considered to be relatively inexpensive computationally and generic; thus, it is readily applicable over a vast range of polymer types. Nonetheless, the fact that it is generic makes its accuracy for describing uncommon molecular architectures questionable. DREIDING does not offer a specific recipe for assigning charges to individual monomers; thus the charges were assigned using the generic Gasteiger⁶² scheme.

The OPLS force field was initially developed by Jorgensen's group^60,61 and has been parameterized for describing accurately very similar polymers; in particular, the same sulfobetaine groups, but shorter by one methylene segment,²¹ and the same SPE group with a different backbone attached to Au nanoparticles.⁶¹ Thus, the potential employed herein was derived by mixing the original OPLS parameters with the force fields in ref. 21 and 61 (see Section S1, ESI†).^63–65 The OPLS force field was applied via an in-house code that was developed for the purposes of this project.

The primary atomistic simulations based on which we parameterized our mesoscopic model were conducted with the OPLS force field. A few representative cases were simulated with DREIDING as well for comparison purposes.

3.1.2 SPCE force field for water. The interactions among water molecules were described with the SPCE three-point-charge force field for water.⁶⁶ SPCE has been employed for modeling very similar systems,¹⁹ and is computationally inexpensive since it involves rigid OH bonds and HÔH bond angles.

3.2 Mesoscopic model

3.2.1 Mapping. Fig. 2 illustrates the mapping between the atomistic and the mesoscopic levels of description. Various coarse graining schemes have been employed in the literature with N_m ranging from 1–5^{31,37,42–44,46,67–69} up to 10⁷–10⁹ water molecules per bead.⁴⁸ In this work, the water molecules are lumped into groups of N_m = 5 water molecules per bead. The mesoscopic representation of SPE includes 4 bead types: SB (relative molecular mass m_C3H5= 41.07 g mol⁻¹), constituting the backbones of the chains; SO (m_C2O2H2 = 58.04 g mol⁻¹), describing the ester group; SN (m_NC4H10 = 72.13 g mol⁻¹), the positively charged quaternary ammonium; SS (m_SO3C2H4 = 108.11 g mol⁻¹), the negatively charged sulfonate group. Each coarse-grained bead of the polymer is placed at the center of mass of the atomistic moiety it represents. Beads are connected together with effective bonds represented by springs and form effective bond-bending angles.

Fig. 2 Atomistic (left) and mesoscopic (right) representation an (a) SPE and (b) water molecules.

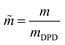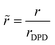3.2.2 Coarse-grained force field for water and reduced units. DPD simulations are usually performed using the following dimensionless quantities for the mass, distance, time, energy, and electric charge, respectively: , , , , . The reference bead mass, m_DPD = N_m·m_H2O, is set equal to the mass of the water bead describing N_m water molecules (m_H2O). is the cutoff distance of the nonbonded interactions with V_H2O being the volume per water molecule as calculated from the density of bulk liquid water under the conditions of interest.³¹ Thus, we find the physical size of the interaction radius. τ_DPD is a reference time and is usually set equal to 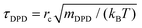. ε_DPD is usually set to k_BT. Note that the aforementioned quantities are functions of the dimensionless DPD number density, which is set to [small rho, Greek, tilde]_DPD = ρ_DPDr_c³ = 3, as in most DPD studies.^30,31,37,70 It should be noted that [small rho, Greek, tilde]_DPD is a free parameter of the model that can be set to any value equal to or larger than 3, which is the lowest value for which the excess pressure retains its proportionality to [small rho, Greek, tilde]_DPD².³⁰ Setting [small rho, Greek, tilde]_DPD > 3, however, has been deemed impractical because the number of interactions scales as ∼[small rho, Greek, tilde]_DPD².³⁰

The commonly used dimensionless friction factor, [small gamma, Greek, tilde]_ij = 4.5 (in units) leads to a very good temperature control; however, it predicts overly enhanced diffusivity for water.^31,45 The effect is demonstrated in Table 1 which depicts the self-diffusion coefficient of experimental⁷¹ and simulated water via MD and DPD. The diffusion coefficient of the DPD water beads, multiplied by N_m = 5, is much higher than the experimental one.

Table 1 Self-diffusion coefficients of water from the experiment,⁷¹ MD (the SPCE model of water with an abrupt cutoff at 10 Å), and DPD (each bead describes five water molecules). The last two rows depict the diffusion coefficient of an SPE monomer infinitely diluted in aqueous solution from MD and DPD. The rightmost column displays the renormalized diffusion coefficient based on τ^renorm_DPD from eqn (5)

System	Method	D (nm^2 ns^−1)	D ^renorm (nm^2 ns^−1)
H2O	EXP^71	2.430	—
H2O	MD-SPCE	2.595	—
W (H2O)5	DPD	10.47	0.486
SPE1	MD-OPLS	0.261	—
SPE1	DPD	4.531	0.210

---

An approach to overcome this problem and reproduce the diffusivity of water exactly is to renormalize the reference time accordingly:^31,45

where and are the simulated and the experimental self-diffusion coefficients of a water bead and a water molecule, respectively.⁷¹ For N_m = 5, τ_DPD = 4.6 ps, whereas was estimated at ∼10.47 × 10⁻⁹ m² s⁻¹ from our simulations (1/6 of the slope of mean square displacement with respect to time). Using these values in eqn (5), the reference time, τ^renorm_DPD, increases by ∼21.5 times (see Table 2). Interestingly, rescaling the time by eqn (5) yields DPD self-diffusivities for SPE which are very close to those obtained by atomistic MD (see the two last rows of Table 1). This reinforces the idea that the rescaling of eqn (5) is physically meaningful.

Table 2 Reference units

Quantity	Real units	DPD units
N m	5 water molecules	5
m DPD	0.09 kg mol^−1	1
τ ^renormDPD	99.245 × 10^−12 s	1
r DPD = rc	7.66 × 10^−10 m	1
ε DPD = kBT	4.14 × 10^−21 J	1
|qDPD|	0.84e = 1.346 × 10^−19 C	7.16
ρ DPD	997 kg m^−3	3
γ ij	1.46 × 10^−13 kg s^−1	4.5
σ ij	3.48 × 10^−17 (J kg s^−1)^0.5	3
a WW	7.34 × 10^−13 N	135.868

---

Regarding the nonbonded interactions among water beads, a common practice is to fit the coefficient a_ij in eqn (4) to a value that in the case of water reproduces the experimental compressibility of the liquid:

with being the dimensionless experimental inverse compressibility of water, where κ_T is the real isothermal compressibility and ρ_n the number density of molecules.³⁰ According to Groot and Warren,³⁰ setting α = (P_DPD − ρ_DPDk_BT)/(a_WWρ_DPD²) to 0.101r_c⁴ provides a good approximation for [small rho, Greek, tilde]_DPD > 2, with P_DPD being the pressure predicted by the DPD simulation. In this work we recalculated it to α = 0.0919r_c⁴, which provides a more accurate estimation of the ratio for [small rho, Greek, tilde]_DPD = 3.

3.2.3 Coarse-grained force field for SPE. In our mesoscopic model, the beads are connected with harmonic strands with the free energy contribution

U_strand = k_strand(r − l₀)² (7)

with k_strand and l₀ being the stiffness and the reference length of the strand, respectively. In addition, consecutive bead triplets form angles which are described with the following harmonic potential:

U_angle = k_angle(θ − θ₀)² (8)

with k_angle and θ₀ being the stiffness and the reference angle of the strand-bending potential. The non-bonded dispersive interactions among like and unlike beads are described with the ramp potential in eqn (4).

Regarding the electrostatics, because of the softness of short-range nonbonded interactions, point charges cannot be used in DPD, for they would bring about collapse of oppositely charged beads upon each other and negatively infinite electrostatic energy. Instead, it is common practice to smear the charge of a bead according to a prescribed density function within a sphere of the prescribed radius. The electrostatic field resulting from the smeared distributions is then summed using the particle–particle particle-mesh (PPPM) or the three-dimensional Ewald summation method (EW3DC).⁷² In our model, the DPD beads experience electrostatic interactions which are described by the following potential⁶⁸ which was introduced by the authors in LAMMPS for the purposes of this project:

where k = (4πε₀ε_r)⁻¹ with ε₀ = 8.85418782 × 10⁻¹² C² J⁻¹ m⁻¹ being the permittivity of free space and ε_r being the relative permittivity (for water at 298 K it equals ε_r = 78.3).³⁹ This potential smears the charge across a DPD bead using a Slater type charge density, with λ being the second moment of the charge distribution.⁶⁸ Note that in the limit λ → 0, the potential recovers its original Coulomb expression, while according to the DPD literature,^45,73,74 the optimal value for λ is 0.25r_c.

In our implementation the DPD nonbonded interactions are zero between 1st neighboring (directly bonded) beads in a molecule, 50% between 2nd bonded neighbors and 100% everywhere else. Regarding the Coulomb interactions, these are zero between 1st–3rd bonded neighbors.

Based on the parameterization procedure that is reported in Appendix A we obtained the coefficients for the mesoscopic force field shown in Tables 3–5. Finally, for the case of brush arrays, the nonbonded coefficients of the atoms comprising the solid surface were set to ã_AA = 200 (in DPD units), whilst the interactions with beads of type j were derived by applying the geometric mixing rule; .

Table 3 Coefficients for the strands (eqn (7)), in DPD units

Bond type	k strand	l 0
SB–SB	993.893	0.390
SB–SO	6536.214	0.375
SN–SO	707.171	0.526
SN–SS	1810.595	0.663

---

Table 4 Coefficients for the strand-angles (eqn (8)), in DPD units

Angle type	k angle	θ 0 (°)
SB–SB–SB	2.744	115.252
SB–SB–SO	6.434	82.982
SB–SO–SN	2.585	130.594
SO–SN–SS	3.094	134.925

---

Table 5 Coefficients for the nonbonded dispersive interactions (a_ij), charges and masses, in DPD units

	SB	SO	SN	SS	W	Charges	Mass
SB	63.69	61.59	62.16	103.44	98.26	0.00	0.456
SO		61.07	39.87	89.33	103.33	0.00	0.645
SN			61.46	77.35	54.45	7.16	0.801
SS				129.03	135.24	−7.16	1.201
W					135.86	0.00	1.000

---

It is worth mentioning here that our implementation involves variable bead-size,⁷⁵ charged DPD beads, and variable a_ii coefficients; thus, it is not straightforward to interpret the physical meaning of the repulsive coefficients listed in Table 5. In detail, the derived a_ij contains information about several molecular-level aspects such as:

• Bead size

• Enthalpic interactions

• Entropic interactions

• Charges and hydrogen-bonding effects

• Geometric constraints imposed by the branched architecture that generate correlations

Even though these aspects are highly convoluted, one could nonetheless attempt to discern some basic trends. Overall, the coefficients increase with bead mass (rightmost column of Table 5) since the beads occupy more space and thus a_ij must become more repulsive. Interestingly, even though m_SN > m_SB and m_SO, their repulsive coefficients are similar. This is attributed to SN being positively charged; the SN–SN repulsive coefficient remains relatively low in order to compensate for electrostatic repulsion between positively charged SN–SN pairs. The same reasoning can be applied to SS beads as well: even though m_SS > m_W, we see that a_SS < a_WW in order to compensate for the repulsive interaction between negatively charged SS beads. Interactions between the beads at the end of the zwitterion (SN and SO) with its backbone (SB) are somewhat more repulsive (e.g., compare SN–SO with SN–SB, and SS–SO with SS–SB, whilst keeping in mind that m_SO > m_SB). This effect could be attributed to the molecular architecture of the polyzwitterions and to excluded volume effects arising due to the presence of the intermediate SO beads.

Finally, the pair-wise friction factors of the SPE beads were set to [small gamma, Greek, tilde]_ij = 4.5. Interestingly, even though we based the time-mapping solely on the dynamics of water, the renormalized diffusion coefficients of the coarse-grained SPEs are in reasonable agreement with the diffusion coefficients of the atomistic ones; e.g., compare the renormalized DPD diffusion coefficient with the atomistic diffusion coefficient in Table 1. The agreement could be potentially improved by optimizing the [small gamma, Greek, tilde]_ij with the target to match the diffusion coefficient of the atomistic and the mesoscopic SPEs.

4. Simulation details

4.1 Atomistic molecular dynamics

The initial configurations were generated with the Amorphous Builder program,⁷⁶ as implemented in the MAPS⁷⁷ package by Scienomics. During the generation phase (chain growth and insertion of water molecules), the system temperature was set to T = 450 K, the density to ρ = 0.8 g mol⁻¹, and the interactions were described by the DREIDING force field⁵⁹ with Gasteiger charges.⁶² For simulations with the OPLS force field the bonded and nonbonded OPLS coefficients were applied using an in-house code.

The atomistic simulations consisted of three main stages:

1. The initial configurations were subjected to sequential energy minimizations, in which the bond and angle stiffness was gradually increased, until these hard degrees of freedom practically reached their equilibrium values. In particular, the initial coefficients for the harmonic, [scr V, script letter V]_bond = k_bond(l − l₀)², SPCE bonds for water were set to k_bond = 100 kcal mol⁻¹ Å⁻¹ and l₀ = 1 Å, and the initial coefficients for the harmonic SPCE angles, [scr V, script letter V]_angle = k_angle(θ − θ₀)², were set to k_angle = 100 kcal mol⁻¹ rad⁻¹ and θ₀ = 109.47 Å. Furthermore, over subsequent energy minimizations, the bond and angle stiffness was increased by powers of 2 until these geometric characteristics practically reached their equilibrium lengths corresponding to infinite stiffness.

2. The energy-minimized atomistic configurations were then simulated for moderate periods of time until they reached their equilibrium properties. In detail, the equilibration stages were the following: (i) first, the samples were simulated for 10 ps using the efficient velocity rescaling thermostat; (ii) then, the samples were simulated in the NVT ensemble using the Nosé–Hoover thermostat for another 10 ps; (iii) finally, the samples were simulated in the NPT ensemble using the Nosé–Hoover thermostat and barostat for up to 160 ps, until they reached their equilibrium density, which is about equal to the density of water, 1 g cm⁻³.^78,79

3. The equilibrated samples were simulated for extended periods of time (up to 0.1 μs).

Note that, in stages (2) and (3), the equations of motion were integrated using the velocity-Verlet algorithm⁸⁰ with a time step set to 1 fs. In addition, the SHAKE algorithm⁸¹ was enabled which applies bond and angle constraints on the bonds and angles of the SPCE water molecules. Throughout the MD simulations we investigated SPEs with 1 up to 64 repeating units at mass ratios ∼10 wt%. Unless otherwise stated, it is assumed that the atomistic simulations are conducted with the OPLS force field, based on which we parameterized our mesoscopic model.

4.2 Mesoscopic simulations

4.2.1 Bulk systems. The simulations of bulk solutions were realized in 3 main phases:

1. The initial mesoscopic configurations for bulk solutions were generated using an in-house builder, PyMeso, which was developed for the purposes of the current project. The code is written in Python3.8 and can generate chains of arbitrary connectivity and chemical constitution based on user input. There is no restriction regarding the number of chain types, polydispersity and the periodic boundary conditions applied at the wall boundaries. For more details about PyMeso see Section S2 (ESI†).⁸²

2. Subsequently, the configurations were energy minimized and then equilibrated for up to [small tau, Greek, tilde] = 10⁴ (∼1 μs).

3. Finally, the trajectories were simulated for extended time periods up to [small tau, Greek, tilde] = 2 × 10⁵ (∼20 μs), for the larger systems considered here.

The equations of motion were integrated using the velocity-Verlet algorithm⁸⁰ in conjunction with the multiple time step Reference System Propagator Algorithm (RESPA),^80,83 with one hierarchical level having a time step equal to 0.005τ_DPD for the bonded interactions and another hierarchical level having a time step equal to 0.015τ_DPD for the nonbonded interactions. The cutoff of the long range interactions was set to r_c = 1 (in DPD units). The summation of the electrostatics was carried out using the Particle–Particle Particle-Mesh (PP-PM) solver⁸⁴ (“pppm/cg” style in LAMMPS which is identical to the “pppm” style except that it incorporates an optimization for systems where most particles are uncharged) with a G-Ewald parameter for the dispersion equal to 1.8, and a maximum relative error of 10⁻⁴. The simulations were performed for SPEs with 1 up to 512 repeating units at 10 wt%.

4.2.2 Brush arrays. Fig. 3 illustrates a brush array with n_SPE = 36 grafted SPE chains of length N_SPE = 5 repeating units in water solution. The edge of the wall lies at z_S = 0.425r_DPD = 0.325 nm, while the grafting point-wall distance is z_g–z_s = 0.5r_DPD ∼ 0.38 nm. The simulations of the brush arrays and the estimation of PMF with umbrella sampling were realized in 5 main phases:

Fig. 3 Coarse-grained representation of a brush array with area/chain = 1.44 nm². The SPE brushes comprise SB (black), SO (red), SN (blue) and SS (yellow) beads, while white beads represent the wall surface. The beads of the wall surface and the grafted beads (SB beads marked with “×”) remain immobile throughout the simulation. z_S and z_g denote the position of the wall surface and the grafted point-wall surface distance, respectively. The violet beads comprise a model foulant particle at z_FL. Water beads are omitted for clarity.

1. The initial mesoscopic configurations for the brush arrays were generated with PyMeso. The solid substrate was modeled by a slice of an 11 × 11 BCC lattice with a lattice constant of 0.8542r_DPD (ρ ∼ 3.2 in DPD units), as shown in Fig. 3. The SPE brushes emanate from grafting points which are distributed periodically across a lattice spanning the lateral directions of the solid surface, with a grafted bead-grafted bead closest distance, where area/chain = σ_g⁻¹, and σ_g is the grafting density.

2. The brush-arrays were then equilibrated in conjunction with a Newton–Raphson scheme that varied the normal dimensions of the simulation box until the normal component of the system pressure matched the pressure of bulk DPD water [P_N ∼ 121.3ε_DPD/r_DPD³ for N_m = 5]. The tolerance value for pressure differences was set to 0.1 and the optimization lasted for up to 7 cycles.

3. The initial snapshots for the umbrella sampling were extracted by Steered Molecular Dynamics (SMD) simulations. In SMD the z-component of the center of mass of the foulant (FL), z_FL, was tethered to the surface with a harmonic spring starting at z_g with stiffness k_spring and equilibrium length l_spring, without applying any constraint along the lateral dimensions; a similar treatment is employed in ref. 19. By adjusting the equilibrium length of the spring one can tune the distance of the FL from the solid surface. The simulations were performed in three stages: (i) the system was initially equilibrated for 500τ_DPD with l_spring = z_init and k_spring rising gradually from 0 to 10 000 (in DPD units). (ii) The system was equilibrated for an additional 100τ_DPD with the same l_spring and k_spring. (iii) The length of the spring decreased gradually from z_init to z_final at a rate Δz/τ_equil, with Δz = (z_init − z_final)/n_bins being the bin width for the umbrella sampling simulations, n_bins being the number of bins, and τ_equil = 100τ_DPD; the FL was thereby gradually moved towards z_g and snapshots of the systems were stored with a frequency τ_equil⁻¹.

4. Starting from the jth snapshot from the SMD simulations an umbrella sampling simulation was performed for 400τ_DPD, l_spring = (z_final − z_init)/j, and k_spring = 500 whilst storing values of (z_FL − z_g) along the generated trajectory.

5. Finally, trajectories started at each snapshot were processed by the implementation of the Weighed Analysis Histogram Method (WHAM) by Grossfield.⁸⁵

Each umbrella sampling experiment was repeated two times with different initial configurations in order to assess the deviation. The latter is very small, probably due to the sufficient equilibration time and relatively large system sizes. It should be noted that, according to our benchmarks, the PMF arising from pulling the FL away from the antifouling layer to infinity (in the reverse direction) is practically identical.

During the simulations both the beads comprising the solid surface and the grafted beads were kept frozen. This treatment, however, can generate artifacts in the calculation of system temperature and pressure; thus, these properties were recomputed based on the atomic velocities and virial of the mobile atoms, respectively. For the calculation of pressure the effective volume of the system was scaled by ; an alternative treatment would be to consider the effective volume of the mobile atoms as the sum of their Voronoi volumes. The systems were periodic along the lateral and aperiodic along the normal directions, whereas reflective (specular) boundary conditions were implemented along the normal direction. The incorporation of fixed wall particles in conjunction with reflective boundaries has been shown to be an effective approach for preventing DPD beads from crossing the top and bottom faces of the simulation box and for enforcing the no slip boundary condition.^33,86,87

During these simulations the equations of motion were integrated using the velocity-Verlet algorithm⁸⁰ with a time step of 0.005τ_DPD. The estimation of the electrostatic interactions in these aperiodic systems was performed with the algorithm by Yeh and Berkowitz⁸⁸ that inserts an empty volume between the images of the system along the aperiodic directions and as a result removes the dipole interactions among the slabs. The parameters of the brush arrays examined in the present work are displayed in Table 6.

Table 6 Parameters of the brush arrays under study

N SPE	Area/chain (nm^2)	a latt (nm)	σ g (nm^−2)	L T (nm)
5, 10, 15, 20	36.9	6.075	0.027	6.075
5, 10, 15, 20	16.4	4.05	0.061	8.1
5, 10, 15, 20	7.29	2.7	0.137	8.1
5, 10, 15, 20	3.24	1.8	0.309	7.2
5, 10, 15, 20	1.44	1.2	0.694	7.2
5, 10, 15, 20	0.64	0.8	1.562	7.2

---

5. Results

5.1 Bulk solutions

Fig. 4 depicts the mean square radius of gyration, 〈R_g²〉, of free SPE in dilute aqueous solution from DPD, MD and from the experimental correlations derived by Mary et al.^14,15 The latter are based on measurements in the presence of NaCl and they refer to the conditions of temperature, SPE and electrolyte concentration under which the upper critical solution temperature of each system exhibits a maximum with respect to the electrolyte concentration. In addition, representative configurations from the atomistic (OPLS) and mesoscopic (DPD) models are displayed in Fig. 5. Overall, atomistic chains as described by the DREIDING and the OPLS force fields exhibit very similar behavior. The size of the atomistic chains—as quantified by 〈R_g²〉—increases sub-linearly with respect to their length in the short chain regime, while for longer chains it follows a scaling law very close to ∼N¹, characteristic of random coils. As far as the mesoscopic chains are concerned, the estimated 〈R_g²〉 values are in very good quantitative agreement with the atomistic ones (compare green triangles with red squares and circles), while for larger chain lengths the scaling exponent becomes slightly higher. The accessible chain length regime from DPD features significant overlap with the experimental correlations by Mary et al.^14,15 Moreover, the predicted square radii of gyration are in quantitative agreement with the experimental correlation which is built-in in the model proposed by Mary et al.: R_g = aM^b_α with a = 0.69 nm, b = 0.48 and M_α being the weight-average (M_w) or number-average (M_n) molar mass.^14,15 (all SPE polymers studied experimentally in ref. 15 were quite polydisperse, with polydispersity indices ranging from 2 to 3.) Small Angle X-ray Scattering (SAXS) measurements, on the other hand, are for N_SPE = 1611 and are a better match with the predictions based on the M_n averaged degree of polymerization.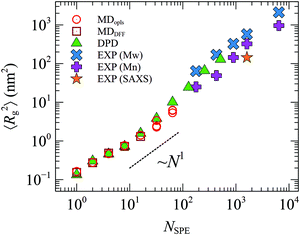

Fig. 4 Mean square radius of gyration from MD with OPLS (○) and DREIDING (□), DPD calculations (▲) and experimental data from ref. 15 (×, + and ★). The experimental data were derived from the correlation R_g = aM^b_α with a = 0.69 nm and b = 0.48, with M_α being either the weight- (M_w, ×) or number- (M_n, +) average molar mass.

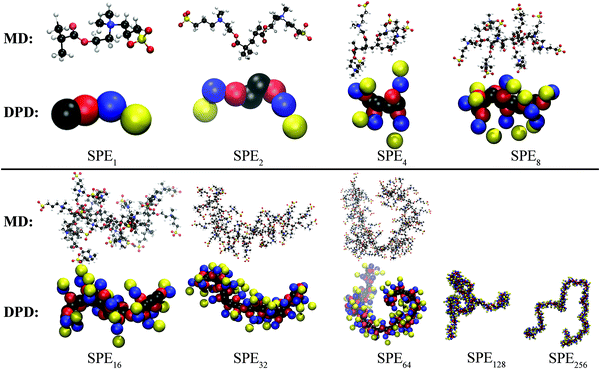Fig. 5 Atomistic (MD with OPLS) and mesoscopic (DPD) representation of representative SPE polymers investigated in this work.

5.2 Brush arrays

Throughout our DPD simulations we investigated polyzwitterionic brush arrays exposed to water similar to those examined by Xiang et al.,¹⁹ over a broad range of molecular parameters such as the area/grafted molecule (i.e., the inverse of the grafting density, σ_g) and the polymerization degree of the grafted SPE chains (N_SPE).

5.2.1 Density profiles. Comparisons of the mass density profiles from DPD against atomistic ones are instructive for assessing the accuracy of our DPD model. It is worth mentioning that the profiles from the DPD simulations considered here differ from the atomistic MD ones by Xiang et al.¹⁹ in the following aspects:

(1) The MD profiles include the additional contribution of the saturated benzene rings with the azide group (C₂₀H₁₉O₃N₄) representing the root of the brush and the polyamide membrane surface.¹⁹

(2) At low grafting densities the polyamide membrane surface employed in the atomistic MD simulations becomes very sparse and as a result the sulfobetaine groups can penetrate it (e.g., see Fig. 6c in ref. 19).

(3) Another difference between these systems is that the atomistic SPEs simulated by Xiang et al.¹⁹ are smaller by one methylene unit, in order to facilitate comparisons with previous simulation works by Shao et al.^16,20–22

These differences have to be accounted for in order to perform meaningful comparisons between these simulations. Therefore, to facilitate comparisons among these models the density profiles in Fig. 6 are visualized against the effective segment-wall distance:

h = z − z_S (10)

with z_S being the effective position of the wall surface. In DPD this is set to the edge of the solid wall, z_S, as indicated in Fig. 3. Consequently, z_S was obtained from the MD profiles in a way that the following mass balance equation is satisfied:In other words, the integration of the density profile from z_S onwards equals the SPE mass per unit area considered in the atomistic system. Consequently, the integrated area below the surface of the wall (i.e., the vertical dashed line in Fig. 6), corresponds to the mass of the polyamide membrane per unit area. Note that comparisons between from MD and DPD are not especially meaningful, since the polyamide membrane is not exactly the same as the solid substrate used in our DPD simulations (see the lattice in Fig. 3).

Fig. 6 Density profiles of SPE (red) and water (blue) from DPD (solid lines) and atomistic MD19 (dots) for area/chain = (a) 3.24, (b) 1.44 and (c) 0.64 nm². The thick vertical line illustrates the effective position of the wall, z_S, whereas the dashed one depicts the grafting point in DPD. The width of the bins of the profile was set to 0.5r_DPD ∼ 0.383 nm.

According to Fig. 6, the density profiles from DPD are in reasonable agreement with the MD¹⁹ density profiles considered by Xiang et al.¹⁹ The DPD profiles appear to be slightly more expanded as compared to the MD ones; the difference can be attributed to the SPEs from the MD study¹⁹ being shorter by one CH₂ segment. In addition, DPD profiles feature a narrow low density region near the surface, since in that case the SPE chains are grafted to a planar solid surface instead of the mobile saturated benzene rings in Xiang et al.¹⁹ As has been demonstrated by numerous works in the past,^38,89–91 the density profiles tend to form steep peaks near rigid planar surfaces. These peaks arise due to excluded volume effects which lead to the formation of layers.^70,92–94 The effect becomes even more intense in DPD with increasing coarse-graining because the interactions among beads become more repulsive⁹⁴ in order to maintain the compressibility at a constant density; e.g., see eqn (6). Nonetheless, setting the width of the profile bin to half the radius of a DPD bead leads to overall smooth profiles, as shown in Fig. 6. In the case corresponding to the highest grafting density examined here, the SPE chains experience intense confinement and as a result some of their beads penetrate the wall surface at the lowest boundary of the simulation box (e.g., see the density states below the solid vertical line in Fig. 6c). The efficacy of DPD to sample the configurations of these densely grafted brushes was quantified in terms of the autocorrelation function of the tangential (with respect to the surface) components of the end-to-end vector of the SPE chains. These results are shown in the Section S3 (ESI†) and demonstrate that the dynamics becomes more sluggish with increasing grafting density, albeit the autocorrelation drops below 10% at times longer than 1000τ_DPD. Another difference between the DPD and MD¹⁹ profiles is the tendency of the water molecules to penetrate the SPE brushes, especially in the dense brush regime. In MD¹⁹ the water molecules can penetrate the SPE brushes over all the grafting densities considered there. In DPD, however, the water beads cannot penetrate the dense brush in Fig. 6c because the water beads are much larger (5 times) than individual water molecules. The profiles of the water beads are similar to those from MD for the sparser brushes (Fig. 6a and b).

5.2.2 Brush thickness. The spatial extent of the polyzwitterionic brushes can be quantified in terms of the root mean square brush thickness:Based on the scaling of its radius of gyration with chain length in dilute aqueous solution (Fig. 4), SPE behaves as if it finds itself in a Θ solvent under the considered conditions. For a polymer brush in a Θ solvent it has been shown that the scaling law 〈h_g²〉^1/2 ∼ N_SPE¹σ_g^1/2 holds.^97–99 We thus examine first how well this scaling describes our simulation results. Fig. 7a depicts 〈h_g²〉^1/2 from DPD and from MD¹⁹ (based on the effective wall projection in eqn (10)), plotted against N_SPE¹σ_g^1/2, appropriate for polymer brushes in Θ solutions.

Fig. 7 (a) 〈h_g²〉^1/2versus N_SPEσ_g^1/2 from MD¹⁹ (filled symbols) and DPD (hollow symbols). (b) 〈h_g²〉^1/2, (c) 〈h_g,99%〉, and (d) 〈h_g,99%〉/〈h_g²〉^1/2versus N_SPEσ_g^1/5. The dashed line in (d) illustrates the prediction from Alexander's model^57,95,96 for incompressible brushes. The markers denote grafting densities, σ_g = 0.027 (●), 0.061 (▲), 0.137 (★), 0.309 (■), 0.694 (+), and 1.562 (×) nm⁻², whereas colors denote different chain lengths, N_SPE = 5 (red), 10 (blue), 15 (green) and 20 (violet). The error bars depict the standard deviation derived from three DPD simulations for each case starting with different initial configurations.

Overall, the brush thickness is a close match between MD¹⁹ and DPD; e.g., compare the red data points for N_SPE = 5. The brush thickness scales linearly with N_SPE, as is indicated by markers with the same shapes and different colors in Fig. 7a; this linear scaling has been shown to hold regardless of whether the solvent is good, theta or poor.⁹⁹ The Θ-scaling with surface grafting density 〈h_g²〉^1/2/N_SPE ∼ σ_g^1/2, however, does not seem to collapse our data fully satisfactorily.

Based on our simulations, the brush thickness is practically insensitive to σ_g at low grafting densities, a feature which indicates that the sparsely grafted chains interact weakly with each other (mushroom regime).¹⁰⁰ At larger grafting densities the chains experience significant confinement and thus the brush thickness increases with σ_g. Nevertheless, this increase appears to be weaker than the prediction for flexible polymer brushes in Θ solvents^97–99 and as a result considerable scattering is seen in Fig. 7a.

Plotting the brush thickness against N_SPE¹σⁿ_g with a scaling exponent n < 1/2 leads to significantly lower scatter. This is clearly demonstrated in Fig. 7b, which depicts 〈h_g²〉^1/2 plotted against N¹σ_g^1/5. The master plot of all data for the brush height in this figure is very satisfactory. Even though long SPE/water solutions behave as Θ solutions under the temperature of interest, the shorter SPE chains considered in Fig. 7 deviate from the expected Θ-solution scaling for brushes of long, randomly coiled chains. This can be attributed to the finite extensibility of the short chains comprising our brushes. Finite extensibility plays a significant role here because of the considerable conformational stiffness exhibited by our SPE chains in water. The inflexibility of our chains is attributable to the large branches on the SPE monomers (SO–SN–SS side groups), which lead to thick and twisted chain contours, and thus to persistent polymer backbones. This effect is especially evident when considering relatively short chains; e.g., please inspect the atomistic and mesoscopic configurations for N_SPE < 40 in Fig. 5.

Finite extensibility leads to a weaker scaling with σ_g. To highlight this, we have performed a simple scaling analysis for a brush of finitely extensible chains in a Θ solvent following ref. 101, which we present in Section S4 (ESI†). A similar effect has been reported for good solvents as well, where, in situations with enhanced chain stretching and orientation, the brush thickness scales more weakly with σ_g, and can even become independent of σ_g in extreme cases.^99,101 It should be noted, however, that in the limit of very high chain molar masses, for which the chains assume random-coil-like configurations, the dependence of 〈h_g²〉^1/2 on grafting density could potentially become stronger, approaching the Θ-chain 〈h_g²〉^1/2 ∼ N_SPE¹σ_g^1/2 scaling.

Another measure for quantifying the shape of a grafted polymer brush is the brush span h_g,99%, which can be defined for planar geometries as the segment-wall distance that encloses 99% of grafted SPE mass:

According to Fig. 7c, h_g,99% exhibits very similar behavior with 〈h_g²〉^1/2, shown in Fig. 7b. Finally, the ratio 〈h_g,99%〉/〈h_g²〉^1/2 is characteristic of the shape of the brush. As shown in Fig. 7d, it appears that, in the limit of large N_SPE and σ_g, this ratio becomes close to which is the prediction from Alexander's model for incompressible brushes.^57,95,96

5.2.3 Potential of mean force of the approaching foulant. The present section investigates the mean force (MF, negative gradient of the potential of mean force) for a foulant (FL) approaching the antifouling (AFL) layer, as modeled by the SPE-covered surface, embedded in a water solvent (W). Negative values of the force denote repulsive FL–AFL tendencies, a feature which is generally preferred in antifouling applications. Positive forces, on the other hand, indicate that there is a tendency for the FL to stick to the grafted brush.

The DPD foulant is modeled as an icosahedron formed by DPD beads connected with harmonic springs. Unless otherwise stated, the spring constant equals k_spring,FL = 500ε_DPD/r_DPD² and the equilibrium length equals, l_0,FL = 0.77 nm (1r_DPD). The repulsive/attractive nature of the resulting mean force depends on an interplay among the strengths of the enthalpic and entropic FL–W, FL–AFL and the W–AFL interactions. In order to explore these tendencies, the repulsive FL–W and FL–AFL interactions were varied systematically, based on the following scaled geometric mixing rules:

with f_FL–W and f_FL–AFL being the corresponding scaling coefficients. In eqn (15) the index j denotes any of the four types of coarse-grained beads SB, SN, SO, and SS used to represent the AFL. Consequently, the resulting relative strength of FL–W and FL–AFL interactions is proportional to the square root of the ratio of the scaling coefficients, as shown in eqn (16):Decreasing/increasing the values of these coefficients leads to more attractive/repulsive interactions with the corresponding species; note that increasing the value of the DPD coefficients corresponds to enhanced repulsion. Also, note that setting f_FL–W = f_FL–AFL = 1 in eqn (14) and (15) recovers the geometric mean expression of the conventional mixing rule.

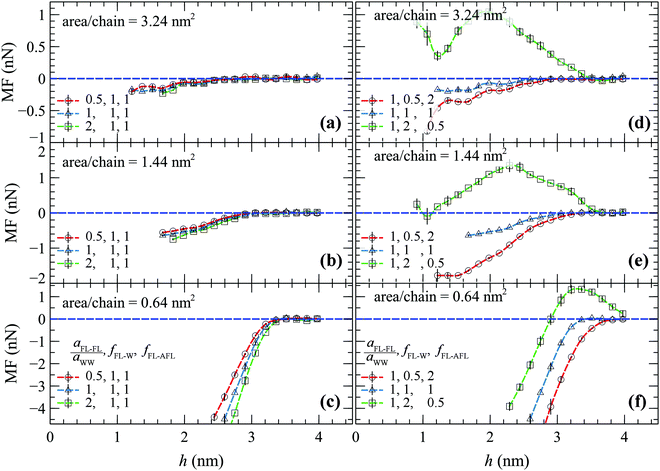
Fig. 8 depicts the MF as obtained from the umbrella sampling DPD simulations on (a and d) sparsely, (b and e) moderately and (c and f) densely grafted brushes, as a function of the separation distance between the FL's center of mass and the wall.

Fig. 8 Mean force (MF) from DPD as a function of the foulant's center of mass-wall surface distance, for area/chain set to (a and d) 3.24 nm², (b and e) 1.44 nm² and (c and f) 0.64 nm². Positive/negative MF indicates attraction/repulsion. Different lines/colors indicate a different combination of (a_FL–FL/a_WW, f_FL–W, f_FL–AFL) as indicated in the legends. In all cases, the equilibrium length of the FL–FL bonds was set to 0.77 nm (r_DPD). The horizontal lines are guides to the eye. The error bars depict the deviation from the mean based on two DPD simulations starting with different initial configurations.

Panels a–c in Fig. 8 depict situations where a_FL–FL is set to 0.5a_WW (circles), a_WW (triangles), and 2a_WW (squares), and f_FL–W = f_FL–AFL = 1. It appears that, regardless of the magnitude of a_FL–FL, the MF remains strictly repulsive. This is to be expected, since the relative strengths of the FL–W and FL–AFL interactions are invariant to a_FL–FL, therefore the overall attractive/repulsive tendencies of the MF are not affected. In practice, since f_FL–W/f_FL–AFL = const, increasing a_FL–FL has the effect of varying the effective bead size of the FL, thus shifting the MF towards slightly larger distances.

The right-hand panels of Fig. 8(d–f) present the effect of varying the relative strength of the FL–W and FL–AFL interactions, whilst fixing a_FL–FL to a_WW. Decreasing f_FL–W/f_FL–AFL (making the foulant more hydrophilic) has the effect of shifting the MF towards larger separation distances, indicating stronger effective FL–AFL repulsion. Increasing f_FL–W/f_FL–AFL, on the other hand (making the foulant more hydrophobic) leads to the emergence of a more complicated picture which could be explained as follows:

(1) At the edge of the AFL brush the MF becomes positive; thus indicating that there is a tendency for the FL to stick on it.

(2) Below a threshold separation distance (which becomes larger with increasing brush density) the MF begins to decrease (becomes more repulsive) due to the manifestation of excluded volume effects; i.e., the foulant is displaced to a region that is already occupied by the brush segments. The effect is more pronounced when considering the densest brush in Fig. 8f, where the MF becomes negative (strictly repulsive) below a distance of 3 nm.

(3) At distances of ∼1 nm where the entire foulant has been submerged into the sparse brush, the MF forms a minimum and begins to rise again (becomes more attractive). This is attributed to the density of the AFL brush having reached approximately its maximum value (where its effect on the MF becomes minor), whereas the density of the (repulsive) water phase declines; hence, favoring the occupation of these low water density-regions.

It is noteworthy that the MF remains strictly positive (attractive) across the full range when considering the sparser brush studied here (Fig. 8d).

The AFL–W interactions play a significant role for the resulting MF, as well. However, we opted not to vary them during our tests since our model has been parameterized for a specific chemical constitution of the antifoulant (AFL). Nonetheless, it is expected that, as the AFL–W interactions become less repulsive there is a tendency for the FL and the AFL to repel each other, since the latter will prefer to interact with the solvent molecules instead of with the FL. More repulsive AFL–W interactions are expected to promote the opposite behavior; i.e., the FL tending to stick to the AFL layer.

Fig. 9 provides qualitative comparisons between the MF from our DPD simulations and from the steered atomistic MD simulations by Xiang et al.¹⁹ In MD, the FL is modeled by an alginate gel via the OPLS force field.¹⁹ In DPD, the equilibrium length of the harmonic springs was set to either l_0,FL = 0.38 nm (0.5r_DPD) or 0.77 nm (r_DPD) in order to explore the effect of varying the size of the foulant. For these comparisons, the FL–AFL and FL–W interactions were estimated via the original geometric mixing rule (f_FL–W = f_FL–AFL = 1). The strength of the repulsive interactions among the beads that comprise the foulant were set to two times those of water (a_FL–FL = 2a_WW), albeit as long as f_FL–W and f_FL–AFL are fixed the overall qualitative behavior is practically the same for lower and higher a_FL–FL values (e.g., see the demonstrations in Fig. 8a–c).

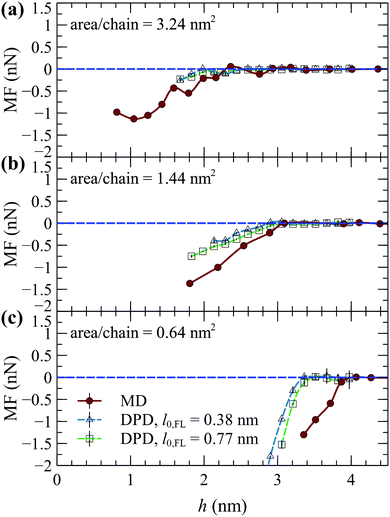Fig. 9 Mean force (MF) from atomistic MD¹⁹ (circles) and DPD with l_0,FL = 0.38 nm (blue triangles) and 0.77 nm (green squares) as a function of the foulant's center of mass-wall surface distance, for area/chain = (a) 3.24 nm², (b) 1.44 nm² and (c) 0.64 nm². Positive/negative MF indicates attraction/repulsion. The horizontal lines are guides to the eye. The error bars depict the deviation from the mean based on two DPD simulations starting with different initial configurations.

The MF is qualitatively similar between DPD and MD; the MF assumes negative (repulsive) values as the foulant approaches the SPE brushes, while it decreases more steeply with increasing grafted density, indicating an enhancement of the antifouling properties of the SPE brush. Increasing the size of the FL by increasing l_0,FL makes the MF slightly more repulsive, albeit the effect is minor. The difference between DPD and MD is to be expected, since the DPD foulant has not been parameterized from an alginate gel, and thus there might be differences in the size and geometry of the foulants considered in each case. For reference, the radius of gyration of the DPD foulant is about with being the golden ratio. It is interesting that, given the simplicity of the biofoulants employed in DPD, the corresponding MFs are in reasonable qualitative agreement with those from MD. The estimation of the PMF arising from the interaction among grafted polyzwitterions and more complex biofoulants (in terms of their chemistry and structure) as a function of their concentration, and in the presence of ionic solutions, is a subject for future research.

6. Concluding remarks

Sulfobetaine-based polyzwitterions constitute promising candidate materials for the design of surfaces with antifouling properties. Several atomistic studies have been conducted in recent years addressing the structure and thermodynamics of these polymers over atomistic length scales.^16,19–22 Nonetheless, the relevant time and length scales of long polyzwitterions are far greater than those that can be reached by conventional atomistic simulations. Hence, there is a need for the development of mesoscopic simulation approaches involving aggressive coarse-graining.

The present work develops a multiscale simulation strategy with two levels of description, entailing an atomistic and a mesoscopic regime. The atomistic regime is investigated with molecular dynamics simulations (MD) using the OPLS force field, whereas the mesoscopic regime is explored by dissipative particle dynamics (DPD) simulations. These two different levels of description are capable of providing access to a very broad spectrum of time- and length-scales, which constitutes an absolute necessity for describing the structural features and thermodynamics of SPE poly-zwitterions. The mesoscopic model is parameterized hand-in-hand with atomistic molecular dynamics simulations across the overlapping regime of chain lengths. More specifically, the coefficients of the mesoscopic force field are optimized to match the atomistically computed strand-length, strand-angle and pair distribution functions via Monte Carlo and machine-learning based approaches.

Overall, the developed potential exhibits good transferability among different concentrations as indicated indirectly, by the good match with molecular dynamics, theory and experiments for both sparse and dense systems. In detail, the structural features of the mesoscopic SPE chains in dilute aqueous solutions reproduce those from the underlying OPLS atomistic model and agree with the experimental findings of Mary et al.^14,15 For sufficiently long SPE chains, the scaling exponent between the mean squared radius of gyration and chain length in dilute aqueous solution is close to 1. The brush array configurations studied herein are investigated in terms of the corresponding brush thickness measures, the local density profiles, and the mean force they exert on an approaching foulant. Results from our DPD simulations are compared with a relevant molecular dynamics study by Xiang et al.¹⁹ In detail, the root mean square brush thickness and the span of the density profiles as quantified by h_g,99% increase approximately linearly with the product of the degree of polymerization and the grafting density to the power of 1/5, a feature that can be explained by scaling considerations for brushes of finitely extensible chains exposed to theta solvents. For very high grafting densities the structure of the brush approaches that of an Alexander-type incompressible brush, also obtained from self-consistent field theory treatment of compressible dense brushes^53,57 in planar geometries.

The repulsive potential of mean force derived from umbrella sampling simulations of a foulant upon approaching the polyzwitterionic brush is in good qualitative agreement with the atomistic findings by Xiang et al.,¹⁹ whereas the discrepancies between atomistic and mesoscopic simulations can be traced to differences between the geometric aspects and the overall parameterization of the model systems.

The repulsive/attractive tendencies of the foulant are governed by an interplay among the foulant–solvent, foulant–antifoulant and the solvent–antifoulant interactions (both enthalpic and entropic). A general design rule for effective nonbiocidal antifoulants would be to enhance antifoulant–solution and the foulant–solution interactions with respect to the antifoulant–foulant ones. For biocidal antifoulants, on the other hand, opposite design rules would be applicable, since sticking the foulant to the antifouling brush would facilitate the biocidal process.

Conflicts of interest

There are no conflicts of interest to declare.

Appendix A

The mesoscopic force field described in Section 3.2.3 was parameterized through a bottom-up mapping procedure aimed at matching the bond and bond-angle distributions and the pair correlation functions between DPD and atomistic trajectories. For the purpose of this matching, the polymer configurations in each atomistic trajectory were geometrically mapped onto coarse-grained configurations. This coarse-graining of atomistic trajectories was performed by lumping the SPE segments into coarse-grained beads (see Fig. 2a) based on the center of mass of the corresponding segments using a code developed in-house:with M_i and r_i being the mass and position of the type i atom, and C_j being a set that includes the atoms that belong to bead j. The mapping procedure we developed can be summarized in the following steps:

1. Derivation of the distributions concerning bonded interactions

2. Boltzmann inversion of the bonded distributions

3. Calibration of the coefficients for the bonded interactions

4. Calibration of the coefficients for the nonbonded interactions

5. Recalibration of the coefficients for the bonded interactions

Details about each step of the mapping procedure are presented in Appendices A1–A5, respectively.

A1. Derivation of the distributions concerning the bonded interactions

Our initial attempt was to extract the strand length (ρ_strand) and strand-angle (ρ_angle) distributions from a coarse-grained trajectory of a single SPE₈ chain immersed in 850 water molecules for extended simulation times (∼0.1 μs). In doing so, we observed that the strand-angle distributions exhibited nonergodic behavior within the time span of the atomistic molecular dynamics; thus, the distributions would not converge within these simulation times. In other words, configurations sampled by the atomistic MD within the accessible simulation time appeared to be trapped in the vicinity of local energy minima, retaining strong memory of their initial characteristics (e.g., angle distributions along consecutive SB–SB–SB triplets differed substantially). Example nonergodic strand-angle distributions are illustrated in Section S5 (ESI†). To circumvent this issue we incorporated a temperature annealing scheme at constant volume and number of particles which proceeds as follows: (i) equilibration of 120 independently generated atomistic samples at T = 900 K with different initial velocities for 2 ns; (ii) temperature annealing from T = 900 K down to 300 K over 2 ns. (iii) Additional relaxation at T = 300 K for 0.5 ns. (iv) Sampling at T = 300 K for 2 ns. Subsequently, the strand length and strand-angle distributions were calculated based on the 120 temperature-annealed atomistic trajectories by placing beads at the centers of mass of atomistically represented groups, configuration by configuration, according to eqn (17). The resulting distributions for strands and strand-angles differed very little across the polymer backbone. The converged ρ_strand and ρ_angle from MD are illustrated in Fig. 10 (red circles). It should be noted that the corresponding box size for this concentration is ∼4 times the radius of gyration of an SPE₈ chain, and as a result interactions between different images of the same chain segments are minimal.⁹⁰

Fig. 10 Strand length (a–d) and strand-angle (e–h) distributions from MD with OPLS (red circles); BI (blue lines); DPD, a_ij = 0, coefficients from BI (green dashes); DPD, a_ij = a_ww, coefficients from BI (purple, dot-dashes); DPD, optimized a_ij coefficients after the final recalibration (orange, dots).

A2. Boltzmann inversion of the distributions

The free energy of the atomistically calculated strand and strand-angle distributions up to an additive constant is given by the following equation:

U(r) = −k_BT ln f(r) (18)

with for strands, and for angles, respectively. Assuming that f follows a Gaussian distribution, then the kind-α strands and the strand-angles can be described by harmonic free energy functions of the form: U_α(x) = k_α(x − μ_α)², with x being the strand length or the angle. Therefore, the stiffness of the strand/strand-angle potential equals k_α = k_BT/(2σ_α²), and the reference length/angle equals μ_α. The blue lines in Fig. 10 depict the theoretical predictions based on the k_α and μ_α coefficients from the Boltzmann inversion (BI). It is worth mentioning that some of the distributions derived from atomistic MD are seen to display complex features. Notable is the bimodality in SB–SB and SO–SN, originating in torsion angles along the backbone and along the side chain adopting trans versus gauche states. These details are not kept in the coarse-grained model.

A3. Calibration of the coefficients for the bonded interactions

As seen in Fig. 10, the strand distributions from DPD with the set of k_α and μ_α for each strand extracted from BI and in the absence of the nonbonded interactions (a_ij = 0) are in good match with the Boltzmann inverted distributions from MD (compare blue lines with the green dashed lines). The strand-angle distributions for SB–SB–SB and SB–SO–SN triplets exhibit a slightly worse match and this is attributed to cross-correlations among different angle types. The introduction of the nonbonded interactions perturbs the distributions significantly; e.g., compare green dashes (a_ij = 0) with the purple dot-dashed lines (a_ij = a_ww) in Fig. 10. To circumvent this issue we developed an optimization scheme that finds the optimal strand and strand-angle coefficients that best reproduce the BI distributions from MD. The scheme optimizes all the coefficients for the target strands and strand-angles at the same time in the presence of the nonbonded interactions, while the whole procedure takes 100–200 iterations. The orange dotted lines in Fig. 10 depict the distributions after the final recalibration (see Appendix A5), which are in excellent match with the fitted (BI) distribution. In other words, the DPD distributions have been optimized with the target to replicate the mean and the standard deviation of their corresponding MD distributions. Introducing more complex functional expressions would allow one to replicate these distributions more closely, but this would introduce additional complications to the model and potentially require even smaller time steps due to the enhanced roughness of the potential hypersurface. Details about the optimization scheme for the bonded interactions are illustrated in S6 (ESI†). An alternative approach for tackling these cross-correlations among different intramolecular components would be to invoke the MRG-GG (molecular renormalization group coarse-graining) scheme devised by Sevalyev et al.¹⁰²

A4. Calibration of the coefficients for the nonbonded interactions

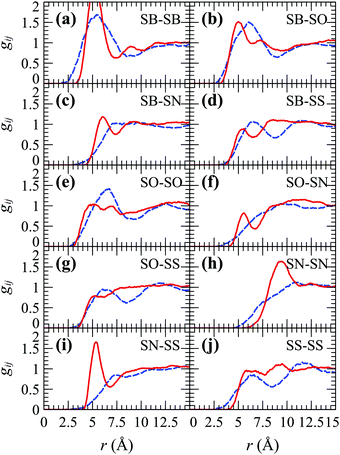
As we discussed in the Introduction section, the χ_ij for the SPE polymers under investigation are inaccessible, and thus we opted for a more direct parameterization approach based on matching the partial pair distribution functions (g_ij) between MD and DPD; the former is shown in Fig. 11 (dashes) and was derived from coarse-graining atomistic trajectories of 4 × SPE monomers in 800 water molecules (concentration ∼7.8 wt%) with a duration of 0.3 μs. The objective function is illustrated in S7 (ESI†). For SPE the objective function to be optimized has as input n_pair = n_types(n_types + 1)/2 − 1 = 14 free parameters (the “−1” has to do with keeping a_WW fixed), while its output (cost) is proportional to the mean squared error between g_ij from MD and DPD averaged over all the n_pair interactions, . To minimize the objective function, initially we performed ∼5000 bounded evaluations for 10 < a_ij < 180, and then we performed Bayesian optimization for ∼3000 steps (having fed the optimized output of the first ∼5000 iterations) to guide us closer to the global minimum using the implementation by Nogueira.¹⁰³ It is worth mentioning that the efficiency of the bounded optimization was comparable to the Bayesian one, since the former was performed in parallel using 128 cpu cores (1 core per simulation). Details about Bayesian optimization can be found in the S8 (ESI†).^103–106

Fig. 11 Pair radial distribution functions from MD with OPLS (dashes) and DPD (solid lines).

With few exceptions, the optimized DPD coefficients allow us to capture very reasonably the overall shape and probability amplitude of the RDFs from MD. The largest discrepancy arises in the SN–SS term of the RDF, wherein the corresponding beads assume opposite charges. The agreement between the atomistic and DPD pair distribution functions could be potentially improved by continuing the Bayesian optimization for much longer times, given that the 14-D objective function is sensitive (spans ∼5 orders of magnitude as shown in Fig. S5, ESI†), somewhat noisy, and that Bayesian optimization lacks appropriate convergence criteria. In addition, one could attempt to introduce additional degrees of freedom, such as varying the absolute values of the charges or the charge smearing radius λ. Here we opted to retain the original bottom-up charges as in most DPD studies, in order to avoid introducing additional complexity to the model. In this way, the interactions with charged foulants are straightforward to describe and do not necessitate additional parameterization. Nonetheless, the aforementioned discrepancies do not appear to affect the performance of the model much, as indicated by the good match of the long range conformational characteristics between MD and DPD presented below in Fig. 4, and the similar density profiles discussed in Section 5.2.1.

Another potential approach for describing the nonbonded interactions would be to incorporate a more complicated expression for the description of the repulsive interactions, or even to invoke tabulated potentials.^52–55

A5. Recalibration of the coefficients for the bonded interactions

The variation of the nonbonded coefficients during the optimization introduced minor perturbations to the strand and strand/angle distributions. To refine these parameters and restore the unperturbed distributions, we performed one last recalibration to the coefficients for the bonded interactions in the presence of the optimized a_ij using the algorithm in S6 (ESI†). This recalibration step had a very minor effect on the partial radial distribution functions; note that the orange dots in Fig. 10 and the red lines in Fig. 11 where calculated using the final form of the potential, after the recalibration process.

Acknowledgements

The authors are grateful for the fruitful discussion with Dr Jean-Yves Delannoy. The contribution of Dr Denis Bendejacq in discussing ref. 14 and 15 with us and pointing our attention to experimental correlations for the SPE radii of gyrations in solution has been valuable. A. P. Sgouros thanks SOLVAY, Brussels, Belgium, for financial support.

References

1. F. Siedenbiedel and J. C. Tiller, Polymers, 2012, 4, 46–71.
2. O. P. Abioye, C. A. Loto and O. S. I. Fayomi, J. Bio- Tribo-Corros., 2019, 5, 22.
3. A. U. Khan, M. Khan, N. Malik, M. H. Cho and M. M. Khan, Bioprocess Biosyst. Eng., 2019, 42, 1–15.
4. Z. K. Zander and M. L. Becker, ACS Macro Lett., 2018, 7, 16–25.
5. K. Thomas, in Woodhead Publishing Series in Metals and Surface Engineering, ed. C. Hellio and D. Yebra, Woodhead Publishing, 2009, pp. 522–553.
6. S. Brooks and M. Waldock, in Woodhead Publishing Series in Metals and Surface Engineering, ed. C. Hellio and D. Yebra, Woodhead Publishing, 2009, pp. 492–521.
7. A. G. Nurioglu, A. C. C. Esteves and G. de With, J. Mater. Chem. B, 2015, 3, 6547–6570.
8. M. Lejars, A. Margaillan and C. Bressy, Chem. Rev., 2012, 112, 4347–4390.
9. S. Nir and M. Reches, Curr. Opin. Biotechnol, 2016, 39, 48–55.
10. G. D. Bixler and B. Bhushan, Philos. Trans. Ser. A, Math. Phys. Eng. Sci., 2012, 370, 2381–2417.
11. A. Marmur, Biofouling, 2006, 22, 107–115.
12. G. B. Hwang, K. Page, A. Patir, S. P. Nair, E. Allan and I. P. Parkin, ACS Nano, 2018, 12, 6050–6058.
13. G. Zhao and W. N. Chen, RSC Adv., 2017, 7, 37990–38000.
14. P. Mary, D. D. Bendejacq, M. P. Labeau and P. Dupuis, J. Phys. Chem. B, 2007, 111, 7767–7777.
15. P. Mary and D. D. Bendejacq, J. Phys. Chem. B, 2008, 112, 2299–2310.
16. Q. Shao and S. Jiang, J. Phys. Chem. B, 2014, 118, 7630–7637.
17. H. Y. Yu, Y. Kang, Y. Liu and B. Mi, J. Membr. Sci., 2014, 449, 50–57.
18. M. Ajmal, S. Demirci, M. Siddiq, N. Aktas and N. Sahiner, Colloids Surf., A, 2015, 486, 29–37.
19. Y. Xiang, R. Xu and Y. Leng, Langmuir, 2018, 34, 2247–2257.
20. Q. Shao, Y. He and S. Jiang, J. Phys. Chem. B, 2011, 115, 8358–8363.
21. Q. Shao, Y. He, A. D. White and S. Jiang, J. Phys. Chem. B, 2010, 114, 16625–16631.
22. Q. Shao, Y. He, A. D. White and S. Jiang, J. Chem. Phys., 2012, 136, 225101.
23. S. Chen, L. Li, C. Zhao and J. Zheng, Polymer, 2010, 51, 5283–5293.
24. S. Lowe, N. M. O’Brien-Simpson and L. A. Connal, Polym. Chem., 2015, 6, 198–212.
25. J. Huo, Z. Chen and J. Zhou, Langmuir, 2019, 35, 1973–1983.
26. H. A. L. Filipe, M. J. Moreno and L. M. S. Loura, Molecules, 2020, 25, 3424.
27. S. Osella and S. Knippenberg, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183494.
28. P. J. Hoogerbruuge and J. M. V. A. Koelman, EPL, 1992, 19, 155.
29. P. Español and P. B. Warren, J. Chem. Phys., 2017, 146, 150901.
30. R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435.
31. R. D. Groot and K. L. Rabone, Biophys. J., 2001, 81, 725–736.
32. R. D. Groot, J. Chem. Phys., 2003, 118, 11265–11277.
33. M. B. Liu, G. R. Liu, L. W. Zhou and J. Z. Chang, Arch. Comput. Methods Eng., 2015, 22, 529–556.
34. A. Karatrantos, N. Clarke, R. J. Composto and K. I. Winey, Soft Matter, 2013, 9, 3877–3884.
35. N. Moreno, S. Nunes and V. M. Calo, Procedia Comput. Sci., 2014, 29, 728–739.
36. F. Alvarez, E. A. Flores, L. V. Castro, J. G. Hernández, A. López and F. Vázquez, Energy Fuels, 2011, 25, 562–567.
37. Y. Ruiz-Morales and O. C. Mullins, Energy Fuels, 2015, 29, 1597–1609.
38. F. Alarcón, E. Pérez and A. Gama Goicochea, Soft Matter, 2013, 9, 3777–3788.
39. C. Ibergay, P. Malfreyt and D. J. Tildesley, J. Phys. Chem. B, 2010, 114, 7274–7285.
40. T. H. Lin, W. P. Shih, C. S. Chen and Y. T. Chiu, 2006 1st IEEE Int. Conf. Nano/Micro Eng. Mol. Syst., 2006, pp. 571–574.
41. M. Liu, P. Meakin and H. Huang, Phys. Fluids, 2006, 18, 017101.
42. J. C. Shillcock and R. Lipowsky, J. Chem. Phys., 2002, 117, 5048–5061.
43. S. Yamamoto and S. A. Hyodo, Polym. J., 2003, 35, 519–527.
44. E. O. Johansson, T. Yamada, B. Sundén and J. Yuan, Int. J. Hydrogen Energy, 2015, 40, 1800–1808.
45. M. T. Lee, A. Vishnyakov and A. V. Neimark, J. Chem. Phys., 2016, 144, 014902.
46. M. T. Lee, A. Vishnyakov and A. V. Neimark, J. Phys. Chem. B, 2013, 117, 10304–10310.
47. M. H. Nafar Sefiddashti, M. Boudaghi-Khajehnobar, B. J. Edwards and B. Khomami, Sci. Rep., 2020, 10, 1–13.
48. A. Kumar, Y. Asako, E. Abu-Nada, M. Krafczyk and M. Faghri, Microfluid. Nanofluid., 2009, 7, 467–477.
49. A. P. Sgouros, G. G. Vogiatzis, G. Megariotis, C. Tzoumanekas and D. N. Theodorou, Macromolecules, 2019, 52, 7503–7523.
50. R. M. Füchslin, H. Fellermann, A. Eriksson and H. J. Ziock, J. Chem. Phys., 2009, 130, 214102.
51. H. Weiß, P. Deglmann, P. J. in’t Veld, M. Cetinkaya and E. Schreiner, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 65–86.
52. A. K. Soper, Chem. Phys., 1996, 202, 295–306.
53. A. P. Sgouros, C. J. Revelas, A. T. Lakkas and D. N. Theodorou, Polymers, 2021, 13, 1197.
54. A. P. Lyubartsev and A. Laaksonen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 3730–3737.
55. A. Lyubartsev, A. Mirzoev, L. J. Chen and A. Laaksonen, Faraday Discuss., 2010, 144, 43–56.
56. G. G. Vogiatzis and D. N. Theodorou, Macromolecules, 2013, 46, 4670–4683.
57. A. T. Lakkas, A. P. Sgouros, C. J. Revelas and D. N. Theodorou, Soft Matter, 2021, 17, 4077–4097.
58. P. Español and P. Warren, EPL, 1995, 30, 191.
59. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909.
60. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
61. T. Yamanaka, A. De Nicola, G. Munaò, T. A. Soares and G. Milano, Chem. Phys. Lett., 2019, 731, 136576.
62. J. Gasteiger and M. Marsili, Tetrahedron Lett., 1978, 19, 3181–3184.
63. J.-P. Ryckaert and A. Bellemans, Faraday Discuss. Chem. Soc., 1978, 66, 95–106.
64. M. J. Abraham, E. Lindahl, B. Hess and D. van der Spoel, GROMACS 2021.1 Manual, 2021 DOI:10.5281/zenodo.5053220.
65. C. Klein, A. Z. Summers, M. W. Thompson, J. B. Gilmer, C. McCabe, P. T. Cummings, J. Sallai and C. R. Iacovella, Comput. Mater. Sci., 2019, 167, 215–227.
66. H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271.
67. C. Li, X. Fu, W. Zhong and J. Liu, ACS Omega, 2019, 4, 10216–10224.
68. R. Vaiwala, S. Jadhav and R. Thaokar, J. Chem. Phys., 2017, 146, 124904.
69. K. Shi, C. Lian, Z. Bai, S. Zhao and H. Liu, Chem. Eng. Sci., 2015, 122, 185–196.
70. M. González-Melchor, E. Mayoral, M. E. Velázquez and J. Alejandre, J. Chem. Phys., 2006, 125, 224107.
71. J. R. Partington, R. F. Hudson and K. W. Bagnall, Nature, 1952, 169, 583–584.
72. C. Ibergay, P. Malfreyt and D. J. Tildesley, J. Chem. Theory Comput., 2009, 5, 3245–3259.
73. P. B. Warren and A. Vlasov, J. Chem. Phys., 2014, 140, 084904.
74. Z. Posel, Z. Limpouchová, K. Šindelka, M. Lísal and K. Procházka, Macromolecules, 2014, 47, 2503–2514.
75. T. P. Liyana-Arachchi, S. N. Jamadagni, D. Eike, P. H. Koenig and J. Ilja Siepmann, J. Chem. Phys., 2015, 142, 044902.
76. D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1467–1478.
77. MAPS®, Scienomics, Paris, 2019.
78. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
79. W. G. Hoover, A. J. C. Ladd and B. Moran, Phys. Rev. Lett., 1982, 48, 1818–1820.
80. M. Tuckerman, B. J. Berne and G. J. Martyna, J. Chem. Phys., 1992, 97, 1990–2001.
81. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
82. R. Mukundan, Proceedings of the 7th Asian Technology Conference in Mathematics 2002, 2002, pp. 97–106.
83. G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. Klein, Mol. Phys., 1996, 87, 1117–1157.
84. R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, Bristol, 1988.
85. A. Grossfield, WHAM: the weighted histogram analysis method, v 2.0.10, http://membrane.urmc.rochester.edu/wordpress/?page_id=126.
86. X. Fan, N. Phan-Thien, S. Chen, X. Wu and T. Yong Ng, Phys. Fluids, 2006, 18, 63102.
87. X. Fan, N. Phan-Thien, N. T. Yong, X. Wu and D. Xu, Phys. Fluids, 2002, 15, 11–21.
88. I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162.
89. K. C. Daoulas, V. A. Harmandaris and V. G. Mavrantzas, Macromolecules, 2005, 38, 5796–5809.
90. A. P. Sgouros, G. G. Vogiatzis, G. Kritikos, A. Boziki, A. Nikolakopoulou, D. Liveris and D. N. Theodorou, Macromolecules, 2017, 50, 8827–8844.
91. G. Kritikos, N. Vergadou and I. G. Economou, J. Phys. Chem. C, 2016, 120, 1013–1024.
92. Particles in Flows, ed. T. Bodnár, P. G. Galdi and Š. Nečasová, Birkhäuser, Cham, 1st edn, 2017.
93. G. E. Karniadakis, A. Beskok and N. Aluru, Systematic coarse-graining of molecular models by the Newton inversion method, Springer, New York, 2nd edn, 2005.
94. I. V. Pivkin and G. E. Karniadakis, Phys. Rev. Lett., 2006, 96, 206001.
95. S. Alexander, J. Phys., 1977, 38, 983–987.
96. P. G. de Gennes, Macromolecules, 1980, 13, 1069–1075.
97. P. Lai and K. Binder, J. Chem. Phys., 1992, 97, 586–595.
98. G. S. Grest and M. Murat, Macromolecules, 1993, 26, 3108–3117.
99. B. Zhao and W. J. Brittain, Prog. Polym. Sci., 2000, 25, 677–710.
100. M. Aubouy, G. H. Fredrickson, P. Pincus and E. Raphael, Macromolecules, 1995, 28, 2979–2981.
101. D. V. Kuznetsov and Z. Y. Chen, J. Chem. Phys., 1998, 109, 7017–7027.
102. A. Savelyev and G. A. Papoian, Biophys. J., 2009, 96, 4044–4052.
103. F. Nogueira, Bayesian Optimization: Open source constrained global optimization tool for Python, 2014, https://github.com/fmfn/BayesianOptimization.
104. P. Frazier, 2018, arXiv:1807.02811.
105. C. E. Rasmussen and K. I. Williams, Gaussian Processes for Machine Learning, the MIT Press, Massachusetts Institute of Technology, 2006.
106. L. P. Kaelbling, M. L. Littman and A. W. Moore, J. Artif. Int. Res., 1996, 4, 237–285.

---

Footnote

† Electronic supplementary information (ESI) available: (S1) OPLS coefficients; (S2) details about the mesoscopic polymer builder PyMeso; (S3) autocorrelation function of the tangential components of the end-to-end vector; (S4) brush-thickness scaling arguments for finitely extensible chains in a theta solvent; (S5) nonergodic angle distributions; (S6) calibration of the bonded coefficients; (S7) optimization of the nonbonded coefficients; (S8) details about the Bayesian optimization. See DOI: 10.1039/d1sm01255j

---